Теория обновления

Теория возобновления — это раздел теории вероятностей , который обобщает процесс Пуассона для произвольного времени удерживания. Вместо экспоненциально распределенных времен удержания процесс обновления может иметь любое независимое и одинаково распределенное (IID) время удержания, имеющее конечное среднее значение. Процесс продления-вознаграждения дополнительно имеет случайную последовательность вознаграждений, получаемых в каждое время удержания, которые являются IID, но не обязательно должны быть независимыми от времени удержания.

Процесс восстановления имеет асимптотические свойства, аналогичные усиленному закону больших чисел и центральной предельной теореме . Функция обновления $m(t)$ (ожидаемое количество прибытий) и функция вознаграждения $g(t)$ (ожидаемая величина вознаграждения) имеют ключевое значение в теории обновления. Функция восстановления удовлетворяет рекурсивному интегральному уравнению — уравнению восстановления. Ключевое уравнение восстановления дает предельное свертки значение $m'(t)$ с подходящей неотрицательной функцией. Суперпозицию процессов восстановления можно изучать как частный случай марковских процессов восстановления .

Приложения включают расчет лучшей стратегии замены изношенного оборудования на заводе и сравнение долгосрочных выгод от различных страховых полисов. Парадокс проверки связан с тем фактом, что наблюдение интервала обновления в момент времени t дает интервал со средним значением, большим, чем средний интервал обновления.

Процессы обновления

Введение

Процесс восстановления является обобщением процесса Пуассона . По сути, процесс Пуассона представляет собой марковский процесс с непрерывным временем для положительных целых чисел (обычно начиная с нуля), который имеет независимые экспоненциально распределенные времена удержания для каждого целого числа. $i$ прежде чем перейти к следующему целому числу, $i+1$. В процессе возобновления время ожидания не обязательно должно иметь экспоненциальное распределение; скорее, времена удержания могут иметь любое распределение по положительным числам, при условии, что времена удержания независимы и одинаково распределены ( IID ) и имеют конечное среднее значение.

Формальное определение

Пример эволюции процесса восстановления со временем удержания S _i и временем скачка J _n .

Позволять $(S_{i})_{i\geq 1}$ быть последовательностью положительных независимых одинаково распределенных случайных величин с конечным математическим ожиданием.

$0<\operatorname {E} [S_{i}]<\infty .$

Мы имеем в виду случайную величину $S_{i}$ как " $i$-е время выдержки".

Определите для каждого n > 0:

$J_{n}=\sum _{i=1}^{n}S_{i},$

каждый $J_{n}$ упоминается как « $n$-е время прыжка" и интервалы $[J_{n},J_{n+1}]$ называются «интервалами обновления».

Затем $(X_{t})_{t\geq 0}$ задается случайной величиной

$X_{t}=\sum _{n=1}^{\infty }\operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}=\sup \left\{\,n:J_{n}\leq t\,\right\}$

где $\operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}$ индикаторная функция

$\operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}={\begin{cases}1,&{\text{if }}J_{n}\leq t\\0,&{\text{otherwise}}\end{cases}}$

$(X_{t})_{t\geq 0}$ представляет количество скачков, произошедших к моменту времени t , и называется процессом восстановления.

Интерпретация

Если рассматривать события, происходящие в случайное время, можно подумать о времени удержания. $\{S_{i}:i\geq 1\}$ как случайное время, прошедшее между двумя последовательными событиями. Например, если процесс обновления моделирует количество поломок различных машин, то время ожидания представляет собой время между выходом одной машины из строя до того, как выйдет из строя другая.

Процесс Пуассона — это уникальный процесс восстановления, обладающий марковским свойством . поскольку экспоненциальное распределение является единственной непрерывной случайной величиной, обладающей свойством безпамяти.

Процессы продления и вознаграждения

Пример эволюции процесса возобновления и вознаграждения со ожидания Si _и , временем перехода J _n вознаграждениями Wi _{временем}

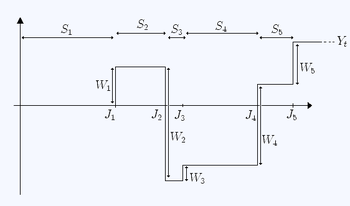
Позволять $W_{1},W_{2},\ldots$ быть последовательностью случайных величин IID ( наград ), удовлетворяющих

$\operatorname {E} |W_{i}|<\infty .\,$

Тогда случайная величина

$Y_{t}=\sum _{i=1}^{X_{t}}W_{i}$

называется процессом возобновления-вознаграждения . Обратите внимание, что в отличие от $S_{i}$, каждый $W_{i}$ может принимать как отрицательные, так и положительные значения.

Случайная величина $Y_{t}$ зависит от двух последовательностей: времени выдержки $S_{1},S_{2},\ldots$ и награды $W_{1},W_{2},\ldots$ Эти две последовательности не обязательно должны быть независимыми. В частности, $W_{i}$ может быть функциейиз $S_{i}$.

Интерпретация

В контексте приведенной выше интерпретации времени выдержки как времени между последовательными неисправностями машины «награды» $W_{1},W_{2},\ldots$ (которые в данном случае оказываются отрицательными) можно рассматривать как последовательные затраты на ремонт, понесенные в результате последовательных неисправностей.

Альтернативная аналогия: у нас есть волшебная гусь, которая откладывает яйца через определенные промежутки времени (время выдержки), распределенное как $S_{i}$. Иногда он откладывает золотые яйца случайного веса, а иногда — токсичные яйца (тоже случайного веса), требующие ответственной (и дорогостоящей) утилизации. «Награды» $W_{i}$ — это последовательные (случайные) финансовые потери/прибыли, возникающие в результате последовательных яиц ( i = 1,2,3,...) и $Y_{t}$ записывает общее финансовое «вознаграждение» в момент времени t .

Функция продления

Мы определяем функцию восстановления как математическое ожидание числа скачков, наблюдавшихся до некоторого момента времени. $t$:

$m(t)=\operatorname {E} [X_{t}].\,$

Элементарная теорема восстановления

Функция восстановления удовлетворяет

$\lim _{t\to \infty }{\frac {1}{t}}m(t)={\frac {1}{\operatorname {E} [S_{1}]}}.$

showДоказательство

The strong law of large numbers for renewal processes implies $\lim _{t\to \infty }{\frac {X_{t}}{t}}={\frac {1}{\operatorname {E} [S_{1}]}}.$ To prove the elementary renewal theorem, it is sufficient to show that $\left\{{\frac {X_{t}}{t}};t\geq 0\right\}$ is uniformly integrable. To do this, consider some truncated renewal process where the holding times are defined by ${\overline {S_{n}}}=a\operatorname {\mathbb {I} } \{S_{n}>a\}$ where $a$ is a point such that $0<F(a)=p<1$ which exists for all non-deterministic renewal processes. This new renewal process ${\overline {X}}_{t}$ is an upper bound on $X_{t}$ and its renewals can only occur on the lattice $\{na;n\in \mathbb {N} \}$. Furthermore, the number of renewals at each time is geometric with parameter $p$. So we have ${\begin{aligned}{\overline {X_{t}}}&\leq \sum _{i=1}^{[at]}\operatorname {Geometric} (p)\\\operatorname {E} \left[\,{\overline {X_{t}}}^{2}\,\right]&\leq C_{1}t+C_{2}t^{2}\\P\left({\frac {X_{t}}{t}}>x\right)&\leq {\frac {\operatorname {E} \left[X_{t}^{2}\right]}{t^{2}x^{2}}}\leq {\frac {\operatorname {E} \left[{\overline {X_{t}}}^{2}\right]}{t^{2}x^{2}}}\leq {\frac {C}{x^{2}}}.\end{aligned}}$

Элементарная теорема возобновления для процессов вознаграждения за возобновление

Определим функцию вознаграждения :

$g(t)=\operatorname {E} [Y_{t}].\,$

Функция вознаграждения удовлетворяет

$\lim _{t\to \infty }{\frac {1}{t}}g(t)={\frac {\operatorname {E} [W_{1}]}{\operatorname {E} [S_{1}]}}.$

Уравнение обновления

Функция восстановления удовлетворяет

$m(t)=F_{S}(t)+\int _{0}^{t}m(t-s)f_{S}(s)\,ds$

где $F_{S}$ — кумулятивная функция распределения $S_{1}$ и $f_{S}$ – соответствующая функция плотности вероятности.

showДоказательство

We may iterate the expectation about the first holding time: $m(t)=\operatorname {E} [X_{t}]=\operatorname {E} [\operatorname {E} (X_{t}\mid S_{1})].\,$ From the definition of the renewal process, we have $\operatorname {E} (X_{t}\mid S_{1}=s)=\operatorname {\mathbb {I} } _{\{t\geq s\}}\left(1+\operatorname {E} [X_{t-s}]\right).\,$ So ${\begin{aligned}m(t)&=\operatorname {E} [X_{t}]\\[12pt]&=\operatorname {E} [\operatorname {E} (X_{t}\mid S_{1})]\\[12pt]&=\int _{0}^{\infty }\operatorname {E} (X_{t}\mid S_{1}=s)f_{S}(s)\,ds\\[12pt]&=\int _{0}^{\infty }\operatorname {\mathbb {I} } _{\{t\geq s\}}\left(1+\operatorname {E} [X_{t-s}]\right)f_{S}(s)\,ds\\[12pt]&=\int _{0}^{t}\left(1+m(t-s)\right)f_{S}(s)\,ds\\[12pt]&=F_{S}(t)+\int _{0}^{t}m(t-s)f_{S}(s)\,ds,\end{aligned}}$ as required.

Ключевая теорема восстановления

Пусть X — процесс восстановления с функцией восстановления $m(t)$ и среднее междувозобновлением $\mu$. Позволять $g:[0,\infty )\rightarrow [0,\infty )$ быть функцией, удовлетворяющей:

• $\int _{0}^{\infty }g(t)\,dt<\infty$
• g монотонно и не возрастает

Ключевая теорема восстановления утверждает, что, поскольку $t\rightarrow \infty$:

$\int _{0}^{t}g(t-x)m'(x)\,dx\rightarrow {\frac {1}{\mu }}\int _{0}^{\infty }g(x)\,dx$

Теорема восстановления

Учитывая $g(x)=\mathbb {I} _{[0,h]}(x)$ для любого $h>0$ дает в качестве частного случая теорему восстановления:

$m(t+h)-m(t)\rightarrow {\frac {h}{\mu }}$ как $t\rightarrow \infty$

Результат можно доказать с помощью интегральных уравнений или аргумента связи . Хотя это частный случай ключевой теоремы восстановления, его можно использовать для вывода полной теоремы путем рассмотрения ступенчатых функций и последующего возрастания последовательностей ступенчатых функций.

Асимптотические свойства

Процессы обновления и процессы возобновления-вознаграждения обладают свойствами, аналогичными усиленному закону больших чисел , который можно вывести из той же теоремы. Если $(X_{t})_{t\geq 0}$ представляет собой процесс обновления и $(Y_{t})_{t\geq 0}$ это процесс обновления-вознаграждения, тогда:

$\lim _{t\to \infty }{\frac {1}{t}}X_{t}={\frac {1}{\operatorname {E} [S_{1}]}}$

$\lim _{t\to \infty }{\frac {1}{t}}Y_{t}={\frac {1}{\operatorname {E} [S_{1}]}}\operatorname {E} [W_{1}]$

почти наверняка.

showДоказательство

First consider $(X_{t})_{t\geq 0}$. By definition we have: $J_{X_{t}}\leq t\leq J_{X_{t}+1}$ for all $t\geq 0$ and so ${\frac {J_{X_{t}}}{X_{t}}}\leq {\frac {t}{X_{t}}}\leq {\frac {J_{X_{t}+1}}{X_{t}}}$ for all t ≥ 0. Now since $0<\operatorname {E} [S_{i}]<\infty$ we have: $X_{t}\to \infty$ as $t\to \infty$ almost surely (with probability 1). Hence: ${\frac {J_{X_{t}}}{X_{t}}}={\frac {J_{n}}{n}}={\frac {1}{n}}\sum _{i=1}^{n}S_{i}\to \operatorname {E} [S_{1}]$ almost surely (using the strong law of large numbers); similarly: ${\frac {J_{X_{t}+1}}{X_{t}}}={\frac {J_{X_{t}+1}}{X_{t}+1}}{\frac {X_{t}+1}{X_{t}}}={\frac {J_{n+1}}{n+1}}{\frac {n+1}{n}}\to \operatorname {E} [S_{1}]\cdot 1$ almost surely. Thus (since $t/X_{t}$ is sandwiched between the two terms) ${\frac {1}{t}}X_{t}\to {\frac {1}{\operatorname {E} [S_{1}]}}$ almost surely. Next consider $(Y_{t})_{t\geq 0}$. We have ${\frac {1}{t}}Y_{t}={\frac {X_{t}}{t}}{\frac {1}{X_{t}}}Y_{t}\to {\frac {1}{\operatorname {E} [S_{1}]}}\cdot \operatorname {E} [W_{1}]$ almost surely (using the first result and using the law of large numbers on $Y_{t}$).

Процессы восстановления дополнительно обладают свойством, аналогичным центральной предельной теореме :

${\frac {X_{t}-t/\mu }{\sqrt {t\sigma ^{2}/\mu ^{3}}}}\to {\mathcal {N}}(0,1)$

Инспекционный парадокс

Интервал обновления, определяемый случайной точкой t (показанной красным), стохастически больше, чем первый интервал обновления.

Смотрите также: Список парадоксов § Математика

Любопытная особенность процессов обновления заключается в том, что если мы подождём какое-то заранее определённое время t , а затем посмотрим, насколько велик интервал обновления, содержащий t , мы должны ожидать, что он обычно будет больше, чем интервал обновления среднего размера.

Математически парадокс проверки гласит: для любого t > 0 интервал обновления, содержащий t, стохастически больше, чем первый интервал обновления. То есть для всех x > 0 и для всех t > 0:

$\operatorname {P} (S_{X_{t}+1}>x)\geq \operatorname {P} (S_{1}>x)=1-F_{S}(x)$

где F _S — кумулятивная функция распределения времен удерживания IID S _i . Ярким примером является парадокс времени ожидания автобуса : при данном случайном распределении прибытия автобусов средний пассажир на автобусной остановке наблюдает больше задержек, чем средний оператор автобусов.

Разрешение парадокса состоит в том, что наше выборочное распределение в момент времени t смещено по размеру (см. смещение выборки ), поскольку вероятность выбора интервала пропорциональна его размеру. Однако интервал обновления среднего размера не зависит от размера.

showДоказательство

Observe that the last jump-time before t is $J_{X_{t}}$; and that the renewal interval containing t is $S_{X_{t}+1}$. Then ${\begin{aligned}\operatorname {P} (S_{X_{t}+1}>x)&{}=\int _{0}^{\infty }\operatorname {P} (S_{X_{t}+1}>x\mid J_{X_{t}}=s)f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }\operatorname {P} (S_{X_{t}+1}>x|S_{X_{t}+1}>t-s)f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }{\frac {\operatorname {P} (S_{X_{t}+1}>x\,,\,S_{X_{t}+1}>t-s)}{\operatorname {P} (S_{X_{t}+1}>t-s)}}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }{\frac {1-F(\max\{x,t-s\})}{1-F(t-s)}}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }\min \left\{{\frac {1-F(x)}{1-F(t-s)}},{\frac {1-F(t-s)}{1-F(t-s)}}\right\}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }\min \left\{{\frac {1-F(x)}{1-F(t-s)}},1\right\}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}\geq \int _{0}^{\infty }(1-F(x))f_{J_{X_{t}}}(s)\,ds=1-F(x)=\operatorname {P} (S_{1}>x),\\[12pt]\end{aligned}}$ since both ${\frac {1-F(x)}{1-F(t-s)}}$ and $1$ are greater than or equal to $1-F(x)$ for all values of s.

Суперпозиция

Если процесс восстановления не является процессом Пуассона, суперпозиция (сумма) двух независимых процессов восстановления не является процессом восстановления. Однако такие процессы можно описать в рамках более широкого класса процессов, называемых процессами марковского обновления . Однако кумулятивная функция распределения первого времени между событиями в процессе суперпозиции определяется выражением

$R(t)=1-\sum _{k=1}^{K}{\frac {\alpha _{k}}{\sum _{l=1}^{K}\alpha _{l}}}(1-R_{k}(t))\prod _{j=1,j\neq k}^{K}\alpha _{j}\int _{t}^{\infty }(1-R_{j}(u))\,{\text{d}}u$

где R _k ( t ) и α _k > 0 — CDF времен между событиями и скорости прибытия процесса k .

Пример приложения

Предприниматель Эрик имеет n машин, срок службы каждой из которых равномерно распределен между нулем и двумя годами. Эрик может позволить каждой машине работать до тех пор, пока она не выйдет из строя, стоимость замены составит 2600 евро; в качестве альтернативы он может заменить машину в любое время, пока она еще работает, за 200 евро.

Какова его оптимальная политика замены?

showРешение

The lifetime of the n machines can be modeled as n independent concurrent renewal-reward processes, so it is sufficient to consider the case n=1. Denote this process by $(Y_{t})_{t\geq 0}$. The successive lifetimes S of the replacement machines are independent and identically distributed, so the optimal policy is the same for all replacement machines in the process. If Eric decides at the start of a machine's life to replace it at time 0 < t < 2 but the machine happens to fail before that time then the lifetime S of the machine is uniformly distributed on [0, t] and thus has expectation 0.5t. So the overall expected lifetime of the machine is: ${\begin{aligned}\operatorname {E} [S]&=\operatorname {E} [S\mid {\text{fails before }}t]\cdot \operatorname {P} [{\text{fails before }}t]+\operatorname {E} [S\mid {\text{does not fail before }}t]\cdot \operatorname {P} [{\text{does not fail before }}t]\\[6pt]&=0.5t({\frac {t}{2}})+t({\frac {2-t}{2}})\end{aligned}}$ and the expected cost W per machine is: ${\begin{aligned}\operatorname {E} [W]&=\operatorname {E} [W\mid {\text{fails before }}t]\cdot \operatorname {P} ({\text{fails before }}t)+\operatorname {E} [W\mid {\text{does not fail before }}t]\cdot \operatorname {P} ({\text{does not fail before }}t)\\[6pt]&=2600({\frac {t}{2}})+200({\frac {2-t}{2}})=1200t+200.\end{aligned}}$ So by the strong law of large numbers, his long-term average cost per unit time is: ${\frac {1}{t}}Y_{t}\simeq {\frac {\operatorname {E} [W]}{\operatorname {E} [S]}}={\frac {4(1200t+200)}{t^{2}+4t-2t^{2}}}$ then differentiating with respect to t: ${\frac {\partial }{\partial t}}{\frac {4(1200t+200)}{t^{2}+4t-2t^{2}}}=4{\frac {(4t-t^{2})(1200)-(4-2t)(1200t+200)}{(t^{2}+4t-2t^{2})^{2}}},$ this implies that the turning points satisfy: ${\begin{aligned}0&=(4t-t^{2})(1200)-(4-2t)(1200t+200)=4800t-1200t^{2}-4800t-800+2400t^{2}+400t\\[6pt]&=-800+400t+1200t^{2},\end{aligned}}$ and thus $0=3t^{2}+t-2=(3t-2)(t+1).$ We take the only solution t in [0, 2]: t = 2/3. This is indeed a minimum (and not a maximum) since the cost per unit time tends to infinity as t tends to zero, meaning that the cost is decreasing as t increases, until the point 2/3 where it starts to increase.

См. также

• Теорема Кэмпбелла (вероятность)
• Сложный процесс Пуассона
• Марковский процесс с непрерывным временем
• Лемма Литтла
• Lotka's integral equation
• Теорема Пальма – Хинчина
• Пуассоновский процесс
• Теория массового обслуживания
• Остаточное время
• Теория руин
• Полумарковский процесс
• Из уравнения Ферстера

Ссылки

• Кокс, Дэвид (1970). Теория обновления . Лондон: Methuen & Co. 142. ИСБН  0-412-20570-Х .
• Дуб, Дж.Л. (1948). «Теория обновления с точки зрения теории вероятностей» (PDF) . Труды Американского математического общества . 63 (3): 422–438. дои : 10.2307/1990567 . JSTOR   1990567 .
• Феллер, Уильям (1971). Введение в теорию вероятностей и ее приложения . Том. 2 (второе изд.). Уайли.
• Гриметт, Греция ; Стирзакер, Д.Р. (1992). Вероятность и случайные процессы (второе изд.). Издательство Оксфордского университета. ISBN  0198572220 .
• Смит, Уолтер Л. (1958). «Теория обновления и ее последствия». Журнал Королевского статистического общества, серия B. 20 (2): 243–302. JSTOR   2983891 .
• Ванли Ван, Йоханнес Х. П. Шульц, Вэйхуа Дэн и Эли Баркай (2018). «Теория обновления с распределенным временем пребывания: типичное и редкое». Физ. Преподобный Е. 98 (4): 042139. arXiv : 1809.05856 . Бибкод : 2018PhRvE..98d2139W . дои : 10.1103/PhysRevE.98.042139 . S2CID   54727926 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )