Раздача риса

В 2D-плоскости выберите фиксированную точку на расстоянии ν от начала координат. Создайте распределение 2D-точек с центром вокруг этой точки, где координаты x и y выбираются независимо от гауссова распределения со стандартным отклонением σ (синяя область). Если R — расстояние от этих точек до начала координат, то R имеет распределение Райса.

Функция плотности вероятности
Кумулятивная функция распределения
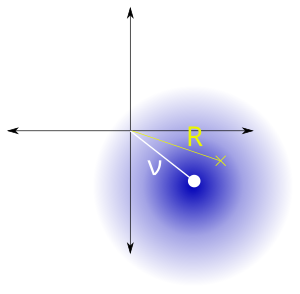
Параметры	$\nu \geq 0$, расстояние между контрольной точкой и центром двумерного распределения, $\sigma \geq 0$, шкала
Поддерживать	$x\in [0,\infty )$
PDF	${\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)$
CDF	$1-Q_{1}\left({\frac {\nu }{\sigma }},{\frac {x}{\sigma }}\right)$ где Q 1 — Q-функция Маркума
Иметь в виду	$\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})$
Дисперсия	$2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{1/2}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)$
асимметрия	(сложный)
Избыточный эксцесс	(сложный)

В теории вероятностей распределение Райса или распределение Райса (или, реже, распределение Райса ) — это вероятностное распределение величины круговой симметричной двумерной нормальной случайной величины , возможно, с ненулевым средним (нецентральным). Он был назван в честь Стивена О. Райса (1907–1986).

Характеристика

Функция плотности вероятности

$f(x\mid \nu ,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),$

где I ₀ ( z ) — модифицированная функция Бесселя первого рода нулевого порядка.

В контексте затухания Райса распределение часто также переписывается с использованием параметра формы. $K={\frac {\nu ^{2}}{2\sigma ^{2}}}$, определяемый как отношение мощности пути прямой видимости к остальным многопутям, и параметр Scale $\Omega =\nu ^{2}+2\sigma ^{2}$, определяемый как общая мощность, полученная по всем путям.

Характеристическая функция распределения Райса задается как:

${\begin{aligned}\chi _{X}(t\mid \nu ,\sigma )=\exp \left(-{\frac {\nu ^{2}}{2\sigma ^{2}}}\right)&\left[\Psi _{2}\left(1;1,{\frac {1}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right.\\[8pt]&\left.{}+i{\sqrt {2}}\sigma t\Psi _{2}\left({\frac {3}{2}};1,{\frac {3}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right],\end{aligned}}$

где $\Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)$ - одна из вырожденных гипергеометрических функций Хорна с двумя переменными, сходящаяся для всех конечных значений $x$ и $y$. Его дают:

$\Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)=\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }{\frac {(\alpha )_{m+n}}{(\gamma )_{m}(\gamma ')_{n}}}{\frac {x^{m}y^{n}}{m!n!}},$

где

$(x)_{n}=x(x+1)\cdots (x+n-1)={\frac {\Gamma (x+n)}{\Gamma (x)}}$

– это возрастающий факториал .

Характеристики

Моменты

Первые несколько резких моментов :

${\begin{aligned}\mu _{1}^{'}&=\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})\\\mu _{2}^{'}&=2\sigma ^{2}+\nu ^{2}\,\\\mu _{3}^{'}&=3\sigma ^{3}{\sqrt {\pi /2}}\,\,L_{3/2}(-\nu ^{2}/2\sigma ^{2})\\\mu _{4}^{'}&=8\sigma ^{4}+8\sigma ^{2}\nu ^{2}+\nu ^{4}\,\\\mu _{5}^{'}&=15\sigma ^{5}{\sqrt {\pi /2}}\,\,L_{5/2}(-\nu ^{2}/2\sigma ^{2})\\\mu _{6}^{'}&=48\sigma ^{6}+72\sigma ^{4}\nu ^{2}+18\sigma ^{2}\nu ^{4}+\nu ^{6}\end{aligned}}$

и вообще, сырые моменты даны

$\mu _{k}^{'}=\sigma ^{k}2^{k/2}\,\Gamma (1\!+\!k/2)\,L_{k/2}(-\nu ^{2}/2\sigma ^{2}).\,$

Здесь L _q ( x ) обозначает полином Лагерра :

$L_{q}(x)=L_{q}^{(0)}(x)=M(-q,1,x)=\,_{1}F_{1}(-q;1;x)$

где $M(a,b,z)=_{1}F_{1}(a;b;z)$ – вырожденная гипергеометрическая функция первого рода. Когда k четно, необработанные моменты становятся простыми полиномами от σ и ν , как в примерах выше.

Для случая q = 1/2:

${\begin{aligned}L_{1/2}(x)&=\,_{1}F_{1}\left(-{\frac {1}{2}};1;x\right)\\&=e^{x/2}\left[\left(1-x\right)I_{0}\left(-{\frac {x}{2}}\right)-xI_{1}\left(-{\frac {x}{2}}\right)\right].\end{aligned}}$

Второй центральный момент , дисперсия , равен

$\mu _{2}=2\sigma ^{2}+\nu ^{2}-(\pi \sigma ^{2}/2)\,L_{1/2}^{2}(-\nu ^{2}/2\sigma ^{2}).$

Обратите внимание, что $L_{1/2}^{2}(\cdot )$ указывает квадрат полинома Лагерра $L_{1/2}(\cdot )$, а не обобщенный полином Лагерра $L_{1/2}^{(2)}(\cdot ).$

Связанные дистрибутивы

• $R\sim \mathrm {Rice} \left(|\nu |,\sigma \right)$ если $R={\sqrt {X^{2}+Y^{2}}}$ где $X\sim N\left(\nu \cos \theta ,\sigma ^{2}\right)$ и $Y\sim N\left(\nu \sin \theta ,\sigma ^{2}\right)$ являются статистически независимыми нормальными случайными величинами и $\theta$ любое действительное число.
• Другой случай, когда $R\sim \mathrm {Rice} \left(\nu ,\sigma \right)$ происходит из следующих шагов:
  1. Генерировать $P$ имеющий распределение Пуассона с параметром (также означает для Пуассона) $\lambda ={\frac {\nu ^{2}}{2\sigma ^{2}}}.$
  2. Генерировать $X$ имеющий распределение хи-квадрат с 2 P + 2 степенями свободы.
  3. Набор $R=\sigma {\sqrt {X}}.$
• Если $R\sim \operatorname {Rice} (\nu ,1)$ затем $R^{2}$ имеет нецентральное распределение хи-квадрат с двумя степенями свободы и параметром нецентральности. $\nu ^{2}$.
• Если $R\sim \operatorname {Rice} (\nu ,1)$ затем $R$ имеет нецентральное распределение хи с двумя степенями свободы и параметром нецентральности. $\nu$.
• Если $R\sim \operatorname {Rice} (0,\sigma )$ затем $R\sim \operatorname {Rayleigh} (\sigma )$, т. е. для частного случая распределения Райса, заданного формулой $\nu =0$, распределение становится распределением Рэлея , для которого дисперсия равна $\mu _{2}={\frac {4-\pi }{2}}\sigma ^{2}$.
• Если $R\sim \operatorname {Rice} (0,\sigma )$ затем $R^{2}$ имеет показательное распределение .
• Если $R\sim \operatorname {Rice} \left(\nu ,\sigma \right)$ затем $1/R$ имеет обратное распределение Райса.
• Свернутое нормальное распределение является одномерным частным случаем распределения Райса.

Предельные случаи

Для больших значений аргумента полином Лагерра принимает вид

$\lim _{x\to -\infty }L_{\nu }(x)={\frac {|x|^{\nu }}{\Gamma (1+\nu )}}.$

Видно, что по мере того, как ν становится большим или σ становится маленьким, среднее значение становится ν , а дисперсия становится σ. ² .

Переход к гауссовскому приближению происходит следующим образом. Из теории функций Бесселя имеем

$I_{\alpha }(z)\to {\frac {e^{z}}{\sqrt {2\pi z}}}\left(1-{\frac {4\alpha ^{2}-1}{8z}}+\cdots \right){\text{ as }}z\rightarrow \infty$

так что в большом $x\nu /\sigma ^{2}$ область, асимптотическое разложение распределения Райса:

${\begin{aligned}f(x,\nu ,\sigma )={}&{\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)\\{\text{ is }}\\&{\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right){\sqrt {\frac {\sigma ^{2}}{2\pi x\nu }}}\exp \left({\frac {2x\nu }{2\sigma ^{2}}}\right)\left(1+{\frac {\sigma ^{2}}{8x\nu }}+\cdots \right)\\\rightarrow {}&{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\nu )^{2}}{2\sigma ^{2}}}\right){\sqrt {\frac {x}{\nu }}},\;\;\;{\text{ as }}{\frac {x\nu }{\sigma ^{2}}}\rightarrow \infty \end{aligned}}$

Более того, когда плотность концентрируется вокруг ${\textstyle \nu }$ и ${\textstyle |x-\nu |\ll \sigma }$ из-за показателя Гаусса мы также можем написать ${\textstyle {\sqrt {{x}/{\nu }}}\approx 1}$ и, наконец, получить нормальное приближение

$f(x,\nu ,\sigma )\approx {\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\nu )^{2}}{2\sigma ^{2}}}\right),\;\;\;{\frac {\nu }{\sigma }}\gg 1$

Приближение становится пригодным для ${\frac {\nu }{\sigma }}>3$

Оценка параметров (метод инверсии Коаи)

Существует три различных метода оценки параметров распределения Райса: (1) метод моментов , (2) метод максимального правдоподобия , и (3) метод наименьших квадратов. В первых двух методах интерес представляет оценка параметров распределения ν и σ по выборке данных. Это можно сделать, используя метод моментов, например, выборочного среднего и выборочного стандартного отклонения. Выборочное среднее — это оценка µ ₁ ^' а выборочное стандартное отклонение представляет собой оценку μ ₂ ^1/2 .

Ниже приводится эффективный метод, известный как «метод инверсии Коаи». для решения оценочных уравнений на основе выборочного среднего и выборочного стандартного отклонения одновременно. Этот метод инверсии также известен как с фиксированной точкой формула SNR . Более ранние работы по методу моментов для решения задачи обычно используют метод поиска корней, который неэффективен.

Во-первых, отношение выборочного среднего к выборочному стандартному отклонению определяется как r , т.е. $r=\mu _{1}^{'}/\mu _{2}^{1/2}$. Формула SNR с фиксированной точкой выражается как

$g(\theta )={\sqrt {\xi {(\theta )}\left[1+r^{2}\right]-2}},$

где $\theta$ – отношение параметров, т.е. $\theta ={\nu }/{\sigma }$, и $\xi {\left(\theta \right)}$ дается:

$\xi {\left(\theta \right)}=2+\theta ^{2}-{\frac {\pi }{8}}\exp {(-\theta ^{2}/2)}\left[(2+\theta ^{2})I_{0}(\theta ^{2}/4)+\theta ^{2}I_{1}(\theta ^{2}/4)\right]^{2},$

где $I_{0}$ и $I_{1}$ — модифицированные функции Бесселя первого рода .

Обратите внимание, что $\xi {\left(\theta \right)}$ является масштабным коэффициентом $\sigma$ и связано с $\mu _{2}$ к:

$\mu _{2}=\xi {\left(\theta \right)}\sigma ^{2}.$

Чтобы найти фиксированную точку, $\theta ^{*}$, из $g$, выбирается начальное решение, ${\theta }_{0}$, что больше нижней границы, которая равна ${\theta }_{\text{lower bound}}=0$ и происходит, когда ${\textstyle r={\sqrt {\pi /(4-\pi )}}}$ (Обратите внимание, что это $r=\mu _{1}^{'}/\mu _{2}^{1/2}$ распределения Рэлея). Это обеспечивает отправную точку для итерации, в которой используется функциональная композиция. и это продолжается до тех пор, пока $\left|g^{i}\left(\theta _{0}\right)-\theta _{i-1}\right|$ меньше некоторого небольшого положительного значения. Здесь, $g^{i}$ обозначает композицию той же функции, $g$, $i$ раз. На практике мы связываем конечный результат $\theta _{n}$ для некоторого целого числа $n$ как фиксированная точка, $\theta ^{*}$, то есть, $\theta ^{*}=g\left(\theta ^{*}\right)$.

После того как фиксированная точка найдена, оценки $\nu$ и $\sigma$ находятся с помощью функции масштабирования, $\xi {\left(\theta \right)}$, следующее:

$\sigma ={\frac {\mu _{2}^{1/2}}{\sqrt {\xi \left(\theta ^{*}\right)}}},$

и

$\nu ={\sqrt {\left(\mu _{1}^{'~2}+\left(\xi \left(\theta ^{*}\right)-2\right)\sigma ^{2}\right)}}.$

Чтобы еще больше ускорить итерацию, можно использовать метод поиска корня Ньютона. Этот конкретный подход очень эффективен.

Приложения

• Евклидова норма двумерного кругово-симметричного нормально распределенного случайного вектора .
• Затухание по Райсу (для многолучевых помех ))
• Влияние ошибки прицеливания на стрельбу по мишеням.
• Анализ разнесения приемников в радиосвязи.
• Распределение эксцентриситетов моделей внутренней части Солнечной системы после длительного численного интегрирования .

См. также

• Распределение Хойта
• Распределение Рэлея

Дальнейшее чтение

• Абрамовиц М. и Стегун И.А. (ред.), Справочник по математическим функциям , Национальное бюро стандартов, 1964; переиздано Dover Publications, 1965. ISBN   0-486-61272-4
• Райс, С.О. , Математический анализ случайного шума. Технический журнал Bell System 24 (1945) 46–156.
• И. Солтани Бозчалуи; Мин Лян (20 ноября 2007 г.). «Подход на основе индекса гладкости к выбору параметров вейвлета при шумоподавлении сигнала и обнаружении неисправностей». Журнал звука и вибрации . 308 (1–2): 253–254. Бибкод : 2007JSV...308..246B . дои : 10.1016/j.jsv.2007.07.038 .
• Ван, Донг; Чжоу, Цян; Цуй, Квок-Леунг (2017). «О распределении модуля вейвлет-коэффициентов Габора и верхней границе безразмерного индекса гладкости в случае аддитивных гауссовских шумов: еще раз». Журнал звука и вибрации . 395 : 393–400. дои : 10.1016/j.jsv.2017.02.013 .
• Лю, Х. и Ханзо, Л., Унифицированный точный анализ производительности BER в асинхронных системах DS-CDMA с использованием модуляции BPSK по каналам с замиранием , Транзакции IEEE в беспроводной связи, том 6, выпуск 10, октябрь 2007 г., стр. 3504–3509.
• Аннамалай А., Телламбура К. и Бхаргава В.К., Производительность приемника с разнесением и равным усилением в беспроводных каналах , Транзакции IEEE в области связи, том 48, октябрь 2000 г., стр. 1732–1745.
• Эрдели А., Магнус В., Оберхеттингер Ф. и Трикоми Ф.Г., Высшие трансцендентные функции, Том 1. Архивировано 11 августа 2011 г. в Wayback Machine McGraw-Hill Book Company Inc., 1953.
• Шривастава, Х.М. и Карлссон, П.В., Множественные гауссовы гипергеометрические ряды. Эллис Хорвуд Лтд., 1985.
• Сийберс Дж., ден Деккер А.Дж., Шеундерс П. и Ван Дайк Д., «Оценка максимального правдоподобия параметров распределения Райса». Архивировано 19 октября 2011 г. в Wayback Machine , IEEE Transactions on Medical Imaging, Vol. 17, №. 3, стр. 357–361 (1998).
• Варадараджан Д. и Халдар Дж. П., «Схема мажорирования-минимизации для МР-изображений Райса и нецентрального хи» , IEEE Transactions on Medical Imaging, Vol. 34, нет. 10, стр. 2191–2202, (2015)
• ден Деккер, AJ; Сийберс, Дж. (декабрь 2014 г.). «Распределение данных на магнитно-резонансных изображениях: обзор». Физика Медика . 30 (7): 725–741. дои : 10.1016/j.ejmp.2014.05.002 . ПМИД   25059432 .
• Коай, К.Г. и Бассер, П.Дж., Аналитически точная схема коррекции для извлечения сигнала из сигналов МР с шумом , Журнал магнитного резонанса, том 179, выпуск = 2, стр. 317–322, (2006)
• Абди А., Тепеделенлиоглу К., Каве М. и Джаннакис Г. Об оценке параметра K для распределения замираний Райса , IEEE Communications Letters, том 5, номер 3, март 2001 г., стр. 92– 94.
• Талукдар, КК; Лоуинг, Уильям Д. (март 1991 г.). «Оценка параметров распределения Райса». Журнал Акустического общества Америки . 89 (3): 1193–1197. Бибкод : 1991ASAJ...89.1193T . дои : 10.1121/1.400532 .
• Бонни, Дж. М.; Рену, JP; Занка, М. (ноябрь 1996 г.). «Оптимальное измерение амплитуды и фазы по данным МРТ». Журнал магнитного резонанса, серия B. 113 (2): 136–144. Бибкод : 1996JMRB..113..136B . дои : 10.1006/jmrb.1996.0166 . ПМИД   8954899 .

Внешние ссылки

• Код MATLAB для распределения Райса/Райсиана (PDF, среднее значение и дисперсия, а также генерация случайных выборок)