Распределение Леви

Для более общего семейства альфа-стабильных распределений Леви, частным случаем которого является это распределение, см. Стабильное распределение .

Леви (без смещения)

Функция плотности вероятности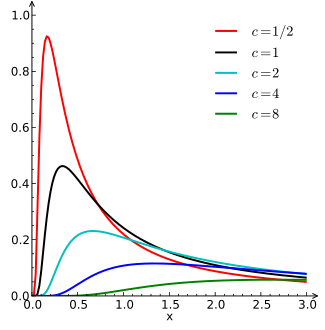
Кумулятивная функция распределения
Параметры	$\mu$ расположение; $c>0\,$ шкала
Поддерживать	$x\in (\mu ,\infty )$
PDF	${\sqrt {\frac {c}{2\pi }}}~~{\frac {e^{-{\frac {c}{2(x-\mu )}}}}{(x-\mu )^{3/2}}}$
CDF	${\textrm {erfc}}\left({\sqrt {\frac {c}{2(x-\mu )}}}\right)$
Квантиль	$\mu +{\frac {\sigma }{2\left({\textrm {erfc}}^{-1}(p)\right)^{2}}}$
Иметь в виду	$\infty$
медиана	$\mu +c/2({\textrm {erfc}}^{-1}(1/2))^{2}\,$
Режим	$\mu +{\frac {c}{3}}$
Дисперсия	$\infty$
асимметрия	неопределенный
Избыточный эксцесс	неопределенный
Энтропия	${\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}$ где $\gamma$ постоянная Эйлера -Машерони
МГФ	неопределенный
CF	$e^{i\mu t-{\sqrt {-2ict}}}$

В теории вероятностей и статистике распределение Леви , названное в честь Поля Леви , представляет собой непрерывное распределение вероятностей для неотрицательной случайной величины . В спектроскопии это распределение с частотой в качестве зависимой переменной известно как профиль Ван-дер-Ваальса . Это частный случай обратного гамма-распределения . Это стабильный дистрибутив .

Определение

Функция плотности вероятности распределения Леви в области $x\geq \mu$ является

$f(x;\mu ,c)={\sqrt {\frac {c}{2\pi }}}\,{\frac {e^{-{\frac {c}{2(x-\mu )}}}}{(x-\mu )^{3/2}}},$

где $\mu$ — параметр местоположения , а $c$ — параметр масштаба . Кумулятивная функция распределения равна

$F(x;\mu ,c)=\operatorname {erfc} \left({\sqrt {\frac {c}{2(x-\mu )}}}\right)=2-2\Phi \left({\sqrt {\frac {c}{(x-\mu )}}}\right),$

где $\operatorname {erfc} (z)$ — дополнительная функция ошибок , а $\Phi (x)$ — функция Лапласа ( CDF стандартного нормального распределения ). Параметр сдвига $\mu$ имеет эффект смещения кривой вправо на величину $\mu$ и заменив опору на интервал [ $\mu$,  $\infty$). Как и все стабильные распределения , распределение Леви имеет стандартную форму f ( x ; 0, 1), которая обладает следующим свойством:

$f(x;\mu ,c)\,dx=f(y;0,1)\,dy,$

где y определяется как

$y={\frac {x-\mu }{c}}.$

Характеристическая функция распределения Леви определяется выражением

$\varphi (t;\mu ,c)=e^{i\mu t-{\sqrt {-2ict}}}.$

Заметим, что характеристическую функцию можно записать и в том же виде, что и для устойчивого распределения с $\alpha =1/2$ и $\beta =1$:

$\varphi (t;\mu ,c)=e^{i\mu t-|ct|^{1/2}(1-i\operatorname {sign} (t))}.$

Предполагая $\mu =0$, n- й момент несмещенного распределения Леви формально определяется выражением

$m_{n}\ {\stackrel {\text{def}}{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {e^{-c/2x}x^{n}}{x^{3/2}}}\,dx,$

который расходится для всех $n\geq 1/2$, так что целые моменты распределения Леви не существуют (только некоторые дробные моменты).

Функция , производящая момент, будет формально определена как

$M(t;c)\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {e^{-c/2x+tx}}{x^{3/2}}}\,dx,$

однако это расходится для $t>0$ и, следовательно, не определена на интервале около нуля, поэтому функция, порождающая момент, фактически не определена.

Как и все стабильные распределения, кроме нормального распределения , крыло функции плотности вероятности демонстрирует поведение тяжелого хвоста, спадающего по степенному закону:

$f(x;\mu ,c)\sim {\sqrt {\frac {c}{2\pi }}}\,{\frac {1}{x^{3/2}}}$ как $x\to \infty ,$

который показывает, что распределение Леви имеет не только «тяжелый хвост» , но и «толстый хвост» . Это проиллюстрировано на диаграмме ниже, на которой функции плотности вероятности для различных значений c и $\mu =0$ строятся на логарифмическом графике :

Функция плотности вероятности для распределения Леви на логарифмическом графике

Стандартное распределение Леви удовлетворяет условию стабильности :

$(X_{1}+X_{2}+\dotsb +X_{n})\sim n^{1/\alpha }X,$

где $X_{1},X_{2},\ldots ,X_{n},X$ являются независимыми стандартными переменными Леви с $\alpha =1/2.$

Связанные дистрибутивы

• Если $X\sim \operatorname {Levy} (\mu ,c)$, затем $kX+b\sim \operatorname {Levy} (k\mu +b,kc).$
• Если $X\sim \operatorname {Levy} (0,c)$, затем $X\sim \operatorname {Inv-Gamma} (1/2,c/2)$ ( обратное гамма-распределение ). Здесь распределение Леви является частным случаем распределения Пирсона типа V.
• Если $Y\sim \operatorname {Normal} (\mu ,\sigma ^{2})$ ( нормальное распределение ), тогда $(Y-\mu )^{-2}\sim \operatorname {Levy} (0,1/\sigma ^{2}).$
• Если $X\sim \operatorname {Normal} (\mu ,1/{\sqrt {\sigma }})$, затем $(X-\mu )^{-2}\sim \operatorname {Levy} (0,\sigma )$.
• Если $X\sim \operatorname {Levy} (\mu ,c)$, затем $X\sim \operatorname {Stable} (1/2,1,c,\mu )$ ( стабильное распространение ).
• Если $X\sim \operatorname {Levy} (0,c)$, затем $X\,\sim \,\operatorname {Scale-inv-\chi ^{2}} (1,c)$ ( масштабированное распределение обратного хи-квадрата ).
• Если $X\sim \operatorname {Levy} (\mu ,c)$, затем $(X-\mu )^{-1/2}\sim \operatorname {FoldedNormal} (0,1/{\sqrt {c}})$ ( свернутое нормальное распределение ).

Генерация случайной выборки

Случайные выборки из распределения Леви могут быть сгенерированы с помощью выборки с обратным преобразованием . Учитывая случайную величину U, полученную из равномерного распределения на единичном интервале (0, 1), переменная X, определяемая формулой

$X=F^{-1}(U)={\frac {c}{(\Phi ^{-1}(1-U/2))^{2}}}+\mu$

распределено по Леви с местоположением $\mu$ и масштабировать $c$. Здесь $\Phi (x)$ — кумулятивная функция распределения стандартного нормального распределения .

Приложения

• Частота геомагнитных инверсий, по-видимому, подчиняется распределению Леви.
• Время попадания в одну точку на расстоянии $\alpha$ от начальной точки, благодаря броуновскому движению, имеет распределение Леви с $c=\alpha ^{2}$. (Для броуновского движения со сносом это время может следовать обратному распределению Гаусса , пределом которого является распределение Леви.)
• Длина пути, пройденного фотоном в мутной среде, соответствует распределению Леви.
• Процесс Коши можно определить как броуновское движение, подчиненное процессу, связанному с распределением Леви.

Ссылки

• «Информация о стабильных дистрибутивах» . Проверено 5 сентября 2021 г. - Введение Джона П. Нолана в устойчивые распределения, некоторые статьи по стабильным законам и бесплатную программу для вычисления стабильных плотностей, кумулятивных функций распределения, квантилей, параметров оценок и т. д. См. особенно « Введение в стабильные распределения», глава 1.

Внешние ссылки

• Вайсштейн, Эрик В. «Распределение Леви» . Математический мир .