Линейная карта
Эта статья включает список общих ссылок , но в ней отсутствуют достаточные соответствующие встроенные цитаты . ( декабрь 2021 г. ) |
В математике , и, более конкретно, в линейной алгебре , линейное отображение (также называемое линейным отображением , линейным преобразованием , гомоморфизмом векторного пространства или в некоторых контекстах линейной функцией ) является отображением между двумя векторными пространствами , сохраняющими операции сложения векторов и скалярного умножения . Те же имена и те же определения используются и для более общего случая модулей над кольцом ; см. Гомоморфизм модулей .
Если линейное отображение является биекцией , то оно называется линейный изоморфизм . В случае, когда линейное отображение называется линейным эндоморфизмом . Иногда этот термин линейный оператор относится к этому случаю, [1] но термин «линейный оператор» может иметь разное значение для разных соглашений: например, его можно использовать, чтобы подчеркнуть, что и являются действительными векторными пространствами (не обязательно с ), [ нужна ссылка ] или его можно использовать, чтобы подчеркнуть это представляет собой функциональное пространство , что является общепринятым соглашением в функциональном анализе . [2] Иногда термин «линейная функция» имеет то же значение, что и «линейная карта» , но в анализе это не так.
Линейная карта из к всегда отображает происхождение к происхождению . Более того, он отображает линейные подпространства в на линейные подпространства в (возможно, меньшего измерения ); [3] например, он отображает плоскость через начало координат в либо к плоскости, проходящей через начало координат в , линия, проходящая через начало координат в или просто начало координат в . Линейные карты часто могут быть представлены в виде матриц , а простые примеры включают линейные преобразования вращения и отражения .
На языке теории категорий линейные карты представляют собой морфизмы векторных пространств и образуют категорию, эквивалентную категории матриц .
Определение и первые последствия
[ редактировать ]Позволять и быть векторными пространствами над одним и тем же полем . Функция называется линейным отображением , если для любых двух векторов и любой скаляр выполняются следующие два условия:
- Аддитивность /операция сложения
- Однородность степени 1 / операция скалярного умножения
Таким образом, линейное отображение называется сохраняющим операции . Другими словами, не имеет значения, применяется ли линейное отображение до (правые части приведенных выше примеров) или после (левые части примеров) операций сложения и скалярного умножения.
В силу ассоциативности операции сложения, обозначенной знаком +, для любых векторов и скаляры имеет место следующее равенство: [4] [5] Таким образом, линейное отображение — это такое, которое сохраняет линейные комбинации .
Обозначая нулевые элементы векторных пространств и к и соответственно, отсюда следует, что Позволять и в уравнении однородности первой степени:
Линейная карта с рассматриваемое как одномерное векторное пространство над собой, называется линейным функционалом . [6]
Эти утверждения распространяются на любой левый модуль по кольцу без изменений и к любому правому модулю после обращения скалярного умножения.
Примеры
[ редактировать ]- Прототипическим примером, дающим имя линейным картам, является функция которого , график представляет собой линию, проходящую через начало координат. [7]
- В более общем смысле любая гомотетия с центром в начале векторного пространства представляет собой линейное отображение (здесь c — скаляр).
- Нулевая карта между двумя векторными пространствами (над одним и тем же полем ) является линейным.
- Тождественное отображение любого модуля представляет собой линейный оператор.
- Для действительных чисел карта не является линейным.
- Для действительных чисел карта не является линейным (но является аффинным преобразованием ).
- Если это реальная матрица , тогда определяет линейную карту из к отправив вектор-столбец вектор-столбцу . И наоборот, любое линейное отображение между конечномерными векторными пространствами может быть представлено таким образом; см. § Матрицы ниже.
- Если является изометрией вещественных нормированных пространств такая, что затем представляет собой линейную карту. Этот результат не обязательно верен для комплексного нормированного пространства. [8]
- Дифференцирование определяет линейное отображение пространства всех дифференцируемых функций в пространство всех функций. Он также определяет линейный оператор в пространстве всех гладких функций (линейный оператор — это линейный эндоморфизм , то есть линейное отображение с той же областью определения и кодомной областью ). Действительно,
- Определенный интеграл на некотором интервале I представляет собой линейное отображение пространства всех вещественнозначных интегрируемых функций на I в . Действительно,
- Неопределенный интеграл (или первообразная ) с фиксированной начальной точкой интегрирования определяет линейное отображение пространства всех вещественнозначных интегрируемых функций на в пространство всех действительных дифференцируемых функций на . Без фиксированной отправной точки первообразная отображается в фактор-пространство дифференцируемых функций с помощью линейного пространства постоянных функций.
- Если и являются конечномерными векторными пространствами над полем F соответствующих размерностей m и n , тогда функция, отображающая линейные отображения к матрицам размера n × m способом, описанным в § Матрицы (ниже), является линейным отображением и даже линейным изоморфизмом .
- Ожидаемое значение ( случайной величины которая на самом деле является функцией и, как таковая, элементом векторного пространства) линейно, как и для случайных величин. и у нас есть и , но дисперсия случайной величины не является линейной.
- Функция с представляет собой линейную карту. Эта функция масштабирует компонент вектора на множитель .
- Функция является аддитивным: не имеет значения, складываются ли векторы сначала, а затем отображаются или они отображаются и наконец добавляются:
- Функция является однородным: не имеет значения, сначала масштабируется вектор, а затем отображается или сначала отображается, а затем масштабируется:
Линейные расширения
[ редактировать ]Часто линейная карта создается путем определения ее на подмножестве векторного пространства, а затем распространяющийся по линейности на линейную оболочку области. Предполагать и являются векторными пространствами и это функция, определенная на некотором подмножестве Тогда линейное продолжение к если оно существует, является линейным отображением определено на который простирается [примечание 1] (имеется в виду, что для всех ) и принимает его значения из кодомена [9] Когда подмножество является векторным подпространством тогда а ( -значное) линейное продолжение всем гарантированно существует, если (и только если) представляет собой линейную карту. [9] В частности, если имеет линейное расширение до то оно имеет линейное расширение на все
Карта можно расширить до линейного отображения тогда и только тогда, когда когда-либо целое число, являются скалярами, а являются векторами такими, что тогда обязательно [10] Если линейное продолжение существует, то линейное расширение является уникальным и держится для всех и как указано выше. [10] Если линейно независима, то каждая функция в любое векторное пространство имеет линейное расширение до (линейного) отображения (верно и обратное).
Например, если и тогда задание и может быть линейно продолжено из линейно независимого набора векторов к линейной карте на Уникальное линейное расширение это карта, которая отправляет к
Каждый (скалярный) линейный функционал определенный в векторном подпространстве вещественного или комплексного векторного пространства имеет линейное распространение на все Действительно, теорема о доминируемом продолжении Хана – Банаха даже гарантирует, что, когда этот линейный функционал доминирует некоторая заданная полунорма (имеется в виду, что держится для всех в области ) то существует линейное расширение до здесь также преобладает
Матрицы
[ редактировать ]Если и являются конечномерными векторными пространствами, и базис , тогда каждое линейное отображение из для каждого векторного пространства определен к может быть представлено матрицей . [11] Это полезно, поскольку позволяет проводить конкретные расчеты. Матрицы дают примеры линейных карт: если настоящий матрица, тогда описывает линейную карту (см. Евклидово пространство ).
Позволять быть основой для . Тогда каждый вектор однозначно определяется коэффициентами в поле :
Если представляет собой линейную карту,
откуда следует, что функция f целиком определяется векторами . Теперь позвольте быть основой для . Тогда мы можем представить каждый вектор как
Таким образом, функция полностью определяется ценностями . Если мы поместим эти значения в матрица , то мы можем удобно использовать его для вычисления векторного вывода для любого вектора в . Получить , каждый столбец из вектор соответствующий как определено выше. Чтобы определить это более четко, для некоторого столбца что соответствует отображению , где это матрица . Другими словами, каждый столбец имеет соответствующий вектор чьи координаты являются элементами столбца . Одна линейная карта может быть представлена множеством матриц. Это связано с тем, что значения элементов матрицы зависят от выбранных базисов.
Матрицы линейного преобразования можно представить визуально:
- Матрица для относительно :
- Матрица для относительно :
- Матрица перехода из к :
- Матрица перехода из к :
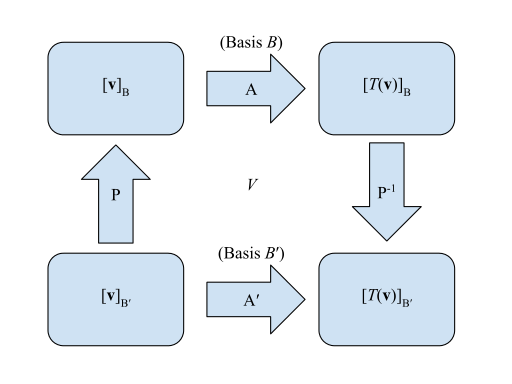
Так, что начиная с нижнего левого угла и ищем правый нижний угол , можно было бы умножить влево, то есть . Эквивалентным методом будет «более длинный» метод, идущий по часовой стрелке от той же точки, такой, что умножается слева на , или .
Примеры в двух измерениях
[ редактировать ]В двумерном пространстве R 2 линейные карты описываются матрицами 2×2 . Вот несколько примеров:
- вращение
- на 90 градусов против часовой стрелки:
- на угол θ против часовой стрелки:
- отражение
- через ось х :
- через ось Y :
- через линию, составляющую угол θ с началом координат:
- масштабирование на 2 во всех направлениях:
- отображение горизонтального сдвига :
- перекос оси y на угол θ :
- сжатие картографии :
- проекция на ось Y :
Если линейная карта состоит только из вращения, отражения и/или равномерного масштабирования, то линейная карта представляет собой конформное линейное преобразование .
Векторное пространство линейных карт
[ редактировать ]Композиция линейных карт линейна: если и линейны, то и их состав линеен . Отсюда следует, что класс всех векторных пространств над данным полем K вместе с K -линейными отображениями как морфизмами образует категорию .
Инверсия . линейной карты, если она определена, снова является линейной картой
Если и линейны, то линейна и их поточечная сумма , который определяется .
Если является линейным и является элементом наземного поля , то карта , определяемый , также является линейным.
Таким образом, набор линейных карт из к сам образует векторное пространство над , [12] иногда обозначается . [13] Кроме того, в случае, если , это векторное пространство, обозначаемое , является ассоциативной алгеброй относительно композиции карт , поскольку композиция двух линейных карт снова является линейной картой, а композиция карт всегда ассоциативна. Более подробно этот случай обсуждается ниже.
Опять же, учитывая конечномерный случай, если были выбраны базисы, то композиция линейных отображений соответствует умножению матриц , сложение линейных отображений соответствует сложению матриц , а умножение линейных отображений на скаляры соответствует умножению матрицы со скалярами.
Эндоморфизмы и автоморфизмы
[ редактировать ]Линейное преобразование является эндоморфизмом ; множество всех таких эндоморфизмов вместе со сложением, композицией и скалярным умножением, как определено выше, образует ассоциативную алгебру с единичным элементом над полем. (и в частности кольцо ). Мультипликативным единичным элементом этой алгебры является тождественное отображение .
Эндоморфизм который также является изоморфизмом называется автоморфизмом , . Композиция двух автоморфизмов снова является автоморфизмом, а множество всех автоморфизмов образует группу , автоморфизмов группу который обозначается или . Поскольку автоморфизмы — это именно те эндоморфизмы , которые обладают обратными относительно композиции, это группа юнитов в кольце .
Если имеет конечную размерность , затем изоморфна ассоциативной алгебре всех матрицы с записями в . Группа автоморфизмов изоморфна группе полной линейной из всех обратимые матрицы с элементами в .
Ядро, образ и теорема о ранге-нулевости
[ редактировать ]Если является линейным, мы ядро и образ или диапазон определяем к
является подпространством и является подпространством . Следующая формула размерности известна как теорема о ранге – недействительности : [14]
Число называют рангом еще и написано как , или иногда, ; [15] [16] число называется ничтожностью и написано как или . [15] [16] Если и конечномерны, базисы выбраны и представлена матрицей , то ранг и ничтожность равны рангу и нулю матрицы , соответственно.
Кокернел
[ редактировать ]Более тонкий инвариант линейного преобразования — это со- ядро , которое определяется как
Это двойственное понятие по отношению к ядру: точно так же, как ядро является подпространством предметной области, со-ядро является фактор- пространством цели . Формально имеем точную последовательность
Их можно интерпретировать следующим образом: учитывая линейное уравнение f ( v ) = w , которое нужно решить,
- ядро — пространство решений однородного ( уравнения f ) = 0, а его размерность — v число степеней свободы в пространстве решений, если оно не пусто;
- коядро — это пространство ограничений , которым должны удовлетворять решения, а его размерность — максимальное количество независимых ограничений.
Размерность совместного ядра и размерность изображения (ранг) в сумме дают размерность целевого пространства. Для конечных размеров это означает, что размерность факторпространства W / f ( V ) равна размерности целевого пространства минус размерность изображения.
В качестве простого примера рассмотрим отображение f : R 2 → Р 2 , заданный выражением f ( x , y ) = (0, y ). Тогда для того, чтобы уравнение f ( x , y ) = ( a , b ) имело решение, мы должны иметь a = 0 (одно ограничение), и в этом случае пространство решения равно ( x , b ) или, что эквивалентно, ( 0, b ) + ( x , 0), (одна степень свободы). Ядро может быть выражено как подпространство ( x , 0) < V : значение x — это свобода решения, тогда как коядро может быть выражено через отображение W → R , : учитывая вектор ( a , b ), значение a является препятствием для нахождения решения.
Примером, иллюстрирующим бесконечномерный случай, является отображение f : R ∞ → Р ∞ , с b 1 = 0 и bn > 0. Его образ состоит из + 1 = a n для n всех последовательностей с первым элементом 0, и, следовательно, его коядро состоит из классов последовательностей с идентичным первым элементом. Таким образом, хотя его ядро имеет размерность 0 (оно отображает только нулевую последовательность в нулевую последовательность), его ко-ядро имеет размерность 1. Поскольку область определения и целевое пространство одинаковы, ранг и размерность ядра складываются. в ту же сумму , что и ранг и размерность коядра ( ), но в бесконечномерном случае нельзя сделать вывод, что ядро и коядро эндоморфизма имеют одинаковую размерность (0 ≠ 1). Обратная ситуация имеет место для отображения h : R ∞ → Р ∞ , с c n знак равно a n + 1 . Его изображение — это все целевое пространство, и, следовательно, его коядро имеет размерность 0, но поскольку он отображает все последовательности, в которых только первый элемент ненулевой, в нулевую последовательность, его ядро имеет размерность 1.
Индекс
[ редактировать ]Для линейного оператора с конечномерным ядром и ко-ядром индекс можно определить как: а именно степени свободы минус количество ограничений.
Для преобразования между конечномерными векторными пространствами это просто разница dim( V ) − dim( W ) по рангу-нулевой. Это дает представление о том, сколько решений или сколько ограничений имеется: при отображении большего пространства в меньшее карта может быть включена и, следовательно, будет иметь степени свободы даже без ограничений. И наоборот, если отображать меньшее пространство в большее, карта не может быть включена, и, следовательно, будут иметься ограничения даже без степеней свободы.
Индекс оператора - это в точности эйлерова характеристика 2-членного комплекса 0 → V → W → 0. В теории операторов индекс операторов Фредгольма является объектом исследования, основным результатом которого является теорема об индексе Атьи – Зингера. . [17]
Алгебраические классификации линейных преобразований
[ редактировать ]Никакая классификация линейных карт не может быть исчерпывающей. В следующем неполном списке перечислены некоторые важные классификации, которые не требуют какой-либо дополнительной структуры в векторном пространстве.
Пусть V и W обозначают векторные пространства над полем F и пусть T : V → W — линейное отображение.
Мономорфизм
[ редактировать ]T называется инъективным или мономорфизмом , если выполняется любое из следующих эквивалентных условий:
- T взаимно однозначно как карта множеств .
- кер Т = {0 В }
- dim(ker T ) = 0
- T является унитарным или сокращаемым слева, то есть для любого векторного пространства U и любой пары линейных отображений R : U → V и S : U → V из уравнения TR = TS следует R = S .
- T обратимо слева , то есть существует линейное отображение S : W → V такое, что является тождественным отображением на V. ST
Эпиморфизм
[ редактировать ]T называется сюръективным или эпиморфизмом, если выполняется любое из следующих эквивалентных условий:
- T представляет собой карту множеств.
- кокс T = {0 Вт }
- T эпическое W или правосократимое, то есть для любого векторного пространства и любой пары линейных отображений R : RT → U и S : W → U уравнение U = ST влечет за собой R = S .
- T обратимо справа , то есть существует линейное отображение S : W → V такое, что — тождественное отображение на W. TS
изоморфизм
[ редактировать ]T называется изоморфизмом, если он обратим как слева, так и справа. Это эквивалентно тому, что T является одновременно взаимно однозначным и на ( биекция множеств), или также тому, что T одновременно является эпическим и моническим и, таким образом, является биморфизмом .
Если T : V → V — эндоморфизм, то:
- Если для некоторого натурального числа n итерация -я T , T n н , тождественно нулю, то T называется нильпотентным .
- Если Т 2 = T , то T называется идемпотентным
- Если T = kI , где k — некоторый скаляр, то T называется масштабирующим преобразованием или отображением скалярного умножения; см. скалярную матрицу .
Изменение базы
[ редактировать ]Учитывая линейное отображение, которое является эндоморфизмом , матрица которого равна A , в базисе B пространства оно преобразует векторные координаты [u] как [v] = A [u]. Поскольку векторы изменяются с обратным преобразованием B (координаты векторов контравариантны ), его обратное преобразование равно [v] = B [v'].
Подставив это в первое выражение следовательно
Следовательно, матрица в новом базисе равна A′ = B −1 AB , будучи B матрицей данного базиса.
Поэтому линейные карты называются 1-ко-1-контравариантными объектами или тензорами типа (1, 1) .
Непрерывность
[ редактировать ]Линейное преобразование между топологическими векторными пространствами , например, нормированными пространствами , может быть непрерывным . Если его область определения и область определения совпадают, то это будет непрерывный линейный оператор . Линейный оператор в нормированном линейном пространстве непрерывен тогда и только тогда, когда он ограничен , например, когда область определения конечномерна. [18] Бесконечномерная область может иметь разрывные линейные операторы .
Примером неограниченного, а значит, и разрывного, линейного преобразования является дифференцирование на пространстве гладких функций, снабженных супремум-нормой (функция с малыми значениями может иметь производную с большими значениями, а производная от 0 равна 0). В конкретном примере sin( nx )/ n сходится к 0, а его производная cos( nx ) — нет, поэтому дифференцирование не является непрерывным в точке 0 (и, если изменить этот аргумент, оно не является непрерывным нигде).
Приложения
[ редактировать ]Конкретным применением линейных карт являются геометрические преобразования , например, выполняемые в компьютерной графике , где перемещение, вращение и масштабирование 2D- или 3D-объектов выполняются с использованием матрицы преобразования . Линейные отображения также используются как механизм описания изменений: например, в исчислении они соответствуют производным; или в теории относительности используется как устройство для отслеживания локальных преобразований систем отсчета.
Другое применение этих преобразований — оптимизация компилятора кода с вложенными циклами и распараллеливание методов компилятора .
См. также
[ редактировать ]- Аддитивное отображение - гомоморфизм Z-модуля
- Антилинейная карта - Сопряженная однородная аддитивная карта.
- Бент-функция – специальный тип логической функции.
- Ограниченный оператор - линейное преобразование между топологическими векторными пространствами.
- Функциональное уравнение Коши – Функциональное уравнение
- Непрерывный линейный оператор
- Линейный функционал — линейная карта векторного пространства с его полем скаляров.
- Линейная изометрия — математическое преобразование, сохраняющее расстояние.
- Категория матриц
- Квазилинеаризация
Примечания
[ редактировать ]- ^ «Линейные преобразования V в V часто называют линейными операторами на V ». Рудин 1976 , с. 207
- ^ Пусть V и W — два вещественных векторных пространства. Отображение a из V в W называется «линейным отображением» или «линейным преобразованием» или «линейным оператором» [...] из V в W , если
для всех ,
для всех и все действительные λ . Бронштейн и Семендяев 2004 , с. 316 - ^ Рудин 1991 , с. 14
Вот некоторые свойства линейных отображений чьи доказательства настолько просты, что мы их опускаем; предполагается, что и :- Если А — подпространство (или выпуклое множество , или сбалансированное множество ), то же самое верно и для
- Если B — подпространство (или выпуклое множество, или сбалансированное множество), то же самое верно и для
- В частности, набор: является подпространством X , называемым нулевым пространством .
- ^ Рудин 1991 , с. 14. Предположим теперь, что X и Y — векторные пространства над одним и тем же скалярным полем . Отображение называется линейным, если для всех и все скаляры и . Обратите внимание, что часто пишут , скорее, чем , когда является линейным.
- ^ Рудин 1976 , с. 206. Отображение A векторного пространства X в векторное пространство Y называется линейным преобразованием, если: для всех и все скаляры c . Обратите внимание, что часто пишут вместо если А линейно.
- ^ Рудин 1991 , с. 14. Линейные отображения X на его скалярное поле называются линейными функционалами .
- ^ «терминология. Что означает слово «линейный» в линейной алгебре?» . Математический обмен стеками . Проверено 17 февраля 2021 г.
- ^ Виланский 2013 , стр. 21–26.
- ^ Jump up to: а б Кубруслый 2001 , с. 57.
- ^ Jump up to: а б Шехтер 1996 , стр. 277–280.
- ^ Рудин 1976 , с. 210Предполагать и являются базами векторных пространств X и Y соответственно. Затем каждый определяет набор чисел такой, что Эти числа удобно представить в виде прямоугольного массива из m строк и n столбцов, называемого размером m на n матрицей : Обратите внимание, что координаты вектора (относительно основания ) появляются в j й столбец . Векторы поэтому иногда называют -столбцами вектор . Используя эту терминологию, диапазон A столбцами охватывается векторами- .
- ^ Экслер (2015) с. 52, § 3.3
- ^ Ту (2011) , стр. 19, § 3.1.
- ^ Horn & Johnson 2013 , 0.2.3 Векторные пространства, связанные с матрицей или линейным преобразованием, с. 6
- ^ Jump up to: а б Кацнельсон и Кацнельсон (2008), стр. 52, § 2.5.1.
- ^ Jump up to: а б Халмош (1974) с. 90, § 50
- ^ Нистор, Виктор (2001) [1994], «Теория индексов» , Энциклопедия математики , EMS Press : «Главный вопрос теории индексов состоит в том, чтобы предоставить формулы индексов для классов операторов Фредгольма... Теория индексов стала предметом ее изучения. стали принадлежать только после того, как М. Ф. Атья и И. Сингер опубликовали свои теоремы об индексах».
- ^ Рудин 1991 , с. 15 1.18. Теорема. Пусть быть линейным функционалом в топологическом векторном пространстве X . Предполагать для некоторых . Тогда каждое из следующих четырех свойств подразумевает остальные три:
- является непрерывным
- Нулевое пространство закрыт.
- не плотно в X .
- ограничен в некоторой окрестности V нуля.
Библиография
[ редактировать ]- Экслер, Шелдон Джей (2015). Линейная алгебра сделана правильно (3-е изд.). Спрингер . ISBN 978-3-319-11079-0 .
- Бронштейн И.Н.; Семендяев К.А. (2004). Справочник по математике (4-е изд.). Нью-Йорк: Springer-Verlag. ISBN 3-540-43491-7 .
- Халмос, Пол Ричард (1974) [1958]. Конечномерные векторные пространства (2-е изд.). Спрингер . ISBN 0-387-90093-4 .
- Хорн, Роджер А.; Джонсон, Чарльз Р. (2013). Матричный анализ (Второе изд.). Издательство Кембриджского университета . ISBN 978-0-521-83940-2 .
- Кацнельсон, Ицхак ; Кацнельсон, Йонатан Р. (2008). (Краткое) Введение в линейную алгебру . Американское математическое общество . ISBN 978-0-8218-4419-9 .
- Кубрусли, Карлос (2001). Элементы теории операторов . Бостон: Биркхойзер. ISBN 978-1-4757-3328-0 . OCLC 754555941 .
- Ланг, Серж (1987), Линейная алгебра (Третье изд.), Нью-Йорк: Springer-Verlag , ISBN 0-387-96412-6
- Рудин, Уолтер (1973). Функциональный анализ . Международная серия по чистой и прикладной математике. Том. 25 (Первое изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN 9780070542259 .
- Рудин, Уолтер (1976). Принципы математического анализа . Студенческая серия Уолтера Рудина по высшей математике (3-е изд.). Нью-Йорк: МакГроу-Хилл. ISBN 978-0-07-054235-8 .
- Рудин, Уолтер (1991). Функциональный анализ . Международная серия по чистой и прикладной математике. Том. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN 978-0-07-054236-5 . OCLC 21163277 .
- Шефер, Хельмут Х .; Вольф, Манфред П. (1999). Топологические векторные пространства . ГТМ . Том. 8 (Второе изд.). Нью-Йорк, Нью-Йорк: Springer New York Выходные данные Springer. ISBN 978-1-4612-7155-0 . OCLC 840278135 .
- Шехтер, Эрик (1996). Справочник по анализу и его основам . Сан-Диего, Калифорния: Academic Press. ISBN 978-0-12-622760-4 . OCLC 175294365 .
- Шварц, Чарльз (1992). Введение в функциональный анализ . Нью-Йорк: М. Деккер. ISBN 978-0-8247-8643-4 . ОСЛК 24909067 .
- Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Спрингер . ISBN 978-0-8218-4419-9 .
- Вилански, Альберт (2013). Современные методы в топологических векторных пространствах . Минеола, Нью-Йорк: ISBN Dover Publications, Inc. 978-0-486-49353-4 . OCLC 849801114 .









































![{\displaystyle E[X+Y]=E[X]+E[Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea2251900ec2b03db1d6f870336155a2a09ff7f1)
![{\displaystyle E[aX]=aE[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e34453ad80cdf674f4d15fab3e8096be81af79a)


































































![{\textstyle \left[\mathbf {v} \right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38ce4e66d088a57d8adb2aadc461213818bc3220)
![{\textstyle \left[T\left(\mathbf {v} \right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/954ce89644d8b424263ec4dac91becfb6672d931)
![{\textstyle A'\left[\mathbf {v} \right]_{B'} =\left[T\left(\mathbf {v} \right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d40bbccc105af68b575ef57b62b1e1943c478aaa)

![{\textstyle P^{-1}AP\left[\mathbf {v} \right]_{B'} =\left[T\left(\mathbf {v} \right)\right]_{B'} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c713b4830cf922213fe7907677ae35be5fffcfc)



















































![{\displaystyle B\left[v'\right]=AB\left[u'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2855717373418c2c2134151c0d0f4d5957292f8)
![{\displaystyle \left[v'\right]=B^{-1}AB\left[u'\right]=A'\left[u'\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65eb8aa4babed0054fcf025303d23fd58309bf7e)

























![{\displaystyle [A]={\begin{bmatrix}a_{1,1}&a_{1,2}&\ldots &a_{1,n}\\a_{2,1}&a_{2,2}&\ ldots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\ldots &a_{m,n}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f53d08efeacd19a7270d82ee81484d772f4e8ef)


![{\текстовый стиль [А]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc7c42d7e9f789e2b3384a4f718faddeb0f2119)






