Споры об исчислении Лейбница-Ньютона

Статуи Исаака Ньютона и Готфрида Вильгельма Лейбница во дворе Музея естественной истории Оксфордского университета , коллаж

В истории исчисления полемика об исчислении ( нем . Prioritätsstreit , букв.   «Спор о приоритете») представляла собой спор между математиками Исааком Ньютоном и Готфридом Вильгельмом Лейбницем о том, кто первым изобрел исчисление . Этот вопрос представлял собой серьезный интеллектуальный спор, который начал закипать в 1699 году и разгорелся в полную силу в 1711 году. Лейбниц первым опубликовал свою работу, но сторонники Ньютона обвинили Лейбница в плагиате неопубликованных идей Ньютона. Лейбниц умер в 1716 году, вскоре после того, как Королевское общество, членом которого был Ньютон, вынесло решение в пользу Ньютона. Современный консенсус состоит в том, что эти двое мужчин разработали свои идеи независимо.

Ньютон сказал, что начал работать над формой исчисления (которую он назвал « методом флюксий и флюэнтов ») в 1666 году, в возрасте 23 лет, но опубликовал ее только в виде незначительной аннотации в конце одной из своих книг. публикации десятилетия спустя (соответствующая рукопись Ньютона от октября 1666 г. теперь опубликована среди его математических статей ). Готфрид Лейбниц начал работать над своим вариантом исчисления в 1674 году, а в 1684 году опубликовал свою первую статью, использующую его, « Новый метод про максимы и минимисы ». Лопиталь опубликовал текст об исчислении Лейбница в 1696 году (в котором он признал, что «Начала» Ньютона 1687 года «почти полностью посвящены этому исчислению»). Между тем, Ньютон, хотя и объяснил свою (геометрическую) форму исчисления в разделе I книги I « Начал» 1687 года, не объяснил свою возможную флюкционную запись для исчисления в печати до 1693 г. (частично) и 1704 г. (полностью).

Преобладающее мнение в XVIII веке было против Лейбница (в Британии, а не в немецкоязычном мире). Сегодня все согласны с тем, что Лейбниц и Ньютон независимо друг от друга изобрели и описали исчисление в Европе в 17 веке.

Несомненно, именно Исаак Ньютон первым разработал новое исчисление бесконечно малых и превратил его в широко расширяемый алгоритм, потенциальные возможности которого он полностью понимал; дифференциальное . и интегральное исчисление , источник великих разработок, продолжавшихся непрерывно с 1684 года до наших дней, было независимо создано Готфридом Лейбницем

- Зал 1980: 1

Один автор определил, что спор идет о «совершенно разных» методах:

Несмотря на... сходство, методы [Ньютона и Лейбница] глубоко различны, поэтому ряд приоритетов становится бессмысленным.

- Грэттан-Гиннесс 1997: 247

С другой стороны, другие авторы подчеркивали эквивалентность и взаимную переводимость методов: здесь Н. Гвиччардини (2003), по-видимому, подтверждает L'Hôpital (1696) (уже цитировавшийся):

школы Ньютона и Лейбница использовали общий математический метод. Они приняли два алгоритма: аналитический метод флюксий, а также дифференциальное и интегральное исчисление, которые можно было перевести один в другой.

- Гвиччардини 2003, стр. 250.

Научный приоритет в 17 веке

В XVII веке, как и в настоящее время, вопрос о научном приоритете имел для ученых большое значение. Однако в этот период только начали появляться научные журналы , а общепринятый механизм фиксации приоритета путем публикации информации об открытии еще не сформировался. Среди методов, использованных учеными, были анаграммы , запечатанные конверты, помещенные в безопасное место, переписка с другими учеными или личное сообщение. Письмо основателю академии наук Французской Марину Мерсенну для французского учёного или секретарю Лондонского королевского общества Генри Ольденбургу для английского языка имело практически статус опубликованной статьи. Первооткрыватель мог «отметить время» момента своего открытия и доказать, что он знал об этом в тот момент, когда письмо было запечатано, и не копировал его ни с чего из опубликованного впоследствии. Тем не менее, если идея была впоследствии опубликована в сочетании с ее использованием в особенно ценном контексте, она могла иметь приоритет над работой более раннего первооткрывателя, которая не имела очевидного применения. Более того, утверждение математика может быть подорвано встречными утверждениями о том, что он на самом деле не изобрел идею, а просто усовершенствовал чью-то идею, усовершенствование, которое не требовало особых навыков и было основано на уже известных фактах.

связана серия громких споров о научном приоритете 17 века — эпохи, которую американский историк науки Д. Мели назвал «золотым веком обливающих грязью споров о приоритетах» С именем Лейбница . Первый из них произошел в начале 1673 года, во время его первого визита в Лондон, когда в присутствии знаменитого математика Джона Пелла он представил свой метод приближения рядов разностями . На замечание Пелла о том, что это открытие уже было сделано Франсуа Реньо и опубликовано в 1670 году в Лионе Габриэлем Мутоном , Лейбниц ответил на следующий день. В письме в Ольденбург он писал, что, просмотрев книгу Мутона, признает правоту Пелла, но в свою защиту может привести свои черновые заметки, в которых есть нюансы, не обнаруженные Рено и Мутоном. Таким образом, честность Лейбница была доказана, но в этом случае его отозвали позже. Во время того же визита в Лондон Лейбниц оказался в противоположной позиции. 1 февраля 1673 года на заседании Лондонского королевского общества он продемонстрировал свой механический калькулятор . Куратор экспериментов Общества Роберт Гук внимательно осмотрел устройство и даже снял для этого заднюю крышку. Несколько дней спустя, в отсутствие Лейбница, Гук раскритиковал машину немецкого учёного, заявив, что тот мог бы создать более простую модель. Лейбниц, узнавший об этом, вернулся в Париж и в письме к Ольденбургу категорически отверг утверждение Гука и сформулировал принципы правильного научного поведения: «Мы знаем, что порядочные и скромные люди предпочитают, когда они думают о чем-то, что согласуется с тем, что сделал кто-то». другие открытия, приписывают первооткрывателю свои собственные улучшения и дополнения, чтобы не возбуждать подозрений в интеллектуальной нечестности, и их должно преследовать стремление к истинному великодушию, а не лживая жажда нечестной прибыли». Чтобы проиллюстрировать правильное поведение, Лейбниц приводит пример Николя-Клод Фабри де Пейреск и Пьер Гассенди , которые выполнили астрономические наблюдения, аналогичные тем, которые ранее сделали Галилео Галилей и Иоганн Гевелий соответственно. Узнав, что не они сделали свои открытия первыми, французские учёные передали свои данные первооткрывателям.

Подход Ньютона к приоритетной проблеме можно проиллюстрировать на примере открытия закона обратных квадратов применительно к динамике тел, движущихся под действием силы тяжести . На основе анализа законов Кеплера и собственных расчетов Роберт Гук сделал предположение, что движение в таких условиях должно происходить по орбитам, подобным эллиптическим . Не имея возможности строго доказать это утверждение, он сообщил об этом Ньютону. Не вступая далее в переписку с Гуком, Ньютон решил эту задачу, как и обратную к ней, доказав, что закон обратных квадратов вытекает из эллиптичности орбит. Это открытие было изложено в его знаменитой работе Philosophiæ Naturalis Principia Mathematica без указания имени Гука. По настоянию астронома Эдмунда Галлея , которому рукопись была передана для редактирования и публикации, в текст была включена фраза о том, что соответствие первого закона Кеплера закону обратных квадратов «независимо одобрено Рен , Гук и Галлей».

По замечанию Владимира Арнольда , Ньютон, выбирая между отказом от публикации своих открытий и постоянной борьбой за приоритет, выбрал и то, и другое.

Фон

Изобретение дифференциального и интегрального исчисления

Основная статья: История исчисления

Дифференциальный треугольник Паскаля

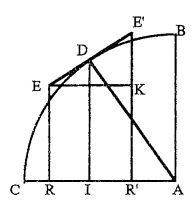
Ко времени Ньютона и Лейбница европейские математики уже внесли значительный вклад в формирование идей математического анализа. занимались голландец Симон Стевин (1548–1620), итальянец Лука Валерио (1553–1618), немец Иоганн Кеплер Разработкой древнего « метода исчерпания » для вычисления площадей и объёмов (1571–1630). Идеи последнего, по-видимому, повлияли – непосредственно или через Галилео Галилея – на « метод неделимых », разработанный Бонавентурой Кавальери (1598–1647).

Последние годы жизни Лейбница, 1710–1716, были омрачены длительными спорами с Джоном Кейлом , Ньютоном и другими по поводу того, открыл ли Лейбниц исчисление независимо от Ньютона, или же он просто изобрел другое обозначение для идей, которые по своей сути были ньютоновскими. . Никто из участников не сомневался, что Ньютон уже разработал свой метод флюксий , когда Лейбниц начал работать над дифференциальным исчислением, однако, по-видимому, не было никаких доказательств, кроме слов Ньютона. Он опубликовал расчет касательной с пометкой: «Это лишь частный случай общего метода, с помощью которого я могу рассчитывать кривые и определять максимумы, минимумы и центры тяжести». Как это было сделано, он объяснил ученику целых 20 лет спустя, когда статьи Лейбница уже были начитаны. Рукописи Ньютона стали известны только после его смерти.

Исчисление бесконечно малых может быть выражено либо в обозначениях флюксий, либо в обозначениях дифференциалов , либо, как отмечалось выше, оно было также выражено Ньютоном в геометрической форме, как в «Началах» 1687 года. Ньютон использовал флюксии еще в 1666 году, но не публиковал отчет о своих обозначениях до 1693 года. Самое раннее использование дифференциалов в записных книжках Лейбница можно отнести к 1675 году. Он использовал эти обозначения в письме Ньютону в 1677 году. Дифференциальная запись также появилась в мемуарах Лейбница 1684 года.

Утверждение о том, что Лейбниц изобрел исчисление независимо от Ньютона, основано на том, что Лейбниц:

1. опубликовал описание своего метода за несколько лет до того, как Ньютон напечатал что-либо о флюксиях,
2. всегда ссылался на это открытие как на свое собственное изобретение (это утверждение не оспаривалось в течение нескольких лет),
3. пользовался сильной презумпцией того, что он действовал добросовестно, и
4. продемонстрировал в своих частных бумагах свое развитие идей исчисления независимо от пути, избранного Ньютоном.

По мнению критиков Лейбница, тот факт, что утверждение Лейбница не оспаривалось в течение нескольких лет, не имеет значения. Чтобы опровергнуть этот случай, достаточно показать, что он:

• видел некоторые статьи Ньютона по этой теме в 1675 году или, по крайней мере, в 1677 году или ранее, и
• получил фундаментальные идеи исчисления из этих работ.

Не было предпринято никаких попыток опровергнуть № 4, который в то время не был известен, но который обеспечивает наиболее убедительное доказательство того, что Лейбниц пришел к исчислению независимо от Ньютона. Эти доказательства, однако, все еще вызывают сомнения, поскольку в ходе расследования и после него было обнаружено, что Лейбниц датировал и изменил основы своих «оригинальных» заметок не только в этом интеллектуальном конфликте, но и в некоторых других. Он также опубликовал «анонимную» клевету на Ньютона относительно их полемики, автор которой первоначально пытался заявить, что он не является его автором.

Однако, если все же предположить добросовестность, заметки Лейбница, представленные на следствии, сначала касались интегрирования , которое он рассматривал как обобщение суммирования бесконечных рядов, тогда как Ньютон начал с производных. Однако рассматривать развитие исчисления как полностью независимое между работами Ньютона и Лейбница упускает из виду тот момент, что оба имели некоторые знания о методах друг друга (хотя Ньютон действительно разработал большинство основ до того, как начал работать Лейбниц) и фактически работали вместе над несколько аспектов, в частности степенной ряд , как показано в письме Генри Ольденбургу от 24 октября 1676 г., где Ньютон отмечает, что Лейбниц разработал ряд методов, один из которых был для него новым. И Лейбниц, и Ньютон могли видеть по этому обмену письмами, что другой далеко продвинулся к исчислению (Лейбниц, в частности, упоминает об этом), но только Лейбниц был этим подтолкнут к публикации.

То, что Лейбниц видел некоторые рукописи Ньютона, всегда было вероятным. В 1849 году К.И. Герхардт , просматривая рукописи Лейбница, нашел выдержки из книги Ньютона « De Analysi per Equationes Numero Terminorum Infinitas » (опубликованной в 1704 году как часть De Quadratura Curvarum, но также ранее циркулировавшей среди математиков, начиная с того, что Ньютон дал копию Исааку Барроу в 1669 год, и Барроу отправляет его Джону Коллинзу. ) почерком Лейбница, о существовании которого ранее не подозревалось, вместе с примечаниями, заново выражающими содержание этих отрывков в дифференциальной записи Лейбница. Следовательно, когда эти экстракты были сделаны, становится крайне важным. Известно, что копия рукописи Ньютона была отправлена ​​Эренфриду Вальтеру фон Чирнхаусу в мае 1675 года, когда он и Лейбниц сотрудничали; не исключено, что эти отрывки были сделаны именно тогда. Также возможно, что они были сделаны в 1676 году, когда Лейбниц обсуждал анализ с помощью бесконечных рядов с Коллинзом и Ольденбургом. Вполне вероятно, что тогда они показали бы ему рукопись Ньютона на эту тему, копия которой наверняка принадлежала одному из них или обоим. С другой стороны, можно предположить, что Лейбниц сделал выдержки из печатной копии в 1704 году или позже. Незадолго до своей смерти Лейбниц признался в письме аббату Антонио Шинелле Конти , что в 1676 году Коллинз показал ему некоторые статьи Ньютона. , но Лейбниц также подразумевал, что они не имеют никакой ценности. Вероятно, он имел в виду письма Ньютона от 13 июня и 24 октября 1676 г., а также письмо от 10 декабря 1672 г. о методе касательные , выдержки из которых сопровождали письмо от 13 июня.

Использовал ли Лейбниц рукопись, из которой он скопировал отрывки, или же он изобрел это исчисление ранее — это вопросы, по которым в настоящее время нет прямых доказательств. Стоит, однако, отметить, что неопубликованные «Портсмутские документы» показывают, что, когда Ньютон в 1711 году внимательно вошел во весь спор, он выбрал именно эту рукопись как ту, которая, вероятно, каким-то образом попала в руки Лейбница. В то время не было прямых доказательств того, что Лейбниц видел рукопись Ньютона до того, как она была напечатана в 1704 году; поэтому гипотеза Ньютона не была опубликована. Но обнаружение Герхардтом копии, сделанной Лейбницем, подтверждает ее точность. Те, кто сомневается в добросовестности Лейбница, утверждают, что для человека его способностей рукопись, особенно если она была дополнена письмом от 10 декабря 1672 года, была достаточна, чтобы дать ему ключ к пониманию методов исчисления. Поскольку в рассматриваемой работе Ньютона действительно использовалась флюзионная система обозначений, любой, кто опирался бы на эту работу, должен был бы изобрести систему обозначений, но некоторые это отрицают.

Разработка

Ссора имела ретроспективный характер. В 1696 году, уже через несколько лет после событий, ставших предметом ссоры, позиция все еще выглядела потенциально мирной: Ньютон и Лейбниц дали ограниченное признание работам друг друга, а книга Лопиталя 1696 года об исчислении от лейбницевца точка зрения также признала опубликованную работу Ньютона 1680-х годов как «почти всю об этом исчислении» (« presque tout de ce Calcul »), одновременно выразив предпочтение удобству обозначений Лейбница .

Поначалу не было никаких оснований подозревать Лейбница в добросовестности. В 1699 году Николя Фатио де Дюйе , швейцарский математик, известный своими работами по проблеме зодиакального света, публично обвинил Лейбница в плагиате Ньютона. хотя он дважды в частном порядке обвинял Лейбница в плагиате в письмах Христиану Гюйгенсу в 1692 году. Лишь после публикации в 1704 году анонимного обзора трактата Ньютона о квадратуре , обзора, подразумевающего, что Ньютон заимствовал идею флюксионного исчисления у Лейбница, ни один ответственный математик не усомнился в том, что Лейбниц изобрел это исчисление независимо от Ньютона. Что касается обзора квадратурной работы Ньютона, все признают, что не было никакого оправдания или авторитета для сделанных в ней утверждений, которые справедливо приписывались Лейбницу. Но последующая дискуссия привела к критическому рассмотрению всего вопроса, и возникли сомнения. Заимствовал ли Лейбниц фундаментальную идею исчисления от Ньютона? Дело против Лейбница, как показалось друзьям Ньютона, было подведено в «Commercium Epistolicum» 1712 года, в котором упоминались все обвинения. Этот документ был тщательно обработан Ньютоном.

Никакого такого изложения (с фактами, датами и ссылками) дела Лейбница его друзья не опубликовали; но Иоганн Бернулли попытался косвенно ослабить доказательства, нападая на личный характер Ньютона в письме от 7 июня 1713 года. Когда Бернулли потребовали объяснений, он самым торжественным образом отрицал, что написал письмо. Принимая отрицание, Ньютон добавил в частном письме Бернулли следующие замечания, в которых Ньютон назвал причины, по которым он принял участие в полемике. Он сказал: «Я никогда не хватался за славу среди чужих народов, но я очень желаю сохранить свой характер за честность, которую автор этого послания, словно авторитетом великого судьи, пытался отобрать у меня. Теперь, когда я стар, мне мало удовольствия от математических исследований, и я никогда не пытался распространять свои мнения по всему миру, но я скорее старался не ввязываться в споры из-за них».

Лейбниц объяснил свое молчание следующим образом в письме Конти от 9 апреля 1716 года:

Чтобы ответить по пунктам на всю опубликованную против меня работу, мне пришлось бы вдаваться в подробности, произошедшие тридцать-сорок лет назад, из которых я мало что помню: мне пришлось бы поискать в своих старых письмах, многие из которых потерянный. Более того, в большинстве случаев я не сохранял копию, а когда и сохранял, копия пряталась в огромной куче бумаг, разобраться в которых я мог только со временем и терпением. Я мало наслаждался досугом, так как в последнее время меня отягощали занятия совершенно иного характера.

Для стойких сторонников Ньютона это было примером слова Лейбница против ряда противоположных и подозрительных деталей. Его непризнанное обладание копией части одной из рукописей Ньютона можно объяснить; но оказывается, что Лейбниц не раз намеренно изменял или добавлял важные документы (например, письмо от 7 июня 1713 г. в Charta Volans и письмо от 8 апреля 1716 г. в Acta Eruditorum ), прежде чем публиковать их, и фальсифицировал дата в рукописи (1675 год изменен на 1673 год). Все это ставит под сомнение его показания.

Учитывая интеллектуальное мастерство Лейбница, о чем свидетельствуют другие его достижения, у него было больше, чем необходимая способность изобрести исчисление. Утверждается, что он получил ряд предложений, а не описание вычислений; возможно, что, поскольку он не публиковал свои результаты с 1677 по 1684 год и поскольку дифференциальная система записи была его изобретением, Лейбниц 30 лет спустя свел к минимуму любую пользу, которую он мог бы получить от чтения рукописи Ньютона. Более того, он, возможно, считал вопрос о том, кто придумал исчисление, несущественным, если сравнивать его с выразительной силой его обозначений.

В любом случае, предвзятость в пользу Ньютона с самого начала испортила все дело. Королевское общество , президентом которого в то время был Исаак Ньютон, в ответ на письмо, полученное от Лейбница, создало комитет для вынесения решения по спору о приоритете. Этот комитет никогда не просил Лейбница изложить свою версию событий. Отчет комиссии, вынесенный в пользу Ньютона, был написан и опубликован Ньютоном под названием «Commercium Epistolicum» (упомянутый выше) в начале 1713 года. Но Лейбниц увидел его только осенью 1714 года.

Смерть Лейбница и конец спора

Лейбниц никогда не соглашался признать приоритет Ньютона в изобретении исчисления. Он также пытался написать свою версию истории дифференциального исчисления, но, как и в случае с историей правителей Брауншвейга, не довел дело до конца. В конце 1715 года Лейбниц принял предложение Иоганна Бернулли организовать еще одно соревнование математиков, в котором различные подходы должны были доказать свою состоятельность. На этот раз задача была взята из области, позже названной вариационным исчислением , — требовалось построить касательную к семейству кривых. Письмо с такой формулировкой было написано 25 ноября и передано в Лондоне Ньютону через Абате Конти . Проблема была сформулирована не очень ясно, и лишь позднее стало ясно, что требуется найти общее, а не частное, как понимал Ньютон, решение. После того как британская сторона опубликовала свое решение, Лейбниц опубликовал свое, более общее, и, таким образом, формально выиграл это соревнование. Со своей стороны Ньютон упорно стремился уничтожить своего противника. Не добившись этого с «Отчетом», он продолжил свои кропотливые исследования, потратив на них сотни часов. Его следующее исследование, озаглавленное «Наблюдения за предыдущим посланием», было вдохновлено письмом Лейбница Конти в марте 1716 года, в котором критиковались философские взгляды Ньютона; никаких новых фактов в этом документе приведено не было. Со смертью Лейбница в ноябре 1716 года споры постепенно утихли. По мнению А. Руперта Холла , после 1722 года этот вопрос перестал интересовать самого Ньютона.

См. также

• Возможность передачи результатов школы Кералы в Европу.
• Список споров о научных приоритетах

Ссылки

• В эту статью включен текст из этого источника, который находится в свободном доступе : Болл, У. В. Роуз (1908). Краткий обзор истории математики . Нью-Йорк: Макмиллан.

Источники

• Арнольд, В. И. (1989). Гюйгенс и Барроу, Ньютон и Гук - Первые шаги математического анализа и теории катастроф . М.: Наука . p. 98. ISBN  5-02-013935-1 .
• Арнольд, Владимир (1990). Гюйгенс и Барроу, Ньютон и Гук: пионеры математического анализа и теории катастроф от эвольвент до квазикристаллов . Перевод Примроуза, Эрик Дж. Ф. Биркхойзер Верлаг . ISBN  3-7643-2383-3 .
• WW Роуз Болл (1908) Краткий обзор истории математики ], 4-е изд.
• Барди, Джейсон Сократ (2006). Войны исчисления: Ньютон, Лейбниц и величайшее математическое столкновение всех времен . Нью-Йорк: Thunder's Mouth Press. ISBN  978-1-56025-992-3 .
• Бойер, CB (1949). История исчисления и его концептуальное развитие . Dover Publications, Inc.
• Ричард К. Браун (2012) Запутанное происхождение исчисления Лейбница: пример математической революции , World Scientific ISBN   9789814390804
• Айвор Граттан-Гиннесс (1997) Нортонская история математических наук . WW Нортон .
• Холл, Арканзас (1980). Философы на войне: Ссора между Ньютоном и Лейбницем . Издательство Кембриджского университета. п. 356. ИСБН  0-521-22732-1 .
• Стивен Хокинг (1988) Краткая история времени от Большого взрыва до черных дыр. Бантамские книги .
• Кандасвами, Ананд. Конфликт Ньютона и Лейбница в контексте .
• Мели, Д.Б. (1993). Эквивалентность и приоритет: Ньютон против Лейбница: включая неопубликованные рукописи Лейбница о «Началах» . Кларендон Пресс. п. 318. ИСБН  0-19-850143-9 .

Внешние ссылки

• Готфрид Вильгельм Лейбниц, Полное собрание сочинений и писем, серия VII: Математические сочинения, том. 5: Бесконечно-малая математика 1674–1676 , Берлин: Akademie Verlag, 2008, стр. 288–295 («Analyseos Tetragonicae pars secunda», 29 октября 1675 г.) и 321–331 («Methodi tangentium inversae exampla», 11 ноября 1675 г.).
• Готфрид Вильгельм Лейбниц, «Новый метод для самых больших и маленьких...», 1684 г. (латинский оригинал) (английский перевод)
• Исаак Ньютон, «Книга мусора Ньютона (Часть 3) (нормализованная версия)»: запись от 16 мая 1666 г. (Проект Ньютона)
• Исаак Ньютон, «De Analysi per Equationes Numero Terminorum Infinitas (О квадратуре кривых и анализе с помощью уравнений бесконечного числа членов)» , в: Два трактата сэра Исаака Ньютона , Джеймс Беттенхэм, 1745.