Логарифм

Графики функций логарифмирования с тремя часто используемыми основаниями. Особые точки log _b   b = 1 обозначены пунктирными линиями, а все кривые пересекаются в log _b 1 = 0 .

В математике логарифм функцией , является обратной возведению в степень . Это означает, что логарифм числа x по основанию   b является показателем степени , до которой b, необходимо возвести чтобы получить x . Например, поскольку 1000 = 10 ³ , основание логарифма  $10$ из 1000 равно 3 или log ₁₀ (1000) = 3 . Логарифм от x по основанию   b обозначается как log _b ( x ) или без круглых скобок, log _b   x . Когда база понятна из контекста или неактуальна, иногда пишут log x .

Логарифм по основанию 10 называется десятичным или десятичным логарифмом и обычно используется в науке и технике. натурального e логарифма лежит число ; ≈ 2,718 В основе его использование широко распространено в математике и физике из-за его очень простой производной . Двоичный 2 логарифм использует базу и часто используется в информатике .

Логарифмы были введены Джоном Непером в 1614 году как средство упрощения вычислений. Они были быстро приняты мореплавателями , учеными, инженерами, геодезистами и другими людьми для облегчения выполнения высокоточных вычислений. Используя таблицы логарифмов , утомительные шаги многозначного умножения можно заменить поиском в таблице и более простым сложением. Это возможно, поскольку логарифм произведения представляет собой сумму логарифмов множителей: $$\log _{b}(xy)=\log _{b}x+\log _{b}y,$$при условии, что b , x и y положительны и b ≠ 1 . , Логарифмическая линейка также основанная на логарифмах, позволяет производить быстрые вычисления без таблиц, но с меньшей точностью. Современное понятие логарифмов исходит от Леонарда Эйлера , который связал их с показательной функцией в 18 веке, а также ввел букву е в качестве основания натуральных логарифмов.

Логарифмические шкалы сводят большие величины к меньшим. Например, децибел (дБ) — это единица измерения отношения в виде логарифмов которых является звуковое давление , в основном для мощности и амплитуды сигнала ( частым примером ). В химии pH — это логарифмическая мера кислотности водного раствора . Логарифмы являются обычным явлением в научных формулах , а также при измерении сложности алгоритмов и геометрических объектов, называемых фракталами . Они помогают описывать частот соотношения музыкальных интервалов , появляются в формулах для подсчета простых чисел или аппроксимации факториалов , служат основой для некоторых моделей в психофизике и могут помочь в судебно-медицинской экспертизе .

Концепция логарифма как обратной возведения в степень распространяется и на другие математические структуры. Однако в общих условиях логарифм имеет тенденцию быть многозначной функцией. Например, комплексный логарифм является многозначной обратной комплексной показательной функции. Точно так же дискретный логарифм является многозначной обратной экспоненциальной функцией в конечных группах; он находит применение в криптографии с открытым ключом .

Мотивация

График ( логарифма по основанию 2 пересекает x ось в точке x = 1 и проходит через точки 2, 1) , (4, 2) и (8, 3) , изображая, например, log ₂ (8) = 3 и 2 ³ = 8 . График подбирается сколь угодно близко к оси Y , но не пересекает ее .

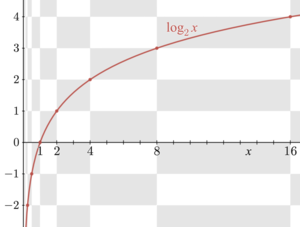
Сложение , умножение и возведение в степень — три наиболее фундаментальные арифметические операции. Обратное действие сложения — вычитание, а обратное умножению — деление . Аналогично, логарифм — это операция, обратная возведению в степень . Возведение в степень - это когда число b , основание , возводится в определенную степень y , показатель степени , чтобы дать значение x ; это обозначается $$b^{y}=x.$$Например, возведение 2 в степень 3 дает 8 : $2^{3}=8.$

Логарифм по основанию b — это обратная операция, которая обеспечивает выход y из входа x . То есть, $y=\log _{b}x$ эквивалентно $x=b^{y}$ если b — положительное действительное число . (Если b не является положительным действительным числом, можно определить и возведение в степень, и логарифм, но они могут принимать несколько значений, что значительно усложняет определения.)

Одной из главных исторических мотиваций введения логарифмов является формула $$\log _{b}(xy)=\log _{b}x+\log _{b}y,$$с помощью которых таблицы логарифмов позволяют свести умножение и деление к сложению и вычитанию, что было большим подспорьем для вычислений до изобретения компьютеров.

Определение

Учитывая положительное действительное число b такое, что b ≠ 1 , логарифм положительного действительного числа x по основанию b — это показатель степени, на которую b, необходимо увеличить чтобы получить x . Другими словами, логарифм x по основанию b — это уникальное действительное число y такое, что $b^{y}=x$.

Логарифм обозначается « log _b   x » (произносится как «логарифм от x по основанию b », « по основанию b логарифм от x » или чаще всего «логарифм по основанию b от x »).

Эквивалентное и более краткое определение состоит в том, что функция log _b является функцией, обратной функции $x\mapsto b^{x}$.

Примеры

• log ₂ 16 = 4 , так как 2 ⁴ = 2 × 2 × 2 × 2 = 16 .
• Логарифмы также могут быть отрицательными: ${\textstyle \log _{2}\!{\frac {1}{2}}=-1}$ с ${\textstyle 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.}$
• log ₁₀ 150 составляет примерно 2,176, что лежит между 2 и 3, точно так же, как 150 лежит между 10. ² = 100 и 10 ³ = 1000 .
• Для любой базы log b b _b   = 1 и log _b 1 = 0 , поскольку b ¹ = б и б ⁰ = 1 соответственно.

Логарифмические тождества

Основная статья: Список логарифмических тождеств

Несколько важных формул, иногда называемых логарифмическими тождествами или логарифмическими законами , связывают логарифмы друг с другом.

Произведение, частное, степень и корень

Логарифм произведения — это сумма логарифмов умножаемых чисел; логарифм отношения двух чисел — это разность логарифмов. Логарифм p -й степени числа в p   раз больше логарифма самого числа; логарифм корня p -й степени равен логарифму числа, разделенного на p . В следующей таблице перечислены эти личности с примерами. Каждое из тождеств можно получить после подстановки определений логарифмов. $x=b^{\,\log _{b}x}$ или $y=b^{\,\log _{b}y}$ в левых сторонах.

	Формула	Пример
Продукт	${\textstyle \log _{b}(xy)=\log _{b}x+\log _{b}y}$	${\textstyle \log _{3}243=\log _{3}(9\cdot 27)=\log _{3}9+\log _{3}27=2+3=5}$
частное	${\textstyle \log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y}$	${\textstyle \log _{2}16=\log _{2}\!{\frac {64}{4}}=\log _{2}64-\log _{2}4=6-2=4}$
Власть	${\textstyle \log _{b}\left(x^{p}\right)=p\log _{b}x}$	${\textstyle \log _{2}64=\log _{2}\left(2^{6}\right)=6\log _{2}2=6}$
Корень	${\textstyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}}$	${\textstyle \log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

Смена базы

Логарифм log _b   x можно вычислить из логарифмов x и b по произвольному основанию k, используя следующую формулу: $$\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.$$

Типичные научные калькуляторы вычисляют логарифмы по основаниям 10 и e . Логарифмы по любой базе b можно определить, используя любой из этих двух логарифмов по предыдущей формуле: $$\log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.$$

Учитывая число x и его логарифм y = log _b   x до неизвестного основания b , основание определяется следующим образом:

$$b=x^{\frac {1}{y}},$$

в чем можно убедиться, взяв определяющее уравнение $x=b^{\,\log _{b}x}=b^{y}$ во власть ${\tfrac {1}{y}}.$

Особые базы

Наложенные графики логарифма по основаниям ⁠ 1/2 е и ⁠ 2 ,

Среди всех вариантов основы особенно распространены три. Это b = 10 , b = e ( иррациональная математическая константа e ≈ 2,71828183 ) и b = 2 ( двоичный логарифм ). В математическом анализе логарифм по основанию e широко распространен из-за аналитических свойств, объясненных ниже. С другой стороны, по основанию 10 логарифмы ( десятичный логарифм ) легко использовать для ручных вычислений в десятичной системе счисления:

$$\ \log _{10}(\ 10\ x\ )\ =\ \log _{10}10\ +\ \log _{10}x\ =\ 1\ +\ \log _{10}x~.$$

Таким образом, log ₁₀ ( x ) связан с количеством десятичных цифр положительного целого числа x : количество цифр — это наименьшее целое число, строго большее, чем log ₁₀ ( x ) . Например, log ₁₀ (5986) равен примерно 3,78. Следующее целое число над ним — 4, что соответствует количеству цифр 5986. В теории информации используются как натуральный логарифм, так и двоичный логарифм , что соответствует использованию натуральных чисел или битов в качестве фундаментальных единиц информации соответственно. Двоичные логарифмы также используются в информатике , где двоичная система распространена повсеместно; в теории музыки , где отношение высоты звука равное двум ( октава ) является повсеместным, а число центов между любыми двумя высотами звука представляет собой масштабированную версию двоичного логарифма или log 2, умноженного на 1200, отношения высоты звука (то есть 100 центов на полутон в обычной равной темперации ) или, что эквивалентно, логарифмическая база 2 ^1/1200 ; а в фотографии логарифмы с измененным масштабом по основанию 2 используются для измерения значений экспозиции , уровней освещенности , времени экспозиции объектива , апертуры и светочувствительности пленки в «стопах».

Аббревиатура log x часто используется, когда предполагаемую базу можно определить на основе контекста или дисциплины или когда база неопределенна или несущественна. Десятичные логарифмы (по основанию 10), исторически используемые в таблицах логарифмов и логарифмических линейках, являются основным инструментом для измерений и вычислений во многих областях науки и техники; в этих контекстах log x по-прежнему часто означает логарифм по основанию десяти. В математике log x обычно означает натуральный логарифм (по основанию e ). В информатике и теории информации журнал часто относится к двоичным логарифмам (основание 2). В следующей таблице перечислены общие обозначения логарифмов по этим основаниям. В столбце «Обозначение ISO» перечислены обозначения, предложенные Международной организацией по стандартизации .

База б	Имя журнала b   x	Обозначение ISO	Другие обозначения
2	двоичный логарифм	фунт х	лд х , журнал х , lg х , журнал 2   х
и	натуральный логарифм	пер х	журнал х , журнал е   х
10	десятичный логарифм	LG х	журнал х , журнал 10   х
б	логарифм по основанию b	журнал б   х

История

Основная статья: История логарифмов

В истории логарифмов в Европе XVII века была открыта новая функция , которая расширила сферу анализа за пределы алгебраических методов. Метод логарифмов был публично предложен Джоном Нейпиром в 1614 году в книге под названием Mirifici Logarithmorum Canonis Descriptio ( «Описание чудесного канона логарифмов »). До изобретения Непера существовали и другие методы аналогичного масштаба, такие как простафаферез или использование таблиц прогрессий, широко разработанные Йостом Бюрги около 1600 года. Нэпьер ввел термин для логарифма на среднелатинском языке «логарифм», происходящий от греческого слова, буквально означающего «число-отношение», от logos «пропорция, соотношение, слово» + arithmos «число».

Десятый логарифм числа — это показатель той степени десяти, которая равна числу. Утверждение о том, что число требует такого количества цифр, является грубым намеком на десятичный логарифм, который Архимед называл «порядком числа». Первые настоящие логарифмы представляли собой эвристические методы, позволяющие превратить умножение в сложение, что облегчило быстрые вычисления. В некоторых из этих методов использовались таблицы, полученные на основе тригонометрических тождеств. Такие методы называются простафаэрезами .

Изобретение функции, ныне известной как натуральный логарифм, началось как попытка выполнить квадратуру прямоугольной гиперболы Грегуаром де Сен-Винсентом , бельгийским иезуитом, проживающим в Праге. Архимед написал «Квадратуру параболы» в третьем веке до нашей эры, но квадратура гиперболы ускользала от всех попыток, пока Сен-Винсент не опубликовал свои результаты в 1647 году. Связь, которую логарифм обеспечивает между геометрической прогрессией в ее аргументе и арифметической прогрессией. значений, побудило А. А. де Сараса установить связь квадратуры Сен-Венсана и традиции логарифмов в простаферезе , что привело к появлению термина «гиперболический логарифм», синонима натурального логарифма. Вскоре новую функцию оценили Христиан Гюйгенс и Джеймс Грегори . Обозначение Logy было принято Лейбницем в 1675 году. а в следующем году подключил его к интегралу ${\textstyle \int {\frac {dy}{y}}.}$

До того, как Эйлер разработал свою современную концепцию комплексных натуральных логарифмов, Роджер Коутс получил почти эквивалентный результат, когда в 1714 году показал, что $$\log(\cos \theta +i\sin \theta )=i\theta .$$

Таблицы логарифмов, логарифмические линейки и исторические приложения

1797 года. в Британской энциклопедии Объяснение логарифмов

Упрощая сложные вычисления до того, как стали доступны калькуляторы и компьютеры, логарифмы способствовали развитию науки, особенно астрономии . Они сыграли решающую роль в развитии геодезии , небесной навигации и других областях. Пьер-Симон Лаплас называл логарифмы.

«...[замечательное изобретение, которое, сокращая до нескольких дней многомесячный труд, удваивает жизнь астронома и избавляет его от ошибок и отвращения, неотделимых от долгих вычислений».

Поскольку функция f ( x ) = b ^х является обратной функцией log _b   x , ее называют антилогарифмом . В настоящее время эту функцию чаще называют показательной функцией .

Таблицы журналов

Ключевым инструментом, позволившим практическое использование логарифмов, была таблица логарифмов . Первая такая таблица была составлена ​​Генри Бриггсом в 1617 году, сразу после изобретения Непера, но с новаторским подходом: в качестве основы использовалось число 10. Первая таблица Бриггса содержала десятичные логарифмы всех целых чисел в диапазоне от 1 до 1000 с точностью до 14 цифр. В дальнейшем были написаны таблицы с увеличивающейся областью применения. В этих таблицах перечислены значения log ₁₀   x для любого числа x в определенном диапазоне и с определенной точностью. Логарифмы с основанием 10 повсеместно использовались для вычислений, отсюда и название «десятигранный логарифм», поскольку числа, которые отличаются в 10 раз, имеют логарифмы, которые отличаются целыми числами. Десятый логарифм x можно разделить на целую и дробную часть , известную как характеристика и мантисса . В таблицы логарифмов необходимо включать только мантиссу, так как характеристику легко определить, посчитав цифры от десятичной точки. Характеристика 10 · x равна единице плюс характеристика x , и их мантиссы одинаковы. Таким образом, используя трехзначную таблицу журналов, логарифм 3542 аппроксимируется выражением

$$\log _{10}3542=\log _{10}(1000\cdot 3.542)=3+\log _{10}3.542\approx 3+\log _{10}3.54$$

Большую точность можно получить интерполяцией :

$$\log _{10}3542\approx 3+\log _{10}3.54+0.2(\log _{10}3.55-\log _{10}3.54)$$

Стоимость 10 ^х можно определить обратным поиском в той же таблице, поскольку логарифм является монотонной функцией .

Вычисления

Произведение и частное двух положительных чисел c и d обычно рассчитывалось как сумма и разность их логарифмов. Произведение cd или частное c / d получено в результате поиска антилогарифма суммы или разности с помощью той же таблицы:

$$cd=10^{\,\log _{10}c}\,10^{\,\log _{10}d}=10^{\,\log _{10}c\,+\,\log _{10}d}$$и $${\frac {c}{d}}=cd^{-1}=10^{\,\log _{10}c\,-\,\log _{10}d}.$$

Для ручных вычислений, требующих сколько-нибудь заметной точности, поиск двух логарифмов, вычисление их суммы или разности и поиск антилогарифма происходит намного быстрее, чем выполнение умножения более ранними методами, такими как простафаферез , который основан на тригонометрических тождествах .

Вычисления степеней и корней сводятся к умножению или делению и поиску по $$c^{d}=\left(10^{\,\log _{10}c}\right)^{d}=10^{\,d\log _{10}c}$$

и $${\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.$$

Тригонометрические расчеты облегчались таблицами, содержащими десятичные логарифмы тригонометрических функций .

Правила слайдов

Еще одним важным приложением была логарифмическая линейка — пара логарифмически разделенных шкал, используемых для вычислений. Нескользящая логарифмическая шкала, правило Гюнтера , была изобретена вскоре после изобретения Нейпира. Уильям Отред усовершенствовал его, создав логарифмическую линейку — пару логарифмических шкал, подвижных относительно друг друга. Числа располагаются на скользящих шкалах на расстояниях, пропорциональных разностям их логарифмов. Соответствующим сдвигом верхней шкалы можно считать механическое сложение логарифмов, как показано здесь:

Схематическое изображение логарифмической линейки. Начиная с 2 на нижней шкале, прибавьте расстояние к 3 на верхней шкале, чтобы получить произведение 6. Логарифмическая линейка работает, потому что она отмечена так, что расстояние от 1 до x пропорционально логарифму x .

Например, прибавление расстояния от 1 до 2 на нижней шкале к расстоянию от 1 до 3 на верхней шкале дает произведение 6, которое считывается в нижней части. Логарифмическая линейка была важным расчетным инструментом для инженеров и ученых до 1970-х годов, поскольку она позволяла, за счет точности, выполнять гораздо более быстрые вычисления, чем методы, основанные на таблицах.

Аналитические свойства

Более глубокое изучение логарифмов требует понятия функции . Функция — это правило, которое по одному числу дает другое число. Примером может служить функция, производящая x -ю степень числа b из любого действительного числа x , где основание b является фиксированным числом. Эта функция записывается как f ( x ) = b ^х . Когда b положительно и не равно 1, ниже мы покажем, что f обратимо, если рассматривать его как функцию от действительных чисел к положительным действительным числам.

Существование

Пусть b — положительное действительное число, не равное 1, и пусть f ( x ) = b ^х .

Стандартный результат реального анализа состоит в том, что любая непрерывная строго монотонная функция является биективной между своей областью определения и областью значений. Этот факт следует из теоремы о промежуточном значении . Теперь f ( строго возрастает при b > 1 ) или строго убывает (при 0 < b < 1 ), непрерывен, имеет область определения $\mathbb {R}$и имеет диапазон $\mathbb {R} _{>0}$. Следовательно, f является биекцией из $\mathbb {R}$ к $\mathbb {R} _{>0}$. Другими словами, для каждого положительного действительного числа y существует ровно одно действительное число x такое, что $b^{x}=y$.

Мы позволяем $\log _{b}\colon \mathbb {R} _{>0}\to \mathbb {R}$ обозначают обратную функцию f . То есть log _by   — это уникальное действительное число x такое, что $b^{x}=y$. Эта функция называется по основанию b функцией логарифма или логарифмической функцией (или просто логарифмом ).

Характеристика по формуле продукта

Функцию log _b   x можно также существенно охарактеризовать формулой произведения $$\log _{b}(xy)=\log _{b}x+\log _{b}y.$$Точнее, логарифм по любому основанию b > 1 — это единственная возрастающая функция f от положительных действительных чисел к действительным числам, удовлетворяющая f ( b ) = 1 и $$f(xy)=f(x)+f(y).$$

График функции логарифма

График функции логарифма log _b ( x ) (синий) получается путем отражения графика функции b ^х (красный) на диагональной линии ( x = y ).

Как обсуждалось выше, функция log _b является обратной экспоненциальной функции. $x\mapsto b^{x}$. Поэтому их графики соответствуют друг другу при обмене координатами x и y (или при отражении от диагональной линии x = y ), как показано справа: точка ( t , u = b ^т ) на графике f дает точку ( u , t = log _b   u ) на графике логарифма и наоборот. Как следствие, log _b ( x ) расходится до бесконечности (становится больше любого заданного числа), если x растет до бесконечности, при условии, что b больше единицы. В этом случае log _b ( x ) — возрастающая функция . Для b < 1 log b ₍ x ) вместо этого стремится к минус бесконечности. Когда x приближается к нулю, log _b   x стремится к минус бесконечности для b > 1 (плюс бесконечности для b < 1 соответственно).

Производная и первообразная

График натурального логарифма (зеленый) и его тангенса при x = 1,5 (черный)

Аналитические свойства функций переходят к обратным к ним. Таким образом, поскольку f ( x ) = b ^х является непрерывной и дифференцируемой функцией , так же как log _by   и . Грубо говоря, непрерывная функция является дифференцируемой, если ее график не имеет острых «углов». , поскольку производная f Более того ( x ) равна ln( b ) b ^х По свойствам экспоненциальной функции цепное правило подразумевает, что производная log _b   x определяется выражением $${\frac {d}{dx}}\log _{b}x={\frac {1}{x\ln b}}.$$То есть наклон касательной , касающейся графика логарифма по основанию b в точке ( x , log _b ( x )) равен 1/( x ln( b )) .

Производная ln( x ) равна 1/ x ; это означает, что ln( x ) является уникальной первообразной 1 / x , которая имеет значение 0 для x = 1 . Именно эта очень простая формула побудила квалифицировать натуральный логарифм как «натуральный»; это также одна из основных причин важности константы e .

Производная с обобщенным функциональным аргументом f ( x ) равна $${\frac {d}{dx}}\ln f(x)={\frac {f'(x)}{f(x)}}.$$ правой части называется логарифмической производной f . Частное в Вычисление f' ( x ) с помощью производной ln( f ( x )) известно как логарифмическое дифференцирование . Первообразная натурального логарифма ln( x ) : $$\int \ln(x)\,dx=x\ln(x)-x+C.$$Связанные формулы , такие как первообразные логарифмов по другим основаниям, могут быть получены из этого уравнения с помощью замены оснований.

Интегральное представление натурального логарифма

Натуральный логарифм t ( — это заштрихованная область под графиком функции f ) x ) = 1/ x (обратная величина x .

Натуральный логарифм t : можно определить как интеграл определенный

$$\ln t=\int _{1}^{t}{\frac {1}{x}}\,dx.$$Преимущество этого определения состоит в том, что оно не опирается на показательную функцию или какие-либо тригонометрические функции; определение дано в терминах интеграла от простой обратной величины. В качестве интеграла ln( t ) равна площади между осью x и графиком функции 1/ x в диапазоне от x = 1 до x = t . Это следствие фундаментальной теоремы исчисления и того факта, что производная ln( x ) равна 1/ x . Из этого определения можно вывести формулы произведения и степенного логарифма. Например, формула произведения ln( tu ) = ln( t ) + ln( u ) выводится как:

$$\ln(tu)=\int _{1}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(1)}{=}}\int _{1}^{t}{\frac {1}{x}}\,dx+\int _{t}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(2)}{=}}\ln(t)+\int _{1}^{u}{\frac {1}{w}}\,dw=\ln(t)+\ln(u).$$

Равенство (1) разбивает интеграл на две части, а равенство (2) представляет собой замену переменной ( w = x / t ). На иллюстрации ниже разделение соответствует разделению области на желтую и синюю части. Изменение масштаба левой синей области по вертикали на коэффициент t и уменьшение ее на тот же коэффициент по горизонтали не меняет ее размера. Переместив его соответствующим образом, область снова соответствует графику функции f ( x ) = 1/ x . Следовательно, левая синяя область, которая является интегралом от f ( x ) от t до tu, такая же, как интеграл от 1 до u . Это подтверждает равенство (2) более геометрическим доказательством.

Наглядное доказательство формулы произведения натурального логарифма.

Формула степени ln( t ^р ) = r ln( t ) может быть получено аналогичным образом:

$$\ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{w^{r}}}\left(rw^{r-1}\,dw\right)=r\int _{1}^{t}{\frac {1}{w}}\,dw=r\ln(t).$$Второе равенство использует замену переменных ( интегрирование подстановкой ), w = x ^{1/ р} .

Сумма по обратным натуральным числам, $$1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},$$называется гармоническим рядом . Он тесно связан с натуральным логарифмом : поскольку n стремится к бесконечности , разница $$\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),$$сходится (т.е. становится сколь угодно близко) к числу, известному как константа Эйлера – Маскерони γ = 0,5772... . Это соотношение помогает анализировать производительность таких алгоритмов, как быстрая сортировка .

Трансцендентность логарифма

Действительные числа , не являющиеся алгебраическими , называются трансцендентными ; например, π и e , но такими числами являются ${\sqrt {2-{\sqrt {3}}}}$ нет. Почти все действительные числа трансцендентны. Логарифм является примером трансцендентной функции . Теорема Гельфонда – Шнайдера утверждает, что логарифмы обычно принимают трансцендентные, то есть «трудные» значения.

Расчет

Клавиши логарифма (LOG для основания 10 и LN для основания e ) на TI-83 Plus . графическом калькуляторе

В некоторых случаях логарифмы легко вычислить, например, log ₁₀ (1000) = 3 . В общем, логарифмы можно вычислять с использованием степенного ряда или среднего арифметико-геометрического значения или получать их из предварительно рассчитанной таблицы логарифмов , обеспечивающей фиксированную точность. Метод Ньютона , итерационный метод приближенного решения уравнений, также может использоваться для вычисления логарифма, поскольку его обратная функция, показательная функция, может быть вычислена эффективно. Используя справочные таблицы, CORDIC -подобные методы можно использовать для вычисления логарифмов, используя только операции сложения и битового сдвига . Более того, алгоритм двоичного логарифма вычисляет lb( x ) рекурсивно , основываясь на повторяющихся возведениях в квадрат x , используя соотношение $$\log _{2}\left(x^{2}\right)=2\log _{2}|x|.$$

Силовая серия

Серия Тейлора

Ряд Тейлора ln( z ) с центром в z = 1 . На анимации показаны первые 10 приближений, а также 99-е и 100-е. Приближения не сходятся дальше, чем на расстоянии 1 от центра.

Для любого действительного числа z , удовлетворяющего условию 0 < z ≤ 2 , справедлива следующая формула:

$${\begin{aligned}\ln(z)&={\frac {(z-1)^{1}}{1}}-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}}-{\frac {(z-1)^{4}}{4}}+\cdots \\&=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {(z-1)^{k}}{k}}.\end{aligned}}$$

Приравнивание функции ln( z ) к этой бесконечной сумме ( ряду ) — это сокращение, говорящее о том, что функция может быть приближена к более и более точному значению с помощью следующих выражений (известных как частичные суммы ):

$$(z-1),\ \ (z-1)-{\frac {(z-1)^{2}}{2}},\ \ (z-1)-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}},\ \ldots$$

Например, при z = 1,5 третье приближение дает 0,4167 , что примерно на 0,011 больше, чем ln(1,5) = 0,405465 , а девятое приближение дает 0,40553 , что всего лишь примерно на 0,0001 больше. я n- частичная сумма может аппроксимировать ln( z ) с произвольной точностью, при условии, что количество слагаемых n достаточно велико.

В элементарном исчислении говорят, что ряд сходится к функции ln( z ) , а эта функция является пределом ряда. Это ряд Тейлора натурального логарифма в точке z = 1 . Ряд Тейлора для ln( z ) обеспечивает особенно полезное приближение к ln(1 + z ), когда z мало, | г | < 1 , с тех пор $$\ln(1+z)=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}-\cdots \approx z.$$

Например, при z = 0,1 аппроксимация первого порядка дает ln(1,1) ≈ 0,1 , что менее чем на 5% отличается от правильного значения 0,0953 .

Обратный гиперболический тангенс

Другой ряд основан на обратной функции гиперболического тангенса : $$\ln(z)=2\cdot \operatorname {artanh} \,{\frac {z-1}{z+1}}=2\left({\frac {z-1}{z+1}}+{\frac {1}{3}}{\left({\frac {z-1}{z+1}}\right)}^{3}+{\frac {1}{5}}{\left({\frac {z-1}{z+1}}\right)}^{5}+\cdots \right),$$для любого действительного числа z > 0 . Используя сигма-нотацию , это также записывается как $$\ln(z)=2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {z-1}{z+1}}\right)^{2k+1}.$$Этот ряд можно получить из приведенного выше ряда Тейлора. Он сходится быстрее, чем ряд Тейлора, особенно если z близко к 1. Например, для z = 1,5 первые три члена второго ряда аппроксимируют ln(1,5) с ошибкой около 3 × 10. ⁻⁶ . Быстрой сходимостью при z, близком к 1, можно воспользоваться следующим образом: задав приближение малой точности y ≈ ln( z ) и положив $$A={\frac {z}{\exp(y)}},$$логарифм z равен: $$\ln(z)=y+\ln(A).$$Чем лучше начальное приближение y , тем ближе A к 1, поэтому его логарифм можно вычислить эффективно. A можно вычислить с помощью экспоненциального ряда , который быстро сходится при условии, что y не слишком велико. Вычисление логарифма больших значений z можно свести к меньшим значениям z, записав z = a · 10. ^б , так что ln( z ) = ln( a ) + b · ln(10) .

Близко связанный метод можно использовать для вычисления логарифма целых чисел. положить $\textstyle z={\frac {n+1}{n}}$ в приведенной выше серии следует, что: $$\ln(n+1)=\ln(n)+2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {1}{2n+1}}\right)^{2k+1}.$$ логарифм большого целого числа n Если известен , то этот ряд дает быстро сходящийся ряд для log( n +1) со сходимости скоростью ${\textstyle \left({\frac {1}{2n+1}}\right)^{2}}$.

Среднее арифметико-геометрическое приближение

Среднее арифметико -геометрическое дает высокоточные аппроксимации натурального логарифма . Сасаки и Канада показали в 1982 году, что он особенно быстр для точности от 400 до 1000 десятичных знаков, в то время как методы рядов Тейлора обычно работают быстрее, когда требуется меньшая точность. В их работе ln( x ) аппроксимируется с точностью до 2 ^{− п} (или p точных битов) по следующей формуле (принадлежащей Карлу Фридриху Гауссу ):

$$\ln(x)\approx {\frac {\pi }{2\,\mathrm {M} \!\left(1,2^{2-m}/x\right)}}-m\ln(2).$$

Здесь M( x , y ) обозначает среднее арифметико- геометрическое x и y . Его получают путем многократного вычисления среднего ( x + y )/2 ( среднего арифметического ) и ${\textstyle {\sqrt {xy}}}$ ( среднее геометрическое ) x и y , тогда пусть эти два числа станут следующими x и y . Эти два числа быстро сходятся к общему пределу, который является значением M( x , y ) . m выбирается таким, что

$$x\,2^{m}>2^{p/2}.\,$$

для обеспечения необходимой точности. Увеличение m приводит к тому, что вычисление M( x , y ) занимает больше шагов (исходные x и y находятся дальше друг от друга, поэтому для сходимости требуется больше шагов), но дает большую точность. Константы π и ln(2) можно вычислить с помощью быстро сходящихся рядов.

Алгоритм Фейнмана

Работая в Национальной лаборатории Лос-Аламоса над Манхэттенским проектом , Ричард Фейнман разработал алгоритм побитовой обработки для вычисления логарифма, который похож на деление в столбики и позже использовался в Соединительной машине . Алгоритм основан на том факте, что каждое действительное число x, где 1 < x < 2, может быть представлено как произведение различных множителей вида 1 + 2. ^{- к} . Алгоритм последовательно строит этот продукт P , начиная с P = 1 и k = 1 : если P · (1 + 2 ^{- к} ) < x меняется , то P на P · (1 + 2 ^{- к} ) . Затем оно увеличивается $k$ по одному независимо. Алгоритм останавливается, когда k становится достаточно большим, чтобы обеспечить желаемую точность. Поскольку log( x ) представляет собой сумму членов вида log(1 + 2 ^{- к} ), соответствующие тем k , для которых множитель 1 + 2 ^{- к} был включен в продукт P , log( x ) можно вычислить простым сложением, используя таблицу log(1 + 2 ^{- к} ) для всех k . Для таблицы логарифмов можно использовать любое основание.

Приложения

Раковина наутилуса с изображением логарифмической спирали.

Логарифмы имеют множество приложений внутри и за пределами математики. Некоторые из этих явлений связаны с понятием масштабной инвариантности . Например, каждая камера раковины наутилуса является приблизительной копией следующей, увеличенной в постоянный коэффициент. Это приводит к возникновению логарифмической спирали . Закон Бенфорда о распределении старших цифр также можно объяснить масштабной инвариантностью. Логарифмы также связаны с самоподобием . Например, логарифмы появляются при анализе алгоритмов, которые решают проблему путем разделения ее на две похожие меньшие проблемы и исправления их решений. На логарифмах основаны и размеры самоподобных геометрических фигур, то есть фигур, части которых напоминают общую картину. Логарифмические шкалы полезны для количественной оценки относительного изменения значения, а не его абсолютной разницы. Более того, поскольку логарифмическая функция log( x ) растет очень медленно при больших x , логарифмические масштабы используются для сжатия крупномасштабных научных данных. Логарифмы также встречаются во многих научных формулах, таких как уравнение ракеты Циолковского , уравнение Фенске или уравнение Нернста .

Логарифмическая шкала

Основная статья: Логарифмическая шкала

Логарифмическая диаграмма, показывающая стоимость одной золотой марки в папьермарках во время немецкой гиперинфляции в 1920-х годах.

Научные величины часто выражаются в виде логарифмов других величин в логарифмической шкале . Например, децибел — это единица измерения , связанная с логарифмического масштаба величинами . Он основан на десятичном мощности десятичном десятичном логарифме коэффициента или в 20 раз большем десятичном логарифме коэффициента трансформации . Он используется для количественной оценки затухания или усиления электрических сигналов. для описания уровней мощности звуков в акустике , и поглощение света в области спектрометрии и оптики . Отношение сигнал /шум, характеризующее количество нежелательного шума по отношению к (значимому) сигналу, также измеряется в децибелах. Аналогичным образом, пиковое отношение сигнал/шум обычно используется для оценки качества звука и методов сжатия изображения с использованием логарифма.

Силу землетрясения измеряют путем десятеричного логарифма энергии, излучаемой при землетрясении. Это используется в моментной шкале магнитуд или шкале магнитуд Рихтера . Например, землетрясение магнитудой 5,0 происходит 32 раза (10 ^1.5 ) и версия 6.0 выпускается 1000 раз (10 ³ ) энергия 4,0. Видимая звездная величина измеряет яркость звезд логарифмически. В химии отрицательный знак десятичного логарифма, десятичная дробь. кологарифм , обозначается буквой р. Например, pH — это десятичный колорарифм активности ионов гидроксония водорода форма ( ионов H ⁺
набрать воды). Активность ионов гидроксония в нейтральной воде составляет 10 ⁻⁷  моль · л ⁻¹ , следовательно, pH равен 7. Уксус обычно имеет pH около 3. Разница в 4 соответствует соотношению 10 ⁴ активности, то есть активность ионов гидроксония уксуса составляет около 10 ⁻³ моль · л ⁻¹ .

Полулогарифмические (логарифмически-линейные) графики используют концепцию логарифмического масштаба для визуализации: одна ось, обычно вертикальная, масштабируется логарифмически. Например, на диаграмме справа резкий рост с 1 миллиона до 1 триллиона сжимается до того же места (по вертикальной оси), что и рост с 1 до 1 миллиона. В таких графиках показательные функции вида f ( x ) = a · b ^х выглядят как прямые линии с наклоном, равным логарифму b . Логарифмические графики масштабируют обе оси логарифмически, что приводит к появлению функций вида f ( x ) = a · x ^к изображать в виде прямых линий с наклоном, равным показателю степени k . Это применяется при визуализации и анализе степенных законов .

Психология

Логарифмы встречаются в нескольких законах, описывающих человеческое восприятие : Закон Хика предполагает логарифмическую зависимость между временем, которое люди тратят на выбор альтернативы, и количеством имеющихся у них вариантов выбора. Закон Фиттса предсказывает, что время, необходимое для быстрого перемещения к целевой области, является логарифмической функцией расстояния до цели и ее размера. В психофизике закон Вебера -Фехнера предлагает логарифмическую связь между стимулом и ощущением , например, фактический и воспринимаемый вес предмета, который несет человек. (Однако этот «закон» менее реалистичен, чем более поздние модели, такие как степенной закон Стивенса . )

Психологические исследования показали, что люди с небольшим математическим образованием склонны оценивать величины логарифмически, то есть располагать число на неотмеченной линии в соответствии с его логарифмом, так что 10 располагается так же близко к 100, как 100 к 1000. Повышение уровня образования меняет это положение. к линейной оценке (расположение 1000 в 10 раз дальше) в некоторых случаях, тогда как логарифмы используются, когда числа, которые нужно нанести на график, трудно построить линейно.

Теория вероятностей и статистика

Три функции плотности вероятности (PDF) случайных величин с логнормальным распределением. Параметр местоположения , который равен нулю для всех трех показанных PDF-файлов, является средним значением логарифма случайной величины, а не средним значением самой переменной.

Распределение первых цифр (в %, красные столбцы) среди населения 237 стран мира. Черные точки указывают на распределение, предсказанное законом Бенфорда.

Логарифмы возникают в теории вероятностей : закон больших чисел диктует, что для честной монеты , когда количество подбрасываний монеты увеличивается до бесконечности, наблюдаемая доля орлов приближается к половине . Колебания этой доли примерно на половину описываются законом повторного логарифма .

Логарифмы также встречаются в логнормальных распределениях . Когда логарифм случайной величины имеет нормальное распределение , говорят, что переменная имеет логнормальное распределение. Логнормальные распределения встречаются во многих областях, где переменная формируется как произведение многих независимых положительных случайных величин, например, при изучении турбулентности.

Логарифмы используются для оценки максимального правдоподобия параметрических статистических моделей . Для такой модели функция правдоподобия зависит как минимум от одного параметра , который необходимо оценить. Максимум функции правдоподобия возникает при том же значении параметра, что и максимум логарифма правдоподобия («логарифм правдоподобия »), поскольку логарифм является возрастающей функцией. Логарифмическое правдоподобие легче максимизировать, особенно для умноженных правдоподобий для независимых случайных величин.

Закон Бенфорда описывает появление цифр во многих наборах данных , например, в высотах зданий. Согласно закону Бенфорда, вероятность того, что первая десятичная цифра элемента в выборке данных равна d (от 1 до 9), равна log ₁₀ ( d + 1) − log ₁₀ ( d ) . независимо от единицы измерения Таким образом, можно ожидать, что около 30% данных будут иметь 1 в качестве первой цифры, 18% начинаются с 2 и т. д. Аудиторы изучают отклонения от закона Бенфорда, чтобы обнаружить мошенничество в бухгалтерском учете.

— Преобразование логарифма это тип преобразования данных, используемый для приближения эмпирического распределения к предполагаемому.

Вычислительная сложность

Анализ алгоритмов — это раздел информатики , изучающий производительность алгоритмов (компьютерных программ , решающих определенную задачу). Логарифмы полезны для описания алгоритмов, которые делят задачу на более мелкие и объединяют решения подзадач.

Например, чтобы найти число в отсортированном списке, алгоритм двоичного поиска проверяет среднюю запись и переходит к половине до или после средней записи, если число все еще не найдено. Этот алгоритм требует в среднем log ₂ ( N ) сравнений, где N — длина списка. Аналогично, алгоритм сортировки слиянием сортирует несортированный список, разделяя список на половины и сначала сортируя их, прежде чем объединять результаты. Алгоритмы сортировки слиянием обычно требуют времени, примерно пропорционального N · log( N ) . Здесь не указывается основание логарифма, поскольку при использовании другого основания результат изменяется только на постоянный коэффициент. Постоянный коэффициент обычно не учитывается при анализе алгоритмов в рамках стандартной модели единой стоимости .

функция f ( x ) Говорят, что растет логарифмически, если f ( x ) (точно или приблизительно) пропорциональна логарифму x . (Однако в биологических описаниях роста организма этот термин используется для обозначения экспоненциальной функции. ) Например, любое натуральное число   N можно представить в двоичном виде не более чем log ₂   N + 1   бит . Другими словами, объем памяти , необходимый для хранения N, растет логарифмически с N. ростом

Энтропия и хаос

Бильярд на овальном бильярдном столе . Две частицы, начиная с центра под углом, отличающимся на один градус, проходят пути, хаотически расходящиеся из-за отражений на границе.

Энтропия в широком смысле является мерой беспорядка некоторой системы. В статистической термодинамике энтропия S некоторой физической системы определяется как $$S=-k\sum _{i}p_{i}\ln(p_{i}).\,$$Сумма рассчитывается по всем возможным состояниям i рассматриваемой системы, например положениям частиц газа в контейнере. Более того, p _i — это вероятность состояния i достижения , а k — постоянная Больцмана . Точно так же энтропия в теории информации измеряет количество информации. Если получатель сообщения может ожидать любого из N возможных сообщений с равной вероятностью, то объем информации, передаваемой любым таким сообщением, определяется количественно как log ₂   N бит.

Показатели Ляпунова используют логарифмы для измерения степени хаотичности динамической системы . Например, для частицы, движущейся по овальному бильярдному столу, даже небольшие изменения начальных условий приводят к совершенно разным траекториям частицы. Такие системы хаотичны детерминированно . , поскольку небольшие ошибки измерения начального состояния предсказуемо приводят к существенно отличающимся конечным состояниям По крайней мере один показатель Ляпунова детерминированно хаотической системы положителен.

Фракталы

Треугольник Серпинского (справа) построен путем многократной замены равносторонних треугольников тремя меньшими.

встречаются в определениях размерности фракталов Логарифмы . Фракталы — это геометрические объекты, самоподобные в том смысле, что небольшие части воспроизводят, хотя бы грубо, всю глобальную структуру. Треугольник Серпинского (на фото) может быть покрыт тремя копиями самого себя, каждая из которых имеет стороны, равные половине исходной длины. Это делает хаусдорфову размерность этой структуры ln(3)/ln(2) ≈ 1,58 . Другое понятие размерности, основанное на логарифме, получается путем подсчета количества ячеек, необходимых для покрытия рассматриваемого фрактала.

Музыка

Четыре разные октавы показаны в линейном масштабе, затем показаны в логарифмическом масштабе (так, как их слышит ухо)

Логарифмы связаны с музыкальными тонами и интервалами . В равнотемперированных настройках соотношение частот зависит только от интервала между двумя тонами, а не от конкретной частоты или высоты отдельных тонов. В 12-тоновой равнотемперированной настройке, распространенной в современной западной музыке, каждая октава (удвоение частоты) разбивается на двенадцать равноотстоящих друг от друга интервалов, называемых полутонами . Например, если нота ля имеет частоту 440 Гц , то нота си-бемоль имеет частоту 466 Гц. Интервал между ля и си-бемоль составляет полутон , как и интервал между си-бемоль и си (частота 493 Гц). Соответственно, соотношения частот совпадают: $${\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.$$

Интервалы между произвольными высотами можно измерить в октавах, взяв по основанию 2 логарифм отношения частот , можно измерить в одинаково умеренных полутонах, взяв логарифм по основанию 2. ^1/12 логарифм ( в 12 раз больше логарифма по основанию 2 ), или может быть измерен в центах , сотых долях полутона, взяв основание 2. ^1/1200 логарифм ( 1200 раз по основанию — 2 логарифма). Последний используется для более точного кодирования, так как он необходим для более точных измерений или неравных темпераментов.

Интервал (играют два тона в то же время)	1/12 тона	Полутон	Просто главная треть	Основная треть	Тритон	Октава
Отношение частот $r$	$2^{\frac {1}{72}}\approx 1.0097$	$2^{\frac {1}{12}}\approx 1.0595$	${\tfrac {5}{4}}=1.25$	${\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}$	${\begin{aligned}2^{\frac {6}{12}}&={\sqrt {2}}\\&\approx 1.4142\end{aligned}}$	$2^{\frac {12}{12}}=2$
Количество полутонов $12\log _{2}r$	${\tfrac {1}{6}}$	$1$	$\approx 3.8631$	$4$	$6$	$12$
Количество центов $1200\log _{2}r$	$16{\tfrac {2}{3}}$	$100$	$\approx 386.31$	$400$	$600$	$1200$

Теория чисел

Натуральные логарифмы тесно связаны с подсчетом простых чисел (2, 3, 5, 7, 11, ...), что является важной темой теории чисел . Для любого целого числа   x количество простых чисел, меньших или равных x, обозначается π ( x ) . Теорема о простых числах утверждает, что π ( x ) приблизительно определяется выражением $${\frac {x}{\ln(x)}},$$в том смысле, что отношение π ( x ) и этой дроби приближается к 1, когда x стремится к бесконечности. Как следствие, вероятность того, что случайно выбранное число между 1 и x является простым, обратно пропорциональна количеству десятичных цифр x . Гораздо лучшая оценка π ( x ) дается смещенной логарифмической интегральной функцией Li( x ) , определенной формулой $$\mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln(t)}}\,dt.$$Гипотеза Римана , одна из старейших открытых математических гипотез , может быть сформулирована в терминах сравнения π ( x ) и Li( x ) . Теорема Эрдеша -Каца, описывающая количество различных простых множителей, также включает натуральный логарифм .

Логарифм n факториала , n ! = 1 · 2 · ... · n , определяется выражением $$\ln(n!)=\ln(1)+\ln(2)+\cdots +\ln(n).$$Это можно использовать для получения формулы Стирлинга , аппроксимации n ! для большого n .

Обобщения

Комплексный логарифм

Основная статья: Комплексный логарифм

Полярная форма z = x + iy . И φ, и φ' являются аргументами z .

Все комплексные числа a, которые решают уравнение

$$e^{a}=z$$

называются комплексными логарифмами ( ) считается z , когда z комплексным числом. Комплексное число обычно представляется как z = x + iy , где x и y — действительные числа, а i — мнимая единица , квадрат которой равен −1. Такое число можно визуализировать с помощью точки на комплексной плоскости , как показано справа. Полярная форма кодирует ненулевое комплексное число z его абсолютным значением , то есть (положительным, действительным) расстоянием r до начала координат и углом между вещественной осью ( x )   Re и линией, проходящей через оба начала координат. и з . называется аргументом z Этот угол .

Абсолютное значение z определяется r выражением

$$\textstyle r={\sqrt {x^{2}+y^{2}}}.$$

Используя геометрическую интерпретацию синуса и косинуса и их периодичность в 2 π , любое комплексное число z можно обозначить как

$$z=x+iy=r(\cos \varphi +i\sin \varphi )=r(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )),$$

для любого целого числа k . Очевидно, аргумент z не определен однозначно: и φ , и φ' = φ + 2 k π являются допустимыми аргументами z для всех целых чисел k , поскольку добавление 2 k π   радиан или k ⋅360° φ на соответствует «обмотке» начала координат против часовой стрелки k   витков . Результирующее комплексное число всегда равно z , как показано справа для k = 1 . Можно выбрать ровно один из возможных аргументов z в качестве так называемого главного аргумента , обозначаемого Arg( z ) с заглавной буквы A , потребовав, чтобы φ принадлежал одному, удобно выбранному повороту, например - π < φ ≤ π или 0 ≤ φ < 2 π . Эти области, где аргумент z определяется однозначно, называются ветвями функции аргумента.

Главная ветвь (- π , π ) комплексного логарифма Log( z ) . Черная точка при z = 1 соответствует нулю абсолютного значения, а более яркие цвета относятся к большим абсолютным значениям. Оттенок цвета кодирует аргумент Log( z ) .

Формула Эйлера связывает тригонометрические функции синус и косинус с комплексной экспонентой : $$e^{i\varphi }=\cos \varphi +i\sin \varphi .$$

Используя эту формулу и снова периодичность, выполняются следующие тождества:

$${\begin{array}{lll}z&=&r\left(\cos \varphi +i\sin \varphi \right)\\&=&r\left(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )\right)\\&=&re^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)}e^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)+i(\varphi +2k\pi )}=e^{a_{k}},\end{array}}$$

где ln( r ) — уникальный действительный натуральный логарифм, a _k обозначает комплексный логарифм z , а k — произвольное целое число. Следовательно, комплексные логарифмы z , которые представляют собой все те комплексные значения a _k, для которых a k _- я степень e равна z , представляют собой бесконечное множество значений.

$a_{k}=\ln(r)+i(\varphi +2k\pi ),\quad$ для произвольных целых чисел k .

Если взять k так, что φ + 2 k π находится в пределах определенного интервала для главных аргументов, тогда a _k называется главным значением логарифма, обозначаемым Log( z ) , опять же с заглавной буквы L . Главный аргумент любого положительного действительного числа x равен 0; следовательно, Log( x ) является действительным числом и равен действительному (натуральному) логарифму. Однако приведенные выше формулы для логарифмов произведений и степеней на главное не обобщаются значение комплексного логарифма.

На иллюстрации справа изображен Log( z ) , ограничивающий аргументы z интервалом (−π, π] . Таким образом, соответствующая ветвь комплексного логарифма имеет разрывы по всей отрицательной действительной оси x , что можно увидеть на рисунке. скачок оттенка здесь возникает из-за перехода на другую границу той же ветви при пересечении границы, т. е. без перехода к соответствующему значению k непрерывно соседней ветви. Такой локус называется разрезом ветки . Отказ от ограничений диапазона аргумента делает отношения «аргумент z » и, следовательно, «логарифм z » многозначными функциями .

Обратные к другим экспоненциальным функциям

Возведение в степень происходит во многих областях математики, и его обратную функцию часто называют логарифмом. Например, логарифм матрицы — это (многозначная) обратная функция матричной экспоненты . Другой пример — p -адический логарифм , обратная функция p -адической экспоненты . Оба определяются через ряд Тейлора, аналогичный реальному случаю. В контексте дифференциальной геометрии экспоненциальное отображение отображает касательное пространство в точке многообразия в окрестность этой точки. Ее обратную карту также называют логарифмической (или логарифмической) картой.

В контексте конечных групп возведение в степень задается путем многократного умножения одного элемента группы b на самого себя. Дискретный логарифм — это целое число n, решающее уравнение $$b^{n}=x,$$где x — элемент группы. Возведение в степень можно выполнить эффективно, но считается, что в некоторых группах вычислить дискретный логарифм очень сложно. Эта асимметрия имеет важные приложения в криптографии с открытым ключом , например, в обмене ключами Диффи-Хеллмана , процедуре, которая позволяет безопасный обмен криптографическими ключами по незащищенным информационным каналам. Логарифм Зеха связан с дискретным логарифмом в мультипликативной группе ненулевых элементов конечного поля .

Другие обратные функции, подобные логарифму, включают двойной логарифм   ln(ln( x )) , супер- или гипер-4-логарифм называется повторным логарифмом (небольшая вариация которого в информатике ), функцию Ламберта W и логит. . Они являются обратными функциями двойной экспоненты , тетрации , f ( w ) = we ^В , и логистической функции соответственно.

Связанные понятия

С точки зрения теории групп , тождество log( cd ) = log( c ) + log( d ) выражает групповой изоморфизм между положительными вещественными числами при умножении и вещественными числами при сложении. Логарифмические функции — единственные непрерывные изоморфизмы между этими группами. Благодаря этому изоморфизму мера Хаара ( мера Лебега ) dx на вещественных числах соответствует мере Хаара dx / x на положительных вещественных числах. Неотрицательные действительные числа имеют не только умножение, но и сложение, и образуют полукольцо , называемое вероятностным полукольцом ; на самом деле это полуполе . Затем логарифм преобразует умножение в сложение (логарифмическое умножение) и сложение в логарифмическое сложение ( LogSumExp ), давая изоморфизм полуколец между вероятностным полукольцом и логарифмическим полукольцом .

Логарифмические одноформы df / f появляются в комплексном анализе и алгебраической геометрии как дифференциальные формы с логарифмическими полюсами .

Полилогарифм формулой — это функция, определяемая $$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}.$$Он связан с натуральным логарифмом соотношением Li ₁ ( z ) = −ln(1 − z ) . Более того, Li _s (1) равна дзета-функции Римана ζ( s ) .

См. также

• Десятичный показатель (dex)
• Экспоненциальная функция
• Указатель статей о логарифмах

Внешние ссылки

• СМИ, связанные с логарифмом, на Викискладе?
• Словарное определение логарифма в Викисловаре
• Цитаты, связанные с историей логарифмов , в Wikiquote
• Урок по логарифмам можно найти в Викиверситете.
• Вайсштейн, Эрик В. , «Логарифм» , MathWorld
• Академия Хана: Логарифмы, бесплатные онлайн-микролекции
• «Логарифмическая функция» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Колин Байфлит, Обучающее видео по логарифмам , получено 12 октября 2010 г.
• Эдвард Райт, Перевод работы Нейпира по логарифмам , заархивировано из оригинала 3 декабря 2002 г. , получено 12 октября 2010 г.
• Глейшер, Джеймс Уитбред Ли (1911), «Логарифм» , в Чисхолме, Хью (редактор), Британская энциклопедия , том. 16 (11-е изд.), Cambridge University Press, стр. 868–77.