Волновая функция

Не путать с волновым уравнением .

Сравнение классической и квантовой концепций гармонического осциллятора для одиночной бесспиновой частицы. Эти два процесса сильно различаются. Классический процесс (А–Б) представляется как движение частицы по траектории. Квантовый процесс (C–H) не имеет такой траектории. Скорее, оно представлено как волна; здесь вертикальная ось показывает действительную часть (синий) и мнимую часть (красный) волновой функции. в виде стоячей волны На панелях (C–F) показаны четыре различных решения уравнения Шредингера . На панелях (G – H) также показаны две разные волновые функции, которые являются решениями уравнения Шредингера, но не стоячими волнами.

Волновая функция изначально очень локализованной свободной частицы.

В квантовой физике ( волновая функция или волновая функция ) — это математическое описание квантового состояния изолированной квантовой системы . Наиболее распространенными символами волновой функции являются греческие буквы ψ и Ψ (строчные и заглавные psi соответственно). Волновые функции являются комплексными . Например, волновая функция может присвоить комплексное число каждой точке в области пространства. Правило Борна предоставляет средства для превращения этих комплексных амплитуд вероятности в реальные вероятности. В одной распространенной форме оно гласит, что квадрат модуля волновой функции, зависящей от положения, представляет собой плотность вероятности измерения . частицы, находящейся в данном месте Интеграл от квадрата модуля волновой функции по всем степеням свободы системы должен быть равен 1, это условие называется нормализацией . Поскольку волновая функция является комплексной, можно измерить только ее относительную фазу и относительную величину; его значение само по себе ничего не говорит о величинах или направлениях измеримых наблюдаемых. необходимо применить квантовые операторы , собственные значения которых соответствуют множествам возможных результатов измерений, К волновой функции ψ и вычислить статистические распределения измеримых величин.

Волновые функции могут быть функциями переменных, отличных от положения, например импульса . Информация, представленная волновой функцией, зависящей от положения, может быть преобразована в волновую функцию, зависящую от импульса, и наоборот, с помощью преобразования Фурье . Некоторые частицы, такие как электроны и фотоны , имеют ненулевой спин , и волновая функция таких частиц включает спин как внутреннюю дискретную степень свободы; также могут быть включены другие дискретные переменные, такие как изоспин . Когда система имеет внутренние степени свободы, волновая функция в каждой точке непрерывных степеней свободы (например, точка в пространстве) присваивает комплексное число каждому возможному значению дискретных степеней свободы (например, z-компонента вращаться). Эти значения часто отображаются в виде матрицы-столбца (например, вектор-столбец 2 × 1 для нерелятивистского электрона со спином 1 ⁄ 2 ).

Согласно принципу суперпозиции квантовой механики, волновые функции можно складывать и умножать на комплексные числа, чтобы сформировать новые волновые функции и сформировать гильбертово пространство . Внутренний продукт между двумя волновыми функциями является мерой перекрытия между соответствующими физическими состояниями и используется в фундаментальной вероятностной интерпретации квантовой механики, правиле Борна , связывающем вероятности перехода со внутренними продуктами. Уравнение Шредингера определяет, как волновые функции изменяются с течением времени, а волновая функция качественно ведет себя так же, как и другие волны , такие как волны на воде или волны на струне, поскольку уравнение Шредингера математически является разновидностью волнового уравнения . Это объясняет название «волновая функция» и порождает корпускулярно-волновой дуализм . Однако волновая функция в квантовой механике описывает своего рода физическое явление, по состоянию на 2023 год все еще открытое для различных интерпретаций , которое фундаментально отличается от классических механических волн.

Историческая справка

В 1900 году Макс Планк постулировал пропорциональность между частотой $f$ фотона и его энергия $E$, $E=hf$, фотона а в 1916 году соответствующее соотношение между импульсом $p$ и длина волны $\lambda$, $\lambda ={\frac {h}{p}}$, где $h$ — постоянная Планка . В 1923 году Де Бройль первым предположил, что соотношение $\lambda ={\frac {h}{p}}$, теперь называемое соотношением Де Бройля , справедливо для массивных частиц, главным ключом к разгадке которого является лоренц-инвариантность , и это можно рассматривать как отправную точку современного развития квантовой механики. Уравнения представляют корпускулярно-волновой дуализм как для безмассовых, так и для массивных частиц.

В 1920-х и 1930-х годах квантовая механика развивалась с использованием исчисления и линейной алгебры . Среди тех, кто использовал методы исчисления, были Луи де Бройль , Эрвин Шредингер и другие, разработавшие « волновую механику ». Среди тех, кто применял методы линейной алгебры, были Вернер Гейзенберг , Макс Борн и другие, разработавшие « матричную механику ». Впоследствии Шрёдингер показал, что эти два подхода эквивалентны.

В 1926 году Шрёдингер опубликовал знаменитое волновое уравнение, теперь названное в его честь — уравнение Шрёдингера . Это уравнение было основано на классическом сохранении энергии с использованием квантовых операторов и соотношений де Бройля, а решения уравнения являются волновыми функциями квантовой системы. Однако никто не знал, как это интерпретировать. Сначала Шредингер и другие думали, что волновые функции представляют собой частицы, которые распределены, причем большая часть частиц находится там, где волновая функция велика. Было показано, что это несовместимо с упругим рассеянием волнового пакета (представляющего частицу) на мишени; оно распространяется во всех направлениях. Хотя рассеянная частица может разлететься в любом направлении, она не разбивается и не разлетается во всех направлениях. В 1926 году Борн предложил концепцию амплитуды вероятности . Это связывает расчеты квантовой механики непосредственно с вероятностными экспериментальными наблюдениями. Это принято как часть Копенгагенской интерпретации квантовой механики. Существует множество других интерпретаций квантовой механики . В 1927 году Хартри и Фок сделали первый шаг в попытке решить волновую функцию N тел и разработали цикл самосогласования : итерационный алгоритм для аппроксимации решения. Теперь он также известен как метод Хартри-Фока . Определитель ) и постоянный элемент были Слейтера (матрицы частью метода, предложенного Джоном К. Слейтером .

Шредингер действительно столкнулся с уравнением для волновой функции, которое удовлетворяло релятивистскому закону сохранения энергии , прежде чем он опубликовал нерелятивистское уравнение, но отбросил его, поскольку оно предсказывало отрицательные вероятности и отрицательные энергии . В 1927 году Кляйн , Гордон и Фок также нашли его, но учли электромагнитное взаимодействие и доказали, что оно лоренц-инвариантно . Де Бройль также пришел к тому же уравнению в 1928 году. Это релятивистское волновое уравнение сейчас наиболее широко известно как уравнение Клейна – Гордона .

В 1927 году Паули феноменологически нашел нерелятивистское уравнение для описания частиц со спином 1/2 в электромагнитных полях, которое теперь называется уравнением Паули . Паули обнаружил, что волновая функция не описывается одной комплексной функцией пространства и времени, а требует двух комплексных чисел, которые соответственно соответствуют состояниям фермиона со спином +1/2 и -1/2. Вскоре после этого, в 1928 году, Дирак нашел уравнение первого успешного объединения специальной теории относительности и квантовой механики, примененное к электрону , которое теперь называется уравнением Дирака . При этом волновая функция представляет собой спинор, представленный четырьмя комплексными компонентами: электрона два для электрона и два для античастицы , позитрона . В нерелятивистском пределе волновая функция Дирака напоминает волновую функцию Паули для электрона. Позже и другие релятивистские волновые уравнения были найдены .

Волновые функции и волновые уравнения в современных теориях

Все эти волновые уравнения имеют непреходящее значение. Уравнение Шрёдингера и уравнение Паули во многих случаях являются превосходными аппроксимациями релятивистских вариантов. Их значительно легче решать практические задачи, чем релятивистские аналоги.

Уравнение Клейна-Гордона и уравнение Дирака , хотя и являются релятивистскими, не представляют собой полного примирения квантовой механики и специальной теории относительности. Раздел квантовой механики, где эти уравнения изучаются так же, как уравнение Шредингера, часто называемый релятивистской квантовой механикой , хотя и очень успешен, имеет свои ограничения (см., например, сдвиг Лэмба ) и концептуальные проблемы (см., например, море Дирака ).

Теория относительности делает неизбежным, что число частиц в системе не является постоянным. Для полного примирения квантовая теория поля . необходима В этой теории волновые уравнения и волновые функции имеют свое место, но в несколько ином виде. Основными объектами интереса являются не волновые функции, а скорее операторы, так называемые операторы поля (или просто поля, где понимается «оператор») в гильбертовом пространстве состояний (которые будут описаны в следующем разделе). Оказывается, исходные релятивистские волновые уравнения и их решения все еще необходимы для построения гильбертова пространства. Более того, операторы свободных полей , т.е. когда предполагается, что взаимодействия не существуют, оказываются (формально) удовлетворяющими тому же уравнению, что и поля (волновые функции) во многих случаях.

Таким образом, уравнение Клейна–Гордона (спин 0 ) и уравнение Дирака (спин 1 ⁄ 2 ) в таком виде остаются в теории. Аналоги с более высокими спинами включают уравнение Прока (спин 1 ), уравнение Рариты – Швингера (спин 3 ⁄ 2 ) и, в более общем плане, уравнения Баргмана–Вигнера . Для безмассовых свободных полей двумя примерами являются уравнение Максвелла свободного поля (спин 1 ) и уравнение Эйнштейна свободного поля (спин 2 ) для операторов поля. Все они по существу являются прямым следствием требования лоренц-инвариантности . Их решения должны трансформироваться при преобразовании Лоренца заданным образом, т. е. при определенном представлении группы Лоренца , и это вместе с некоторыми другими разумными требованиями, например, свойством кластерной декомпозиции , с учетом причинно-следственной связи, достаточно, чтобы исправить уравнения.

Это относится к уравнениям свободного поля; взаимодействие не учитывается. Если доступна лагранжева плотность (включая взаимодействия), то лагранжев формализм даст уравнение движения на классическом уровне. Это уравнение может быть очень сложным и не поддающимся решению. Любое решение будет относиться к фиксированному числу частиц и не будет учитывать термин «взаимодействие», упомянутый в этих теориях, который включает в себя создание и уничтожение частиц, а не внешние потенциалы, как в обычной «первоквантованной» квантовой теории.

В теории струн ситуация остается аналогичной. Например, волновая функция в импульсном пространстве играет роль коэффициента разложения Фурье в общем состоянии частицы (струны) с импульсом, который не определен четко.

Определение (одна бесспиновая частица в одном измерении)

Стоячие волны для частицы в ящике , примеры стационарных состояний .

Бегущие волны свободной частицы.

Действительные части волновой функции положения Ψ( x ) и волновой функции импульса Φ( p ) и соответствующие плотности вероятности |Ψ( x )| ² и |Φ( p )| ² , для одной частицы со спином 0 в одном x или p измерении . Непрозрачность цвета частиц соответствует плотности вероятности ( а не волновой функции) обнаружения частицы в положении x или импульсе p .

А пока рассмотрим простой случай нерелятивистской одиночной частицы без спина в одном пространственном измерении. Более общие случаи обсуждаются ниже.

Согласно постулатам квантовой механики , состояние физической системы в фиксированный момент времени $t$, задается волновой функцией, принадлежащей сепарабельному комплексному гильбертовому пространству . Таким образом, скалярный продукт двух волновых функций Ψ ₁ и Ψ ₂ можно определить как комплексное число (в момент времени t )

$(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty$.

Более подробная информация приведена ниже . Однако скалярное произведение волновой функции Ψ на саму себя,

$(\Psi ,\Psi )=\|\Psi \|^{2}$,

всегда . положительное действительное число Число ‖ Ψ ‖ (не ‖ Ψ ‖ ² ) называется нормой волновой функции Ψ . сепарабельное гильбертово пространство Рассматриваемое бесконечномерно . это означает, что не существует конечного набора функций, интегрируемых с квадратом , которые можно складывать в различных комбинациях, чтобы создать любую возможную интегрируемую с квадратом функцию .

Волновые функции в позиционном пространстве

Состояние такой частицы полностью описывается ее волновой функцией: $$\Psi (x,t)\,,$$ где x — положение, а t — время. Это комплексная функция двух вещественных переменных x и t .

Для одной бесспиновой частицы в одном измерении, если волновую функцию интерпретировать как амплитуду вероятности ; квадрат модуля волновой функции, положительное действительное число $$\left|\Psi (x,t)\right|^{2}=\Psi ^{*}(x,t)\Psi (x,t)=\rho (x),$$интерпретируется как плотность вероятности измерения положения частицы в данный момент времени t . Звездочка указывает на комплексно-сопряженное соединение . Если положение частицы измерено , его местоположение не может быть определено из волновой функции, а описывается распределением вероятностей .

Условие нормализации

Вероятность того, что его положение x окажется в интервале a ≤ x ≤ b, является интегралом от плотности по этому интервалу: $$P_{a\leq x\leq b}(t)=\int _{a}^{b}\,|\Psi (x,t)|^{2}dx$$где t — время измерения частицы. Это приводит к условию нормализации : $$\int _{-\infty }^{\infty }\,|\Psi (x,t)|^{2}dx=1\,,$$потому что если частицу измерить, то есть 100% вероятность, что она где-то окажется .

Для данной системы набор всех возможных нормируемых волновых функций (в любой момент времени) образует абстрактное математическое векторное пространство , что означает, что можно складывать различные волновые функции и умножать волновые функции на комплексные числа. Технически волновые функции образуют луч в проективном гильбертовом пространстве, а не в обычном векторном пространстве.

Квантовые состояния как векторы

См. также: Математическая формулировка квантовой механики , обозначение Бракета и оператор положения.

В конкретный момент времени все значения волновой функции Ψ( x , t ) являются компонентами вектора. Их несчетно бесконечно много и вместо суммирования используется интегрирование. В обозначениях Бракета этот вектор записывается $$|\Psi (t)\rangle =\int \Psi (x,t)|x\rangle dx$$и называется «вектором квантового состояния» или просто «квантовым состоянием». Есть несколько преимуществ понимания волновых функций как элементов абстрактного векторного пространства:

• Все мощные инструменты линейной алгебры можно использовать для манипулирования волновыми функциями и их понимания. Например:
  • Линейная алгебра объясняет, как векторному пространству можно задать базис , а затем любой вектор в векторном пространстве можно выразить в этом базисе. Это объясняет взаимосвязь между волновой функцией в пространстве положений и волновой функцией в пространстве импульсов и предполагает, что существуют и другие возможности.
  • Обозначение Бракета можно использовать для манипулирования волновыми функциями.
• Идея о том, что квантовые состояния являются векторами в абстрактном векторном пространстве, является совершенно общей для всех аспектов квантовой механики и квантовой теории поля , тогда как идея о том, что квантовые состояния являются комплексными «волновыми» функциями пространства, верна только в определенных ситуациях.

Параметр времени часто скрывается и будет в дальнейшем. Координата x является непрерывным индексом. | ​ x ⟩ называются несобственными векторами , которые, в отличие от правильных векторов , нормируемых к единице, могут быть нормализованы только к дельта-функции Дирака. $$\langle x'|x\rangle =\delta (x'-x)$$таким образом $$\langle x'|\Psi \rangle =\int \Psi (x)\langle x'|x\rangle dx=\Psi (x')$$и $$|\Psi \rangle =\int |x\rangle \langle x|\Psi \rangle dx=\left(\int |x\rangle \langle x|dx\right)|\Psi \rangle$$который освещает идентификационный оператор $$I=\int |x\rangle \langle x|dx\,.$$что аналогично соотношению полноты ортонормированного базиса в N-мерном гильбертовом пространстве.

Нахождение тождественного оператора в базисе позволяет явно выразить абстрактное состояние в базисе и многое другое (внутренний продукт между двумя векторами состояния и другие операторы для наблюдаемых могут быть выражены в базисе).

Волновые функции в импульсном пространстве

Частица также имеет волновую функцию в пространстве импульсов : $$\Phi (p,t)$$где p — импульс в одном измерении, который может иметь любое значение от −∞ до +∞ , а t — время.

Аналогично случаю положения, скалярное произведение двух волновых функций Φ ₁ ( p , t ) и Φ ₂ ( p , t ) может быть определено как: $$(\Phi _{1},\Phi _{2})=\int _{-\infty }^{\infty }\,\Phi _{1}^{*}(p,t)\Phi _{2}(p,t)dp\,.$$

Одним из частных решений независимого от времени уравнения Шредингера является $$\Psi _{p}(x)=e^{ipx/\hbar },$$плоская волна , которую можно использовать при описании частицы с импульсом точно p , поскольку она является собственной функцией оператора импульса. Эти функции не нормализуются к единице (они не интегрируемы с квадратом), поэтому на самом деле они не являются элементами физического гильбертова пространства. Набор $$\{\Psi _{p}(x,t),-\infty \leq p\leq \infty \}$$образует то, что называется базисом импульса . Этот «базис» не является базисом в обычном математическом смысле. Во-первых, поскольку функции не нормализуются, вместо этого они нормализуются до дельта-функции . $$(\Psi _{p},\Psi _{p'})=\delta (p-p').$$

Во-вторых, хотя они линейно независимы, их слишком много (они образуют несчетное множество) для основы физического гильбертова пространства. Их по-прежнему можно использовать для выражения всех функций в нем с помощью преобразований Фурье, как описано ниже.

Отношения между представлениями положения и импульса

Представления x и p : $${\begin{aligned}|\Psi \rangle =I|\Psi \rangle &=\int |x\rangle \langle x|\Psi \rangle dx=\int \Psi (x)|x\rangle dx,\\|\Psi \rangle =I|\Psi \rangle &=\int |p\rangle \langle p|\Psi \rangle dp=\int \Phi (p)|p\rangle dp.\end{aligned}}$$

Теперь возьмем проекцию состояния Ψ на собственные функции импульса, используя последнее выражение в двух уравнениях: $$\int \Psi (x)\langle p|x\rangle dx=\int \Phi (p')\langle p|p'\rangle dp'=\int \Phi (p')\delta (p-p')dp'=\Phi (p).$$

Затем, используя известное выражение для подходящим образом нормализованных собственных состояний импульса в решениях позиционного представления свободного уравнения Шредингера $$\langle x|p\rangle =p(x)={\frac {1}{\sqrt {2\pi \hbar }}}e^{{\frac {i}{\hbar }}px}\Rightarrow \langle p|x\rangle ={\frac {1}{\sqrt {2\pi \hbar }}}e^{-{\frac {i}{\hbar }}px},$$получается $$\Phi (p)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Psi (x)e^{-{\frac {i}{\hbar }}px}dx\,.$$

Аналогично, используя собственные функции положения, $$\Psi (x)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Phi (p)e^{{\frac {i}{\hbar }}px}dp\,.$$

Таким образом, оказывается, что волновые функции в пространстве положения и пространстве импульса являются преобразованиями Фурье друг друга. Это два представителя одного и того же государства; содержат одну и ту же информацию, и любого из них достаточно для расчета любого свойства частицы.

На практике волновая функция в пространстве-положении используется гораздо чаще, чем волновая функция в пространстве-импульсе. Потенциал, входящий в соответствующее уравнение (Шрёдингера, Дирака и т. д.), определяет, в каком базисе описание проще всего. Для осциллятора гармонического x и p входят симметрично, поэтому не имеет значения, какое описание использовать. Получается то же уравнение (по модулю констант). Отсюда, немного подумав, следует, что решения волнового уравнения гармонического осциллятора являются собственными функциями преобразования Фурье в L ² .

Определения (другие случаи)

Ниже приведены общие формы волновой функции для систем более высоких измерений и большего количества частиц, а также включающие другие степени свободы, кроме координат положения или компонентов импульса.

Конечномерное гильбертово пространство

Хотя гильбертовы пространства изначально относятся к бесконечномерным пространствам с полным внутренним произведением, включают конечномерные пространства с полным внутренним произведением . они, по определению, также В физике их часто называют конечномерными гильбертовыми пространствами . Для каждого конечномерного гильбертова пространства существуют ортонормированные базисные наборы, охватывающие все гильбертово пространство.

Если N -мерное множество ${\textstyle \{|\phi _{i}\rangle \}}$ ортонормирован, то оператор проектирования пространства, охватываемого этими состояниями, имеет вид:

$$P=\sum _{i}|\phi _{i}\rangle \langle \phi _{i}|=I$$где проекция эквивалентна тождественному оператору, поскольку ${\textstyle \{|\phi _{i}\rangle \}}$ охватывает все гильбертово пространство, оставляя любой вектор из гильбертова пространства неизменным. Это также известно как отношение полноты конечномерного гильбертова пространства.

Вместо этого волновая функция определяется следующим образом:

$$|\psi \rangle =I|\psi \rangle =\sum _{i}|\phi _{i}\rangle \langle \phi _{i}|\psi \rangle$$где ${\textstyle \{\langle \phi _{i}|\psi \rangle \}}$, представляет собой набор комплексных чисел, которые можно использовать для построения волновой функции по приведенной выше формуле.

Вероятностная интерпретация внутреннего продукта

Если набор ${\textstyle \{|\phi _{i}\rangle \}}$ являются собственными невырожденными наблюдаемыми с собственными значениями ${\textstyle \lambda _{i}}$, согласно постулатам квантовой механики , вероятность измерения наблюдаемой равна ${\textstyle \lambda _{i}}$ определяется по правилу Борна как:

$$P_{\psi }(\lambda _{i})=|\langle \phi _{i}|\psi \rangle |^{2}$$

Для невырожденных ${\textstyle \{|\phi _{i}\rangle \}}$ некоторой наблюдаемой, если собственные значения ${\textstyle \lambda }$ имеют подмножество собственных векторов, обозначенных как ${\textstyle \{|\lambda ^{(j)}\rangle \}}$, согласно постулатам квантовой механики , вероятность измерения наблюдаемой равна ${\textstyle \lambda _{i}}$ дается:

$$P_{\psi }(\lambda )=\sum _{j}|\langle \lambda ^{(j)}|\psi \rangle |^{2}=|{\widehat {P}}_{\lambda }|\psi \rangle |^{2}$$где ${\textstyle {\widehat {P}}_{\lambda }=\sum _{j}|\lambda ^{(j)}\rangle \langle \lambda ^{(j)}|}$ является оператором проектирования состояний в подпространство, натянутое на ${\textstyle \{|\lambda ^{(j)}\rangle \}}$. Равенство следует из ортогональной природы ${\textstyle \{|\phi _{i}\rangle \}}$.

Следовательно, ${\textstyle \{\langle \phi _{i}|\psi \rangle \}}$ которые определяют состояние квантовомеханической системы, имеют величины, квадрат которых дает вероятность измерения соответствующих ${\textstyle |\phi _{i}\rangle }$ состояние.

Физическое значение относительной фазы

В то время как относительная фаза имеет наблюдаемые эффекты в экспериментах, глобальная фаза системы экспериментально неразличима. Например, в частице, находящейся в суперпозиции двух состояний, глобальную фазу частицы невозможно отличить путем определения математического ожидания наблюдаемой или вероятности наблюдения различных состояний, но относительные фазы могут влиять на математические ожидания наблюдаемых.

Хотя общая фаза системы считается произвольной, относительная фаза для каждого состояния ${\textstyle |\phi _{i}\rangle }$ состояния подготовленного состояния в суперпозиции можно определить, исходя из физического смысла подготовленного состояния и его симметрии. Например, построение спиновых состояний вдоль направления x как суперпозиции спиновых состояний вдоль направления z можно выполнить путем применения соответствующего преобразования вращения к состояниям спина вдоль z, которое обеспечивает соответствующую фазу состояний относительно друг друга.

Заявка на включение спина

Пример конечномерного гильбертова пространства можно построить с использованием собственных спиновых сетей ${\textstyle s}$-спиновые частицы, образующие ${\textstyle 2s+1}$ мерное гильбертово пространство . Однако общая волновая функция частицы, которая полностью описывает ее состояние, всегда принадлежит бесконечномерному гильбертовому пространству , поскольку она включает в себя тензорное произведение с гильбертовым пространством, относящимся к положению или импульсу частицы. Тем не менее, методы, разработанные для конечномерного гильбертова пространства, полезны, поскольку их можно рассматривать независимо или рассматривать с учетом линейности тензорного произведения.

Поскольку оператор спина для данного ${\textstyle s}$-спиновые частицы можно представить как конечные ${\textstyle (2s+1)^{2}}$ матрица , которая действует на ${\textstyle 2s+1}$ независимые компоненты вектора спина, обычно предпочтительнее обозначать компоненты спина, используя обозначение матрица/столбец/строка, где это применимо.

Например, каждый | s _z ⟩ обычно идентифицируется как вектор-столбец: $$|s\rangle \leftrightarrow {\begin{bmatrix}1\\0\\\vdots \\0\\0\\\end{bmatrix}}\,,\quad |s-1\rangle \leftrightarrow {\begin{bmatrix}0\\1\\\vdots \\0\\0\\\end{bmatrix}}\,,\ldots \,,\quad |-(s-1)\rangle \leftrightarrow {\begin{bmatrix}0\\0\\\vdots \\1\\0\\\end{bmatrix}}\,,\quad |-s\rangle \leftrightarrow {\begin{bmatrix}0\\0\\\vdots \\0\\1\\\end{bmatrix}}$$

но это обычное злоупотребление обозначениями, потому что кеты | s _z ⟩ не являются синонимами и не равны векторам-столбцам. Векторы-столбцы просто предоставляют удобный способ выразить компоненты спина.

В соответствии с обозначениями оператор спина z-компоненты можно записать как: $${\frac {1}{\hbar }}{\hat {S}}_{z}={\begin{bmatrix}s&0&\cdots &0&0\\0&s-1&\cdots &0&0\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\cdots &-(s-1)&0\\0&0&\cdots &0&-s\end{bmatrix}}$$

поскольку собственные векторы оператора спина z-компоненты представляют собой указанные выше векторы-столбцы, а собственные значения представляют собой соответствующие квантовые числа спина.

Таким образом, в соответствии с обозначениями вектор из такого конечномерного гильбертова пространства представляется как:

$$|\phi \rangle ={\begin{bmatrix}\langle s|\phi \rangle \\\langle s-1|\phi \rangle \\\vdots \\\langle -(s-1)|\phi \rangle \\\langle -s|\phi \rangle \\\end{bmatrix}}={\begin{bmatrix}\varepsilon _{s}\\\varepsilon _{s-1}\\\vdots \\\varepsilon _{-s+1}\\\varepsilon _{-s}\\\end{bmatrix}}$$где ${\textstyle \{\varepsilon _{i}\}}$ соответствующие комплексные числа.

В следующем обсуждении спина полная волновая функция рассматривается как тензорное произведение спиновых состояний из конечномерных гильбертовых пространств и волновой функции, которая была разработана ранее. Таким образом, рассматривается основа этого гильбертова пространства: $|\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle |s_{z}\rangle$.

Одночастичные состояния в трехмерном позиционном пространстве

Волновая функция в позиционном пространстве одиночной частицы без спина в трех пространственных измерениях аналогична случаю одного пространственного измерения, описанному выше: $$\Psi (\mathbf {r} ,t)$$ где r — вектор положения в трехмерном пространстве, а t — время. Как всегда Ψ( r , t ) является комплексной функцией действительных переменных. Как один вектор в обозначениях Дирака $$|\Psi (t)\rangle =\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r} ,t)\,|\mathbf {r} \rangle$$

Все предыдущие замечания о внутренних произведениях, волновых функциях импульсного пространства, преобразованиях Фурье и т. д. распространяются и на более высокие измерения.

Для частицы со спином , игнорируя положения степеней свободы, волновая функция является функцией только спина (время является параметром); $$\xi (s_{z},t)$$где s _z — квантовое число проекции спина вдоль оси z . ( Ось z выбирается произвольно; вместо нее можно использовать другие оси, если волновая функция преобразуется соответствующим образом, см. ниже.) Параметр s _z , в отличие от r и t , является дискретной переменной . Например, для со спином 1/2 частицы s _z может быть только +1/2 или -1/2 , а не каким-либо другим значением. (В общем, для спина s s s _z может быть − s , 1 , ..., − s + 1, − s ). Подстановка каждого квантового числа дает комплексную функцию пространства и времени, их + 2 1 . Их можно объединить в вектор-столбец.

$$\xi ={\begin{bmatrix}\xi (s,t)\\\xi (s-1,t)\\\vdots \\\xi (-(s-1),t)\\\xi (-s,t)\\\end{bmatrix}}=\xi (s,t){\begin{bmatrix}1\\0\\\vdots \\0\\0\\\end{bmatrix}}+\xi (s-1,t){\begin{bmatrix}0\\1\\\vdots \\0\\0\\\end{bmatrix}}+\cdots +\xi (-(s-1),t){\begin{bmatrix}0\\0\\\vdots \\1\\0\\\end{bmatrix}}+\xi (-s,t){\begin{bmatrix}0\\0\\\vdots \\0\\1\\\end{bmatrix}}$$

В нотации Бракет они легко группируются в компоненты вектора: $$|\xi (t)\rangle =\sum _{s_{z}=-s}^{s}\xi (s_{z},t)\,|s_{z}\rangle$$

Весь вектор ξ является решением уравнения Шрёдингера (с подходящим гамильтонианом), которое разворачивается в связанную систему 2 s + 1 обыкновенных дифференциальных уравнений с решениями ξ ( s , t ), ξ ( s − 1, t ), ..., ξ (− s , т ) . Некоторые авторы используют термин «спиновая функция» вместо «волновая функция». Это контрастирует с решениями волновых функций позиционного пространства, координаты положения которых представляют собой непрерывные степени свободы, потому что тогда уравнение Шредингера действительно принимает форму волнового уравнения.

В более общем смысле, для трехмерной частицы с любым спином волновую функцию можно записать в «пространстве позиция-спин» как: $$\Psi (\mathbf {r} ,s_{z},t)$$и их также можно объединить в вектор-столбец $$\Psi (\mathbf {r} ,t)={\begin{bmatrix}\Psi (\mathbf {r} ,s,t)\\\Psi (\mathbf {r} ,s-1,t)\\\vdots \\\Psi (\mathbf {r} ,-(s-1),t)\\\Psi (\mathbf {r} ,-s,t)\\\end{bmatrix}}$$в котором спиновая зависимость помещена в индексацию записей, а волновая функция представляет собой комплексную векторную функцию только пространства и времени.

Все значения волновой функции не только дискретных, но и непрерывных переменных собираются в один вектор. $$|\Psi (t)\rangle =\sum _{s_{z}}\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r} ,s_{z},t)\,|\mathbf {r} ,s_{z}\rangle$$

Для одиночной частицы тензорное произведение ⊗ ее вектора состояния положения | ψ ⟩ и вектор спинового состояния | ξ ⟩ дает составной вектор состояния позиционного спина $$|\psi (t)\rangle \!\otimes \!|\xi (t)\rangle =\sum _{s_{z}}\int d^{3}\!\mathbf {r} \,\psi (\mathbf {r} ,t)\,\xi (s_{z},t)\,|\mathbf {r} \rangle \!\otimes \!|s_{z}\rangle$$с идентификацией $$|\Psi (t)\rangle =|\psi (t)\rangle \!\otimes \!|\xi (t)\rangle$$$$\Psi (\mathbf {r} ,s_{z},t)=\psi (\mathbf {r} ,t)\,\xi (s_{z},t)$$$$|\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle \!\otimes \!|s_{z}\rangle$$

Факторизация тензорного произведения собственных состояний энергии всегда возможна, если орбитальный и спиновый угловые моменты частицы разделимы в гамильтониане, лежащем в основе динамики системы (другими словами, гамильтониан можно разбить на сумму орбитальных и спиновых членов ). Зависимость от времени можно отнести к любому фактору, и эволюцию каждого фактора во времени можно изучать отдельно. В соответствии с такими гамильтонианами любое состояние тензорного произведения превращается в другое состояние тензорного произведения, что, по сути, означает, что любое незапутанное состояние остается незапутанным при эволюции во времени. Говорят, что это происходит, когда нет физического взаимодействия между состояниями тензорных произведений. В случае несепарабельных гамильтонианов собственные состояния энергии называются некоторой линейной комбинацией таких состояний, которые не обязательно факторизуются; примеры включают частицу в магнитном поле и спин-орбитальную связь .

Предыдущее обсуждение не ограничивается спином как дискретной переменной: полный угловой момент J. также можно использовать Другие дискретные степени свободы, такие как изоспин , могут быть выражены аналогично случаю спина, описанному выше.

Многочастичные состояния в трехмерном позиционном пространстве

Бегущие волны двух свободных частиц с подавлением двух или трех измерений. Вверху — волновая функция в пространстве положения, внизу — волновая функция в пространстве импульса с соответствующими плотностями вероятности.

Если частиц много, то, как правило, существует только одна волновая функция, а не отдельная волновая функция для каждой частицы. Тот факт, что одна волновая функция описывает множество частиц, делает возможными квантовую запутанность и парадокс ЭПР . Волновая функция в позиционном пространстве для N частиц записывается: $$\Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t)$$где r _i — положение i -й частицы в трёхмерном пространстве, а t — время. В целом это комплексная функция от 3 N + 1 вещественных переменных.

В квантовой механике существует фундаментальное различие между идентичными и различимыми частицами. Например, любые два электрона идентичны и принципиально неотличимы друг от друга; законы физики не позволяют «проставить идентификационный номер» на определенном электроне, чтобы отслеживать его. Это приводит к требованию к волновой функции системы одинаковых частиц: $$\Psi \left(\ldots \mathbf {r} _{a},\ldots ,\mathbf {r} _{b},\ldots \right)=\pm \Psi \left(\ldots \mathbf {r} _{b},\ldots ,\mathbf {r} _{a},\ldots \right)$$где знак + частицы являются стоит, если все бозонами , и знак - , если все они фермионы . Другими словами, волновая функция либо полностью симметрична в положениях бозонов, либо полностью антисимметрична в положениях фермионов. Физический обмен частицами соответствует математическому переключению аргументов в волновой функции. Антисимметрия фермионных волновых функций приводит к принципу Паули . Как правило, требования бозонной и фермионной симметрии являются проявлением статистики частиц и присутствуют в других формализмах квантовых состояний.

Для N различимых частиц (ни одна из которых не является одинаковой , т.е. нет двух, имеющих одинаковый набор квантовых чисел), нет требования, чтобы волновая функция была симметричной или антисимметричной.

Для совокупности частиц, некоторые из которых идентичны с координатами r ₁ , r ₂ , ..., а другие различимы x ₁ , x ₂ , ... (не тождественны друг другу и не идентичны вышеупомянутым тождественным частицам), волна функция симметрична или антисимметрична только в одинаковых координатах частицы r _i : $$\Psi \left(\ldots \mathbf {r} _{a},\ldots ,\mathbf {r} _{b},\ldots ,\mathbf {x} _{1},\mathbf {x} _{2},\ldots \right)=\pm \Psi \left(\ldots \mathbf {r} _{b},\ldots ,\mathbf {r} _{a},\ldots ,\mathbf {x} _{1},\mathbf {x} _{2},\ldots \right)$$

Опять же, не существует требований симметрии для различимых координат частиц x _i .

Волновая функция для N частиц, каждая из которых имеет спин, представляет собой комплексную функцию $$\Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},s_{z\,1},s_{z\,2}\cdots s_{z\,N},t)$$

Собрав все эти компоненты в один вектор,

$$|\Psi \rangle =\overbrace {\sum _{s_{z\,1},\ldots ,s_{z\,N}}} ^{\text{discrete labels}}\overbrace {\int _{R_{N}}d^{3}\mathbf {r} _{N}\cdots \int _{R_{1}}d^{3}\mathbf {r} _{1}} ^{\text{continuous labels}}\;\underbrace {{\Psi }(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},s_{z\,1},\ldots ,s_{z\,N})} _{\begin{array}{c}{\text{wave function (component of }}\\{\text{ state vector along basis state)}}\end{array}}\;\underbrace {|\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},s_{z\,1},\ldots ,s_{z\,N}\rangle } _{\text{basis state (basis ket)}}\,.$$

Для идентичных частиц требования симметрии применяются как к аргументам положения, так и к аргументам спина волновой функции, поэтому она имеет в целом правильную симметрию.

Формулы для скалярных произведений представляют собой интегралы по всем координатам или импульсам и суммы по всем спиновым квантовым числам. Для общего случая N частиц со спином в 3-м измерении: $$(\Psi _{1},\Psi _{2})=\sum _{s_{z\,N}}\cdots \sum _{s_{z\,2}}\sum _{s_{z\,1}}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{1}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{2}\cdots \int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{N}\Psi _{1}^{*}\left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)\Psi _{2}\left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)$$это всего N трехмерных объемных интегралов и N сумм по спинам. Элементы дифференциального объема d ³ r _i также пишутся « dV _i » или « dx _i dy _i dz _i ».

Многомерные преобразования Фурье пространственных волновых функций положения или положения-спин дают пространственно-волновые функции импульса или импульса-спин.

Вероятностная интерпретация

Для общего случая N частиц со спином в 3d, если Ψ интерпретировать как амплитуду вероятности, плотность вероятности равна $$\rho \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)=\left|\Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)\right|^{2}$$

а вероятность того, что частица 1 находится в области R ₁ со спином s _{z 1} = m ₁ , а частица 2 находится в области R ₂ со спином s _{z 2} = m ₂ и т. д. в момент времени t является интегралом плотности вероятности по этим областям. и оценивается по этим числам вращения:

$P_{\mathbf {r} _{1}\in R_{1},s_{z\,1}=m_{1},\ldots ,\mathbf {r} _{N}\in R_{N},s_{z\,N}=m_{N}}(t)=\int _{R_{1}}d^{3}\mathbf {r} _{1}\int _{R_{2}}d^{3}\mathbf {r} _{2}\cdots \int _{R_{N}}d^{3}\mathbf {r} _{N}\left|\Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},m_{1}\cdots m_{N},t\right)\right|^{2}$

Физический смысл фазы

В нерелятивистской квантовой механике с помощью волнового уравнения Шредингера, зависящего от времени, можно показать, что уравнение:

$${\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {J} =0$$удовлетворен, где ${\textstyle \rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}}$ плотность вероятности и ${\textstyle \mathbf {J} (\mathbf {x} ,t)={\frac {\hbar }{2im}}(\psi ^{*}\nabla \psi -\psi \nabla \psi ^{*})={\frac {\hbar }{m}}{\text{Im}}(\psi ^{*}\nabla \psi )}$, известен как поток вероятности в соответствии с формой уравнения непрерывности приведенного выше уравнения.

Используя следующее выражение для волновой функции: $$\psi (\mathbf {x} ,t)={\sqrt {\rho (\mathbf {x} ,t)}}\exp {\frac {iS(\mathbf {x} ,t)}{\hbar }}$$где ${\textstyle \rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}}$ плотность вероятности и ${\textstyle S(\mathbf {x} ,t)}$ является фазой волновой функции, можно показать, что:

$$\mathbf {J} (\mathbf {x} ,t)={\frac {\rho \nabla S}{m}}$$

Следовательно, пространственное изменение фазы характеризует поток вероятности .

По классической аналогии, для ${\textstyle \mathbf {J} =\rho \mathbf {v} }$, количество ${\textstyle {\frac {\nabla S}{m}}}$ аналогично скорости. Обратите внимание, что это не подразумевает буквального толкования ${\textstyle {\frac {\nabla S}{m}}}$ как скорость, поскольку скорость и положение не могут быть определены одновременно в соответствии с принципом неопределенности . Подставив форму волновой функции в зависящее от времени волновое уравнение Шредингера и приняв классический предел, ${\textstyle \hbar |\nabla ^{2}S|\ll |\nabla S|^{2}}$:

$${\frac {1}{2m}}|\nabla S(\mathbf {x} ,t)|^{2}+V(\mathbf {x} )+{\frac {\partial S}{\partial t}}=0$$

Что аналогично уравнению Гамильтона-Якоби из классической механики. Эта интерпретация соответствует теории Гамильтона – Якоби , в которой ${\textstyle \mathbf {P} _{\text{class.}}=\nabla S}$, где S — главная функция Гамильтона .

Зависимость от времени

Основная статья: Динамические картинки

Для систем с не зависящими от времени потенциалами волновую функцию всегда можно записать как функцию степеней свободы, умноженных на зависящий от времени фазовый фактор, вид которого задается уравнением Шредингера. Для N частиц, учитывая только их положение и подавляя другие степени свободы, $$\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N},t)=e^{-iEt/\hbar }\,\psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})\,,$$где E — собственное значение энергии системы, соответствующее собственному состоянию Ψ . Волновые функции такого вида называются стационарными состояниями .

Временная зависимость квантового состояния и операторов может быть размещена в соответствии с унитарными преобразованиями операторов и состояний. Для любого квантового состояния |Ψ⟩ и оператора O в картине Шредингера |Ψ( t )⟩ изменяется со временем в соответствии с уравнением Шредингера, в то время как O является постоянным. В картине Гейзенберга все наоборот: |Ψ⟩ является постоянным, в то время как O ( t ) меняется со временем в соответствии с уравнением движения Гейзенберга. Картина Дирака (или взаимодействия) является промежуточной, зависимость от времени имеет место как в операторах, так и в состояниях, которые развиваются согласно уравнениям движения. Это полезно прежде всего при вычислении элементов S-матрицы .

Нерелятивистские примеры

Ниже приведены решения уравнения Шредингера для одной нерелятивистской бесспиновой частицы.

Конечный потенциальный барьер

Рассеяние на конечном потенциальном барьере высотой V ₀ . Указаны амплитуды и направление движущихся левых и правых волн. Красным цветом обозначены волны, использованные для определения амплитуды отражения и передачи. E > V ₀ для этой иллюстрации.

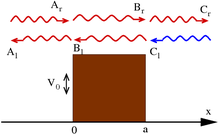
Одной из наиболее выдающихся особенностей волновой механики является возможность частицы достигать места с запредельным (в классической механике) силовым потенциалом . Распространенной моделью является « потенциальный барьер », одномерный случай имеет потенциал $$V(x)={\begin{cases}V_{0}&|x|<a\\0&|x|\geq a\end{cases}}$$а стационарные решения волнового уравнения имеют вид (при некоторых константах k , κ ) $$\Psi (x)={\begin{cases}A_{\mathrm {r} }e^{ikx}+A_{\mathrm {l} }e^{-ikx}&x<-a,\\B_{\mathrm {r} }e^{\kappa x}+B_{\mathrm {l} }e^{-\kappa x}&|x|\leq a,\\C_{\mathrm {r} }e^{ikx}+C_{\mathrm {l} }e^{-ikx}&x>a.\end{cases}}$$

Обратите внимание, что эти волновые функции не нормированы; см . в теории рассеяния обсуждение .

Стандартная интерпретация этого состоит в том, что поток частиц выпускается на шаг слева (направление отрицательного x ): установка A _r = 1 соответствует выбросу частиц по отдельности; термины, содержащие r _и C r _, означают движение вправо, а Al _A и C _l – влево. В соответствии с этой интерпретацией луча положите C _l = 0, поскольку частицы не приходят справа. Таким образом, применяя непрерывность волновых функций и их производных на границах, можно определить указанные выше константы.

Волновые функции трехмерных электронов в квантовой точке. Здесь показаны квантовые точки прямоугольной и треугольной формы. Энергетические состояния в прямоугольных точках относятся скорее к s-типу и p-типу . Однако в треугольной точке волновые функции смешаны из-за симметрии конфайнмента. (Нажмите, чтобы увидеть анимацию)

В полупроводниковом кристаллите, радиус которого меньше размера его экситона Боровского радиуса , экситоны сжимаются, что приводит к квантовому ограничению . Затем уровни энергии можно смоделировать с использованием модели частицы в ящике , в которой энергия различных состояний зависит от длины ящика.

Квантовый гармонический осциллятор

Волновые функции квантового гармонического осциллятора можно выразить через полиномы Эрмита H _n , они имеют вид $$\Psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}{\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)}$$где n = 0, 1, 2, ... .

Плотность вероятности электронов для первых нескольких атома водорода электронных орбиталей показана в виде поперечных сечений. Эти орбитали образуют ортонормированный базис волновой функции электрона. Различные орбитали изображены в разном масштабе.

Атом водорода

Волновые функции электрона в атоме водорода выражаются через сферические гармоники и обобщенные полиномы Лагерра (разные авторы определяют их по-разному - см. основную статью о них и об атоме водорода).

Удобно использовать сферические координаты, а волновую функцию можно разделить на функции каждой координаты: $$\Psi _{n\ell m}(r,\theta ,\phi )=R(r)\,\,Y_{\ell }^{m}\!(\theta ,\phi )$$где R — радиальные функции, а Y ^м
_ℓ ( θ , φ ) — сферические гармоники степени ℓ и порядка m . Это единственный атом, для которого уравнение Шрёдингера решено точно. Многоэлектронные атомы требуют аппроксимативных методов. Семейство решений: $$\Psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )$$где а ₀ = 4 πε ₀ ħ ² / я _е е ² – радиус Бора , л ^{2ℓ + 1}
_{n − ℓ − 1} — обобщенные полиномы Лагерра степени n — ℓ — 1 , n = 1, 2, ... — главное квантовое число , ℓ = 0, 1, ..., n − 1 — азимутальное квантовое число , m = - ℓ , - ℓ + 1, ..., ℓ - 1, ℓ магнитное квантовое число . Водородоподобные атомы имеют очень похожие решения.

Это решение не учитывает спин электрона.

На рисунке водородных орбиталей 19 фрагментов изображения представляют собой изображения волновых функций в пространстве позиций (их квадрат нормы). Волновые функции представляют собой абстрактное состояние, характеризующееся тройкой квантовых чисел ( n , ℓ , m ) в правом нижнем углу каждого изображения. Это главное квантовое число, квантовое число орбитального углового момента и магнитное квантовое число. Вместе с одним квантовым числом спин-проекции электрона это полный набор наблюдаемых.

Рисунок может служить иллюстрацией некоторых дополнительных свойств функциональных пространств волновых функций.

• В этом случае волновые функции интегрируемы с квадратом. Первоначально можно принять функциональное пространство как пространство суммируемых с квадратом функций, обычно обозначаемых L ² .
• Отображаемые функции являются решениями уравнения Шрёдингера. Очевидно, что не каждая функция из L ² удовлетворяет уравнению Шрёдингера для атома водорода. Таким образом, функциональное пространство является подпространством L ² .
• Отображаемые функции составляют основу функционального пространства. Каждой тройке ( n , ℓ , m ) соответствует базисная волновая функция. Если принять во внимание спин, то для каждой тройки имеется две базисные функции. Таким образом, функциональное пространство имеет счетный базис .
• Базисные функции взаимно ортонормированы .

Волновые функции и функциональные пространства

Понятие функциональных пространств естественным образом возникает при обсуждении волновых функций. Функциональное пространство — это набор функций, обычно с некоторыми определяющими требованиями к функциям (в данном случае они интегрируются с квадратом ), иногда с алгебраической структурой на множестве (в данном случае структура векторного пространства со скалярным произведением ), вместе с топологией на множестве. подмножества функционального пространства Последнее здесь будет использоваться редко, оно необходимо только для получения точного определения того, что означает замкнутость . Ниже будет сделан вывод, что функциональное пространство волновых функций является гильбертовым пространством . Это наблюдение является основой преобладающей математической формулировки квантовой механики.

Структура векторного пространства

Волновая функция — это элемент функционального пространства, частично характеризуемый следующими конкретными и абстрактными описаниями.

• Уравнение Шрёдингера линейно. Это означает, что ее решения, волновые функции, можно складывать и умножать на скаляры, чтобы получить новое решение. Множество решений уравнения Шрёдингера представляет собой векторное пространство.
• Принцип суперпозиции квантовой механики. Если Ψ и Φ — два состояния в абстрактном пространстве состояний квантово-механической системы, а a и b — любые два комплексных числа, то a Ψ + b Φ также является допустимым состоянием. (Считается ли нулевой вектор действительным состоянием («система отсутствует»), является вопросом определения. Нулевой вектор не ни в коем случае описывает состояние вакуума в квантовой теории поля.) Набор допустимых состояний представляет собой векторное пространство. .

Это сходство, конечно, не случайно. Следует также учитывать различия между помещениями.

Представительства

Базовые состояния характеризуются набором квантовых чисел. Это набор собственных значений набора наблюдаемых коммутирующих максимального . Физические наблюдаемые представляются линейными операторами, также называемыми наблюдаемыми, в векторном пространстве. Максимальность означает, что к множеству нельзя добавить никаких дополнительных алгебраически независимых наблюдаемых, которые коммутируют с уже существующими. Выбор такого множества можно назвать выбором представления .

• Постулат квантовой механики гласит, что физически наблюдаемая величина системы, такая как положение, импульс или спин, представляется линейным эрмитовым оператором в пространстве состояний. Возможными результатами измерения величины являются собственные значения оператора. На более глубоком уровне большинство наблюдаемых, а возможно, и все, возникают как генераторы симметрий .
• Физическая интерпретация заключается в том, что такой набор представляет собой то, что теоретически можно одновременно измерить с произвольной точностью. Соотношение неопределенности Гейзенберга запрещает одновременные точные измерения двух некоммутирующих наблюдаемых.
• Набор не уникален. Например, для одночастичной системы это может быть z -проекция положения и спина ( x , S _z ) импульса и спина y , или это может быть проекция ( p , S _y ) . В этом случае оператор, соответствующий положению ( оператор умножения в представлении положения), и оператор, соответствующий импульсу ( дифференциальный оператор в представлении положения), не коммутируют.
• После того, как представление выбрано, произвол все равно остается. Осталось выбрать систему координат. Это может, например, соответствовать выбору осей x , y и z или выбору криволинейных координат , примером которых являются сферические координаты, используемые для волновых функций атомов водорода. Этот окончательный выбор также фиксирует базис в абстрактном гильбертовом пространстве. Базовые состояния помечены квантовыми числами, соответствующими максимальному набору коммутирующих наблюдаемых и соответствующей системе координат.

Абстрактные состояния «абстрактны» только в том смысле, что произвольный выбор, необходимый для конкретного явного не дан описания. Это то же самое, что сказать, что не дан выбор максимального набора коммутирующих наблюдаемых. Это аналогично векторному пространству без заданного базиса. Волновые функции, соответствующие состоянию, соответственно, не уникальны. Эта неединственность отражает неединственность выбора максимального набора коммутирующих наблюдаемых. Для одной частицы со спином в одном измерении определенному состоянию соответствуют две волновые функции: x , Sz ) _Ψ и Ψ ( p , Sy ₍ ) , обе описывающие одно и то же состояние.

• Для каждого выбора максимальных коммутирующих наборов наблюдаемых для абстрактного пространства состояний существует соответствующее представление, которое связано с функциональным пространством волновых функций.
• Между всеми этими различными функциональными пространствами и абстрактным пространством состояний существуют взаимно однозначные соответствия (здесь без учета нормализации и ненаблюдаемых фазовых факторов), причем общим знаменателем здесь является конкретное абстрактное состояние. Например, связь между пространственными волновыми функциями импульса и положения, описывающими одно и то же состояние, представляет собой преобразование Фурье .

Каждый выбор представления следует рассматривать как определение уникального функционального пространства, в котором живут волновые функции, соответствующие этому выбору представления. Это различие лучше всего соблюдать, даже если можно утверждать, что два таких функциональных пространства математически равны, например, представляют собой набор функций, интегрируемых с квадратом. Тогда можно думать о функциональных пространствах как о двух различных копиях этого набора.

Внутренний продукт

Существует дополнительная алгебраическая структура векторных пространств волновых функций и абстрактного пространства состояний.

• С физической точки зрения различные волновые функции интерпретируются как перекрывающиеся в некоторой степени. Система в состоянии Ψ , которое не перекрывается с состоянием Φ, не может быть обнаружена в состоянии Φ при измерении. Но если Φ ₁ , Φ ₂ , … степени перекрывают Ψ в некоторой , есть шанс, что измерение системы, описываемой Ψ, будет найдено в состояниях Φ ₁ , Φ ₂ , … . Также правила отбора соблюдаются . Обычно они формулируются с учетом сохранения некоторых квантовых чисел. Это означает, что некоторые процессы, допустимые с некоторых точек зрения (например, сохранение энергии и импульса), не происходят, поскольку начальная и конечная полные волновые функции не перекрываются.
• Математически оказывается, что решения уравнения Шрёдингера для конкретных потенциалов каким-то образом ортогональны , обычно это описывается интегралом $$\int \Psi _{m}^{*}\Psi _{n}w\,dV=\delta _{nm},$$ где m , n — (наборы) индексов (квантовых чисел), обозначающих различные решения, строго положительная функция w называется весовой функцией, а δ _mn — дельта Кронекера . Интеграция осуществляется по всему соответствующему пространству.

Это мотивирует введение внутреннего продукта в векторном пространстве абстрактных квантовых состояний, совместимого с приведенными выше математическими наблюдениями при переходе к представлению. Его обозначают (Ψ, Φ) или в обозначениях Бракета ⟨Ψ|Φ⟩ . Получается комплексное число. Что касается внутреннего продукта, функциональное пространство является пространством внутреннего продукта . Явное появление скалярного произведения (обычно интеграла или суммы интегралов) зависит от выбора представления, а комплексное число (Ψ, Φ) — нет. Большая часть физической интерпретации квантовой механики проистекает из правила Борна . Он утверждает, что вероятность p обнаружить при измерении состояние Φ , если система находится в состоянии Ψ, равна $$p=|(\Phi ,\Psi )|^{2},$$где Φ и Ψ считаются нормированными. Рассмотрим эксперимент по рассеянию . В квантовой теории поля, если Φ _out описывает состояние в «далеком будущем» («внешнее состояние») после прекращения взаимодействия между рассеивающими частицами, а Ψ _в «включенном состоянии» в «далеком прошлом», то величины (Φ _out , Ψ _in ) , где Φ _out и Ψ _in варьируются по полному набору входных и выходных состояний соответственно, называется S-матрицей или матрицей рассеяния . Знание этого, по сути, означает решение имеющейся теории, по крайней мере, в том, что касается предсказаний. Измеримые величины, такие как скорость затухания и сечения рассеяния, можно рассчитать по S-матрице.

Гильбертово пространство

Приведенные выше наблюдения отражают суть функциональных пространств, элементами которых являются волновые функции. Однако описание еще не полное. Существует еще одно техническое требование к функциональному пространству, а именно полнота , которое позволяет определить пределы последовательностей в функциональном пространстве и гарантировать, что, если предел существует, он является элементом функционального пространства. Полное пространство внутреннего произведения называется гильбертовым пространством . Свойство полноты имеет решающее значение в современных методах лечения и применениях квантовой механики. Например, существование операторов проектирования или ортогональных проекций зависит от полноты пространства. Эти операторы проектирования, в свою очередь, необходимы для формулировки и доказательства многих полезных теорем, например спектральной теоремы . Это не очень важно для вводного курса квантовой механики, а технические подробности и ссылки можно найти в сносках, подобных следующей. Пространство Л ² представляет собой гильбертово пространство, внутренний продукт которого представлен позже. Функциональное пространство примера на рисунке является подпространством L ² . Подпространство гильбертова пространства называется гильбертовым пространством, если оно замкнуто.

Таким образом, набор всех возможных нормируемых волновых функций для системы с определенным выбором базиса вместе с нулевым вектором составляют гильбертово пространство.

Не все интересующие функции являются элементами некоторого гильбертова пространства, скажем L ² . Наиболее ярким примером является набор функций e ^{2 πi п · х ⁄ ч} . Это плоские волновые решения уравнения Шредингера для свободной частицы, но они не нормируемы, следовательно, не в L ² . Но они, тем не менее, являются основополагающими для описания. С их помощью можно выражать функции, нормируемые с помощью волновых пакетов . В некотором смысле они являются базисом (но не базисом гильбертова пространства или базисом Гамеля ), в котором могут быть выражены интересующие волновые функции. Существует также артефакт «нормализация к дельта-функции», который часто используется для удобства обозначений, см. ниже. Сами дельта-функции также не интегрируемы с квадратом.

Приведенное выше описание функционального пространства, содержащего волновые функции, в основном мотивировано математически. Функциональные пространства из-за полноты очень велики в определенном смысле . Не все функции являются реалистичным описанием любой физической системы. Например, в функциональном пространстве L ² можно найти функцию, которая принимает значение 0 для всех рациональных чисел и для -i иррациональных чисел в интервале [0, 1] . Это квадратично интегрируемо, но вряд ли может представлять физическое состояние.

Общие гильбертовы пространства

Хотя пространство решений в целом является гильбертовым пространством, существует множество других гильбертовых пространств, которые обычно встречаются в качестве ингредиентов.

• Квадратно интегрируемые комплексные функции на интервале [0, 2 π ] . Набор { e ^{интервал} /2 π , n ∈ Z } — базис гильбертова пространства, т. е. максимальное ортонормированное множество.
• Преобразование Фурье переводит функции из указанного выше пространства в элементы l ² ( Z ) , пространство суммируемых с квадратом функций Z → C . Последнее пространство является гильбертовым пространством, а преобразование Фурье является изоморфизмом гильбертовых пространств. Его основой является { е _я , я ∈ Z } с е _я ( j ) знак равно δ _ij , я , j ∈ Z .
• Самый простой пример остовных полиномов находится в пространстве функций, интегрируемых с квадратом на интервале [–1, 1] , для которого полиномы Лежандра являются базисом гильбертова пространства (полное ортонормированное множество).
• Интегрируемые с квадратом функции на единичной сфере S ² является гильбертовым пространством. Базисными функциями в этом случае являются сферические гармоники . Полиномы Лежандра являются составляющими сферических гармоник. Большинство задач с вращательной симметрией будут иметь «одно и то же» (известное) решение относительно этой симметрии, поэтому исходная проблема сводится к проблеме меньшей размерности.
• Соответствующие полиномы Лагерра появляются в задаче о водородной волновой функции после исключения сферических гармоник. Они охватывают гильбертово пространство суммируемых с квадратом функций на полубесконечном интервале [0, ∞) .

В более общем плане можно рассмотреть единую трактовку всех полиномиальных решений второго порядка уравнений Штурма – Лиувилля в рамках гильбертова пространства. К ним относятся полиномы Лежандра и Лагерра, а также полиномы Чебышева , полиномы Якоби и полиномы Эрмита . Все это на самом деле проявляется в физических задачах, последние — в гармоническом осцилляторе , и то, что в противном случае представляет собой сбивающий с толку лабиринт свойств специальных функций, становится организованной совокупностью фактов. Подробнее см. Byron & Fuller (1992 , глава 5).

Встречаются и конечномерные гильбертовы пространства. Пространство С ^н является гильбертовым пространством размерности n . Внутренний продукт — это стандартный внутренний продукт в этих пространствах. В нем находится «спиновая часть» волновой функции одной частицы.

• В нерелятивистском описании электрона n = 2 , а полная волновая функция является решением уравнения Паули .
• В соответствующей релятивистской трактовке n = 4 и волновая функция решает уравнение Дирака .

При большем количестве частиц ситуация усложняется. Необходимо использовать тензорные произведения и использовать теорию представлений задействованных групп симметрии ( группы вращения и группы Лоренца соответственно), чтобы извлечь из тензорного произведения пространства, в которых находятся (полные) спиновые волновые функции. (Дальнейшие проблемы возникают в релятивистском случае, если только частицы не являются свободными. См. уравнение Бете-Солпитера .) Соответствующие замечания относятся к понятию изоспина , для которого группа симметрии равна SU(2) . В моделях ядерных сил шестидесятых годов (полезных и сегодня, см. ядерная сила ) использовалась группа симметрии SU(3) . И в этом случае часть волновых функций, соответствующих внутренним симметриям, находится в некотором C ^н или подпространства тензорных произведений таких пространств.

• В квантовой теории поля основным гильбертовым пространством является пространство Фока . Он строится из свободных одночастичных состояний, т.е. волновых функций, если выбрано представление, и может вмещать любое конечное, не обязательно постоянное во времени, число частиц. Интересная (или, скорее, понятная ) динамика заключается не в волновых функциях, а в операторах поля , которые являются операторами, действующими в пространстве Фока. Таким образом, картина Гейзенберга является наиболее распространенным выбором (постоянные состояния, изменяющиеся во времени операторы).

Из-за бесконечномерной природы системы соответствующие математические инструменты являются объектами изучения функционального анализа .

Упрощенное описание

Непрерывность волновой функции и ее первой пространственной производной (в направлении x , координаты y и z не показаны) в некоторый момент времени t .

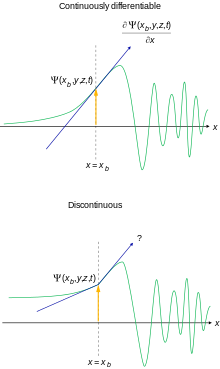
Не все вводные учебники идут по длинному пути и знакомят с полным гильбертовым пространственным механизмом, но основное внимание уделяется нерелятивистскому уравнению Шредингера в позиционном представлении для некоторых стандартных потенциалов. Следующие ограничения на волновую функцию иногда формулируются явно, чтобы расчеты и физическая интерпретация имели смысл:

• Волновая функция должна быть интегрируемой с квадратом . Это мотивировано копенгагенской интерпретацией волновой функции как амплитуды вероятности.
• Оно должно быть всюду непрерывным и всюду непрерывно дифференцируемым . Это мотивировано появлением уравнения Шрёдингера для большинства физически разумных потенциалов.

Для особых целей можно несколько смягчить эти условия. Если эти требования не выполняются, интерпретировать волновую функцию как амплитуду вероятности невозможно. Заметим, что из правила непрерывности производных могут возникнуть исключения в точках бесконечного разрыва потенциального поля. Например, в частице в ящике , где производная волновой функции может быть разрывной на границе ящика, где известно, что потенциал имеет бесконечный разрыв.

Это не меняет структуру гильбертова пространства, в котором обитают эти конкретные волновые функции, но меняет подпространство интегрируемых с квадратом функций L ² , которое является гильбертовым пространством, удовлетворяющим второму требованию, не замкнуто в L ² , следовательно, не является гильбертовым пространством само по себе. Функции, не соответствующие требованиям, по-прежнему необходимы как по техническим, так и по практическим причинам.

Подробнее о волновых функциях и абстрактном пространстве состояний

Основная статья: Квантовое состояние

Как было показано, набор всех возможных волновых функций в некотором представлении системы образует, вообще говоря, бесконечномерное гильбертово пространство. Из-за множества возможных вариантов базиса представления эти гильбертовы пространства не уникальны. Поэтому говорят об абстрактном гильбертовом пространстве, пространстве состояний , где выбор представления и базиса остается неопределенным. В частности, каждое состояние представлено как абстрактный вектор в пространстве состояний. Квантовое состояние |Ψ⟩ в любом представлении обычно выражается как вектор $$|\Psi \rangle =\sum _{\boldsymbol {\alpha }}\int d^{m}\!{\boldsymbol {\omega }}\,\,\Psi ({\boldsymbol {\alpha }},{\boldsymbol {\omega }},t)\,|{\boldsymbol {\alpha }},{\boldsymbol {\omega }}\rangle$$где

• | α , ω ⟩ базисные векторы выбранного представления
• д ^м ω = dω ₁ dω ₂ ... dω _m « элемент дифференциального объема » в непрерывных степенях свободы
• Ψ( α , ω , t ) компонента вектора |Ψ⟩ , называемая волновой функцией системы
• α = ( α ₁ , α ₂ , ..., α _n ) безразмерные дискретные квантовые числа
• ω = ( ω ₁ , ω ₂ , ..., ω _m ) непрерывные переменные (не обязательно безразмерные)

Эти квантовые числа индексируют компоненты вектора состояния. Более того, все α находятся в n- мерном множестве A = A ₁ × A ₂ × ... × An _, где каждое A _i представляет собой набор разрешенных значений для α _i ; все ω находятся в m -мерном «объеме» Ω ⊆ ℝ ^м где Ω = Ω ₁ × Ω ₂ × ... × Ω _m и каждое Ω _i ⊆ R представляет собой набор разрешенных значений для ω _i , подмножества действительных чисел R . Для общности n и m не обязательно равны.

Пример:

1. Для одной частицы в 3d со спином s , пренебрегая другими степенями свободы, используя декартовы координаты, мы могли бы взять α = ( s _z ) для спинового квантового числа частицы вдоль направления z, и ω = ( x , y , z ) для координат положения частицы. Здесь A = {− s , − s + 1, ..., s − 1, s } — набор разрешенных спиновых квантовых чисел, а Ω = R ³ представляет собой набор всех возможных положений частиц в трехмерном позиционном пространстве.
2. Альтернативный выбор — α = ( s _y ) для спинового квантового числа вдоль направления y и = ( p _x , py _, ω p _z ) для компонентов импульса частицы. В этом случае A и Ω такие же, как и раньше.

Плотность вероятности обнаружения системы в момент времени $t$в штате | α , ω ⟩ ​ $$\rho _{\alpha ,\omega }(t)=|\Psi ({\boldsymbol {\alpha }},{\boldsymbol {\omega }},t)|^{2}$$

Вероятность найти систему с α в некоторых или всех возможных конфигурациях с дискретными переменными, D ⊆ A , и ω в некоторых или всех возможных конфигурациях с непрерывными переменными, C ⊆ Ω , представляет собой сумму и интеграл по плотности, $$P(t)=\sum _{{\boldsymbol {\alpha }}\in D}\int _{C}\rho _{\alpha ,\omega }(t)\,\,d^{m}\!{\boldsymbol {\omega }}$$

Поскольку сумма всех вероятностей должна быть равна 1, условие нормировки $$1=\sum _{{\boldsymbol {\alpha }}\in A}\int _{\Omega }\rho _{\alpha ,\omega }(t)\,d^{m}\!{\boldsymbol {\omega }}$$должно соблюдаться на всех этапах эволюции системы.

Условие нормировки требует ρ d ^м Чтобы ω было безразмерным, согласно размерному анализу Ψ должно иметь те же единицы измерения, что и ( ω ₁ ω ₂ ... ω _m ) ^−1/2 .

Онтология

Основная статья: Интерпретации квантовой механики

Существует ли волновая функция на самом деле и что она собой представляет, являются основными вопросами интерпретации квантовой механики . Над этой проблемой ломали голову многие известные физики предыдущего поколения, такие как Шрёдингер , Эйнштейн и Бор . Некоторые защищают формулировки или варианты копенгагенской интерпретации (например, Бор, Вигнер и фон Нейман ), в то время как другие, такие как Уиллер или Джейнс , придерживаются более классического подхода. и рассматривать волновую функцию как представление информации в сознании наблюдателя, т.е. как меру нашего знания реальности. Некоторые, в том числе Шредингер, Бом , Эверетт и другие, утверждали, что волновая функция должна иметь объективное физическое существование. Эйнштейн считал, что полное описание физической реальности должно относиться непосредственно к физическому пространству и времени, в отличие от волновой функции, которая относится к абстрактному математическому пространству.

См. также

• Бозон
• Теория де Бройля – Бома
• Двухщелевой эксперимент
• Волна Фарадея
• Фермион
• Формулировка в фазовом пространстве
• Уравнение Шрёдингера
• Коллапс волновой функции
• Волновой пакет

Общие источники

• «Приложения квантовой механики» . Конспект лекций по курсу AP3303 . Кафедра квантовых нанонаучных исследований Делфтского технического университета. 2022.
• Аронс, AB; Пеппард, МБ (1965). «Предложение Эйнштейна о концепции фотона: перевод статьи Annalen der Physik 1905 года» (PDF) . Американский журнал физики . 33 (5): 367. Бибкод : 1965AmJPh..33..367A . дои : 10.1119/1.1971542 .
• Аткинс, PW (1974). Кванта: Справочник концепций . Кларендон Пресс. ISBN  978-0-19-855494-3 .
• Бор, Н. (1985). Калькар, Дж. (ред.). Нильс Бор — Собрание сочинений: Основы квантовой физики I (1926 — 1932) . Том. 6. Амстердам: Северная Голландия. ISBN  978-044453289-3 .
• Борн, М. (1926а). «К квантовой механике столкновительных процессов». З. Физ . 37 (12): 863–867. Бибкод : 1926ZPhy...37..863B . дои : 10.1007/bf01397477 . S2CID   119896026 .
• Борн, М. (1926б). «Квантовая механика столкновительных процессов». З. Физ . 38 (11–12): 803–827. Бибкод : 1926ZPhy...38..803B . дои : 10.1007/bf01397184 . S2CID   126244962 .
• Борн, М. (1927). «Физические аспекты квантовой механики» . Природа . 119 (2992): 354–357. Бибкод : 1927Natur.119..354B . дои : 10.1038/119354a0 .
• Родился М. (11 декабря 1954 г.). «Статистическая интерпретация квантовой механики» . Нобелевская лекция . 122 (3172). Нобелевский фонд : 675–9. дои : 10.1126/science.122.3172.675 . ПМИД   17798674 .
• де Бройль, Л. (1923). «Радиации — Ondes et quanta» [Радиация — Волны и кванты]. Comptes Rendus (на французском языке). 177 : 507–510, 548, 630. Интернет-копия (на французском языке) Интернет-копия (на английском языке)
• де Бройль, Л. (1960). Нелинейная волновая механика: причинная интерпретация . Амстердам: Elsevier – через Интернет-архив .
• Байрон, ФРВ; Фуллер, Р.В. (1992) [Впервые опубликовано в 1969 году]. Математика классической и квантовой физики . Дуврские книги по физике (переработанная редакция). Дуврские публикации . ISBN  978-0-486-67164-2 – через Интернет-архив .
• Камиллери, К. (2009). Гейзенберг и интерпретация квантовой механики: физик как философ . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-88484-6 .
• Конвей, Дж. Б. (1990). Курс функционального анализа . Тексты для аспирантов по математике. Том. 96. Спрингер Верлаг . ISBN  978-0-387-97245-9 .
• Дирак, ПАМ (1939). «Новые обозначения квантовой механики». Математические труды Кембриджского философского общества . 35 (3): 416–418. Бибкод : 1939PCPS...35..416D . дои : 10.1017/S0305004100021162 . S2CID   121466183 .
• Дирак, ПАМ (1982). Принципы квантовой механики . Международная серия монографий по физике (4-е изд.). Издательство Оксфордского университета. ISBN  0-19-852011-5 .
• Эйнштейн, А. (1905). «Об эвристическом взгляде на образование и преобразование света» . Анналы физики (на немецком языке). 17 (6): 132–148. Бибкод : 1905АнП...322..132Е . дои : 10.1002/andp.19053220607 .
• Эйнштейн, А. (1916). «К квантовой теории излучения». Объявления Физического общества Цюриха . 18 :47–62.
• Эйнштейн, А. (1917). «К квантовой теории излучения». Физический журнал (на немецком языке). 18 :121-128. Бибкод : 1917PhyZ...18..121E .
• Эйнштейн, А. (1998). Шилпп, Пенсильвания (ред.). Альберт Эйнштейн: философ-ученый . Библиотека живых философов. Том. VII (3-е изд.). Издательская компания La Salle, Иллинойс: Открытый суд. ISBN  978-0-87548-133-3 .
• Айсберг, Роберт Мартин; Резник, Роберт (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Джон Уайли и сыновья. ISBN  978-0-471-87373-0 – через Интернет-архив .
• Грейнер, В .; Рейнхардт, Дж. (2008). Квантовая электродинамика (4-е изд.). спрингер. ISBN  978-354087560-4 .
• Гриффитс, диджей (2004). Введение в квантовую механику (2-е изд.). Эссекс, Англия: Pearson Education. ISBN  978-013111892-8 .
• Гриффитс, Дэвид (2008). Введение в элементарные частицы . Вайли-ВЧ. стр. 162 и далее. ISBN  978-3-527-40601-2 .
• тер Хаар, Д. (1967). Старая квантовая теория . Пергамон Пресс . стр. 167–183 . LCCN   66029628 – через Интернет-архив .
• Ханле, Пенсильвания (1977), «Реакция Эрвина Шрёдингера на диссертацию Луи де Бройля по квантовой теории», Isis , 68 (4): 606–609, doi : 10.1086/351880 , S2CID   121913205
• Гейзенберг, В. (1958). Физика и философия: революция в современной науке . Нью-Йорк: Harper & Row – через Интернет-архив .
• Джейнс, ET (2003). Ларри, Дж. (ред.). Теория вероятностей: логика науки . Издательство Кембриджского университета . ISBN  978-0-521 59271-0 .
• Ландау, LD ; Лифшиц, Э.М. (1977). Квантовая механика: нерелятивистская теория . Том. 3 (3-е изд.). Пергамон Пресс . ISBN  978-0-08-020940-1 . Онлайн-копия
• Ландсман, Н.П. (2009). «Правило рождения и его интерпретация» (PDF) . Сборник квантовой физики . Берлин, Гейдельберг: Springer Berlin Heidelberg. стр. 64–70. дои : 10.1007/978-3-540-70626-7_20 . ISBN  978-3-540-70622-9 .
• Лернер, Р.Г. ; Тригг, Г.Л. (1991). Энциклопедия физики (2-е изд.). Издательство ВХК. ISBN  978-0-89573-752-6 – через Интернет-архив .
• Людвиг, Г. (1968). Волновая механика . Оксфорд, Великобритания: Пергамон Пресс. ISBN  978-0-08-203204-5 . LCCN   66-30631 – через Интернет-архив .
• Мартин, БР; Шоу, Г. (2008). Физика элементарных частиц . Манчестерская серия по физике (3-е изд.). Джон Уайли и сыновья. ISBN  978-0-470-03294-7 .
• Мердок, Д. (1987). Философия физики Нильса Бора . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-33320-7 – через Интернет-архив .
• Ньютон, Р.Г. (2002). Квантовая физика: Учебник для аспиранта . Нью-Йорк: Спрингер. ISBN  978-0-387-95473-8 .
• Паули, Вольфганг (1927). «К квантовой механике магнитного электрона». Журнал физики (на немецком языке). 43 (9–10): 601–623. Бибкод : 1927ZPhy...43..601P . дои : 10.1007/bf01397326 . S2CID   128228729 .
• Пелег, Ю.; Пнини, Р.; Заарур, Э.; Хехт, Э. (2010). Квантовая механика . Очерки Шаума (2-е изд.). МакГроу Хилл. ISBN  978-0-07-162358-2 .
• Рэй, AIM (2008). Квантовая механика . Том. 2 (5-е изд.). Группа Тейлор и Фрэнсис. ISBN  978-1-5848-89700 .
• Шрёдингер, Э. (1926). «Волновая теория механики атомов и молекул» (PDF) . Физический обзор . 28 (6): 1049–1070. Бибкод : 1926PhRv...28.1049S . дои : 10.1103/PhysRev.28.1049 . Архивировано из оригинала (PDF) 17 декабря 2008 года.
• Шанкар, Р. (1994). Принципы квантовой механики (2-е изд.). ISBN  978-030644790-7 .
• Типлер, Пенсильвания; Моска, Г.; Фриман (2008). Физика для ученых и инженеров - с современной физикой (6-е изд.). У. Х. Фриман. ISBN  978-0-7167-8964-2 .
• Тревес, Франсуа (2006). Топологические векторные пространства, распределения и ядра . Минеола, Нью-Йорк: Курьерская корпорация. ISBN  978-0-486-45352-1 .
• Вайнберг, С. (2002), Квантовая теория полей , том. 1, Издательство Кембриджского университета, ISBN  978-0-521-55001-7 – через Интернет-архив
• Вайнберг, С. (2013), Лекции по квантовой механике , Cambridge University Press, ISBN  978-1-107-02872-2
• Уилер, Дж.А. ; Журек, WH (1983). Квантовая теория и измерения . Принстон, штат Нью-Джерси: Издательство Принстонского университета.
• Янг, HD; Фридман, РА (2008). Пирсон (ред.). Физика Университета Сирса и Земански (12-е изд.). Аддисон-Уэсли. ISBN  978-0-321-50130-1 .
• Зеттили, Н. (2009). Квантовая механика: концепции и приложения (2-е изд.). Уайли. ISBN  978-0-470-02679-3 .
• Цвибах, Бартон (2009). Первый курс теории струн . Издательство Кембриджского университета. ISBN  978-0-521-88032-9 .

Дальнейшее чтение

• Ким, Ён Ки (2 сентября 2000 г.). Практическая атомная физика (PDF) . Национальный институт стандартов и технологий. стр. 1 (55 с). Архивировано из оригинала (PDF) 22 июля 2011 года.
• Полкингхорн, Джон (2002). Квантовая теория, очень краткое введение . Издательство Оксфордского университета. ISBN  978-0-19-280252-1 .

Внешние ссылки

• Квантовая механика для инженеров
• Спин-волновые функции Нью-Йоркского университета
• Возвращение к идентичным частицам, Майкл Фаулер
• Природа многоэлектронных волновых функций
• Квантовая механика и квантовые вычисления в BerkeleyX. Архивировано 13 мая 2013 г. в Wayback Machine.
• Эйнштейн, Квантовая теория излучения