Распределение Бернулли

Распределение Бернулли

Функция массы вероятности 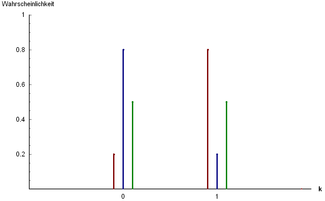Три примера распределения Бернулли:   $P(x=0)=0{.}2$ и $P(x=1)=0{.}8$   $P(x=0)=0{.}8$ и $P(x=1)=0{.}2$   $P(x=0)=0{.}5$ и $P(x=1)=0{.}5$
Параметры	$0\leq p\leq 1$ $q=1-p$
Поддерживать	$k\in \{0,1\}$
ПМФ	${\begin{cases}q=1-p&{\text{if }}k=0\\p&{\text{if }}k=1\end{cases}}$
CDF	${\begin{cases}0&{\text{if }}k<0\\1-p&{\text{if }}0\leq k<1\\1&{\text{if }}k\geq 1\end{cases}}$
Иметь в виду	$p$
медиана	${\begin{cases}0&{\text{if }}p<1/2\\\left[0,1\right]&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}$
Режим	${\begin{cases}0&{\text{if }}p<1/2\\0,1&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}$
Дисперсия	$p(1-p)=pq$
БЕЗУМНЫЙ	$2p(1-p)=2pq$
асимметрия	${\frac {q-p}{\sqrt {pq}}}$
Избыточный эксцесс	${\frac {1-6pq}{pq}}$
Энтропия	$-q\ln q-p\ln p$
МГФ	$q+pe^{t}$
CF	$q+pe^{it}$
ПГФ	$q+pz$
Информация о Фишере	${\frac {1}{pq}}$

В теории вероятностей и статистике распределение Бернулли , названное в честь швейцарского математика Якоба Бернулли , - дискретное распределение вероятностей случайной величины , принимающей значение 1 с вероятностью $p$ и значение 0 с вероятностью $q=1-p$. Менее формально его можно рассматривать как модель набора возможных результатов любого отдельного эксперимента , в котором задается вопрос «да-нет» . Такие вопросы приводят к результатам , имеющим булево значение: один бит , значение которого равно успех/ да / истина / единица с вероятностью p и отказ/нет/ ложь / ноль с вероятностью q . Его можно использовать для представления (возможно, необъективного) подбрасывания монеты , где 1 и 0 будут обозначать «орёл» и «решку» соответственно, а p будет вероятностью выпадения монеты орлом (или наоборот, где 1 будет обозначать решку). и p будет вероятностью решки). В частности, недобросовестные монеты имели бы $p\neq 1/2.$

Распределение Бернулли — это частный случай биномиального распределения , когда проводится одно испытание (поэтому для такого биномиального распределения n будет равно 1). Это также частный случай двухточечного распределения , для которого возможные результаты не обязательно должны быть 0 и 1.

Характеристики

Если $X$ — случайная величина с распределением Бернулли, то:

$\Pr(X=1)=p=1-\Pr(X=0)=1-q.$

Функция вероятностной массы $f$ этого распределения по возможным результатам k , есть

$f(k;p)={\begin{cases}p&{\text{if }}k=1,\\q=1-p&{\text{if }}k=0.\end{cases}}$

Это также можно выразить как

$f(k;p)=p^{k}(1-p)^{1-k}\quad {\text{for }}k\in \{0,1\}$

или как

$f(k;p)=pk+(1-p)(1-k)\quad {\text{for }}k\in \{0,1\}.$

Распределение Бернулли является частным случаем биномиального распределения с $n=1.$

Эксцесс значений стремится к бесконечности для высоких и низких $p,$ но для $p=1/2$ двухточечные распределения, включая распределение Бернулли, имеют меньший избыточный эксцесс , а именно -2, чем любое другое распределение вероятностей.

Распределения Бернулли для $0\leq p\leq 1$ образуют экспоненциальное семейство .

максимального правдоподобия Оценка $p$ на основе случайной выборки – это выборочное среднее .

Функция распределения вероятностей по массе эксперимента Бернулли вместе с соответствующей кумулятивной функцией распределения.

Иметь в виду

Ожидаемое значение случайной величины Бернулли $X$ является

$\operatorname {E} [X]=p$

Это связано с тем, что для распределенной по Бернулли случайной величины $X$ с $\Pr(X=1)=p$ и $\Pr(X=0)=q$ мы находим

$\operatorname {E} [X]=\Pr(X=1)\cdot 1+\Pr(X=0)\cdot 0=p\cdot 1+q\cdot 0=p.$

Дисперсия

Дисперсия распределения Бернулли $X$ является

$\operatorname {Var} [X]=pq=p(1-p)$

Сначала мы находим

$\operatorname {E} [X^{2}]=\Pr(X=1)\cdot 1^{2}+\Pr(X=0)\cdot 0^{2}=p\cdot 1^{2}+q\cdot 0^{2}=p=\operatorname {E} [X]$

Из этого следует

$\operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=\operatorname {E} [X]-\operatorname {E} [X]^{2}=p-p^{2}=p(1-p)=pq$

Имея этот результат, легко доказать, что для любого распределения Бернулли его дисперсия будет иметь значение внутри $[0,1/4]$.

асимметрия

Асимметрия ​ ​ ${\frac {q-p}{\sqrt {pq}}}={\frac {1-2p}{\sqrt {pq}}}$. Когда мы берем стандартизированную распределенную случайную величину Бернулли ${\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}$ мы находим, что эта случайная величина достигает ${\frac {q}{\sqrt {pq}}}$ с вероятностью $p$ и достигает $-{\frac {p}{\sqrt {pq}}}$ с вероятностью $q$. Таким образом мы получаем

${\begin{aligned}\gamma _{1}&=\operatorname {E} \left[\left({\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}\right)^{3}\right]\\&=p\cdot \left({\frac {q}{\sqrt {pq}}}\right)^{3}+q\cdot \left(-{\frac {p}{\sqrt {pq}}}\right)^{3}\\&={\frac {1}{{\sqrt {pq}}^{3}}}\left(pq^{3}-qp^{3}\right)\\&={\frac {pq}{{\sqrt {pq}}^{3}}}(q-p)\\&={\frac {q-p}{\sqrt {pq}}}.\end{aligned}}$

Высшие моменты и кумулянты

Все необработанные моменты равны из-за того, что $1^{k}=1$ и $0^{k}=0$.

$\operatorname {E} [X^{k}]=\Pr(X=1)\cdot 1^{k}+\Pr(X=0)\cdot 0^{k}=p\cdot 1+q\cdot 0=p=\operatorname {E} [X].$

Центральный момент заказа $k$ дается

$\mu _{k}=(1-p)(-p)^{k}+p(1-p)^{k}.$

Первые шесть центральных моментов

${\begin{aligned}\mu _{1}&=0,\\\mu _{2}&=p(1-p),\\\mu _{3}&=p(1-p)(1-2p),\\\mu _{4}&=p(1-p)(1-3p(1-p)),\\\mu _{5}&=p(1-p)(1-2p)(1-2p(1-p)),\\\mu _{6}&=p(1-p)(1-5p(1-p)(1-p(1-p))).\end{aligned}}$

Высшие центральные моменты можно более компактно выразить через $\mu _{2}$ и $\mu _{3}$

${\begin{aligned}\mu _{4}&=\mu _{2}(1-3\mu _{2}),\\\mu _{5}&=\mu _{3}(1-2\mu _{2}),\\\mu _{6}&=\mu _{2}(1-5\mu _{2}(1-\mu _{2})).\end{aligned}}$

Первые шесть кумулянтов

${\begin{aligned}\kappa _{1}&=p,\\\kappa _{2}&=\mu _{2},\\\kappa _{3}&=\mu _{3},\\\kappa _{4}&=\mu _{2}(1-6\mu _{2}),\\\kappa _{5}&=\mu _{3}(1-12\mu _{2}),\\\kappa _{6}&=\mu _{2}(1-30\mu _{2}(1-4\mu _{2})).\end{aligned}}$

Связанные дистрибутивы

• Если $X_{1},\dots ,X_{n}$ являются независимыми, одинаково распределенными ( iid ) случайными величинами, все испытания Бернулли с вероятностью успеха p , то их сумма распределяется согласно биномиальному распределению с параметрами n и p :

  $\sum _{k=1}^{n}X_{k}\sim \operatorname {B} (n,p)$ ( биномиальное распределение ).

Распределение Бернулли — это просто $\operatorname {B} (1,p)$, также записанный как ${\textstyle \mathrm {Bernoulli} (p).}$

• Категориальное распределение является обобщением распределения Бернулли для переменных с любым постоянным числом дискретных значений.
• является Бета-распределение сопряженным априорным распределением Бернулли.
• Геометрическое распределение моделирует количество независимых и идентичных испытаний Бернулли, необходимых для достижения одного успеха.
• Если ${\textstyle Y\sim \mathrm {Bernoulli} \left({\frac {1}{2}}\right)}$, затем ${\textstyle 2Y-1}$ имеет распределение Радемахера .

См. также

• Процесс Бернулли — случайный процесс, состоящий из последовательности независимых испытаний Бернулли.
• Выборка Бернулли
• Бинарная функция энтропии
• Бинарная диаграмма решений

Дальнейшее чтение

• Джонсон, Нидерланды; Коц, С.; Кемп, А. (1993). Одномерные дискретные распределения (2-е изд.). Уайли. ISBN  0-471-54897-9 .
• Питман, Джон Г. (1963). Введение в прикладную статистику . Нью-Йорк: Харпер и Роу. стр. 162–171.

Внешние ссылки

• «Биномиальное распределение» , Математическая энциклопедия , EMS Press , 2001 [1994] .
• Вайсштейн, Эрик В. «Распределение Бернулли» . Математический мир .
• Интерактивная графика: Одномерные отношения распределения .