Равномерный 5-многогранник

Графы правильных и однородных 5-многогранников.
5-симплекс	Выпрямленный 5-симплекс		Усеченный 5-симплекс
Согнутый 5-симплекс	Ранцинированный 5-симплекс		Стерический 5-симплекс
5-ортоплекс	Усеченный 5-ортоплекс		Выпрямленный 5-ортоплекс
Сочлененный 5-ортоплекс		Ранцинированный 5-ортоплекс
Согнутый 5-куб	Ранцинированный 5-кубовый		Стерилизованный 5-куб.
5-куб	Усеченный 5-куб		Ректифицированный 5-куб
5-демикуб		Усеченный 5-микуб
Согнутый 5-демикуб		Ранцинированный 5-демикуб

В геометрии однородный — это 5-многогранник пятимерный однородный многогранник . По определению однородный 5-многогранник является вершинно-транзитивным и построен из однородных 4- многогранников .

Полный набор выпуклых однородных 5-многогранников не определен, но многие из них можно построить как конструкции Витхоффа из небольшого набора групп симметрии . Эти операции построения представлены перестановками колец диаграмм Кокстера .

История открытия

Правильные многогранники : (выпуклые грани)
- 1852 : Людвиг Шлефли доказал в своей рукописной теории множественной непрерывности , что существует ровно 3 правильных многогранника в 5 или более измерениях .
Выпуклые полуправильные многогранники категории Коксетера : (Различные определения до однородной )
- 1900 : Торольд Госсет перечислил список непризматических полуправильных выпуклых многогранников с правильными гранями ( выпуклые правильные 4-многогранники ) в своей публикации «О правильных и полуправильных фигурах в пространстве n измерений» . ^[1]
Выпуклые однородные многогранники :
- 1940–1988 : Поиск систематически расширялся Х. С. М. Коксетером в его публикации «Правильные и полуправильные многогранники I, II и III» .
- 1966 : Норман В. Джонсон защитил докторскую диссертацию. Диссертация под руководством Кокстера, «Теория однородных многогранников и сот» , Университет Торонто.
Невыпуклые однородные многогранники :
- 1966 : Джонсон в своей диссертации описывает две невыпуклые однородные антипризмы в пятимерном пространстве. ^[2]
- 2000–2024 : Джонатан Бауэрс и другие исследователи ищут другие невыпуклые однородные 5-многогранники. ^[3] с текущим количеством известных однородных 5-многогранников 1348 вне бесконечных семейств (выпуклых и невыпуклых), исключая призмы однородных 4-многогранников. Список не является полным. ^[4]^[5]

Правильные 5-многогранники

Правильные 5-многогранники могут быть представлены символом Шлефли {p,q,r,s} с s {p,q,r} 4-многогранниками вокруг каждой грани . Таких правильных многогранников ровно три, все выпуклые:

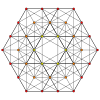
{3,3,3,3} - 5-симплекс
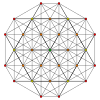
{4,3,3,3} - 5-куб
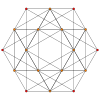
{3,3,3,4} - 5-ортоплекс

Не существует невыпуклых правильных многогранников в пяти измерениях и выше.

Выпуклые однородные 5-многогранники

Нерешенная задача по математике :

Каков полный набор выпуклых однородных 5-многогранников? ^[6]

(еще нерешенные задачи по математике)

Известно 104 выпуклых однородных 5-многогранников, а также ряд бесконечных семейств дуопризм и дуопризм многоугольник-многогранник. Все, кроме большой призмы антипризмы, основаны на конструкциях Витхоффа , симметрии отражения, созданной с помощью групп Кокстера . ^{[ нужна ссылка ]}

Симметрия однородных 5-многогранников в четырех измерениях

— 5-симплекс правильная форма семейства A ₅ . 5 -куб и 5-ортоплекс — правильные формы _{семейства B5} . Бифуркационный граф семейства D ₅ содержит 5-ортоплекс , а также 5-демикуб , который является чередующимся 5-кубом .

Каждый отражающий однородный 5-многогранник может быть построен в одной или нескольких отражающих точечных группах в 5 измерениях с помощью конструкции Витхоффа , представленной кольцами вокруг перестановок узлов на диаграмме Коксетера . Зеркальные гиперплоскости можно сгруппировать, как видно по цветным узлам, разделенным четными ветвями. Группы симметрии вида [a,b,b,a] имеют расширенную симметрию [[a,b,b,a]], как и [3,3,3,3], удваивая порядок симметрии. Однородные многогранники в этой группе с симметричными кольцами содержат эту расширенную симметрию.

Если все зеркала данного цвета не имеют кольца (неактивны) в данном однородном многограннике, он будет иметь конструкцию с более низкой симметрией за счет удаления всех неактивных зеркал. Если все узлы данного цвета окольцованы (активны), операция чередования может создать новый 5-многогранник с киральной симметрией, показанный как «пустые» узлы в кружке», но геометрия обычно не настраивается для создания единых решений.

Фундаментальные семьи ^[7]

Группа символ	Заказ	Кронштейн обозначение	Коммутатор подгруппа	Коксетер число (час)	Размышления м = 5/2 ч ^[8]
A_А5	720	[3,3,3,3]	[3,3,3,3] ⁺	6		15
Д ₅	1920	[3,3,3 ^1,1]	[3,3,3 ^1,1] ⁺	8		20
Б ₅	3840	[4,3,3,3]	[3,3,3 ^1,1] ⁺	10	5	20

Однородные призмы

Существует 5 конечных категориальных однородных призматических семейств многогранников, основанных на непризматических однородных 4-многогранниках . Существует одно бесконечное семейство 5-многогранников, основанное на призмах равномерных дуопризм {p}×{q}×{ }.

Коксетер группа	Заказ	Коксетер обозначение	Коммутатор подгруппа	Размышления
А ₄ А ₁	120	[3,3,3,2] = [3,3,3]×[ ]	[3,3,3] ⁺			10		1
Д ₄ А ₁	384	[3 ^1,1,1,2] = [3 ^1,1,1]×[ ]	[3 ^1,1,1] ⁺			12		1
Б ₄ А ₁	768	[4,3,3,2] = [4,3,3]×[ ]	[3 ^1,1,1] ⁺		4	12		1
Ф ₄ А ₁	2304	[3,4,3,2] = [3,4,3]×[ ]	[3 ⁺,4,3 ⁺]		12	12		1
Ч ₄ А ₁	28800	[5,3,3,2] = [3,4,3]×[ ]	[5,3,3] ⁺			60		1
Дуопризматические призмы (для четных изображений используйте 2p и 2q)
Я ₂ ( п )Я ₂ ( q )А ₁	8 шт.	[p,2,q,2] = [p]×[q]×[ ]	[п ⁺,2,д ⁺]		п	д		1
Я ₂ (2 п )Я ₂ ( q )А ₁	16 кв.м.	[2p,2,q,2] = [2p]×[q]×[ ]		п	п	д		1
Я ₂ (2 п )И ₂ (2 р )А ₁	32 кв.м.	[2p,2,2q,2] = [2p]×[2q]×[ ]		п	п	д	д	1

Равномерные дуопризмы

Существует 3 категориальных однородных дуопризматических семейства многогранников, основанных на декартовых произведениях однородных многогранников и правильных многоугольников : { q , r }×{ p }.

Коксетер группа	Заказ	Коксетер обозначение	Коммутатор подгруппа	Размышления
Призматические группы (для четных используйте 2p)
А ₃ I ₂ ( п )	48 р	[3,3,2, п ] = [3,3]×[ п ]	[(3,3) ⁺,2, п ⁺]		6	п
А ₃ И ₂ ( 2п )	96 р	[3,3,2,2 п ] = [3,3]×[2 п ]			6	п	п
Б ₃ я ₂ ( п )	96 р	[4,3,2, п ] = [4,3]×[ п ]		3	6	п
Б ₃ И ₂ ( 2п )	192 стр.	[4,3,2,2 п ] = [4,3]×[2 п ]		3	6	п	п
Ч ₃ я ₂ ( п )	240 р.	[5,3,2, п ] = [5,3]×[ п ]	[(5,3) ⁺,2, п ⁺]		15	п
Ч ₃ И ₂ ( 2п )	480 р.	[5,3,2,2 п ] = [5,3]×[2 п ]	[(5,3) ⁺,2, п ⁺]		15	п	п

Перечисление выпуклых однородных 5-многогранников

Семейство симплекс : А ₅ [3 ⁴]
- 19 однородных 5-многогранников
Гиперкуб / Ортоплекс Семейство _{: B 5} [4,3 ³]
- 31 однородный 5-многогранник
Демигиперкуб Д ₅ /Е _{5 : [3}Семейство ^2,1,1]
- 23 однородных 5-многогранника (8 уникальных)
Полихоральные призмы:
- 56 однородных 5-многогранников (45 уникальных) конструкций на основе призматических семейств: [3,3,3]×[ ], [4,3,3]×[ ], [5,3,3]×[ ], [3 ^1,1,1]×[ ].
- Один невитоффиан . Призма большой антипризмы — единственный известный невитоффов выпуклый однородный 5-многогранник, построенный из двух больших антипризм, соединенных многогранными призмами.

В результате получается: 19+31+8+45+1=104.

Кроме того, имеются:

Бесконечно много однородных 5-многогранных конструкций на основе призматических семейств дуопризм: [ p ]×[ q ]×[ ].
Бесконечно множество однородных 5-многогранных конструкций на основе дуопризматических семейств: [3,3]×[ p ], [4,3]×[ p ], [5,3]×[ p ].

А ₅Семья

Существует 19 форм, основанных на всех перестановках диаграмм Кокстера с одним или несколькими кольцами. (16+4-1 случаев)

Они названы Норманом Джонсоном в честь строительных операций Уитхоффа на основе обычного 5-симплекса (гексатерона).

Семейство A ₅ факториал имеет симметрию порядка 720 (6- ) . 7 из 19 фигур с симметрично обведенными диаграммами Кокстера имеют двойную симметрию, порядок 1440.

Координаты однородных 5-многогранников с 5-симплексной симметрией могут быть сгенерированы как перестановки простых целых чисел в 6-мерном пространстве, все в гиперплоскостях с нормальным вектором (1,1,1,1,1,1).

#	Базовая точка	Джонсона Система именования Имя Бауэрса и (аббревиатура) Диаграмма Кокстера	Количество элементов k-грани					Вертекс фигура	Количество фасетов по местоположению: [3,3,3,3]
#	Базовая точка		4	3	2	1	0	Вертекс фигура	[3,3,3] (6)	[3,3,2] (15)	[3,2,3] (20)	[2,3,3] (15)	[3,3,3] (6)	Все
1	(0,0,0,0,0,1) или (0,1,1,1,1,1)	5-симплекс гексатерон (хикс)	6	15	20	15	6	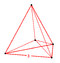{3,3,3}	{3,3,3}	-	-	-	-
2	(0,0,0,0,1,1) или (0,0,1,1,1,1)	Выпрямленный 5-симплекс выпрямленный гексатерон (rix)	12	45	80	60	15	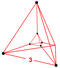т{3,3}×{ }	г {3,3,3}	-	-	-	{3,3,3}
3	(0,0,0,0,1,2) или (0,1,2,2,2,2)	Усеченный 5-симплекс усеченный гексатерон (тикс)	12	45	80	75	30	Тетрах.pyr	т{3,3,3}	-	-	-	{3,3,3}
4	(0,0,0,1,1,2) или (0,1,1,2,2,2)	Согнутый 5-симплекс маленький ромбический гексатерон (саркс)	27	135	290	240	60	призма-клин	рр{3,3,3}	-	-	{ }×{3,3}	г {3,3,3}
5	(0,0,0,1,2,2) или (0,0,1,2,2,2)	Битусеченный 5-симплекс усеченный гексатерон (биттикс)	12	60	140	150	60		2т{3,3,3}	-	-	-	т{3,3,3}
6	(0,0,0,1,2,3) или (0,1,2,3,3,3)	Количественно усеченный 5-симплекс большой ромбический гексатерон (гаркс)	27	135	290	300	120		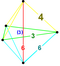тр{3,3,3}	-	-	{ }×{3,3}	т{3,3,3}
7	(0,0,1,1,1,2) или (0,1,1,1,2,2)	Ранцинированный 5-симплекс маленький призматичный гексатерон (спикс)	47	255	420	270	60		т _0,3 {3,3,3}	-	{3}×{3}	{ }×r{3,3}	г {3,3,3}
8	(0,0,1,1,2,3) или (0,1,2,2,3,3)	Runcitусеченный 5-симплекс призматоусеченный гексатерон (паттикс)	47	315	720	630	180		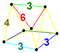т _0,1,3 {3,3,3}	-	{6}×{3}	{ }×r{3,3}	рр{3,3,3}
9	(0,0,1,2,2,3) или (0,1,1,2,3,3)	Рунцикантеллярный 5-симплекс призматоромбовидный гексатерон (пиркс)	47	255	570	540	180		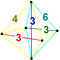т _0,1,3 {3,3,3}	-	{3}×{3}	{ }×t{3,3}	2т{3,3,3}
10	(0,0,1,2,3,4) или (0,1,2,3,4,4)	Ранчикантиусеченный 5-симплекс большой призматический гексатерон (гиппикс)	47	315	810	900	360	Ирр. 5-клеточный	т _0,1,2,3 {3,3,3}	-	{3}×{6}	{ }×t{3,3}	тр{3,3,3}
11	(0,1,1,1,2,3) или (0,1,2,2,2,3)	Стеритусеченный 5-симплекс целлипризматический гексатерон (каппикс)	62	330	570	420	120		т{3,3,3}	{ }×t{3,3}	{3}×{6}	{ }×{3,3}	т _0,3 {3,3,3}
12	(0,1,1,2,3,4) или (0,1,2,3,3,4)	Стерикантиусеченный 5-симплекс целлигреатор ромбовидный гексатерон (когракс)	62	480	1140	1080	360		тр{3,3,3}	{ }×tr{3,3}	{3}×{6}	{ }×rr{3,3}	т _0,1,3 {3,3,3}
13	(0,0,0,1,1,1)	Биректифицированный 5-симплекс додекатерон (точка)	12	60	120	90	20	{3}×{3}	г {3,3,3}	-	-	-	г {3,3,3}
14	(0,0,1,1,2,2)	Двукантельчатый 5-симплекс небольшой бирромбированный додекатерон (сибрид)	32	180	420	360	90		рр{3,3,3}	-	{3}×{3}	-	рр{3,3,3}
15	(0,0,1,2,3,3)	Бикантиусеченный 5-симплекс большой бирромбовидный додекатерон (гибрид)	32	180	420	450	180		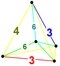тр{3,3,3}	-	{3}×{3}	-	тр{3,3,3}
16	(0,1,1,1,1,2)	Стерический 5-симплекс мелкий клеточный додекатерон (ставрон)	62	180	210	120	30	Ирр. 16-ячеечный	{3,3,3}	{ }×{3,3}	{3}×{3}	{ }×{3,3}	{3,3,3}
17	(0,1,1,2,2,3)	Стериконтеллярный 5-симплекс маленький целлиромбовидный додекатерон (карточка)	62	420	900	720	180		рр{3,3,3}	{ }×rr{3,3}	{3}×{3}	{ }×rr{3,3}	рр{3,3,3}
18	(0,1,2,2,3,4)	Стерунцитусеченный 5-симплекс целлипризматоусеченный додекатерон (каптид)	62	450	1110	1080	360		т _0,1,3 {3,3,3}	{ }×t{3,3}	{6}×{6}	{ }×t{3,3}	т _0,1,3 {3,3,3}
19	(0,1,2,3,4,5)	Всеусеченный 5-симплекс большой клеточный додекатерон (гокад)	62	540	1560	1800	720	Ирр. {3,3,3}	т _0,1,2,3 {3,3,3}	{ }×tr{3,3}	{6}×{6}	{ }×tr{3,3}	т _0,1,2,3 {3,3,3}
Неоднородный		Омниснуб 5-симплекс курносый додекатерон (снод) курносый гексатерон (сникс)	422	2340	4080	2520	360		чт _0,1,2,3 {3,3,3}	чт _0,1,2,3 {3,3,2}	чт _0,1,2,3 {3,2,3}	чт _0,1,2,3 {3,3,2}	чт _0,1,2,3 {3,3,3}	(360) Ирр. {3,3,3}

Б ₅Семья

Семейство B ₅ 2 имеет симметрию порядка 3840 (5!× ⁵).

В этой семье 2 ⁵−1=31 Однородные многогранники Витоффа, созданные путем маркировки одного или нескольких узлов диаграммы Кокстера . Также добавлены 8 однородных многогранников, сгенерированных как чередования с половинной симметрией, которые образуют полную копию семейства D ₅ как ... = ..... (Есть и другие чередования, которые не указаны, поскольку они производят только повторения, как ... = .... и ... = .... Это дало бы полное дублирование однородных 5-многогранников с номерами от 20 до 34 с нарушенной пополам симметрией.)

Для простоты она разделена на две подгруппы, в каждой по 12 форм, и 7 «средних» форм, одинаково принадлежащих обеим.

Семейство 5-кубов 5-многогранников задается выпуклыми оболочками базовых точек, перечисленных в следующей таблице, со всеми перестановками координат и знаков. Каждая базовая точка порождает отдельный однородный 5-многогранник. Все координаты соответствуют однородным 5-многогранникам с длиной ребра 2.

#	Базовая точка	Имя Диаграмма Кокстера	Количество элементов					Вертекс фигура	Количество фасетов по местоположению: [4,3,3,3]
#	Базовая точка	Имя Диаграмма Кокстера	4	3	2	1	0	Вертекс фигура	[4,3,3] (10)	[4,3,2] (40)	[4,2,3] (80)	[2,3,3] (80)	[3,3,3] (32)	Все
20	(0,0,0,0,1)√2	5-ортоплекс триаконтадитерон (так)	32	80	80	40	10	{3,3,4}	-	-	-	-	{3,3,3}
21	(0,0,0,1,1)√2	Выпрямленный 5-ортоплекс ректифицированный триаконтадитерон (крыса)	42	240	400	240	40	{ }×{3,4}	{3,3,4}	-	-	-	г {3,3,3}
22	(0,0,0,1,2)√2	Усеченный 5-ортоплекс усеченный триаконтадитерон (общий)	42	240	400	280	80	(Окта.пир)	{3,3,4}	-	-	-	т{3,3,3}
23	(0,0,1,1,1)√2	Биректифицированный 5-куб пентерактитриаконтадитерон (нит) (Биректифицированный 5-ортоплекс)	42	280	640	480	80	{4}×{3}	г {3,3,4}	-	-	-	г {3,3,3}
24	(0,0,1,1,2)√2	Сочлененный 5-ортоплекс маленький ромбовидный триаконтадитерон (сарт)	82	640	1520	1200	240	Призма-клин	г {3,3,4}	{ }×{3,4}	-	-	рр{3,3,3}
25	(0,0,1,2,2)√2	Битусеченный 5-ортоплекс усеченный триаконтадитерон (биттит)	42	280	720	720	240		т{3,3,4}	-	-	-	2т{3,3,3}
26	(0,0,1,2,3)√2	Кантиусеченный 5-ортоплекс большой ромбовидный триаконтадитерон (гарт)	82	640	1520	1440	480		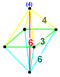т{3,3,4}	{ }×{3,4}	-	-	т _0,1,3 {3,3,3}
27	(0,1,1,1,1)√2	Ректифицированный 5-куб пентеракт ректификованный (рин)	42	200	400	320	80	{3,3}×{ }	г {4,3,3}	-	-	-	{3,3,3}
28	(0,1,1,1,2)√2	Ранцинированный 5-ортоплекс маленький призматичный триаконтадитерон (плюна)	162	1200	2160	1440	320		г {4,3,3}	{ }×r{3,4}	{3}×{4}		т _0,3 {3,3,3}
29	(0,1,1,2,2)√2	Двускатный 5-куб небольшой биромбированный пентерактитриаконтадитерон (сибрант) (двукантелленый 5-ортоплекс)	122	840	2160	1920	480		рр{3,3,4}	-	{4}×{3}	-	рр{3,3,3}
30	(0,1,1,2,3)√2	Ранцитусеченный 5-ортоплекс призматоусеченный триаконтадитерон (паттит)	162	1440	3680	3360	960		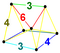рр{3,3,4}	{ }×r{3,4}	{6}×{4}	-	т _0,1,3 {3,3,3}
31	(0,1,2,2,2)√2	Битусеченный 5-куб усеченный пентеракт (биттин)	42	280	720	800	320		2т{4,3,3}	-	-	-	т{3,3,3}
32	(0,1,2,2,3)√2	Рунцикантеллярный 5-ортоплекс призматорромбовидный триаконтадитерон (пирт)	162	1200	2960	2880	960		2т{4,3,3}	{ }×t{3,4}	{3}×{4}	-	т _0,1,3 {3,3,3}
33	(0,1,2,3,3)√2	Бикантиусеченный 5-куб большой бирромбатированный триаконтадитерон (гибрант) (Двукантиусеченный 5-ортоплекс)	122	840	2160	2400	960		тр{3,3,4}	-	{4}×{3}	-	рр{3,3,3}
34	(0,1,2,3,4)√2	Ранцикантиусеченный 5-ортоплекс большой призматичный триаконтадитерон (гиппит)	162	1440	4160	4800	1920		тр{3,3,4}	{ }×t{3,4}	{6}×{4}	-	т _0,1,2,3 {3,3,3}
35	(1,1,1,1,1)	5-куб пентеракт (пентеракт)	10	40	80	80	32	{3,3,3}	{4,3,3}	-	-	-	-
36	(1,1,1,1,1) + (0,0,0,0,1)√2	Стерилизованный 5-куб. мелкоклеточный пентерактитриаконтадитерон (скудный) (стерифицированный 5-ортоплекс)	242	800	1040	640	160	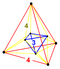Тетр.антипрм	{4,3,3}	{4,3}×{ }	{4}×{3}	{ }×{3,3}	{3,3,3}
37	(1,1,1,1,1) + (0,0,0,1,1)√2	Ранцинированный 5-кубовый малый призматический пентеракт (пролет)	202	1240	2160	1440	320		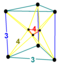т _0,3 {4,3,3}	-	{4}×{3}	{ }×r{3,3}	г {3,3,3}
38	(1,1,1,1,1) + (0,0,0,1,2)√2	Стеритусеченный 5-ортоплекс целлипризматический триаконтадитерон (каппин)	242	1520	2880	2240	640		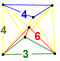т _0,3 {4,3,3}	{4,3}×{ }	{6}×{4}	{ }×t{3,3}	т{3,3,3}
39	(1,1,1,1,1) + (0,0,1,1,1)√2	Согнутый 5-куб малый ромбовидный пентеракт (сирн)	122	680	1520	1280	320	Призма-клин	рр{4,3,3}	-	-	{ }×{3,3}	г {3,3,3}
40	(1,1,1,1,1) + (0,0,1,1,2)√2	Стериконтеллярный 5-кубовый целлиромбированный пентерактитриаконтадитерон (карнит) (стерикантеллярный 5-ортоплекс)	242	2080	4720	3840	960		рр{4,3,3}	рр{4,3}×{ }	{4}×{3}	{ }×rr{3,3}	рр{3,3,3}
41	(1,1,1,1,1) + (0,0,1,2,2)√2	Рунцикантеллярный 5-куб призматор ромбовидный пентеракт (принт)	202	1240	2960	2880	960		т _0,2,3 {4,3,3}	-	{4}×{3}	{ }×t{3,3}	2т{3,3,3}
42	(1,1,1,1,1) + (0,0,1,2,3)√2	Стерикантиусеченный 5-ортоплекс целлигреаторромбовидный триаконтадитерон (когарт)	242	2320	5920	5760	1920		т _0,2,3 {4,3,3}	рр{4,3}×{ }	{6}×{4}	{ }×tr{3,3}	тр{3,3,3}
43	(1,1,1,1,1) + (0,1,1,1,1)√2	Усеченный 5-куб усеченный пентеракт (тан)	42	200	400	400	160	Тетрах.pyr	т{4,3,3}	-	-	-	{3,3,3}
44	(1,1,1,1,1) + (0,1,1,1,2)√2	Стерильный усеченный 5-куб. целлипризматический триаконтадитерон (капт)	242	1600	2960	2240	640		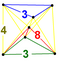т{4,3,3}	т{4,3}×{ }	{8}×{3}	{ }×{3,3}	т _0,3 {3,3,3}
45	(1,1,1,1,1) + (0,1,1,2,2)√2	Усеченный 5-куб призматоусеченный пентеракт (паттин)	202	1560	3760	3360	960		т _0,1,3 {4,3,3}	-	{8}×{3}	{ }×r{3,3}	рр{3,3,3}
46	(1,1,1,1,1) + (0,1,1,2,3)√2	Стерильныйусеченный 5-куб. целлипризматоусеченный пентерактитриаконтадитерон (каптинт) (стериусеченный 5-ортоплекс)	242	2160	5760	5760	1920		т _0,1,3 {4,3,3}	т{4,3}×{ }	{8}×{6}	{ }×t{3,3}	т _0,1,3 {3,3,3}
47	(1,1,1,1,1) + (0,1,2,2,2)√2	Количественный усеченный 5-куб большой ромбовидный пентеракт (гирн)	122	680	1520	1600	640		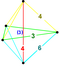тр{4,3,3}	-	-	{ }×{3,3}	т{3,3,3}
48	(1,1,1,1,1) + (0,1,2,2,3)√2	Стерикантиусеченный 5-кубовый целлигреатор, ромбовидный пентеракт (когрин)	242	2400	6000	5760	1920		тр{4,3,3}	тр{4,3}×{ }	{8}×{3}	{ }×rr{3,3}	т _0,1,3 {3,3,3}
49	(1,1,1,1,1) + (0,1,2,3,3)√2	Ранцикантиусеченный 5-куб большой призматический пентеракт (гиппин)	202	1560	4240	4800	1920		т _0,1,2,3 {4,3,3}	-	{8}×{3}	{ }×t{3,3}	тр{3,3,3}
50	(1,1,1,1,1) + (0,1,2,3,4)√2	Всеусеченный 5-куб большой клеточный пентерактитриаконтадитерон (гакнет) (всеусеченный 5-ортоплекс)	242	2640	8160	9600	3840	Ирр. {3,3,3}	тр{4,3}×{ }	тр{4,3}×{ }	{8}×{6}	{ }×tr{3,3}	т _0,1,2,3 {3,3,3}
51		5-демикуб гемипентеракт (хин) =	26	120	160	80	16	г {3,3,3}	ч{4,3,3}	-	-	-	-	(16) {3,3,3}
52		Кантик 5-кубовый Усеченный гемипентеракт (тонкий) =	42	280	640	560	160		ч ₂ {4,3,3}	-	-	-	(16) г {3,3,3}	(16) т{3,3,3}
53		Руничич 5-куб. Малый ромбовидный гемипентеракт (сирхин) =	42	360	880	720	160		ч ₃ {4,3,3}	-	-	-	(16) г {3,3,3}	(16) рр{3,3,3}
54		Стерический 5-кубовый Малый призматический гемипентеракт (сифин) =	82	480	720	400	80		ч{4,3,3}	ч{4,3}×{}	-	-	(16) {3,3,3}	(16) т _0,3 {3,3,3}
55		Рунцикантик 5-куб. Большой ромбовидный гемипентеракт (гирхин) =	42	360	1040	1200	480		ч _2,3 {4,3,3}	-	-	-	(16) 2т{3,3,3}	(16) тр{3,3,3}
56		Стерикантический 5-кубовый Призматоусеченный гемипентеракт (питин) =	82	720	1840	1680	480		ч ₂ {4,3,3}	ч ₂ {4,3}×{}	-	-	(16) рр{3,3,3}	(16) т _0,1,3 {3,3,3}
57		Стерирунный 5-куб. Призматоромбовидный гемипентеракт (пирхин) =	82	560	1280	1120	320		ч ₃ {4,3,3}	ч{4,3}×{}	-	-	(16) т{3,3,3}	(16) т _0,1,3 {3,3,3}
58		Стерилизатор 5-кубовый Большой призматический гемипентеракт (гифин) =	82	720	2080	2400	960		ч _2,3 {4,3,3}	ч ₂ {4,3}×{}	-	-	(16) тр{3,3,3}	(16) т _0,1,2,3 {3,3,3}
Неоднородный		Чередованный ранцикантиусеченный 5-ортоплекс Курносый призматотриаконтадитерон (фрагмент) Курносый гемипентеракт (снахин) =	1122	6240	10880	6720	960		ср{3,3,4}	ср{2,3,4}	ср{3,2,4}	-	чт _0,1,2,3 {3,3,3}	(960) Ирр. {3,3,3}
Неоднородный		Краеугольно-вздернутый 5-ортоплекс Пиритоснуб пентеракт (писнан)	1202	7920	15360	10560	1920		ср ₃ {3,3,4}	ср ₃ {2,3,4}	ср ₃ {3,2,4}	с{3,3}×{ }	чт _0,1,2,3 {3,3,3}	(960) Ирр. {3,3}×{ }
Неоднородный		Курносый 5-куб. Курносый пентеракт (снан)	2162	12240	21600	13440	960		чт _0,1,2,3 {3,3,4}	чт _0,1,2,3 {2,3,4}	чт _0,1,2,3 {3,2,4}	чт _0,1,2,3 {3,3,2}	чт _0,1,2,3 {3,3,3}	(1920) Ирр. {3,3,3}

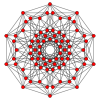
Д ₅Семья

Семейство D ₅ 2 имеет симметрию порядка 1920 (5! x ⁴).

Это семейство состоит из 23 однородных многогранников Витоффа, полученных из перестановок 3×8-1 D ₅ диаграммы Кокстера с одним или несколькими кольцами. 15 (2×8-1) повторяются из семейства B5 _, а 8 уникальны для этого семейства, хотя даже эти 8 дублируют чередования из _{семейства B5} .

В 15 повторах оба узла, заканчивающиеся ветвями длины 1, имеют кольцо, поэтому два типа элементы идентичны, а симметрия удваивается: отношения ... = .... и ... = ..., создавая полную копию однородных 5-многогранников с 20 по 34 выше. В 8 новых формах один такой узел окольцован, а другой нет, причем отношение ... = ... дублируя однородные 5-многогранники с 51 по 58 выше.

#	Диаграмма Кокстера Шлефли Символы Имена Джонсона и Бауэрса	Количество элементов					Вертекс фигура	Фасеты по местоположению: [3 ^1,2,1]
#	Диаграмма Кокстера Шлефли Символы Имена Джонсона и Бауэрса	4	3	2	1	0	Вертекс фигура	[3,3,3] (16)	[3 ^1,1,1] (10)	[3,3]×[ ] (40)	[ ]×[3]×[ ] (80)	[3,3,3] (16)	Все
[51]	= h{4,3,3,3}, 5-демикуб Гемипентеракт (хин)	26	120	160	80	16	г {3,3,3}	{3,3,3}	ч{4,3,3}	-	-	-
[52]	= h ₂ {4,3,3,3}, кантика 5-куба Усеченный гемипентеракт (тонкий)	42	280	640	560	160		т{3,3,3}	ч ₂ {4,3,3}	-	-	г {3,3,3}
[53]	= h ₃ {4,3,3,3}, рунический 5-куб Малый ромбовидный гемипентеракт (сирхин)	42	360	880	720	160		рр{3,3,3}	ч ₃ {4,3,3}	-	-	г {3,3,3}
[54]	= h ₄ {4,3,3,3}, стерический 5-куб Малый призматический гемипентеракт (сифин)	82	480	720	400	80		т _0,3 {3,3,3}	ч{4,3,3}	ч{4,3}×{}	-	{3,3,3}
[55]	= h _2,3 {4,3,3,3}, рунообразный 5-куб Большой ромбовидный гемипентеракт (гирхин)	42	360	1040	1200	480		2т{3,3,3}	ч _2,3 {4,3,3}	-	-	тр{3,3,3}
[56]	= h _2,4 {4,3,3,3}, стерикантный 5-куб Призматоусеченный гемипентеракт (питин)	82	720	1840	1680	480		т _0,1,3 {3,3,3}	ч ₂ {4,3,3}	ч ₂ {4,3}×{}	-	рр{3,3,3}
[57]	= h _3,4 {4,3,3,3}, стерильный 5-куб. Призматоромбовидный гемипентеракт (пирхин)	82	560	1280	1120	320		т _0,1,3 {3,3,3}	ч ₃ {4,3,3}	ч{4,3}×{}	-	т{3,3,3}
[58]	= h _2,3,4 {4,3,3,3}, стерирункантный 5-куб Большой призматический гемипентеракт (гифин)	82	720	2080	2400	960		т _0,1,2,3 {3,3,3}	ч _2,3 {4,3,3}	ч ₂ {4,3}×{}	-	тр{3,3,3}
Неоднородный	= ht _0,1,2,3 {3,3,3,4}, чередующийся продолговато-усеченный 5-ортоплекс Курносый гемипентеракт (снахин)	1122	6240	10880	6720	960		чт _0,1,2,3 {3,3,3}	ср{3,3,4}	ср{2,3,4}	ср{3,2,4}	чт _0,1,2,3 {3,3,3}	(960) Ирр. {3,3,3}

Равномерные призматические формы

Существует 5 конечных категориальных однородных призматических семейств многогранников, основанных на непризматических однородных 4-многогранниках . Для простоты большинство чередований не показано.

A ₄ × A ₁

Это призматическое семейство имеет 9 форм :

Семейство А ₁ х А ₄ . имеет симметрию порядка 240 (2*5!)

#	Диаграмма Кокстера и Шлефли символы Имя	Количество элементов
#	Диаграмма Кокстера и Шлефли символы Имя	Фасеты	Клетки	Лица	Края	Вершины
59	= {3,3,3}×{ } 5-ячеечная призма (пенп)	7	20	30	25	10
60	= г{3,3,3}×{ } Призма выпрямленная 5-ячеечная (раппип)	12	50	90	70	20
61	= т{3,3,3}×{ } Усеченная 5-ячеечная призма (типпип)	12	50	100	100	40
62	= rr{3,3,3}×{ } Скошенная 5-ячеечная призма (сриппип)	22	120	250	210	60
63	= т _0,3 {3,3,3}×{ } Сморщенная 5-ячеечная призма (спиддип)	32	130	200	140	40
64	= 2t{3,3,3}×{ } Усеченная 5-ячеечная призма (декапичная)	12	60	140	150	60
65	= tr{3,3,3}×{ } Скошенная 5-ячеечная призма (гриппип)	22	120	280	300	120
66	= т _0,1,3 {3,3,3}×{ } Усеченная 5-ячеечная призма (приппип)	32	180	390	360	120
67	= т _0,1,2,3 {3,3,3}×{ } Всеусеченная 5-ячеечная призма (гиппиддип)	32	210	540	600	240

Б ₄ × А ₁

Это призматическое семейство имеет 16 форм . (Три являются общими для семейства [3,4,3]×[ ])

Семейство A ₁ ×B ₄ 2 имеет симметрию порядка 768 ( ⁵4!).

Последние три курносых можно реализовать с ребрами одинаковой длины, но они все равно окажутся неоднородными, поскольку некоторые из их 4-граней не являются однородными 4-многогранниками.

#	Диаграмма Кокстера и Шлефли символы Имя	Количество элементов
#	Диаграмма Кокстера и Шлефли символы Имя	Фасеты	Клетки	Лица	Края	Вершины
[16]	= {4,3,3}×{ } Тессерактическая призма (пятиугольная) (То же, что и 5-куб )	10	40	80	80	32
68	= г{4,3,3}×{ } Выпрямленная тессерактическая призма (риттип)	26	136	272	224	64
69	= т{4,3,3}×{ } Усеченная тессерактическая призма (таттип)	26	136	304	320	128
70	= rr{4,3,3}×{ } Кантелляционная тессерактическая призма (сриттип)	58	360	784	672	192
71	= т _0,3 {4,3,3}×{ } Сморщенная тессерактическая призма (сидпитип)	82	368	608	448	128
72	= 2t{4,3,3}×{ } Двуусеченная тессерактическая призма (тахп)	26	168	432	480	192
73	= tr{4,3,3}×{ } Кантиусеченная тессерактическая призма (наконечник)	58	360	880	960	384
74	= т _0,1,3 {4,3,3}×{ } Закругленная тессерактическая призма (прохп)	82	528	1216	1152	384
75	= т _0,1,2,3 {4,3,3}×{ } Всеусеченная тессерактическая призма (гидпитип)	82	624	1696	1920	768
76	= {3,3,4}×{ } 16-ячеечная призма (шестигранная)	18	64	88	56	16
77	= г{3,3,4}×{ } Выпрямленная 16-ячеечная призма (icope) (То же, что и 24-ячеечная призма )	26	144	288	216	48
78	= т{3,3,4}×{ } Усеченная 16-ячеечная призма (thexip)	26	144	312	288	96
79	= rr{3,3,4}×{ } Скошенная 16-ячеечная призма (рикопа) (То же, что и выпрямленная 24-ячеечная призма )	50	336	768	672	192
80	= tr{3,3,4}×{ } Скошенная 16-ячеечная призма (тикопе) (То же, что и усеченная 24-ячеечная призма )	50	336	864	960	384
81	= т _0,1,3 {3,3,4}×{ } Усеченная 16-ячеечная призма (приттип)	82	528	1216	1152	384
82	= ср{3,3,4}×{ } курносая 24-ячеечная призма (садип)	146	768	1392	960	192
Неоднородный	исправленная тессерактическая альтерпризма (рита)	50	288	464	288	64
Неоднородный	усеченная 16-ячеечная альтерпризма (текса)	26	168	384	336	96
Неоднородный	усеченная тессерактическая альтерпризма (таха)	50	288	624	576	192

Ф ₄ × А ₁

Это призматическое семейство имеет 10 форм .

Семейство A ₁ x F ₄ . имеет симметрию порядка 2304 (2*1152) Три многогранника 85, 86 и 89 (зеленый фон) имеют двойную симметрию [[3,4,3],2], порядка 4608. Последний, курносая 24-ячеечная призма (синий фон), имеет [3 ⁺,4,3,2] симметрия, порядок 1152.

#	Диаграмма Кокстера и Шлефли символы Имя	Количество элементов
#	Диаграмма Кокстера и Шлефли символы Имя	Фасеты	Клетки	Лица	Края	Вершины
[77]	= {3,4,3}×{ } 24-ячеечная призма (icope)	26	144	288	216	48
[79]	= г{3,4,3}×{ } выпрямленная 24-ячеечная призма (рикопе)	50	336	768	672	192
[80]	= т{3,4,3}×{ } усеченная 24-ячеечная призма (тикопе)	50	336	864	960	384
83	= rr{3,4,3}×{ } кантеллированная 24-ячеечная призма (срикопе)	146	1008	2304	2016	576
84	= т _0,3 {3,4,3}×{ } сморщенная 24-ячеечная призма (остроконечная)	242	1152	1920	1296	288
85	= 2t{3,4,3}×{ } 24-ячеечная призма с усеченной битой (контип)	50	432	1248	1440	576
86	= tr{3,4,3}×{ } кантиусеченная 24-ячеечная призма (грикопа)	146	1008	2592	2880	1152
87	= т _0,1,3 {3,4,3}×{ } усеченная 24-ячеечная призма (прикопа)	242	1584	3648	3456	1152
88	= т _0,1,2,3 {3,4,3}×{ } всеусеченная 24-ячеечная призма (гиппикчап)	242	1872	5088	5760	2304
[82]	= s{3,4,3}×{ } курносая 24-ячеечная призма (садип)	146	768	1392	960	192

Н ₄ × А ₁

Это призматическое семейство имеет 15 форм :

Семейство A ₁ x H ₄ . имеет симметрию порядка 28800 (2*14400)

#	Диаграмма Кокстера и Шлефли символы Имя	Количество элементов
#	Диаграмма Кокстера и Шлефли символы Имя	Фасеты	Клетки	Лица	Края	Вершины
89	= {5,3,3}×{ } 120-ячеечная призма (хайп)	122	960	2640	3000	1200
90	= г{5,3,3}×{ } Призма выпрямленная 120-ячеечная (рахипе)	722	4560	9840	8400	2400
91	= т{5,3,3}×{ } Усеченная 120-ячеечная призма (типе)	722	4560	11040	12000	4800
92	= rr{5,3,3}×{ } Кантелеллированная 120-ячеечная призма (срахип)	1922	12960	29040	25200	7200
93	= т _0,3 {5,3,3}×{ } Сморщенная 120-ячеечная призма (сидпиксип)	2642	12720	22080	16800	4800
94	= 2t{5,3,3}×{ } Усеченная 120-ячеечная призма (xhip)	722	5760	15840	18000	7200
95	= tr{5,3,3}×{ } Скошенная 120-ячеечная призма (грахип)	1922	12960	32640	36000	14400
96	= т _0,1,3 {5,3,3}×{ } Усеченная 120-ячеечная призма (приксип)	2642	18720	44880	43200	14400
97	= т _0,1,2,3 {5,3,3}×{ } Всеусеченная 120-ячеечная призма (гидпиксип)	2642	22320	62880	72000	28800
98	= {3,3,5}×{ } 600-ячеечная призма (exip)	602	2400	3120	1560	240
99	= г{3,3,5}×{ } Призма выпрямленная 600-ячеечная (роксип)	722	5040	10800	7920	1440
100	= т{3,3,5}×{ } Усеченная 600-ячеечная призма (texip)	722	5040	11520	10080	2880
101	= rr{3,3,5}×{ } Кантелляционная призма из 600 ячеек (шриксип)	1442	11520	28080	25200	7200
102	= tr{3,3,5}×{ } Скошенная 600-ячеечная призма (grixip)	1442	11520	31680	36000	14400
103	= т _0,1,3 {3,3,5}×{ } Усеченная призма из 600 ячеек (прагип)	2642	18720	44880	43200	14400

Дуопризма призмы

Равномерные призмы дуопризмы, { p }×{ q }×{ }, образуют бесконечный класс для всех целых чисел p , q >2. {4}×{4}×{ } образует форму более низкой симметрии 5-куба .

Расширенный f-вектор { p }×{ q }×{ } вычисляется как ( p , p , 1 )*( q , q , 1 )*(2, 1 ) = (2 pq ,5 pq ,4 pq +2 p +2 q ,3 pq +3 p +3 q , p + q +2, 1 ).

Диаграмма Кокстера	Имена	Количество элементов
Диаграмма Кокстера	Имена	4-ликий	Клетки	Лица	Края	Вершины
	{ п }×{ q }×{ } ^[9]	п + д +2	3 пк +3 п +3 кв	4 пк +2 п +2 кв	5 кв.м.	2 шт.
	{ п } ²×{ }	2( р +1)	3 п ( п +1)	4 п ( п +1)	5 р. ²	2 р ²
	{3} ²×{ }	8	36	48	45	18
	{4} ²×{ } = 5-куб	10	40	80	80	32

Большая призма-антипризма

Призма большой антипризмы — единственный известный выпуклый невитоффов однородный 5-многогранник. Он имеет 200 вершин, 1100 ребер, 1940 граней (40 пятиугольников, 500 квадратов, 1400 треугольников), 1360 ячеек (600 тетраэдров , 40 пятиугольных антипризм , 700 треугольных призм , 20 пятиугольных призм ) и 322 гиперячейки (2 большие антипризмы) . , 20 пятиугольных призм -антипризм , и 300 тетраэдрических призм ).

#	Имя	Количество элементов
#	Имя	Фасеты	Клетки	Лица	Края	Вершины
104	большая призма-антипризма (гаппип) ^[10]	322	1360	1940	1100	200

Замечания о конструкции Витгофа для однородных 5-многогранников.

Построение отражающих 5-мерных однородных многогранников осуществляется с помощью процесса построения Витхоффа и представляется с помощью диаграммы Кокстера , где каждый узел представляет зеркало. Узлы окольцованы, чтобы указать, какие зеркала активны. Полный набор генерируемых однородных многогранников основан на уникальных перестановках кольцевых узлов. Однородные 5-многогранники называются в соответствии с правильными многогранниками каждого семейства. Некоторые семейства имеют два обычных конструктора и, следовательно, могут иметь два способа их именования.

Вот основные операторы, доступные для построения и именования однородных 5-многогранников.

Последняя операция, пренебрежение и, в более общем смысле, чередование, — это операции, которые могут создавать нерефлексивные формы. Они нарисованы с «полыми кольцами» в узлах.

Призматические формы и раздвоенные графы могут использовать одну и ту же нотацию индексации усечения, но для ясности требуют явной системы нумерации узлов.

Операция	Расширенный Символ Шлефли		Описание
Родитель	т ₀ {p,q,r,s}	{п, д, г, с}	Любой правильный 5-многогранник
Исправленный	т ₁ {p,q,r,s}	r{p,q,r,s}	Края полностью усекаются в отдельные точки. 5-многогранник теперь имеет объединенные грани родительского и двойственного многогранников.
биректифицированный	т ₂ {p,q,r,s}	2r{p,q,r,s}	Биректификация сводит грани к точкам, клетки к их двойникам .
Триректифицированный	т ₃ {p,q,r,s}	3r{p,q,r,s}	Триректификация сводит ячейки к точкам. (Двойное исправление)
Квадриректифицированный	т ₄ {p,q,r,s}	4r{p,q,r,s}	Квадриректификация сводит 4-грани к точкам. (Двойной)
Усечено	т _0,1 {p,q,r,s}	t{p,q,r,s}	Каждая исходная вершина отсекается, а пробел заполняет новая грань. Усечение имеет степень свободы, которая имеет одно решение, создающее однородный усеченный 5-многогранник. 5-многогранник имеет исходные грани, удвоенные по сторонам, и содержит грани двойственного.
Отмененный	т _0,2 {p,q,r,s}	rr{p,q,r,s}	Помимо усечения вершин, каждое исходное ребро скашивается, и на их месте появляются новые прямоугольные грани.
рухлый	т _0,3 {p,q,r,s}		Рансинация уменьшает ячейки и создает новые ячейки в вершинах и краях.
стерилизованный	т _0,4 {p,q,r,s}	2r2r{p,q,r,s}	Стерикация уменьшает количество граней и создает новые грани (гиперячейки) в вершинах и краях зазоров. (То же, что и операция расширения для 5-многогранников.)
Всеусеченный	т _0,1,2,3,4 {p,q,r,s}		Применяются все четыре оператора: усечение, кантелляция, рансинация и стерикация.
Половина	ч{2p,3,q,r}		Чередование , то же, что
Кантик	ч ₂ {2p,3,q,r}		То же, что
Рунцич	ч ₃ {2p,3,q,r}		То же, что
Рансикантический	ч _2,3 {2p,3,q,r}		То же, что
Стерик	ч ₄ {2p,3,q,r}		То же, что
Стерирунчич	ч _3,4 {2p,3,q,r}		То же, что
Стерикантический	ч _2,4 {2p,3,q,r}		То же, что
Стерилунцикантический	ч _2,3,4 {2p,3,q,r}		То же, что
пренебрежительное отношение	с{p,2q,r,s}		Попеременное усечение
Курносый исправлен	ср{п,q,2r,s}		Попеременное усеченное выпрямление
	ht _0,1,2,3 {p,q,r,s}		Попеременное сокращение
Полный пренебрежение	ht _0,1,2,3,4 {p,q,r,s}		Попеременное всеусечение

Регулярные и однородные соты

Существует пять фундаментальных аффинных групп Кокстера и 13 призматических групп, которые генерируют регулярные и равномерные мозаики в евклидовом 4-мерном пространстве. ^[11]^[12]

Фундаментальные группы
#	Группа Коксетера			Диаграмма Кокстера	Формы
1	${\tilde {A}}_{4}$	[3 ^[5]]	[(3,3,3,3,3)]		7
2	${\tilde {C}}_{4}$	[4,3,3,4]			19
3	${\tilde {B}}_{4}$	[4,3,3 ^1,1]	[4,3,3,4,1 ⁺]	=	23 (8 новых)
4	${\tilde {D}}_{4}$	[3 ^1,1,1,1]	[1 ⁺,4,3,3,4,1 ⁺]	=	9 (0 новых)
5	${\tilde {F}}_{4}$	[3,4,3,3]			31 (21 новый)

Существует три правильных соты евклидова 4-мерного пространства:

тессерактические соты с символами {4,3,3,4}, = . В этом семействе 19 однородных сот.
Соты из 24 ячеек с символами {3,4,3,3}, . В этом семействе имеется 31 светоотражающая однородная сота и одна чередующаяся форма.
- Усеченные соты из 24 ячеек с символами t{3,4,3,3},
- Курносые 24-ячеистые соты с символами s{3,4,3,3}, и построен из четырех курносых 24-ячеек , одной 16-ячеек и пяти 5-ячеек в каждой вершине.
16-ячеечная сота с символами {3,3,4,3},

Другие семейства, образующие однородные соты:

имеется 23 формы с уникальными кольцами, 8 новых В семействе 16-клеточных сот . С символами h{4,3 ²,4} геометрически идентична 16-ячеистой соте , =
Существует 7 форм с уникальными кольцами. ${\tilde {A}}_{4}$ ${\tilde {A}}_{4}$ , семейное, все новое, в том числе:
В составе 9 уникально кольцевых форм. ${\tilde {D}}_{4}$ : [3 ^1,1,1,1] семейство, два новых, в том числе четверть тессерактических сот , = и усеченные тессерактические соты , = .

Не-Витоффовы однородные мозаики в 4-мерном пространстве также существуют за счет удлинения (вставки слоев) и вращения (вращения слоев) этих отражающих форм.

Призматические группы
#	Группа Коксетера
1	${\tilde {C}}_{3}$ × ${\tilde {I}}_{1}$	[4,3,4,2,∞]
2	${\tilde {B}}_{3}$ × ${\tilde {I}}_{1}$	[4,3 ^1,1,2,∞]
3	${\tilde {A}}_{3}$ × ${\tilde {I}}_{1}$	[3 ^[4],2,∞]
4	${\tilde {C}}_{2}$ × ${\tilde {I}}_{1}$ х ${\tilde {I}}_{1}$	[4,4,2,∞,2,∞]
5	${\tilde {H}}_{2}$ × ${\tilde {I}}_{1}$ х ${\tilde {I}}_{1}$	[6,3,2,∞,2,∞]
6	${\tilde {A}}_{2}$ × ${\tilde {I}}_{1}$ х ${\tilde {I}}_{1}$	[3 ^[3],2,∞,2,∞]
7	${\tilde {I}}_{1}$ × ${\tilde {I}}_{1}$ х ${\tilde {I}}_{1}$ х ${\tilde {I}}_{1}$	[∞,2,∞,2,∞,2,∞]
8	${\tilde {A}}_{2}$ х ${\tilde {A}}_{2}$	[3 ^[3],2,3 ^[3]]
9	${\tilde {A}}_{2}$ × ${\tilde {B}}_{2}$	[3 ^[3],2,4,4]
10	${\tilde {A}}_{2}$ × ${\tilde {G}}_{2}$	[3 ^[3],2,6,3]
11	${\tilde {B}}_{2}$ × ${\tilde {B}}_{2}$	[4,4,2,4,4]
12	${\tilde {B}}_{2}$ × ${\tilde {G}}_{2}$	[4,4,2,6,3]
13	${\tilde {G}}_{2}$ × ${\tilde {G}}_{2}$	[6,3,2,6,3]

Правильные и однородные гиперболические соты

Гиперболические компактные группы

Существует 5 компактных гиперболических групп Кокстера ранга 5, каждая из которых порождает однородные соты в гиперболическом 4-мерном пространстве как перестановки колец диаграмм Кокстера.

${\widehat {AF}}_{4}$ = [(3,3,3,3,4)]:	${\bar {DH}}_{4}$ = [5,3,3 ^1,1]:	${\bar {H}}_{4}$ = [3,3,3,5]: ${\bar {BH}}_{4}$ = [4,3,3,5]: ${\bar {K}}_{4}$ = [5,3,3,5]:

В H имеется 5 правильных компактных выпуклых гиперболических сот. ⁴ космос: ^[13]

Компактные правильные выпуклые гиперболические соты
Сотовое имя	Шлефли Символ {п, д, г, с}	Фасет тип {п, д, г}	Клетка тип {п, д}	Лицо тип {р}	Лицо фигура {с}	Край фигура {р,с}	Вертекс фигура {д, г, с}	Двойной
Орден-5 5-клеточный (пенте)	{3,3,3,5}	{3,3,3}	{3,3}	{3}	{5}	{3,5}	{3,3,5}	{5,3,3,3}
Орден-3 120 ячейка (найти)	{5,3,3,3}	{5,3,3}	{5,3}	{5}	{3}	{3,3}	{3,3,3}	{3,3,3,5}
Тессерактик Ордена-5 (питест)	{4,3,3,5}	{4,3,3}	{4,3}	{4}	{5}	{3,5}	{3,3,5}	{5,3,3,4}
Орден-4 120-ячеечный (дерьмо)	{5,3,3,4}	{5,3,3}	{5,3}	{5}	{4}	{3,4}	{3,3,4}	{4,3,3,5}
Орден-5 120-кл (фитте)	{5,3,3,5}	{5,3,3}	{5,3}	{5}	{5}	{3,5}	{3,3,5}	Самодвойственный

В H также имеются 4 правильных компактных гиперболических соты-звезды. ⁴ космос:

Компактные правильные гиперболические соты-звезды
Сотовое имя	Шлефли Символ {п, д, г, с}	Фасет тип {п, д, г}	Клетка тип {п, д}	Лицо тип {р}	Лицо фигура {с}	Край фигура {р,с}	Вертекс фигура {д, г, с}	Двойной
Орден-3 малый звездчатый 120-ячеечный	{5/2,5,3,3}	{5/2,5,3}	{5/2,5}	{5}	{5}	{3,3}	{5,3,3}	{3,3,5,5/2}
Заказ-5/2 600-ячеечный	{3,3,5,5/2}	{3,3,5}	{3,3}	{3}	{5/2}	{5,5/2}	{3,5,5/2}	{5/2,5,3,3}
Икосаэдрический 120-ячеечный порядка 5	{3,5,5/2,5}	{3,5,5/2}	{3,5}	{3}	{5}	{5/2,5}	{5,5/2,5}	{5,5/2,5,3}
Орден-3 отличный 120-ячеечный	{5,5/2,5,3}	{5,5/2,5}	{5,5/2}	{5}	{3}	{5,3}	{5/2,5,3}	{3,5,5/2,5}

Гиперболические паракомпактные группы

Существует 9 паракомпактных гиперболических групп Кокстера ранга 5 , каждая из которых порождает однородные соты в 4-мерном пространстве как перестановки колец диаграмм Кокстера. Паракомпактные группы порождают соты с бесконечными гранями или фигурами вершин .

${\bar {P}}_{4}$ = [3,3 ^[4]]: ${\bar {BP}}_{4}$ = [4,3 ^[4]]: ${\bar {FR}}_{4}$ = [(3,3,4,3,4)]: ${\bar {DP}}_{4}$ = [3 ^[3]×[]]:	${\bar {N}}_{4}$ = [4,/3\,3,4]: ${\bar {O}}_{4}$ = [3,4,3 ^1,1]: ${\bar {S}}_{4}$ = [4,3 ^2,1]: ${\bar {M}}_{4}$ = [4,3 ^1,1,1]:	${\bar {R}}_{4}$ = [3,4,3,4]:

Примечания

^ Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900 г.
^ Многомерный глоссарий , Георгий Ольшевский.
^ Бауэрс, Джонатан (2000). «Равномерная Полихора» (PDF) . В Резе Сархаги (ред.). Мосты 2000 . Конференция по мостам. стр. 239–246.
^ Униформа Политера , Джонатан Бауэрс
^ Однородный многогранник
^ ACW (24 мая 2012 г.), «Выпуклые однородные 5-многогранники» , Открытый сад задач , заархивировано из оригинала 5 октября 2016 г. , получено 4 октября 2016 г.
^ Регулярные и полуправильные многогранники III, стр.315 Три конечные группы 5-мерных измерений
^ Коксетер , Правильные многогранники , §12.6 Число отражений, уравнение 12.61
^ «Н,к-диппип» .
^ «Гаппип» .
^ Правильные многогранники, стр.297. Таблица IV. Фундаментальные области для неприводимых групп, порожденных отражениями.
^ Правильные и полуправильные многогранники, II, стр. 298-302 Четырехмерные соты
^ Коксетер, Красота геометрии: двенадцать эссе, Глава 10: Правильные соты в гиперболическом пространстве, Сводные таблицы IV, стр. 213

Ссылки

Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики , Макмиллан, 1900 (3 правильных и один полуправильный 4-мерный многогранник)
А. Буль Стотт : Геометрический вывод полуправильных многогранников из правильных многогранников и пространственного заполнения , Трактаты о единице ширины Королевской академии наук Амстердам, Первый раздел 11,1, Амстердам, 1910 г.
ХСМ Коксетер :
- HSM Coxeter , Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 (стр. 297 Фундаментальные области для неприводимых групп, порожденных отражениями, сферическими и евклидовыми)
- HSM Coxeter , Красота геометрии: двенадцать эссе (Глава 10: Правильные соты в гиперболическом пространстве, Сводные таблицы IV, стр. 213)
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591] (стр. 287 5D евклидовы группы, стр. 298 Четырехмерные соты)
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
Джеймс Э. Хамфрис, Группы отражения и группы Кокстера , Кембриджские исследования по высшей математике, 29 (1990) (стр. 141, 6.9 Список гиперболических групп Кокстера, рисунок 2) [2]

Внешние ссылки

Клитцинг, Ричард. «5D однородные многогранники (политеры)» . – включает невыпуклые формы, а также конструкции-дубликаты из _{B 5} и D _5. семейств

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁

[1] Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900 г.

[2] Многомерный глоссарий , Георгий Ольшевский.

[3] Бауэрс, Джонатан (2000). «Равномерная Полихора» (PDF) . В Резе Сархаги (ред.). Мосты 2000 . Конференция по мостам. стр. 239–246.

[4] Униформа Политера , Джонатан Бауэрс

[5] Однородный многогранник

[6] ACW (24 мая 2012 г.), «Выпуклые однородные 5-многогранники» , Открытый сад задач , заархивировано из оригинала 5 октября 2016 г. , получено 4 октября 2016 г.

[7] Регулярные и полуправильные многогранники III, стр.315 Три конечные группы 5-мерных измерений

[8] Коксетер , Правильные многогранники , §12.6 Число отражений, уравнение 12.61

[9] «Н,к-диппип» .

[10] «Гаппип» .

[11] Правильные многогранники, стр.297. Таблица IV. Фундаментальные области для неприводимых групп, порожденных отражениями.

[12] Правильные и полуправильные многогранники, II, стр. 298-302 Четырехмерные соты

[13] Коксетер, Красота геометрии: двенадцать эссе, Глава 10: Правильные соты в гиперболическом пространстве, Сводные таблицы IV, стр. 213

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]