Список правильных многогранников
| Правильные (2D) многоугольники | |
|---|---|
| Выпуклый | Звезда |
 {5} |  {5/2} |
| Regular (3D) polyhedra | |
| Выпуклый | Звезда |
 {5,3} |  {5/2,5} |
| Правильные 4D-многогранники | |
| Выпуклый | Звезда |
 {5,3,3} |  {5/2,5,3} |
| Обычные 2D-мозаики | |
| евклидов | гиперболический |
 {4,4} |  {5,4} |
| Обычные 3D-мозаики | |
| евклидов | гиперболический |
 {4,3,4} |  {5,3,4} |
В этой статье перечислены правильные многогранники в евклидовом , сферическом и гиперболическом пространствах.
Обзор
[ редактировать ]В этой таблице показана сводка количества правильных многогранников по рангам.
| Классифицировать | Конечный | евклидов | гиперболический | Абстрактный | |||||
|---|---|---|---|---|---|---|---|---|---|
| Компактный | Паракомпакт | ||||||||
| Выпуклый | Звезда | Перекос [а] [1] | Выпуклый | Перекос [а] [1] | Выпуклый | Звезда | Выпуклый | ||
| 1 | 1 | никто | никто | никто | никто | никто | никто | никто | 1 |
| 2 | никто | 1 | никто | 1 | никто | никто | |||
| 3 | 5 | 4 | 9 | 3 | 3 | ||||
| 4 | 6 | 10 | 18 | 1 | 7 | 4 | никто | 11 | |
| 5 | 3 | никто | 3 | 3 | 15 | 5 | 4 | 2 | |
| 6 | 3 | никто | 3 | 1 | 7 | никто | никто | 5 | |
| 7+ | 3 | никто | 3 | 1 | 7 | никто | никто | никто | |
- ^ Jump up to: а б Считаем только многогранники полного ранга. В более высоких измерениях существует больше правильных многогранников каждого ранга > 1.
Не существует евклидовых правильных звездных мозаик ни в каком количестве измерений.
1-многогранники
[ редактировать ] | Диаграмма Кокстера представляет зеркальные «плоскости» как узлы и помещает кольцо вокруг узла, если точка не находится на плоскости. Дион , { } |
Существует только один многогранник ранга 1 (1-многогранник), замкнутый отрезок, ограниченный двумя своими концами. Любая реализация этого 1-многогранника регулярна. Он имеет символ Шлефли { }, [2] [3] или диаграмма Кокстера с одним кольцевым узлом, ![]() . Норман Джонсон называет это дионом [4] и присваивает ему символ Шлефли { }.
. Норман Джонсон называет это дионом [4] и присваивает ему символ Шлефли { }.
Несмотря на то, что это тривиальный многогранник, он выглядит как ребра многоугольников и других многогранников более высокой размерности. [5] Он используется в определении однородных призм, таких как символ Шлефли { } × {p} или диаграмма Кокстера. ![]()
![]()
![]()
![]()
![]() как декартово произведение отрезка и правильного многоугольника. [6]
как декартово произведение отрезка и правильного многоугольника. [6]
2-многогранники (многоугольники)
[ редактировать ]Многогранники ранга 2 (2-многогранники) называются многоугольниками . Правильные многоугольники бывают равносторонними и циклическими . -угольный правильный многоугольник p обозначается символом Шлефли {p}.
Многие источники рассматривают только выпуклые многоугольники , но звездчатые многоугольники , как и пентаграмма , при их рассмотрении также могут быть правильными. Они используют те же вершины, что и выпуклые формы, но соединяются альтернативной связностью, которая для завершения проходит по кругу более одного раза.
Выпуклый
[ редактировать ]Символ Шлефли {p} представляет правильный p -угольник .
| Имя | Треугольник ( 2-симплекс ) | Квадрат ( 2-ортоплекс ) ( 2-куб ) | Пентагон ( 2-пятиугольный многогранник ) | Шестиугольник | Семиугольник | Октагон | |
|---|---|---|---|---|---|---|---|
| Шлефли | {3} | {4} | {5} | {6} | {7} | {8} | |
| Симметрия | Д 3 , [3] | Д 4 , [4] | Д 5 , [5] | Д 6 , [6] | D 7 , [7] | Д 8 , [8] | |
| Коксетер | |||||||
| Изображение |  |  |  |  |  |  | |
| Имя | Нонагон (Девятиугольник) | Декагон | Хендекагон | Додекагон | Тридекагон | Тетрадекагон | |
| Шлефли | {9} | {10} | {11} | {12} | {13} | {14} | |
| Симметрия | Д 9 , [9] | Д 10 , [10] | Д 11 , [11] | Д 12 , [12] | Д 13 , [13] | Д 14 , [14] | |
| Дынкин | |||||||
| Изображение |  |  |  |  |  |  | |
| Имя | Пятиугольник | Шестиугольник | Гептадекагон | Октадекагон | Эннеадекагон | Икосагон | ...п-гон |
| Шлефли | {15} | {16} | {17} | {18} | {19} | {20} | { п } |
| Симметрия | Д 15 , [15] | D 16 , [16] | Д 17 , [17] | Д 18 , [18] | Д 19 , [19] | Д 20 , [20] | Д п , [п] |
| Дынкин | |||||||
| Изображение |  |  |  |  |  |  |  |
сферический
[ редактировать ]Правильный двуугольник {2} можно считать вырожденным правильным многоугольником. Его можно реализовать невырожденно в некоторых неевклидовых пространствах, например на поверхности сферы или тора . Например, дигон можно невырожденно реализовать как сферическую луну . Моногон . {1} также можно реализовать на сфере как одну точку с большим кругом, проходящим через нее [7] Однако моногон не является допустимым абстрактным многогранником , поскольку его единственное ребро инцидентно только одной вершине, а не двум.
| Имя | моногон | Достаточно |
|---|---|---|
| Символ Шлефли | {1} | {2} |
| Симметрия | Д 1 , [ ] | Д2 ] , [2 |
| Диаграмма Кокстера | ||
| Изображение |  |  |
Звезды
[ редактировать ]Существует бесконечно много правильных звездных многогранников в двух измерениях, символы Шлефли которых состоят из рациональных чисел { n / m } . Они называются звездчатыми многоугольниками и имеют то же расположение вершин, что и выпуклые правильные многоугольники.
В общем, для любого натурального числа n существуют правильные n -конечные звезды с символами Шлефли { n / m } для всех m такие, что m < n / 2 (строго говоря, { n / m } = { n / ( n − m )} ), а m и n просты взаимно (поэтому все звездчатые многоугольника с простым числом сторон будут правильными звездами). Символы, в которых m и n не являются взаимно простыми, могут использоваться для обозначения составных многоугольников .
| Имя | Пентаграмма | Гептаграммы | Октаграмма | Эннеаграммы | Декаграмма | ... н-граммы | ||
|---|---|---|---|---|---|---|---|---|
| Шлефли | {5/2} | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | { п/к } |
| Симметрия | Д 5 , [5] | D 7 , [7] | Д 8 , [8] | Д 9 , [9], | Д 10 , [10] | Д п , [ п ] | ||
| Коксетер | ||||||||
| Изображение |  |  |  |  |  |  |  | |
Могут существовать звездчатые многоугольники, которые могут существовать только в виде сферических мозаик, подобно моногону и двуугольнику (например: {3/2}, {5/3}, {5/4}, {7/4}, {9/ 5}), однако они, по-видимому, не были детально изучены.
Также существуют неудавшиеся звездчатые многоугольники, такие как треугольник , которые не покрывают поверхность круга конечное число раз. [8]
Наклонить полигоны
[ редактировать ]Помимо плоских правильных многоугольников существует бесконечно много правильных косых многоугольников . Наклонные полигоны можно создать с помощью операции смешивания.
Смесь двух многоугольников P и Q , записываемая P # Q , может быть построена следующим образом:
- возьмем декартово произведение их вершин V P × V Q .
- добавить ребра ( p 0 × q 0 , p 1 × q 1 ) , где ( p 0 , p 1 ) - ребро P и ( q 0 , q 1 ) - ребро Q .
- выбрать произвольную связную составляющую результата.
Альтернативно, смесь представляет собой многоугольник ⟨ ρ 0 σ 0 , ρ 1 σ 1 ⟩ , где ρ и σ — образующие зеркала P и Q, помещенные в ортогональные подпространства. [9] Операция смешивания является коммутативной, ассоциативной и идемпотентной.
Каждый правильный косой многоугольник можно выразить как смесь уникальных [а] набор плоских многоугольников. [9] Если P и Q не имеют общих факторов, то Dim( P # Q ) = Dim( P ) + Dim( Q ) .
В 3 пространстве
[ редактировать ]Правильные конечные многоугольники в трех измерениях представляют собой в точности смесь плоских многоугольников (размерность 2) с двуугольником (размерность 1). Они имеют вершины, соответствующие призме ( { n / m }#{} , где n нечетно) или антипризме ( { n / m }#{} , где n четно). Все многоугольники в трехмерном пространстве имеют четное количество вершин и ребер.
Некоторые из них выглядят как многоугольники Петри правильных многогранников.
В 4 пространстве
[ редактировать ]Правильные конечные многоугольники в 4 измерениях — это в точности многоугольники, образованные смесью двух различных плоских многоугольников. Они имеют вершины, лежащие на торе Клиффорда и связанные клиффордовым смещением . В отличие от трехмерных многоугольников, перекошенные многоугольники при двойном вращении могут иметь нечетное количество сторон.
3-многогранники (многогранники)
[ редактировать ]Многогранники ранга 3 называются многогранниками :
Правильный многогранник с символом Шлефли { p , q } , диаграммы Коксетера ![]()
![]()
![]()
![]()
![]() , имеет правильный тип грани { p } и правильную вершинную фигуру { q } .
, имеет правильный тип грани { p } и правильную вершинную фигуру { q } .
Вершинная фигура (многогранника) — это многоугольник, видимый путем соединения тех вершин, которые находятся на расстоянии одного ребра от данной вершины. Для правильных многогранников эта вершинная фигура всегда является правильным (и плоским) многоугольником.
Существование правильного многогранника { p , q } ограничено неравенством, связанным с дефектом угла вершинной фигуры :
Перечисляя перестановки , мы находим пять выпуклых форм, четыре звездчатые формы и три плоских мозаики, все с многоугольниками { p } и { q }, ограниченными: {3}, {4}, {5}, {5/2}, и {6}.
За пределами евклидова пространства существует бесконечное множество правильных гиперболических мозаик.
Выпуклый
[ редактировать ]Пять выпуклых правильных многогранников называются Платоновыми телами . Число вершин дается с каждым количеством вершин. Все эти многогранники имеют эйлерову характеристику (χ), равную 2.
| Имя | Шлефли { п , q } | Коксетер | Изображение (твердый) | Изображение (сфера) | Лица { п } | Края | Вершины { q } | Симметрия | Двойной |
|---|---|---|---|---|---|---|---|---|---|
| Тетраэдр ( 3-симплекс ) | {3,3} |  |  | 4 {3} | 6 | 4 {3} | Т д [3,3] (*332) | (себя) | |
| Шестигранник Куб ( 3-куб ) | {4,3} |  |  | 6 {4} | 12 | 8 {3} | Ой [4,3] (*432) | Октаэдр | |
| Октаэдр ( 3-ортоплекс ) | {3,4} |  |  | 8 {3} | 12 | 6 {4} | Ой [4,3] (*432) | Куб | |
| Додекаэдр | {5,3} |  |  | 12 {5} | 30 | 20 {3} | I h [5,3] (*532) | Икосаэдр | |
| Икосаэдр | {3,5} |  |  | 20 {3} | 30 | 12 {5} | I h [5,3] (*532) | Додекаэдр |
сферический
[ редактировать ]В сферической геометрии существуют правильные сферические многогранники ( мозаики сферы ) , которые в противном случае были бы вырождены в многогранники. Это осоэдры {2,n} и двойственные им диэдры {n,2}. Коксетер называет эти случаи «неправильными» мозаиками. [10]
Первые несколько случаев (n от 2 до 6) перечислены ниже.
| Имя | Шлефли {2,р} | Коксетер диаграмма | Изображение (сфера) | Лица {2} π/п | Края | Вершины {р} | Симметрия | Двойной |
|---|---|---|---|---|---|---|---|---|
| Дигональный осоэдр | {2,2} | 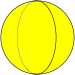 | 2 {2} п/2 | 2 | 2 {2} п/2 | Д 2 часа [2,2] (*222) | Себя | |
| Треугольный осоэдр | {2,3} |  | 3 {2} п/3 | 3 | 2 {3} | Д 3 часа [2,3] (*322) | Треугольный диэдр | |
| Квадратный осоэдр | {2,4} | 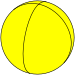 | 4 {2} п/4 | 4 | 2 {4} | Д 4 часа [2,4] (*422) | Квадратный двугранник | |
| Пятиугольный осоэдр | {2,5} | 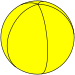 | 5 {2} п/5 | 5 | 2 {5} | Д 5ч [2,5] (*522) | Пятиугольный диэдр | |
| Шестиугольный осоэдр | {2,6} |  | 6 {2} стр/6 | 6 | 2 {6} | Д 6ч [2,6] (*622) | Шестиугольный диэдр |
| Имя | Шлефли {п, 2} | Коксетер диаграмма | Изображение (сфера) | Лица {р} | Края | Вершины {2} | Симметрия | Двойной |
|---|---|---|---|---|---|---|---|---|
| Дигональный диэдр | {2,2} |  | 2 {2} п/2 | 2 | 2 {2} п/2 | Д 2 часа [2,2] (*222) | Себя | |
| Треугольный диэдр | {3,2} |  | 2 {3} | 3 | 3 {2} п/3 | Д 3 часа [3,2] (*322) | Треугольный осоэдр | |
| Квадратный двугранник | {4,2} |  | 2 {4} | 4 | 4 {2} п/4 | Д 4 часа [4,2] (*422) | Квадратный осоэдр | |
| Пятиугольный диэдр | {5,2} |  | 2 {5} | 5 | 5 {2} п/5 | Д 5ч [5,2] (*522) | Пятиугольный осоэдр | |
| Шестиугольный диэдр | {6,2} |  | 2 {6} | 6 | 6 {2} стр/6 | Д 6ч [6,2] (*622) | Шестиугольный осоэдр |
Звездчатые диэдры и осоэдры { p / q , 2} и {2, p / q } также существуют для любого звездчатого многоугольника { p / q } .
Звезды
[ редактировать ]Правильные многогранники называются многогранниками Кеплера – Пуансо , и их четыре, в зависимости от расположения вершин додекаэдра звездчатые {5,3} и икосаэдра {3,5}:
Будучи сферическими мозаиками , эти звездные формы перекрывают сферу несколько раз, что называется ее плотностью , равной 3 или 7 для этих форм. На мозаичных изображениях показана одна сферическая полигональная грань желтого цвета.
| Имя | Изображение (скелетный) | Изображение (твердый) | Изображение (сфера) | Звездчатость диаграмма | Шлефли { п , q } и Коксетер | Лица { п } | Края | Вершины { q } краска. | час | Плотность | Симметрия | Двойной |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Малый звездчатый додекаэдр |  |  |  |  | {5/2,5} | 12 {5/2} | 30 | 12 {5} | −6 | 3 | I h [5,3] (*532) | Большой додекаэдр |
| Большой додекаэдр |  |  |  |  | {5,5/2} | 12 {5} | 30 | 12 {5/2} | −6 | 3 | I h [5,3] (*532) | Малый звездчатый додекаэдр |
| Большой звездчатый додекаэдр |  |  |  |  | {5/2,3} | 12 {5/2} | 30 | 20 {3} | 2 | 7 | I h [5,3] (*532) | Большой икосаэдр |
| Большой икосаэдр |  |  | 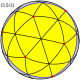 |  | {3,5/2} | 20 {3} | 30 | 12 {5/2} | 2 | 7 | I h [5,3] (*532) | Большой звездчатый додекаэдр |
Существует бесконечно много неудавшихся звездчатых многогранников. Это также сферические мозаики со звездчатыми многоугольниками в символах Шлефли, но они не покрывают сферу конечное число раз. Некоторые примеры: {5/2,4}, {5/2,9}, {7/2,3}, {5/2,5/2}, {7/2,7/3}, {4, 5/2} и {3,7/3}.
Перекос многогранников
[ редактировать ]Этот раздел нуждается в расширении . Вы можете помочь, добавив к нему . ( январь 2024 г. ) |
Правильные косые многогранники являются обобщениями набора правильных многогранников , которые включают возможность неплоских вершинных фигур .
Для 4-мерных косых многогранников Коксетер предложил для этих фигур модифицированный символ Шлефли {l,m|n}, где {l,m} подразумевает фигуру вершины , m l-угольников вокруг вершины и n -угольных отверстий. Их вершинные фигуры представляют собой косые многоугольники , зигзагообразные между двумя плоскостями.
Правильные косые многогранники, представленные {l,m|n}, подчиняются этому уравнению:
Четыре из них можно увидеть в 4-х измерениях как подмножество граней четырёх правильных 4-многогранников , имеющих одинаковое расположение вершин и расположение ребер :
 |  |  |  |
| {4, 6 | 3} | {6, 4 | 3} | {4, 8 | 3} | {8, 4 | 3} |
|---|
4-многогранники
[ редактировать ]Правильные 4-многогранники с символом Шлефли имеют клетки типа , лица типа , краевые фигуры и вершинные фигуры .
- Вершинная фигура (4-многогранника) — это многогранник, видимый по расположению соседних вершин вокруг данной вершины. Для правильных 4-многогранников эта вершинная фигура представляет собой правильный многогранник.
- Краевая фигура — это многоугольник, который можно увидеть по расположению граней вокруг края. Для правильных 4-многогранников эта реберная фигура всегда будет правильным многоугольником.
Существование правильного 4-многогранника ограничено существованием правильных многогранников . Предлагаемое название для 4-многогранников — «полихорон». [11]
Каждый из них будет существовать в пространстве, зависящем от этого выражения:
- : Гиперсферические трехмерные соты или четырехмерные многогранники.
- : Евклидовы трехмерные соты
- : Гиперболические трехмерные соты
Эти ограничения допускают 21 форму: 6 — выпуклые, 10 — невыпуклые, одна — евклидовы трехмерные соты и 4 — гиперболические соты.
Эйлерова характеристика для выпуклых 4-многогранников равно нулю:
Выпуклый
[ редактировать ]Шесть выпуклых правильных 4-многогранников показаны в таблице ниже. Все эти 4-многогранники имеют эйлерову характеристику (χ), равную 0.
| Имя | Шлефли {п, д, г} | Коксетер | Клетки {п, д} | Лица {р} | Края {р} | Вершины {q,r} | Двойной {р, д, р} |
|---|---|---|---|---|---|---|---|
| 5-клеточный ( 4-симплекс ) | {3,3,3} | 5 {3,3} | 10 {3} | 10 {3} | 5 {3,3} | (себя) | |
| 8-ячеечный ( 4-куб ) (Тессеракт) | {4,3,3} | 8 {4,3} | 24 {4} | 32 {3} | 16 {3,3} | 16-ячеечный | |
| 16-ячеечный ( 4-ортоплекс ) | {3,3,4} | 16 {3,3} | 32 {3} | 24 {4} | 8 {3,4} | Тессеракт | |
| 24-ячеечный | {3,4,3} | 24 {3,4} | 96 {3} | 96 {3} | 24 {4,3} | (себя) | |
| 120-ячеечный | {5,3,3} | 120 {5,3} | 720 {5} | 1200 {3} | 600 {3,3} | 600-ячеечный | |
| 600-ячеечный | {3,3,5} | 600 {3,3} | 1200 {3} | 720 {5} | 120 {3,5} | 120-ячеечный |
| 5-клеточный | 8-ячеечный | 16-ячеечный | 24-ячеечный | 120-ячеечный | 600-ячеечный |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
| Каркас ( многоугольник Петри ) с наклоном ортогональных проекций | |||||
 |  |  |  |  |  |
| Твердые орфографические проекции | |||||
 четырехгранный конверт (ячейка/ вершинно-центрированный) |  кубическая оболочка (клеточно-центрированный) |  кубическая оболочка (клеточно-центрированный) |  кубооктаэдрический конверт (клеточно-центрированный) |  усеченный ромб триаконтаэдр конверт (клеточно-центрированный) |  Пентакис икосододекаэдрический конверт (вершинно-центрированный) |
| Каркасные диаграммы Шлегеля ( Перспективная проекция ) | |||||
 (клеточно-центрированный) |  (клеточно-центрированный) |  (клеточно-центрированный) |  (клеточно-центрированный) |  (клеточно-центрированный) |  (вершинно-центрированный) |
| Каркасные стереографические проекции ( гиперсферические ) | |||||
 |  |  |  |  |  |
сферический
[ редактировать ]Ди-4-топы и хосо-4-топы существуют как правильные мозаики 3-сферы .
К регулярным ди-4-топам (2 грани) относятся: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2. }, {p,2,2} и их хосо-4-топы двойственные (2 вершины): {2,3,3}, {2,4,3}, {2,3,4}, {2, 3,5}, {2,5,3}, {2,2, п }. 4-многогранники вида {2, p , 2} — это то же самое, что {2,2, p }. Существуют также случаи { p ,2, q }, которые имеют двугранные ячейки и одногранные вершинные фигуры.
| Шлефли {2, п , q } | Коксетер | Клетки {2, р } π/ q | Лица {2} π/ п ,π/ q | Края | Вершины | Вершинная фигура { п , q } | Симметрия | Двойной |
|---|---|---|---|---|---|---|---|---|
| {2,3,3} | 4 {2,3} π/3  | 6 {2} π/3,π/3 | 4 | 2 | {3,3}  | [2,3,3] | {3,3,2} | |
| {2,4,3} | 6 {2,4} π/3  | 12 {2} π/4,π/3 | 8 | 2 | {4,3}  | [2,4,3] | {3,4,2} | |
| {2,3,4} | 8 {2,3} п/4  | 12 {2} п/3,п/4 | 6 | 2 | {3,4}  | [2,4,3] | {4,3,2} | |
| {2,5,3} | 12 {2.5} π/3  | 30 {2} π/5,π/3 | 20 | 2 | {5,3}  | [2,5,3] | {3,5,2} | |
| {2,3,5} | 20 {2,3} п/5  | 30 {2} п/3, п/5 | 12 | 2 | {3,5}  | [2,5,3] | {5,3,2} |
Звезды
[ редактировать ]Существует десять правильных звездчатых 4-многогранников , которые называются 4-многогранниками Шлефли – Гесса . Их вершины основаны на выпуклых 120-ячеечных {5,3,3} и 600-клеточных {3,3,5} .
Людвиг Шлефли нашел четыре из них и пропустил последние шесть, потому что он не допускал форм, не удовлетворяющих эйлеровой характеристике, в ячейках или фигурах вершин (для торов с нулевыми отверстиями: F+V−E=2). Эдмунд Гесс (1843–1903) завершил полный список десяти в своей немецкой книге « Введение в теорию сферического деления со специальным рассмотрением ее применения к теории равноповерхностей и равноугольных многогранников» (1883) [1] .
Существует 4 уникальных расположения ребер и 7 уникальных расположений граней из этих 10 правильных звездчатых 4-многогранников, показанных в виде ортогональных проекций :
| Имя | Каркас | Твердый | Шлефли {p, q, r} Коксетер | Клетки {п, д} | Лица {р} | Края {р} | Вершины {q, р} | Плотность | час | Группа симметрии | Двойной {р, д, р} |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Икосаэдрический 120-ячеечный (граненый, 600-ячеечный) |  |  | {3,5,5/2} | 120 {3,5} | 1200 {3} | 720 {5/2} | 120 {5,5/2} | 4 | 480 | Ч 4 [5,3,3] | Маленький звездчатый, 120 ячеек. |
| Маленький звездчатый, 120 ячеек. |  |  | {5/2,5,3} | 120 {5/2,5} | 720 {5/2} | 1200 {3} | 120 {5,3} | 4 | −480 | Ч 4 [5,3,3] | Икосаэдрический 120-ячеечный |
| Отличный 120-ячеечный |  |  | {5,5/2,5} | 120 {5,5/2} | 720 {5} | 720 {5} | 120 {5/2,5} | 6 | 0 | Ч 4 [5,3,3] | Самодвойственный |
| Гранд, 120 ячеек |  |  | {5,3,5/2} | 120 {5,3} | 720 {5} | 720 {5/2} | 120 {3,5/2} | 20 | 0 | Ч 4 [5,3,3] | Большой звездчатый 120-ячеечный |
| Большой звездчатый 120-ячеечный |  |  | {5/2,3,5} | 120 {5/2,3} | 720 {5/2} | 720 {5} | 120 {3,5} | 20 | 0 | Ч 4 [5,3,3] | Гранд, 120 ячеек |
| Большой звездчатый, 120 ячеек |  |  | {5/2,5,5/2} | 120 {5/2,5} | 720 {5/2} | 720 {5/2} | 120 {5,5/2} | 66 | 0 | Ч 4 [5,3,3] | Самодвойственный |
| Большой гранд, 120 ячеек |  |  | {5,5/2,3} | 120 {5,5/2} | 720 {5} | 1200 {3} | 120 {5/2,3} | 76 | −480 | Ч 4 [5,3,3] | Большой икосаэдр, 120 ячеек. |
| Большой икосаэдр, 120 ячеек. (большой граненый, 600 ячеек) |  |  | {3,5/2,5} | 120 {3,5/2} | 1200 {3} | 720 {5} | 120 {5/2,5} | 76 | 480 | Ч 4 [5,3,3] | Большой гранд, 120 ячеек |
| Гранд 600-ячеечный |  |  | {3,3,5/2} | 600 {3,3} | 1200 {3} | 720 {5/2} | 120 {3,5/2} | 191 | 0 | Ч 4 [5,3,3] | Большой гранд звездчатый, 120 ячеек. |
| Большой гранд звездчатый, 120 ячеек. |  |  | {5/2,3,3} | 120 {5/2,3} | 720 {5/2} | 1200 {3} | 600 {3,3} | 191 | 0 | Ч 4 [5,3,3] | Гранд 600-ячеечный |
Существует 4 неудавшихся потенциальных регулярных звездчатых 4-многогранника перестановки: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5. /2}. Их ячейки и вершинные фигуры существуют, но они не покрывают гиперсферу с конечным числом повторений.
Перекос 4-многогранников
[ редактировать ]Этот раздел нуждается в расширении . Вы можете помочь, добавив к нему . ( январь 2024 г. ) |
Помимо 16 плоских 4-многогранников, указанных выше, существует 18 конечных косых многогранников. [12] Один из них получается как Петриал тессеракта, а остальные 17 могут быть сформированы путем применения операции каппа к плоским многогранникам и Петриалу тессеракта.
Ранги 5 и выше
[ редактировать ]5-многогранникам можно присвоить символ где это четырехликий тип, тип клетки, тип лица, и это фигура лица, - краевая фигура, а это вершинная фигура.
- ( Вершинная фигура 5-многогранника) — это 4-многогранник, если рассматривать расположение вершин, соседних с каждой вершиной.
- Реберная фигура (5-многогранника) представляет собой многогранник, который можно увидеть по расположению граней вокруг каждого ребра.
- Фигура грани (5-мерного многогранника) представляет собой многоугольник, который можно увидеть по расположению ячеек вокруг каждой грани.
Правильный 5-многогранник существует только если и являются правильными 4-многогранниками.
Пространство, в котором он помещается, основано на выражении:
- : Сферическая 4-мерная мозаика или 5-мерный многогранник.
- : Евклидова 4-мерная мозаика
- : гиперболическая 4-мерная мозаика
Перечисление этих ограничений дает 3 выпуклых многогранника, отсутствие звездчатых многогранников, 3 мозаики евклидова 4-мерного пространства и 5 мозаик паракомпактного гиперболического 4-мерного пространства. Единственные невыпуклые правильные многогранники ранга 5 и выше — это косые.
Выпуклый
[ редактировать ]В размерностях 5 и выше существует только три вида выпуклых правильных многогранников. [13]
| Имя | Шлефли Символ {p 1 ,...,p n −1 } | Коксетер | k -грани | Фасет тип | Вертекс фигура | Двойной |
|---|---|---|---|---|---|---|
| n -симплекс | {3 п -1 } | {3 п -2 } | {3 п -2 } | Самодвойственный | ||
| n- куб | {4,3 п -2 } | {4,3 п -3 } | {3 п -2 } | n- ортоплекс | ||
| n- ортоплекс | {3 п -2 ,4} | {3 п -2 } | {3 п -3 ,4} | n- куб |
Существуют также неправильные случаи, когда некоторые числа в символе Шлефли равны 2. Например, {p,q,r,...2} — неправильный правильный сферический многогранник, если {p,q,r...} — правильный сферический многогранник, а {2,...p,q,r} — несобственный правильный сферический многогранник, если {...p,q,r} — правильный сферический многогранник. Такие многогранники также можно использовать в качестве граней, получая такие формы, как {p,q,...2...y,z}.
5 измерений
[ редактировать ]| Имя | Шлефли Символ {п, д, г, с} Коксетер | Фасеты {п, д, г} | Клетки {п, д} | Лица {р} | Края | Вершины | Лицо фигура {с} | Край фигура {р,с} | Вертекс фигура {д, г, с} |
|---|---|---|---|---|---|---|---|---|---|
| 5-симплекс | {3,3,3,3} | 6 {3,3,3} | 15 {3,3} | 20 {3} | 15 | 6 | {3} | {3,3} | {3,3,3} |
| 5-куб | {4,3,3,3} | 10 {4,3,3} | 40 {4,3} | 80 {4} | 80 | 32 | {3} | {3,3} | {3,3,3} |
| 5-ортоплекс | {3,3,3,4} | 32 {3,3,3} | 80 {3,3} | 80 {3} | 40 | 10 | {4} | {3,4} | {3,3,4} |
 5-симплекс |  5-куб |  5-ортоплекс |
6 измерений
[ редактировать ]| Имя | Шлефли | Вершины | Края | Лица | Клетки | 4-ликий | 5-гранный | час |
|---|---|---|---|---|---|---|---|---|
| 6-симплекс | {3,3,3,3,3} | 7 | 21 | 35 | 35 | 21 | 7 | 0 |
| 6-куб. | {4,3,3,3,3} | 64 | 192 | 240 | 160 | 60 | 12 | 0 |
| 6-ортоплекс | {3,3,3,3,4} | 12 | 60 | 160 | 240 | 192 | 64 | 0 |
 6-симплекс |  6-куб. |  6-ортоплекс |
7 измерений
[ редактировать ]| Имя | Шлефли | Вершины | Края | Лица | Клетки | 4-ликий | 5-гранный | 6-гранный | час |
|---|---|---|---|---|---|---|---|---|---|
| 7-симплекс | {3,3,3,3,3,3} | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 2 |
| 7-куб | {4,3,3,3,3,3} | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 2 |
| 7-ортоплекс | {3,3,3,3,3,4} | 14 | 84 | 280 | 560 | 672 | 448 | 128 | 2 |
 7-симплекс |  7-куб |  7-ортоплекс |
8 измерений
[ редактировать ]| Имя | Шлефли | Вершины | Края | Лица | Клетки | 4-ликий | 5-гранный | 6-гранный | 7-гранный | час |
|---|---|---|---|---|---|---|---|---|---|---|
| 8-симплекс | {3,3,3,3,3,3,3} | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 0 |
| 8-кубовый | {4,3,3,3,3,3,3} | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 0 |
| 8-ортоплекс | {3,3,3,3,3,3,4} | 16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | 0 |
 8-симплекс |  8-кубовый |  8-ортоплекс |
9 измерений
[ редактировать ]| Имя | Шлефли | Вершины | Края | Лица | Клетки | 4-ликий | 5-гранный | 6-гранный | 7-гранный | 8-гранный | час |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-симплекс | {3 8 } | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 2 |
| 9-куб | {4,3 7 } | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 2 |
| 9-ортоплекс | {3 7 ,4} | 18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | 2 |
 9-симплекс |  9-куб |  9-ортоплекс |
10 измерений
[ редактировать ]| Имя | Шлефли | Вершины | Края | Лица | Клетки | 4-ликий | 5-гранный | 6-гранный | 7-гранный | 8-гранный | 9-ликий | час |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10-симплекс | {3 9 } | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 0 |
| 10-кубовый | {4,3 8 } | 1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | 0 |
| 10-ортоплекс | {3 8 ,4} | 20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | 0 |
 10-симплекс |  10-кубовый |  10-ортоплекс |
Звездные многогранники
[ редактировать ]Не существует правильных звездчатых многогранников ранга 5 и выше, за исключением вырожденных многогранников, созданных звездным произведением звездчатых многогранников более низкого ранга. например, гомотопы и дитопы.
Правильные проективные многогранники
[ редактировать ]Проективный правильный ( n +1) -многогранник существует, когда исходная правильная n -сферическая мозаика {p,q,...} центрально симметрична . Такой многогранник называется полу-{p,q,...} и содержит вдвое меньше элементов. Коксетер дает символ {p,q,...}/2, а Макмаллен пишет {p,q,...} h/2 с h в качестве числа Кокстера . [14]
с четными сторонами Правильные многоугольники имеют проективные многоугольники в форме полуугольника 2n , {2p}/2.
относятся 4 правильных проективных многогранника К 4 из 5 Платоновых тел .
Полукуб и гемиоктаэдр обобщаются как гемин- n -кубы и геми -n - ортоплексы любого ранга.
Правильные проективные многогранники
[ редактировать ]| Имя | Коксетер МакМаллен | Изображение | Лица | Края | Вершины | час | скелетный график |
|---|---|---|---|---|---|---|---|
| полукуб | {4,3}/2 {4,3} 3 |  | 3 | 6 | 4 | 1 | К 4 |
| Полуоктаэдр | {3,4}/2 {3,4} 3 |  | 4 | 6 | 3 | 1 | Двусторонний К 3 |
| Полудодекаэдр | {5,3}/2 {5,3} 5 |  | 6 | 15 | 10 | 1 | Г(5,2) |
| Полу-икосаэдр | {3,5}/2 {3,5} 5 |  | 10 | 15 | 6 | 1 | К 6 |
Правильные проективные 4-многогранники
[ редактировать ]5 из 6 выпуклых правильных 4-многогранников являются центрально-симметричными, порождающими проективные 4-многогранники. Тремя особыми случаями являются геми-24 клетки, геми-600 клеток и геми-120 клеток.
| Имя | Коксетер символ | МакМаллен Символ | Клетки | Лица | Края | Вершины | час | Скелетный график |
|---|---|---|---|---|---|---|---|---|
| полудессеракт | {4,3,3}/2 | {4,3,3} 4 | 4 | 12 | 16 | 8 | 0 | К 4,4 |
| Геми- 16-клеточный | {3,3,4}/2 | {3,3,4} 4 | 8 | 16 | 12 | 4 | 0 | обоюдоострый К 4 |
| Геми- 24-клеточный | {3,4,3}/2 | {3,4,3} 6 | 12 | 48 | 48 | 12 | 0 | |
| Геми- 120-ячеечный | {5,3,3}/2 | {5,3,3} 15 | 60 | 360 | 600 | 300 | 0 | |
| Геми- 600-ячеечный | {3,3,5}/2 | {3,3,5} 15 | 300 | 600 | 360 | 60 | 0 |
Правильные проективные 5-многогранники
[ редактировать ]Только 2 из 3 правильных сферических многогранников центрально симметричны для рангов 5 и выше: они являются полуверсиями правильного гиперкуба и ортоплекса. Они приведены в таблице ниже для ранга 5, например:
| Имя | Шлефли | 4-ликий | Клетки | Лица | Края | Вершины | час | Скелетный график |
|---|---|---|---|---|---|---|---|---|
| геми- пентеракт | {4,3,3,3}/2 | 5 | 20 | 40 | 40 | 16 | 1 | Скелет Тессеракта + 8 центральных диагоналей |
| полупентакросс | {3,3,3,4}/2 | 16 | 40 | 40 | 20 | 5 | 1 | обоюдоострый К 5 |
Апейротопы
[ редактировать ]Апейротоп , или бесконечный многогранник — это многогранник который имеет бесконечно много граней . n - апейротоп — это бесконечный n -многогранник: 2-апейротоп или апейрогон — бесконечный многоугольник, 3-апейротоп или апейроэдр — бесконечный многогранник и т. д.
Существует два основных геометрических класса апейротопа: [15]
- Правильные соты измерений n , полностью заполняющие n -мерное пространство.
- Правильные косые апейротопы , содержащие n -мерное многообразие в высшем пространстве.
2-апейротопы (апейрогоны)
[ редактировать ]Прямой апейрогон представляет собой правильное замощение линии, подразделяющее ее на бесконечное число равных отрезков. Он имеет бесконечно много вершин и ребер. Его символ Шлефли — {∞}, а диаграмма Кокстера ![]()
![]()
![]() .
.
Он существует как предел p -угольника, когда p стремится к бесконечности, следующим образом:
| Имя | моногон | Достаточно | Треугольник | Квадрат | Пентагон | Шестиугольник | Семиугольник | п-гон | Апейрогон |
|---|---|---|---|---|---|---|---|---|---|
| Шлефли | {1} | {2} | {3} | {4} | {5} | {6} | {7} | { п } | {∞} |
| Симметрия | Д 1 , [ ] | Д2 ] , [2 | Д 3 , [3] | Д 4 , [4] | Д 5 , [5] | Д 6 , [6] | D 7 , [7] | [п] | |
| Коксетер | |||||||||
| Изображение |  |  |  |  |  |  |  |
Апейрогоны на гиперболической плоскости , особенно правильный апейрогон , {∞}, могут иметь кривизну, как и конечные многоугольники евклидовой плоскости, с вершинами, описанными орициклами или гиперциклами, а не кругами .
Регулярные апейрогоны, масштабированные так, чтобы сходиться на бесконечности, имеют символ {∞} и существуют на орициклах, хотя в более общем смысле они могут существовать на гиперциклах.
| {∞} | {пи/мин} |
|---|---|
 Апейрогон на орицикле |  Апейрогон на гиперцикле |
Выше показаны два правильных гиперболических апейрогона в модели диска Пуанкаре , правый показывает перпендикулярные линии отражения расходящихся фундаментальных областей , разделенных длиной λ.
Косые апейрогоны
[ редактировать ]Косой апейрогон в двух измерениях образует на плоскости зигзагообразную линию. Если зигзаг ровный и симметричный, то апейрогон правильный.
Косые апейрогоны можно построить в любом количестве измерений. В трех измерениях правильный косой апейрогон образует спиральную спираль и может быть как левосторонним, так и правосторонним.
| 2 измерения | 3 измерения |
|---|---|
 Зигзагообразный апейрогон |  Хеликс апейрогон |
3-апейротопы (апейроэдры)
[ редактировать ]Евклидовы мозаики
[ редактировать ]Есть три регулярных мозаики плоскости.
| Имя | Квадратная плитка (кадриль) | Треугольная плитка (для дельты) | Шестиугольная плитка (гекстиль) |
|---|---|---|---|
| Симметрия | п4м, [4,4], (*442) | п6м, [6,3], (*632) | |
| Шлефли {p,q} | {4,4} | {3,6} | {6,3} |
| Диаграмма Кокстера | |||
| Изображение |  |  |  |
Есть два неправильных правильных мозаики: {∞,2}, апейрогон , состоящий из двух апейрогонов , каждый из которых заполняет половину плоскости; и, во-вторых, его двойственный {2,∞}, апейрогональный осоэдр , рассматриваемый как бесконечный набор параллельных прямых.
 {∞,2} , |  {2,∞} , |
Евклидовы звездные мозаики
[ редактировать ]Не существует правильных плоских мозаик звездчатых многоугольников . Есть много перечислений, которые укладываются в плоскость (1/ p + 1/ q = 1/2), например {8/3,8}, {10/3,5}, {5/2,10}, {12 /5,12} и т. д., но ни одно из них не повторяется периодически.
Гиперболические мозаики
[ редактировать ]Мозаики гиперболического 2-мерного пространства представляют собой гиперболические мозаики . В H существует бесконечно много правильных мозаик. 2 . Как указано выше, каждая пара натуральных чисел { p , q } такая, что 1/ p + 1/ q < 1/2, дает гиперболическую мозаику. Фактически, для общего треугольника Шварца ( p , q , r ) то же самое справедливо для 1/ p + 1/ q + 1/ r < 1.
Существует несколько различных способов отображения гиперболической плоскости, включая модель диска Пуанкаре, которая отображает плоскость в виде круга, как показано ниже. Следует признать, что все грани многоугольников на мозаике ниже имеют одинаковый размер и кажутся уменьшающимися только вблизи краев из-за примененной проекции, что очень похоже на эффект объектива «рыбий глаз» камеры .
Существует бесконечно много плоских правильных 3-апейротопов (апеироэдров) как правильных мозаик гиперболической плоскости вида {p,q} с p+q<pq/2.
- {3,7}, {3,8}, {3,9} ... {3,∞}
- {4,5}, {4,6}, {4,7} ... {4,∞}
- {5,4}, {5,5}, {5,6} ... {5,∞}
- {6,4}, {6,5}, {6,6} ... {6,∞}
- {7,3}, {7,4}, {7,5} ... {7,∞}
- {8,3}, {8,4}, {8,5} ... {8,∞}
- {9,3}, {9,4}, {9,5} ... {9,∞}
- ...
- {∞,3}, {∞,4}, {∞,5} ... {∞,∞}
Выборка:
| Обычная таблица гиперболической мозаики |
|---|
Разбиения {p, ∞} имеют идеальные вершины на краю модели диска Пуанкаре. Их дуальные {∞, p} имеют идеальные апейрогональные грани, т. е. вписаны в орициклы . Можно пойти дальше (как это сделано в таблице выше) и найти замощения с ультраидеальными вершинами вне диска Пуанкаре, двойственные плиткам, вписанным в гиперциклы ; в том, что обозначено выше как {p, iπ/λ}, вокруг каждой ультраидеальной вершины по-прежнему помещается бесконечное количество плиток. [16] (Параллельные линии в расширенном гиперболическом пространстве встречаются в идеальной точке; ультрапараллельные линии встречаются в ультраидеальной точке.) [17]
Гиперболические звездные мозаики
[ редактировать ]Существуют две бесконечные формы гиперболических мозаик, чьи грани или вершинные фигуры представляют собой звездчатые многоугольники: { m /2, m } и двойственные им { m , m /2} с m = 7, 9, 11, .... { m /2, m } — это звездчатые мозаики { m , 3}, а двойственные мозаики { m , m /2} — это фасеты мозаик {3, m } и увеличе- ния мозаик { m , 3}.
Паттерны { m /2, m } и { m , m /2} продолжаются при нечетных m < 7 как многогранники : при m = 5 мы получаем малый звездчатый додекаэдр и большой додекаэдр , а при m = 3 случай вырождается до тетраэдра . Два других многогранника Кеплера-Пуансо ( большой звездчатый додекаэдр и большой икосаэдр ) не имеют аналогов правильной гиперболической мозаики. Если m четно, в зависимости от того, как мы решим определить { m /2}, мы можем получить либо вырожденные двойные покрытия других мозаик, либо составные мозаики.
| Имя | Шлефли | Диаграмма Кокстера | Изображение | Тип лица {р} | Вершинная фигура {д} | Плотность | Симметрия | Двойной |
|---|---|---|---|---|---|---|---|---|
| Гептаграммная плитка порядка 7 | {7/2,7} |  | {7/2} | {7} | 3 | *732 [7,3] | Семиугольная мозаика гептаграммного порядка | |
| Семиугольная мозаика гептаграммного порядка | {7,7/2} |  | {7} | {7/2} | 3 | *732 [7,3] | Гептаграммная плитка порядка 7 | |
| Эннеаграмматическая мозаика порядка 9 | {9/2,9} |  | {9/2} | {9} | 3 | *932 [9,3] | Эннеагональная мозаика эннеаграммического порядка | |
| Эннеагональная мозаика эннеаграммического порядка | {9,9/2} |  | {9} | {9/2} | 3 | *932 [9,3] | Эннеаграмматическая мозаика порядка 9 | |
| Гендекаграммная плитка порядка 11 | {11/2,11} |  | {11/2} | {11} | 3 | *11.3.2 [11,3] | Шестнадцатиугольная мозаика эндекаграммного порядка | |
| Шестнадцатиугольная мозаика эндекаграммного порядка | {11,11/2} |  | {11} | {11/2} | 3 | *11.3.2 [11,3] | Гендекаграммная плитка порядка 11 | |
| Порядок- p p -грамматическое замощение | { п /2, р } | { п /2} | { п } | 3 | * стр. 32 [стр, 3] | p - грамматический порядок p -угольная мозаика | ||
| p - грамматический порядок p -угольная мозаика | { п , п /2} | { п } | { п /2} | 3 | * стр. 32 [стр, 3] | Порядок- p p -грамматическое замощение |
Перекос апейроэдров в евклидовом трехмерном пространстве
[ редактировать ]Этот раздел нуждается в расширении . Вы можете помочь, добавив к нему . ( январь 2024 г. ) |
есть три правильных косых апейроэдра с плоскими гранями. В евклидовом трехмерном пространстве [18] [19] [20] Они имеют такое же расположение вершин и расположение краев , что и 3 выпуклых однородных сот .
- 6 квадратов вокруг каждой вершины: {4,6|4}
- 4 шестиугольника вокруг каждой вершины: {6,4|4}
- 6 шестиугольников вокруг каждой вершины: {6,6|3}

| Правильные косые многогранники с плоскими гранями. | ||
|---|---|---|
 {4,6|4} |  {6,4|4} |  {6,6|3} |
С учетом перекоса граней в евклидовом трехмерном пространстве имеется 24 правильных апейроэдра. [22] К ним относятся 12 апейроэдров, созданных путем слияния с евклидовыми апейроэдрами, и 12 чистых апейроэдров, включая 3 вышеперечисленных, которые нельзя выразить как нетривиальную смесь.
Эти чистые апейроэдры:
- {4,6|4} , мукуб
- {∞,6} 4,4 , Петриал мукуба
- {6,6|3} , мутетраэдр
- {∞,6} 6,3 , Петриал мутетраэдра
- {6,4|4} , муоктаэдр
- {∞,4} 6,4 , Петриал муоктаэдра
- {6,6} 4 , разделение мукуба пополам
- {4,6} 6 , Петриал {6,6} 4
- {∞,4} ·,*3 , перекос муоктаэдра
- {6,4} 6 , Петриал {∞,4} ·,*3
- {∞,3} ( а )
- {∞,3} ( б )
Косые апейроэдры в гиперболическом трехмерном пространстве
[ редактировать ]существует 31 правильный косой апейроэдр с выпуклыми гранями с компактной или паракомпактной симметрией: В гиперболическом трехмерном пространстве [23]
- 14 компактны: {8,10|3}, {10,8|3}, {10,4|3}, {4,10|3}, {6,4|5}, {4,6|5 }, {10,6|3}, {6,10|3}, {8,8|3}, {6,6|4}, {10,10|3},{6,6|5}, {8,6|3} и {6,8|3}.
- 17 являются паракомпактными: {12,10|3}, {10,12|3}, {12,4|3}, {4,12|3}, {6,4|6}, {4,6|6 }, {8,4|4}, {4,8|4}, {12,6|3}, {6,12|3}, {12,12|3}, {6,6|6}, {8,6|4}, {6,8|4}, {12,8|3}, {8,12|3} и {8,8|4}.
4-апейротопы
[ редактировать ]Мозаики евклидова трехмерного пространства
[ редактировать ]
Существует только одна невырожденная правильная мозаика 3-мерного пространства ( соты ), {4, 3, 4}: [24]
| Имя | Шлефли {п, д, г} | Коксетер | Клетка тип {п, д} | Лицо тип {р} | Край фигура {р} | Вертекс фигура {q,r} | час | Двойной |
|---|---|---|---|---|---|---|---|---|
| Кубические соты | {4,3,4} | {4,3} | {4} | {4} | {3,4} | 0 | Самодвойственный |
Неправильные мозаики евклидова трехмерного пространства
[ редактировать ]
Существует шесть неправильных правильных мозаик, пар, основанных на трех правильных евклидовых мозаиках. Все их ячейки и вершинные фигуры представляют собой правильные осоэдры {2,n}, диэдры , {n,2} и евклидовы мозаики. Эти неправильные регулярные мозаики конструктивно связаны с призматическими однородными сотами посредством операций усечения. Они представляют собой многомерные аналоги апейрогонального мозаики второго порядка и апейрогонального осоэдра .
| Шлефли {п, д, г} | Коксетер диаграмма | Клетка тип {п, д} | Лицо тип {р} | Край фигура {р} | Вертекс фигура {q,r} |
|---|---|---|---|---|---|
| {2,4,4} | {2,4} | {2} | {4} | {4,4} | |
| {2,3,6} | {2,3} | {2} | {6} | {3,6} | |
| {2,6,3} | {2,6} | {2} | {3} | {6,3} | |
| {4,4,2} | {4,4} | {4} | {2} | {4,2} | |
| {3,6,2} | {3,6} | {3} | {2} | {6,2} | |
| {6,3,2} | {6,3} | {6} | {2} | {3,2} |
Мозаики гиперболического трехмерного пространства
[ редактировать ]Существует десять плоских правильных сот гиперболического трехмерного пространства: [25]
- 4 компактны: {3,5,3}, {4,3,5}, {5,3,4} и {5,3,5}.
- а 6 паракомпактных: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3, 6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6,3,6}.
| ||||
|
Тесселяции гиперболического трехмерного пространства можно назвать гиперболическими сотами . В H 15 гиперболических сот. 3 , 4 компактных и 11 паракомпактных.
| Имя | Шлефли Символ {п, д, г} | Коксетер | Клетка тип {п, д} | Лицо тип {р} | Край фигура {р} | Вертекс фигура {q,r} | час | Двойной |
|---|---|---|---|---|---|---|---|---|
| Икосаэдрические соты | {3,5,3} | {3,5} | {3} | {3} | {5,3} | 0 | Самодвойственный | |
| Заказ-5 куб.сот | {4,3,5} | {4,3} | {4} | {5} | {3,5} | 0 | {5,3,4} | |
| Додекаэдрические соты порядка 4 | {5,3,4} | {5,3} | {5} | {4} | {3,4} | 0 | {4,3,5} | |
| Додекаэдрические соты порядка 5 | {5,3,5} | {5,3} | {5} | {5} | {3,5} | 0 | Самодвойственный |
Также есть 11 паракомпактных H. 3 соты (с бесконечными (евклидовыми) ячейками и/или фигурами вершин): {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3 ,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6, 3,6}.
| Имя | Шлефли Символ {п, д, г} | Коксетер | Клетка тип {п, д} | Лицо тип {р} | Край фигура {р} | Вертекс фигура {q,r} | час | Двойной |
|---|---|---|---|---|---|---|---|---|
| Тетраэдрические соты порядка 6 | {3,3,6} | {3,3} | {3} | {6} | {3,6} | 0 | {6,3,3} | |
| Шестиугольная сотовая плитка | {6,3,3} | {6,3} | {6} | {3} | {3,3} | 0 | {3,3,6} | |
| Октаэдрические соты порядка 4 | {3,4,4} | {3,4} | {3} | {4} | {4,4} | 0 | {4,4,3} | |
| Квадратная сотовая плитка | {4,4,3} | {4,4} | {4} | {3} | {4,3} | 0 | {3,3,4} | |
| Треугольные соты для плитки | {3,6,3} | {3,6} | {3} | {3} | {6,3} | 0 | Самодвойственный | |
| Заказ-6 куб.сот | {4,3,6} | {4,3} | {4} | {4} | {3,6} | 0 | {6,3,4} | |
| Шестиугольная плитка Order-4 сотовая | {6,3,4} | {6,3} | {6} | {4} | {3,4} | 0 | {4,3,6} | |
| Заказать-4 квадратные соты для плитки | {4,4,4} | {4,4} | {4} | {4} | {4,4} | 0 | Самодвойственный | |
| Додекаэдрические соты порядка 6 | {5,3,6} | {5,3} | {5} | {5} | {3,6} | 0 | {6,3,5} | |
| Шестиугольная плитка Орден-5 сотовая | {6,3,5} | {6,3} | {6} | {5} | {3,5} | 0 | {5,3,6} | |
| Шестиугольная плитка Орден-6 сотовая | {6,3,6} | {6,3} | {6} | {6} | {3,6} | 0 | Самодвойственный |
Некомпактные решения существуют как лоренцевы группы Кокстера и могут быть визуализированы с помощью открытых областей в гиперболическом пространстве (фундаментальный тетраэдр, имеющий ультраидеальные вершины). Все соты с гиперболическими ячейками или фигурами вершин и не имеющие 2 в символе Шлефли, некомпактны.
| { п ,3} \ р | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... ∞ |
|---|---|---|---|---|---|---|---|---|
{2,3}  |  {2,3,2} | {2,3,3} | {2,3,4} | {2,3,5} | {2,3,6} | {2,3,7} | {2,3,8} | {2,3,∞} |
{3,3}  |  {3,3,2} |  {3,3,3} |  {3,3,4} |  {3,3,5} |  {3,3,6} |  {3,3,7} |  {3,3,8} |  {3,3,∞} |
| {4,3} |  {4,3,2} |  {4,3,3} |  {4,3,4} |  {4,3,5} |  {4,3,6} |  {4,3,7} |  {4,3,8} |  {4,3,∞} |
{5,3}  |  {5,3,2} |  {5,3,3} |  {5,3,4} |  {5,3,5} |  {5,3,6} |  {5,3,7} |  {5,3,8} |  {5,3,∞} |
{6,3}  |  {6,3,2} |  {6,3,3} |  {6,3,4} |  {6,3,5} |  {6,3,6} |  {6,3,7} |  {6,3,8} |  {6,3,∞} |
{7,3}  | {7,3,2} |  {7,3,3} |  {7,3,4} |  {7,3,5} |  {7,3,6} |  {7,3,7} |  {7,3,8} |  {7,3,∞} |
{8,3}  | {8,3,2} |  {8,3,3} |  {8,3,4} |  {8,3,5} |  {8,3,6} |  {8,3,7} |  {8,3,8} |  {8,3,∞} |
... {∞,3}  | {∞,3,2} |  {∞,3,3} |  {∞,3,4} |  {∞,3,5} |  {∞,3,6} |  {∞,3,7} |  {∞,3,8} |  {∞,3,∞} |
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
В H нет правильных гиперболических звездочек-сот 3 : все формы с правильным звездчатым многогранником в качестве ячейки, вершины или того и другого в конечном итоге оказываются сферическими.
Идеальные вершины теперь появляются, когда фигура вершины представляет собой евклидову мозаику, и ее можно вписать в орисферу, а не в сферу. Они двойственны идеальным ячейкам (евклидовы мозаики, а не конечные многогранники). По мере дальнейшего увеличения последнего числа в символе Шлефли фигура вершины становится гиперболической, а вершины становятся ультраидеальными (поэтому ребра не пересекаются в гиперболическом пространстве). В сотах {p, q, ∞} ребра пересекают шар Пуанкаре только в одной идеальной точке; в остальном край стал ультраидеальным. Дальнейшее продолжение привело бы к ребрам, которые являются совершенно ультраидеальными как для сот, так и для фундаментального симплекса (хотя на таких рёбрах всё равно будет встречаться бесконечно много {p, q}). В общем случае, когда последнее число символа Шлефли становится ∞, грани коразмерности два пересекают гипершар Пуанкаре только в одной идеальной точке. [16]
5-апейротопы
[ редактировать ]Мозаики евклидова 4-мерного пространства
[ редактировать ]Существует три вида бесконечных регулярных мозаик ( сот ), которые могут мозаизировать евклидово четырехмерное пространство:
| Имя | Шлефли Символ {п, д, г, с} | Фасет тип {п, д, г} | Клетка тип {п, д} | Лицо тип {р} | Лицо фигура {с} | Край фигура {р,с} | Вертекс фигура {д, г, с} | Двойной |
|---|---|---|---|---|---|---|---|---|
| Тессерактические соты | {4,3,3,4} | {4,3,3} | {4,3} | {4} | {4} | {3,4} | {3,3,4} | Самодвойственный |
| 16-ячеечная сотовая связь | {3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,4,3,3} |
| 24-ячеистые соты | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {4,3,3} | {3,3,4,3} |
 Прогнозируемая часть {4,3,3,4} (Тессерактические соты) |  Прогнозируемая часть {3,3,4,3} (16-ячеистые соты) |  Прогнозируемая часть {3,4,3,3} (24-ячеистые соты) |
Также существуют два неправильных случая {4,3,4,2} и {2,4,3,4}.
Существуют три плоские правильные соты евклидова 4-мерного пространства: [24]
- {4,3,3,4}, {3,3,4,3} и {3,4,3,3}.
Существует семь плоских правильных выпуклых сот гиперболического 4-мерного пространства: [25]
- 5 компактны: {3,3,3,5}, {5,3,3,3}, {4,3,3,5}, {5,3,3,4}, {5,3,3 ,5}
- 2 являются паракомпактными: {3,4,3,4} и {4,3,4,3}.
Есть четыре плоских правильных звездчатых соты гиперболического 4-мерного пространства: [25]
- {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5} и {5,5/2,5,3}.
Мозаики гиперболического 4-мерного пространства
[ редактировать ]В H семь выпуклых правильных сот и четыре звезды-соты. 4 космос. [26] Пять выпуклых компактны, а два паракомпактны.
Пять компактных регулярных сот в формате H 4 :
| Имя | Шлефли Символ {п, д, г, с} | Фасет тип {п, д, г} | Клетка тип {п, д} | Лицо тип {р} | Лицо фигура {с} | Край фигура {р,с} | Вертекс фигура {д, г, с} | Двойной |
|---|---|---|---|---|---|---|---|---|
| Заказ-5 5-ячеечный сот | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} |
| 120-ячеечная сотовая связь | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} |
| Тессерактические соты порядка 5 | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} |
| Заказ-4 сотовый, 120 ячеек | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} |
| Заказ-5 120-ячеечный сот | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Самодвойственный |
Два паракомпактных регулярных H 4 соты: {3,4,3,4}, {4,3,4,3}.
| Имя | Шлефли Символ {п, д, г, с} | Фасет тип {п, д, г} | Клетка тип {п, д} | Лицо тип {р} | Лицо фигура {с} | Край фигура {р,с} | Вертекс фигура {д, г, с} | Двойной |
|---|---|---|---|---|---|---|---|---|
| Соты Order-4, 24 ячейки | {3,4,3,4} | {3,4,3} | {3,4} | {3} | {4} | {3,4} | {4,3,4} | {4,3,4,3} |
| Кубические соты | {4,3,4,3} | {4,3,4} | {4,3} | {4} | {3} | {4,3} | {3,4,3} | {3,4,3,4} |
Некомпактные решения существуют как лоренцевы группы Кокстера и могут быть визуализированы с помощью открытых областей в гиперболическом пространстве (фундаментальная 5-ячеечная структура имеет некоторые части, недоступные за пределами бесконечности). Все соты, которые не показаны в таблице ниже и не имеют 2 в символе Шлефли, являются некомпактными.
| Сферические / евклидовы /гиперболические ( компактные / паракомпактные / некомпактные ) соты {p,q,r,s} | ||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
Звездные мозаики гиперболического 4-мерного пространства
[ редактировать ]В H четыре правильных звездочки-соты. 4 простор, все компактно:
| Имя | Шлефли Символ {п, д, г, с} | Фасет тип {п, д, г} | Клетка тип {п, д} | Лицо тип {р} | Лицо фигура {с} | Край фигура {р,с} | Вертекс фигура {д, г, с} | Двойной | Плотность |
|---|---|---|---|---|---|---|---|---|---|
| Небольшие звездчатые соты из 120 ячеек. | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5/2} | {3} | {3,3} | {5,3,3} | {3,3,5,5/2} | 5 |
| Соты пентаграммного порядка из 600 ячеек | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} | 5 |
| Икосаэдрические 120-ячеистые соты порядка 5 | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} | 10 |
| Большие соты из 120 ячеек | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} | 10 |
6-апейротопы
[ редактировать ]Существует только одна плоская правильная сота евклидова 5-мерного пространства: (ранее указанная выше как мозаика) [24]
- {4,3,3,3,4}
Существует пять плоских правильных сот гиперболического 5-мерного пространства, все паракомпактные: (ранее перечисленные выше как мозаики) [25]
- {3,3,3,4,3}, {3,4,3,3,3}, {3,3,4,3,3}, {3,4,3,3,4} и { 4,3,3,4,3}
Мозаики евклидова 5-мерного пространства
[ редактировать ]Гиперкубические соты — единственное семейство правильных сот, которые могут замощить каждое измерение, пять или выше, образованное гранями гиперкуба , по четыре вокруг каждого гребня .
| Имя | Шлефли { п 1 , п 2 , ..., п п -1 } | Фасет тип | Вертекс фигура | Двойной |
|---|---|---|---|---|
| Квадратная плитка | {4,4} | {4} | {4} | Самодвойственный |
| Кубические соты | {4,3,4} | {4,3} | {3,4} | Самодвойственный |
| Тессерактические соты | {4,3 2 ,4} | {4,3 2 } | {3 2 ,4} | Самодвойственный |
| 5-кубовые соты | {4,3 3 ,4} | {4,3 3 } | {3 3 ,4} | Самодвойственный |
| 6-кубовые соты | {4,3 4 ,4} | {4,3 4 } | {3 4 ,4} | Самодвойственный |
| 7-кубовые соты | {4,3 5 ,4} | {4,3 5 } | {3 5 ,4} | Самодвойственный |
| 8-кубовые соты | {4,3 6 ,4} | {4,3 6 } | {3 6 ,4} | Самодвойственный |
| n- гиперкубические соты | {4,3 n−2 ,4} | {4,3 n−2 } | {3 n−2 ,4} | Самодвойственный |
В Е 5 , существуют также несобственные случаи {4,3,3,4,2}, {2,4,3,3,4}, {3,3,4,3,2}, {2,3,3, 4,3}, {3,4,3,3,2} и {2,3,4,3,3}. В Е н , {4,3 n−3 ,4,2} и {2,4,3 n−3 ,4} всегда являются неправильными евклидовыми мозаиками.
Мозаики гиперболического 5-мерного пространства
[ редактировать ]В H есть 5 обычных сот. 5 , все паракомпактные, которые включают бесконечные (евклидовы) грани или вершинные фигуры: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3} , {3,4,3,3,4} и {4,3,3,4,3}.
Не существует компактных регулярных мозаик гиперболического пространства размерности 5 и выше, а также нет паракомпактных регулярных мозаик в гиперболическом пространстве размерности 6 и выше.
| Имя | Шлефли Символ {p,q,r,s,t} | Фасет тип {п, д, г, с} | 4-сторонний тип {п, д, г} | Клетка тип {п, д} | Лицо тип {р} | Клетка фигура {т} | Лицо фигура {с, т} | Край фигура {р,с,т} | Вертекс фигура {q,r,s,t} | Двойной |
|---|---|---|---|---|---|---|---|---|---|---|
| 5-ортоплексные соты | {3,3,3,4,3} | {3,3,3,4} | {3,3,3} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,3,4,3} | {3,4,3,3,3} |
| Соты из 24 ячеек | {3,4,3,3,3} | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {3,3,3} | {4,3,3,3} | {3,3,3,4,3} |
| 16-ячеечный сотовый сот | {3,3,4,3,3} | {3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {3,3} | {4,3,3} | {3,4,3,3} | самодвойственный |
| Заказ-4 24-ячеечный сотовый сот | {3,4,3,3,4} | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {4} | {3,4} | {3,3,4} | {4,3,3,4} | {4,3,3,4,3} |
| Тессерактические соты | {4,3,3,4,3} | {4,3,3,4} | {4,3,3} | {4,3} | {4} | {3} | {4,3} | {3,4,3} | {3,3,4,3} | {3,4,3,3,4} |
≥ 5 не существует правильных звездных n Поскольку для n -многогранников , которые могли бы быть потенциальными ячейками или вершинными фигурами, в H больше нет гиперболических звездных сот. н для n ≥ 5.
Апейротопы ранга 7 и выше
[ редактировать ]Мозаики гиперболического 6-мерного пространства и выше
[ редактировать ]Не существует регулярных компактных или паракомпактных мозаик гиперболического пространства размерности 6 и выше. Однако любой символ Шлефли формы {p,q,r,s,...}, не рассмотренный выше (p,q,r,s,... натуральные числа выше 2 или бесконечности), будет образовывать некомпактную мозаику гиперболическое n -пространство. [16]
Абстрактные многогранники
[ редактировать ]Абстрактные многогранники возникли в результате попытки изучить многогранники отдельно от геометрического пространства, в которое они встроены. Они включают мозаику сферического, евклидова и гиперболического пространства, а также других многообразий . Существует бесконечно много каждого ранга выше 1. Пример см . в этом атласе . Некоторыми примечательными примерами абстрактных правильных многогранников, которые не встречаются нигде в этом списке, являются 11-ячеечный , {3,5,3} и 57-ячеечный , {5,3,5}, которые имеют правильные проективные многогранники в качестве ячеек. и вершинные фигуры.
Элементами абстрактного многогранника являются его тело (максимальный элемент), его грани, ребра, вершины и нулевой многогранник или пустое множество. Эти абстрактные элементы можно отобразить в обычном пространстве или реализовать в виде геометрических фигур. Некоторые абстрактные многогранники имеют правильно сформированную или точную реализацию, другие — нет. Флаг — это связное множество элементов каждого ранга — для многогранника это тело, грань, ребро грани, вершина ребра и нулевой многогранник. Абстрактный многогранник называется правильным, если его комбинаторные симметрии транзитивны относительно его флагов, то есть любой флаг может быть отображен на любой другой при условии симметрии многогранника. Абстрактные правильные многогранники остаются активной областью исследований.
Пять таких правильных абстрактных многогранников, которые не могут быть реализованы точно и симметрично, были идентифицированы Х. С. М. Коксетером в его книге «Правильные многогранники» (1977) и снова Дж. М. Уиллсом в его статье «Комбинаторно правильные многогранники индекса 2» (1987). [27] Все они топологически эквивалентны тороидам . Их построение путем расположения n граней вокруг каждой вершины можно повторять бесконечно как мозаику гиперболической плоскости . На диаграммах ниже изображения гиперболических мозаик имеют цвета, соответствующие цветам изображений многогранников.
Многогранник 
Медиальный ромбический триаконтаэдр
Додекадодекаэдр
Медиальный триамбический икосаэдр
Дитригональный додекадодекаэдр
Раскопанный додекаэдрВершинная фигура {5}, {5/2} 

(5.5/2) 2 
{5}, {5/2} 

(5.5/3) 3 

Лица 30 ромбов 
12 пятиугольников
12 пентаграмм

20 шестиугольников 
12 пятиугольников
12 пентаграмм

20 гексаграмм 
Укладка плитки 
{4, 5}
{5, 4}
{6, 5}
{5, 6}
{6, 6}час −6 −6 −16 −16 −20
Они встречаются как двойные пары следующим образом:
- Медиальный ромбический триаконтаэдр и додекадодекаэдр двойственны друг другу.
- Медиальный триамбический икосаэдр и дитригональный додекадодекаэдр двойственны друг другу.
- самодвойственен Раскопанный додекаэдр .
См. также
[ редактировать ]- Полигон
- Многогранник
- Правильный многогранник (5 правильных платоновых тел и 4 тела Кеплера – Пуансо )
- каменный
- 4-многогранник
- Правильный 4-многогранник (16 правильных 4-многогранников, 4 выпуклых и 10 звездочек (Шлефли – Гесса))
- Равномерный 4-многогранник
- Тесселяция
- Правильный многогранник
- Регулярное отображение (теория графов)
Примечания
[ редактировать ]- ^ до тождества и идемпотентности
Ссылки
[ редактировать ]- ^ Jump up to: а б МакМаллен, Питер (2004), «Регулярные многогранники полного ранга» , Дискретная и вычислительная геометрия , 32 : 1–35, doi : 10.1007/s00454-004-0848-5 , S2CID 46707382
- ^ Коксетер (1973) , с. 129.
- ^ Макмаллен и Шульте (2002) , с. 30.
- ^ Джонсон, Северо-Запад (2018). «Глава 11: Конечные группы симметрии». Геометрии и преобразования . Издательство Кембриджского университета. 11.1 Многогранники и соты, с. 224. ИСБН 978-1-107-10340-5 .
- ^ Коксетер (1973) , с. 120.
- ^ Коксетер (1973) , с. 124.
- ^ Коксетер, Правильные комплексные многогранники , с. 9
- ^ Дункан, Хью (28 сентября 2017 г.). «Между квадратным камнем и твердым пятиугольником: дробные многоугольники» . меловая пыль .
- ^ Jump up to: а б Макмаллен и Шульте 2002 .
- ^ Коксетер (1973) , стр. 66–67.
- ^ Тезисы (PDF) . Выпуклые и абстрактные многогранники (19–21 мая 2005 г.) и День многогранников в Калгари (22 мая 2005 г.).
- ^ МакМаллен (2004) .
- ^ Коксетер (1973) , Таблица I: Правильные многогранники, (iii) Три правильных многогранника в n измерениях (n>=5), стр. 294–295.
- ^ МакМаллен и Шульте (2002) , «Проективные правильные многогранники 6C», стр. 162-165 .
- ^ Грюнбаум, Б. (1977). «Правильные многогранники — старые и новые». уравнения Математические 16 (1–2): 1–20. дои : 10.1007/BF01836414 . S2CID 125049930 .
- ^ Jump up to: а б с Ройс Нельсон и Генри Сегерман, Визуализация гиперболических сот
- ^ Ирвинг Адлер, Новый взгляд на геометрию (Дуврское издание 2012 г.), стр.233
- ^ Коксетер, HSM (1938). «Правильные косые многогранники в трех и четырех измерениях». Учеб. Лондонская математика. Соц . 2. 43 : 33–62. дои : 10.1112/plms/s2-43.1.33 .
- ^ Коксетер, HSM (1985). «Правильные и полуправильные многогранники II». Математический журнал . 188 (4): 559–591. дои : 10.1007/BF01161657 . S2CID 120429557 .
- ^ Конвей, Джон Х.; Бургель, Хайди; Гудман-Штраус, Хаим (2008). «Глава 23: Объекты с первичной симметрией, бесконечные платоновые многогранники». Симметрии вещей . Тейлор и Фрэнсис. стр. 333–335. ISBN 978-1-568-81220-5 .
- ^ Макмаллен и Шульте (2002) , с. 224.
- ^ МакМаллен и Шульте (2002) , Раздел 7E.
- ^ Гарнер, CWL (1967). «Правильные косые многогранники в гиперболическом трехмерном пространстве» . Может. Дж. Математика . 19 : 1179–1186. дои : 10.4153/CJM-1967-106-9 . S2CID 124086497 . Примечание: в его статье говорится, что их 32, но один самодвойственный, поэтому остается 31.
- ^ Jump up to: а б с Коксетер (1973) , Таблица II: Правильные соты, с. 296.
- ^ Jump up to: а б с д Коксетер (1999) , «Глава 10».
- ^ Коксетер (1999) , «Глава 10», Таблица IV, стр. 10. 213.
- ^ Дэвид А. Рихтер. «Правильные многогранники (индекса два)» . Архивировано из оригинала 4 марта 2016 г. Проверено 13 марта 2015 г.
Цитаты
[ редактировать ]- Коксетер, HSM (1999), «Глава 10: Правильные соты в гиперболическом пространстве», Красота геометрии: двенадцать эссе , Минеола, Нью-Йорк: Dover Publications, Inc., стр. 199–214, ISBN 0-486-40919-8 , LCCN 99035678 , МР 1717154 . См., в частности, сводные таблицы II, III, IV, V, стр. 212–213.
- Первоначально опубликовано в Коксетер, HSM (1956), «Регулярные соты в гиперболическом пространстве» (PDF) , Труды Международного конгресса математиков, 1954, Амстердам , том. III, Амстердам: North-Holland Publishing Co., стр. 155–169, MR 0087114 , заархивировано из оригинала (PDF) 02 апреля 2015 г.
- Коксетер, HSM (1973) [1948]. Правильные многогранники (Третье изд.). Нью-Йорк: Dover Publications. ISBN 0-486-61480-8 . МР 0370327 . OCLC 798003 . См., в частности, Таблицы I и II: Правильные многогранники и соты, стр. 294–296.
- Джонсон, Норман В. (2012), «Регулярные инверсные многогранники» (PDF) , Международная конференция по математике расстояний и приложениям (2–5 июля 2012 г., Варна, Болгария) , стр. 85–95, документ 27
- МакМаллен, Питер ; Шульте, Эгон (2002), Абстрактные правильные многогранники , Энциклопедия математики и ее приложений, том. 92, Кембридж: Издательство Кембриджского университета, номер номера : 10.1017/CBO9780511546686 , ISBN. 0-521-81496-0 , MR 1965665 , S2CID 115688843
- МакМаллен, Питер (2018), «Новые регулярные соединения 4-многогранников», Новые тенденции в интуитивной геометрии , Математические исследования Общества Боляи, том. 27, стр. 307–320, номер документа : 10.1007/978-3-662-57413-3_12 , ISBN. 978-3-662-57412-6 .
- Нельсон, Ройс; Сегерман, Генри (2015). «Визуализация гиперболических сот». arXiv : 1511.02851 [ math.HO ]. Hyperbolichoneycombs.org/
- Соммервилл, ДМЮ (1958), Введение в геометрию n измерений , Нью-Йорк: Dover Publications, Inc., MR 0100239 . Перепечатка изд. 1930 г., опубликованная Э. П. Даттоном. См., в частности, главу X: Правильные многогранники.
Внешние ссылки
[ редактировать ]- Платоновые тела
- Многогранники Кеплера-Пуансо
- Обычные четырехмерные многогранники
- Многомерный глоссарий (поищите Hexacosichoron и Hecatonicosachoron )
- Средство просмотра многогранников
- Многогранники и оптимальная упаковка p точек в n мерных сферах
- Атлас маленьких правильных многогранников
- Правильные многогранники во времени И. Хабард, Многогранники, карты и их симметрии
- Правильные звездчатые многогранники , Нан Ма
| Космос | Семья | / / | ||||
|---|---|---|---|---|---|---|
| И 2 | Равномерная укладка плитки | {3 [3] } | д 3 | HD 3 | квартал 3 | Шестиугольный |
| И 3 | Равномерные выпуклые соты | {3 [4] } | д 4 | HD 4 | 4 квартала | |
| И 4 | Униформа 4-сотовая | {3 [5] } | д 5 | hδ 5 | qδ 5 | 24-ячеистые соты |
| И 5 | Униформа 5-сотовая | {3 [6] } | д 6 | HD 6 | qδ 6 | |
| И 6 | Униформа 6-сотовая | {3 [7] } | д 7 | hδ 7 | qδ 7 | 2 22 |
| И 7 | Униформа 7-сотовая | {3 [8] } | д 8 | hδ 8 | 8 кварталов | 1 33 • 3 31 |
| И 8 | Униформа 8-сотовая | {3 [9] } | д 9 | HD 9 | qδ 9 | 1 52 • 2 51 • 5 21 |
| И 9 | Униформа 9-сотовая | {3 [10] } | д 10 | HD 10 | 10 кварталов | |
| И 10 | Униформа 10-сотовая | {3 [11] } | д 11 | HD 11 | qδ 11 | |
| И п -1 | Равномерный ( n -1)- сотовый | {3 [н] } | δ н | hδ н | qδ н | 1 лиц 2 • 2 лиц 1 • лиц 21 |







































![{\displaystyle {\begin{aligned}&{\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}:{\text{Многогранник (существующий) в евклидовом 3-мерном пространстве)}}\\[6pt]&{\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}:{\text {Замощение евклидовой плоскости}}\\[6pt]&{\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}:{\text{Hyperbolic мозаика плоскости}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b3e3112344f5e050eb160928c5170cabb51bcf8)


































































































































































































































































































