Осоэдр
| Набор правильных n -угольных осоэдров | |
|---|---|
 Пример правильного шестиугольного осоэдра на сфере | |
| Тип | правильный многогранник или сферическая мозаика |
| Лица | n дигонов |
| Края | н |
| Вершины | 2 |
| Эйлер чар. | 2 |
| Конфигурация вершин | 2 н |
| Символ Витхоффа | п | 2 2 |
| Символ Шлефли | {2, п } |
| Диаграмма Кокстера | |
| Группа симметрии | Д н ч [2, н] (*22n) заказ 4 н. |
| Группа вращения | Д н [2, н] + (22н) заказ 2 н. |
| Двойной многогранник | правильный n -угольный диэдр |

В сферической геометрии на сферической поверхности , так что каждая n-угольный осоэдр представляет собой мозаику лунок лунка имеет одни и те же две полярно противоположные вершины.
Правильный { n -угольный осоэдр имеет символ Шлефли 2, n }, при этом каждый сферический лунец имеет внутренний угол 2 π / n radians ( 360 / n градусов). [1] [2]
Осоэдры как правильные многогранники
[ редактировать ]Для правильного многогранника, символ Шлефли которого равен { m , n }, количество многоугольных граней равно:
Известные в древности Платоновые тела являются единственными целочисленными решениями для m ≥ 3 и n ≥ 3. Ограничение m ≥ 3 требует, чтобы многоугольные грани имели как минимум три стороны.
При рассмотрении многогранников как сферической мозаики это ограничение можно ослабить, поскольку дигоны (2-угольники) можно представить как сферические лунки , имеющие ненулевую площадь .
Если допустить m = 2, то
и допускает новый бесконечный класс правильных многогранников — осоэдров. На сферической поверхности многогранник {2, n } изображается как n примыкающих друг к другу лунок с внутренними углами 2 π / п . Все эти сферические луны имеют две общие вершины.
| Космос | сферический | евклидов | |||||
|---|---|---|---|---|---|---|---|
| Укладка плитки имя | шестиугольный осоэдр | Дигональный осоэдр | Треугольный осоэдр | Квадрат осоэдр | пятиугольный осоэдр | ... | Апейрогональный осоэдр |
| Укладка плитки изображение |  | 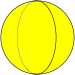 |  | 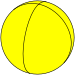 | 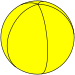 | ... | |
| Шлефли символ | {2,1} | {2,2} | {2,3} | {2,4} | {2,5} | ... | {2,∞} |
| Коксетер диаграмма | ... | ||||||
| Лица и края | 1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Вершины | 2 | 2 | 2 | 2 | 2 | ... | 2 |
| Вертекс конфиг. | 2 | 2.2 | 2 3 | 2 4 | 2 5 | ... | 2 ∞ |
Калейдоскопическая симметрия
[ редактировать ]The двуугольные сферические лунные грани -осоэдр, , представляют фундаментальные области двугранной симметрии в трех измерениях : циклическую симметрию , , , заказ . Области отражения могут быть показаны попеременно окрашенными лунками в виде зеркальных изображений.
Разделение каждой луны на два сферических треугольника создает -угольная бипирамида , представляющая двугранную симметрию , заказ .
| Симметрия (порядок ) | Обозначение Шенфлиса | |||||||
|---|---|---|---|---|---|---|---|---|
| Обозначение орбифолда | ||||||||
| Диаграмма Кокстера | ||||||||
| -угольный осоэдр | Символ Шлефли | |||||||
| Фундаментальные домены разного цвета |  |  |  |  |  |  | ||
Связь с телом Штейнмеца
[ редактировать ]Тетрагональный осоэдр топологически эквивалентен бицилиндрическому телу Штейнмеца , пересечению двух цилиндров под прямым углом. [3]
Производные многогранники
[ редактировать ]Двойственным к n-угольному осоэдру {2, n } является n -угольный диэдр , { n , 2}. Многогранник {2,2} самодуален и является одновременно осоэдром и диэдром.
Осоэдр можно модифицировать так же, как и другие многогранники, чтобы получить усеченную вариацию. Усеченный n -угольный осоэдр — это n-угольная призма .
Апейрогональный осоэдр
[ редактировать ]В пределе осоэдр становится апейрогональным осоэдром как двумерная мозаика:
Гозотопы
[ редактировать ]Многомерные аналоги вообще называются гомотопами . Правильный гомотоп с символом Шлефли {2, p ,..., q } имеет две вершины, каждая из которых имеет фигуру вершины { p ,..., q }.
Двумерный гозотоп {2} является двуугольником .
Этимология
[ редактировать ]Термин «осоэдр», по-видимому, происходит от греческого ὅσος ( hosos ) «столько», идея состоит в том, что осоэдр может иметь « столько граней, сколько пожелает». [4] Его представил Вито Каравелли в восемнадцатом веке. [5]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Коксетер, Правильные многогранники , с. 12
- ^ Аннотация Правильные многогранники, с. 161
- ^ Вайсштейн, Эрик В. «Солид Штейнмеца» . Математический мир .
- ^ Стивен Шварцман (1 января 1994 г.). Слова математики: этимологический словарь математических терминов, используемых на английском языке . МАА. С. 108–109 . ISBN 978-0-88385-511-9 .
- ^ Коксетер, HSM (1974). Правильные комплексные многогранники . Лондон: Издательство Кембриджского университета. п. 20. ISBN 0-521-20125-Х .
Осоэдр {2,p} (в несколько искаженном виде) был назван Вито Каравелли (1724–1800)…
- МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Cambridge University Press , ISBN 0-521-81496-0
- Коксетер, HSM , Правильные многогранники (третье издание), Dover Publications Inc., ISBN 0-486-61480-8







![{\displaystyle [п]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)
















![{\displaystyle [\,\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fa4c06a6c3b5a7bee90e2c44f7530e3f2a46bf8)
![{\displaystyle [2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa32363c093f4cfd50ecba68068bcfd396ea8bff)
![{\displaystyle [3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f671027d56f9c24d65c03a4a26eb0d3b933f4f15)
![{\displaystyle [4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d865272ff436d713d5069ae3066bbe07a000a99)
![{\displaystyle [5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/958ef87021d704de46ad116821bc677e07d9a5fe)
![{\displaystyle [6]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/162951515fcb56919dffe17b119f4a0aa7e9dae6)








