График функции

В математике график функции $f$ это набор упорядоченных пар $(x,y)$ , где $f(x)=y.$ В общем случае, когда $x$ и $f(x)$ являются действительными числами , эти пары представляют собой декартовы координаты точек на плоскости и часто образуют кривую .Графическое представление графика функции также известно как график .

В случае функций двух переменных , то есть функций, область определения которых состоит из пар $(x,y)$ – граф обычно относится к множеству упорядоченных троек $(x,y,z)$ где $f(x,y)=z$ . Это подмножество трехмерного пространства ; для непрерывной вещественной функции двух действительных переменных ее график образует поверхность , которую можно визуализировать как график поверхности .

В науке , технике , технологиях , финансах и других областях графики — это инструменты, используемые для многих целей. В простейшем случае одна переменная отображается как функция другой, обычно с использованием прямоугольных осей ; см . в разделе График (графика) подробности .

График функции является частным случаем отношения . В современных основах математики и, как правило, в теории множеств функция фактически равна своему графику. ^[1] Однако часто бывает полезно рассматривать функции как отображения . ^[2] которые состоят не только из отношения между входом и выходом, но также из того, какой набор является доменом, а какой набор является кодоменом . Например, чтобы сказать, что функция находится на ( сюръективной ) или нет, следует учитывать кодомен. График функции сам по себе не определяет кодомен. Это обычное дело ^[3] использовать оба термина «функция» и «график функции», поскольку, даже если рассматривать один и тот же объект, они указывают на его рассмотрение с другой точки зрения.

Определение

Дана функция $f:X\to Y$ из набора $X$ ( домен ) в набор $Y$ ( кодомен ), графиком функции является множество ^[4] $G(f)=\{(x,f(x)):x\in X\},$ которое является подмножеством декартова произведения $X\times Y$ . При определении функции в терминах теории множеств принято отождествлять функцию с ее графиком, хотя формально функция образуется тройкой, состоящей из ее области определения, ее кодомена и ее графика.

Примеры

Функции одной переменной

График функции $f:\{1,2,3\}\to \{a,b,c,d\}$ определяется $f(x)={\begin{cases}a,&{\text{if }}x=1,\\d,&{\text{if }}x=2,\\c,&{\text{if }}x=3,\end{cases}}$ является подмножеством множества $\{1,2,3\}\times \{a,b,c,d\}$ $G(f)=\{(1,a),(2,d),(3,c)\}.$

Судя по графику, область $\{1,2,3\}$ восстанавливается как набор первых компонентов каждой пары в графе $\{1,2,3\}=\{x:\ \exists y,{\text{ such that }}(x,y)\in G(f)\}$ .Аналогично, диапазон можно восстановить как $\{a,c,d\}=\{y:\exists x,{\text{ such that }}(x,y)\in G(f)\}$ .Кодомен $\{a,b,c,d\}$ Однако невозможно определить только по графику.

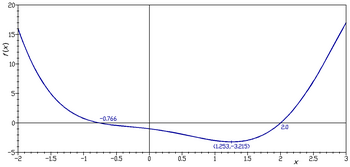
График кубического многочлена на вещественной прямой $f(x)=x^{3}-9x$ является $\{(x,x^{3}-9x):x{\text{ is a real number}}\}.$

Если этот набор нанести на декартову плоскость , результатом будет кривая (см. рисунок).

Функции двух переменных

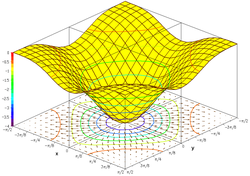
График тригонометрической функции $f(x,y)=\sin(x^{2})\cos(y^{2})$ является $\{(x,y,\sin(x^{2})\cos(y^{2})):x{\text{ and }}y{\text{ are real numbers}}\}.$

Если этот набор нанести на трехмерную декартову систему координат , результатом будет поверхность (см. рисунок).

Часто бывает полезно показать на графике градиент функции и несколько кривых уровня. Кривые уровня могут быть отображены на функциональной поверхности или спроецированы на нижнюю плоскость. На втором рисунке представлен такой рисунок графика функции: $f(x,y)=-(\cos(x^{2})+\cos(y^{2}))^{2}.$

См. также

Ссылки

^ Чарльз Пинтер (2014) [1971]. Книга по теории множеств . Дуврские публикации. п. 49. ИСБН 978-0-486-79549-2 .
^ ТМ Апостол (1981). Математический анализ . Аддисон-Уэсли. п. 35.
^ П.Р. Халмош (1982). Книга задач о гильбертовом пространстве . Спрингер Верлаг. п. 31 . ISBN 0-387-90685-1 .
^ Д.С. Бриджес (1991). Основы реального и абстрактного анализа . Спрингер. п. 285 . ISBN 0-387-98239-6 .

Дальнейшее чтение

Залинеску, Константин (30 июля 2002 г.). Выпуклый анализ в общих векторных пространствах . Ривер Эдж, Нью-Джерси, Лондон: World Scientific Publishing . ISBN 978-981-4488-15-0 . МР 1921556 . OCLC 285163112 – через Интернет-архив .

Внешние ссылки

Вайсштейн, Эрик В. « Функциональный график ». Из MathWorld — веб-ресурса Wolfram.

[Pinter2014-1] Чарльз Пинтер (2014) [1971]. Книга по теории множеств . Дуврские публикации. п. 49. ИСБН 978-0-486-79549-2 .

[2] ТМ Апостол (1981). Математический анализ . Аддисон-Уэсли. п. 35.

[3] П.Р. Халмош (1982). Книга задач о гильбертовом пространстве . Спрингер Верлаг. п. 31 . ISBN 0-387-90685-1 .

[4] Д.С. Бриджес (1991). Основы реального и абстрактного анализа . Спрингер. п. 285 . ISBN 0-387-98239-6 .

[1]

[2]

[3]

[4]