Обратное распределение Гаусса

О распределении 1/x, когда x является гауссовым, см. Взаимное нормальное распределение .

Обратный Гауссов

Функция плотности вероятности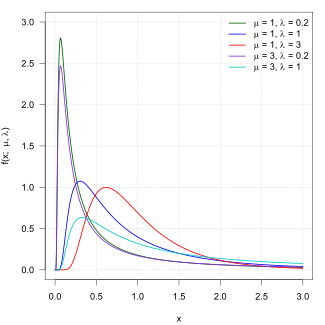
Кумулятивная функция распределения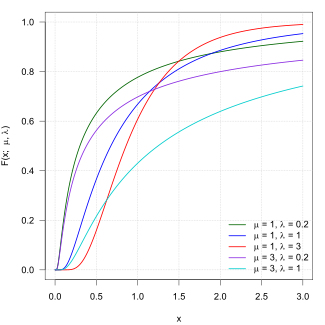
Обозначения	$\operatorname {IG} \left(\mu ,\lambda \right)$
Параметры	$\mu >0$ $\lambda >0$
Поддерживать	$x\in (0,\infty )$
PDF	${\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp \left[-{\frac {\lambda (x-\mu )^{2}}{2\mu ^{2}x}}\right]$
CDF	$\Phi \left({\sqrt {\frac {\lambda }{x}}}\left({\frac {x}{\mu }}-1\right)\right)$ ${}+\exp \left({\frac {2\lambda }{\mu }}\right)\Phi \left(-{\sqrt {\frac {\lambda }{x}}}\left({\frac {x}{\mu }}+1\right)\right)$ где $\Phi$ — стандартное нормальное (стандартное гауссово) распределение cdf
Иметь в виду	$\operatorname {E} [X]=\mu$ $\operatorname {E} [{\frac {1}{X}}]={\frac {1}{\mu }}+{\frac {1}{\lambda }}$
Режим	$\mu \left[\left(1+{\frac {9\mu ^{2}}{4\lambda ^{2}}}\right)^{\frac {1}{2}}-{\frac {3\mu }{2\lambda }}\right]$
Дисперсия	$\operatorname {Var} [X]={\frac {\mu ^{3}}{\lambda }}$ $\operatorname {Var} [{\frac {1}{X}}]={\frac {1}{\mu \lambda }}+{\frac {2}{\lambda ^{2}}}$
асимметрия	$3\left({\frac {\mu }{\lambda }}\right)^{1/2}$
Избыточный эксцесс	${\frac {15\mu }{\lambda }}$
МГФ	$\exp \left[{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}t}{\lambda }}}}\right)}\right]$
CF	$\exp \left[{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}\mathrm {i} t}{\lambda }}}}\right)}\right]$

В теории вероятностей обратное распределение Гаусса (также известное как распределение Вальда ) представляет собой двухпараметрическое семейство непрерывных распределений вероятностей с поддержкой на (0,∞).

Его функция плотности вероятности определяется выражением

$f(x;\mu ,\lambda )={\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp {\biggl (}-{\frac {\lambda (x-\mu )^{2}}{2\mu ^{2}x}}{\biggr )}$

для x > 0, где $\mu >0$ это среднее и $\lambda >0$ является параметром формы.

Обратное распределение Гаусса имеет несколько свойств, аналогичных распределению Гаусса. Название может вводить в заблуждение: оно является «обратным» только в том смысле, что, в то время как гауссиан описывает уровень броуновского движения в фиксированное время, обратный гауссиан описывает распределение времени, которое требуется броуновскому движению с положительным дрейфом для достижения фиксированного положительного значения. уровень.

Его кумулянтная производящая функция (логарифм характеристической функции) является обратной кумулянтной производящей функцией гауссовой случайной величины.

Чтобы указать, что случайная величина X имеет обратное гауссово распределение со средним значением µ и параметром формы λ, мы пишем $X\sim \operatorname {IG} (\mu ,\lambda )\,\!$.

Характеристики

Форма с одним параметром

Функция плотности вероятности (pdf) обратного распределения Гаусса имеет форму с одним параметром, определяемую выражением

$f(x;\mu ,\mu ^{2})={\frac {\mu }{\sqrt {2\pi x^{3}}}}\exp {\biggl (}-{\frac {(x-\mu )^{2}}{2x}}{\biggr )}.$

В этой форме среднее значение и дисперсия распределения равны, $\mathbb {E} [X]={\text{Var}}(X).$

Кроме того, кумулятивная функция распределения (cdf) однопараметрического обратного распределения Гаусса связана со стандартным нормальным распределением соотношением

${\begin{aligned}\Pr(X<x)&=\Phi (-z_{1})+e^{2\mu }\Phi (-z_{2}),\end{aligned}}$

где $z_{1}={\frac {\mu }{x^{1/2}}}-x^{1/2}$, $z_{2}={\frac {\mu }{x^{1/2}}}+x^{1/2},$ и $\Phi$ — это CDF стандартного нормального распределения. Переменные $z_{1}$ и $z_{2}$ связаны друг с другом тождеством $z_{2}^{2}=z_{1}^{2}+4\mu .$

В форме с одним параметром MGF упрощается до

$M(t)=\exp[\mu (1-{\sqrt {1-2t}})].$

Обратное распределение Гаусса в форме двух параметров $f(x;\mu ,\lambda )$ может быть преобразовано в форму с одним параметром $f(y;\mu _{0},\mu _{0}^{2})$ путем соответствующего масштабирования $y={\frac {\mu ^{2}x}{\lambda }},$ где $\mu _{0}=\mu ^{3}/\lambda .$

Стандартная форма обратного распределения Гаусса:

$f(x;1,1)={\frac {1}{\sqrt {2\pi x^{3}}}}\exp {\biggl (}-{\frac {(x-1)^{2}}{2x}}{\biggr )}.$

Суммирование

Если X _i имеет $\operatorname {IG} (\mu _{0}w_{i},\lambda _{0}w_{i}^{2})\,\!$ распределение для i = 1, 2, ..., n и Xi _{независимы} все то ,

$S=\sum _{i=1}^{n}X_{i}\sim \operatorname {IG} \left(\mu _{0}\sum w_{i},\lambda _{0}\left(\sum w_{i}\right)^{2}\right).$

Обратите внимание, что

${\frac {\operatorname {Var} (X_{i})}{\operatorname {E} (X_{i})}}={\frac {\mu _{0}^{2}w_{i}^{2}}{\lambda _{0}w_{i}^{2}}}={\frac {\mu _{0}^{2}}{\lambda _{0}}}$

является постоянным для всех i . Это необходимое условие суммирования. В противном случае S не было бы распределено по обратному Гауссу.

Масштабирование

Для любого t > 0 справедливо равенство

$X\sim \operatorname {IG} (\mu ,\lambda )\,\,\,\,\,\,\Rightarrow \,\,\,\,\,\,tX\sim \operatorname {IG} (t\mu ,t\lambda ).$

Экспоненциальное семейство

Обратное распределение Гаусса представляет собой двухпараметрическое экспоненциальное семейство с натуральными параметрами − λ /(2 µ ² ) и − λ /2, а также естественные статистики X и 1/ X .

Для $\lambda >0$ фиксированное, это также однопараметрическое естественное экспоненциальное семейное распределение где базовое распределение имеет плотность

$h(x)={\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp \left(-{\frac {\lambda }{2x}}\right)\mathbb {1} _{[0,\infty )}(x)\,.$

Действительно, с $\theta \leq 0$,

$p(x;\theta )={\frac {\exp(\theta x)h(x)}{\int \exp(\theta y)h(y)dy}}$

плотность выше реального. Вычислив интеграл, получим

$p(x;\theta )={\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp \left(-{\frac {\lambda }{2x}}+\theta x-{\sqrt {-2\lambda \theta }}\right)\mathbb {1} _{[0,\infty )}(x)\,.$

Замена $\theta =-\lambda /(2\mu ^{2})$ делает приведенное выше выражение равным $f(x;\mu ,\lambda )$.

Связь с броуновским движением

Пример остановленных случайных блужданий с $\alpha =1,\nu =0.1,\sigma =0.2$. На верхнем рисунке показана гистограмма времени ожидания, а также прогноз в соответствии с обратным распределением Гаусса. На нижнем рисунке показаны траектории.

Пусть случайный процесс X _t задается формулой

$X_{0}=0\quad$

$X_{t}=\nu t+\sigma W_{t}\quad \quad \quad \quad$

где W _t — стандартное броуновское движение . То есть X _t — броуновское движение со сносом $\nu >0$.

Тогда время первого прохождения фиксированного уровня $\alpha >0$ по X _t распределяется по обратно-гауссову закону:

$T_{\alpha }=\inf\{t>0\mid X_{t}=\alpha \}\sim \operatorname {IG} \left({\frac {\alpha }{\nu }},\left({\frac {\alpha }{\sigma }}\right)^{2}\right)={\frac {\alpha }{\sigma {\sqrt {2\pi x^{3}}}}}\exp {\biggl (}-{\frac {(\alpha -\nu x)^{2}}{2\sigma ^{2}x}}{\biggr )}$

то есть

$P(T_{\alpha }\in (T,T+dT))={\frac {\alpha }{\sigma {\sqrt {2\pi T^{3}}}}}\exp {\biggl (}-{\frac {(\alpha -\nu T)^{2}}{2\sigma ^{2}T}}{\biggr )}dT$

(см. Шрёдингер уравнение 19, Смолуховский , уравнение 8 и Фолкс , уравнение 1).

показывать Вывод распределения времени первого прохождения

Suppose that we have a Brownian motion $X_{t}$ with drift $\nu$ defined by: $X_{t}=\nu t+\sigma W_{t},\quad X(0)=x_{0}$ And suppose that we wish to find the probability density function for the time when the process first hits some barrier $\alpha >x_{0}$ - known as the first passage time. The Fokker-Planck equation describing the evolution of the probability distribution $p(t,x)$ is: ${\partial p \over {\partial t}}+\nu {\partial p \over {\partial x}}={1 \over {2}}\sigma ^{2}{\partial ^{2}p \over {\partial x^{2}}},\quad {\begin{cases}p(0,x)&=\delta (x-x_{0})\\p(t,\alpha )&=0\end{cases}}$ where $\delta (\cdot )$ is the Dirac delta function. This is a boundary value problem (BVP) with a single absorbing boundary condition $p(t,\alpha )=0$, which may be solved using the method of images. Based on the initial condition, the fundamental solution to the Fokker-Planck equation, denoted by $\varphi (t,x)$, is: $\varphi (t,x)={1 \over {\sqrt {2\pi \sigma ^{2}t}}}\exp \left[-{(x-x_{0}-\nu t)^{2} \over {2\sigma ^{2}t}}\right]$ Define a point $m$, such that $m>\alpha$. This will allow the original and mirror solutions to cancel out exactly at the barrier at each instant in time. This implies that the initial condition should be augmented to become: $p(0,x)=\delta (x-x_{0})-A\delta (x-m)$ where $A$ is a constant. Due to the linearity of the BVP, the solution to the Fokker-Planck equation with this initial condition is: $p(t,x)={1 \over {\sqrt {2\pi \sigma ^{2}t}}}\left\{\exp \left[-{(x-x_{0}-\nu t)^{2} \over {2\sigma ^{2}t}}\right]-A\exp \left[-{(x-m-\nu t)^{2} \over {2\sigma ^{2}t}}\right]\right\}$ Now we must determine the value of $A$. The fully absorbing boundary condition implies that: $(\alpha -x_{0}-\nu t)^{2}=-2\sigma ^{2}t\log A+(\alpha -m-\nu t)^{2}$ At $p(0,\alpha )$, we have that $(\alpha -x_{0})^{2}=(\alpha -m)^{2}\implies m=2\alpha -x_{0}$. Substituting this back into the above equation, we find that: $A=e^{2\nu (\alpha -x_{0})/\sigma ^{2}}$ Therefore, the full solution to the BVP is: $p(t,x)={1 \over {\sqrt {2\pi \sigma ^{2}t}}}\left\{\exp \left[-{(x-x_{0}-\nu t)^{2} \over {2\sigma ^{2}t}}\right]-e^{2\nu (\alpha -x_{0})/\sigma ^{2}}\exp \left[-{(x+x_{0}-2\alpha -\nu t)^{2} \over {2\sigma ^{2}t}}\right]\right\}$ Now that we have the full probability density function, we are ready to find the first passage time distribution $f(t)$. The simplest route is to first compute the survival function $S(t)$, which is defined as: ${\begin{aligned}S(t)&=\int _{-\infty }^{\alpha }p(t,x)dx\\&=\Phi \left({\alpha -x_{0}-\nu t \over {\sigma {\sqrt {t}}}}\right)-e^{2\nu (\alpha -x_{0})/\sigma ^{2}}\Phi \left({-\alpha +x_{0}-\nu t \over {\sigma {\sqrt {t}}}}\right)\end{aligned}}$ where $\Phi (\cdot )$ is the cumulative distribution function of the standard normal distribution. The survival function gives us the probability that the Brownian motion process has not crossed the barrier $\alpha$ at some time $t$. Finally, the first passage time distribution $f(t)$ is obtained from the identity: ${\begin{aligned}f(t)&=-{dS \over {dt}}\\&={(\alpha -x_{0}) \over {\sqrt {2\pi \sigma ^{2}t^{3}}}}e^{-(\alpha -x_{0}-\nu t)^{2}/2\sigma ^{2}t}\end{aligned}}$ Assuming that $x_{0}=0$, the first passage time follows an inverse Gaussian distribution: $f(t)={\alpha \over {\sqrt {2\pi \sigma ^{2}t^{3}}}}e^{-(\alpha -\nu t)^{2}/2\sigma ^{2}t}\sim {\text{IG}}\left[{\alpha \over {\nu }},\left({\alpha \over {\sigma }}\right)^{2}\right]$

Когда дрейф равен нулю

Общий частный случай изложенного выше возникает, когда броуновское движение не имеет дрейфа. В этом случае параметр µ стремится к бесконечности, а время первого прохождения фиксированного уровня α имеет функцию плотности вероятности

$f\left(x;0,\left({\frac {\alpha }{\sigma }}\right)^{2}\right)={\frac {\alpha }{\sigma {\sqrt {2\pi x^{3}}}}}\exp \left(-{\frac {\alpha ^{2}}{2\sigma ^{2}x}}\right)$

(см. также Башелье ). Это распределение Леви с параметрами $c=\left({\frac {\alpha }{\sigma }}\right)^{2}$ и $\mu =0$.

Максимальная вероятность

Модель, где

$X_{i}\sim \operatorname {IG} (\mu ,\lambda w_{i}),\,\,\,\,\,\,i=1,2,\ldots ,n$

со всеми wi _{известными} , ( μ , λ ) неизвестными и всеми X _i, независимыми имеет следующую функцию правдоподобия

$L(\mu ,\lambda )=\left({\frac {\lambda }{2\pi }}\right)^{\frac {n}{2}}\left(\prod _{i=1}^{n}{\frac {w_{i}}{X_{i}^{3}}}\right)^{\frac {1}{2}}\exp \left({\frac {\lambda }{\mu }}\sum _{i=1}^{n}w_{i}-{\frac {\lambda }{2\mu ^{2}}}\sum _{i=1}^{n}w_{i}X_{i}-{\frac {\lambda }{2}}\sum _{i=1}^{n}w_{i}{\frac {1}{X_{i}}}\right).$

Решение уравнения правдоподобия дает следующие оценки максимального правдоподобия.

${\widehat {\mu }}={\frac {\sum _{i=1}^{n}w_{i}X_{i}}{\sum _{i=1}^{n}w_{i}}},\,\,\,\,\,\,\,\,{\frac {1}{\widehat {\lambda }}}={\frac {1}{n}}\sum _{i=1}^{n}w_{i}\left({\frac {1}{X_{i}}}-{\frac {1}{\widehat {\mu }}}\right).$

${\widehat {\mu }}$ и ${\widehat {\lambda }}$ независимы и

${\widehat {\mu }}\sim \operatorname {IG} \left(\mu ,\lambda \sum _{i=1}^{n}w_{i}\right),\qquad {\frac {n}{\widehat {\lambda }}}\sim {\frac {1}{\lambda }}\chi _{n-1}^{2}.$

Выборка из обратного распределения Гаусса

Можно использовать следующий алгоритм.

Сгенерируйте случайную величину из нормального распределения со средним значением 0 и стандартным отклонением, равным 1.

$\displaystyle \nu \sim N(0,1).$

Возведите значение в квадрат

$\displaystyle y=\nu ^{2}$

и использовать соотношение

$x=\mu +{\frac {\mu ^{2}y}{2\lambda }}-{\frac {\mu }{2\lambda }}{\sqrt {4\mu \lambda y+\mu ^{2}y^{2}}}.$

Создайте еще одну случайную величину, на этот раз выбранную из равномерного распределения от 0 до 1.

$\displaystyle z\sim U(0,1).$

Если $z\leq {\frac {\mu }{\mu +x}}$ затем вернись $\displaystyle x$ иначе возврат ${\frac {\mu ^{2}}{x}}.$

Пример кода на Java :

public double inverseGaussian(double mu, double lambda) {
    Random rand = new Random();
    double v = rand.nextGaussian();  // Sample from a normal distribution with a mean of 0 and 1 standard deviation
    double y = v * v;
    double x = mu + (mu * mu * y) / (2 * lambda) - (mu / (2 * lambda)) * Math.sqrt(4 * mu * lambda * y + mu * mu * y * y);
    double test = rand.nextDouble();  // Sample from a uniform distribution between 0 and 1
    if (test <= (mu) / (mu + x))
        return x;
    else
        return (mu * mu) / x;
}

Распределение Уолда с использованием Python с помощью matplotlib и NumPy.

И чтобы построить график распределения Вальда в Python, используя matplotlib и NumPy :

import matplotlib.pyplot as plt
import numpy as np

h = plt.hist(np.random.wald(3, 2, 100000), bins=200, density=True)

plt.show()

Связанные дистрибутивы

• Если $X\sim \operatorname {IG} (\mu ,\lambda )$, затем $kX\sim \operatorname {IG} (k\mu ,k\lambda )$ на любое число $k>0.$
• Если $X_{i}\sim \operatorname {IG} (\mu ,\lambda )\,$ затем $\sum _{i=1}^{n}X_{i}\sim \operatorname {IG} (n\mu ,n^{2}\lambda )\,$
• Если $X_{i}\sim \operatorname {IG} (\mu ,\lambda )\,$ для $i=1,\ldots ,n\,$ затем ${\bar {X}}\sim \operatorname {IG} (\mu ,n\lambda )\,$
• Если $X_{i}\sim \operatorname {IG} (\mu _{i},2\mu _{i}^{2})\,$ затем $\sum _{i=1}^{n}X_{i}\sim \operatorname {IG} \left(\sum _{i=1}^{n}\mu _{i},2\left(\sum _{i=1}^{n}\mu _{i}\right)^{2}\right)\,$
• Если $X\sim \operatorname {IG} (\mu ,\lambda )$, затем $\lambda (X-\mu )^{2}/\mu ^{2}X\sim \chi ^{2}(1)$.

Свертка обратного распределения Гаусса (распределение Вальда) и экспоненциального распределения (распределение Экс-Вальда) используется в качестве модели для определения времени отклика в психологии. с визуальным поиском в качестве примера.

История

Похоже, что это распределение было впервые получено в 1900 году Луи Башелье. как момент, когда акция впервые достигает определенной цены. В 1915 году его независимо использовал Эрвин Шредингер. и Мариан против Смолуховского как время первого прохождения броуновского движения. В области моделирования воспроизводства она известна как функция Хадвигера, в честь Хьюго Хадвигера, описавшего ее в 1940 году. Авраам Вальд повторно получил это распределение в 1944 году. как предельная форма выборки в последовательном тесте отношения вероятностей. Название «обратная гауссовая» было предложено Морисом Твиди в 1945 году. Твиди исследовал это распределение в 1956 году. и 1957 год и установил некоторые его статистические свойства. Распространение было подробно рассмотрено Фолксом и Чикарой в 1978 году.

Численные вычисления и программное обеспечение

Несмотря на простую формулу функции плотности вероятности, численные расчеты вероятности для обратного распределения Гаусса, тем не менее, требуют особой осторожности для достижения полной машинной точности в арифметике с плавающей запятой для всех значений параметров. Функции для обратного распределения Гаусса предоставляются для языка программирования R несколькими пакетами, включая rmutil, СуппДистс, ЗВЕЗДА, инвГаусс, ЛапласДемон, и статмод.

См. также

• Обобщенное обратное распределение Гаусса
• Распределения Твиди . Обратное распределение Гаусса является членом семейства моделей экспоненциальной дисперсии Твиди.
• Остановка времени

Дальнейшее чтение

• Høyland, Арнльот ; Раусанд, Марвин (1994). Теория надежности систем . Нью-Йорк: Уайли. ISBN  978-0-471-59397-3 .
• Seshadri, V. (1993). The Inverse Gaussian Distribution . Oxford University Press. ISBN  978-0-19-852243-0 .

Внешние ссылки

• Обратное распределение Гаусса на веб-сайте Wolfram.