Система Катапаяди

Эта статья содержит индийский текст . Без надлежащей поддержки рендеринга вы можете увидеть вопросительные знаки или рамки , неправильно расположенные гласные или отсутствующие союзы. вместо индийского текста

Kaṭapayādi system (Devanagari: कटपयादि, also known as Paralppēru, Malayalam: പരല്‍പ്പേര്) of numerical notation is an ancient Indian alphasyllabic numeral system to depict letters to numeralsСистема катапаяди (деванагари: कटपयादि, также известная как Паралппперу, малаялам: പരല്‍പ്പേര്) числовой записи — это древняя индийская буквенно-сложная система счисления, позволяющая для удобства изображать буквы в цифрах. запоминание чисел в виде слов или стихов . Приписывая одной цифре более одной буквы и аннулируя некоторые другие буквы как бесполезные, эта система обеспечивает гибкость в формировании осмысленных слов из чисел, которые можно легко запомнить.

История

Самое старое доступное свидетельство использования системы Катапаяди कटपयादि) взято из Грахачаранибандханы Харидатты (санскрит : в 683 году нашей эры . ^{[ 1 ]} Оно использовалось в «Лагхубхаскария-виваране», написанном Шанкара-нараяной 869 году нашей эры. в ^{[ 2 ]}

В некоторых астрономических текстах, популярных в Керале, положения планет были закодированы в системе Катапаяди. Первой такой работой считается « Чандра-вакьяни» , Вараручи которую традиционно относят к четвертому веку нашей эры . Таким образом, можно разумно предположить, что происхождение системы Катапаяди зародилось где-то в начале первого тысячелетия . ^{[ 3 ]}

Известно, что Арьябхата в своем трактате «Арьябхатия» использовал аналогичную, более сложную систему для представления астрономических чисел . Нет точных доказательств того, что система Ка-та-па-йа-ди произошла от нумерации Арьябхаты . ^{[ 4 ]}

Географическое распространение использования

Почти все свидетельства использования системы Ка-та-па-йа-ди происходят из Южной Индии , особенно из Кералы . О его использовании в Северной Индии известно немного. Однако на санскритской астролябии , обнаруженной в Северной Индии , градусы высоты отмечены в системе Катапаяди . Он хранится в библиотеке Сарасвати Бхавана Сампурнанандского санскритского университета в Варанаси . ^{[ 5 ]}

Система Ка-та-па-йа-ди распространена не только в Индии. Некоторые палийские хронограммы, основанные на системе Ка-та-па-йа-ди, были обнаружены в Бирме . ^{[ 6 ]}

Правила и практики

Следующий стих из » Шанкаравармана «Садратнамалы объясняет механизм системы. ^{[ 7 ]}^{[ 8 ]}

Существительные также являются пустыми числами, например катапайя.
В смеси количество халов заканчивается и о звуке хал думать не приходится.

Транслитерация:

наньявачаща шуньяни санкхйах катапаядайах
мишре тупантьяхал санкхья на ча чинтйо халасварах

Перевод: na (न), ña (ञ) и a (अ)-s, т. е. гласные обозначают ноль . Девять целых чисел представлены группой согласных , начинающейся с ка , та , па , я . В союзной согласной учитывается только последняя из согласных. Согласную без гласной следует игнорировать.

Пояснение: Буквы и цифры располагаются в следующем порядке (в алфавитах деванагари, каннада, телугу и малаялам соответственно).

1	2	3	4	5	6	7	8	9	0
ка к к к к	ха ха ха ха ха ха	высокий ग ग ग ग	гха д ಘ ఘ ഘ	ಙ Г	ca ch ಚ చ ച	отец छ ಛ ఛ ഛ	Я ஜ ஜ ஜ ஜ	джа джа джа джа	ня – ఞ ഞ
та т т т т	хорошая вещь ఠ ഠ	да ड ಡ డ ഡ	Дха พ พ พ พ	ана ࣣ ࣣ ࣣ ࣣ	та त ತ త ത	да эт эт эт эт	да да да да да	дха дха ధ ധ	и न न न न
на প પ પ પ	фа फ फ फ फ	не б б б	бха бха бха бха	Я не знаю	–	–	–	–	–
да य ಯ య യ	ра र र र र	ل ل ل ل	идет व ವ వ വ	śa श ಶ శ ശ	ষ ষ ষ ষ ষ	са са са са са са	если ह ह ह ह	–	–

Согласным присвоены цифры согласно таблице выше. Например, ба (ब) всегда равно 3, тогда как 5 может быть представлено либо нга (ङ), либо ана (ण), либо ма (म), либо ша (श).
Всем отдельным гласным, таким как ( अ) и ṛ (ऋ), присваивается ноль.
В случае союза согласные, присоединенные к негласной, не имеют значения. Например, кья (क्य) образуется из: k (क्) + y (य्) + a (अ). Единственная согласная, стоящая рядом с гласной, — это йа (य). Таким образом, соответствующая цифра для кья (क्य) будет 1.
невозможно представить десятичный разделитель . В системе
Индийцы использовали индуистско-арабскую систему счисления для нумерации, традиционно записываемую с возрастанием разрядов слева направо. Это соответствует правилу «अङ्कानां वामतो गतिः», которое означает, что числа идут справа налево.

Вариации

Согласный в ḷ (малаялам: ল, деванагари: ಳ, каннада: ಲ) используется в произведениях, использующих систему Катапаяди, например, таблице синусов Мадхавы .
Практики позднего средневековья не приравнивают отдельные гласные к нулю. Но иногда это считается бесполезным.

Использование

Математика и астрономия

Таблица синусов Мадхавы, построенная из Кералы математиком и астрономом XIV века Мадхавой из Сангамаграмы, использует систему Катапаяди для перечисления тригонометрических синусов углов.
В Карана-паддхати , написанном в 15 веке, есть следующая шлока для значения числа пи (π):

Анунанананнананунананнанитьяй-

Саммахатащакракалавибхактах

Чандамшучандрадхамакумбхипалаир-

Вьясастадардхам Трибхамаурвика Сьят

Транслитерация

анунануннаннананануннанитьяй

ссмахаташчакра калавибхактох

Чандамшучандрадхамакумбхипалаир

вьясастадарддхам трибхамаурвика сйат

Он дает длину окружности диаметром анунануннанананануннанитьяи (10 000 000 000) как чандамшучандрадхамакумбхипалаир (31415926536).

В «Садратнамале» Шанкаравармана используется система Катапаяди. Первый стих главы 4 Садратнамалы заканчивается строкой: ^{[ 9 ]}

(Это было бы) Бхадрамбудхисиддхаджанмаганитасраддха сма йад бхупаги:

Транслитерация

(сйад) бхадрамбудхисиддхаджанмаганиташраддха сма йад бхупагих

Разделение согласных в соответствующей фразе дает:

да да	д д	день день	м м	бу бу	д д	дхи-дхи	си си	д д	дха дха	да да	нн н	м ма	ग га	Ни Ни	त та	श श	ра-ра	д д	дха дха	स् s	м ма	य ya	д д	भू भू	нет	ги ги
4	–	2	–	3	–	9	7	–	9	8	–	5	3	5	6	–	2	–	9	–	5	1	–	4	1	3

Меняя цифры на современный порядок убывания десятичных знаков, мы получаем 314159265358979324 , что представляет собой значение числа Пи (π) до 17 десятичных знаков, за исключением того, что последняя цифра может быть округлена до 4.

В этом стихе зашифровано значение числа Пи (π) до 31 десятичного знака.

 गोपीभाग्यमधुव्रात-शृङ्गिशोदधिसन्धिग॥
 खलजीवितखाताव गलहालारसंधर॥

 ಗೋಪೀಭಾಗ್ಯಮಧುವ್ರಾತ-ಶೃಂಗಿಶೋದಧಿಸಂಧಿಗ ||
 ಖಲಜೀವಿತಖಾತಾವ ಗಲಹಾಲಾರಸಂಧರ ||

Этот стих напрямую дает десятичный эквивалент числа Пи, разделенного на 10: Пи/10 = 0,31415926535897932384626433832792.

 గోపీభాగ్యమధువ్రాత-శృంగిశోదధిసంధిగ |
 ఖలజీవితఖాతావ గలహాలారసంధర ||

Традиционно в системе катапаяди порядок цифр меняется на обратный для образования числа. В данной шлоке это правило нарушено.

Карнатическая музыка

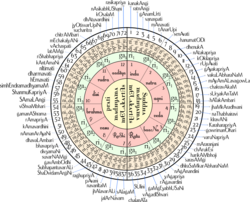
Мелакарта - раги музыки Карнатика названы так, что первые два слога названия дают его номер. Эту систему иногда называют Ка-та-па-йа-ди санкхья . Свары . «Са» и «Па» фиксированы, и вот как получить другие свары из числа мелакарты

Мелакарты с 1 по 36 имеют Ma1, а мелакарты с 37 по 72 — Ma2.
Остальные примечания получаются путем записи частного (целой части) и остатка, когда единица меньше числа мелакарты делится на 6. Если число мелакарты больше 36, перед выполнением этого шага вычтите 36 из числа мелакарты.
Позиции «Ри» и «Га»: в раге будут:
- Ri1 и Ga1, если частное равно 0
- Ri1 и Ga2, если частное равно 1
- Ri1 и Ga3, если частное равно 2
- Ri2 и Ga2, если частное равно 3
- Ri2 и Ga3, если частное равно 4
- Ri3 и Ga3, если частное равно 5
Позиции «Да» и «Ни»: в раге будут:
- Da1 и Ni1, если остаток равен 0
- Da1 и Ni2, если остаток равен 1
- Da1 и Ni3, если остаток равен 2
- Da2 и Ni2, если остаток равен 3
- Da2 и Ni3, если остаток равен 4
- Da3 и Ni3, если остаток равен 5

см . в сварах в музыке Карнатика . Подробную информацию о приведенных выше обозначениях

Рага Дхирасанкарабхаранам

Схема катапаяди связывает дха $\leftrightarrow$ 9 и ра $\leftrightarrow$ 2, следовательно, число мелакарты раги равно 29 (92 перевернутое). 29 меньше 36, следовательно, Дхирасанкарабхаранам имеет Ma1. Делим 28 (1 меньше 29) на 6, частное 4 и остаток 4. Следовательно, в этой раге есть Ri2, Ga3 (частное 4) и Da2, Ni3 (остаток 4). Следовательно, масштаб этой раги — Sa Ri2 Ga3 Ma1 Pa Da2 Ni3 SA .

Рага Меха Кальяни

Из схемы кодирования Ма $\leftrightarrow$ 5, гл. $\leftrightarrow$ 6. Следовательно, число мелакарты раги равно 65 (56 в перевернутом виде). 65 больше 36. Итак, у МехаКальяни Ма2. Поскольку число раги больше 36, вычтите из него 36. 65–36=29. 28 (1 меньше 29) разделить на 6: частное=4, остаток=4. Встречается Ri2 Ga3. Встречается Da2 Ni3. Итак, у МехаКаляни есть ноты Sa Ri2 Ga3 Ma2 Pa Da2 Ni3 SA .

Исключение для Симхендрамадхьямама.

Согласно приведенному выше расчету, мы должны получить Sa $\leftrightarrow$ 7, Ха $\leftrightarrow$ 8 дает число 87 вместо 57 для Симхендрамадхьямама. В идеале это должно быть Са. $\leftrightarrow$ 7, Ма $\leftrightarrow$ 5, дающее число 57. Поэтому считается, что имя следует писать как Симендрамадхьямам (как в случае с Брахманой на санскрите).

Представление дат

Важные даты запоминались путем их преобразования с использованием системы Катапаяди . Эти даты обычно представляются как количество дней с начала Кали-Юги . Иногда ее называют калидина санкхья .

Календарь малаялам, известный как коллаваршам (малаялам: Коллаваршам), был принят в Керале начиная с 825 года нашей эры, в результате чего некоторые календари были обновлены . Эта дата запомнилась как ачарья вагбхада , преобразованная с помощью катапаяди в 1434160 дней с начала Кали-юги . ^{[ 10 ]}
Нараяниям , написанная Мелпатуром Нараяной Бхаттатири , заканчивается строкой āyurārogyasaukhyam (ആയുരാരോഗ്യസൌഖ്യം), что означает долгую жизнь, здоровье и счастье. ^{[ 11 ]}

На малаялам	Здоровье
В Деванагари	Долголетия, здоровья и счастья
В ИАСТ	Аюрарогьясаукхьям
Стоимость по Катапаяди	1712210

Это число представляет собой время завершения работы, выраженное в количестве дней с начала Кали-юги по календарю малаялам .

Другие

Некоторые люди используют систему Катапаяди для обозначения новорожденных. ^{[ 12 ]}^{[ 13 ]}
Следующий стих, составленный на малаялам Кодуналлуром Куньниккуттаном Тампураном с использованием Катапаяди, представляет собой количество дней в месяцах по григорианскому календарю .

Палахаре палу хорош

Илла Паленну Гопалан – День Англамаса Крамал

Транслитерация

палахаре палу наллу, пуларннало калаккилам

илла паленну гопалан – ангхамасадинам крамал

Перевод: Молоко лучше всего готовить на завтрак, утром его следует размешать. Но Гопалан говорит, что молока нет – количество дней в английских месяцах по порядку.

Преобразование пар букв с использованием катапаяди дает: пала — 31, харе — 28, палу = 31, наллу — 30, пулар — 31, ннало — кала 30, кала) — 31, ккилам (килам) — 31, илла (илла) — 30, Пале — 31, нну го — 30, Палану — 31.

См. также

Ссылки

^ Шрирамамула Раджешвара Сарма, КАТАПАЯДИ СИСТЕМА ЧИСЛОВЫХ обозначений И ЕЕ РАСПРОСТРАНЕНИЕ ЗА ПРЕДЕЛАМИ КЕРАЛЫ, преподобный о. истории математики 18 (2012) [1]
^ Джей Джей О'Коннор; Э. Ф. Робертсон (ноябрь 2000 г.). «Шанкара Нараяна» . Школа математики и статистики, Университет Сент-Эндрюс, Шотландия . Проверено 1 января 2010 г.
^ Плофкер, Ким (2009). Математика в Индии . Издательство Принстонского университета . п. 384. ИСБН 978-0-691-12067-6 .
^ JF Fleet (апрель 1912 г.). «Нотации Ка-та-па-йа-ди Второй Арья-Сиддханты» . Журнал Королевского азиатского общества Великобритании и Ирландии . 44 . Королевское азиатское общество Великобритании и Ирландии : 459–462. дои : 10.1017/S0035869X00043197 . JSTOR 25190035 . S2CID 163907655 .
^ Шрирамамула Раджешвара Сарма (1999), Обозначения Катапаяди на санскритской астролябии. Индийский Дж. Хист. Sc.34(4) (1999) [2]
^ JF Fleet (июль 1911 г.). «Система выражения чисел катапаяди» . Журнал Королевского азиатского общества Великобритании и Ирландии . 43 (3). Королевское азиатское общество Великобритании и Ирландии : 788–794. дои : 10.1017/S0035869X00041952 . JSTOR 25189917 . S2CID 163597699 .
^ Сарма, КВ (2001). «Садратнамала Шанкара Вармана». Индийский журнал истории науки (Индийская национальная академия наук, Нью-Дели) 36 (3–4 (Приложение)): 1–58. «Архивная копия» (PDF) . Архивировано из оригинала (PDF) 2 апреля 2015 года . Проверено 17 декабря 2009 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )
^ Ананд Раман. «Древняя формула катапаяди и современный метод хеширования» (PDF) . Архивировано из оригинала (PDF) 16 июня 2011 года. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ Сарма (2001), с. 26
^ Фрэнсис Циммерман, 1989, Лилавати, милостивая арифметика - Индия - Математический загадочный тур «Лилавати, милостивая арифметика - Индия - математический загадочный тур | Курьер ЮНЕСКО | Найдите статьи на BNET» . Архивировано из оригинала 6 сентября 2009 года . Проверено 3 января 2010 г.
^ Доктор. C Кришнан Намбудири, Чекракал Иллам, Каликут, Namboothiti.com Доктор C Кришнан Намбудири. « Катапаяади» или «Паральпперу » . Доверие веб-сайтов Намбутири . Проверено 1 января 2010 г.
^ Висти Ларсен, Выбор благоприятного имени ^{[ постоянная мертвая ссылка ]}
^ «Принципы именования» .

Внешние ссылки

Катапаяди Санкхья, система кодирования-декодирования Катапаяди.

Дальнейшее чтение

А. А. Хаттангади, Исследования в области математики, Universities Press (Индия) Pvt. Ltd., Хайдарабад (2001 г.) ISBN 81-7371-387-1 [3]

[astro-1] Шрирамамула Раджешвара Сарма, КАТАПАЯДИ СИСТЕМА ЧИСЛОВЫХ обозначений И ЕЕ РАСПРОСТРАНЕНИЕ ЗА ПРЕДЕЛАМИ КЕРАЛЫ, преподобный о. истории математики 18 (2012) [1]

[2] Джей Джей О'Коннор; Э. Ф. Робертсон (ноябрь 2000 г.). «Шанкара Нараяна» . Школа математики и статистики, Университет Сент-Эндрюс, Шотландия . Проверено 1 января 2010 г.

[3] Плофкер, Ким (2009). Математика в Индии . Издательство Принстонского университета . п. 384. ИСБН 978-0-691-12067-6 .

[4] JF Fleet (апрель 1912 г.). «Нотации Ка-та-па-йа-ди Второй Арья-Сиддханты» . Журнал Королевского азиатского общества Великобритании и Ирландии . 44 . Королевское азиатское общество Великобритании и Ирландии : 459–462. дои : 10.1017/S0035869X00043197 . JSTOR 25190035 . S2CID 163907655 .

[5] Шрирамамула Раджешвара Сарма (1999), Обозначения Катапаяди на санскритской астролябии. Индийский Дж. Хист. Sc.34(4) (1999) [2]

[6] JF Fleet (июль 1911 г.). «Система выражения чисел катапаяди» . Журнал Королевского азиатского общества Великобритании и Ирландии . 43 (3). Королевское азиатское общество Великобритании и Ирландии : 788–794. дои : 10.1017/S0035869X00041952 . JSTOR 25189917 . S2CID 163597699 .

[7] Сарма, КВ (2001). «Садратнамала Шанкара Вармана». Индийский журнал истории науки (Индийская национальная академия наук, Нью-Дели) 36 (3–4 (Приложение)): 1–58. «Архивная копия» (PDF) . Архивировано из оригинала (PDF) 2 апреля 2015 года . Проверено 17 декабря 2009 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )

[8] Ананд Раман. «Древняя формула катапаяди и современный метод хеширования» (PDF) . Архивировано из оригинала (PDF) 16 июня 2011 года. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[9] Сарма (2001), с. 26

[10] Фрэнсис Циммерман, 1989, Лилавати, милостивая арифметика - Индия - Математический загадочный тур «Лилавати, милостивая арифметика - Индия - математический загадочный тур | Курьер ЮНЕСКО | Найдите статьи на BNET» . Архивировано из оригинала 6 сентября 2009 года . Проверено 3 января 2010 г.

[11] Доктор. C Кришнан Намбудири, Чекракал Иллам, Каликут, Namboothiti.com Доктор C Кришнан Намбудири. « Катапаяади» или «Паральпперу » . Доверие веб-сайтов Намбутири . Проверено 1 января 2010 г.

[12] Висти Ларсен, Выбор благоприятного имени ^{[ постоянная мертвая ссылка ]}

[13] «Принципы именования» .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

v т и Керальская школа астрономии и математики
Astronomers and mathematicians	(Complete list) Acyuta Piṣāraṭi Azhvāñceri Taṃprākkaḷ Citrabhānu Dāmodara of Vațaśreņi Devācārya Govinda Bhattathiri Govindasvāmin Haridatta Jyeṣṭhadeva Kochukrishnan Asan Madhava of Sangamagrama Mazhamaṅgalaṃ Nārāyaṇan Naṃpūtiri Nīlakaņțha Sōmayāji Nīlakaṇṭha II Parameśvara of Vațaśśeri Śaṅkaranārāyaṇa Śaṅkara of Mahiṣamaṅgalam Putumana Somayāji Śankara Vāriyar Śaṅkara Varma of Kaṭattanāṭ Udayadivākara Vararuci I Vidyamadhava
Treatises	Aryabhatiya-bhashya (Nīlakaņțha Sōmayāji) Candrachayaganita Dasādhyāyi Drigganita Dṛkkaraṇa Gaṇitayuktayah Golavada Golasara Grahacāraṇinibandhana Jātaka-sāara-saṃgraha Jyotirmimamsa Jyotiśśāstra-saṃgraha Kanakkusāraṃ Karaṇapaddhati Kriyakramakari Laghuvivṛti (commentary on Tantrasamgraha) Madhyamanayanaprakara Mahābhāskarīya Bhāshya Pañcabodha Sadratnamālā Sidhhantadarpana Spuṭanirṇaya Tantrasamgraha Venvaroha Yuktibhāṣā
Concepts/Topics	Chandravakyas Drigganita system Kaṭapayādi system Madhava's correction terms Madhava series Madhava's sine table Parahita system
Places associated with members of the school	Athavanad (Azhvanchery Thamprakkal) Alathiyur (Govinda Bhattathiri, etc) Kadathanadu (Sankara Varman) Mahodayapuram (Kodungallur) (Sankaranarayana) Kudallur (Madhava of Sangamagrama) Peruvanam (Mahishamangalam Sankaran Namputhiri) Thrikkandiyur (Nilakantha Somayaji, etc) Sivapuram (Thrissur) (Putumana Somayaji, etc) Tirunavaya (Haridatta)

v т и Научные исследования в Керале
Pre 19th Century	Achyuta Pisharati Candravakyas Citrabhanu Damodara Ganita-yukti-bhasa Govinda Bhattathiri Haridatta Jyā, koti-jyā and utkrama-jyā Jyeṣṭhadeva Jyotirmimamsa Karanapaddhati Katapayadi system Kriyakramakari Madhava of Sangamagrama Madhava series Madhava's sine table Melpathur Narayana Bhattathiri Nilakantha Somayaji Parameshvara Sadratnamala Śaṅkaranārāyaṇa Tantrasamgraha
Organizations	C-DAC Thiruvananthapuram Centre for Development Studies Centre for Earth Science Studies Centre for Mathematical Sciences (Kerala) Centre for Rural Management Centre of Science and Technology for Rural Development Cyberpark Kerala Mathematical Association Kerala Science and Technology Museum Kerala Science Congress Kerala Soil Museum Kerala State Council for Science, Technology and Environment Krishi Vigyan Kendra Kannur Liquid Propulsion Systems Centre Rajiv Gandhi Centre for Biotechnology Regional Agricultural Research Station, Pattambi Rice Research Station, Moncombu Vikram Sarabhai Space Centre
Institutions	Agricultural Research Station, Anakkayam Agricultural Research Station, Mannuthy Agronomic Research Station, Chalakudy Amrita Institute of Medical Sciences and Research Centre Aromatic and Medicinal Plants Research Station, Odakkali Banana Research Station, Kannara Cashew Research Station, Madakkathara Central Institute of Fisheries Technology Central Marine Fisheries Research Institute Central Tuber Crops Research Institute Centre for Marine Living Resources & Ecology College of Horticulture Crocodile Rehabilitation and Research Centre Institute of Handloom and Textile Technology Indian Institute of Science Education and Research, Thiruvananthapuram Indian Institute of Space Science and Technology Indian Institute of Spices Research Jubilee Mission Medical College and Research Institute Kerala Forest Research Institute Kerala School of Mathematics, Kozhikode Mar Athanasios College for Advanced Studies, Tiruvalla National Institute for Interdisciplinary Science and Technology National Institute of Speech and Hearing National Research Institute for Panchakarma Naval Physical and Oceanographic Laboratory Oriental Research Institute & Manuscripts Library Sree Chitra Tirunal Institute for Medical Sciences and Technology Srinivasa Ramanujan Institute of Basic Sciences St. Ephrem Ecumenical Research Institute Tropical Botanical Garden and Research Institute Vadakke Madham Brahmaswam Vedic Research Centre
Scientists	Ajit Varki C. V. Subramanian Dileep George E. C. George Sudarshan G. Madhavan Nair George Varghese K. R. Ramanathan K. Radhakrishnan M. G. K. Menon Matthew Pothen Thekaekara P. N. Vinayachandran Pisharoth Rama Pisharoty Pulickel Ajayan R. S. Krishnan Sainudeen Pattazhy T. A. Venkitasubramanian Thanu Padmanabhan Thomas Zacharia Vainu Bappu Varghese Mathai Vinod Scaria
Assorted articles	A Passage to Infinity FORV Sagar Sampada Swatantra 2014 Techno-lodge Technology Business Incubator TBI-NITC A History of the Kerala School of Hindu Astronomy
Templates Category WikiProject India portal