дополнение Минковского

Красная фигура представляет собой сумму Минковского синей и зеленой фигур.

В геометрии двух сумма Минковского наборов векторов положения A и B в евклидовом пространстве формируется путем добавления каждого вектора из A к каждому вектору из B :

$A+B=\{\mathbf {a} +\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}$

Разница Минковского (также вычитание Минковского , разложение Минковского или геометрическая разность ) является соответствующим обратным, где $(A-B)$ создает набор, который можно суммировать с для восстановления A. B Это определяется как дополнение суммы Минковского дополнения A с отражением B относительно начала координат.

$-B=\{\mathbf {-b} \,|\,\mathbf {b} \in B\}$

$A-B=(A^{\complement }+(-B))^{\complement }$

Это определение допускает симметричную связь между суммой и разностью Минковского. Обратите внимание, что поочередное взятие суммы и разности с B не обязательно эквивалентно. Сумма может заполнить пробелы, которые разница не может открыть вновь, а разница может стереть маленькие островки, которые сумма не может воссоздать из ничего.

$(A-B)+B\subseteq A$

$(A+B)-B\supseteq A$

$A-B=(A^{\complement }+(-B))^{\complement }$

$A+B=(A^{\complement }-(-B))^{\complement }$

При обработке 2D-изображений сумма и разность Минковского известны как расширение и эрозия .

Альтернативное определение разности Минковского иногда используется для вычисления пересечения выпуклых фигур. Это не эквивалентно предыдущему определению и не является обратной операцией суммирования. Вместо этого он заменяет векторное сложение суммы Минковского векторным вычитанием . Если две выпуклые фигуры пересекаются, результирующий набор будет содержать начало координат.

$A-B=\{\mathbf {a} -\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}=A+(-B)$

Концепция названа в честь Германа Минковского .

Пример

Сумма Минковского A + B

Например, если у нас есть два множества A и B , каждое из которых состоит из трех векторов положения (неформально, трех точек), представляющих вершины двух треугольников в $\mathbb {R} ^{2}$, с координатами

$A=\{(1,0),(0,1),(0,-1)\}$

и

$B=\{(0,0),(1,1),(1,-1)\}$

то их сумма Минковского равна

$A+B=\{(1,0),(2,1),(2,-1),(0,1),(1,2),(1,0),(0,-1),(1,0),(1,-2)\},$

который состоит из вершин шестиугольника и его центра.

Для сложения Минковского нулевой набор , $\{0\},$ содержащий только нулевой вектор 0, является единичным элементом : для каждого подмножества S векторного пространства

$S+\{0\}=S.$

Пустой набор важен для сложения Минковского, потому что пустой набор аннулирует все остальные подмножества: для каждого подмножества S векторного пространства его сумма с пустым набором пуста:

$S+\emptyset =\emptyset .$

В качестве другого примера рассмотрим суммы Минковского открытых или закрытых шаров в поле $\mathbb {K} ,$ это либо действительные числа $\mathbb {R}$ или комплексные числа $\mathbb {C} .$ Если $B_{r}:=\{s\in \mathbb {K} :|s|\leq r\}$ представляет собой закрытый шар радиуса $r\in [0,\infty ]$ сосредоточено в $0$ в $\mathbb {K}$ тогда для любого $r,s\in [0,\infty ],$ $B_{r}+B_{s}=B_{r+s}$ а также $cB_{r}=B_{|c|r}$ будет выполняться для любого скаляра $c\in \mathbb {K}$ такой, что продукт $|c|r$ определяется (что происходит, когда $c\neq 0$ или $r\neq \infty$). Если $r,s,$ и $c$ все отличны от нуля, то те же равенства сохраняли бы силу, если бы $B_{r}$ был определен как открытый шар, а не закрытый шар с центром в $0$ (необходимо ненулевое предположение, поскольку открытый шар радиуса $0$ пустое множество). Сумма Минковского закрытого шара и открытого шара есть открытый шар. В более общем смысле, сумма Минковского открытого подмножества с любым другим набором будет открытым подмножеством.

Если $G=\{(x,1/x):0\neq x\in \mathbb {R} \}$ это график ​ $f(x)={\frac {1}{x}}$ и если и $Y=\{0\}\times \mathbb {R}$ это $y$-ось в $X=\mathbb {R} ^{2}$ то сумма Минковского этих двух замкнутых подмножеств плоскости является открытым множеством. $G+Y=\{(x,y)\in \mathbb {R} ^{2}:x\neq 0\}=\mathbb {R} ^{2}\setminus Y$ состоящее из всего, кроме $y$-ось. Это показывает, что сумма Минковского двух замкнутых множеств не обязательно является замкнутым множеством. Однако сумма Минковского двух замкнутых подмножеств будет замкнутым подмножеством, если хотя бы одно из этих множеств также является компактным подмножеством .

Выпуклые оболочки сумм Минковского

Сложение Минковского хорошо ведет себя по отношению к операции взятия выпуклых оболочек , как показывает следующее предложение:

Для всех непустых подмножеств $S_{1}$ и $S_{2}$ реального векторного пространства выпуклая оболочка их суммы Минковского является суммой Минковского их выпуклых оболочек:

$\operatorname {Conv} (S_{1}+S_{2})=\operatorname {Conv} (S_{1})+\operatorname {Conv} (S_{2}).$

В более общем смысле этот результат справедлив для любого конечного набора непустых множеств:

${\textstyle \operatorname {Conv} \left(\sum {S_{n}}\right)=\sum \operatorname {Conv} (S_{n}).}$

В математической терминологии операции суммирования Минковского и формирования выпуклых оболочек являются коммутирующими операциями.

Если $S$ является выпуклым множеством, то $\mu S+\lambda S$ также является выпуклым множеством; более того

$\mu S+\lambda S=(\mu +\lambda )S$

для каждого $\mu ,\lambda \geq 0$. И наоборот, если это « распределительное свойство » справедливо для всех неотрицательных действительных чисел, $\mu ,\lambda$, то множество выпукло.

Пример невыпуклого множества такого, что $A+A\neq 2A.$

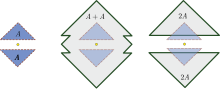
На рисунке справа показан пример невыпуклого множества, для которого $A+A\subsetneq 2A.$

Пример в $1$ размерность: $B=[1,2]\cup [4,5].$ Можно легко подсчитать, что $2B=[2,4]\cup [8,10]$ но $B+B=[2,4]\cup [5,7]\cup [8,10],$ отсюда еще раз $B+B\subsetneq 2B.$

Суммы Минковского действуют линейно на периметре двумерных выпуклых тел: периметр суммы равен сумме периметров. Кроме того, если $K$ является (внутренней частью) кривой постоянной ширины , то сумма Минковского $K$ и его $180^{\circ }$ вращение - диск. Эти два факта можно объединить, чтобы дать краткое доказательство теоремы Барбье о периметре кривых постоянной ширины.

Приложения

Сложение Минковского играет центральную роль в математической морфологии . Он возникает в «кисть и мазок» парадигме 2D компьютерной графики (с различными вариантами использования, в частности, Дональдом Э. Кнутом в Metafont ), а также как операция сплошной развертки в 3D компьютерной графике . Также было показано, что оно тесно связано с расстоянием движения землеройной машины и, как следствие, с оптимальной транспортировкой .

Планирование движения

Суммы Минковского используются при планировании движения объекта среди препятствий. Они используются для расчета конфигурационного пространства , которое представляет собой набор всех допустимых положений объекта. В простой модели поступательного движения объекта на плоскости, где положение объекта может быть однозначно задано положением неподвижной точки этого объекта, конфигурационным пространством является сумма Минковского множества препятствий и подвижных объектов. объект помещен в начало координат и повернут на 180 градусов.

Обработка с числовым программным управлением (NC)

При обработке с числовым программным управлением программирование инструмента с ЧПУ использует тот факт, что сумма Минковского режущей детали с ее траекторией задает форму разреза в материале.

3D solid modeling

В OpenSCAD суммы Минковского используются для очерчивания одной формы другой фигурой, создавая смесь обеих фигур.

Теория агрегации

Суммы Минковского также часто используются в теории агрегирования, когда отдельные объекты, подлежащие агрегированию, характеризуются через множества.

Обнаружение столкновений

Суммы Минковского, в частности разности Минковского, часто используются вместе с алгоритмами GJK для вычисления обнаружения столкновений выпуклых оболочек в физических движках .

Алгоритмы вычисления сумм Минковского

Сложение Минковского и выпуклые оболочки. Шестнадцать темно-красных точек (справа) образуют сумму Минковского четырех невыпуклых множеств (слева), каждое из которых состоит из пары красных точек. Их выпуклые оболочки (затенены розовым) содержат знаки плюс (+): правый знак плюс представляет собой сумму левых знаков плюс.

Плоский случай

Два выпуклых многоугольника на плоскости

Для двух выпуклых многоугольников P и Q на плоскости с m и n вершинами их сумма Минковского представляет собой выпуклый многоугольник с не более чем m + n вершинами и может быть вычислена за время O( m + n ) с помощью очень простой процедуры, которая может неофициально описать следующим образом. Предположим, что заданы края многоугольника и направление, скажем, против часовой стрелки, вдоль границы многоугольника. Тогда легко видеть, что эти ребра выпуклого многоугольника упорядочены по полярному углу . Объединим упорядоченные последовательности направленных ребер из P и Q в одну упорядоченную последовательность S . Представьте, что эти края представляют собой сплошные стрелки , которые можно свободно перемещать, сохраняя при этом параллельность исходному направлению. Соберите эти стрелки в порядке последовательности S, прикрепив хвост следующей стрелки к головке предыдущей стрелы. Оказывается, что полученная цепочка на самом деле будет выпуклым многоугольником, который представляет собой сумму Минковского P и Q. ломаная

Другой

Если один многоугольник выпуклый, а другой нет, сложность их суммы Минковского равна O( nm ). Если они оба невыпуклые, их сложность суммы Минковского равна O(( mn ) ² ).

Существенная сумма Минковского

Существует также понятие существенной суммы Минковского + _e двух подмножеств евклидова пространства. Обычную сумму Минковского можно записать как

$A+B=\left\{z\in \mathbb {R} ^{n}\,|\,A\cap (z-B)\neq \emptyset \right\}.$

Таким образом, существенная сумма Минковского определяется формулой

$A+_{\mathrm {e} }B=\left\{z\in \mathbb {R} ^{n}\,|\,\mu \left[A\cap (z-B)\right]>0\right\},$

где µ обозначает n - мерную меру Лебега . Причиной термина «существенный» является следующее свойство индикаторных функций : при этом

$1_{A\,+\,B}(z)=\sup _{x\,\in \,\mathbb {R} ^{n}}1_{A}(x)1_{B}(z-x),$

видно, что

$1_{A\,+_{\mathrm {e} }\,B}(z)=\mathop {\mathrm {ess\,sup} } _{x\,\in \,\mathbb {R} ^{n}}1_{A}(x)1_{B}(z-x),$

где «ess sup» обозначает существенную супремум .

л ^п сумма Минковского

Для K и L компактных выпуклых подмножеств в $\mathbb {R} ^{n}$, сумма Минковского может быть описана опорной функцией выпуклых множеств:

$h_{K+L}=h_{K}+h_{L}.$

Для p ≥ 1 Файри определил L ^п Сумма Минковского K + _p L компактных выпуклых множеств K и L в $\mathbb {R} ^{n}$ содержащий источник как

$h_{K+_{p}L}^{p}=h_{K}^{p}+h_{L}^{p}.$

По неравенству Минковского функция h _{K+ p L} снова является положительно однородной и выпуклой и, следовательно, является опорной функцией выпуклого компактного множества. Это определение является основополагающим в L ^п Теория Брунна-Минковского.

См. также

• Сумма Бляшке - многогранник, объединяющий два меньших многогранника.
• Теорема Брунна–Минковского - теорема по геометрии. Страницы, отображающие описания викиданных в качестве запасного варианта , неравенство объемов сумм Минковского.
• Свертка - интеграл, выражающий степень перекрытия одной функции при ее смещении над другой.
• Расширение - операция в математической морфологии
• Эрозия - основные операции в математической морфологии.
• Интервальная арифметика - метод ограничения ошибок численных вычислений.
• Смешанный объем (он же Quermassintegral или внутренний объем )
• Параллельная кривая
• Лемма Шепли – Фолкмана . Суммы наборов векторов почти выпуклы.
• Sumset – набор всех возможных сумм элемента набора A и элемента набора B. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Топологическое векторное пространство # Свойства - Векторное пространство с понятием близости.
• Зонотоп - выпуклый многогранник, проецируемый из гиперкуба. Страницы с краткими описаниями целей перенаправления.

Ссылки

• Эрроу, Кеннет Дж .; Хан, Фрэнк Х. (1980). Общий конкурентный анализ . Продвинутые учебники по экономике. Том. 12 (перепечатка (1971) Сан-Франциско, Калифорния: Holden-Day, Inc. Тексты по математической экономике. 6 изд.). Амстердам: Северная Голландия. ISBN  978-0-444-85497-1 . МР   0439057 .
• Гарднер, Ричард Дж. (2002), «Неравенство Брунна-Минковского», Bull. амер. Математика. Соц. (NS) , 39 (3): 355–405 (электронный), doi : 10.1090/S0273-0979-02-00941-2
• Грин, Джерри; Хеллер, Уолтер П. (1981). «1 Математический анализ и выпуклость с приложениями к экономике». В «Стреле», Кеннет Джозеф ; Интрилигатор, Майкл Д. (ред.). Справочник по математической экономике, I. том Справочники по экономике. Том. 1. Амстердам: Издательство North-Holland Publishing Co., стр. 15–52. дои : 10.1016/S1573-4382(81)01005-9 . ISBN  978-0-444-86126-9 . МР   0634800 .
• Генри Манн (1976), Теоремы сложения: Теоремы сложения теории групп и теории чисел (исправленное переиздание издания Wiley 1965 года), Хантингтон, Нью-Йорк: Издательство Роберта Э. Кригера, ISBN  978-0-88275-418-5 – через www.krieger-publishing.com/subcats/MathematicsandStatistics/mathematicsandstatistics.html.
• Рокафеллар, Р. Тиррелл (1997). Выпуклый анализ . Принстонские вехи в математике (перепечатка математической серии Принстона 1979 года, 28 изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. стр. xviii+451. ISBN  978-0-691-01586-6 . МР   1451876 .
• Натансон, Мелвин Б. (1996), Аддитивная теория чисел: обратные задачи и геометрия сумм , GTM, vol. 165, Шпрингер, Збл   0859.11003 .
• Окс, Эдуард; Шарир, Миха (2006), «Суммы Минковского монотонных и общих простых многоугольников», Discrete & Computational Geometry , 35 (2): 223–240, doi : 10.1007/s00454-005-1206-y .
• Шнайдер, Рольф (1993), Выпуклые тела: теория Брунна-Минковского , Кембридж: Издательство Кембриджского университета .
• Тао, Теренс и Ву, Ван (2006), Аддитивная комбинаторика , Издательство Кембриджского университета .
• Майер, А.; Зеленюк, В. (2014). «Агрегация индексов производительности Мальмквиста с учетом перераспределения ресурсов» . Европейский журнал операционных исследований . 238 (3): 774–785. дои : 10.1016/j.ejor.2014.04.003 .
• Зеленюк, В (2015). «Агрегация эффективности масштаба» . Европейский журнал операционных исследований . 240 (1): 269–277. дои : 10.1016/j.ejor.2014.06.038 .

Внешние ссылки

• «Сложение Минковского» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Хоу, Роджер (1979), О тенденции к выпуклости векторной суммы множеств , Дискуссионные документы Фонда Коулза, том. 538, Фонд экономических исследований Коулза , Йельский университет.
• Суммы Минковского в библиотеке алгоритмов вычислительной геометрии
• Сумма Минковского двух треугольников и Сумма Минковского диска и многоугольника Джорджа Бека, Демонстрационный проект Вольфрама .
• Дополнение Минковского выпуклых форм Александра Богомольного : апплет
• Wikibooks:Руководство пользователя OpenSCAD/Преобразования#minkowski Мариуса Кинтеля: Приложение
• Применение Минковского. Дополнение к робототехнике Джоан Джерард.
• Демонстрация аддитивности Минковского, выпуклой монотонности и других свойств расстояния Earth Movers.