Теорема Белла

Теорема Белла — это термин, охватывающий ряд тесно связанных результатов в физике , каждый из которых определяет, что квантовая механика несовместима с локальными теориями скрытых переменных , учитывая некоторые основные предположения о природе измерения. «Локальный» здесь относится к принципу локальности , идее о том, что на частицу может влиять только ее непосредственное окружение, и что взаимодействия, опосредованные физическими полями, не могут распространяться быстрее скорости света . « Скрытые переменные » — это предполагаемые свойства квантовых частиц, которые не включены в квантовую теорию, но, тем не менее, влияют на результат экспериментов. По словам физика Джона Стюарта Белла , в честь которого названо это семейство результатов: «Если [теория скрытых переменных] локальна, она не будет согласовываться с квантовой механикой, а если она согласуется с квантовой механикой, она не будет локальной. " ^[1]

Первый такой результат был представлен Беллом в 1964 году на основе парадокса Эйнштейна-Подольского-Розена , который привлек внимание к явлению квантовой запутанности . Белл пришел к выводу, что если измерения выполняются независимо на двух разделенных частицах запутанной пары, то предположение о том, что результаты зависят от скрытых переменных внутри каждой половины, подразумевает математическое ограничение на то, как коррелируют результаты двух измерений. Такое ограничение позже будет названо неравенством Белла . Затем Белл показал, что квантовая физика предсказывает корреляции, нарушающие это неравенство. В последующие годы было предложено множество вариаций теоремы Белла с использованием различных предположений и получением различных неравенств Белла (или неравенства «типа Белла»).

Первый элементарный эксперимент, предназначенный для проверки теоремы Белла, был выполнен в 1972 году Джоном Клаузером и Стюартом Фридманом . ^[2] более сложные эксперименты, известные под общим названием « тесты Белла» С тех пор много раз проводились . Часто эти эксперименты преследовали цель «закрыть лазейки», то есть улучшить проблемы планирования или постановки эксперимента, которые в принципе могли повлиять на достоверность результатов более ранних тестов Белла. Тесты Белла постоянно обнаруживают, что физические системы подчиняются квантовой механике и нарушают неравенства Белла; то есть результаты этих экспериментов несовместимы с какой-либо локальной теорией скрытых переменных. ^[3]^[4]

Точная природа предположений, необходимых для доказательства ограничения корреляций типа Белла, обсуждается физиками и философами . Хотя значение теоремы Белла не вызывает сомнений, ее полное значение для интерпретации квантовой механики остается нерешенным.

Теорема

Существует множество вариаций основной идеи, некоторые из которых основаны на более строгих математических предположениях, чем другие. ^[5] Примечательно, что теоремы типа Белла не относятся к какой-либо конкретной теории локальных скрытых переменных, а вместо этого показывают, что квантовая физика нарушает общие предположения, лежащие в основе классических картин природы. Исходная теорема, доказанная Беллом в 1964 году, не очень поддается экспериментированию, и жанр неравенств типа Белла удобно представить на более позднем примере. ^[6]

Гипотетические персонажи Алиса и Боб стоят в далеко отстоящих друг от друга местах. Их коллега Виктор готовит пару частиц и отправляет одну Алисе, а другую Бобу. Когда Алиса получает свою частицу, она решает выполнить одно из двух возможных измерений (возможно, подбрасывая монету, чтобы решить, какое именно). Обозначим эти измерения через $A_{0}$ и $A_{1}$ . Оба $A_{0}$ и $A_{1}$ двоичные измерения : результат $A_{0}$ либо $+1$ или $-1$ , и аналогично для $A_{1}$ . Когда Боб получает свою частицу, он выбирает одно из двух измерений: $B_{0}$ и $B_{1}$ , которые также являются двоичными.

Предположим, что каждое измерение обнаруживает свойство, которым уже обладала частица. Например, если Алиса решит измерить $A_{0}$ и получает результат $+1$ , то полученная ею частица имела значение $+1$ для недвижимости $a_{0}$ . ^{[примечание 1]} Рассмотрим комбинацию $a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}=(a_{0}+a_{1})b_{0}+(a_{0}-a_{1})b_{1}\,.$ Потому что оба $a_{0}$ и $a_{1}$ принять значения $\pm 1$ , то либо $a_{0}=a_{1}$ или $a_{0}=-a_{1}$ . В первом случае количество $(a_{0}-a_{1})b_{1}$ должно равняться 0, а в последнем случае $(a_{0}+a_{1})b_{0}=0$ . Таким образом, одно из слагаемых в правой части приведенного выше выражения обратится в нуль, а другое будет равно $\pm 2$ . Следовательно, если эксперимент повторяется во многих попытках, и Виктор готовит новые пары частиц, абсолютное значение среднего значения комбинации $a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}$ во всех испытаниях будет меньше или равно 2. Ни одно испытание не может измерить эту величину, поскольку Алиса и Боб могут выбрать только одно измерение каждый, но в предположении, что основные свойства существуют, среднее значение суммы равно сумма средних значений за каждый срок. Использование угловых скобок для обозначения средних значений $|\langle A_{0}B_{0}\rangle +\langle A_{0}B_{1}\rangle +\langle A_{1}B_{0}\rangle -\langle A_{1}B_{1}\rangle |\leq 2\,.$ Это неравенство Белла, а именно неравенство CHSH . ^[6]^: 115 Его вывод здесь зависит от двух предположений: во-первых, что основные физические свойства $a_{0},a_{1},b_{0},$ и $b_{1}$ существовать независимо от того, что за ними наблюдают или измеряют (иногда это называется предположением о реализме ); и во-вторых, выбор действия Алисы не может повлиять на результат Боба или наоборот (часто это называется предположением о локальности ). ^[6]^: 117

Квантовая механика может нарушать неравенство CHSH следующим образом. Виктор готовит пару кубитов , которые он описывает состоянием Белла. $|\psi \rangle ={\frac {|0\rangle \otimes |1\rangle -|1\rangle \otimes |0\rangle }{\sqrt {2}}},$ где $|0\rangle$ и $|1\rangle$ являются собственными состояниями одной из матриц Паули , $\sigma _{z}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}.$ Затем Виктор передает первый кубит Алисе, а второй Бобу. Алисой и Бобом Выбор возможных измерений также определяется в терминах матриц Паули. Алиса измеряет любую из двух наблюдаемых $\sigma _{z}$ и $\sigma _{x}$ : $A_{0}=\sigma _{z},\ A_{1}=\sigma _{x}={\begin{pmatrix}0&1\\1&0\end{pmatrix}};$ и Боб измеряет любую из двух наблюдаемых $B_{0}=-{\frac {\sigma _{x}+\sigma _{z}}{\sqrt {2}}},\ B_{1}={\frac {\sigma _{x}-\sigma _{z}}{\sqrt {2}}}.$ Виктор может вычислить значения квантового ожидания для пар этих наблюдаемых, используя правило Борна : $\langle A_{0}\otimes B_{0}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{0}\otimes B_{1}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{1}\otimes B_{0}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{1}\otimes B_{1}\rangle =-{\frac {1}{\sqrt {2}}}\,.$ Хотя за одну попытку эксперимента можно провести только одно из этих четырех измерений, сумма $\langle A_{0}\otimes B_{0}\rangle +\langle A_{0}\otimes B_{1}\rangle +\langle A_{1}\otimes B_{0}\rangle -\langle A_{1}\otimes B_{1}\rangle =2{\sqrt {2}}$ дает сумму средних значений, которые Виктор ожидает найти в нескольких испытаниях. Это значение превышает классическую верхнюю границу 2, выведенную из гипотезы локальных скрытых переменных. ^[6]^: 116 Значение $2{\sqrt {2}}$ на самом деле это самое большое значение, которое квантовая физика допускает для этой комбинации значений математического ожидания, что делает его границей Цирельсона . ^[9]^: 140

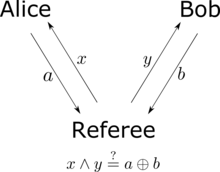
Иллюстрация игры CHSH: рефери Виктор отправляет по биту Алисе и Бобу, а Алиса и Боб отправляют по биту обратно рефери.

Неравенство CHSH также можно рассматривать как игру , в которой Алиса и Боб пытаются скоординировать свои действия . ^[10]^[11] Виктор готовит два кусочка, $x$ и $y$ независимо и случайно. Он посылает бит $x$ Алисе и немного $y$ Бобу. Алиса и Боб выиграют, если вернут биты ответа. $a$ и $b$ Виктору, удовлетворяя $xy=a+b\mod 2\,.$ Или, что то же самое, Алиса и Боб выигрывают, если выполняется логическое И из $x$ и $y$ это логическое исключающее ИЛИ $a$ и $b$ . Алиса и Боб могут согласовать любую стратегию до игры, но они не могут общаться после начала игры. В любой теории, основанной на локальных скрытых переменных, вероятность победы Алисы и Боба не превышает $3/4$ , независимо от того, о какой стратегии они договорились заранее. Однако, если они имеют запутанное квантовое состояние, их вероятность победы может быть столь же велика, как ${\frac {2+{\sqrt {2}}}{4}}\approx 0.85\,.$

Вариации и связанные результаты

Белл (1964)

В статье Белла 1964 года указывается, что при ограниченных условиях локальные модели скрытых переменных могут воспроизводить предсказания квантовой механики. Затем он демонстрирует, что это не может быть верным в целом. ^[12] Белл рассматривает усовершенствование Дэвида Бома мысленного эксперимента Эйнштейна-Подольского-Розена (ЭПР). В этом сценарии пара частиц образуется вместе таким образом, что они описываются спиновым синглетным состоянием (которое является примером запутанного состояния). Затем частицы расходятся в противоположных направлениях. Каждая частица измеряется устройством Штерна-Герлаха , измерительным инструментом, который может быть ориентирован в разных направлениях и который сообщает об одном из двух возможных результатов, которые можно представить как $+1$ и $-1$ . Конфигурация каждого измерительного прибора представлена единичным вектором , а квантовомеханический прогноз корреляции между двумя детекторами с настройками ${\vec {a}}$ и ${\vec {b}}$ является $P({\vec {a}},{\vec {b}})=-{\vec {a}}\cdot {\vec {b}}.$ В частности, если ориентация двух детекторов одинакова ( ${\vec {a}}={\vec {b}}$ ), то результат одного измерения наверняка будет отрицательным по сравнению с результатом другого, что дает $P({\vec {a}},{\vec {a}})=-1$ . А если ориентации двух детекторов ортогональны ( ${\vec {a}}\cdot {\vec {b}}=0$ ), то результаты некоррелированы, и $P({\vec {a}},{\vec {b}})=0$ . Белл на своем примере доказывает, что эти особые случаи можно объяснить с помощью скрытых переменных, а затем продолжает показывать, что весь спектр возможностей, связанных с промежуточными углами, не может быть объяснен с помощью скрытых переменных .

Белл утверждал, что локальная модель скрытых переменных для этих корреляций объяснит их с точки зрения интеграла по возможным значениям некоторого скрытого параметра. $\lambda$ : $P({\vec {a}},{\vec {b}})=\int d\lambda \,\rho (\lambda )A({\vec {a}},\lambda )B({\vec {b}},\lambda ),$ где $\rho (\lambda )$ представляет собой функцию плотности вероятности . Две функции $A({\vec {a}},\lambda )$ и $B({\vec {b}},\lambda )$ предоставьте ответы двух детекторов с учетом векторов ориентации и скрытой переменной: $A({\vec {a}},\lambda )=\pm 1,\,B({\vec {b}},\lambda )=\pm 1.$ Важно отметить, что результат детектора $A$ не зависит от ${\vec {b}}$ , а также результат $B$ не зависит от ${\vec {a}}$ , поскольку два детектора физически разделены. Теперь предположим, что у экспериментатора есть выбор настроек второго детектора: его можно установить либо на ${\vec {b}}$ или чтобы ${\vec {c}}$ . Белл доказывает, что разница в корреляции между этими двумя вариантами настройки детектора должна удовлетворять неравенству $|P({\vec {a}},{\vec {b}})-P({\vec {a}},{\vec {c}})|\leq 1+P({\vec {b}},{\vec {c}}).$ Однако легко найти ситуации, когда квантовая механика нарушает неравенство Белла. ^[13]^{: 425–426} Например, пусть векторы ${\vec {a}}$ и ${\vec {b}}$ ортогональны, и пусть ${\vec {c}}$ лежат в их плоскости под углом 45° к ним обоим. Затем $P({\vec {a}},{\vec {b}})=0,$ пока $P({\vec {a}},{\vec {c}})=P({\vec {b}},{\vec {c}})=-{\frac {\sqrt {2}}{2}},$ но ${\frac {\sqrt {2}}{2}}\nleq 1-{\frac {\sqrt {2}}{2}}.$ Следовательно, не существует локальной модели со скрытыми переменными, которая могла бы воспроизвести предсказания квантовой механики для всех вариантов выбора. ${\vec {a}}$ , ${\vec {b}}$ , и ${\vec {c}}.$ Экспериментальные результаты противоречат классическим кривым и соответствуют кривой, предсказанной квантовой механикой, если учитывать экспериментальные недостатки. ^[5]

Теорема Белла 1964 года требует возможности идеальных антикорреляций: способности делать прогноз с вероятностью 1 о результате второго детектора, зная результат первого. Это связано с «ЭПР-критерием реальности», концепцией, введенной в статье 1935 года Эйнштейном, Подольским и Розеном. В этой статье утверждается: «Если, никоим образом не нарушая систему, мы можем предсказать с уверенностью (т. е. с вероятностью, равной единице) значение физической величины, то существует элемент реальности, соответствующий этой величине». ^[14]

GHZ – Мермин (1990)

Дэниел Гринбергер , Майкл А. Хорн и Антон Зейлингер в 1990 году представили мысленный эксперимент с четырьмя частицами, который Дэвид Мермин затем упростил, чтобы использовать только три частицы. ^[15]^[16] В этом мысленном эксперименте Виктор генерирует набор из трех частиц со спином 1/2, описываемых квантовым состоянием. $|\psi \rangle ={\frac {1}{\sqrt {2}}}(|000\rangle -|111\rangle )\,,$ где, как указано выше, $|0\rangle$ и $|1\rangle$ — собственные векторы матрицы Паули $\sigma _{z}$ . Затем Виктор отправляет по частице Алисе, Бобу и Чарли, которые ждут в далеко отстоящих друг от друга местах. Алиса измеряет либо $\sigma _{x}$ или $\sigma _{y}$ на ее частице, как и Боб и Чарли. Результатом каждого измерения является либо $+1$ или $-1$ . Применение правила Борна к трехкубитному состоянию $|\psi \rangle$ Виктор предсказывает, что всякий раз, когда три измерения включают одно $\sigma _{x}$ и два $\sigma _{y}$ , продукт результатов всегда будет $+1$ . Это следует из того, что $|\psi \rangle$ является собственным вектором $\sigma _{x}\otimes \sigma _{y}\otimes \sigma _{y}$ с собственным значением $+1$ , и аналогично для $\sigma _{y}\otimes \sigma _{x}\otimes \sigma _{y}$ и $\sigma _{y}\otimes \sigma _{y}\otimes \sigma _{x}$ . Следовательно, зная результат Алисы для $\sigma _{x}$ измерение и результат Боба для $\sigma _{y}$ измерения Виктор может предсказать с вероятностью 1, какой результат получит Чарли за $\sigma _{y}$ измерение. Согласно критерию реальности ЭПР, существует «элемент реальности», соответствующий результату $\sigma _{y}$ измерение кубита Чарли. Действительно, та же самая логика применима как к измерениям, так и ко всем трем кубитам. Таким образом, согласно критерию реальности ЭПР, каждая частица содержит «набор инструкций», который определяет результат $\sigma _{x}$ или $\sigma _{y}$ измерение на нем. Тогда набор всех трех частиц будет описываться набором команд $(a_{x},a_{y},b_{x},b_{y},c_{x},c_{y})\,,$ при этом каждая запись является либо $-1$ или $+1$ и каждый $\sigma _{x}$ или $\sigma _{y}$ измерение просто возвращает соответствующее значение.

Если Алиса, Боб и Чарли выполняют $\sigma _{x}$ измерения, то произведение их результатов будет $a_{x}b_{x}c_{x}$ . Это значение можно вывести из $(a_{x}b_{y}c_{y})(a_{y}b_{x}c_{y})(a_{y}b_{y}c_{x})=a_{x}b_{x}c_{x}a_{y}^{2}b_{y}^{2}c_{y}^{2}=a_{x}b_{x}c_{x}\,,$ потому что квадрат любого $-1$ или $+1$ является $1$ . Каждый множитель в скобках равен $+1$ , так $a_{x}b_{x}c_{x}=+1\,,$ и произведение результатов Алисы, Боба и Чарли будет $+1$ с вероятностью единица. Но это несовместимо с квантовой физикой: Виктор может предсказать, используя состояние $|\psi \rangle$ что измерение $\sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}$ вместо этого даст $-1$ с вероятностью единица.

Этот мысленный эксперимент также можно преобразовать в традиционное неравенство Белла или, что то же самое, в нелокальную игру в том же духе, что и игра CHSH. ^[17] В нем Алиса, Боб и Чарли получают биты. $x,y,z$ от Виктора обещал, что их всегда будет четное количество, т.е. $x\oplus y\oplus z=0$ и отправить ему обратно биты $a,b,c$ . Они выиграют игру, если $a,b,c$ иметь нечетное количество единиц для всех входов, кроме $x=y=z=0$ , когда их должно быть четное количество. То есть они выигрывают игру тогда и только тогда, когда $a\oplus b\oplus c=x\lor y\lor z$ . С локальными скрытыми переменными наибольшая вероятность победы составляет 3/4, тогда как, используя описанную выше квантовую стратегию, они выигрывают с уверенностью. Это пример квантовой псевдотелепатии .

Теорема Кука – Спекера (1967)

В квантовой теории ортонормированные основы гильбертова пространства представляют собой измерения, которые можно выполнить в системе, имеющей это гильбертово пространство. Каждый вектор в базисе представляет собой возможный результат этого измерения. ^{[примечание 2]} Предположим, что скрытая переменная $\lambda$ существует, так что, зная ценность $\lambda$ подразумевает уверенность в результате любого измерения. Учитывая значение $\lambda$ , каждый результат измерения, то есть каждый вектор в гильбертовом пространстве, либо невозможен , либо гарантирован. Конфигурация Кохена-Спкера представляет собой конечный набор векторов, состоящих из нескольких взаимосвязанных базисов, со свойством, что вектор в нем всегда будет невозможен, если рассматривать его как принадлежащий одному базису, и гарантированно, если считать его принадлежащим другому. Другими словами, конфигурация Кохена – Спекера представляет собой «неокрашиваемый набор», который демонстрирует непоследовательность предположения о скрытой переменной. $\lambda$ можно контролировать результаты измерений. ^[22]^{: 196–201}

Теорема о свободе воли

Аргументы типа Кохена – Спекера, использующие конфигурации взаимосвязанных оснований, можно объединить с идеей измерения запутанных пар, которая лежит в основе неравенств типа Белла. Это было отмечено еще в 1970-х годах Кохеном, ^[23] Хейвуд и Рыжая, ^[24] Лестница, ^[25] и Браун и Светличный. ^[26] Как отметил ЭПР, получение результата измерения на одной половине запутанной пары подразумевает уверенность в результате соответствующего измерения на другой половине. «ЭПР-критерий реальности» утверждает, что, поскольку вторая половина пары не была нарушена, эта уверенность должна быть обусловлена принадлежащим ей физическим свойством. ^[27] Другими словами, по этому критерию скрытая переменная $\lambda$ должно существовать в пределах второй, еще не измеренной половины пары. Никакого противоречия не возникает, если рассматривать только одно измерение на первой половине. Однако если у наблюдателя есть выбор из нескольких возможных измерений, а векторы, определяющие эти измерения, образуют конфигурацию Кохена – Спекера, то некоторый результат второй половины будет одновременно невозможен и гарантирован.

Этот тип аргумента привлек внимание, когда его пример был выдвинут Джоном Конвеем и Саймоном Кохеном под названием «Теорема о свободе воли» . ^[28]^[29]^[30] Теорема Конвея-Кохена использует пару запутанных кутритов и конфигурацию Кохена-Спкера, открытую Ашером Пересом . ^[31]

Квазиклассическая запутанность

Как отметил Белл, некоторые предсказания квантовой механики могут быть воспроизведены в локальных моделях скрытых переменных, включая особые случаи корреляций, возникающих в результате запутанности. Эта тема систематически изучалась со времени появления теоремы Белла. В 1989 году Рейнхард Вернер представил то, что сейчас называется состояниями Вернера , — совместные квантовые состояния для пары систем, которые дают корреляции типа ЭПР, но также допускают модель со скрытыми переменными. ^[32] Состояния Вернера — это двудольные квантовые состояния, инвариантные относительно унитарной формы симметричного тензорного произведения : $\rho _{AB}=(U\otimes U)\rho _{AB}(U^{\dagger }\otimes U^{\dagger }).$ В 2004 году Роберт Спеккенс представил игрушечную модель , которая начинается с предпосылки о локальных дискретных степенях свободы, а затем вводит «принцип баланса знаний», который ограничивает то, как много наблюдатель может знать об этих степенях свободы, тем самым превращая их в скрытые переменные. . Разрешенные состояния знаний («эпистемические состояния») об основных переменных («онтические состояния») имитируют некоторые особенности квантовых состояний. Корреляции в игрушечной модели могут имитировать некоторые аспекты запутанности, например моногамию , но по своей конструкции игрушечная модель никогда не может нарушать неравенство Белла. ^[33]^[34]

История

Фон

Вопрос о том, может ли квантовая механика быть «дополненной» скрытыми переменными, возник еще в первые годы существования квантовой теории. В своем учебнике по квантовой механике 1932 года эрудит венгерского происхождения Джон фон Нейман представил, как он утверждал, доказательство того, что не может быть никаких «скрытых параметров». Справедливость и окончательность доказательства фон Неймана были подвергнуты сомнению Гансом Райхенбахом , более подробно Гретой Германн и, возможно, в беседе, но не в печати, Альбертом Эйнштейном. ^{[примечание 3]} ( Саймон Кохен и Эрнст Шпекер отвергли ключевое предположение фон Неймана еще в 1961 году, но не публиковали его критику до 1967 года. ^[40])

Эйнштейн настойчиво утверждал, что квантовая механика не может быть законченной теорией. Его предпочтительный аргумент основывался на принципе локальности:

Рассмотрим механическую систему, состоящую из двух частичных систем A и B , которые взаимодействуют друг с другом только в течение ограниченного времени. Пусть задана функция ψ до их взаимодействия. Тогда уравнение Шредингера даст функцию ψ после того, как произойдет их взаимодействие. Определим теперь физическое состояние частичной системы А как можно полнее путем измерений. Тогда квантовая механика позволяет нам определить ψ-функцию частичной системы B на основе проведенных измерений и ψ-функцию всей системы. Однако это определение дает результат, который зависит от того, какая из определяющих величин, определяющих состояние А, была измерена (например, координаты или импульсы). Поскольку после взаимодействия может существовать только одно физическое состояние B , которое нельзя разумно рассматривать как зависящее от конкретного измерения, которое мы выполняем в системе A, отделенной от B, можно заключить, что функция ψ не скоординирована однозначно с физическим состоянием. состояние. Это согласование нескольких ψ-функций при одном и том же физическом состоянии системы. B еще раз показывает, что функцию ψ нельзя интерпретировать как (полное) описание физического состояния единичной системы. ^[41]

Мысленный эксперимент ЭПР аналогичен, в нем также рассматриваются две отдельные системы A и B, описываемые совместной волновой функцией. Однако статья ЭПР добавляет идею, позже известную как ЭПР-критерий реальности, согласно которой способность предсказывать с вероятностью 1 результат измерения B подразумевает существование «элемента реальности» внутри B . ^[42]

В 1951 году Дэвид Бом предложил вариант мысленного эксперимента ЭПР, в котором измерения имеют дискретные диапазоны возможных результатов, в отличие от измерений положения и импульса, рассматриваемых ЭПР. ^[43] Годом ранее Чиен-Шиунг Ву и Ирвинг Шакнов успешно измерили поляризацию фотонов, образующихся в запутанных парах, что сделало версию мысленного эксперимента Бома практически осуществимой. ^[44]

К концу 1940-х годов математик Джордж Макки заинтересовался основами квантовой физики, и в 1957 году он составил список постулатов, которые он считал точным определением квантовой механики. ^[45] Макки предположил, что один из постулатов является избыточным, и вскоре после этого Эндрю М. Глисон доказал, что его действительно можно вывести из других постулатов. ^[46]^[47] Теорема Глисона предоставила аргумент в пользу того, что широкий класс теорий скрытых переменных несовместим с квантовой механикой. ^{[примечание 4]} Более конкретно, теорема Глисона исключает модели со скрытыми переменными, которые являются «неконтекстуальными». Любая модель скрытых переменных для квантовой механики должна, чтобы избежать следствий теоремы Глисона, включать скрытые переменные, которые не являются свойствами, принадлежащими только измеряемой системе, но также зависят от внешнего контекста, в котором производятся измерения. Этот тип зависимости часто рассматривается как надуманный или нежелательный; в некоторых случаях это несовместимо со специальной теорией относительности . ^[49]^[50] Теорема Кохена – Спекера уточняет это утверждение, создавая конкретное конечное подмножество лучей, на котором не может быть определена такая вероятностная мера. ^[49]^[51]

Цунг-Дао Ли был близок к выводу теоремы Белла в 1960 году. Он рассмотрел события, в которых рождались два каона, движущиеся в противоположных направлениях, и пришел к выводу, что скрытые переменные не могут объяснить корреляции, которые можно было получить в таких ситуациях. Однако возникли сложности из-за того, что каоны распадаются, и он не дошел до вывода неравенства типа Белла. ^{[примечание 5]}

Публикации Белла

Белл решил опубликовать свою теорему в сравнительно малоизвестном журнале, потому что она не требовала платы за страницу , фактически платя авторам, которые публиковались там в то время. Однако, поскольку журнал не предоставлял авторам бесплатные перепечатки статей для распространения, Беллу пришлось потратить полученные деньги на покупку копий, которые он мог бы отправить другим физикам. ^[52] Хотя в самих статьях, напечатанных в журнале, название издания было указано просто « Физика» , на обложках была трехъязычная версия «Физика Физика Физика», чтобы указать, что статьи будут печатать на английском, французском и русском языках. ^[39]^{: 92–100, 289}

Прежде чем доказать свой результат 1964 года, Белл также доказал результат, эквивалентный теореме Кохена-Спкера (поэтому последнюю иногда также называют теоремой Белла-Кохена-Спкера или теоремой Белла-КС). Однако публикация этой теоремы была случайно отложена до 1966 года. ^[49]^[53] В этой статье Белл утверждал, что, поскольку объяснение квантовых явлений с помощью скрытых переменных потребует нелокальности, парадокс ЭПР «разрешается так, как Эйнштейну меньше всего хотелось бы». ^[53]

Эксперименты

**Схема «двухканального» теста Белла**
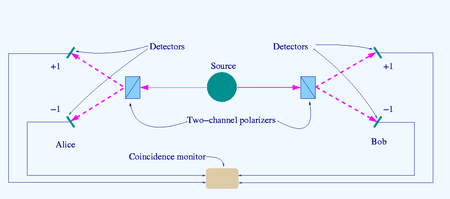
Источник S производит пары «фотонов», посланных в противоположных направлениях. Каждый фотон сталкивается с двухканальным поляризатором, ориентацию которого (a или b) может задать экспериментатор. Появляющиеся сигналы из каждого канала обнаруживаются и совпадения четырех типов (++, −−, +− и −+) подсчитываются монитором совпадений.

В 1967 году необычное название « Физика, телосложение, физика» привлекло внимание Джона Клаузера , который затем обнаружил статью Белла и начал обдумывать, как провести тест Белла в лаборатории. ^[54] Клаузер и Стюарт Фридман провели тест Белла в 1972 году. ^[55]^[56] Это был лишь ограниченный тест, поскольку выбор настроек детектора производился до того, как фотоны покинули источник. В 1982 году Ален Аспект и его коллеги провели первый тест Белла, чтобы устранить это ограничение. ^[57] Это положило начало тенденции к все более строгим тестам Белла. Мысленный эксперимент GHZ был реализован на практике с использованием запутанных тройек фотонов в 2000 году. ^[58] К 2002 году проверка неравенства CHSH стала возможной на лабораторных курсах бакалавриата. ^[59]

В тестах Белла могут возникнуть проблемы с планированием или постановкой эксперимента, которые влияют на достоверность экспериментальных результатов. Эти проблемы часто называют «лазейками». Цель эксперимента — проверить, можно ли описать природу с помощью локальной теории скрытых переменных , которая противоречила бы предсказаниям квантовой механики.

Наиболее распространенными лазейками в реальных экспериментах являются лазейки обнаружения и локализации . ^[60] Лазейка для обнаружения открывается, когда в эксперименте обнаруживается небольшая часть частиц (обычно фотонов), что позволяет объяснить данные с помощью локальных скрытых переменных, предполагая, что обнаруженные частицы представляют собой нерепрезентативную выборку. Лазейка в отношении локальности открывается, когда обнаружения не выполняются с пространственным разделением , что позволяет результату одного измерения влиять на другое, не противореча теории относительности. В некоторых экспериментах могут быть дополнительные дефекты, которые делают возможным объяснение нарушений теста Белла с помощью локальных скрытых переменных. ^[61]

Хотя в разных экспериментах были закрыты как лазейки для определения местоположения, так и для обнаружения, давняя проблема заключалась в том, чтобы закрыть обе лазейки одновременно в одном и том же эксперименте. Наконец, это было достигнуто в трех экспериментах в 2015 году. ^[62]^[63]^[64]^[65]^[66]Что касается этих результатов, Ален Аспект пишет, что «ни один эксперимент... нельзя назвать полностью свободным от лазеек», но он говорит, что эксперименты «устраняют последние сомнения в том, что нам следует отказаться» от локальных скрытых переменных, и ссылается на примеры оставшихся лазейки как «надуманные» и «чуждые обычному способу рассуждения в физике». ^[67]

Эти попытки экспериментально подтвердить нарушения неравенств Белла позже привели к тому, что Клаузер, Аспект и Антон Цайлингер были удостоены Нобелевской премии по физике 2022 года . ^[68]

Интерпретации

Реакции на теорему Белла были многочисленными и разнообразными. Максимилиан Шлоссхауэр, Йоханнес Кофлер и Цайлингер пишут, что неравенства Белла представляют собой «прекрасный пример того, как мы можем получить строгий теоретический результат, проверенный многочисленными экспериментами, и при этом не согласиться с выводами». ^[69]

Копенгагенская интерпретация

Интерпретации копенгагенского типа обычно рассматривают нарушение неравенств Белла как основание для отклонения предположения, часто называемого контрфактической определенностью или «реализмом», что не обязательно означает отказ от реализма в более широком философском смысле. ^[70]^[71] Например, Ролан Омнес выступает за отказ от скрытых переменных и заключает, что «квантовая механика, вероятно, настолько же реалистична, насколько когда-либо будет реалистична любая теория ее масштаба и зрелости». ^[72]^: 531 Точно так же Рудольф Пайерлс понял, что суть теоремы Белла заключается в том, что, поскольку предпосылка локальности физически разумна, «скрытые переменные не могут быть введены без отказа от некоторых результатов квантовой механики». ^[73]^[74]

По этому же пути идут интерпретации, восходящие к копенгагенской традиции, такие как последовательные истории (часто рекламируемые как «Копенгаген сделан правильно»), ^[75]^{: 2839} а также кбизм . ^[76]

Многомировая интерпретация квантовой механики

Интерпретация многих миров , также известная как интерпретация Эверетта , является динамически локальной, то есть не требует действий на расстоянии . ^[77]^: 17 и детерминированный, потому что он представляет собой единую часть квантовой механики без коллапса. Он может генерировать корреляции, нарушающие неравенство Белла, поскольку нарушает неявное предположение Белла о том, что измерения имеют единственный результат. Фактически, теорема Белла может быть доказана в рамках многомировой модели, исходя из предположения, что измерение имеет единственный результат. Следовательно, нарушение неравенства Белла можно интерпретировать как демонстрацию того, что измерения имеют несколько результатов. ^[78]

Объяснение корреляций Белла состоит в том, что когда Алиса и Боб проводят измерения, они разделяются на локальные ветви. С точки зрения каждой копии Алисы существует множество копий Боба, получающих разные результаты, поэтому у Боба не может быть определенного результата, и то же самое верно с точки зрения каждой копии Боба. Они получат взаимно четко определенный результат только тогда, когда их будущие световые конусы перекроются. На этом этапе можно сказать, что корреляция Белла начинает существовать, но она возникла по чисто локальному механизму. Поэтому нарушение неравенства Белла нельзя интерпретировать как доказательство нелокальности. ^[77]^{: 28}

Нелокальные скрытые переменные

Большинство сторонников идеи скрытых переменных считают, что эксперименты исключили локальные скрытые переменные. ^{[примечание 6]} Они готовы отказаться от локальности, объясняя нарушение неравенства Белла средствами нелокальной теории скрытых переменных , в которой частицы обмениваются информацией о своих состояниях. Это основа интерпретации Бома квантовой механики, которая требует, чтобы все частицы во Вселенной были способны мгновенно обмениваться информацией со всеми остальными. Одной из задач нелокальных теорий скрытых переменных является объяснение, почему эта мгновенная связь может существовать на уровне скрытых переменных, но ее нельзя использовать для отправки сигналов. ^[81] Эксперимент 2007 года исключил большой класс небомовских нелокальных теорий скрытых переменных, но не саму бомовскую механику. ^[82]

Транзакционная интерпретация , постулирующая волны, распространяющиеся как назад, так и вперед во времени, также нелокальна. ^[83]

Супердетерминизм

Необходимым предположением для вывода теоремы Белла является то, что скрытые переменные не коррелируют с настройками измерения. Это предположение было оправдано тем, что экспериментатор имеет « свободную волю » выбирать настройки и что в первую очередь необходимо заниматься наукой. (Гипотетическая) теория, в которой выбор измерения обязательно коррелирует с измеряемой системой, известна как супердетерминированная . ^[60]

Некоторые сторонники детерминистских моделей не отказались от локальных скрытых переменных. Например, Жерар 'т Хофт утверждал, что супердетерминизм нельзя отвергать. ^[84]

См. также

Примечания

^ Для удобства мы предполагаем, что реакция детектора на основное свойство является детерминированной. Это предположение можно заменить; это эквивалентно постулированию совместного распределения вероятностей по всем наблюдаемым эксперимента. ^[7]^[8]
^ Более подробно, как разработал Поль Дирак , ^[18] Дэвид Хилберт , ^[19] Джон фон Нейман , ^[20] и Герман Вейль , ^[21] состояние квантовомеханической системы является вектором $|\psi \rangle$ принадлежащий ( сепарабельному ) гильбертовому пространству ${\mathcal {H}}$ . Интересующие физические величины — положение, импульс, энергия, спин — представлены «наблюдаемыми», которые представляют собой самосопряженные линейные операторы , действующие в гильбертовом пространстве. Когда измеряется наблюдаемая величина, результатом будет одно из ее собственных значений с вероятностью, определяемой правилом Борна : в простейшем случае собственное значение $\eta$ невырожден, а вероятность определяется выражением $|\langle \eta |\psi \rangle |^{2}$ , где $|\eta \rangle$ является связанным с ним собственным вектором. В более общем смысле собственное значение вырождено, а вероятность определяется выражением $\langle \psi |P_{\eta }\psi \rangle$ , где $P_{\eta }$ является проектором на связанное с ним собственное пространство. Для целей данного обсуждения мы можем считать собственные значения невырожденными.
^ См. Райхенбах. ^[35] и Джаммер, ^[36]^: 276 Мермин и Шак, ^[37] а за замечания Эйнштейна Клаузер и Шимони ^[38] и Вик. ^[39]^: 286
^ теория скрытых переменных Детерминированная подразумевает, что вероятность данного результата всегда равна 0 или 1. Например, измерение Штерна-Герлаха на атоме со спином 1 покажет, что угловой момент атома вдоль выбранной оси равен одно из трех возможных значений, которое можно обозначить $-$ , $0$ и $+$ . В детерминированной теории скрытых переменных существует основное физическое свойство, которое фиксирует результат, полученный при измерении. В зависимости от ценности лежащего в основе физического свойства любой данный результат (например, результат $+$ ) должно быть либо невозможно, либо гарантировано. Но из теоремы Глисона следует, что такой детерминированной вероятностной меры не может быть, поскольку она доказывает, что любая вероятностная мера должна принимать форму отображения $u\to \langle \rho u,u\rangle$ для некоторого оператора плотности $\rho$ . Это отображение непрерывно на единичной сфере гильбертова пространства, и поскольку эта единичная сфера связна , никакая непрерывная вероятностная мера на ней не может быть детерминированной. ^[48]^: §1.3
^ Об этом сообщил Макс Джаммер . ^[36]^: 308 Ли наиболее известен своим совместно с Чэнь-Нин Яном предсказанием о нарушении сохранения четности, предсказанием, которое принесло им Нобелевскую премию после того, как оно было подтверждено Цзянь-Шюн Ву , который не участвовал в премии.
^ ET Джейнс был одним исключением, ^[79] но аргументы Джейнса в целом не были признаны убедительными. ^[80]

Ссылки

^ Белл, Джон С. (1987). Выразимое и невыразимое в квантовой механике . Издательство Кембриджского университета. п. 65. ИСБН 9780521368698 . ОСЛК 15053677 .
^ «Нобелевская премия по физике 2022» . Нобелевская премия (Пресс-релиз). Шведская королевская академия наук . 4 октября 2022 г. . Проверено 6 октября 2022 г.
^ Сотрудничество BIG Bell Test (9 мая 2018 г.). «Вызов местному реализму с помощью человеческого выбора». Природа . 557 (7704): 212–216. arXiv : 1805.04431 . Бибкод : 2018Natur.557..212B . дои : 10.1038/s41586-018-0085-3 . ПМИД 29743691 . S2CID 13665914 .
^ Волчовер, Натали (07 февраля 2017 г.). «Эксперимент подтверждает квантовую странность» . Журнал Кванта . Проверено 08 февраля 2020 г.
↑ Перейти обратно: Перейти обратно: ^а ^б Шимони, Эбнер . «Теорема Белла» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д Нильсен, Майкл А .; Чуанг, Исаак Л. (2010). Квантовые вычисления и квантовая информация (2-е изд.). Кембридж: Издательство Кембриджского университета. ISBN 978-1-107-00217-3 . OCLC 844974180 .
^ Хорошо, Артур (1 февраля 1982 г.). «Скрытые переменные, совместная вероятность и неравенства Белла» . Письма о физических отзывах . 48 (5): 291–295. Бибкод : 1982PhRvL..48..291F . doi : 10.1103/PhysRevLett.48.291 . ISSN 0031-9007 .
^ Браунштейн, Сэмюэл Л.; Кейвс, Карлтон М. (август 1990 г.). «Выявление лучшего неравенства Белла». Анналы физики . 202 (1): 22–56. Бибкод : 1990АнФиз.202...22Б . дои : 10.1016/0003-4916(90)90339-П .
^ Рау, Йохен (2021). Квантовая теория: подход к обработке информации . Издательство Оксфордского университета. ISBN 978-0-192-65027-6 . OCLC 1256446911 .
^ Умный . ; Хойер, П.; Тонер, Б.; Уотрус, Дж. (2004). «Последствия и пределы нелокальных стратегий». Слушания. 19-я ежегодная конференция IEEE по сложности вычислений, 2004 г. ИИЭЭ . стр. 236–249. arXiv : Quant-ph/0404076 . Бибкод : 2004quant.ph..4076C . дои : 10.1109/CCC.2004.1313847 . ISBN 0-7695-2120-7 . OCLC 55954993 . S2CID 8077237 .
^ Барнум, Х.; Бейги, С.; Бойшо, С.; Эллиотт, МБ; Венер, С. (6 апреля 2010 г.). «Локальное квантовое измерение и отсутствие сигналов подразумевают квантовые корреляции». Письма о физических отзывах . 104 (14): 140401. arXiv : 0910.3952 . Бибкод : 2010PhRvL.104n0401B . doi : 10.1103/PhysRevLett.104.140401 . ISSN 0031-9007 . ПМИД 20481921 . S2CID 17298392 .
^ Белл, Дж. С. (1964). «О парадоксе Эйнштейна-Подольского-Розена» (PDF) . Физика Телосложение Физика . 1 (3): 195–200. doi : 10.1103/PhysicsPhysiqueFizika.1.195 .
^ Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику (2-е изд.). Река Аппер-Сэддл, Нью-Джерси: Пирсон Прентис Холл. ISBN 0-13-111892-7 . OCLC 53926857 .
^ Эйнштейн, А .; Подольский, Б. ; Розен, Н. (15 мая 1935 г.). «Можно ли квантово-механическое описание физической реальности считать полным?» . Физический обзор . 47 (10): 777–780. Бибкод : 1935PhRv...47..777E . дои : 10.1103/PhysRev.47.777 .
^ Гринбергер, Д .; Хорн, М .; Шимони, А. ; Цайлингер, А. (1990). «Теорема Белла без неравенств» . Американский журнал физики . 58 (12): 1131. Бибкод : 1990AmJPh..58.1131G . дои : 10.1119/1.16243 .
^ Мермин, Н. Дэвид (1990). «Возвращение к квантовым тайнам». Американский журнал физики . 58 (8): 731–734. Бибкод : 1990AmJPh..58..731M . дои : 10.1119/1.16503 .
^ Брассар, Жиль ; Бродбент, Энн ; Тапп, Ален (2005). «Переработка многопользовательской игры Мермина в рамки псевдотелепатии». Квантовая информация и вычисления . 5 (7): 538–550. arXiv : Quant-ph/0408052 . Бибкод : 2004quant.ph..8052B . дои : 10.26421/QIC5.7-2 .
^ Дирак, Поль Адриен Морис (1930). Принципы квантовой механики . Оксфорд: Кларендон Пресс.
^ Гильберт, Дэвид (2009). Зауэр, Тилман; Майер, Ульрих (ред.). Лекции по основам физики 1915–1927: теория относительности, квантовая теория и эпистемология . Спрингер. дои : 10.1007/b12915 . ISBN 978-3-540-20606-4 . OCLC 463777694 .
^ фон Нейман, Джон (1932). Математические основы квантовой механики . Берлин: Шпрингер. Английский перевод: Математические основы квантовой механики . Перевод Бейера, Издательство Роберта Т. Принстонского университета. 1955.
^ Вейль, Герман (1950) [1931]. Теория групп и квантовая механика . Перевод Робертсона, HP Dover. ISBN 978-0-486-60269-1 . В переводе с немецкого Теория групп и квантовая механика (2-е изд.). С. Хирзель Верлаг [ де ] . 1931 год.
^ Перес, Ашер (1993). Квантовая теория: концепции и методы . Клювер . ISBN 0-7923-2549-4 . ОСЛК 28854083 .
^ Рыжий, Майкл ; Браун, Харви (1 июля 1991 г.). «Нелокальность в квантовой механике». Труды Аристотелевского общества, дополнительные тома . 65 (1): 119–160. дои : 10.1093/аристотелиансупп/65.1.119 . ISSN 0309-7013 . JSTOR 4106773 . К аналогичному подходу независимо пришел Саймон Кохен, хотя он никогда не публиковался (частное сообщение).
^ Хейвуд, Питер; Рыжий, Майкл Л.Г. (май 1983 г.). «Нелокальность и парадокс Кохена – Спекера». Основы физики . 13 (5): 481–499. Бибкод : 1983FoPh...13..481H . дои : 10.1007/BF00729511 . ISSN 0015-9018 . S2CID 120340929 .
^ Лестница, Аллен (декабрь 1983 г.). «Квантовая логика, реализм и определенность ценностей». Философия науки . 50 (4): 578–602. дои : 10.1086/289140 . ISSN 0031-8248 . S2CID 122885859 .
^ Браун, HR ; Светличный, Г. (ноябрь 1990 г.). «Нелокальность и лемма Глисона. Часть I. Детерминистические теории». Основы физики . 20 (11): 1379–1387. Бибкод : 1990FoPh...20.1379B . дои : 10.1007/BF01883492 . ISSN 0015-9018 . S2CID 122868901 .
^ Глик, Дэвид; Боге, Флориан Дж. (22 октября 2019 г.). «Является ли критерий реальности аналитическим?». Эркеннтнис . 86 (6): 1445–1451. arXiv : 1909.11893 . Бибкод : 2019arXiv190911893G . дои : 10.1007/s10670-019-00163-w . ISSN 0165-0106 . S2CID 202889160 .
^ Конвей, Джон ; Кохен, Саймон (2006). «Теорема свободы воли». Основы физики . 36 (10): 1441. arXiv : quant-ph/0604079 . Бибкод : 2006FoPh...36.1441C . дои : 10.1007/s10701-006-9068-6 . S2CID 12999337 .
^ Ремейер, Джули (15 августа 2008 г.). «Есть ли у субатомных частиц свободная воля?» . Новости науки . Проверено 23 апреля 2022 г.
^ Томас, Рэйчел (27 декабря 2011 г.). «Джон Конвей – открытие свободы воли (часть I)» . Плюс журнал . Проверено 23 апреля 2022 г.
^ Конвей, Джон Х .; Кохен, Саймон (2009). «Сильная теорема о свободе воли» (PDF) . Уведомления АМС . 56 (2): 226–232.
^ Вернер, Рейнхард Ф. (1 октября 1989 г.). «Квантовые состояния с корреляциями Эйнштейна – Подольского – Розена, допускающие модель скрытой переменной». Физический обзор А. 40 (8): 4277–4281. Бибкод : 1989PhRvA..40.4277W . дои : 10.1103/PhysRevA.40.4277 . ISSN 0556-2791 . ПМИД 9902666 .
^ Спеккенс, Роберт В. (19 марта 2007 г.). «Доказательства эпистемического взгляда на квантовые состояния: игрушечная теория». Физический обзор А. 75 (3): 032110. arXiv : quant-ph/0401052 . Бибкод : 2007PhRvA..75c2110S . дои : 10.1103/PhysRevA.75.032110 . ISSN 1050-2947 . S2CID 117284016 .
^ Катани, Лоренцо; Браун, Дэн Э. (27 июля 2017 г.). «Игрушечная модель Спеккенса во всех измерениях и ее связь со стабилизатором квантовой механики» . Новый журнал физики . 19 (7): 073035. arXiv : 1701.07801 . Бибкод : 2017NJPh...19g3035C . дои : 10.1088/1367-2630/aa781c . ISSN 1367-2630 . S2CID 119428107 .
^ Райхенбах, Ганс (1944). Философские основы квантовой механики . Издательство Калифорнийского университета. п. 14. OCLC 872622725 .
↑ Перейти обратно: Перейти обратно: ^а ^б Джаммер, Макс (1974). Философия квантовой механики . Джон Уайли и сыновья. ISBN 0-471-43958-4 .
^ Мермин, Н. Дэвид ; Шак, Рюдигер (2018). «Гомер кивнул: удивительная оплошность фон Неймана». Основы физики . 48 (9): 1007–1020. arXiv : 1805.10311 . Бибкод : 2018FoPh...48.1007M . дои : 10.1007/s10701-018-0197-5 . S2CID 118951033 .
^ Клаузер, Дж. Ф.; Шимони, А. (1978). «Теорема Белла: экспериментальные проверки и выводы» (PDF) . Отчеты о прогрессе в физике . 41 (12): 1881–1927. Бибкод : 1978РПФ...41.1881С . CiteSeerX 10.1.1.482.4728 . дои : 10.1088/0034-4885/41/12/002 . S2CID 250885175 . Архивировано (PDF) из оригинала 23 сентября 2017 г. Проверено 28 октября 2017 г.
↑ Перейти обратно: Перейти обратно: ^а ^б Уик, Дэвид (1995). «Теорема Белла». Печально известная граница: семь десятилетий ереси в квантовой физике . Нью-Йорк: Спрингер. стр. 92–100. дои : 10.1007/978-1-4612-4030-3_11 . ISBN 978-0-387-94726-6 .
^ Конвей, Джон ; Кохен, Саймон (2002). «Геометрия квантовых парадоксов». В Бертльманне, Рейнгольд А .; Цайлингер, Антон (ред.). Квантовые [не]говоримые: от Белла к квантовой информации . Берлин: Шпрингер. стр. 257–269. ISBN 3-540-42756-2 . ОСЛК 49404213 .
^ Эйнштейн, Альберт (март 1936 г.). «Физика и реальность». Журнал Института Франклина . 221 (3): 349–382. Бибкод : 1936FrInJ.221..349E . дои : 10.1016/S0016-0032(36)91047-5 .
^ Харриган, Николас; Спеккенс, Роберт В. (2010). «Эйнштейн, неполнота и эпистемический взгляд на квантовые состояния». Основы физики . 40 (2): 125. arXiv : 0706.2661 . Бибкод : 2010FoPh...40..125H . дои : 10.1007/s10701-009-9347-0 . S2CID 32755624 .
^ Бом, Дэвид (1989) [1951]. Квантовая теория (переиздание в Дувре). Прентис-Холл. стр. 614–623. ISBN 978-0-486-65969-5 . OCLC 1103789975 .
^ Ву, К.-С. ; Шахнов И. (1950). «Угловая корреляция рассеянного аннигиляционного излучения». Физический обзор . 77 (1): 136. Бибкод : 1950PhRv...77..136W . дои : 10.1103/PhysRev.77.136 .
^ Макки, Джордж В. (1957). «Квантовая механика и гильбертово пространство». Американский математический ежемесячник . 64 (8П2): 45–57. дои : 10.1080/00029890.1957.11989120 . JSTOR 2308516 .
^ Глисон, Эндрю М. (1957). «Меры на замкнутых подпространствах гильбертова пространства» . Математический журнал Университета Индианы . 6 (4): 885–893. дои : 10.1512/iumj.1957.6.56050 . МР 0096113 .
^ Чернофф, Пол Р. «Энди Глисон и квантовая механика» (PDF) . Уведомления АМС . 56 (10): 1253–1259.
^ Вилце, А. (2017). «Квантовая логика и теория вероятностей» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Мермин, Н. Дэвид (июль 1993 г.). «Скрытые переменные и две теоремы Джона Белла» (PDF) . Обзоры современной физики . 65 (3): 803–815. arXiv : 1802.10119 . Бибкод : 1993РвМП...65..803М . дои : 10.1103/RevModPhys.65.803 . S2CID 119546199 .
^ Шимони, Абнер (1984). «Контекстные теории скрытых переменных и неравенства Белла». Британский журнал философии науки . 35 (1): 25–45. дои : 10.1093/bjps/35.1.25 .
^ Перес, Ашер (1991). «Два простых доказательства теоремы Кохена-Спкера» . Журнал физики A: Математический и общий . 24 (4): Л175–Л178. Бибкод : 1991JPhA...24L.175P . дои : 10.1088/0305-4470/24/4/003 . ISSN 0305-4470 .
^ Уитакер, Эндрю (2016). Джон Стюарт Белл и физика двадцатого века: видение и целостность . Издательство Оксфордского университета. ISBN 978-0-19-874299-9 .
↑ Перейти обратно: Перейти обратно: ^а ^б Белл, Дж. С. (1966). «К проблеме скрытых переменных в квантовой механике». Обзоры современной физики . 38 (3): 447–452. Бибкод : 1966РвМП...38..447Б . дои : 10.1103/revmodphys.38.447 . ОСТИ 1444158 .
^ Кайзер, Дэвид (30 января 2012 г.). «Как хиппи спасли физику: наука, контркультура и квантовое возрождение [отрывок]» . Научный американец . Проверено 11 февраля 2020 г.
^ Фридман, С.Дж .; Клаузер, Дж. Ф. (1972). «Экспериментальная проверка локальных теорий скрытых переменных» (PDF) . Письма о физических отзывах . 28 (938): 938–941. Бибкод : 1972PhRvL..28..938F . doi : 10.1103/PhysRevLett.28.938 .
^ Фридман, Стюарт Джей (5 мая 1972 г.). Экспериментальная проверка локальных теорий скрытых переменных (PDF) (доктор философии). Калифорнийский университет, Беркли.
^ Аспект, Ален; Далибар, Жан; Роджер, Жерар (1982). «Экспериментальная проверка неравенств Белла с использованием анализаторов, изменяющихся во времени» . Письма о физических отзывах . 49 (25): 1804–7. Бибкод : 1982PhRvL..49.1804A . doi : 10.1103/PhysRevLett.49.1804 .
^ Пан, Цзянь-Вэй; Баумистер, Д.; Дэниел, М.; Вайнфуртер, Х.; Цайлингер, А. (2000). «Экспериментальная проверка квантовой нелокальности в трехфотонной ГГЦ-запутанности». Природа . 403 (6769): 515–519. Бибкод : 2000Natur.403..515P . дои : 10.1038/35000514 . ПМИД 10676953 . S2CID 4309261 .
^ Делингер, Дитрих; Митчелл, М.В. (2002). «Запутанные фотоны, нелокальность и неравенства Белла в студенческой лаборатории». Американский журнал физики . 70 (9): 903–910. arXiv : Quant-ph/0205171 . Бибкод : 2002AmJPh..70..903D . дои : 10.1119/1.1498860 . S2CID 49487096 .
↑ Перейти обратно: Перейти обратно: ^а ^б Ларссон, Ян-Оке (2014). «Лазовки в тестах неравенства Белла локального реализма». Физический журнал A: Математический и теоретический . 47 (42): 424003. arXiv : 1407.0363 . Бибкод : 2014JPhA...47P4003L . дои : 10.1088/1751-8113/47/42/424003 . S2CID 40332044 .
^ Герхардт, И.; Лю, К.; Ламас-Линарес, А.; Скаар, Дж.; Скарани, В.; и др. (2011). «Экспериментальная имитация нарушения неравенств Белла». Письма о физических отзывах . 107 (17): 170404. arXiv : 1106.3224 . Бибкод : 2011PhRvL.107q0404G . doi : 10.1103/PhysRevLett.107.170404 . ПМИД 22107491 . S2CID 16306493 .
^ Мерали, Зия (27 августа 2015 г.). «Квантовая «жуткость» прошла самое жесткое испытание» . Новости природы . 525 (7567): 14–15. Бибкод : 2015Natur.525...14M . дои : 10.1038/nature.2015.18255 . ПМИД 26333448 . S2CID 4409566 .
^ Маркофф, Джек (21 октября 2015 г.). «Прости, Эйнштейн. Квантовое исследование показало, что «жуткие действия» реальны» . Нью-Йорк Таймс . Проверено 21 октября 2015 г.
^ Хенсен, Б.; и др. (21 октября 2015 г.). «Нарушение неравенства Белла без лазеек с использованием спинов электронов, разделенных на 1,3 километра». Природа . 526 (7575): 682–686. arXiv : 1508.05949 . Бибкод : 2015Natur.526..682H . дои : 10.1038/nature15759 . ПМИД 26503041 . S2CID 205246446 .
^ Шальм, ЛК; и др. (16 декабря 2015 г.). «Сильная проверка локального реализма без лазеек» . Письма о физических отзывах . 115 (25): 250402. arXiv : 1511.03189 . Бибкод : 2015PhRvL.115y0402S . doi : 10.1103/PhysRevLett.115.250402 . ПМЦ 5815856 . ПМИД 26722906 .
^ Джустина, М.; и др. (16 декабря 2015 г.). «Проверка теоремы Белла со запутанными фотонами без существенных лазеек». Письма о физических отзывах . 115 (25): 250401. arXiv : 1511.03190 . Бибкод : 2015PhRvL.115y0401G . doi : 10.1103/PhysRevLett.115.250401 . ПМИД 26722905 . S2CID 13789503 .
^ Аспект, Ален (16 декабря 2015 г.). «Закрывая дверь к квантовым дебатам Эйнштейна и Бора» . Физика . 8 : 123. Бибкод : 2015PhyOJ...8..123A . дои : 10.1103/Физика.8.123 .
^ Аландер, Йохан; Бургер, Людвиг; Поллард, Никлас (04 октября 2022 г.). «Нобелевская премия по физике достаётся исследователям «жуткой» квантовой науки» . Рейтер . Проверено 4 октября 2022 г.
^ Шлоссауэр, Максимилиан; Кофлер, Йоханнес; Цайлингер, Антон (6 января 2013 г.). «Снимок фундаментального отношения к квантовой механике». Исследования по истории и философии науки. Часть B: Исследования по истории и философии современной физики . 44 (3): 222–230. arXiv : 1301.1069 . Бибкод : 2013ШПМП..44..222С . дои : 10.1016/j.shpsb.2013.04.004 . S2CID 55537196 .
^ Вернер, Райнхард Ф. (24 октября 2014 г.). «Комментарий к статье «Что сделал Белл» ». Физический журнал A: Математический и теоретический . 47 (42): 424011. Бибкод : 2014JPhA...47P4011W . дои : 10.1088/1751-8113/47/42/424011 . ISSN 1751-8113 . S2CID 122180759 .
^ Жуковский, Марек (2017). «Теорема Белла говорит нам не о том, что такое квантовая механика, а о том, чем квантовая механика не является». В Бертльманне, Рейнгольде; Цайлингер, Антон (ред.). Квантовые [Un]Speakables II . Коллекция «Границы». Чам: Международное издательство Springer. стр. 175–185. arXiv : 1501.05640 . дои : 10.1007/978-3-319-38987-5_10 . ISBN 978-3-319-38985-1 . S2CID 119214547 .
^ Омнес, Р. (1994). Интерпретация квантовой механики . Издательство Принстонского университета. ISBN 978-0-691-03669-4 . OCLC 439453957 .
^ Пайерлс, Рудольф (1979). Сюрпризы в теоретической физике . Издательство Принстонского университета. стр. 26–29. ISBN 0-691-08241-3 .
^ Мермин, Северная Дакота (1999). «Что эти корреляции знают о реальности? Нелокальность и абсурд». Основы физики . 29 (4): 571–587. arXiv : Quant-ph/9807055 . Бибкод : 1998quant.ph..7055M . дои : 10.1023/А:1018864225930 .
^ Хоэнберг, ПК (05 октября 2010 г.). «Коллоквиум: Введение в последовательную квантовую теорию». Обзоры современной физики . 82 (4): 2835–2844. arXiv : 0909.2359 . Бибкод : 2010RvMP...82.2835H . дои : 10.1103/RevModPhys.82.2835 . ISSN 0034-6861 . S2CID 20551033 .
^ Хили, Ричард (2016). «Квантово-байесовский и прагматический взгляды на квантовую теорию» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета. Архивировано из оригинала 17 августа 2021 г. Проверено 16 сентября 2021 г.
↑ Перейти обратно: Перейти обратно: ^а ^б Браун, Харви Р .; Тимпсон, Кристофер Г. (2016). «Белл о теореме Белла: меняющееся лицо нелокальности». В Белле, Мэри; Гао, Шан (ред.). Квантовая нелокальность и реальность: 50 лет теоремы Белла . Издательство Кембриджского университета. стр. 91–123. arXiv : 1501.03521 . дои : 10.1017/CBO9781316219393.008 . ISBN 9781316219393 . S2CID 118686956 .
^ Дойч, Дэвид ; Хайден, Патрик (2000). «Информационный поток в запутанных квантовых системах». Труды Королевского общества А. 456 (1999): 1759–1774. arXiv : Quant-ph/9906007 . Бибкод : 2000RSPSA.456.1759D . дои : 10.1098/rspa.2000.0585 . S2CID 13998168 .
^ Джейнс, ET (1989). «Разъяснение тайн — первоначальная цель». Максимальная энтропия и байесовские методы (PDF) . стр. 1–27. CiteSeerX 10.1.1.46.1264 . дои : 10.1007/978-94-015-7860-8_1 . ISBN 978-90-481-4044-2 . Архивировано (PDF) из оригинала 28 октября 2011 г. Проверено 18 октября 2011 г.
^ Гилл, Ричард Д. (2002). «Время, конечная статистика и пятая позиция Белла». Материалы конференции «Основы теории вероятностей и физики-2»: Векшё (Соланд), Швеция, 2-7 июня 2002 г. Том. 5. Издательство Университета Векшё. стр. 179–206. arXiv : Quant-ph/0301059 .
^ Вуд, Кристофер Дж.; Спеккенс, Роберт В. (3 марта 2015 г.). «Урок алгоритмов причинного обнаружения квантовых корреляций: причинные объяснения нарушений неравенства Белла требуют тонкой настройки» . Новый журнал физики . 17 (3): 033002. arXiv : 1208.4119 . Бибкод : 2015NJPh...17c3002W . дои : 10.1088/1367-2630/17/3/033002 . ISSN 1367-2630 . S2CID 118518558 .
^ Грёблахер, Симон; Патерек, Томаш; Кальтенбек, Райнер; Брукнер, Часлав; Жуковский, Марек; Аспельмейер, Маркус; Цайлингер, Антон (2007). «Экспериментальная проверка нелокального реализма». Природа . 446 (7138): 871–5. arXiv : 0704.2529 . Бибкод : 2007Natur.446..871G . дои : 10.1038/nature05677 . ПМИД 17443179 . S2CID 4412358 .
^ Кастнер, Рут Э. (май 2010 г.). «Квантовый эксперимент лжеца в транзакционной интерпретации Крамера» . Исследования по истории и философии науки. Часть B: Исследования по истории и философии современной физики . 41 (2): 86–92. arXiv : 0906.1626 . Бибкод : 2010ШПМП..41...86К . дои : 10.1016/j.shpsb.2010.01.001 . S2CID 16242184 . Архивировано из оригинала 24 июня 2018 г. Проверено 16 сентября 2021 г.
^ 'т Хоофт, Джерард (2016). Интерпретация квантовой механики клеточным автоматом . Фундаментальные теории физики. Том. 185. Спрингер. дои : 10.1007/978-3-319-41285-6 . ISBN 978-3-319-41284-9 . OCLC 951761277 . S2CID 7779840 . Архивировано из оригинала 29 декабря 2021 г. Проверено 27 августа 2020 г.

Дальнейшее чтение

Следующие материалы предназначены для широкой аудитории.

Аксель, Амир Д. (2001). Запутывание: величайшая загадка физики . Нью-Йорк: Четыре стены, восемь окон.
Африат, А.; Селлери, Ф. (1999). Парадокс Эйнштейна, Подольского и Розена . Нью-Йорк и Лондон: Пленум Пресс.
Бэгготт, Дж. (1992). Смысл квантовой теории . Издательство Оксфордского университета.
Гилдер, Луиза (2008). Эпоха запутанности: когда квантовая физика возродилась . Нью-Йорк: Альфред А. Кнопф.
Грин, Брайан (2004). Ткань Космоса . Винтаж. ISBN 0-375-72720-5 .
Мермин, Н. Дэвид (1981). «Возвращение домой атомного мира: квантовые тайны для всех». Американский журнал физики . 49 (10): 940–943. Бибкод : 1981AmJPh..49..940M . дои : 10.1119/1.12594 . S2CID 122724592 .
Мермин, Н. Дэвид (апрель 1985 г.). «Существует ли Луна, когда никто не смотрит? Реальность и квантовая теория». Физика сегодня . 38 (4): 38–47. Бибкод : 1985ФТ....38д..38М . дои : 10.1063/1.880968 .

Следующие более технически ориентированы.

Аспект, А .; и др. (1981). «Экспериментальная проверка реалистичных локальных теорий с помощью теоремы Белла» . Физ. Преподобный Летт . 47 (7): 460–463. Бибкод : 1981PhRvL..47..460A . дои : 10.1103/physrevlett.47.460 .
Аспект, А.; и др. (1982). «Экспериментальная реализация мысленного эксперимента Эйнштейна-Подольского-Розена-Бома: новое нарушение неравенств Белла» . Физ. Преподобный Летт . 49 (2): 91–94. Бибкод : 1982PhRvL..49...91A . дои : 10.1103/physrevlett.49.91 .
Аспект, А.; Гранжер, П. (1985). «О резонансном рассеянии и других гипотетических эффектах в атомно-каскадном эксперименте Орсе для проверки неравенств Белла: обсуждение и некоторые новые экспериментальные данные». Lettere al Nuovo Cimento . 43 (8): 345–348. дои : 10.1007/bf02746964 . S2CID 120840672 .
Белл, Дж. С. (1971). «Введение в вопрос о скрытой переменной». Труды Международной школы физики «Энрико Ферми», курс IL, «Основы квантовой механики» . стр. 171–81.
Белл, Дж. С. (2004). «Носки Бертльмана и природа реальности». Выразимое и невыразимое в квантовой механике . Издательство Кембриджского университета. стр. 139–158.
Д'Эспанья, Б. (1979). «Квантовая теория и реальность» (PDF) . Научный американец . 241 (5): 158–181. Бибкод : 1979SciAm.241e.158D . doi : 10.1038/scientificamerican1179-158 . Архивировано (PDF) из оригинала 27 марта 2009 г. Проверено 18 марта 2009 г.
Фрай, ES; Вальтер, Т.; Ли, С. (1995). «Предложение по проверке неравенств Белла без лазеек» (PDF) . Физ. Преподобный А. 52 (6): 4381–4395. Бибкод : 1995PhRvA..52.4381F . дои : 10.1103/physreva.52.4381 . hdl : 1969.1/126533 . ПМИД 9912775 . Архивировано из оригинала 29 декабря 2021 г. Проверено 19 марта 2018 г.
Фрай, ES; Вальтер, Т. (2002). «Атомные тесты неравенств Белла — наследие Джона Белла продолжается». В Бертльманне, РА; Цайлингер, А. (ред.). Квантовые [не]выразимые слова . Берлин-Гейдельберг-Нью-Йорк: Springer. стр. 103–117.
Гольдштейн, Шелдон; и др. (2011). «Теорема Белла» . Схоларпедия . 6 (10): 8378. Бибкод : 2011SchpJ...6.8378G . doi : 10.4249/scholarpedia.8378 .
Гриффитс, РБ (2001). Непротиворечивая квантовая теория . Издательство Кембриджского университета. ISBN 978-0-521-80349-6 . OCLC 1180958776 .
Харди, Л. (1993). «Нелокальность для двух частиц без неравенств почти для всех запутанных состояний». Письма о физических отзывах . 71 (11): 1665–1668. Бибкод : 1993PhRvL..71.1665H . дои : 10.1103/physrevlett.71.1665 . ПМИД 10054467 . S2CID 11839894 .
Мацукевич, Д.Н.; Маунц, П.; Меринг, Д.Л.; Ольмшенк, С.; Монро, К. (2008). «Нарушение неравенства Белла с двумя удаленными атомными кубитами». Физ. Преподобный Летт . 100 (15): 150404. arXiv : 0801.2184 . Бибкод : 2008PhRvL.100o0404M . дои : 10.1103/physrevlett.100.150404 . ПМИД 18518088 . S2CID 11536757 .
Риффель, Элеонора Г .; Полак, Вольфганг Х. (4 марта 2011 г.). «4.4 Парадокс ЭПР и теорема Белла». Квантовые вычисления: краткое введение . МТИ Пресс. стр. 60–65. ISBN 978-0-262-01506-6 .
Сулькс, С. (2003). «Природа света и экспериментальная физика двадцатого века». Основы науки . 8 (4): 365–391. дои : 10.1023/A:1026323203487 . S2CID 118769677 .
ван Фраассен, Британская Колумбия (1991). Квантовая механика: взгляд эмпирика . Кларендон Пресс. ISBN 978-0-198-24861-3 . ОСЛК 22906474 .

Внешние ссылки

[9] Для удобства мы предполагаем, что реакция детектора на основное свойство является детерминированной. Это предположение можно заменить; это эквивалентно постулированию совместного распределения вероятностей по всем наблюдаемым эксперимента. ^[7]^[8]

[23] Более подробно, как разработал Поль Дирак , ^[18] Дэвид Хилберт , ^[19] Джон фон Нейман , ^[20] и Герман Вейль , ^[21] состояние квантовомеханической системы является вектором $|\psi \rangle$ принадлежащий ( сепарабельному ) гильбертовому пространству ${\mathcal {H}}$ . Интересующие физические величины — положение, импульс, энергия, спин — представлены «наблюдаемыми», которые представляют собой самосопряженные линейные операторы , действующие в гильбертовом пространстве. Когда измеряется наблюдаемая величина, результатом будет одно из ее собственных значений с вероятностью, определяемой правилом Борна : в простейшем случае собственное значение $\eta$ невырожден, а вероятность определяется выражением $|\langle \eta |\psi \rangle |^{2}$ , где $|\eta \rangle$ является связанным с ним собственным вектором. В более общем смысле собственное значение вырождено, а вероятность определяется выражением $\langle \psi |P_{\eta }\psi \rangle$ , где $P_{\eta }$ является проектором на связанное с ним собственное пространство. Для целей данного обсуждения мы можем считать собственные значения невырожденными.

[42] См. Райхенбах. ^[35] и Джаммер, ^[36]^: 276 Мермин и Шак, ^[37] а за замечания Эйнштейна Клаузер и Шимони ^[38] и Вик. ^[39]^: 286

[52] теория скрытых переменных Детерминированная подразумевает, что вероятность данного результата всегда равна 0 или 1. Например, измерение Штерна-Герлаха на атоме со спином 1 покажет, что угловой момент атома вдоль выбранной оси равен одно из трех возможных значений, которое можно обозначить $-$ , $0$ и $+$ . В детерминированной теории скрытых переменных существует основное физическое свойство, которое фиксирует результат, полученный при измерении. В зависимости от ценности лежащего в основе физического свойства любой данный результат (например, результат $+$ ) должно быть либо невозможно, либо гарантировано. Но из теоремы Глисона следует, что такой детерминированной вероятностной меры не может быть, поскольку она доказывает, что любая вероятностная мера должна принимать форму отображения $u\to \langle \rho u,u\rangle$ для некоторого оператора плотности $\rho$ . Это отображение непрерывно на единичной сфере гильбертова пространства, и поскольку эта единичная сфера связна , никакая непрерывная вероятностная мера на ней не может быть детерминированной. ^[48]^: §1.3

[56] Об этом сообщил Макс Джаммер . ^[36]^: 308 Ли наиболее известен своим совместно с Чэнь-Нин Яном предсказанием о нарушении сохранения четности, предсказанием, которое принесло им Нобелевскую премию после того, как оно было подтверждено Цзянь-Шюн Ву , который не участвовал в премии.

[86] ET Джейнс был одним исключением, ^[79] но аргументы Джейнса в целом не были признаны убедительными. ^[80]

[1] Белл, Джон С. (1987). Выразимое и невыразимое в квантовой механике . Издательство Кембриджского университета. п. 65. ИСБН 9780521368698 . ОСЛК 15053677 .

[2] «Нобелевская премия по физике 2022» . Нобелевская премия (Пресс-релиз). Шведская королевская академия наук . 4 октября 2022 г. . Проверено 6 октября 2022 г.

[NAT-20180509-3] Сотрудничество BIG Bell Test (9 мая 2018 г.). «Вызов местному реализму с помощью человеческого выбора». Природа . 557 (7704): 212–216. arXiv : 1805.04431 . Бибкод : 2018Natur.557..212B . дои : 10.1038/s41586-018-0085-3 . ПМИД 29743691 . S2CID 13665914 .

[4] Волчовер, Натали (07 февраля 2017 г.). «Эксперимент подтверждает квантовую странность» . Журнал Кванта . Проверено 08 февраля 2020 г.

[Stanford-5] Перейти обратно: Перейти обратно: ^а ^б Шимони, Эбнер . «Теорема Белла» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .

[mike-and-ike-6] Перейти обратно: Перейти обратно: ^а ^б ^с ^д Нильсен, Майкл А .; Чуанг, Исаак Л. (2010). Квантовые вычисления и квантовая информация (2-е изд.). Кембридж: Издательство Кембриджского университета. ISBN 978-1-107-00217-3 . OCLC 844974180 .

[7] Хорошо, Артур (1 февраля 1982 г.). «Скрытые переменные, совместная вероятность и неравенства Белла» . Письма о физических отзывах . 48 (5): 291–295. Бибкод : 1982PhRvL..48..291F . doi : 10.1103/PhysRevLett.48.291 . ISSN 0031-9007 .

[8] Браунштейн, Сэмюэл Л.; Кейвс, Карлтон М. (август 1990 г.). «Выявление лучшего неравенства Белла». Анналы физики . 202 (1): 22–56. Бибкод : 1990АнФиз.202...22Б . дои : 10.1016/0003-4916(90)90339-П .

[10] Рау, Йохен (2021). Квантовая теория: подход к обработке информации . Издательство Оксфордского университета. ISBN 978-0-192-65027-6 . OCLC 1256446911 .

[11] Умный . ; Хойер, П.; Тонер, Б.; Уотрус, Дж. (2004). «Последствия и пределы нелокальных стратегий». Слушания. 19-я ежегодная конференция IEEE по сложности вычислений, 2004 г. ИИЭЭ . стр. 236–249. arXiv : Quant-ph/0404076 . Бибкод : 2004quant.ph..4076C . дои : 10.1109/CCC.2004.1313847 . ISBN 0-7695-2120-7 . OCLC 55954993 . S2CID 8077237 .

[12] Барнум, Х.; Бейги, С.; Бойшо, С.; Эллиотт, МБ; Венер, С. (6 апреля 2010 г.). «Локальное квантовое измерение и отсутствие сигналов подразумевают квантовые корреляции». Письма о физических отзывах . 104 (14): 140401. arXiv : 0910.3952 . Бибкод : 2010PhRvL.104n0401B . doi : 10.1103/PhysRevLett.104.140401 . ISSN 0031-9007 . ПМИД 20481921 . S2CID 17298392 .

[Bell1964-13] Белл, Дж. С. (1964). «О парадоксе Эйнштейна-Подольского-Розена» (PDF) . Физика Телосложение Физика . 1 (3): 195–200. doi : 10.1103/PhysicsPhysiqueFizika.1.195 .

[14] Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику (2-е изд.). Река Аппер-Сэддл, Нью-Джерси: Пирсон Прентис Холл. ISBN 0-13-111892-7 . OCLC 53926857 .

[EPR-15] Эйнштейн, А .; Подольский, Б. ; Розен, Н. (15 мая 1935 г.). «Можно ли квантово-механическое описание физической реальности считать полным?» . Физический обзор . 47 (10): 777–780. Бибкод : 1935PhRv...47..777E . дои : 10.1103/PhysRev.47.777 .

[GHZ1990-16] Гринбергер, Д .; Хорн, М .; Шимони, А. ; Цайлингер, А. (1990). «Теорема Белла без неравенств» . Американский журнал физики . 58 (12): 1131. Бибкод : 1990AmJPh..58.1131G . дои : 10.1119/1.16243 .

[mermin1990-17] Мермин, Н. Дэвид (1990). «Возвращение к квантовым тайнам». Американский журнал физики . 58 (8): 731–734. Бибкод : 1990AmJPh..58..731M . дои : 10.1119/1.16503 .

[Brassard_2004-18] Брассар, Жиль ; Бродбент, Энн ; Тапп, Ален (2005). «Переработка многопользовательской игры Мермина в рамки псевдотелепатии». Квантовая информация и вычисления . 5 (7): 538–550. arXiv : Quant-ph/0408052 . Бибкод : 2004quant.ph..8052B . дои : 10.26421/QIC5.7-2 .

[19] Дирак, Поль Адриен Морис (1930). Принципы квантовой механики . Оксфорд: Кларендон Пресс.

[20] Гильберт, Дэвид (2009). Зауэр, Тилман; Майер, Ульрих (ред.). Лекции по основам физики 1915–1927: теория относительности, квантовая теория и эпистемология . Спрингер. дои : 10.1007/b12915 . ISBN 978-3-540-20606-4 . OCLC 463777694 .

[21] фон Нейман, Джон (1932). Математические основы квантовой механики . Берлин: Шпрингер. Английский перевод: Математические основы квантовой механики . Перевод Бейера, Издательство Роберта Т. Принстонского университета. 1955.

[22] Вейль, Герман (1950) [1931]. Теория групп и квантовая механика . Перевод Робертсона, HP Dover. ISBN 978-0-486-60269-1 . В переводе с немецкого Теория групп и квантовая механика (2-е изд.). С. Хирзель Верлаг [ де ] . 1931 год.

[24] Перес, Ашер (1993). Квантовая теория: концепции и методы . Клювер . ISBN 0-7923-2549-4 . ОСЛК 28854083 .

[25] Рыжий, Майкл ; Браун, Харви (1 июля 1991 г.). «Нелокальность в квантовой механике». Труды Аристотелевского общества, дополнительные тома . 65 (1): 119–160. дои : 10.1093/аристотелиансупп/65.1.119 . ISSN 0309-7013 . JSTOR 4106773 . К аналогичному подходу независимо пришел Саймон Кохен, хотя он никогда не публиковался (частное сообщение).

[26] Хейвуд, Питер; Рыжий, Майкл Л.Г. (май 1983 г.). «Нелокальность и парадокс Кохена – Спекера». Основы физики . 13 (5): 481–499. Бибкод : 1983FoPh...13..481H . дои : 10.1007/BF00729511 . ISSN 0015-9018 . S2CID 120340929 .

[27] Лестница, Аллен (декабрь 1983 г.). «Квантовая логика, реализм и определенность ценностей». Философия науки . 50 (4): 578–602. дои : 10.1086/289140 . ISSN 0031-8248 . S2CID 122885859 .

[28] Браун, HR ; Светличный, Г. (ноябрь 1990 г.). «Нелокальность и лемма Глисона. Часть I. Детерминистические теории». Основы физики . 20 (11): 1379–1387. Бибкод : 1990FoPh...20.1379B . дои : 10.1007/BF01883492 . ISSN 0015-9018 . S2CID 122868901 .

[29] Глик, Дэвид; Боге, Флориан Дж. (22 октября 2019 г.). «Является ли критерий реальности аналитическим?». Эркеннтнис . 86 (6): 1445–1451. arXiv : 1909.11893 . Бибкод : 2019arXiv190911893G . дои : 10.1007/s10670-019-00163-w . ISSN 0165-0106 . S2CID 202889160 .

[30] Конвей, Джон ; Кохен, Саймон (2006). «Теорема свободы воли». Основы физики . 36 (10): 1441. arXiv : quant-ph/0604079 . Бибкод : 2006FoPh...36.1441C . дои : 10.1007/s10701-006-9068-6 . S2CID 12999337 .

[31] Ремейер, Джули (15 августа 2008 г.). «Есть ли у субатомных частиц свободная воля?» . Новости науки . Проверено 23 апреля 2022 г.

[32] Томас, Рэйчел (27 декабря 2011 г.). «Джон Конвей – открытие свободы воли (часть I)» . Плюс журнал . Проверено 23 апреля 2022 г.

[33] Конвей, Джон Х .; Кохен, Саймон (2009). «Сильная теорема о свободе воли» (PDF) . Уведомления АМС . 56 (2): 226–232.

[34] Вернер, Рейнхард Ф. (1 октября 1989 г.). «Квантовые состояния с корреляциями Эйнштейна – Подольского – Розена, допускающие модель скрытой переменной». Физический обзор А. 40 (8): 4277–4281. Бибкод : 1989PhRvA..40.4277W . дои : 10.1103/PhysRevA.40.4277 . ISSN 0556-2791 . ПМИД 9902666 .

[35] Спеккенс, Роберт В. (19 марта 2007 г.). «Доказательства эпистемического взгляда на квантовые состояния: игрушечная теория». Физический обзор А. 75 (3): 032110. arXiv : quant-ph/0401052 . Бибкод : 2007PhRvA..75c2110S . дои : 10.1103/PhysRevA.75.032110 . ISSN 1050-2947 . S2CID 117284016 .

[36] Катани, Лоренцо; Браун, Дэн Э. (27 июля 2017 г.). «Игрушечная модель Спеккенса во всех измерениях и ее связь со стабилизатором квантовой механики» . Новый журнал физики . 19 (7): 073035. arXiv : 1701.07801 . Бибкод : 2017NJPh...19g3035C . дои : 10.1088/1367-2630/aa781c . ISSN 1367-2630 . S2CID 119428107 .

[37] Райхенбах, Ганс (1944). Философские основы квантовой механики . Издательство Калифорнийского университета. п. 14. OCLC 872622725 .

[jammer1974-38] Перейти обратно: Перейти обратно: ^а ^б Джаммер, Макс (1974). Философия квантовой механики . Джон Уайли и сыновья. ISBN 0-471-43958-4 .

[39] Мермин, Н. Дэвид ; Шак, Рюдигер (2018). «Гомер кивнул: удивительная оплошность фон Неймана». Основы физики . 48 (9): 1007–1020. arXiv : 1805.10311 . Бибкод : 2018FoPh...48.1007M . дои : 10.1007/s10701-018-0197-5 . S2CID 118951033 .

[40] Клаузер, Дж. Ф.; Шимони, А. (1978). «Теорема Белла: экспериментальные проверки и выводы» (PDF) . Отчеты о прогрессе в физике . 41 (12): 1881–1927. Бибкод : 1978РПФ...41.1881С . CiteSeerX 10.1.1.482.4728 . дои : 10.1088/0034-4885/41/12/002 . S2CID 250885175 . Архивировано (PDF) из оригинала 23 сентября 2017 г. Проверено 28 октября 2017 г.

[:1-41] Перейти обратно: Перейти обратно: ^а ^б Уик, Дэвид (1995). «Теорема Белла». Печально известная граница: семь десятилетий ереси в квантовой физике . Нью-Йорк: Спрингер. стр. 92–100. дои : 10.1007/978-1-4612-4030-3_11 . ISBN 978-0-387-94726-6 .

[43] Конвей, Джон ; Кохен, Саймон (2002). «Геометрия квантовых парадоксов». В Бертльманне, Рейнгольд А .; Цайлингер, Антон (ред.). Квантовые [не]говоримые: от Белла к квантовой информации . Берлин: Шпрингер. стр. 257–269. ISBN 3-540-42756-2 . ОСЛК 49404213 .

[44] Эйнштейн, Альберт (март 1936 г.). «Физика и реальность». Журнал Института Франклина . 221 (3): 349–382. Бибкод : 1936FrInJ.221..349E . дои : 10.1016/S0016-0032(36)91047-5 .

[45] Харриган, Николас; Спеккенс, Роберт В. (2010). «Эйнштейн, неполнота и эпистемический взгляд на квантовые состояния». Основы физики . 40 (2): 125. arXiv : 0706.2661 . Бибкод : 2010FoPh...40..125H . дои : 10.1007/s10701-009-9347-0 . S2CID 32755624 .

[46] Бом, Дэвид (1989) [1951]. Квантовая теория (переиздание в Дувре). Прентис-Холл. стр. 614–623. ISBN 978-0-486-65969-5 . OCLC 1103789975 .

[47] Ву, К.-С. ; Шахнов И. (1950). «Угловая корреляция рассеянного аннигиляционного излучения». Физический обзор . 77 (1): 136. Бибкод : 1950PhRv...77..136W . дои : 10.1103/PhysRev.77.136 .

[48] Макки, Джордж В. (1957). «Квантовая механика и гильбертово пространство». Американский математический ежемесячник . 64 (8П2): 45–57. дои : 10.1080/00029890.1957.11989120 . JSTOR 2308516 .

[gleason1957-49] Глисон, Эндрю М. (1957). «Меры на замкнутых подпространствах гильбертова пространства» . Математический журнал Университета Индианы . 6 (4): 885–893. дои : 10.1512/iumj.1957.6.56050 . МР 0096113 .

[chernoff2009-50] Чернофф, Пол Р. «Энди Глисон и квантовая механика» (PDF) . Уведомления АМС . 56 (10): 1253–1259.

[wilce2017-51] Вилце, А. (2017). «Квантовая логика и теория вероятностей» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета.

[ND_Mermin_1993-07-53] Перейти обратно: Перейти обратно: ^а ^б ^с Мермин, Н. Дэвид (июль 1993 г.). «Скрытые переменные и две теоремы Джона Белла» (PDF) . Обзоры современной физики . 65 (3): 803–815. arXiv : 1802.10119 . Бибкод : 1993РвМП...65..803М . дои : 10.1103/RevModPhys.65.803 . S2CID 119546199 .

[54] Шимони, Абнер (1984). «Контекстные теории скрытых переменных и неравенства Белла». Британский журнал философии науки . 35 (1): 25–45. дои : 10.1093/bjps/35.1.25 .

[55] Перес, Ашер (1991). «Два простых доказательства теоремы Кохена-Спкера» . Журнал физики A: Математический и общий . 24 (4): Л175–Л178. Бибкод : 1991JPhA...24L.175P . дои : 10.1088/0305-4470/24/4/003 . ISSN 0305-4470 .

[:0-57] Уитакер, Эндрю (2016). Джон Стюарт Белл и физика двадцатого века: видение и целостность . Издательство Оксфордского университета. ISBN 978-0-19-874299-9 .

[Bell1966-58] Перейти обратно: Перейти обратно: ^а ^б Белл, Дж. С. (1966). «К проблеме скрытых переменных в квантовой механике». Обзоры современной физики . 38 (3): 447–452. Бибкод : 1966РвМП...38..447Б . дои : 10.1103/revmodphys.38.447 . ОСТИ 1444158 .

[59] Кайзер, Дэвид (30 января 2012 г.). «Как хиппи спасли физику: наука, контркультура и квантовое возрождение [отрывок]» . Научный американец . Проверено 11 февраля 2020 г.

[60] Фридман, С.Дж .; Клаузер, Дж. Ф. (1972). «Экспериментальная проверка локальных теорий скрытых переменных» (PDF) . Письма о физических отзывах . 28 (938): 938–941. Бибкод : 1972PhRvL..28..938F . doi : 10.1103/PhysRevLett.28.938 .

[61] Фридман, Стюарт Джей (5 мая 1972 г.). Экспериментальная проверка локальных теорий скрытых переменных (PDF) (доктор философии). Калифорнийский университет, Беркли.

[62] Аспект, Ален; Далибар, Жан; Роджер, Жерар (1982). «Экспериментальная проверка неравенств Белла с использованием анализаторов, изменяющихся во времени» . Письма о физических отзывах . 49 (25): 1804–7. Бибкод : 1982PhRvL..49.1804A . doi : 10.1103/PhysRevLett.49.1804 .

[GHZ2000-63] Пан, Цзянь-Вэй; Баумистер, Д.; Дэниел, М.; Вайнфуртер, Х.; Цайлингер, А. (2000). «Экспериментальная проверка квантовой нелокальности в трехфотонной ГГЦ-запутанности». Природа . 403 (6769): 515–519. Бибкод : 2000Natur.403..515P . дои : 10.1038/35000514 . ПМИД 10676953 . S2CID 4309261 .

[64] Делингер, Дитрих; Митчелл, М.В. (2002). «Запутанные фотоны, нелокальность и неравенства Белла в студенческой лаборатории». Американский журнал физики . 70 (9): 903–910. arXiv : Quant-ph/0205171 . Бибкод : 2002AmJPh..70..903D . дои : 10.1119/1.1498860 . S2CID 49487096 .

[larsson14-65] Перейти обратно: Перейти обратно: ^а ^б Ларссон, Ян-Оке (2014). «Лазовки в тестах неравенства Белла локального реализма». Физический журнал A: Математический и теоретический . 47 (42): 424003. arXiv : 1407.0363 . Бибкод : 2014JPhA...47P4003L . дои : 10.1088/1751-8113/47/42/424003 . S2CID 40332044 .

[66] Герхардт, И.; Лю, К.; Ламас-Линарес, А.; Скаар, Дж.; Скарани, В.; и др. (2011). «Экспериментальная имитация нарушения неравенств Белла». Письма о физических отзывах . 107 (17): 170404. arXiv : 1106.3224 . Бибкод : 2011PhRvL.107q0404G . doi : 10.1103/PhysRevLett.107.170404 . ПМИД 22107491 . S2CID 16306493 .

[67] Мерали, Зия (27 августа 2015 г.). «Квантовая «жуткость» прошла самое жесткое испытание» . Новости природы . 525 (7567): 14–15. Бибкод : 2015Natur.525...14M . дои : 10.1038/nature.2015.18255 . ПМИД 26333448 . S2CID 4409566 .

[NYT-20151021-68] Маркофф, Джек (21 октября 2015 г.). «Прости, Эйнштейн. Квантовое исследование показало, что «жуткие действия» реальны» . Нью-Йорк Таймс . Проверено 21 октября 2015 г.

[NTR-20151021-69] Хенсен, Б.; и др. (21 октября 2015 г.). «Нарушение неравенства Белла без лазеек с использованием спинов электронов, разделенных на 1,3 километра». Природа . 526 (7575): 682–686. arXiv : 1508.05949 . Бибкод : 2015Natur.526..682H . дои : 10.1038/nature15759 . ПМИД 26503041 . S2CID 205246446 .

[PRL115-250402-70] Шальм, ЛК; и др. (16 декабря 2015 г.). «Сильная проверка локального реализма без лазеек» . Письма о физических отзывах . 115 (25): 250402. arXiv : 1511.03189 . Бибкод : 2015PhRvL.115y0402S . doi : 10.1103/PhysRevLett.115.250402 . ПМЦ 5815856 . ПМИД 26722906 .

[PRL115-250401-71] Джустина, М.; и др. (16 декабря 2015 г.). «Проверка теоремы Белла со запутанными фотонами без существенных лазеек». Письма о физических отзывах . 115 (25): 250401. arXiv : 1511.03190 . Бибкод : 2015PhRvL.115y0401G . doi : 10.1103/PhysRevLett.115.250401 . ПМИД 26722905 . S2CID 13789503 .

[72] Аспект, Ален (16 декабря 2015 г.). «Закрывая дверь к квантовым дебатам Эйнштейна и Бора» . Физика . 8 : 123. Бибкод : 2015PhyOJ...8..123A . дои : 10.1103/Физика.8.123 .

[73] Аландер, Йохан; Бургер, Людвиг; Поллард, Никлас (04 октября 2022 г.). «Нобелевская премия по физике достаётся исследователям «жуткой» квантовой науки» . Рейтер . Проверено 4 октября 2022 г.

[74] Шлоссауэр, Максимилиан; Кофлер, Йоханнес; Цайлингер, Антон (6 января 2013 г.). «Снимок фундаментального отношения к квантовой механике». Исследования по истории и философии науки. Часть B: Исследования по истории и философии современной физики . 44 (3): 222–230. arXiv : 1301.1069 . Бибкод : 2013ШПМП..44..222С . дои : 10.1016/j.shpsb.2013.04.004 . S2CID 55537196 .

[75] Вернер, Райнхард Ф. (24 октября 2014 г.). «Комментарий к статье «Что сделал Белл» ». Физический журнал A: Математический и теоретический . 47 (42): 424011. Бибкод : 2014JPhA...47P4011W . дои : 10.1088/1751-8113/47/42/424011 . ISSN 1751-8113 . S2CID 122180759 .

[76] Жуковский, Марек (2017). «Теорема Белла говорит нам не о том, что такое квантовая механика, а о том, чем квантовая механика не является». В Бертльманне, Рейнгольде; Цайлингер, Антон (ред.). Квантовые [Un]Speakables II . Коллекция «Границы». Чам: Международное издательство Springer. стр. 175–185. arXiv : 1501.05640 . дои : 10.1007/978-3-319-38987-5_10 . ISBN 978-3-319-38985-1 . S2CID 119214547 .

[omnes-77] Омнес, Р. (1994). Интерпретация квантовой механики . Издательство Принстонского университета. ISBN 978-0-691-03669-4 . OCLC 439453957 .

[78] Пайерлс, Рудольф (1979). Сюрпризы в теоретической физике . Издательство Принстонского университета. стр. 26–29. ISBN 0-691-08241-3 .

[79] Мермин, Северная Дакота (1999). «Что эти корреляции знают о реальности? Нелокальность и абсурд». Основы физики . 29 (4): 571–587. arXiv : Quant-ph/9807055 . Бибкод : 1998quant.ph..7055M . дои : 10.1023/А:1018864225930 .

[80] Хоэнберг, ПК (05 октября 2010 г.). «Коллоквиум: Введение в последовательную квантовую теорию». Обзоры современной физики . 82 (4): 2835–2844. arXiv : 0909.2359 . Бибкод : 2010RvMP...82.2835H . дои : 10.1103/RevModPhys.82.2835 . ISSN 0034-6861 . S2CID 20551033 .

[81] Хили, Ричард (2016). «Квантово-байесовский и прагматический взгляды на квантовую теорию» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета. Архивировано из оригинала 17 августа 2021 г. Проверено 16 сентября 2021 г.

[BrownTimpson-82] Перейти обратно: Перейти обратно: ^а ^б Браун, Харви Р .; Тимпсон, Кристофер Г. (2016). «Белл о теореме Белла: меняющееся лицо нелокальности». В Белле, Мэри; Гао, Шан (ред.). Квантовая нелокальность и реальность: 50 лет теоремы Белла . Издательство Кембриджского университета. стр. 91–123. arXiv : 1501.03521 . дои : 10.1017/CBO9781316219393.008 . ISBN 9781316219393 . S2CID 118686956 .

[83] Дойч, Дэвид ; Хайден, Патрик (2000). «Информационный поток в запутанных квантовых системах». Труды Королевского общества А. 456 (1999): 1759–1774. arXiv : Quant-ph/9906007 . Бибкод : 2000RSPSA.456.1759D . дои : 10.1098/rspa.2000.0585 . S2CID 13998168 .

[E.T._Jaynes_1989-84] Джейнс, ET (1989). «Разъяснение тайн — первоначальная цель». Максимальная энтропия и байесовские методы (PDF) . стр. 1–27. CiteSeerX 10.1.1.46.1264 . дои : 10.1007/978-94-015-7860-8_1 . ISBN 978-90-481-4044-2 . Архивировано (PDF) из оригинала 28 октября 2011 г. Проверено 18 октября 2011 г.

[Gill2002-85] Гилл, Ричард Д. (2002). «Время, конечная статистика и пятая позиция Белла». Материалы конференции «Основы теории вероятностей и физики-2»: Векшё (Соланд), Швеция, 2-7 июня 2002 г. Том. 5. Издательство Университета Векшё. стр. 179–206. arXiv : Quant-ph/0301059 .

[87] Вуд, Кристофер Дж.; Спеккенс, Роберт В. (3 марта 2015 г.). «Урок алгоритмов причинного обнаружения квантовых корреляций: причинные объяснения нарушений неравенства Белла требуют тонкой настройки» . Новый журнал физики . 17 (3): 033002. arXiv : 1208.4119 . Бибкод : 2015NJPh...17c3002W . дои : 10.1088/1367-2630/17/3/033002 . ISSN 1367-2630 . S2CID 118518558 .

[88] Грёблахер, Симон; Патерек, Томаш; Кальтенбек, Райнер; Брукнер, Часлав; Жуковский, Марек; Аспельмейер, Маркус; Цайлингер, Антон (2007). «Экспериментальная проверка нелокального реализма». Природа . 446 (7138): 871–5. arXiv : 0704.2529 . Бибкод : 2007Natur.446..871G . дои : 10.1038/nature05677 . ПМИД 17443179 . S2CID 4412358 .

[89] Кастнер, Рут Э. (май 2010 г.). «Квантовый эксперимент лжеца в транзакционной интерпретации Крамера» . Исследования по истории и философии науки. Часть B: Исследования по истории и философии современной физики . 41 (2): 86–92. arXiv : 0906.1626 . Бибкод : 2010ШПМП..41...86К . дои : 10.1016/j.shpsb.2010.01.001 . S2CID 16242184 . Архивировано из оригинала 24 июня 2018 г. Проверено 16 сентября 2021 г.

[90] 'т Хоофт, Джерард (2016). Интерпретация квантовой механики клеточным автоматом . Фундаментальные теории физики. Том. 185. Спрингер. дои : 10.1007/978-3-319-41285-6 . ISBN 978-3-319-41284-9 . OCLC 951761277 . S2CID 7779840 . Архивировано из оригинала 29 декабря 2021 г. Проверено 27 августа 2020 г.

[1]

[2]

[3]

[4]

[5]

[6]

[примечание 1]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[примечание 2]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[примечание 3]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[примечание 4]

[49]

[50]

[51]

[примечание 5]

[52]

[39]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[примечание 6]

[81]

[82]

[83]

[84]

[7]

[8]

[18]

[19]

[20]

[21]

[35]

[36]

[37]

[38]

[48]

[79]

[80]

v т и Квантовая механика
Background	Introduction History Timeline Classical mechanics Old quantum theory Glossary
Fundamentals	Born rule Bra–ket notation Complementarity Density matrix Energy level Ground state Excited state Degenerate levels Zero-point energy Entanglement Hamiltonian Interference Decoherence Measurement Nonlocality Quantum state Superposition Tunnelling Scattering theory Symmetry in quantum mechanics Uncertainty Wave function Collapse Wave–particle duality
Formulations	Formulations Heisenberg Interaction Matrix mechanics Schrödinger Path integral formulation Phase space
Equations	Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations	Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective collapse Quantum logic Relational Transactional Von Neumann–Wigner
Experiments	Bell test Davisson–Germer Delayed-choice quantum eraser Double-slit Franck–Hertz Mach–Zehnder interferometer Elitzur–Vaidman Popper Quantum eraser Stern–Gerlach Wheeler's delayed choice
Science	Quantum biology Quantum chemistry Quantum chaos Quantum cosmology Quantum differential calculus Quantum dynamics Quantum geometry Quantum measurement problem Quantum mind Quantum stochastic calculus Quantum spacetime
Technology	Quantum algorithms Quantum amplifier Quantum bus Quantum cellular automata Quantum finite automata Quantum channel Quantum circuit Quantum complexity theory Quantum computing Timeline Quantum cryptography Quantum electronics Quantum error correction Quantum imaging Quantum image processing Quantum information Quantum key distribution Quantum logic Quantum logic gates Quantum machine Quantum machine learning Quantum metamaterial Quantum metrology Quantum network Quantum neural network Quantum optics Quantum programming Quantum sensing Quantum simulator Quantum teleportation
Extensions	Quantum fluctuation Casimir effect Quantum statistical mechanics Quantum field theory History Quantum gravity Relativistic quantum mechanics
Related	Schrödinger's cat in popular culture Wigner's friend EPR paradox Quantum mysticism
Category

Базы данных авторитетного контроля
International	FAST
National	France BnF data Germany Israel United States
Other	IdRef