Китайская математика

Математика возникла независимо в Китае в 11 веке до нашей эры. Китайцы самостоятельно разработали действительную систему счисления , включающую в себя значительно большие и отрицательные числа , более чем одну систему счисления ( двоичную и десятичную ), алгебру , геометрию , теорию чисел и тригонометрию .

Со времен династии Хань , когда диофантова аппроксимация была выдающимся численным методом , китайцы добились существенного прогресса в области полиномиальной оценки . Алгоритмы, такие как regula falsi , и выражения, такие как непрерывные дроби, широко используются и с тех пор хорошо документированы. Они намеренно находят главный n-й корень степени из положительных чисел и корни уравнений . Основные тексты того периода, «Девять глав о математическом искусстве» и « Книга о числах и вычислениях», подробно описывают процессы решения различных математических задач в повседневной жизни. В обоих текстах все процедуры были рассчитаны с использованием счетной доски и включали обратные элементы, а также евклидовы деления . В текстах представлены процедуры, аналогичные методу исключения Гаусса и методу Горнера для линейной алгебры . Достижения китайской алгебры достигли апогея в 13 веке во времена династии Юань с развитием Тянь юань шу .

Предполагается, что в результате очевидных лингвистических и географических барьеров, а также содержания китайская математика и математика древнего Средиземноморья развивались более или менее независимо до того времени, когда «Девять глав о математическом искусстве» достигли своей окончательной формы. , а «Книга о числах и вычислениях» и «Хуайнаньцзы» примерно современны классической греческой математике. Вероятен некоторый обмен идеями по всей Азии посредством известных культурных обменов, по крайней мере, со времен Римской империи. Часто элементы математики ранних обществ соответствуют элементарным результатам, найденным позже в таких областях современной математики, как геометрия или теория чисел. теорема Пифагора Например, была засвидетельствована во времена герцога Чжоу . Также было показано, что знание треугольника Паскаля существовало в Китае за несколько столетий до Паскаля . например, эрудит эпохи Сун Шэнь Го .

Доимперская эпоха

Визуальное доказательство треугольника (3, 4, 5), как в Чжоуби Суаньцзин 500–200 гг. До н.э.

Система счисления костяного алфавита Oracle

Счетная стержень, десятичное значение разряда

Династия Шан (1600–1050 до н. э.). Одним из старейших сохранившихся математических трудов является « И Цзин» , оказавший большое влияние на письменную литературу во времена династии Чжоу (1050–256 гг. до н.э.). Что касается математики, книга включала сложное использование гексаграмм . Лейбниц указывал, что И Цзин (И Цзин) содержит элементы двоичных чисел .

Начиная с периода Шан, китайцы уже полностью разработали десятичную систему. С давних времен китайцы понимали основы арифметики (которая доминировала в истории Дальнего Востока), алгебру, уравнения и отрицательные числа со счетными палочками . Хотя китайцы были больше сосредоточены на арифметике и продвинутой алгебре для астрономических целей, они также были первыми, кто разработал отрицательные числа, алгебраическую геометрию и использование десятичных дробей.

Математика была одним из шести предметов искусства, которые студенты должны были освоить во времена династии Чжоу (1122–256 гг. До н.э.). Чтобы выучить их все в совершенстве, нужно было стать совершенным джентльменом, сравнимым с понятием « человек эпохи Возрождения ». Шесть искусств берут свое начало в конфуцианской философии .

Самая старая из существующих в Китае работ по геометрии происходит из философского мохистского канона ок. 330 г. до н. э. , составлено последователями Мози (470–390 гг. до н. э.). « Мо Цзин» описал различные аспекты многих областей, связанных с физической наукой, а также предоставил небольшой объем информации по математике. Он дал «атомарное» определение геометрической точки, заявив, что линия разделена на части, а часть, которая не имеет оставшихся частей (т. е. не может быть разделена на более мелкие части) и, таким образом, образует крайний конец линии, является точкой. . Подобно « первому и третьему определениям Евклида и Мо началу линии» Платона, Цзин утверждает, что «точка может стоять в конце (линии) или в ее начале, как предлежание головы при родах. (Что касается его невидимости), то нет ничего похожего на него». Подобно атомистам Демокрита утверждал , , Мо Цзин что точка — это наименьшая единица, и ее нельзя разрезать пополам, поскольку «ничто» не может быть разделено пополам». Там говорилось, что две линии одинаковой длины всегда будут заканчиваться в одном и том же месте». давая определения для сравнения длин и параллелей ». наряду с принципами пространства и ограниченного пространства. Там также описывался тот факт, что плоскости без качества толщины не могут складываться в кучу, поскольку они не могут взаимно соприкасаться. В книге предусмотрено распознавание слов для обозначения окружности, диаметра и радиуса, а также определение объема.

В истории развития математики отсутствуют некоторые доказательства. По поводу некоторых математических классиков до сих пор ведутся споры. Например, « Чжоуби Суаньцзин» датируется примерно 1200–1000 гг. до н. э., однако многие ученые полагают, что он был написан между 300 и 250 гг. до н. э. Чжоуби Суаньцзин содержит углубленное доказательство теоремы Гоугу (частный случай теоремы Пифагора ), но больше фокусируется на астрономических расчетах. Однако недавнее археологическое открытие бамбуковых пластинок Цинхуа , датированных ок. 305 г. до н.э. , раскрыл некоторые аспекты математики доциньской эпохи, такие как первая известная десятичная таблица умножения .

Впервые счеты были упомянуты во втором веке до нашей эры, наряду с «счетом с помощью палочек» ( суань-цзы ), при котором маленькие бамбуковые палочки помещались в последовательные квадраты шахматной доски.

Династия Цинь

известно немногое О математике династии Цинь или раньше из-за сожжения книг и захоронения ученых , около 213–210 гг. до н.э. Знания об этом периоде можно определить на основе гражданских проектов и исторических свидетельств. Династия Цинь создала стандартную систему весов. Гражданские проекты династии Цинь были значительным достижением человеческой инженерии. Император Цинь Ши Хуан приказал многим мужчинам построить большие статуи в натуральную величину для дворцовой гробницы, а также других храмов и святынь, а форма гробницы была разработана с учетом геометрических навыков архитектуры. Несомненно, одно из величайших достижений человеческой истории — Великая Китайская стена — потребовало использования многих математических методов. Во всех зданиях и грандиозных проектах династии Цинь использовались передовые формулы расчета объема, площади и пропорций.

Наличка из бамбука Цинь, приобретенная на антикварном рынке Гонконга Академией Юэлу , по предварительным данным, содержит самый ранний эпиграфический образец математического трактата.

Династия Хань

Дополнительная информация: Наука и техника династии Хань § Математика и астрономия.

Девять глав о математическом искусстве

Во времена династии Хань числа были преобразованы в десятичную систему разрядов и использовались на счетной доске с набором счетных стержней, называемых стержневым исчислением , состоящих всего из девяти символов с пустым местом на счетной доске, обозначающим ноль. Отрицательные числа и дроби также использовались в решениях великих математических текстов того периода. Математические тексты того времени, « Книга чисел и вычислений» и «Цзючжан суаньшу», решали основные арифметические задачи, такие как сложение, вычитание, умножение и деление. Кроме того, они описали процессы извлечения квадратных и кубических корней, которые в конечном итоге были применены для решения квадратных уравнений до третьего порядка. Оба текста также добились существенного прогресса в линейной алгебре, а именно в решении систем уравнений с множеством неизвестных. Значение числа пи в обоих текстах принято равным трем. Однако математики Лю Синь (ум. 23) и Чжан Хэн (78–139) дали более точные приближения для числа Пи , чем использовали китайцы предыдущих столетий. Математика была разработана для решения практических задач того времени, таких как раздел земли или проблемы, связанные с разделением платежей. Китайцы не сосредоточивались на теоретических доказательствах, основанных на геометрии или алгебре в современном смысле доказательства уравнений для нахождения площади или объема. «Книга вычислений» и «Девять глав математического искусства» содержат множество практических примеров, которые можно использовать в повседневной жизни.

Книга по числам и вычислениям

Книга «Числа и вычисления» содержит около семи тысяч знаков и написана на 190 бамбуковых полосках. Он был обнаружен вместе с другими письменами в 1984 году, когда археологи открыли гробницу в Чжанцзяшане в провинции Хубэй . Из документальных свидетельств известно, что эта гробница была закрыта в 186 г. до н.э., в начале правления династии Западная Хань . Хотя его связь с Девятью главами все еще обсуждается учеными, некоторые его содержания явно имеют там параллели. Однако текст « Суань шу шу» гораздо менее систематичен, чем «Девять глав», и, по-видимому, состоит из ряда более или менее независимых коротких фрагментов текста, взятых из ряда источников.

Книга вычислений содержит множество пояснений к решению задач, которые будут подробно рассмотрены в «Девяти главах математического искусства». Пример элементарной математики в Суан сю сю : квадратный корень аппроксимируется с использованием метода ложного положения , который гласит: «объединить избыток и недостаток в качестве делителя; (взяв) числитель недостатка, умноженный на знаменатель избытка и числитель избытка. умножить на знаменатель дефицита, объединить их в дивиденд». Более того, «Книга вычислений» решает системы двух уравнений и двух неизвестных, используя тот же метод ложного положения.

Девять глав

«Девять глав о математическом искусстве» археологически датируются 179 годом нашей эры, хотя традиционно они датируются 1000 годом до нашей эры, но они были написаны, возможно, еще в 300–200 годах до нашей эры. Хотя автор(ы) неизвестны, они внесли большой вклад в восточном мире. Проблемы создаются с помощью вопросов, за которыми сразу следуют ответы и процедура. В тексте нет формальных математических доказательств, только пошаговая процедура. Комментарий Лю Хуэя предоставил геометрические и алгебраические доказательства проблем, изложенных в тексте.

«Девять глав математического искусства» были одной из самых влиятельных из всех китайских математических книг и состояли из 246 задач. Позже оно было включено в « Десять вычислительных канонов» , которые стали основой математического образования в последующие столетия. В эту книгу вошли 246 задач по геодезии, сельскому хозяйству, партнерству, инженерному делу, налогообложению, расчетам, решению уравнений и свойствам прямоугольных треугольников. Девять глав внесли существенные дополнения в решение квадратных уравнений способом, аналогичным методу Горнера . Он также внес значительный вклад в фанчэн , или то, что сейчас известно как линейная алгебра. В седьмой главе решается система линейных уравнений с двумя неизвестными с использованием метода ложного положения, аналогично книге вычислений. Восьмая глава посвящена решению одновременных определенных и неопределенных линейных уравнений с использованием положительных и отрицательных чисел, причем одна задача связана с решением четырех уравнений с пятью неизвестными. Девять глав решают системы уравнений, используя методы, аналогичные современному исключению Гаусса и обратной замене .

Версия «Девяти глав» , послужившая основой для современных интерпретаций, стала результатом усилий ученого Дай Чжэня. Записав задачи непосредственно из энциклопедии Юнлэ , он затем приступил к внесению изменений в исходный текст, а также к включению своих собственных заметок, объясняющих причины внесения изменений. Его законченная работа будет впервые опубликована в 1774 году, но в 1776 году будет опубликована новая редакция, исправляющая различные ошибки, а также включающая версию « Девяти глав из Южной песни», содержащую комментарии Луи Хуэя и Ли Чуньфэна. Окончательная версия работы Дай Чжэня вышла в 1777 году под названием «Павильон пульсации» , причем эта окончательная версия получила широкое распространение и стала стандартом для современных версий «Девяти глав» . Однако эта версия подверглась тщательному анализу со стороны Го Шучэня, утверждающего, что отредактированная версия все еще содержит множество ошибок и что не все первоначальные поправки были внесены самим Дай Чжэнем.

Расчет числа Пи

В задачах «Девяти глав математического искусства» число «пи» принимается равным трем при расчете задач, связанных с кругами и сферами, например, с площадью сферической поверхности. В тексте нет явной формулы для вычисления числа Пи, равного трем, но она используется в задачах как «Девяти глав математического искусства», так и «Записей ремесленника», которые были созданы в один и тот же период времени. Историки полагают, что эта цифра Пи была рассчитана с использованием соотношения 3:1 между длиной окружности и диаметром круга. Некоторые ханьские математики пытались улучшить это число, например Лю Синь, который, как полагают, оценил число Пи в 3,154. Позже Лю Хуэй попытался улучшить расчет, вычислив число Пи равным 3,141024. Лю рассчитал это число, используя многоугольники внутри шестиугольника в качестве нижнего предела по сравнению с кругом. Позже Цзу Чунчжи обнаружил, что число пи составляет 3,1415926 < π < 3,1415927, используя многоугольники с 24 576 сторонами. Этот расчет был обнаружен в Европе в 16 веке.

Не существует явного метода или записи того, как он рассчитал эту оценку.

Деление и извлечение корня

Основные арифметические процессы, такие как сложение, вычитание, умножение и деление, существовали еще до династии Хань. В «Девяти главах математического искусства» эти основные операции воспринимаются как нечто само собой разумеющееся и просто инструктируются читателем их выполнять. Математики Хань вычисляли квадратные и кубические корни аналогично делению, а задачи деления и извлечения корня встречаются в четвертой главе « Девяти глав математического искусства» . Вычисление квадратных и кубических корней чисел осуществляется путем последовательного приближения, так же, как и деление, и часто используются аналогичные термины, такие как делимое ( ши ) и делитель ( фа ). на протяжении всего процесса Затем этот процесс последовательного приближения был распространен на решение квадратичных уравнений второго и третьего порядка, таких как $x^{2}+a=b$, используя метод, аналогичный методу Горнера. Во времена династии Хань метод не был распространен на решение квадратичных уравнений n-го порядка; однако этот метод в конечном итоге был использован для решения этих уравнений.

Фанчэн на счетной доске

Линейная алгебра

Книга вычислений — первый известный текст по решению систем уравнений с двумя неизвестными. есть три набора задач, Всего в «Книге вычислений» связанных с решением систем уравнений с помощью метода ложного положения, которые снова воплощены в практические термины. Седьмая глава из «Девяти глав о математическом искусстве» также посвящена решению системы двух уравнений с двумя неизвестными с помощью метода ложного положения. Чтобы определить большее из двух неизвестных, метод ложного положения предлагает читателю перекрестно умножить второстепенные члены или zi (которые представляют собой значения, заданные для избытка и дефицита) с главными членами mu . Чтобы найти меньшее из двух неизвестных, просто сложите второстепенные члены.

Восьмая глава из девяти глав математического искусства посвящена решению бесконечных уравнений с бесконечным количеством неизвестных. На протяжении всей главы этот процесс называется «процедурой фанчэн». Многие историки предпочли оставить термин фанчэн непереведенным из-за противоречивых свидетельств того, что этот термин означает. Многие историки сегодня переводят это слово на линейную алгебру . В этой главе процесс исключения Гаусса и обратной замены используется для решения систем уравнений со многими неизвестными. Задачи решались на счетной доске и включали в себя использование как отрицательных чисел, так и дробей. Счетная доска фактически представляла собой матрицу , где верхняя строка — это первая переменная одного уравнения, а нижняя — последняя.

Комментарий Лю Хуэя к Девяти главам математического

Метод истощения Лю Хуэя

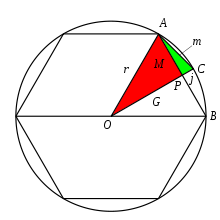
Лю Хуэя Комментарий к «Девяти главам математического искусства» является самым ранним доступным изданием оригинального текста. Многие считают, что Хуэй стал математиком вскоре после династии Хань. В своем комментарии Хуэй уточнил и доказал некоторые проблемы с алгебраической или геометрической точки зрения. Например, в « Девяти главах математического искусства » значение числа «пи» принимается равным трем в задачах, касающихся кругов и сфер. В своем комментарии Лю Хуэй находит более точную оценку числа пи с помощью метода исчерпывания . Этот метод предполагает создание последовательных многоугольников внутри круга, так что в конечном итоге площадь многоугольника более высокого порядка будет идентична площади круга. Используя этот метод, Лю Хуэй установил, что значение числа Пи составляет около 3,14. Лю Хуэй также представил геометрическое доказательство извлечения квадратного и кубического корня, аналогичное греческому методу, который включал разрезание квадрата или куба по любой линии или сечению и определение квадратного корня посредством симметрии остальных прямоугольников.

Троецарствие, Джин и шестнадцать королевств

Обзор морского острова Лю Хуэем

Алгоритм Сунзи для деления 400 г. н.э.

Разделение аль-Хорезми в 9 веке

Статуя Цзу Чунчжи .

В третьем веке Лю Хуэй написал свой комментарий к Девяти главам, а также написал Хайдао Суаньцзин , в котором речь шла об использовании теоремы Пифагора (уже известной по девяти главам) и тройной, четверной триангуляции для геодезии; его достижения в области математических изысканий на тысячелетие превзошли достижения Запада. Он был первым китайским математиком, вычислившим π = 3,1416 с помощью своего π- алгоритма . Он обнаружил использование принципа Кавальери для нахождения точной формулы объема цилиндра, а также разработал элементы исчисления бесконечно малых в III веке нашей эры.

дробная интерполяция для числа Пи

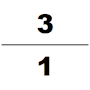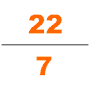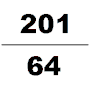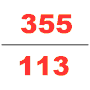
В четвертом веке другой влиятельный математик по имени Цзу Чунчжи представил Да Мин Ли. Этот календарь был специально рассчитан для предсказания множества космологических циклов, которые произойдут в определенный период времени. О его жизни на самом деле известно очень мало. Сегодня единственными источниками являются «Книга Суй» , теперь мы знаем, что Цзу Чунчжи был одним из поколений математиков. Он использовал пи-алгоритм Лю Хуэя, примененный к 12288-угольникам, и получил значение числа пи с точностью до 7 десятичных знаков (между 3,1415926 и 3,1415927), что останется наиболее точным приближением числа π, доступным в течение следующих 900 лет. Он также применил интерполяцию Хэ Чэнтяня для приближения иррационального числа дробью в своих астрономических и математических работах и ​​получил ${\tfrac {355}{113}}$ как хорошее приближение дроби для числа Пи; Ёсио Миками заметил, что ни греки, ни индусы, ни арабы не знали об этом приближении дроби к числу пи, пока голландский математик Адриан Антонисзум не открыл его заново в 1585 году, «поэтому китайцы обладали этим самым необычным из всех дробных значений за всю историю человечества». на целое тысячелетие раньше, чем Европа».

Вместе со своим сыном Цзу Гэном Цзу Чунчжи применил принцип Кавальери, чтобы найти точное решение для расчета объема сферы. Помимо формул для объема сферы, его книга также включала формулы кубических уравнений и точное значение числа Пи. Его работа «Чжуй Шу» была исключена из программы математики во времена династии Сун и утеряна. Многие считали, что Чжуй Шу содержит формулы и методы линейной , матричной алгебры , алгоритм вычисления значения π , формулы объёма сферы. Текст должен также ассоциироваться с его астрономическими методами интерполяции, которые содержали бы знания, подобные нашей современной математике.

Математическое руководство под названием « Математическая классика Сунзи», датированное периодом между 200 и 400 годами нашей эры, содержало наиболее подробное пошаговое описание алгоритма умножения и деления со счетными палочками. Любопытно, что Сунзи , возможно, повлиял на развитие систем стоимости мест и систем стоимости мест и связанного с ними подразделения Галер на Западе. Европейские источники узнали о методах определения стоимости в 13 веке из латинского перевода работы Аль-Хорезми начала 9 века . Представление Хорезми почти идентично алгоритму деления в Сунци , даже в отношении стилистических вопросов (например, использование пробелов для обозначения конечных нулей); сходство предполагает, что результаты, возможно, не были независимым открытием. Исламские комментаторы работы Аль-Хорезми полагали, что она в первую очередь обобщает индуистские знания; Неспособность аль-Хорезми процитировать свои источники затрудняет определение того, научились ли эти источники этой процедуре в Китае.

В пятом веке в руководстве под названием « Чжан Цюцзянь суаньцзин » обсуждались линейные и квадратные уравнения. К этому моменту у китайцев появилась концепция отрицательных чисел .

Династия Тан

Во времена династии Тан изучение математики было довольно стандартным в великих школах. «Десять вычислительных канонов» представляли собой сборник из десяти китайских математических работ, составленный математиком ранней династии Тан Ли Чуньфэном (李淳風 602–670) в качестве официальных математических текстов для императорских экзаменов по математике. Династии Суй и Тан управляли «Школой вычислений».

Ван Сяотун был великим математиком в начале династии Тан , и он написал книгу: Цзигу Суаньцзин ( Продолжение древней математики ), где впервые появляются численные решения общих кубических уравнений.

Первые знания по математике (арифметике) тибетцы получили из Китая во время правления Намри сронг бцана , умершего в 630 году.

Таблицы , составленную в 718 году синусов нашей эры во индийского математика Арьябхаты были переведены в китайскую математическую книгу Кайюань Чжаньцзин времена династии Тан. Хотя китайцы преуспели в других областях математики, таких как твердотельная геометрия , биномиальная теорема и сложные алгебраические формулы, ранние формы тригонометрии не получили такого широкого признания, как в современной индийской и исламской математике .

И Сину , математику и буддийскому монаху, приписывают вычисление таблицы касательных. Вместо этого ранние китайцы использовали эмпирическую замену, известную как чунг ча , в то время как практическое использование плоской тригонометрии для использования синуса, тангенса и секанса было известно. И Син был известен своим гением и, как известно, подсчитывал количество возможных позиций в настольной игре го (хотя без символа нуля ему было трудно выразить это число).

Династии Сун и Юань

династии Северная Сун Математик Цзя Сянь разработал аддитивный мультипликативный метод извлечения квадратного и кубического корня, который реализовал правило «Хорнера».

Треугольник Ян Хуэй ( треугольник Паскаля ) с использованием стержневых цифр, как показано в публикации Чжу Шицзе в 1303 году нашей эры.

Четыре выдающихся математика возникли во времена династий Сун и Юань , особенно в двенадцатом и тринадцатом веках: Ян Хуэй , Цинь Цзюшао , Ли Чжи (Ли Е) и Чжу Шицзе . использовали метод Горнера - Руффини Ян Хуэй, Цинь Цзюшао, Чжу Шицзе шестьсот лет назад для решения определенных типов одновременных уравнений, корневых, квадратных, кубических уравнений и уравнений четвертой степени. Ян Хуэй также был первым человеком в истории, который открыл и доказал « треугольник Паскаля », а также его биномиальное доказательство (хотя самое раннее упоминание о треугольнике Паскаля в Китае существует до одиннадцатого века нашей эры). Ли Чжи, с другой стороны, исследовал форму алгебраической геометрии, основанную на тянь юань шю . Его книга; Цэюань Хайцзин произвел революцию в идее вписания круга в треугольники, превратив эту геометрическую задачу с помощью алгебры вместо традиционного метода использования теоремы Пифагора. Го Шоуцзин того времени также работал над сферической тригонометрией для точных астрономических расчетов. На этом этапе математической истории многие современные западные математики уже были открыты китайскими математиками. На какое-то время все стихло, пока не наступил Ренессанс китайской математики в тринадцатом веке. Это привело к тому, что китайские математики решали уравнения методами, которые Европа не знала до восемнадцатого века. Кульминацией этой эпохи стало Чжу Шицзе Две книги «Суаньсюэ цимэн» и « Нефритовое зеркало четырех неизвестных» . Сообщается, что в одном случае он предложил метод, эквивалентный стержневой конденсации Гаусса .

Цинь Цзюшао ( ок. 1202–1261 ) был первым, кто ввел символ нуля ». в китайскую математику вместо нулей использовались пробелы До этого нововведения в системе счетных палочек . Одним из наиболее важных вкладов Цинь Цзюшао был его метод решения числовых уравнений высокого порядка. Ссылаясь на решение Цинь уравнения 4-го порядка, Ёсио Миками сказал: «Кто может отрицать тот факт, что выдающийся процесс Горнера использовался в Китае, по крайней мере, почти на шесть долгих веков раньше, чем в Европе?» Цинь также решил уравнение 10-го порядка.

Треугольник Паскаля впервые был проиллюстрирован в Китае Ян Хуэем в его книге «Сянцзе Цзючжан Суаньфа» (詳解九章算法), хотя ранее около 1100 года он был описан Цзя Сянем . Хотя « Введение в вычислительные исследования» (算學啓蒙), написанное Чжу Шицзе ( эт. XIII век) в 1299 году, не содержало ничего нового в китайской алгебре, оно оказало большое влияние на развитие японской математики .

Алгебра

Цэюань Хайцзин

Основная статья: Цэюань Хайцзин

Вписанный круг Ли Е в треугольник: схема круглого города

Магические концентрические круги Ян Хуэя - сумма чисел на каждом круге и диаметре (игнорируя средние 9) дает 138.

Цейюань хайцзин ( китайский : 測圓海鏡 ; пиньинь : Cèyuán Hώijìng ), или Морское зеркало измерений круга , представляет собой сборник из 692 формул и 170 задач, связанных с вписанным кругом в треугольник, написанный Ли Чжи (или Ли Е). ) (1192–1272 гг. н.э.). Он использовал Тянь юань шу для преобразования сложных геометрических задач в задачи чистой алгебры. Затем он использовал фан фа , или метод Горнера , для решения уравнений степени до шести, хотя он не описал свой метод решения уравнений. «Ли Чжи (или Ли Е, 1192–1279), пекинский математик, которому Хубилай-хан предложил в 1206 году правительственный пост, но он вежливо нашел предлог отклонить его. Его Цзе-юань хай-цзин ( «Море- Зеркало измерений круга ) включает 170 задач, касающихся [...] некоторых задач, приводящих к полиномиальным уравнениям шестой степени. Хотя он не описал свой метод решения уравнений, похоже, он мало чем отличался от этого. метод Хорнера использовали Чу Ши-цзе и Хорнер. Другими, кто использовал метод Хорнера, были Цинь Цзю-шао (ок. 1202 – ок. 1261) и Ян Хуэй (ок. 1261–1275).

четырех

Факсимиле Нефритового зеркала четырех неизвестных

« Нефритовое зеркало четырех неизвестных» было написано Чжу Шицзе в 1303 году нашей эры и знаменует собой пик развития китайской алгебры. Четыре элемента, называемые небом, землей, человеком и материей, представляли четыре неизвестных величины в его алгебраических уравнениях. Речь идет об одновременных уравнениях и уравнениях степени до четырнадцати. Для решения этих уравнений автор использует метод веера fa , сегодня называемый методом Горнера.

есть много уравнений рядов суммирования, приведенных без доказательства В «Зеркале» . Некоторые из серий суммирования:

$1^{2}+2^{2}+3^{2}+\cdots +n^{2}={n(n+1)(2n+1) \over 3!}$$1+8+30+80+\cdots +{n^{2}(n+1)(n+2) \over 3!}={n(n+1)(n+2)(n+3)(4n+1) \over 5!}$

в девяти

« Математический трактат в девяти разделах » был написан богатым правителем и министром Цинь Цзю-шао ( ок. 1202 – ок. 1261 ) и с изобретением метода решения одновременных сравнений знаменует высшую точку китайской неопределенности. анализ.

Магические квадраты и магические круги

Самые ранние известные магические квадраты порядка больше трех приписываются Ян Хуэю (ок. 1261–1275), который работал с магическими квадратами порядка десяти. «То же самое устройство «Горнера» использовал Ян Хуэй, о жизни которого почти ничего не известно и чьи работы сохранились лишь частично. Среди его дошедших до нас вкладов — самые ранние китайские магические квадраты порядка больше трех, в том числе по два каждый. приказов с четвертого по восьмой и по одному приказу девятого и десятого». Он также работал с магическим кругом .

Тригонометрия

Зародышевое состояние тригонометрии в Китае начало медленно меняться и развиваться во время династии Сун (960–1279), когда китайские математики начали уделять больше внимания необходимости сферической тригонометрии в календарной науке и астрономических расчетах. Эрудит Шэнь и чиновник Го (1031–1095) использовал тригонометрические функции для решения математических задач о хордах и дугах. Джозеф В. Добен отмечает, что в формуле Шена «техника пересекающихся кругов» он создает аппроксимацию дуги окружности s выражением s = c + 2 v. ² / d , где d — диаметр , v — версинус , c — длина хорды c, стягивающей дугу. Сал Рестиво пишет, что работы Шена по длинам дуг окружностей легли в основу сферической тригонометрии, разработанной в 13 веке математиком и астрономом Го Шоуцзином (1231–1316). Гоше и Нидэм заявляют, что Го использовал сферическую тригонометрию в своих расчетах для улучшения китайского календаря и астрономии . Наряду с китайской иллюстрацией математических доказательств Го, датированной более поздним XVII веком, Нидхэм пишет:

Го использовал четырехугольную сферическую пирамиду, базальный четырехугольник которой состоял из одной экваториальной и одной эклиптической дуги вместе с двумя дугами меридиана , одна из которых проходила через точку летнего солнцестояния ... Такими методами он смог получить ду люй. (градусы экватора, соответствующие градусам эклиптики), джи ча (значения хорд для заданных дуг эклиптики) и ча лю (разница между хордами дуг, отличающихся на 1 градус).

Несмотря на достижения работ Шэня и Го в области тригонометрии, еще одна существенная работа по китайской тригонометрии не будет опубликована снова до 1607 года, когда «Начала Евклида» были опубликованы одновременно китайским чиновником и астрономом Сюй Гуанци (1562–1633) и итальянским иезуитом Маттео Риччи. (1552–1610).

Династия Мин

После свержения династии Юань Китай стал с подозрением относиться к знаниям, предпочитаемым монголами. Суд отказался от математики и физики в пользу ботаники и фармакологии . Имперские экзамены включали мало математики, и то немногое, что они включали, игнорировало последние события. Марцлов пишет:

В конце XVI века китайская автохтонная математика, известная самим китайцам, не представляла собой почти ничего, не более чем расчет на счетах, тогда как в XVII и XVIII веках ничто не могло сравниться с революционным прогрессом на театре европейской науки. . Более того, в этот же период никто не мог сообщить о том, что происходило в более отдаленном прошлом, поскольку сами китайцы имели об этом лишь отрывочные сведения. Не следует забывать, что в самом Китае автохтонная математика не была заново открыта в больших масштабах до последней четверти XVIII века.

Соответственно, ученые меньше внимания уделяли математике; выдающиеся математики, такие как Гу Инсян и Тан Шуньчжи, похоже, не знали о методе «умножить умножить» . Без устных собеседников, которые могли бы их объяснить, тексты быстро становились непонятными; что еще хуже, большинство проблем можно решить более элементарными методами. Таким образом, для среднего ученого Тяньюань казалась нумерологией. Когда У Цзин сопоставил все математические труды предыдущих династий в «Аннотациях вычислений в девяти главах математического искусства» , он опустил Тянь юань шу и метод увеличения умножения.

Счеты.

Вместо этого математический прогресс сосредоточился на вычислительных инструментах. В 15 веке счеты приобрели форму суан-пан . Простой в использовании и переноске, быстрый и точный, он быстро вытеснил стержневой исчисление в качестве предпочтительной формы вычислений. Чжусуань , арифметические вычисления на счетах, вдохновил на создание множества новых работ. Суанфа Тунцзонг («Общий источник вычислительных методов»), 17-томный труд, опубликованный в 1592 году Ченг Давеем , использовался более 300 лет. Чжу Цзайюй, принц Чжэна, использовал 81-позиционные счеты для вычисления квадратного корня и кубического корня с точностью от 2 до 25 цифр, точность, которая позволила ему разработать систему равного темперамента .

В конце 16 века Маттео Риччи решил публиковать западные научные труды, чтобы занять должность при императорском дворе. С помощью Сюй Гуанци он смог перевести «Начала » Евклида , используя те же методы, которые используются для преподавания классических буддийских текстов. Его примеру последовали и другие миссионеры, переводившие западные труды по специальным функциям (тригонометрии и логарифмам), которым пренебрегали в китайской традиции. Однако современные учёные сочли акцент на доказательствах, а не на решённых задачах, сбивающим с толку, и большинство из них продолжали работать только на классических текстах.

Династия Цин

При императоре Канси , который изучал западную математику у иезуитов и был открыт для внешних знаний и идей, китайская математика пользовалась кратким периодом официальной поддержки. По указанию Канси Мэй Гоучэн и трое других выдающихся математиков составили 53-томный труд под названием Шули Цзинъюнь («Сущность математического исследования»), который был напечатан в 1723 году и дал систематическое введение в западные математические знания. В то же время Мэй Гоучэн также развился до Мэйши Цуншу Цзияна («Сборник сочинений Мэй»). Мэйши Цуншу Цзиян представлял собой энциклопедическое изложение почти всех школ китайской математики того времени, но оно также включало межкультурные работы Мэй Вэньдинга (1633–1721), дедушки Гоучэна. Предприятие стремилось облегчить китайским математикам, работающим над западной математикой, трудности с отслеживанием цитат.

Однако едва были изданы энциклопедии, как император Юнчжэн взошел на престол. Юнчжэн внес резкий антизападный поворот в китайскую политику и изгнал большинство миссионеров из двора. Не имея доступа ни к западным текстам, ни к понятным китайским текстам, китайская математика находилась в застое.

В 1773 году император Цяньлун решил составить Полную библиотеку Четырех сокровищниц (или Сику Цюаньшу ). Дай Чжэнь (1724–1777) выбрал и вычитал «Девять глав математического искусства» из энциклопедии Юнлэ и несколько других математических работ династий Хань и Тан. Давно пропавшие математические работы династий Сун и Юань, такие как Сы-юань Ю-цзянь и Цэюань Хайцзин , также были найдены и напечатаны, что непосредственно привело к волне новых исследований. Наиболее аннотированными работами были «Цзючжан суаньшу ксиаотушуо» («Иллюстрации процесса вычислений к девяти главам математического искусства »), предоставленные Ли Хуаном, и Сиюань юйцзянь сякао («Подробное объяснение сы-юань юй-цзянь») Ло Шилиня.

влияния

В 1840 году Первая опиумная война вынудила Китай открыть свои двери и взглянуть на внешний мир, что также привело к притоку западных математических исследований темпами, не имеющими себе равных в предыдущие столетия. В 1852 году китайский математик Ли Шаньлан и британский миссионер Александр Уайли совместно перевели последние девять томов « Элементов» и 13 томов по алгебре . При содействии Джозефа Эдкинса вскоре последовали новые работы по астрономии и математическому анализу. Китайские ученые поначалу не были уверены, стоит ли подходить к новым работам: было ли изучение западных знаний формой подчинения иностранным захватчикам ? Но к концу века стало ясно, что Китай может начать восстанавливать свой суверенитет только путем внедрения западных достижений. Китайские ученые, обучавшиеся в западных миссионерских школах на основе (переведенных) западных текстов, быстро потеряли связь с местной традицией. Те, кто обучался самостоятельно или принадлежал к традиционалистским кругам, тем не менее продолжали работать в традиционных рамках алгоритмической математики, не прибегая к западному символизму. Однако, как отмечает Марцлофф, «начиная с 1911 года в Китае практиковалась исключительно западная математика».

В современном Китае

Китайская математика пережила мощный всплеск возрождения после создания современной китайской республики в 1912 году . С тех пор современные китайские математики добились многочисленных достижений в различных математических областях.

Некоторые известные современные этнические китайские математики включают:

• Шиинг-Шен Черн широко известен как лидер в области геометрии и один из величайших математиков двадцатого века и был удостоен премии Вольфа за огромный вклад в математику.
• Кай Фан внес огромный фундаментальный вклад во многие различные области математики. Его работы по теории неподвижной точки , помимо влияния на нелинейный функциональный анализ, нашли широкое применение в математической экономике и теории игр, теории потенциала, вариационном исчислении и дифференциальных уравнениях.
• Шинг-Тунг Яу , его вклад повлиял как на физику, так и на математику, он активно работал на стыке геометрии и теоретической физики и впоследствии был награжден медалью Филдса за свой вклад.
• Теренс Тао , вундеркинд по национальности китаец , получивший степень магистра в 16 лет, был самым молодым участником за всю историю Международной математической олимпиады , впервые участвуя в соревнованиях в возрасте десяти лет и выиграв бронзовую, серебряную и золотую медали. Он остается самым молодым обладателем каждой из трех медалей в истории Олимпиады. Он получил медаль Филдса .
• Итан Чжан , теоретик чисел , установивший первую конечную границу промежутков между простыми числами.
• Чэнь Цзинжунь , теоретик чисел , доказавший, что каждое достаточно большое четное число можно записать как сумму либо двух простых чисел , либо простого и полупростого числа (произведение двух простых чисел), что теперь называется теоремой Чена . Его работа была известна как веха в исследовании гипотезы Гольдбаха .

Китайская Народная Республика

В 1949 году, в начале основания Китайской Народной Республики, правительство уделяло большое внимание делу науки, хотя страна находилась в затруднительном положении из-за нехватки средств. Китайская академия наук была основана в ноябре 1949 года. Институт математики был официально основан в июле 1952 года. Затем Китайское математическое общество и его учредительные журналы восстановили и добавили другие специальные журналы. За 18 лет после 1949 года количество опубликованных статей более чем в три раза превысило общее количество статей до 1949 года. Многие из них не только заполнили пробелы в прошлом Китая, но и достигли передового мирового уровня.

Во время хаоса Культурной революции наука пришла в упадок. В области математики, помимо Чэнь Цзинжуня, Хуа Луоген, Чжан Гуанхоу и другие математики изо всех сил пытаются продолжить свою работу. После катастрофы, с публикацией литературной книги Го Моро «Весна науки», китайские науки и математика пережили возрождение. В 1977 г. в Пекине был сформулирован новый план развития математики, была возобновлена ​​работа математического общества, переиздан журнал, стал издаваться академический журнал, усилилось математическое образование, усилились фундаментальные теоретические исследования.

Важным математическим достижением китайского математика в направлении системы власти является то, как Ся Чжихун доказал гипотезу Пенлеве в 1988 году. При наличии некоторых начальных состояний N небесных тел одно из небесных тел убегало до бесконечности или скорости за ограниченное время. время. Достигнута бесконечность, т. е. имеются нестолкновительные особенности. Гипотеза Пенлеве - важная гипотеза в области энергетических систем, предложенная в 1895 году. Очень важным недавним развитием проблемы четырех тел является то, что Сюэ Цзиньсинь и Долгопят доказали особенность отсутствия столкновений в упрощенной версии системы четырех тел. около 2013 года.

Кроме того, в 2007 году Шен Вэйсяо и Козловски Ван-Стриен доказали гипотезу реального Фату : вещественные гиперболические многочлены плотны в пространстве вещественных многочленов с фиксированной степенью. Эту гипотезу можно проследить до Фату в 1920-х годах, а позже Смейла сформулировал ее в 1960-х годах. Доказательство гипотезы Реального Фату — одно из наиболее важных достижений в области конформной динамики за последнее десятилетие.

Производительность IMO

По сравнению с другими странами-участницами Международной математической олимпиады , Китай имеет самые высокие командные результаты и наибольшее количество раз выигрывал золото IMO для всех членов с полной командой.

В образовании

Первое упоминание о книге, используемой при изучении математики в Китае, датируется вторым веком нашей эры ( Хоу Ханьшу : 24, 862; 35,1207). Нам говорят, что Ма Сюй, молодой человек c. 110 , и Чжэн Сюань (127–200) изучали Девять глав о математических процедурах . Кристофер Каллен утверждает, что математика, как и медицина, преподавалась устно. Стилистика Суань сю из Чжанцзяшаня позволяет предположить, что текст был собран из различных источников, а затем подвергся кодификации.

См. также

• Китайская астрономия
• История математики
  • Индийская математика
  • Исламская математика
  • Японская математика
• Список китайских открытий
• Список китайских математиков
• Числа в китайской культуре

Ссылки

Цитируемые работы

• Бойер, CB (1991). История математики . обр. Ута К. Мерцбах (изд. в мягкой обложке). Уайли. ISBN  0-471-54397-7 .
• Бреар, Андреа (2019). Девять глав о математической современности: очерки о глобальных исторических затруднениях науки о числах в Китае . Транскультурные исследования - Гейдельбергские исследования Азии и Европы в глобальном контексте. Чам: Спрингер. ISBN  978-3-319-93695-6 .
• Добен, Джозеф В. (2007). «Китайская математика». В Каце, Виктор Дж. (ред.). Математика Египта, Месопотамии, Китая, Индии и ислама: справочник . Издательство Принстонского университета. ISBN  978-0-691-11485-9 .
• Добен, Джозеф В. (2008). «算数書 Суан Шу Шу Книга о числах и вычислениях: английский перевод с комментариями». Архив истории точных наук . 62 (2): 91–178. дои : 10.1007/s00407-007-0124-1 . JSTOR   41134274 . S2CID   125757029 .
• Добен, Джозеф В. (2013). «九章筭术 Цзю чжан суань шу (Девять глав об искусстве математики) - оценка текста, его изданий и переводов» . Архив Зудхоффа (на немецком языке). 97 (2): 199–235. doi : 10.25162/sudhoff-2013-0017 . ISSN   0039-4564 . JSTOR   43694474 . ПМИД   24707775 . S2CID   1159700 .
• Ландер, Брайан (10 апреля 2014 г.). «Государственное управление речными дамбами в раннем Китае: новые источники по экологической истории Центрального региона Янцзы» . Тунг Пао . 100 (4–5): 325–362. дои : 10.1163/15685322-10045P02 . ISSN   0082-5433 .
• Либбрехт, Ульрих (1973). Китайская математика в тринадцатом веке: Шу-шу цю-чан Цинь Цзю-шао . Научная серия MIT о Восточной Азии. Кембридж, Массачусетс: MIT Press. ISBN  978-0-262-12043-2 .
• Харт, Роджер (2011). Китайские корни линейной алгебры . Балтимор: Издательство Университета Джонса Хопкинса. ISBN  978-0-8018-9755-9 .
• Конг Гопин (kongguópíng) (октябрь 2012 г.). Чжунгуо сюсюэ шу шан зуй гуан хуи де пьян чжан Самая славная глава в истории китайской математики [ Самая блестящая глава в истории китайской математики ] (на китайском языке). Цзилиньская научно-техническая пресса. ISBN  9787538461541 .
• Кун Гопин (Kong Guoping) (2015) . История китайской математической мысли [ Интеллектуальная история китайской математики ] (на китайском языке). Издательство Нанкинского университета. ISBN  9787305147050 .
• Марцлофф, Жан-Клод (1987). История китайской математики . Перевод Уилсона, Стивена С. Берлина: Springer. ISBN  9783540337836 . OCLC   262687287 . Проверено 17 ноября 2023 г.
• Миками, Ёсио (1961) [1913]. Развитие математики в Китае и Японии (2-е изд.). Нью-Йорк: Челси. ISBN  978-0-8284-0149-4 . ЛЦН   62-001997 .
• Нидхэм, Джозеф (1955). «Метод Горнера в китайской математике». Тунг Пао . Вторая серия. 43 (5): 345–401. JSTOR   4527405 .
• Нидхэм, Джозеф (1959). Математика и науки о небе и земле . Наука и цивилизация в Китае. Том. 3. Издательство Кембриджского университета. ISBN  978-0-521-05801-8 .
• Сиу, Ман-Кеунг (1993). «Доказательство и педагогика в Древнем Китае». Образовательные исследования по математике . 24 (4): 345–357. дои : 10.1007/BF01273370 . JSTOR   3482649 . S2CID   120420378 .
•  В эту статью включен текст из «Британской энциклопедии: словаря искусств, наук, литературы и общей информации», том 26 , Хью Чизхолма, публикации 1911 года, которая сейчас находится в свободном доступе в Соединенных Штатах.
•  В эту статью включен текст из «Жизни Будды и ранней истории его ордена», взятый из тибетских работ в Бках-хгюр и Бстан-хгьюр, за которыми следуют заметки о ранней истории Тибета и Хотена , переведенные Уильямом Вудвиллом Рокхиллом, Эрнст Леуманн, Бунью Наньцзио, публикация 1907 года, сейчас находящаяся в свободном доступе в США.

Внешние ссылки

• Тексты по ранней математике (китайский) - Chinese Text Project
• Обзор китайской математики
• Китайская математика во времена династии Хань
• Букварь математики Чжу Шицзе