Е 7 (математика)

В математике — это E7 _{алгебраических} название нескольких тесно связанных групп Ли , линейных групп или их алгебр Ли e7 _, все из которых имеют размерность 133; то же обозначение E7 _{используется} для соответствующей корневой решетки , имеющей ранг 7. Обозначение E7 _{происходит} из классификации Картана–Киллинга комплексных простых алгебр Ли , которые распадаются на четыре бесконечные серии, обозначенные An _, Bn _, C _n , D _n и пять исключительных случаев, обозначенных E ₆ , E ₇ , E ₈ , F ₄ и G ₂ . алгебра E7 _{Таким образом ,} является одним из пяти исключительных случаев.

Фундаментальной группой (присоединенной) комплексной формы, компактной вещественной формы или любой алгебраической версии E7 _{является} циклическая группа Z /2 Z , а ее внешняя группа автоморфизмов — тривиальная группа . Размерность его фундаментального представления равна 56.

Реальные и сложные формы

Существует единственная комплексная алгебра Ли типа E ₇ , соответствующая комплексной группе комплексной размерности 133. Комплексную присоединенную группу Ли E ₇ комплексной размерности 133 можно рассматривать как простую вещественную группу Ли вещественной размерности 266. Это имеет фундаментальное значение. группа Z /2 Z , имеет максимальную компактную подгруппу компактной формы (см. ниже) группы E ₇ и имеет внешнюю группу автоморфизмов порядка 2, порожденную комплексным сопряжением.

Помимо комплексной группы Ли типа E7 _, существуют четыре действительные формы алгебры Ли и, соответственно, четыре вещественные формы группы с тривиальным центром (все из которых имеют алгебраическое двойное накрытие, а три из них имеют дополнительные не -алгебраические накрытия, придающие дальнейшие вещественные формы), все вещественной размерности 133, а именно:

• Компактная форма (которая обычно имеется в виду, если не указана другая информация), которая имеет фундаментальную группу Z /2 Z и тривиальную внешнюю группу автоморфизмов.
• Расщепляемая форма EV (или E ₇₍₇₎ ), которая имеет максимальную компактную подгруппу SU(8)/{±1}, циклическую фундаментальную группу порядка 4 и группу внешних автоморфизмов порядка 2.
• EVI (или E7 _(-5) ), которая имеет максимальную компактную подгруппу SU(2)·SO(12)/(центр), нециклическую фундаментальную группу порядка 4 и тривиальную внешнюю группу автоморфизмов.
• EVII (или E _7(-25) ), которая имеет максимальную компактную подгруппу SO(2) · E ₆ /(центр), бесконечную циклическую фундаментальную группу и внешнюю группу автоморфизмов порядка 2.

Полный список вещественных форм простых алгебр Ли см. в списке простых групп Ли .

Компактная вещественная форма E7 _— это группа изометрий 64-мерного исключительного компактного риманова симметрического пространства Картана EVI (в классификации ). Она неофициально известна как « кватероктонионная проективная плоскость », поскольку ее можно построить с использованием алгебры, которая является тензорным произведением кватернионов и октонионов , а также известна как проективная плоскость Розенфельда , хотя она не подчиняется обычным аксиомам проективная плоскость. Это можно систематически увидеть, используя конструкцию, известную как магический квадрат , предложенную Гансом Фройденталем и Жаком Титсом .

Конструкция Титса-Кехера производит формы алгебры Ли E ₇ из алгебр Альберта , 27-мерных исключительных йордановых алгебр .

E ₇ как алгебраическая группа

С помощью базиса Шевалле для алгебры Ли можно определить Е7 _как линейную алгебраическую группу над целыми числами и, следовательно, над любым коммутативным кольцом и, в частности, над любым полем: это определяет так называемое расщепление (иногда также известное как как «раскрученный») присоединенная форма E ₇ . Над алгебраически замкнутым полем это и его двойное накрытие являются единственными формами; однако над другими полями часто существует множество других форм или «поворотов» E ₇ , которые классифицируются в общих рамках когомологий Галуа (над совершенным полем k ) множеством H ¹ ( k , Aut(E ₇ )), которая, поскольку диаграмма Дынкина группы E ₇ (см. ниже ) не имеет автоморфизмов, совпадает с H ¹ ( к , Е7 _{, объявление} ).

В поле действительных чисел вещественный компонент идентичности этих алгебраически скрученных форм E ₇ совпадает с тремя упомянутыми выше вещественными группами Ли , но с тонкостью, касающейся фундаментальной группы: все присоединенные формы E ₇ имеют фундаментальную группу Z. /2 Z в смысле алгебраической геометрии, т. е. допускают ровно одно двойное накрытие; поэтому дальнейшие некомпактные вещественные формы группы Ли группы Ли E7 _не являются алгебраическими и не допускают точных конечномерных представлений.

Над конечными полями из теоремы Ланга–Стейнберга следует, что H ¹ ( k , E ₇ ) = 0, что означает, что E ₇ не имеет скрученных форм: см. ниже .

Алгебра

Диаграмма Дынкина

Диаграмма Дынкина для E ₇ имеет вид .

Корневая система

126 вершин многогранника 31 _{представляют} 2 собой корневые векторы E ₇ , как показано в этой на плоскость Кокстера. проекции
Диаграмма Кокстера – Дынкина :

Показано в 3D-проекции с использованием базисных векторов [u,v,w], обеспечивающих симметрию H3:
и = (1, φ , 0, -1, φ , 0,0)
v = ( φ , 0, 1, φ , 0, -1,0)
ш = (0, 1, φ , 0, -1, φ , 0)
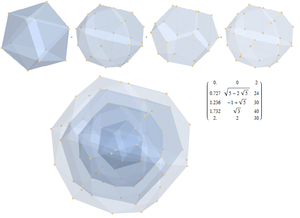
Спроецированные 2 ₃₁ вершины многогранников сортируются и подсчитываются по их трехмерным нормам, в результате чего создаются все более прозрачные оболочки каждого набора подсчитанных норм. Они показывают:
1) 2 точки в начале координат
2) 2 икосаэдра
3) 1 икосадодекаэдр
4) 2 додекаэдра
5) 1 икосадодекаэдр
всего 126 вершин.

Хотя корни охватывают 7-мерное пространство, более симметрично и удобно представлять их в виде векторов, лежащих в 7-мерном подпространстве 8-мерного векторного пространства.

Корнями являются все перестановки 8×7 числа (1,−1,0,0,0,0,0,0) и все ${\begin{pmatrix}8\\4\end{pmatrix}}$ перестановки ( ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ )

Обратите внимание, что 7-мерное подпространство — это подпространство, в котором сумма всех восьми координат равна нулю. Всего корней 126.

– Простые корни это

(0,−1,1,0,0,0,0,0)

(0,0,−1,1,0,0,0,0)

(0,0,0,−1,1,0,0,0)

(0,0,0,0,−1,1,0,0)

(0,0,0,0,0,−1,1,0)

(0,0,0,0,0,0,−1,1)

( ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ ,− ⁠ 1 / 2 ⁠ )

Они перечислены так, что соответствующие им узлы на диаграмме Дынкина расположены слева направо (на диаграмме, изображенной выше), причем боковой узел последним.

Альтернативное описание

Альтернативное (7-мерное) описание корневой системы, которое полезно при рассмотрении E ₇ × SU(2) как подгруппы E ₈ , выглядит следующим образом:

Все $4\times {\begin{pmatrix}6\\2\end{pmatrix}}$ перестановки (±1,±1,0,0,0,0,0), сохраняющие ноль в последней записи, все следующие корни с четным числом + ⁠ 1 / 2 ⁠

$\left(\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over {\sqrt {2}}}\right)$

и два следующих корня

$\left(0,0,0,0,0,0,\pm {\sqrt {2}}\right).$

генераторы состоят из 66-мерной so (12) подалгебры, а также 64 генераторов, которые преобразуются как в два самосопряженных спинора Вейля спина Таким образом , (12) противоположной киральности, так и в их генератор киральности, и в два других генератора киральности. $\pm {\sqrt {2}}$.

E ₇ Учитывая матрицу Картана (ниже) и диаграммы Дынкина : порядок узлов

один выбор простых корней задается строками следующей матрицы:

${\begin{bmatrix}1&-1&0&0&0&0&0\\0&1&-1&0&0&0&0\\0&0&1&-1&0&0&0\\0&0&0&1&-1&0&0\\0&0&0&0&1&1&0\\-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&{\frac {\sqrt {2}}{2}}\\0&0&0&0&1&-1&0\\\end{bmatrix}}.$

Диаграмма Хассе E ₇ корневого частичного набора с метками ребер, обозначающими добавленное простое положение корня

Группа Вейля

Группа Вейля группы E ₇ имеет порядок 2903040: это прямое произведение циклической группы порядка 2 и единственной простой группы порядка 1451520 (которую можно описать как PSp ₆ (2) или PSΩ ₇ (2)).

Матрица Картана

${\begin{bmatrix}2&-1&0&0&0&0&0\\-1&2&-1&0&0&0&0\\0&-1&2&-1&0&0&0\\0&0&-1&2&-1&0&-1\\0&0&0&-1&2&-1&0\\0&0&0&0&-1&2&0\\0&0&0&-1&0&0&2\end{bmatrix}}.$

Важные подалгебры и представления

Вложения максимальных подгрупп E ₇ до размерности 133 показаны с соответствующей матрицей проекции.

E ₇ имеет подалгебру SU(8), о чем свидетельствует тот факт, что в 8-мерном описании корневой системы первая группа корней идентична корням SU(8) (с той же подалгеброй Картана , что и в Е ₇ ).

В дополнение к 133-мерному присоединенному представлению существует 56-мерное «векторное» представление , которое можно найти в _{присоединенном представлении E8} .

Все характеры конечномерных представлений вещественных и комплексных алгебр и групп Ли задаются формулой характеров Вейля . Размеры наименьших неприводимых представлений (последовательность A121736 в OEIS ):

1 , 56, 133 , 912, 1463 , 1539 , 6480, 7371 , 8645 , 24320, 27664, 40755 , 51072, 86184, 150822 , 152152 , 238602 , 253935 , 293930 , 320112, 362880, 365750 , 573440 , 617253 , 861840, 885248, 915705 , 980343 , 2273920, 2282280, 2785552, 3424256 , 3635840...

Подчеркнутые члены в приведенной выше последовательности — это размерности тех неприводимых представлений, которыми обладает присоединенная форма E ₇ (т. е. тех, чьи веса принадлежат корневой решетке E ₇ ), тогда как полная последовательность дает размерности неприводимых представлений E 7 . односвязная форма E ₇ . Существуют неизоморфные неприводимые представления размерностей 1903725824, 16349520330 и т. д.

Фундаментальными представлениями являются представления с размерностями 133, 8645, 365750, 27664, 1539, 56 и 912 (соответствующие семи узлам диаграммы Дынкина в порядке, выбранном для приведенной выше матрицы Картана , т. е. узлы читаются в шестимерном формате). сначала цепочка узлов, причем последний узел подключается к третьему).

вложения максимальных подгрупп группы E ₇ Справа показаны до размерности 133.

E ₇ Polynomial Invariants

E ₇ — группа автоморфизмов следующей пары полиномов от 56 некоммутативных переменных. Мы делим переменные на две группы по 28: ( p , P ) и ( q , Q ), где p и q — действительные переменные, а P и Q 3×3 октонионов — эрмитовые матрицы . Тогда первый инвариант — это симплектический инвариант Sp(56, R ):

$C_{1}=pq-qp+Tr[PQ]-Tr[QP]$

Второй более сложный инвариант — это симметричный многочлен четвертой степени:

$C_{2}=(pq+Tr[P\circ Q])^{2}+pTr[Q\circ {\tilde {Q}}]+qTr[P\circ {\tilde {P}}]+Tr[{\tilde {P}}\circ {\tilde {Q}}]$

Где ${\tilde {P}}\equiv \det(P)P^{-1}$ а оператор двоичного круга определяется выражением $A\circ B=(AB+BA)/2$.

Альтернативный полиномиальный инвариант четвертой степени, построенный Картаном, использует две антисимметричные матрицы размером 8x8, каждая из которых содержит 28 компонентов.

$C_{2}=Tr[(XY)^{2}]-{\dfrac {1}{4}}Tr[XY]^{2}+{\frac {1}{96}}\epsilon _{ijklmnop}\left(X^{ij}X^{kl}X^{mn}X^{op}+Y^{ij}Y^{kl}Y^{mn}Y^{op}\right)$

Chevalley groups of type E ₇

Точки над конечным полем с q элементами (расщепимой) алгебраической группы Е7 ₍ см. выше ), будь то присоединенной (бесцентровой) или односвязной формы (ее алгебраическое универсальное накрытие), дают конечную группу Шевалле . Это тесно связано с группой, записанной E ₇ ( q ), однако в этом обозначении есть двусмысленность, которая может означать несколько вещей:

• конечная группа, состоящая из точек над F _q односвязной формы E ₇ (для наглядности ее можно записать E _7,sc ( q ) и известна как «универсальная» группа Шевалле типа E ₇ над F _q ),
• (реже) конечная группа, состоящая из точек над F _q присоединенной формы к E ₇ (для наглядности ее можно записать E _7,ad ( q ), и известна как «присоединенная» группа Шевалле типа E ₇ над F _q ), или
• конечная группа, которая является образом естественного отображения первой во вторую: это то, что в дальнейшем будет обозначаться E7 ₍ q ) , как это чаще всего встречается в текстах, посвященных конечным группам.

С точки зрения конечной группы, отношения между этими тремя группами, которые совершенно аналогичны отношениям между SL( n , q ), PGL( n , q ) и PSL( n , q ), можно резюмировать следующим образом: E ₇ ( q ) является простым для любого q , E _7,sc ( q ) — его накрытие Шура , а E _7,ad ( q ) лежит в своей группе автоморфизмов; более того, когда q является степенью 2, все три совпадают, а в противном случае (когда q нечетно) множитель Шура E ₇ ( q ) равен 2, а E ₇ ( q ) имеет индекс 2 в E _7,ad ( q ), что объясняет, почему E _7,sc ( q ) и E _7,ad ( q ) часто записываются как 2·E ₇ ( q ) и E ₇ ( q )·2. ) реже _{С точки зрения алгебраической группы, E 7} ( q относится к конечной простой группе, поскольку последняя не является естественным образом множеством точек алгебраической группы над F _q в отличие от E _7,sc ( q ) и E _7,ad ( q ).

Как упоминалось выше, E ₇ ( q ) прост для любого q , и оно составляет одно из бесконечных семейств, к которым обращается классификация конечных простых групп . Его количество элементов задается формулой (последовательность A008870 в OEIS ):

${\frac {1}{\mathrm {gcd} (2,q-1)}}q^{63}(q^{18}-1)(q^{14}-1)(q^{12}-1)(q^{10}-1)(q^{8}-1)(q^{6}-1)(q^{2}-1)$

Порядок E _7,sc ( q ) или E _7,ad ( q ) (оба равны) можно получить, удалив разделительный множитель gcd(2, q −1) (последовательность A008869 в OEIS ). Множитель Шура E ₇ ( q ) равен НОД(2, q −1), а его внешняя группа автоморфизмов является произведением диагональной группы автоморфизмов Z /gcd(2, q −1) Z (задаваемой действием E _7,ad ( q )) и группу полевых автоморфизмов (т. е. циклических порядка f, если q = p ^ж где p — простое число).

Важность в физике

N = 8 Супергравитация в четырех измерениях, которая является размерной редукцией одиннадцатимерной супергравитации , допускает бозонную глобальную симметрию E ₇ SU (8) и бозонную локальную симметрию . Фермионы находятся в представлениях SU(8), калибровочные поля — в представлении E7 _, а скаляры — в представлении обоих (Гравитоны являются синглетами относительно обоих). Физические состояния находятся в представлениях смежного класса E ₇ / SU(8) .

В теории струн E7 _{появляется} как часть калибровочной группы одной из (нестабильных и несуперсимметричных ) версий гетеротической струны . Он также может появиться в неразрывной калибровочной группе E ₈ × E ₇ в шестимерных компактификациях гетеротической теории струн, например на четырехмерной поверхности K3 .

См. также

• И (алгебра Ли)
• Классификация ADE
• Список простых групп Ли

Ссылки

• Адамс, Дж. Франк (1996), Лекции по исключительным группам Ли , Чикагские лекции по математике, University of Chicago Press , ISBN  978-0-226-00526-3 , МР   1428422
• Джон Баэз , Октонионы , Раздел 4.5: E ₇ , Bull. амер. Математика. Соц. 39 (2002), 145-205 . Интернет-версия HTML по адресу http://math.ucr.edu/home/baez/octonions/node18.html .
• Э. Креммер и Б. Джулия, Теория супергравитации N = 8 . 1. Лагранжиан , Phys.Lett.B80:48,1978. Отсканированная онлайн-версия по адресу http://ac.els-cdn.com/0370269378903039/1-s2.0-0370269378903039-main.pdf?_tid=79273 f80-539d-11e4-a133-00000aab0f6c&acdnat=1413289833_5f3539a6365149b108ddcec889200964 .