Равный темперамент

Сравнение некоторых равных темпераментов. График охватывает одну октаву горизонтально (откройте изображение, чтобы просмотреть всю ширину), а каждый затененный прямоугольник - ширина одного шага в масштабе. Справедливые коэффициенты интервала разделены в ряды по их основным пределам .

12 тонального темперамента хроматической шкалы на C , одна полная октава, поднимаясь, известная только с помощью Sharps.

Равный темперамент - это музыкальный темперамент или система настройки , которая приближается только к интервалу , разделяя октаву (или другой интервал) на шаги, так что отношение частот любой смежной пары нот одинакова. Эта система дает шаги шага , воспринимаемые как равные по размеру из -за логарифмических изменений частоты шага.

В классической музыке и западной музыке в целом наиболее распространенной системой настройки с 18 -го века было 12 равный темперамент (также известный как 12 тонального растущего темперамента , 12 Тет или 12 ET , неофициально сокращенные как 12 равных ), что делит октаву на 12 части, все из которых равны в логарифмической шкале , с соотношением, равным 12 -м корне 2 ( ¹² √ 2 ≈ 1,05946). Что в результате наименьший интервал, ⁠ 1/12 ⁠ наполовину или Ширина октавы называется полутоном шагом. В западных странах термин равный темперамент без квалификации, как правило, означает 12 тет .

В наше время 12 TET обычно настраивается относительно стандартного шага 440 Гц, называемого 440 , что означает, что одна нота, A , настраивается на 440 герц , и все остальные ноты определяются как некоторые кратные полутоны от него, либо выше или ниже по частоте. Стандартный шаг не всегда был 440 Гц; Он значительно варьировался и в целом вырос за последние несколько сотен лет.

Другие равные температуры делят октаву по -разному. Например, некоторая музыка была написана в 19 TET и 31 TET , в то время как в системе арабского тона используется 24 TET .

Вместо того, чтобы разделить октаву, равный темперамент также может разделить другой интервал, как и равный вспышка версии шкалы Болен-Пьера , которая делит справедливый интервал октавы и пятую (соотношение 3: 1), называемое A » Tritave "или" псевдо-октава "в этой системе, на 13 равных частей.

Для систем настройки, которые разделяют октаву одинаково, но не являются приближениями только интервалов, термин равного деления октавы или EDO можно использовать .

Unfretted String Ansembles , которые могут регулировать настройку всех заметок, за исключением открытых строк , и вокальных групп, которые не имеют ограничений механической настройки, иногда используют настройку гораздо ближе к просто интонации по акустическим причинам. Другие инструменты, такие как некоторые инструменты ветра , клавиатура и надуваемых , часто только приближаются к одинаковому темпераменту, где технические ограничения предотвращают точные настройки. Некоторые ветровые инструменты, которые могут легко и спонтанно сгибать свой тон, особенно тромбоны , используют настройку, похожую на струнные ансамбли и голосовые группы.

Сравнение равных темпераментов между 10 ТЕТ и 60 ТЕТ на каждом основном интервале с небольшими основными пределами (красный: ⁠ 3/2 , ⁠ зеленый : ⁠ 5/4 , ⁠ : индиго ⁠ 7/4 , ⁠ желтый : ⁠ 11/8 , ⁠ : Голубой ⁠ 13/8 ​ ⁠ ) . Каждый цветной график показывает, сколько ошибки происходит (в центах) на ближайшем приближении соответствующего справедливого интервала (черная линия в центре). Две черные кривые, окружающие график с обеих сторон, представляют максимально возможную ошибку, в то время как серые внутри них указывают половину.

Общие свойства

При равном темпераменте расстояние между двумя смежными этапами шкалы составляет один и тот же интервал . Поскольку воспринимаемая идентичность интервала зависит от его соотношения , эта шкала в ровных шагах представляет собой геометрическую последовательность умножений. ( Арифметическая последовательность интервалов не будет звучать равномерно распределенной и не позволила бы транспозиции в разные ключи .) В частности, наименьший интервал в равной температуре-это отношение:

$\ r^{n}=p\$

$\ r={\sqrt[{n}]{p\ }}\$

где соотношение r делит соотношение p (обычно октава, которая составляет 2: 1) на n равных частей. ( См. Двенадцать тонов равного темперамента ниже. )

Шкалы часто измеряются в центах , которые делят октаву на 1200 равных интервалов (каждый называемый центом). Эта логарифмическая шкала облегчает сравнение различных систем настройки, чем сравнение соотношений, и имеет значительное использование в этномузикологии . Основной шаг в центах для любого равного темперамента можно найти, взяв ширину P выше в центах (обычно октава, которая имеет ширину 1200 центов), называемой ниже W , и деление на n частей:

$\ c={\frac {\ w\ }{n}}\$

В музыкальном анализе материал, принадлежащий равному темпераменту, часто дается целочисленную нотацию , что означает, что для представления каждого шага используется одно целое число. Это упрощает и обобщает обсуждение материала высоты тона в темпераменте так же, как принятие логарифма умножения уменьшает его до добавления. Кроме того, применяя модульную арифметику , где модуль представляет собой количество подразделений октавы (обычно 12), эти целые числа могут быть уменьшены до классов шага , что удаляет различие (или признает сходство) между одноименными высоты, например , C - это 0 независимо от реестра октав. Стандарт кодирования MIDI использует обозначения Integer Note.

Двенадцать тонов равного темперамента

Основная статья: 12 равный темперамент

12 тонального темперамента, который делит октаву на 12 интервалов одинакового размера, является музыкальной системой, наиболее широко используемой сегодня, особенно в западной музыке.

История

Две фигуры, которые часто приписывают достижение точного расчета равного темперамента,-это Чжу Зайю (также романизированный как Чу-цайю. Китайский: 朱載堉 ) в 1584 году и Саймон Стевин в 1585 году. Согласно Фа Куттнеру, критику отдачи Чжу, Известно, что Чжу «представил весьма точный, простой и изобретательный метод для арифметического расчета моно-крошек равного темперамента в 1584 году», и что Стевин «предложил математическое определение равного темперамента плюс несколько менее точное вычисление соответствующих численных значений в 1585 или позже ».

События произошли независимо.

Кеннет Робинсон приписывает изобретению равного темперамента Чжу и предоставляет текстовые цитаты в качестве доказательства. В 1584 году Чжу написал:

Я основал новую систему. Я устанавливаю одну ногу как число, из которого должны быть извлечены другие, и используя пропорции, которые я их извлекаю. В целом, нужно найти точные фигуры для пиппортов в двенадцати операциях.

Куттнер не согласен и замечает, что его утверждение «не может считаться правильным без основной квалификации». Куттнер предполагает, что ни Чжу, ни Стевин не достигли равного темперамента и нельзя считать его изобретателем.

Китай

Zhu Zaiyu Трубы с равной температурой

Китайские теоретики ранее придумали приближения для 12 Тет , но Чжу был первым человеком, который математически решал 12 тонального растущего темперамента, который он описал в двух книгах, опубликованных в 1580 году и 1584. Нидхэм также дает расширенный счет.

Чжу получил свой результат, последовательно разделив длину струны и трубы на ¹² √ 2 ≈ 1,059463 и для длины трубы на ²⁴ √ 2  ≈ 1.029302 , так что после 12 подразделений (октава) длина была вдвое.

Чжу создал несколько инструментов, настроенных на его систему, включая бамбуковые трубы.

Европа

Некоторые из первых европейцев, защищающих равного темперамента, были Lutenists Vincenzo Galilei , Giacomo Gorzanis и Francesco Spinacino , все из которых писали в ней музыку.

Саймон Стевин был первым, кто разработал 12 Тет на основе двенадцатого корня из двух , который он описал в Ван -де -Спигелинге Дер Сингконсте ( ок. 1605 ), опубликованном посмертно в 1884 году.

Остальные игроки для инструментов (Lutenists и гитаристы), как правило, предпочитали равный темперамент, в то время как другие были более разделены. В конце концов, 12-тонный равный темперамент победил. Это позволило энгармоническую модуляцию , новые стили симметричной тональности и политональности , атональную музыку, такую ​​как написанная с 12-тональной техникой или сериализмом , и джаз (по крайней мере, его пианино-компонент) для развития и процветания.

Математика

Одна октава из 12 тет на монохорде

В 12 тональном равный темперамент, который делит октаву на 12 равных частей, ширина семитона , то есть соотношение частоты интервала между двумя соседними нотами - это двенадцатый корень из двух :

${\sqrt[{12}]{2\ }}=2^{\tfrac {1}{12}}\approx 1.059463$

Этот интервал разделен на 100 центов.

Расчет абсолютных частот

См. Также: Ключевые частоты фортепиано

Чтобы найти частоту, p _n , примечания в 12 Тет , можно использовать следующую формулу:

$\ P_{n}=P_{a}\ \cdot \ {\Bigl (}\ {\sqrt[{12}]{2\ }}\ {\Bigr )}^{n-a}\$

В этой формуле P _N представляет высоту или частоту (обычно в Герце ) вы пытаетесь найти. P _A - частота эталонного шага. Индийские числа n и a - это этикетки, назначенные желаемому шагу ( n ) и эталонному шагу ( a ). Эти два числа из списка последовательных целых чисел, назначенных для последовательных полутонов. Например, 4 _{(эталонный шаг) представляет собой} 49 -й ключ с левого конца пианино (настроенный на 440 Гц ) и C ₄ ( середина C ), а F ♯ ₄ - 40 -й и 46 -й клавиши, соответственно. Эти числа могут быть использованы для поиска частоты C ₄ и F ♯ ₄ :

$P_{40}=440\ {\mathsf {Hz}}\ \cdot \ {\Bigl (}{\sqrt[{12}]{2}}\ {\Bigr )}^{(40-49)}\approx 261.626\ {\mathsf {Hz}}\$

$P_{46}=440\ {\mathsf {Hz}}\ \cdot \ {\Bigl (}{\sqrt[{12}]{2}}\ {\Bigr )}^{(46-49)}\approx 369.994\ {\mathsf {Hz}}\$

Преобразование частот в их аналоги с равным темпераментом

Чтобы преобразовать частоту (в Гц) в его равные 12 -ТЕТ -аналоги, можно использовать следующую формулу:

$\ E_{n}=E_{a}\ \cdot \ 2^{\ x}\ \quad$ где в общем $\quad \ x\ \equiv \ {\frac {1}{\ 12\ }}\ \operatorname {round} \!{\Biggl (}12\log _{2}\left({\frac {\ n\ }{a}}\right){\Biggr )}~.$

Сравнение интервалов в 12-метровой с простой интонацией

E _n - частота шага в равной темпераменте, а e _A - частота эталонного шага. Например, если мы позволим эталонному шагу равняться 440 Гц, мы видим, что E ₅ и C ♯ ₅ имеют следующие частоты соответственно:

$E_{660}=440\ {\mathsf {Hz}}\ \cdot \ 2^{\left({\frac {7}{\ 12\ }}\right)}\ \approx \ 659.255\ {\mathsf {Hz}}\ \quad$ где в этом случае $\quad x={\frac {1}{\ 12\ }}\ \operatorname {round} \!{\Biggl (}\ 12\log _{2}\left({\frac {\ 660\ }{440}}\right)\ {\Biggr )}={\frac {7}{\ 12\ }}~.$

$E_{550}=440\ {\mathsf {Hz}}\ \cdot \ 2^{\left({\frac {1}{\ 3\ }}\right)}\ \approx \ 554.365\ {\mathsf {Hz}}\ \quad$ где в этом случае $\quad x={\frac {1}{\ 12\ }}\ \operatorname {round} \!{\Biggl (}12\log _{2}\left({\frac {\ 550\ }{440}}\right){\Biggr )}={\frac {4}{\ 12\ }}={\frac {1}{\ 3\ }}~.$

Сравнение с просто интонацией

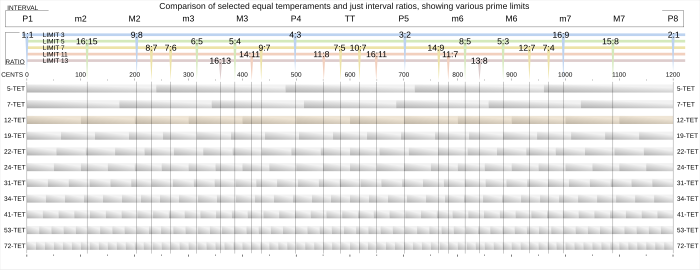
Интервалы 12 тет близко приближаются к некоторым интервалу в просто интонации . Пятые и четвертые почти неразличимо близки к просто с интервалами, в то время как трети и шестой находятся дальше.

В следующей таблице размеры различных справедливых интервалов сравниваются с их одинаковыми аналогами, приведенными в качестве соотношения, а также центов.

Имя интервала	Точное значение в 12 тет	Десятичное значение в 12 тет	Войти в	Просто интервал интонации	Центы в просто интонации	12 центов ​ Ошибка настройки
Унисон ( с )	2 0 ⁄ 12 = 1	1	0	⁠ 1 / 1 ⁠ = 1	0	0
Незначительный второй ( D ♭ )	2 1 ⁄ 12 = 12 √ 2	1.059463	100	⁠ 16 / 15 ⁠ = 1.06666...	111.73	-11.73
Крупный второй ( D )	2 2 ⁄ 12 = 6 √ 2	1.122462	200	⁠ 9 / 8 ⁠ = 1.125	203.91	-3.91
Незначительный третий ( E ♭ )	2 3 ⁄ 12 = 4 √ 2	1.189207	300	⁠ 6 / 5 ⁠ = 1.2	315.64	-15.64
Основной третий ( e )	2 4 ⁄ 12 = 3 √ 2	1.259921	400	⁠ 5 / 4 ⁠ = 1.25	386.31	+13.69
Идеальный четвертый ( F )	2 5 ⁄ 12 = 12 √ 32	1.33484	500	⁠ 4 / 3 ⁠ = 1.33333...	498.04	+1.96
Тритон ( G ♭ )	2 6 ⁄ 12 = √ 2	1.414214	600	⁠ 64 / 45 ⁠ = 1.42222...	609.78	-9.78
Идеальный пятый ( г )	2 7 ⁄ 12 = 12 √ 128	1.498307	700	⁠ 3 / 2 ⁠ = 1.5	701.96	-1.96
( a Незначительный шестой )	2 8 ⁄ 12 = 3 √ 4	1.587401	800	⁠ 8 / 5 ⁠ = 1.6	813.69	-13.69
Основной шестой ( а )	2 9 ⁄ 12 = 4 √ 8	1.681793	900	⁠ 5 / 3 ⁠ = 1.66666...	884.36	+15.64
Незначительный седьмой ( B ♭ )	2 10 ⁄ 12 = 6 √ 32	1.781797	1000	⁠ 16 / 9 ⁠ = 1.77777...	996.09	+3.91
Крупный седьмой ( б )	2 11 ⁄ 12 = 12 √ 2048	1.887749	1100	⁠ 15 / 8 ⁠ = 1.875	1088.270	+11.73
Октава ( с )	2 12 ⁄ 12 = 2	2	1200	⁠ 2 / 1 ⁠ = 2	1200.00	0

Семьтоновое равное разделение пятого

Скрипки, альты и виолончели настраиваются в совершенных пятых ( gdae для скрипок и CGDA для ободи и виолончели), что говорит о том, что их соотношение семитона немного выше, чем при обычном 12 тоне. Поскольку идеальная пятая - в соотношении 3: 2 с его базовым тоном, и этот интервал содержит семь шагов, каждый тон находится в соотношении ⁷ √ ⁠ 3/2 а ⁠ соотношением ≈ 517 к следующему (100,28 центов), что обеспечивает идеальную пятую с соотношением 3: 2, но слегка расширенная октава с : 258 или ≈ 2,00388: 1, не обычная 2: 2: 1, потому что 12 идеальных пятых не равны семи октавам. Однако во время фактической игры скрипачи выбирают высоты на слух, и только четыре неутагнутых шага струн гарантированно продемонстрируют это соотношение 3: 2.

Другие равные температуры

Смотрите также: звук 13

Темпераменты с пятью, семью и девятью в этномузикологии

Приближение 7 Тет

Пяти- и семитоновый равный темперамент ( 5 TET и {{7 tet }} 240 центов и 171 цент Шаги, соответственно, довольно распространены.

5 Tet и 7 Tet отмечают конечные точки достоверного диапазона настройки синтонского темперамента , как показано на рисунке 1 .

• В 5 Tet закаленная идеальная пятая шириной 720 центов (в верхней части континуума настройки) и отмечает конечную точку на континууме настройки , при которой ширина второго второго ужимается до ширины 0 центов.
• В 7 Tet , закаленная идеальная пятая пятая имеет ширину 686 центов (в нижней части континуума настройки) и отмечает конечную точку на континууме настройки, в котором второй второй расширяется, как и главная вторая (по 171 центам каждый )

5 тона и 9 тона равный темперамент

По словам Кунста (1949), индонезийские гамеланы настроены на 5 Тет , но, согласно Худу (1966) и Макфи (1966), их настройка широко варьируется, и, по словам Тензера (2000), они содержат растянутые октавы . В настоящее время принято из двух основных систем настройки в Gamelan Music, Slendro и Pelog , только Slendro несколько напоминает пятитонный равный темперамент, в то время как Pelog очень неравен; Тем не менее, в 1972 году Surjodiningrat, Sudarjana и Susanto анализируют Pelog как эквивалент 9-tet ( ).

7-тонный равный темперамент

Тайский ксилофон , измеренный Мортоном в 1974 году «варьировался только плюс или минус 5 центов» от 7 Тет . По словам Мортона,

«Тайские инструменты фиксированной высоты настроены на равноправную систему из семи шагов на октаву ... Как и в западной традиционной музыке, однако все виды системы настройки не используются в одном режиме (часто называемая« масштаб »); В тайской системе пять из семи используются в основных шагах в любом режиме, тем самым устанавливая схему невидистых интервалов для режима ».

В 1969 году в 1969 году шкала южноамериканских индейцев из доинструментальной культуры, измеренной с помощью коилью в 1969 году, показал 175 центов с семью тональным темпераментом, который немного растягивает октаву, как и в случае с инструментальной музыкальной музыкой.

Китайская музыка традиционно использовала 7 тет .

Различные равные температуры

Система нотации Исли Блэквуд для 16 равных темпераментов: интервалы отмечены аналогично тем, что они приближаются, и меньше экранмонических эквивалентов.

Сравнение равных темпераментов от 9 до 25

19 или

Многие инструменты были построены с использованием 19 EDO Tuning. Эквивалентно ⁠ 1/3 ​ ⁠ Компа ​ ​Третий и основной шестой, чем 19 Эдо 232 Эдо. Его идеальный четвертый (на 505 центов), на семь центов острее, чем просто интонация и пять центов острее, чем 12 Эдо.

22 или

22 EDO является одним из самых точных EDO, представляющих суперпийский темперамент (где 7: 4 и 16: 9 - тот же интервал) и находится рядом с оптимальным генератором для темперамента дикобраза. Пятые настолько острые, что основные и второстепенные трети, которые мы получаем от пятых, станут третьими (9/7) и субминором (7/6). На шаг ближе друг к другу находятся классические основные и незначительные трети (5/4 и 6/5).

23 или

23 Эдо является крупнейшим Эдо, который не может приблизительно приближать 3 -й, 5 -й, 7 -й и 11 -й гармоник (3: 2, 5: 4, 7: 4, 11: 8) в пределах 20 центов. Тем не менее, он очень хорошо соответствует некоторым соотношениям между ними (например, второстепенной третьей 6: 5), что делает его привлекательным для микротоналистов, ищущих необычную гармоническую территорию.

24 или

24 Edo , четвертьтона , особенно популярна, так как представляет собой удобную точку доступа для композиторов, обусловленных стандартными Western 12 Edo Pitch и записи, которые также заинтересованы в микротональности. Поскольку 24 Edo содержит все поля 12 EDO, музыканты используют дополнительные цвета, не теряя никакой тактики, доступной в 12 тональной гармонии. Это 24, кратное 12, также делает 24 EDO легко достичь инструментальных инструментов, используя два традиционных 12-инструмента EDO, настроенных на четверть тона, такие как два пианино, что также позволяет каждому исполнителю (или один исполнитель, играющий на фортепиано с каждой рукой. ) читать знакомые 12 тональных обозначений. Различные композиторы, в том числе Чарльз Айвз , экспериментировали с музыкой для квартал-тональных пианино. 24 Эдо также очень хорошо приближается к 11 -м и 13 -м гармоникам, в отличие от 12 Эдо.

26 или

26 является знаменателем сходительного к log ₂ (7), настраивая 7 -ю гармонику (7: 4) с менее чем половиной цента ошибки. Несмотря на то, что он предназначен для темперамента, он очень плоский, с четырьмя его идеальными пятыми, производящими основную квартиру третьего 17 центов (приравнивается к нейтральной третьей трети 11: 9). 26 Эдо имеет две малые трети и две малые шестой, и он может быть альтернативным темпераментом для гармонии парикмахерской .

27 или

27 является самым низким числом равных подразделений октавы, которые уникально представляют все интервалы, включающие первые восемь гармоник. Это вытаскивает септимальную запятую , но не синтоническую запятую .

29 или

29 - это самое низкое количество равных подразделений октавы, идеальная пятая пятая, чем в 12 EDO, в котором пятая - 1,5 цента, а не 2 цента. Его классический основной третий примерно такой же неточный, как 12 Эдо, но настраивается на 14 центов, а не 14 центов. Он также настраивает 7 -й, 11 -й и 13 -й гармоники плоской примерно на то же количество, что позволяет 29 EDO соответствовать интервалу, таким как 7: 5, 11: 7 и 13:11 очень точно. Резка все 29 интервалов пополам производит 58 EDO , что допускает более низкие ошибки для некоторых только тонов.

31 или

31 Эдо был защищен Кристианом Хейгенсом и Адрианом Фоккером и представляет собой стандартизацию четверть коммерки . 31 EDO не имеет столь точной пятой, как 12 EDO (например, 19 EDO), но его основные трети и незначительные шестой находятся менее чем на 1 цент от всего лишь. Это также обеспечивает хорошие матчи для гармоник до 11, из которых седьмая гармоника особенно точна.

34 или

34 EDO дает немного более низкие общие комбинированные ошибки приближения к 3: 2, 5: 4, 6: 5, а их инверсии, чем 31 EDO, несмотря на немного менее точную посадку в течение 5: 4. 34 EDO не точно приближается к седьмой гармонике или соотношению с участием 7, и не подразумевается, поскольку его пятая часть является острым, а не плоским. Это позволяет тритону на 600 центов, поскольку 34 - равномерное число.

41 или

41 - следующий Эдо с лучшим идеальным пятым, чем 29 Эдо и 12 Эдо. Его классическая крупная треть также является более точной, всего лишь шесть центов. Это не подразделенный темперамент, поэтому он различает 10: 9 и 9: 8, а также классические и пифагорские мажор, в отличие от 31 Эдо. Это более точное в 13 пределе, чем 31 Эдо.

46 или

46 EDO предоставляет основные трети и идеальные пятые, которые немного острые, и многие Скажите, что это дает крупным триадам характерный яркий звук. Основные гармоники до 17 находятся в пределах 6 центов от точности, а 10: 9 и 9: 5 - пятая часть цента от чистого. Поскольку это не система подразделенной, она различает 10: 9 и 9: 8.

53 или

53 EDO только случайно применял, но лучше приближается к традиционным справедливости, чем 12, 19 или 31 EDO. Его чрезвычайно точные идеальные пятые делают его эквивалентным расширенной пифагорской настройке , так как 53 является знаменателем сходящегося в log ₂ (3). С его точным циклом пятых и многоцелевого шага запятой, 53 EDO использовался в теории турецкой музыки . Это не подразделенный темперамент, который ставит хорошие трети в течение легкого досягаемости, укладывая пятые; Вместо этого, как и все расколовые температуры , самые согласные трети представлены пифагорейским дефицитом четвертого (CF ♭ ), достигнутыми путем укладки восемь идеальных четвертых. Это также вытаскивает Kleisma , позволяя ее пятую, чтобы быть достигнут стопкой из шести малых третей (6: 5).

58 или

58 Равный темперамент - это дублирование 29 Эдо, которое он содержит как встроенный темперамент. Как и 29 Эдо, он может соответствовать интервалу, таким как 7: 4, 7: 5, 11: 7 и 13:11 очень точно, а также лучшие приблизительные только трети и шестые.

72 или

72 Эдо хорошо приближается к многим интервалу интонации , обеспечивая почти только эквиваленты 3-го, 5-го, 7-го и 11-го гармоники. 72 Эдо преподавали, написали и исполняли на практике Джо Манери и его ученики (чьи атональные склонности обычно избегают какой -либо ссылки на просто интонацию ). Поскольку это кратно 12, 72 EDO можно считать расширением 12 EDO, содержащих шесть копий из 12 EDO, начиная с разных поля, три копии из 24 EDO и две копии из 36 EDO.

96 или

96 Эдо приближает все интервалы в пределах 6,25 цента, что едва ли различено. Как восьмикратное кратное 12, его можно полностью использовать, как общий 12 EDO. Это отстаивало несколько композиторов, особенно Джулиан Каррильо .

Другие равные подразделения октавы, которые обнаружили случайное использование, включают 13 Эдо , 15 Эдо и 17 Эдо .

2, 5, 12, 41, 53, 306, 665 и 15601 являются знаменателями первых конвергентов Log ₂ (3), SO 2, 5, 12, 41, 53, 306, 665 и 15601 Двенадцы (и пятые), существо В корреспонденте равные температуры, равные целочисленному числу октава, являются лучшими приближениями 2, 5, 12, 41, 53, 306, 665 и 15601 только двенадцатых/пятых, чем в любом равном темпераменте с меньшим количеством тонов.

1, 2, 3, 5, 7, 12, 29, 41, 53, 200, ... (последовательность A060528 в OEI ) - это последовательность подразделений октавы, которая обеспечивает лучшие и лучшие приближения идеальной пятой. Связанные последовательности, содержащие подразделения, приближающиеся к другим справедливым интервалам, перечислены в сноске.

Равные температуры не-октавных интервалов

Равная температурная версия шкалы Болен-Пьерса состоит из соотношения 3: 1 (1902 цента), традиционно идеальной пятой плюс октава (то есть идеального двенадцатого), называемого в этой теории ( игра ( ) и разделен на 13 равных частей. Это обеспечивает очень близкое совпадение с справедливо настроенными соотношениями, состоящими только из нечетных чисел. Каждый шаг составляет 146,3 цента ( ), или ¹³ √ 3 .

Венди Карлос создала три необычных равных темперамента после тщательного изучения свойств возможных темпераментов с размером шага от 30 до 120 центов. Они назывались альфа , бета и гамма . Их можно считать равными подразделениями идеальной пятой. Каждый из них обеспечивает очень хорошее приближение нескольких интервалов. Их размеры шагов:

• Альфа : ⁹ √ ⁠ 3/2 Игра ⁠ ( )
• Бета : ¹¹ √ ⁠ 3/2 игра ⁠ ( )
• Гамма : ²⁰ √ ⁠ 3/2 игра ⁠ ( )

Альфа и бета могут быть услышаны на заглавном треке альбома Carlos в 1986 году Beauty in the Beast .

Пропорции между полутоном и всем тоном

В этом разделе у полутона и целого тон могут не быть своих обычных значений EDO, так как в нем обсуждается, как они могут быть смягчены по -разному, от своих справедливых версий до создания желаемых отношений. Пусть количество шагов в полутоне будет S , и количество шагов в тоне будет t .

Есть ровно одно семейство равных темпераментов, которое исправляет полутон на любую правильную долю всего тона, сохраняя при этом заметки в правильном порядке (это означает, что, например, C , D , E , F и F ♯ поднимаются Закажите, если они сохраняют свои обычные отношения с C ). То есть исправление Q к правильной фракции в отношениях QT = S также определяет уникальное семейство одного растущего темперамента и его мультипликатора, которые выполняют эту связь.

Например, где k - целое число, 12 К Эдо наборы q = ⁠ 1/2 ​ ⁠ ​ , 19 K EDO SETS Q = ⁠ 1/3 ​ ⁠ ​ ​ и 31 K EDO SETS Q = ⁠ 2/5 ​ ⁠ ​ . Наименьшие кратные в этих семьях (например, 12, 19 и 31 выше) имеют дополнительное свойство, не имеющих заметок за пределами круга пятых . (Это не так в целом; в 24 Эдо , полу-шиппестные и полуфлаты не находятся в круге пятых, начиная с c .) Чрезвычайные случаи- 5 К Эдо , где Q = 0 , а полутон становится Unison, и 7 K Edo , где Q = 1 и полутон и тон - один и тот же интервал.

Как только кто -то узнает, сколько шагов находится в полутоне и тон в этом равном темпераменте, можно найти количество шагов, которые он имеет в октаве. Равный темперамент с вышеупомянутыми свойствами (включая отсутствие заметок за пределами круга пятых) делит октаву на 7 T - 2 с шагами идеальную пятую на 4 T - S. и Если есть примечания за пределами круга пятых, необходимо увеличить эти результаты на n , количество непересекающихся кругов пятых, необходимых для создания всех заметок (например, два из 24 Эдо , шесть из 72 Эдо ). (С этой целью нужно взять небольшой семитон: 19 у Эдо есть два полутона, один из них ⁠ 1/3 , Тон ⁠ а другое - ⁠ 2/3 ​ ⁠ ​ . Точно так же 31 EDO имеет два полутона, один из которых ⁠ 2/5 , Тон ⁠ а другое - ⁠  3  / 5 ⁠ ).

Наименьшим из этих семей является 12 К Эдо , и, в частности, 12 Эдо является наименьшим равным темпераментом с вышеуказанными свойствами. Кроме того, это делает семитон ровно половину всего тона, самым простым возможным отношением. Это некоторые из причин, по которой 12 Эдо стал наиболее часто используемым равным темпераментом. (Другая причина заключается в том, что 12 EDO является наименьшим равным темпераментом, чтобы приблизительно приблизительно 5 лимит-гармонии, следующим образом является 19-й из них 19 Edo.)

Каждый выбор фракции Q для взаимосвязи приводит к тому, что один из равных темпераментов, но обратное неправда: 47 EDO имеет два разных полутона, где один ⁠ 1/7 , Тон ⁠ а другой - ⁠ 8/9 19 ⁠ , которые не являются дополнениями друг друга, как в Эдо ( ⁠ 1/3 ​ ⁠ и ​ ⁠ 2/3 ​ ⁠ ) . Принимая каждый семитон приводит к другому выбору идеального пятого.

Связанные системы настройки

Регулярные диатонические настройки

Рисунок 1: Регулярные континуум диатонических настроек , которые включают в себя много заметных настроек «равного темперамента».

Диатоническая настройка в 12 тональном растущем темпераменте (12 Тет ) может быть обобщена на любую обычную диатоническую настройку, делящую октаву как последовательность этапов   T T T T T T S   (или некоторого кругового сдвига или «вращения»). Чтобы называться обычной диатонической настройкой, каждый из двух полутонов ( ы ) должен быть меньше, чем любой из тонов ( больший тон , t и меньший тон , t ). Запятая κ подразумевается как отношение размера между большими и меньшими тонами: выражено как частоты κ = ⁠   T   / T ⁠ , или в качестве центов   κ = t - t   .

Примечания в обычной диатонической настройке связаны в «спирали пятых», которая не закрывается (в отличие от круга пятых в 12 Тет ). Начиная с субдомиминантного F (в ключе от C ) есть три идеальных пятых подряд - F - C , C - G и G - D - сочиняйте некоторую перестановку меньших интервалов   TT TS . Три пятых настройки прерваны могилой пятой d - a =   t tts   ( могила означает «квартира за запятой »), за которым следует еще одна идеальная пятая, e - b , и еще одна могила пятая, b - f ♯ и и и затем перезагрузка в острых островах с F ♯ - C ♯ ; Тот же паттерн повторяется через острые ноты, затем двойные шины и т. Д., Неопределенный. Но каждая октава полностью натуральных или всеотраслевых или все-двойных шиповников выравнивается на две запятой с каждым переходом от натуральных к шарпам или отдельных шарпах к двойным островам и т. Д. Паттерн также является обратным симметричным в квартирах: Спускается на четвертых, рисунок взаимно обостряет примечания по двум запятой с каждым переходом от естественных нот к сплющенным нотам или квартирам к двойным квартирам и т. Д. Если оставлены немодифицированными, две могилы в каждом блоке полностью натуральных нот или все-шарпс , или примечания к всесторонним Интервалы "Волк" : каждый из могил пятых из мелодий диатонической запятой .

Поскольку запятая, κ , расширяет меньший тонус   T = SC , в больший тонус ,   t = SC κ , октава только T   T T T T S   может быть разбит на последовательность   SC κ SC S SC SC SC κ S S S κ S , (или круговой сдвиг ) диатонических полутонов S , хроматических полутонов C и запятых   κ . Различные равные температуры изменяют размеры интервалов, обычно разбивая три запятые, а затем перераспределяют их части в семь диатонических полутонов или в пять хроматических полутонов C или в как S , так и с C , с некоторыми фиксированными пропорциями для каждого типа семитона Полем

Последовательность интервалов S , C и κ может быть неоднократно добавлять к себе в большую спираль в 12 пятых и сделана для подключения на дальние конца путем небольших корректировок к размеру одного или нескольких интервалов или оставленных не Случайно менее чем идеальные пятые, плоские запятыми.

Превращать диатонические настройки в Эдо

Равный темперамент может быть создан, если размеры основных и второстепенных тонов ( t , t ) изменены как одинаковые (скажем, путем установки κ = 0 , а другие расширились, чтобы все еще заполнить октаву), и оба полутона ( s и c ) Тот же размер, затем двенадцать равных полутонов, два на тон, результат. В 12 Tet полутон, S , ровно вдвое меньше всего того же размера целых тонов t = t .

Некоторые из промежуточных размеров тонов и семитонов также могут быть получены в системах равных темпераментов путем изменения размеров запятой и семитонов. Получает 7 Тет в пределе, как размер C и κ, имеет тенденцию к нулю, а октава сохраняется фиксированной, а 5 Тет в пределе, как S и κ, имеют тенденцию к нулю; 12 Тет , конечно, случай   S = C   и   κ = 0 . Например:

5 Тет и 7 Тет

Есть два экстремальных случая, которые связаны с этой структурой: когда S и κ уменьшаются до нуля, а размер октавы остается фиксированным, результат - TTTTT , 5 -тональный равный темперамент. По мере того, как S становится все больше (и поглощает пространство, ранее используемое для запятой κ ), в конечном итоге шаги-все одинаковый размер, ttttttt , и результат-равный темперамент с семью тонами. Эти две крайности не включены как «обычные» диатонические настройки.

19 Tet

Если диатоновый семитон установлен вдвое больше, чем размер хроматического полутона, то есть   S = 2 C (в центах) и   κ = 0 , результат - 19 Тет , с одним шагом для хроматического семитона C , два шага для диатонического семитона S , три шага для тонов T = T и общее количество шагов 3 T + 2 T + 2 S = 9 + 6 + 4 = 19 шагов. Встроенная 12 тональная подсистема внимательно приближается к исторически важной ⁠ 1/3 ​ Защита ⁠ подразумевающая система .

31 тет

Если хроматический семитон составляет две трети размера диатонического семитона, т.е. c = ⁠ 2/3 для диатонического семитона ⁠ , с двумя шагами для хроматического полутона, три шага с , с κ = 0 , результат составляет 31 Тет и пять шагов для тона, где 3 T + 2 T + 2 S = 15 + 10 + 6 = 31 шаг . Встроенная 12 тональная подсистема внимательно приближается к исторически важной ⁠ 1/4 4 ⁠ один параграф означало .

43 Тет

Если хроматический семитон составляет три четверти размера диатонического семитона, т.е. c = ⁠ 3/4 шага для диатонического семитона ⁠ , с тремя шагами для хроматического полутона, четыре S , с κ = 0 , результат составляет 43 Тет и семь шагов для тона, где 3 T + 2 T + 2 S = 21 + 14 + 8 = 43. Встроенная 12 тональная подсистема близко приближается ⁠ 1/5 ⁠ один параграф означало .

53 Тет

хроматический семитон сделан такого же размера, как три запятых,   κ в центах   частоте   c = κ ³   ) диатонические   , Если c 3 по = ( S + C = 8 κ , и более высокий тон девять,   t = S + C + κ = 9 κ . Следовательно, 3 T + 2 T + 2 S = 27 κ + 16 κ + 10 κ = 53 κ для 53 стадий по одной запятой каждый. Размер запятой / размер шага равен   κ = ⁠ 1300/53 = ¢ ⁠ ¢ точно, или   κ 22,642 ¢   ≈ 21,506 , синтонская запятая . Это чрезвычайно близкое приближение к 5-лимитной просто интонации и пифагорской настройке, и является основой для теории турецкой музыки .

Смотрите также

• Просто интонация
• Музыкальная акустика
  (Физика музыки)
• Музыка и математика
• Микротунер
• Микротональная музыка
• Настройка фортепиано
• СПИСОК ИНДАКОВЫХ интервалов
• Диатонический и хроматический
• Электронный тюнер
• Музыкальная настройка

Источники

• Boiles, J. (1969). «Терпехуа, хотя и песня». Этномузикология . 13 : 42–47.
• Чо, Джин Джинсионг (2003). Открытие музыкального равного темперамента в Китае и Европе в шестнадцатом веке . Льюистон, Нью -Йорк: Эдвин Меллен Пресс .
• Даффин, Росс В. (2007). Как равный темперамент разрушил гармонию (и почему вы должны заботиться) . Нью -Йорк, Нью -Йорк: Wwnorton & Company. ISBN  978-0-39306227-4 .
• Jorgensen, Owen (1991). Настройка . Издательство штата Мичиган Университет. ISBN  0-87013-290-3 .
• Сетарес, Уильям А. (2005). Настройка, тембра, спектр, масштаб (2 -е изд.). Лондон, Великобритания: Springer-Verlag. ISBN  1-85233-797-4 .
• Сдача, W.; Внезапно PJ; Поддержание, А. (1972). Тона вокруг Яванея за пределами яванского плана, который Jogjakta, In: Получите Madade Press University. Как метод «Шкала Центральной Явы Gamelan в качестве примера негармонического музыкального масштаба» . Telia.com . Нейробиология музыки. Архивировано из оригинала 27 января 2005 года . Получено 19 мая 2006 года .
• Стюарт, PJ (2006) [январь 1999]. От галактики до галактики: музыка сфер (отчет). 8096295 - через Academia.edu. "Alt. Link 1" . 269108386 - через ResearchGate.net. "Alt. Link 2" - через Google Docs.
• Храмов, Михайло (26–29 июля 2008 г.). Приближение 5-лимитной просто интонации . Компьютерное MIDI моделирование в негативных системах равных подразделений октавы. Международная конференция SIGMAP-2008 . Порту . С. 181–184. ISBN  978-989-8111-60-9 .

Дальнейшее чтение

• Helmholtz, H. (2005) [1877 (4 -е немецкое изд.), 1885 (2 -е английское изд.)]. По ощущениям тона как физиологической основы для теории музыки . Перевод Эллис, AJ (переиздание изд.). Whitefish, MT: Kellinger Publishing. ISBN  978-1-41917893-1 Полем OCLC   71425252 - через интернет -архив (archive.org).
  - основополагающая работа по акустике и восприятию звука. Особенно материал в Приложении XX: дополнения переводчиком , страницы 430–556 (PDF -страницы 451–577) (см. Также статью Wiki о ощущениях тона )

Внешние ссылки

• Введение в исторические настройки Кайла Ганна
• Xenharmonic Wiki на Edos Vs. Равные температуры
• Фонд Хуйгенс-Фоккера Центра микротональной музыки
• A.Orlandini: музыка акустика
• «Темперамент» от добавки к циклопдии мистера Чемберса (1753)
• Барбиери, Патрицио. Энфармонические инструменты и музыка, 1470–1900 . (2008) Латина, публикация библиотеки Levante
• Фрактальная микротональная музыка , Джим размер .
• Все существующие цитаты 18 -го века на JS Bach и темперамент
• Доминик Экерсли: « Rosetta Revisited: очень обычный темперамент Баха »
• Скважина темпераменты, основанные на определении Werckmeister
• F aepred cardinality ​ от кальсов ​ ​ от perter b uch