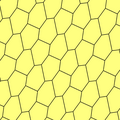
Шестиугольная плитка

Шестиугольная плитка

Тип	Обычная плитка
Конфигурация вершин	6.6.6 (или 6 ³)
Конфигурация лица	V3.3.3.3.3.3 (или V3 ⁶)
Символ (ы) Шлефли	{6,3} т{3,6}
Символ (ы) Витхоффа	3 \| 6 2 2 6 \| 3 3 3 3 \|
Диаграмма(ы) Кокстера
Симметрия	p6m , [6,3], (*632)
Симметрия вращения	р6 , [6,3] ⁺, (632)
Двойной	Треугольная плитка
Характеристики	Вершинно-транзитивный , ребро-транзитивный , грани-транзитивный

В геометрии шестиугольная мозаика или шестиугольная мозаика — это правильная мозаика евклидовой плоскости , в которой ровно три шестиугольника в каждой вершине встречаются . Он имеет Шлефли символ ${6,3}$ или $t {3,6}$ (как усеченная треугольная мозаика).

Английский математик Джон Конвей назвал это гекстилем .

шестиугольника Внутренний угол составляет 120 градусов, поэтому три шестиугольника в одной точке составляют полные 360 градусов. Это одно из трех правильных замощений плоскости . Два других — это треугольная мозаика и квадратная мозаика .

Приложения

Шестиугольная плитка — это самый плотный способ расположить круги в двух измерениях. Гипотеза о сотах утверждает, что шестиугольная мозаика — лучший способ разделить поверхность на области равной площади с наименьшим общим периметром. Оптимальную трехмерную структуру для изготовления сот (вернее, мыльных пузырей) исследовал лорд Кельвин , который считал, что структура Кельвина (или объемноцентрированная кубическая решетка) является оптимальной. Однако менее регулярная структура Вейра – Фелана немного лучше.

Эта структура существует в природе в виде графита , где каждый лист графена напоминает проволочную сетку с сильными ковалентными углеродными связями. Были синтезированы трубчатые листы графена, известные как углеродные нанотрубки . Они имеют множество потенциальных применений благодаря своей высокой прочности на разрыв и электрическим свойствам. Силицен аналогичен.

Проволочная сетка состоит из шестиугольной решетки (часто нерегулярной) проволок.

Самая плотная упаковка кругов на этой мозаике устроена как шестиугольники.
из проволочной сетки Ограждение
Графен
можно Углеродную нанотрубку рассматривать как шестиугольную плитку на цилиндрической поверхности.
Шестиугольная персидская плитка около 1955 г.

Шестиугольная черепица появляется во многих кристаллах. В трех измерениях гранецентрированная кубическая и гексагональная плотная упаковка распространенными кристаллическими структурами являются . Это самые плотные упаковки сфер в трех измерениях. Структурно они представляют собой параллельные слои шестиугольных плиток, аналогичные структуре графита. Они отличаются тем, что слои расположены в шахматном порядке друг от друга, при этом гранецентрированный куб является более правильным из двух. Чистая медь , среди других материалов, образует гранецентрированную кубическую решетку.

Равномерные раскраски

Существует три различных однородных цвета шестиугольной мозаики, все они созданы на основе отражательной симметрии конструкций Витхоффа . ( h , k ) представляют собой периодическое повторение одной цветной плитки, считая шестиугольные расстояния сначала h , а затем k . Тот же подсчет используется в многогранниках Гольдберга с обозначением { p +,3} _{h , k} и может быть применен к гиперболическим мозаикам для p > 6.

к -равномерный	1-униформа			2-униформа		3-униформа
Симметрия	п6м, (*632)		p3m1, (*333)	п6м, (*632)		п6, (632)
Картина
Цвета	1	2	3	2	4	2	7
(ч,к)	(1,0)	(1,1)		(2,0)		(2,1)
Шлефли	{6,3}	т{3,6}	т{3 ^[3]}
Витхофф	3 \| 6 2	2 6 \| 3	3 3 3 \|
Коксетер
Конвей	ЧАС	tΔ		cH=t6daH		wH=t6dsH

Трехцветная мозаика представляет собой мозаику, созданную пермутоэдрами третьего порядка .

Шестиугольная плитка со скошенными краями

Шестиугольная мозаика со скошенной кромкой заменяет ребра новыми шестиугольниками и преобразуется в другую шестиугольную мозаику. В пределе исходные грани исчезают, а новые шестиугольники вырождаются в ромбы, и получается ромбическая мозаика .

Шестиугольная *мозаика со скошенными краями* вырождается в ромбовидную мозаику. на пределе

Шестиугольники (H)	Шестигранники с фаской (cH)			Ромби (даХ)

Связанные мозаики

Шестиугольники можно разбить на наборы по 6 треугольников. Этот процесс приводит к двум 2-однородным мозаикам и треугольным мозаикам :

Обычная плитка	Диссекция	2-однородные мозаики		Обычная плитка	Вставка	Двойные мозаики
Оригинал		1/3 рассечённая	2/3 рассеченный	полностью рассеченный		от E до IH, от FH до H

Шестиугольную мозаику можно рассматривать как вытянутую ромбическую мозаику , где каждая вершина ромбической мозаики растягивается до нового ребра. Это похоже на соотношение мозаики ромбического додекаэдра и ромбо-шестиугольного додекаэдра в трех измерениях.

Ромбическая плитка	Шестиугольная плитка	Фехтование использует это соотношение

Также возможно разделить прототипы некоторых шестиугольных мозаик на два, три, четыре или девять равных пятиугольников:

Пятиугольная мозаика типа 1 с наложением правильных шестиугольников (каждый состоит из двух пятиугольников).	пятиугольная черепица типа 3 с наложениями правильных шестиугольников (каждый из которых состоит из 3 пятиугольников).	Пятиугольная черепица типа 4 с наложениями полуправильных шестиугольников (каждый из которых состоит из 4 пятиугольников).	Пятиугольная черепица типа 3 с наложением правильных шестиугольников двух размеров (содержащих 3 и 9 пятиугольников соответственно).

Мутации симметрии

Это разбиение топологически связано как часть последовательности правильных разбиений с шестиугольными гранями, начиная с шестиугольного разбиения, с символом Шлефли {6,n} и диаграммой Кокстера. , стремясь к бесконечности.

* n 62 мутация симметрии правильных мозаик: {6, n } v т и
Spherical	Euclidean	Hyperbolic tilings
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

Это разбиение топологически связано с правильными многогранниками с фигурой вершины n. ³, как часть последовательности, продолжающейся в гиперболическую плоскость .

* n 32 мутация симметрии правильных мозаик: { n ,3} v т и
Spherical				Euclidean	Compact hyperb.		Paraco.	Noncompact hyperbolic

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Аналогично это относится к однородным усеченным многогранникам с фигурой вершины n .6.6.

* n 32 мутация симметрии усеченных мозаик: n .6.6 v т и
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Это замощение также является частью последовательности усеченных ромбических многогранников и замощений с симметрией группы Кокстера [n,3] . Куб можно рассматривать как ромбический шестигранник, где ромбы — это квадраты. Усеченные формы имеют в усеченных вершинах правильные n-угольники и неправильные шестиугольные грани.

Мутации симметрии двойственных квазирегулярных мозаик: V(3.n) ²
*n32	Spherical			Euclidean	Hyperbolic
*n32	*332	*432	*532	*632	*732	*832...	*∞32
Tiling
Conf.	V(3.3)²	V(3.4)²	V(3.5)²	V(3.6)²	V(3.7)²	V(3.8)²	V(3.∞)²

Конструкции Витгофа из шестиугольных и треугольных мозаик.

Как и в случае с однородными многогранниками, существует восемь однородных мозаик , которые могут быть основаны на правильной шестиугольной мозаике (или двойной треугольной мозаике ).

Если нарисовать плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, получится 8 форм, 7 из которых топологически различны. ( Усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)

Однородные шестиугольные/треугольные плитки
Fundamental domains	Symmetry: [6,3], (*632)							[6,3]⁺, (632)
	{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}


Config.	6³	3.12.12	(6.3)²	6.6.6	3⁶	3.4.6.4	4.6.12	3.3.3.3.6

Моноэдральные выпуклые шестиугольные мозаики

Существует 3 типа моноэдральных выпуклых шестиугольных мозаик. ^[1] Все они изоэдральные . Каждый из них имеет параметрические вариации в пределах фиксированной симметрии. Тип 2 содержит скользящие отражения и является 2-изоэдральным, сохраняя различимость киральных пар.

3 типа моноэдральных выпуклых шестиугольных мозаик
1	2		3
п2, 2222	пгг, 22×	п2, 2222	стр3, 333

б = е Б + С + Г = 360°	б = е, d = е Б + С + Е = 360°		а = е, б = с, d = е Б = Д = Ф = 120°
2-плиточная решетка	4-плиточная решетка		3-х плиточная решетка

Топологически эквивалентные мозаики

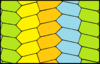
Шестиугольные мозаики могут быть созданы с той же топологией {6,3}, что и обычные мозаики (3 шестиугольника вокруг каждой вершины). У изоэдральных граней существует 13 вариантов. Данная симметрия предполагает, что все лица одного цвета. Цвета здесь обозначают позиции решетки. ^[2] Одноцветные (1-плиточные) решетки представляют собой шестиугольники- параллелограммы .

13 шестиугольников с изоэдральной черепицей
пг (××)	п3 (333)	пмг (22*)

пгг (22×)	п31м (3*3)	р2 (2222)	см (2*22)	п6м (*632)

Другие топологические шестиугольные мозаики с изоэдральной плиткой рассматриваются как четырехугольники и пятиугольники, которые не являются смежными, а интерпретируются как коллинеарные смежные края:

Четырехугольники с изоэдральной черепицей
пмг (22*)		пгг (22×)			см (2*22)	р2 (2222)
Параллелограмм	Трапеция	Параллелограмм	Прямоугольник	Параллелограмм	Прямоугольник	Прямоугольник

Пятиугольники с изоэдральной черепицей
р2 (2222)	пгг (22×)	п3 (333)

2-однородные и 3-однородные мозаики имеют степень свободы вращения, которая искажает 2/3 шестиугольников, включая коллинеарный случай, который также можно рассматривать как мозаику шестиугольников и более крупных треугольников без края к краю. ^[3]

Его также можно исказить в хиральный четырехцветный трехнаправленный узор, искажая некоторые шестиугольники в параллелограммы . Сплетенный узор с 2 цветными гранями имеет вращательную симметрию 632 (p6) . Шевронный узор имеет симметрию pmg (22 * ), которая понижается до p1 (°) с 3 или 4 цветными плитками.

Обычный	вращающийся	Обычный	Тканый	Шеврон
п6м, (*632)	п6, (632)	п6м (*632)	п6 (632)	р1 (°)

p3m1, (*333)	п3, (333)	п6м (*632)	р2 (2222)	р1 (°)

Упаковка круга

Шестиугольную мозаику можно использовать в качестве упаковки кругов , размещая круги одинакового диаметра в центре каждой точки. Каждый круг соприкасается с тремя другими кругами упаковки ( число поцелуя ). ^[4] Зазор внутри каждого шестиугольника позволяет разместить один круг, создавая наиболее плотную упаковку из треугольной мозаики , при этом каждый круг соприкасается максимум с 6 кругами.

Родственные регулярные сложные апейрогоны

Есть два правильных сложных апейрогона , разделяющие вершины шестиугольной мозаики. Правильные комплексные апейрогоны имеют вершины и ребра, причем ребра могут содержать 2 и более вершин. Правильные апейрогоны p { q } r ограничены следующим образом: 1/ p + 2/ q + 1/ r = 1. Ребра имеют p вершин, а вершинные фигуры являются r -угольными. ^[5]

Первый состоит из двух ребер, по три вокруг каждой вершины, второй имеет шестиугольные ребра, по три вокруг каждой вершины. Третий комплексный апейрогон, имеющий те же вершины, является квазиправильным, в котором чередуются 2-ребра и 6-рёбра.

2{12}3 или	6{4}3 или

См. также

Ссылки

^ Плитки и узоры , Разд. 9.3 Другие моноэдральные замощения выпуклыми многоугольниками
^ Плитки и узоры , из списка 107 изоэдральных мозаик, стр. 473–481.
^ Плитки и узоры , однородные плитки, не расположенные от края до края.
^ Порядок в пространстве: справочник по дизайну, Кейт Кричлоу, стр. 74–75, образец 2.
^ Коксетер, Правильные комплексные многогранники, стр. 111–112, стр. 111–112. 136.

Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 стр. 296, Таблица II: Обычные соты.
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1 . (Глава 2.1: Правильные и однородные мозаики , стр. 58–65)
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 35. ISBN 0-486-23729-Х .
Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1]

Внешние ссылки

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеечная сотовая связь
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	. _{7 кв}	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	11 _{квартал}
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁

[1] Плитки и узоры , Разд. 9.3 Другие моноэдральные замощения выпуклыми многоугольниками

[2] Плитки и узоры , из списка 107 изоэдральных мозаик, стр. 473–481.

[3] Плитки и узоры , однородные плитки, не расположенные от края до края.

[Critchlow-4] Порядок в пространстве: справочник по дизайну, Кейт Кричлоу, стр. 74–75, образец 2.

[5] Коксетер, Правильные комплексные многогранники, стр. 111–112, стр. 111–112. 136.

[1]

[2]

[3]

[4]

[5]