Экспоненциальное распределение

Не путать с экспоненциальным семейством вероятностных распределений.

Экспоненциальный

Функция плотности вероятности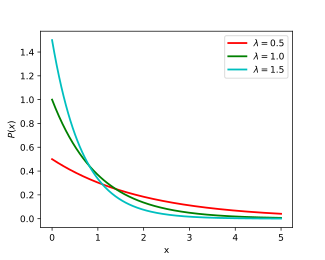
Кумулятивная функция распределения
Параметры	$\lambda >0,$ ставка или обратная шкала
Поддерживать	$x\in [0,\infty )$
PDF	$\lambda e^{-\lambda x}$
CDF	$1-e^{-\lambda x}$
Квантиль	$-{\frac {\ln(1-p)}{\lambda }}$
Иметь в виду	${\frac {1}{\lambda }}$
медиана	${\frac {\ln 2}{\lambda }}$
Режим	$0$
Дисперсия	${\frac {1}{\lambda ^{2}}}$
асимметрия	$2$
Избыточный эксцесс	$6$
Энтропия	$1-\ln \lambda$
МГФ	${\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda$
CF	${\frac {\lambda }{\lambda -it}}$
Информация о Фишере	${\frac {1}{\lambda ^{2}}}$
Расхождение Кульбака – Лейблера	$\ln {\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda }{\lambda _{0}}}-1$
Ожидаемый дефицит	${\frac {-\ln(1-p)+1}{\lambda }}$

В теории вероятностей и статистике экспоненциальное распределение или отрицательное экспоненциальное распределение — это распределение вероятностей расстояния между событиями в точечном процессе Пуассона , т. е. процессе, в котором события происходят непрерывно и независимо с постоянной средней скоростью; параметром расстояния может быть любая значимая одномерная мера процесса, например, время между производственными ошибками или длина рулона ткани в процессе ткацкого производства. Это частный случай гамма -распределения . Это непрерывный аналог геометрического распределения , и его ключевым свойством является отсутствие памяти . Помимо использования для анализа точечных процессов Пуассона, он встречается и в различных других контекстах.

Показательное распределение — это не то же самое, что класс экспоненциальных семейств распределений. Это большой класс вероятностных распределений, который включает экспоненциальное распределение в качестве одного из своих членов, но также включает в себя множество других распределений, таких как нормальное , биномиальное , гамма- распределение и распределение Пуассона .

Определения

Функция плотности вероятности

Функция плотности вероятности (pdf) экспоненциального распределения равна

$f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

Здесь λ > 0 — параметр распределения, часто называемый параметром скорости . Распределение поддерживается на интервале [0, ∞) . Если случайная величина X имеет такое распределение, мы пишем X ~ Exp( λ ) .

Экспоненциальное распределение демонстрирует бесконечную делимость .

Кумулятивная функция распределения

Кумулятивная функция распределения определяется выражением

$F(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

Альтернативная параметризация

Экспоненциальное распределение иногда параметризуется с помощью масштабного параметра β = 1/ λ , который также является средним значением: $$f(x;\beta )={\begin{cases}{\frac {1}{\beta }}e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}\qquad \qquad F(x;\beta )={\begin{cases}1-e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}$$

Характеристики

Среднее значение, дисперсия, моменты и медиана

Среднее значение — это вероятностный центр масс, то есть первый момент .

Медиана — это прообраз F ⁻¹ (1/2).

Среднее или ожидаемое значение экспоненциально распределенной случайной величины X с параметром скорости λ определяется выражением $$\operatorname {E} [X]={\frac {1}{\lambda }}.$$

В свете приведенных ниже примеров это имеет смысл; человек, который принимает в среднем два телефонных звонка в час, может рассчитывать, что время между последовательными звонками составит 0,5 часа или 30 минут.

Дисперсия выражением X ​ определяется $$\operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},$$поэтому стандартное отклонение равно среднему значению.

Моменты ​ X для , $n\in \mathbb {N}$ даны $$\operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.$$

Центральные моменты X для , $n\in \mathbb {N}$ даны $$\mu _{n}={\frac {!n}{\lambda ^{n}}}={\frac {n!}{\lambda ^{n}}}\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.$$где ! n является субфакториалом n ​

Медиана ​ X выражением определяется $$\operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],$$где ln относится к натуральному логарифму . Таким образом, абсолютная разница между средним значением и медианой равна $$\left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],$$

в соответствии с медианно-средним неравенством .

Свойство безпамяти экспоненциальной случайной величины

Экспоненциально распределенная случайная величина T подчиняется соотношению $$\Pr \left(T>s+t\mid T>s\right)=\Pr(T>t),\qquad \forall s,t\geq 0.$$

В этом можно убедиться, рассмотрев дополнительную кумулятивную функцию распределения : $${\begin{aligned}\Pr \left(T>s+t\mid T>s\right)&={\frac {\Pr \left(T>s+t\cap T>s\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {\Pr \left(T>s+t\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}\\[4pt]&=e^{-\lambda t}\\[4pt]&=\Pr(T>t).\end{aligned}}$$

Когда T интерпретируется как время ожидания возникновения события относительно некоторого начального времени, это соотношение подразумевает, что, если T обусловлено невозможностью наблюдения события в течение некоторого начального периода времени s , распределение оставшегося времени ожидания такое же, как исходное безусловное распределение. Например, если событие не произошло через 30 секунд, условная вероятность того, что возникновение займет еще как минимум 10 секунд, равна безусловной вероятности наблюдения события более чем через 10 секунд после начального времени.

Экспоненциальное распределение и геометрическое распределение являются единственными распределениями вероятностей без памяти .

Следовательно, экспоненциальное распределение также обязательно является единственным непрерывным распределением вероятностей, имеющим постоянную частоту отказов .

Квантили

Критерии Тьюки для аномалий.

Функция квантиля (обратная кумулятивная функция распределения) для Exp( λ ) равна $$F^{-1}(p;\lambda )={\frac {-\ln(1-p)}{\lambda }},\qquad 0\leq p<1$$

составляют Таким образом , квартили :

• первый квартиль: ln(4/3)/ λ
• медиана : ln(2)/ λ
• третий квартиль: ln(4)/ λ

И, как следствие, межквартильный размах равен ln(3)/ λ .

Условная стоимость под угрозой (ожидаемый дефицит)

Условное значение риска (CVaR), также известное как ожидаемый дефицит или суперквантиль для Exp( λ ), рассчитывается следующим образом:

$${\begin{aligned}{\bar {q}}_{\alpha }(X)&={\frac {1}{1-\alpha }}\int _{\alpha }^{1}q_{p}(X)dp\\&={\frac {1}{(1-\alpha )}}\int _{\alpha }^{1}{\frac {-\ln(1-p)}{\lambda }}dp\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{1-\alpha }^{0}-\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{0}^{1-\alpha }\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}[(1-\alpha )\ln(1-\alpha )-(1-\alpha )]\\&={\frac {-\ln(1-\alpha )+1}{\lambda }}\\\end{aligned}}$$

Буферизованная вероятность превышения (bPOE)

Основная статья: Буферизованная вероятность превышения

Буферизованная вероятность превышения равна единице минус уровень вероятности, при котором CVaR равен порогу. $x$. Его получают следующим образом:

$${\begin{aligned}{\bar {p}}_{x}(X)&=\{1-\alpha |{\bar {q}}_{\alpha }(X)=x\}\\&=\{1-\alpha |{\frac {-\ln(1-\alpha )+1}{\lambda }}=x\}\\&=\{1-\alpha |\ln(1-\alpha )=1-\lambda x\}\\&=\{1-\alpha |e^{\ln(1-\alpha )}=e^{1-\lambda x}\}=\{1-\alpha |1-\alpha =e^{1-\lambda x}\}=e^{1-\lambda x}\end{aligned}}$$

Расхождение Кульбака – Лейблера

Направленное расхождение Кульбака–Лейблера в нац . $e^{\lambda }$ («приблизительное» распределение) от $e^{\lambda _{0}}$ («истинное» распределение) определяется выражением $${\begin{aligned}\Delta (\lambda _{0}\parallel \lambda )&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {p_{\lambda _{0}}(x)}{p_{\lambda }(x)}}\right)\\&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {\lambda _{0}e^{\lambda _{0}x}}{\lambda e^{\lambda x}}}\right)\\&=\log(\lambda _{0})-\log(\lambda )-(\lambda _{0}-\lambda )E_{\lambda _{0}}(x)\\&=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1.\end{aligned}}$$

Максимальное распределение энтропии

Среди всех непрерывных распределений вероятностей с носителем [0, ∞) и средним значением µ экспоненциальное распределение с λ = 1/ µ имеет наибольшую дифференциальную энтропию . Другими словами, это максимальное распределение вероятностей энтропии для случайной величины X , которая больше или равна нулю и для которой E[ X ] фиксировано.

Распределение минимума экспоненциальных случайных величин

Пусть X ₁ , …, X _n – независимые экспоненциально распределенные случайные величины со скоростными параметрами λ ₁ , …, λ _n . Затем $$\min \left\{X_{1},\dotsc ,X_{n}\right\}$$также распределено экспоненциально с параметром $$\lambda =\lambda _{1}+\dotsb +\lambda _{n}.$$

В этом можно убедиться, рассмотрев дополнительную кумулятивную функцию распределения : $${\begin{aligned}&\Pr \left(\min\{X_{1},\dotsc ,X_{n}\}>x\right)\\={}&\Pr \left(X_{1}>x,\dotsc ,X_{n}>x\right)\\={}&\prod _{i=1}^{n}\Pr \left(X_{i}>x\right)\\={}&\prod _{i=1}^{n}\exp \left(-x\lambda _{i}\right)=\exp \left(-x\sum _{i=1}^{n}\lambda _{i}\right).\end{aligned}}$$

Индекс переменной, достигшей минимума, распределяется согласно категориальному распределению. $$\Pr \left(X_{k}=\min\{X_{1},\dotsc ,X_{n}\}\right)={\frac {\lambda _{k}}{\lambda _{1}+\dotsb +\lambda _{n}}}.$$

Доказательство можно увидеть, позволив $I=\operatorname {argmin} _{i\in \{1,\dotsb ,n\}}\{X_{1},\dotsc ,X_{n}\}$. Затем, $${\begin{aligned}\Pr(I=k)&=\int _{0}^{\infty }\Pr(X_{k}=x)\Pr(\forall _{i\neq k}X_{i}>x)\,dx\\&=\int _{0}^{\infty }\lambda _{k}e^{-\lambda _{k}x}\left(\prod _{i=1,i\neq k}^{n}e^{-\lambda _{i}x}\right)dx\\&=\lambda _{k}\int _{0}^{\infty }e^{-\left(\lambda _{1}+\dotsb +\lambda _{n}\right)x}dx\\&={\frac {\lambda _{k}}{\lambda _{1}+\dotsb +\lambda _{n}}}.\end{aligned}}$$

Обратите внимание, что $$\max\{X_{1},\dotsc ,X_{n}\}$$не распределяется экспоненциально, если X ₁ , …, X _{n имеют параметр 0.} не все

Совместные моменты статистики экспоненциального порядка iid

Позволять $X_{1},\dotsc ,X_{n}$ быть $n$ независимые и одинаково распределенные экспоненциальные случайные величины с параметром скорости λ . Позволять $X_{(1)},\dotsc ,X_{(n)}$ обозначают соответствующую порядковую статистику . Для $i<j$ , совместный момент $\operatorname {E} \left[X_{(i)}X_{(j)}\right]$ статистики заказов $X_{(i)}$ и $X_{(j)}$ дается $${\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right]\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}+\sum _{k=0}^{i-1}{\frac {1}{((n-k)\lambda )^{2}}}+\left(\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}\right)^{2}.\end{aligned}}$$

В этом можно убедиться, обратившись к закону полного ожидания и свойству отсутствия памяти: $${\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\int _{0}^{\infty }\operatorname {E} \left[X_{(i)}X_{(j)}\mid X_{(i)}=x\right]f_{X_{(i)}}(x)\,dx\\&=\int _{x=0}^{\infty }x\operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]f_{X_{(i)}}(x)\,dx&&\left({\textrm {since}}~X_{(i)}=x\implies X_{(j)}\geq x\right)\\&=\int _{x=0}^{\infty }x\left[\operatorname {E} \left[X_{(j)}\right]+x\right]f_{X_{(i)}}(x)\,dx&&\left({\text{by the memoryless property}}\right)\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right].\end{aligned}}$$

Первое уравнение следует из закона полного ожидания .Второе уравнение использует тот факт, что как только мы ставим условие на $X_{(i)}=x$, из этого должно следовать, что $X_{(j)}\geq x$. Третье уравнение основано на свойстве отсутствия памяти для замены $\operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]$ с $\operatorname {E} \left[X_{(j)}\right]+x$.

Сумма двух независимых экспоненциальных случайных величин

Функция распределения вероятностей (PDF) суммы двух независимых случайных величин представляет собой свертку их отдельных PDF-файлов . Если $X_{1}$ и $X_{2}$ являются независимыми экспоненциальными случайными величинами с соответствующими параметрами скорости $\lambda _{1}$ и $\lambda _{2},$ тогда плотность вероятности $Z=X_{1}+X_{2}$ дается $${\begin{aligned}f_{Z}(z)&=\int _{-\infty }^{\infty }f_{X_{1}}(x_{1})f_{X_{2}}(z-x_{1})\,dx_{1}\\&=\int _{0}^{z}\lambda _{1}e^{-\lambda _{1}x_{1}}\lambda _{2}e^{-\lambda _{2}(z-x_{1})}\,dx_{1}\\&=\lambda _{1}\lambda _{2}e^{-\lambda _{2}z}\int _{0}^{z}e^{(\lambda _{2}-\lambda _{1})x_{1}}\,dx_{1}\\&={\begin{cases}{\dfrac {\lambda _{1}\lambda _{2}}{\lambda _{2}-\lambda _{1}}}\left(e^{-\lambda _{1}z}-e^{-\lambda _{2}z}\right)&{\text{ if }}\lambda _{1}\neq \lambda _{2}\\[4pt]\lambda ^{2}ze^{-\lambda z}&{\text{ if }}\lambda _{1}=\lambda _{2}=\lambda .\end{cases}}\end{aligned}}$$Энтропия этого распределения доступна в закрытой форме: полагая $\lambda _{1}>\lambda _{2}$ (без ограничения общности), тогда $${\begin{aligned}H(Z)&=1+\gamma +\ln \left({\frac {\lambda _{1}-\lambda _{2}}{\lambda _{1}\lambda _{2}}}\right)+\psi \left({\frac {\lambda _{1}}{\lambda _{1}-\lambda _{2}}}\right),\end{aligned}}$$где $\gamma$ – постоянная Эйлера-Машерони , а $\psi (\cdot )$ это дигамма-функция .

В случае равных параметров скорости результатом является распределение Эрланга с формой 2 и параметром $\lambda ,$ что, в свою очередь, является частным случаем гамма-распределения .

Сумма n независимых Exp( λ) экспоненциальных случайных величин распределена по схеме Gamma(n, λ) .

Связанные дистрибутивы

• Если X ~ Лапласа(μ, β ⁻¹ ) , то | Икс - мкм| ~ Эксп(β).
• Если X ~ Парето(1, λ) , то log( X ) ~ Exp(λ).
• Если X ~ SkewLogistic(θ) , то $\log \left(1+e^{-X}\right)\sim \operatorname {Exp} (\theta )$.
• Если X _i ~ U (0, 1), то $$\lim _{n\to \infty }n\min \left(X_{1},\ldots ,X_{n}\right)\sim \operatorname {Exp} (1)$$
• Экспоненциальное распределение является пределом масштабированного бета-распределения : $$\lim _{n\to \infty }n\operatorname {Beta} (1,n)=\operatorname {Exp} (1).$$
• Экспоненциальное распределение является частным случаем распределения Пирсона 3-го типа .
• Экспоненциальное распределение является частным случаем гамма-распределения с параметром формы 1.
• Если X ~ Exp(λ) и X _i ~ Exp(λ _i ), то:
  • $kX\sim \operatorname {Exp} \left({\frac {\lambda }{k}}\right)$, замыкание при масштабировании положительным коэффициентом.
  • 1 + X ~ Бенктандер-Вейбулл (λ, 1), что сводится к усеченному экспоненциальному распределению.
  • тот ^Х ~ Парето ( k , λ).
  • и ^−X ~ Бета (л, 1).
  • ⁠ 1 / k ⁠ e ^Х ~ PowerLaw ( k , λ)
  • ${\sqrt {X}}\sim \operatorname {Rayleigh} \left({\frac {1}{\sqrt {2\lambda }}}\right)$, распределение Рэлея
  • $X\sim \operatorname {Weibull} \left({\frac {1}{\lambda }},1\right)$, распределение Вейбулла
  • $X^{2}\sim \operatorname {Weibull} \left({\frac {1}{\lambda ^{2}}},{\frac {1}{2}}\right)$
  • µ − β log(λ X ) ∼ Гумбел (µ, β) .
  • $\lfloor X\rfloor \sim \operatorname {Geometric} \left(1-e^{-\lambda }\right)$, геометрическое распределение на 0,1,2,3,...
  • $\lceil X\rceil \sim \operatorname {Geometric} \left(1-e^{-\lambda }\right)$, геометрическое распределение на 1,2,3,4,...
  • Если также Y ~ Erlang( n , λ) или $Y\sim \Gamma \left(n,{\frac {1}{\lambda }}\right)$ затем ${\frac {X}{Y}}+1\sim \operatorname {Pareto} (1,n)$
  • Если также λ ~ Gamma ( k , θ) (параметризация формы, масштаба), то маргинальное распределение X равно Lomax ( k , 1/θ), гамма- смесь
  • λ ₁ Икс ₁ - λ ₂ Y ₂ ~ Лаплас(0, 1) .
  • min{ X ₁ , ..., X _n } ~ Exp(λ ₁ + ... + λ _n ).
  • Если также λ _i = λ, то:
    • $X_{1}+\cdots +X_{k}=\sum _{i}X_{i}\sim$ Эрланг ( k , λ) = Гамма ( k , λ ⁻¹ ) = Gamma( k , λ) (в параметризации ( k , θ ) и (α, β) соответственно) с целочисленным параметром формы k.
    • Если $T=(X_{1}+\cdots +X_{n})=\sum _{i=1}^{n}X_{i}$, затем $2\lambda T\sim \chi _{2n}^{2}$.
    • X _i − X _j ~ Лапласа(0, λ ⁻¹ ).
  • Если также X _i независимы, то:
    • ${\frac {X_{i}}{X_{i}+X_{j}}}$ ~ В (0, 1)
    • $Z={\frac {\lambda _{i}X_{i}}{\lambda _{j}X_{j}}}$ имеет функцию плотности вероятности $f_{Z}(z)={\frac {1}{(z+1)^{2}}}$. Это можно использовать для получения доверительного интервала для ${\frac {\lambda _{i}}{\lambda _{j}}}$.
  • Если также λ = 1:
    • $\mu -\beta \log \left({\frac {e^{-X}}{1-e^{-X}}}\right)\sim \operatorname {Logistic} (\mu ,\beta )$, логистическое распределение
    • $\mu -\beta \log \left({\frac {X_{i}}{X_{j}}}\right)\sim \operatorname {Logistic} (\mu ,\beta )$
    • μ − σ log( X ) ~ GEV(μ, σ, 0) .
    • Далее, если $Y\sim \Gamma \left(\alpha ,{\frac {\beta }{\alpha }}\right)$ затем ${\sqrt {XY}}\sim \operatorname {K} (\alpha ,\beta )$ ( K-распределение )
  • Если также λ = 1/2, то X ∼ χ ²
    ₂ ; т. е. X имеет распределение хи-квадрат с 2 степенями свободы . Следовательно: $$\operatorname {Exp} (\lambda )={\frac {1}{2\lambda }}\operatorname {Exp} \left({\frac {1}{2}}\right)\sim {\frac {1}{2\lambda }}\chi _{2}^{2}\Rightarrow \sum _{i=1}^{n}\operatorname {Exp} (\lambda )\sim {\frac {1}{2\lambda }}\chi _{2n}^{2}$$
• Если $X\sim \operatorname {Exp} \left({\frac {1}{\lambda }}\right)$ и $Y\mid X$ ~ Пуассон( X ) тогда $Y\sim \operatorname {Geometric} \left({\frac {1}{1+\lambda }}\right)$ ( геометрическое распределение )
• Распределение Хойта можно получить из экспоненциального распределения и арксинусного распределения.
• Экспоненциальное распределение является пределом κ -экспоненциального распределения в $\kappa =0$ случай.
• Экспоненциальное распределение является пределом κ-обобщенного гамма-распределения в $\alpha =1$ и $\nu =1$ случаи:

  $\lim _{(\alpha ,\nu )\to (0,1)}p_{\kappa }(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\Big )}}}{\frac {\alpha \lambda ^{\nu }}{\Gamma (\nu )}}x^{\alpha \nu -1}\exp _{\kappa }(-\lambda x^{\alpha })=\lambda e^{-\lambda x}$

Другие связанные дистрибутивы:

• Гиперэкспоненциальное распределение – распределение, плотность которого представляет собой взвешенную сумму экспоненциальных плотностей.
• Гипоэкспоненциальное распределение – распределение общей суммы экспоненциальных случайных величин.
• exGaussianраспределение – сумма экспоненциального распределения и нормального распределения .

Статистический вывод

Ниже предположим, что случайная величина X распределена экспоненциально с параметром скорости λ, и $x_{1},\dotsc ,x_{n}$ являются n независимыми выборками из X со средним значением выборки ${\bar {x}}$.

Оценка параметров

Оценка максимального правдоподобия для λ строится следующим образом.

Функция правдоподобия для λ, учитывая независимую и одинаково распределенную выборку x = ( x ₁ , …, x _n ), полученную из переменной, равна: $$L(\lambda )=\prod _{i=1}^{n}\lambda \exp(-\lambda x_{i})=\lambda ^{n}\exp \left(-\lambda \sum _{i=1}^{n}x_{i}\right)=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right),$$

где: $${\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$$– выборочное среднее.

Производная логарифма функции правдоподобия равна: $${\frac {d}{d\lambda }}\ln L(\lambda )={\frac {d}{d\lambda }}\left(n\ln \lambda -\lambda n{\overline {x}}\right)={\frac {n}{\lambda }}-n{\overline {x}}\ {\begin{cases}>0,&0<\lambda <{\frac {1}{\overline {x}}},\\[8pt]=0,&\lambda ={\frac {1}{\overline {x}}},\\[8pt]<0,&\lambda >{\frac {1}{\overline {x}}}.\end{cases}}$$

Следовательно, оценка максимального правдоподобия для параметра скорости равна: $${\widehat {\lambda }}_{\text{mle}}={\frac {1}{\overline {x}}}={\frac {n}{\sum _{i}x_{i}}}$$

Это не объективная оценка ​ $\lambda ,$ хотя ${\overline {x}}$ является беспристрастным МЛЭ оценщик $1/\lambda$ и среднее распределение.

Предвзятость ${\widehat {\lambda }}_{\text{mle}}$ равно $$B\equiv \operatorname {E} \left[\left({\widehat {\lambda }}_{\text{mle}}-\lambda \right)\right]={\frac {\lambda }{n-1}}$$что дает оценку максимального правдоподобия с поправкой на смещение $${\widehat {\lambda }}_{\text{mle}}^{*}={\widehat {\lambda }}_{\text{mle}}-B.$$

Приблизительный минимизатор среднеквадратической ошибки (см. также: компромисс между смещением и дисперсией ) можно найти, предполагая, что размер выборки больше двух, с поправочным коэффициентом для MLE: $${\widehat {\lambda }}=\left({\frac {n-2}{n}}\right)\left({\frac {1}{\bar {x}}}\right)={\frac {n-2}{\sum _{i}x_{i}}}$$Это получено из среднего значения и дисперсии обратного гамма-распределения , ${\textstyle {\mbox{Inv-Gamma}}(n,\lambda )}$.

Информация о Фишере

Информация Фишера , обозначаемая ${\mathcal {I}}(\lambda )$, для оценки параметра скорости $\lambda$ дается как: $${\mathcal {I}}(\lambda )=\operatorname {E} \left[\left.\left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}\right|\lambda \right]=\int \left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}f(x;\lambda )\,dx$$

Подключение распределения и решение дает: $${\mathcal {I}}(\lambda )=\int _{0}^{\infty }\left({\frac {\partial }{\partial \lambda }}\log \lambda e^{-\lambda x}\right)^{2}\lambda e^{-\lambda x}\,dx=\int _{0}^{\infty }\left({\frac {1}{\lambda }}-x\right)^{2}\lambda e^{-\lambda x}\,dx=\lambda ^{-2}.$$

Это определяет объем информации, которую несет каждая независимая выборка экспоненциального распределения о неизвестном параметре скорости. $\lambda$.

Доверительные интервалы

Точный 100(1 - α)% доверительный интервал для параметра скорости экспоненциального распределения определяется следующим образом: $${\frac {2n}{{\widehat {\lambda }}_{\textrm {mle}}\chi _{{\frac {\alpha }{2}},2n}^{2}}}<{\frac {1}{\lambda }}<{\frac {2n}{{\widehat {\lambda }}_{\textrm {mle}}\chi _{1-{\frac {\alpha }{2}},2n}^{2}}}\,,$$что также равно $${\frac {2n{\overline {x}}}{\chi _{{\frac {\alpha }{2}},2n}^{2}}}<{\frac {1}{\lambda }}<{\frac {2n{\overline {x}}}{\chi _{1-{\frac {\alpha }{2}},2n}^{2}}}\,,$$где х ²
_{p , v} — 100( p ) процентиль распределения хи-квадрат с v степенями свободы , n — количество наблюдений, а x-bar — среднее значение выборки. Простую аппроксимацию точных конечных точек интервала можно получить, используя нормальную аппроксимацию χ ²
_{p , v} распределение. Это приближение дает следующие значения для 95% доверительного интервала: $${\begin{aligned}\lambda _{\text{lower}}&={\widehat {\lambda }}\left(1-{\frac {1.96}{\sqrt {n}}}\right)\\\lambda _{\text{upper}}&={\widehat {\lambda }}\left(1+{\frac {1.96}{\sqrt {n}}}\right)\end{aligned}}$$

Такое приближение может быть приемлемым для образцов, содержащих не менее 15–20 элементов.

Байесовский вывод

Сопряженным априором экспоненциального распределения является гамма-распределение (частным случаем которого является экспоненциальное распределение). Полезна следующая параметризация функции плотности вероятности гамма-излучения:

$$\operatorname {Gamma} (\lambda ;\alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\lambda ^{\alpha -1}\exp(-\lambda \beta ).$$

Затем апостериорное распределение p можно выразить через функцию правдоподобия, определенную выше, и априорную гамму:

$${\begin{aligned}p(\lambda )&\propto L(\lambda )\Gamma (\lambda ;\alpha ,\beta )\\&=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right){\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\lambda ^{\alpha -1}\exp(-\lambda \beta )\\&\propto \lambda ^{(\alpha +n)-1}\exp(-\lambda \left(\beta +n{\overline {x}}\right)).\end{aligned}}$$

Теперь апостериорная плотность p задана с точностью до отсутствующей нормировочной константы. Поскольку он имеет форму гамма-pdf, его можно легко заполнить и получить:

$$p(\lambda )=\operatorname {Gamma} (\lambda ;\alpha +n,\beta +n{\overline {x}}).$$

Здесь гиперпараметр α можно интерпретировать как количество предыдущих наблюдений, а β — как сумму предыдущих наблюдений.Апостериорное среднее здесь равно: $${\frac {\alpha +n}{\beta +n{\overline {x}}}}.$$

Возникновение и применение

Возникновение событий

Экспоненциальное распределение возникает естественным образом при описании длин времен между приходами в однородном пуассоновском процессе .

Экспоненциальное распределение можно рассматривать как непрерывный аналог геометрического распределения , которое описывает количество испытаний Бернулли, необходимых для того, чтобы дискретный процесс изменил состояние. Напротив, экспоненциальное распределение описывает время, в течение которого непрерывный процесс меняет состояние.

В реальных сценариях предположение о постоянной скорости (или вероятности в единицу времени) редко выполняется. Например, скорость входящих телефонных звонков различается в зависимости от времени суток. Но если мы сосредоточимся на временном интервале, в течение которого скорость примерно постоянна, например, с 14 до 16 часов в рабочие дни, экспоненциальное распределение можно использовать в качестве хорошей приближенной модели времени до следующего телефонного звонка. Аналогичные предостережения применимы к следующим примерам, которые дают примерно экспоненциально распределенные переменные:

• Время до распада радиоактивной частицы , или время между щелчками счетчика Гейгера
• Время между получением одного телефонного звонка и следующего
• Время до дефолта (при выплате держателям долгов компании) при моделировании кредитного риска в сокращенной форме

Экспоненциальные переменные также можно использовать для моделирования ситуаций, когда определенные события происходят с постоянной вероятностью на единицу длины, например, расстояние между мутациями в цепи ДНК или между дорожно-транспортными происшествиями на данной дороге.

В теории массового обслуживания время обслуживания агентов в системе (например, сколько времени требуется кассиру банка и т. д. для обслуживания клиента) часто моделируется как экспоненциально распределенные переменные. (Например, поступление клиентов также моделируется распределением Пуассона , если поступления независимы и распределены одинаково.) Длина процесса, который можно рассматривать как последовательность нескольких независимых задач, соответствует распределению Эрланга (которое представляет собой распределение суммы нескольких независимых экспоненциально распределенных переменных). Теория надежности и инженерия надежности также широко используют экспоненциальное распределение. Из-за отсутствия памяти у этого распределения оно хорошо подходит для моделирования с постоянной степенью опасности, части кривой ванны используемой в теории надежности. можно легко добавить интенсивность отказов Это также очень удобно, поскольку в модель надежности . Однако экспоненциальное распределение не подходит для моделирования общего срока службы организмов или технических устройств, поскольку «частота отказов» здесь не постоянна: больше отказов происходит как для очень молодых, так и для очень старых систем.

Подобрано кумулятивное экспоненциальное распределение максимального годового количества осадков за 1 день с использованием CumFreq.

В физике , если вы наблюдаете газ при фиксированной температуре и давлении в однородном гравитационном поле , высоты различных молекул также подчиняются приблизительному экспоненциальному распределению, известному как барометрическая формула . Это следствие упомянутого ниже свойства энтропии.

В гидрологии экспоненциальное распределение используется для анализа экстремальных значений таких переменных, как месячные и годовые максимальные значения суточного количества осадков и объемы речного стока.

Синее изображение иллюстрирует пример подбора экспоненциального распределения к ранжированному максимальному годовому количеству осадков за один день, демонстрируя также 90% доверительный интервал, основанный на биномиальном распределении . Данные об осадках представлены в виде координат на графике в рамках кумулятивного частотного анализа .

В управлении операционными залами - распределение продолжительности операции по категориям операций без типичного содержания труда (например, в отделении неотложной помощи, охватывающее все виды операций).

Прогноз

После наблюдения выборки из n точек данных из неизвестного экспоненциального распределения общая задача состоит в том, чтобы использовать эти выборки для прогнозирования будущих данных из того же источника. Распространенным прогнозным распределением по будущим выборкам является так называемое подключаемое распределение, формируемое путем включения подходящей оценки параметра скорости λ в функцию экспоненциальной плотности. Обычным выбором оценки является тот, который обеспечивается принципом максимального правдоподобия, и его использование дает прогнозную плотность для будущей выборки x _{n +1} , обусловленную наблюдаемыми выборками x = ( x ₁ , ..., x _n ) данный $$p_{\rm {ML}}(x_{n+1}\mid x_{1},\ldots ,x_{n})=\left({\frac {1}{\overline {x}}}\right)\exp \left(-{\frac {x_{n+1}}{\overline {x}}}\right).$$

Байесовский подход обеспечивает прогнозируемое распределение, которое учитывает неопределенность оцениваемого параметра, хотя это может решающим образом зависеть от выбора априора.

Прогнозирующее распределение, свободное от проблем выбора априорных значений, возникающих при субъективном байесовском подходе, - это

$$p_{\rm {CNML}}(x_{n+1}\mid x_{1},\ldots ,x_{n})={\frac {n^{n+1}\left({\overline {x}}\right)^{n}}{\left(n{\overline {x}}+x_{n+1}\right)^{n+1}}},$$

который можно рассматривать как

1. частотное доверительное распределение , полученное из распределения основной величины ${x_{n+1}}/{\overline {x}}$;
2. прогнозируемая вероятность профиля, полученная путем исключения параметра λ из совместной вероятности x _{n +1} и λ путем максимизации;
3. объективное байесовское предсказательное апостериорное распределение, полученное с использованием неинформативного Джеффриса априорного 1/ λ ;
4. прогнозируемое распределение условного нормализованного максимального правдоподобия (CNML), исходя из соображений теории информации.

Точность прогнозируемого распределения может быть измерена с использованием расстояния или расхождения между истинным экспоненциальным распределением с параметром скорости λ ₀ и прогнозным распределением, основанным на выборке x . Дивергенция Кульбака -Лейблера - это широко используемая, не требующая параметризации мера разницы между двумя распределениями. Обозначая Δ( λ ₀ || p ) расхождение Кульбака – Лейблера между экспонентой с параметром скорости λ ₀ и прогнозирующим распределением p, можно показать, что

$${\begin{aligned}\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {ML}})\right]&=\psi (n)+{\frac {1}{n-1}}-\log(n)\\\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {CNML}})\right]&=\psi (n)+{\frac {1}{n}}-\log(n)\end{aligned}}$$

где математическое ожидание берется относительно экспоненциального распределения с параметром скорости λ ₀ ∈ (0, ∞) , а ψ( · ) – дигамма-функция. Ясно, что прогнозирующее распределение CNML строго превосходит подключаемое распределение максимального правдоподобия с точки зрения среднего расхождения Кульбака-Лейблера для всех размеров выборки n > 0 .

Генерация случайной переменной

Дополнительная информация: Генерация неоднородных случайных величин.

Концептуально очень простой метод генерации экспоненциальных переменных основан на выборке обратного преобразования : учитывая случайную величину U, полученную из равномерного распределения на единичном интервале (0, 1) , переменная

$$T=F^{-1}(U)$$

имеет показательное распределение, где F ⁻¹ — функция квантиля , определяемая формулой

$$F^{-1}(p)={\frac {-\ln(1-p)}{\lambda }}.$$

Более того, если U равномерен на (0, 1), то и 1 − U равномерен . Это означает, что можно генерировать экспоненциальные переменные следующим образом:

$$T={\frac {-\ln(U)}{\lambda }}.$$

Другие методы генерации экспоненциальных переменных обсуждаются Кнутом. и Деврой.

Также доступен быстрый метод генерации набора готовых упорядоченных экспоненциальных переменных без использования процедуры сортировки.

См. также

• Мертвое время - применение экспоненциального распределения к анализу детектора частиц.
• Распределение Лапласа , или «двойное экспоненциальное распределение».
• Отношения между распределениями вероятностей
• Экспоненциальное распределение Маршалла – Олкина

Внешние ссылки

• «Экспоненциальное распределение» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Онлайн калькулятор экспоненциального распределения