Греки (финансы)

В математических финансах греки ; первый или выше) , представляют собой величины (известные в исчислении как частичные производные представляющие чувствительность цены производного инструмента, такого как вариант изменений в одном или нескольких базовых параметрах , на которых значение значения Инструмент или портфель финансовых инструментов зависят. Название используется, потому что наиболее распространенная из этих чувствительности обозначается греческими буквами (как и некоторые другие финансовые меры). В совокупности они также назывались чувствительностью к риску , ^{[ 1 ]} меры риска ^{[ 2 ]}^: 742 или параметры хеджирования . ^{[ 3 ]}

Использование греков

В основе параметр	Параметр параметра
В основе параметр	Точечная цена С	Волатильность $\sigma$	Проход время
Значение (v)	$\Delta$ Дельта	${\mathcal {V}}$ Вега	$\Theta$ Тета
Дельта ( $\Delta$ )	$\Gamma$ Гамма	Ванна	Шарм
Вега ( ${\mathcal {V}}$ )	Ванна	Ром	Знать
Тета ( $\Theta$ )	Шарм	Знать
Гамма ( $\Gamma$ )	Скорость	Зомма	Цвет
Ром		Последний

Определение греков как чувствительность цены и риска опции (в первом ряду) к базовому параметру (в первом столбце).
Греки первого порядка находятся в синем, греки второго порядка в зеленом, а греки третьего порядка-желтый.
Ванна, очарование и вета появляются дважды, так как частичные перекрестные производные равны теореме Шварца . Rho, Lambda, Epsilon и Vera не так, как они не так важны, как остальные. Три места в таблице не заняты, потому что соответствующие величины еще не были определены в финансовой литературе.

Греки являются жизненно важными инструментами в управлении рисками . Каждый греческий измеряет чувствительность стоимости портфеля к небольшому изменению данного базового параметра, так что компонентные риски могут рассматриваться в изоляции, и портфель соответственно перебалансировал для достижения желаемого воздействия; Смотрите, например, дельта хеджирование .

Греки в модели чернокожих -шолсов (относительно простая идеализированная модель определенных финансовых рынков) относительно легко рассчитать - желаемая собственность финансовых моделей - и очень полезны для торговцев деривативами, особенно для тех, кто стремится хеджировать свои портфели от неблагоприятных Изменения в рыночных условиях. По этой причине те греки, которые особенно полезны для хеджирования, такие как Delta, Theta и Vega, хорошо определены для измерения изменений в параметрах точечной цены, времени и волатильности. Хотя Rho (частичная производная по отношению к бесконечной процентной ставке ) является первичным вводом в модель чернокожих-шол. Как правило, незначительные и, следовательно, производные более высокого порядка, включающие безрисковую процентную ставку, не являются общими.

Наиболее распространенными из греков являются производные первого порядка: Дельта , Вега , Тета и Ро ; а также гамма , производное второго порядка функции значения. Оставшаяся чувствительность в этом списке достаточно распространена, чтобы иметь общие имена, но этот список ни в коем случае не исчерпывает.

Игроки на рынке совершают конкурентные сделки с участием много миллиардов (из $, £ или €), базовых каждый день, поэтому важно правильно сделать суммы. На практике они будут использовать более сложные модели, которые выходят за рамки упрощенных предположений, используемых в модели Black-Scholes, и, следовательно, в греках.

Имена

Использование имен греческих букв, по -видимому, является расширением от общих финансов, альфа и бета , а также использование Sigma (стандартное отклонение логарифмических возвратов) и тау (время для истечения) в модели ценообразования опции чернокожих . Несколько имен, таких как «Vega» (символ которого похож на греческую букву NU ; Использование этого имени могло привести к путанице) и «Zomma», изобретены, но звучат похожи на греческие буквы. Названия «цвет» и «очарование», по -видимому, вытекают из использования этих терминов для экзотических свойств кварков в физике частиц .

Греки первого порядка

Дельта

Дельта , ^{[ 4 ]} $\Delta$ , измеряет ставку изменения теоретического значения опции в отношении изменений в цене базового актива. Delta является первой производной значения $V$ опции в отношении цены базового инструмента $S$ .

\Delta ={\frac {\partial V}{\partial S}}

Практическое использование

Для ванильной опции Delta составит число от 0,0 до 1,0 для длительного вызова (или короткого пута) и 0,0 и -1,0 для длительного пункта (или короткого звонка); В зависимости от цены опция вызова ведет себя так, как будто кто -то владеет 1 акцией базовой акции (если в глубокой в деньгах) или ничего не владеет (если далеко от денег), или что -то среднее, и, наоборот, для опциона. Разница между дельтой вызова и дельтой точки на том же ударе равна одному. По паритету PUT -SALL , длинный вызов и короткий пут эквивалентен форварду F , который является линейным в точках S, с коэффициентом единицы, поэтому производная DF/DS является 1. См. Формулы ниже.

Эти цифры обычно представляются в процентах от общего количества акций, представленных опционным договором. Это удобно, потому что вариант (мгновенно) ведут себя как количество акций, указанных Delta. Например, если портфель из 100 американских вариантов вызовов на XYZ имеет дельту 0,25 (= 25%), он получит или потеряет стоимость, как 2500 акций XYZ, поскольку цена изменяется за небольшие ценовые движения (100 опционных контрактов покрывают покрытия. 10000 акций). Знак и процент часто сбрасываются - знак подразумевается в типе опции (отрицательный для пута, положительный для вызовов), и процент понят. Наиболее часто цитируемыми являются 25 Delta Put, 50 Delta Put/50 Delta Call и 25 Delta Call. 50 Delta Put и 50 Delta Call не совсем идентичны из -за точки и вперед, отличающиеся от фактора дисконтирования, но они часто объединяются.

Delta всегда положительна для длинных звонков и отрицательно для длинных путов (если они не нулевые). Общая дельта сложного портфеля позиций на одном и том же базовом активе может быть рассчитана, просто взяв сумму дельт для каждой отдельной позиции - дельта портфеля является линейным для составляющих. Поскольку дельта базового актива всегда составляет 1,0, трейдер может дельта-задержать всю свою позицию в базовой основе, покупая или сократив количество акций, указанных общей дельтой. Например, если дельта портфеля опционов в XYZ (выраженная как акции базовых) составляет +2,75, трейдер сможет дельта-поддерживать портфель, продав короткие 2,75 акции базовых. Затем этот портфель сохранит свою общую стоимость независимо от того, в каком направлении движется цена XYZ. (Хотя для лишь небольших движений в основе, короткое количество времени и не с учетом изменений в других рыночных условиях, таких как волатильность и норму прибыли для бесконечных инвестиций).

Как прокси для вероятности

(Абсолютная стоимость) дельта близок к, но не идентична процентной денег , то есть, то есть подразумеваемая вероятность того, что этот вариант истекает в деньгах (если рынок перемещается под движением Браун в риске. нейтральная мера ). ^{[ 5 ]} По этой причине некоторые трейдеры опционов используют абсолютную стоимость Delta в качестве приближения к процентной денег. Например, если вариант вызова за пределами денег имеет дельту 0,15, трейдер может оценить, что вариант имеет приблизительно 15% вероятность истечения срока действия в деньгах. Аналогичным образом, если контракт на PUT имеет дельту составляет -0,25, трейдер может ожидать, что вариант будет иметь 25% вероятность истечения срока действия в деньгах. Вызовы и поставки в деньгах имеют дельту приблизительно 0,5 и -0,5 соответственно с небольшим смещением в сторону более высоких дельт для вызовов ATM, поскольку безрисковая ставка вносит некоторое смещение в дельту. Негативная вероятность скидки на опцию, заканчивающаяся в деньгах при истечении срока действия, называется двойной дельтой , которая является первой производной цены опционов в отношении забастовки. ^{[ 6 ]}

Отношения между Call и Delta

Учитывая европейский вызов и вариант поставки для того же базового, цена удара и время до зрелости, а также без дивидендов, сумма абсолютных значений дельты каждой опции будет 1 - точнее, дельта вызова ( положительный) минус дельта пут (отрицательный) равен 1. Это связано с паритетом пута : длинный вызов плюс короткий пункт (вызов за вызов пут) повторяет форвард, который имеет дельта 1

Если значение дельты для опции известно, можно рассчитать значение дельты опции той же цены удара, в основе и зрелости, но противоположных справа, вычитая 1 из известной дельты вызовов или добавив 1 в известную Delta Put Delta Полем

\Delta ({\text{call}})-\Delta ({\text{put}})=1,{\text{ therefore: }}\Delta ({\text{call}})=\Delta ({\text{put}})+1{\text{ and }}\Delta ({\text{put}})=\Delta ({\text{call}})-1.

Например, если дельта вызова составляет 0,42, то можно вычислить дельту соответствующего пута по той же цене удара на 0,42 - 1 = -0,58. Чтобы получить дельту вызова из пут, можно аналогично потребоваться -0,58 и добавить 1, чтобы получить 0,42.

Вега

Вега ^{[ 4 ]} Измеряет чувствительность к волатильности . Vega является производной значения опции в отношении волатильности базового актива.

{\mathcal {V}}={\frac {\partial V}{\partial \sigma }}

Вега - это не имя какого -либо греческого письма. Используемый глиф-это нестандартная версия греческой буквы NU ( ${\textstyle \nu }$ ), написано как ${\mathcal {V}}$ Полем Предположительно, название Вега было принято, потому что греческая буква NU выглядела как латинский Vee , и Vega была получена из Vee по аналогии с тем, как бета , ETA и Theta произносится на американском английском.

Символ каппа , $\kappa$ иногда используется (учеными) вместо Веги (как тау (тау ( $\tau$ ) или столичная лямбда ( $\Lambda$ ), ^{[ 7 ]} ^: 315 хотя они редки).

Vega обычно выражается как сумма денег за основную долю, которую стоимость опции будет получена или проиграет по мере роста волатильности или падает на 1 процентный пункт . Все варианты (как вызовы, так и поставки) получат ценность с ростом волатильности.

Vega может быть важным греческим для мониторинга для трейдера опционов, особенно на летучих рынках, поскольку значение некоторых стратегий опционов может быть особенно чувствительным к изменениям волатильности. значение опции «Аттрактическое опцию» Например, чрезвычайно зависит от изменений волатильности. См. Риск волатильности .

Тета

Тета , ^{[ 4 ]} $\Theta$ , измеряет чувствительность значения производной к течению времени (см. Значение опции ): «распад времени».

\Theta =-{\frac {\partial V}{\partial \tau }}

Со временем, с уменьшением времени до истечения срока действия и равным, внешнее значение опции уменьшается. Обычно (но см. Ниже), это означает, что опция теряет значение со временем, которое обычно называют длинными вариантами, обычно имеющими короткие (отрицательные) тета. На самом деле, как правило, буквальное первое производное время WRT значения опции является положительным числом. Изменение значения опции обычно отрицательно, потому что прохождение времени является отрицательным числом ( уменьшение до $\tau \,$ , время с истечением). Однако, согласно соглашению, практикующие обычно предпочитают ссылаться на экспозицию тета («распад») длительного варианта как негативного (вместо того, чтобы пройти время как негативное), и поэтому тета обычно сообщается в -1 раза превышающей первую производную, как выше.

В то время как внешнее значение уменьшается с прохождением времени, иногда противодействующий фактор дисконтируется. Для вариантов глубоких денег некоторых типов (для Put in Black-Scholes, PUT и вызовов в черных), поскольку факторы дисконтирования увеличиваются до 1 с течением времени, то есть элемент увеличения стоимости в длинном варианте Полем Иногда варианты в глубине денег получают больше от увеличения коэффициентов дисконтирования, чем они теряют от уменьшения внешней стоимости, и сообщаемая тета будет положительным значением для длинного варианта, а не более типичного отрицательного значения (и вариант будет Ранний кандидат в физические упражнения, если они используются, и европейский вариант может стать меньше, чем паритет).

Согласно соглашению в опциональных формулах, $\tau \,$ Время до истечения, определено в годы. Практикующие обычно предпочитают просматривать тета с точки зрения изменения количества дней с истечения срока действия, а не количество лет до истечения срока действия. Поэтому сообщается, что тета обычно делится на количество дней в год. (Будь то считать календарные дни или рабочие дни варьируются в зависимости от личного выбора, с аргументами для обоих.)

Родовой

Ро , ^{[ 4 ]} $\rho$ , измерения чувствительности к процентной ставке: это производная значения опциона в отношении бесконечной процентной ставки (для соответствующего непогашенного срока).

\rho ={\frac {\partial V}{\partial r}}

За исключением экстремальных обстоятельств, значение опции менее чувствительно к изменениям в бесконечной процентной ставке, чем к изменениям в других параметрах. По этой причине RHO является наименее используемым из греков первого порядка.

RHO обычно выражается как сумма денег, на акцию базового, что стоимость опциона будет выиграть или проиграть, поскольку безрисковая процентная ставка увеличивается или падает на 1,0% в год (100 базисных пунктов).

Лямбда

Лямбда , ^{[ 4 ]} $\lambda$ , омега , ^{[ 8 ]} $\Omega$ , или эластичность ^{[ 4 ]} Является ли процентное изменение стоимости опционов на процентное изменение в базовой цене, мера левереджа , иногда называемое передач.

\lambda =\Omega ={\frac {\partial V}{\partial S}}\times {\frac {S}{V}}

Это держит это $\lambda =\Omega =\Delta \times {\frac {S}{V}}$ .

Это похоже на концепцию дельты, но выражается в процентах, а не абсолютных терминах.

Эпсилон

Эпсилон , ^{[ 9 ]} $\varepsilon$ (также известен как PSI, $\psi$ ), это процентное изменение стоимости опциона на процентное изменение в основной дивидендной доходности, мера дивидендного риска. Воздействие дивидендов на практике определяется с использованием увеличения этой урожайности на 10%. Очевидно, что эта чувствительность может применяться только к производным инструментам продуктов акционерного капитала .

\varepsilon =\psi ={\frac {\partial V}{\partial q}}

Численно, все чувствительность первого порядка можно интерпретировать как спреды в ожидаемых доходах. ^{[ 10 ]} Информационная геометрия предлагает другую (тригонометрическую) интерпретацию. ^{[ 10 ]}

Греки второго порядка

Гамма

Гамма , ^{[ 4 ]} $\Gamma$ , измеряет ставку изменения в дельте в отношении изменений в базовой цене. Гамма является второй производной функции стоимости по отношению к базовой цене.

\Gamma ={\frac {\partial \Delta }{\partial S}}={\frac {\partial ^{2}V}{\partial S^{2}}}

Большинство длинных вариантов имеют положительную гамма, а большинство коротких вариантов имеют отрицательную гамма. Длинные варианты имеют положительную связь с гаммой, потому что по мере увеличения цены гамма также увеличивается, что приводит к тому, что Delta приближается к 1 от 0 (опция длинных вызовов) и 0 из -1 (опция длинного пута). Обращение верно для коротких вариантов. ^{[ 11 ]}

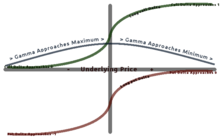
Гамма является наибольшей приблизительно в деньгах (ATM) и уменьшает дальше, чем вы идете либо в деньги (ITM), либо из-за денег (OTM). Гамма важна, потому что она исправляет для выпуклости ценности.

Когда трейдер стремится установить эффективную дельта-догона для портфеля, трейдер также может попытаться нейтрализовать гамма портфеля, поскольку это гарантирует, что хеджирование будет эффективно в более широком диапазоне основных цен на цену.

Ванна

Ванна , ^{[ 4 ]} также называется DVEGADSPOT ^{[ 13 ]} и ddeltadvol , ^{[ 13 ]} является производным второго порядка значения опции, один раз до базовой точечной цены и один раз к волатильности. Он математически эквивалентен DDELTADVOL , чувствительности Delta Option в отношении изменения волатильности; Или, в качестве альтернативы, частично Vega по цене базового инструмента. Vanna может быть полезной чувствительностью для мониторинга при поддержании портфеля дельта или Vega, поскольку Vann Основная точечная цена.

Если базовое значение имеет непрерывные вторые частичные производные, то тогда ${\text{Vanna}}={\frac {\partial \Delta }{\partial \sigma }}={\frac {\partial {\mathcal {V}}}{\partial S}}={\frac {\partial ^{2}V}{\partial S\,\partial \sigma }}.$

Шарм

Шарм ^{[ 4 ]} или дельта -распад ^{[ 14 ]} Измеряет мгновенную скорость смены дельты в течение срока времени.

{\text{Charm}}=-{\frac {\partial \Delta }{\partial \tau }}={\frac {\partial \Theta }{\partial S}}=-{\frac {\partial ^{2}V}{\partial \tau \,\partial S}}

Очарование также называлось DDELTADTIME . ^{[ 13 ]} Очарование может быть важным греческим для измерения/мониторинга, когда дельта выдерживает позицию в течение выходных. Charm-это производная второго порядка значения опции, один раз до цены и один раз до текущего времени. Тогда это является производной тета по цене базовой.

Математический результат формулы для очарования (см. Ниже) выражается в Delta/Year. Часто полезно разделить это на количество дней в год, чтобы прибыть в дельта -распад в день. Это использование довольно точное, когда количество дней оставалось до тех пор, пока не станет большим. Когда вариант приближается к истечению, сама очарование может быстро измениться, что оценивает оценки дельта -распада неточным.

Ром

Vomma , ^{[ 4 ]} Волга , ^{[ 15 ]} Вега выпуклость , ^{[ 15 ]} или dvegadvol ^{[ 15 ]} Измеряет чувствительность второго порядка к волатильности . Vomma является вторым производным значения опции в отношении волатильности, или, по -другому, Vomma измеряет скорость изменения в VEGA в качестве изменений волатильности.

{\text{Vomma}}={\frac {\partial {\mathcal {V}}}{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma ^{2}}}

С помощью положительной Vomma позиция станет длинной вегой, поскольку подразумеваемая волатильность увеличивается и короткая Vega по мере его уменьшения, что может быть скальпировано таким образом, аналогично длинной гамме. И первоначально вега-нейтральная позиция с длинной водой может быть построена из соотношений вариантов на разных ударах. Vomma положительно для длинных вариантов от денег и первоначально увеличивается с расстоянием от денег (но выходит из -за того, что Вега выходит). (В частности, Vomma является положительным, если обычные термины D ₁ и D ₂ имеют тот же знак, который верно, когда D ₁ <0 или D ₂ > 0.)

Знать

VetaЗнает ^{[ 16 ]} Vega Decay или Dvegadtime ^{[ 15 ]} Измеряет скорость изменения в Веге в отношении течения времени. VETA является вторым производным функции значения; Оказавшись волатильностью и один раз от времени.

{\text{Veta}}={\frac {\partial {\mathcal {V}}}{\partial \tau }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial \tau }}

Обычной практикой является разделение математического результата VETA в 100 раз превышает количество дней в год, чтобы снизить стоимость до процентного изменения в VEGA за один день.

Оставаться

Оставаться ^{[ 17 ]} (Иногда Rhova ) ^{[ 17 ]} Измеряет скорость изменения в RHO в отношении волатильности. Vera является вторым производным функции значения; Один раз к волатильности и один раз до процентной ставки.

{\text{Vera}}={\frac {\partial \rho }{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial r}}

Слово «Vera» было придумано R. naryshkin в начале 2012 года, когда эта чувствительность должна была использоваться на практике для оценки влияния изменений волатильности на Rho-Hedging, но в доступной литературе еще не было названия. «Вера» была выбрана, чтобы звучать похоже на комбинацию Vega и Rho, соответствующих греков первого порядка. Это имя теперь в более широком использовании, в том числе, например, программное обеспечение Algebra Computer Computer (которое имеет функцию «Blackscholesvera» в своем финансовом пакете).

Частичная производная второго порядка по отношению к удару K

Это частичное производное играет фундаментальную роль в формуле Breeden -Litzenberger, ^{[ 18 ]} который использует котируемые цены на опционы вызовов для оценки нейтральных вероятностей, подразумеваемых такими ценами.

\varpi ={\frac {\partial ^{2}V}{\partial K^{2}}}

Для вариантов вызовов это может быть аппроксимировано с использованием бесконечно малых портфелей стратегий бабочки .

Греки третьего порядка

Скорость

Скорость ^{[ 4 ]} Измеряет ставку изменения в гамме в отношении изменений в базовой цене.

{\text{Speed}}={\frac {\partial \Gamma }{\partial S}}={\frac {\partial ^{3}V}{\partial S^{3}}}

Это также иногда называют гаммой гаммы ^{[ 2 ]}^: 799 или dgammadspot . ^{[ 13 ]} Скорость является третьей производной функции стоимости в отношении базовой точечной цены. Скорость может быть важна для контроля при притяжении Delta или гамма-выписке портфеля.

Зомма

Зомма ^{[ 4 ]} Измеряет скорость изменения гаммы в отношении изменений волатильности.

{\text{Zomma}}={\frac {\partial \Gamma }{\partial \sigma }}={\frac {\partial {\text{vanna}}}{\partial S}}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \sigma }}

Zomma также называлась Dgammadvol . ^{[ 13 ]} Zomma является третьей производной значения опции, дважды до базовой цены активов и один раз к волатильности. Zomma может быть полезной чувствительностью для мониторинга при поддержании гамма-обтягиваемого портфеля, поскольку Zomma поможет трейдеру предвидеть изменения в эффективности хеджирования в качестве изменений волатильности.

Цвет

Цвет , ^{[ 13 ]} гамма -распад ^{[ 19 ]} или dgammadtime ^{[ 13 ]} Измеряет скорость смены гаммы за время.

{\text{Color}}={\frac {\partial \Gamma }{\partial \tau }}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \tau }}

Цвет-это производная третьего порядка значения опции, дважды до базовой цены активов и один раз от времени. Цвет может быть важной чувствительностью для мониторинга при поддержании гамма-обтягиваемого портфеля, поскольку он может помочь трейдеру предвидеть эффективность хеджирования с течением времени.

Математический результат формулы для цвета (см. Ниже) выражается в гамме в год. Часто полезно разделить это на количество дней в год, чтобы прийти к изменению гаммы в день. Это использование довольно точное, когда количество дней оставалось до тех пор, пока не станет большим. Когда вариант приближается к истечению, сам цвет может быстро измениться, что приведет к тому, что оценки гамма -изменений в гамма -изменении.

Последний

Последний ^{[ 4 ]} Измеряет чувствительность опции vomma в отношении изменения волатильности.

{\text{Ultima}}={\frac {\partial {\text{vomma}}}{\partial \sigma }}={\frac {\partial ^{3}V}{\partial \sigma ^{3}}}

Ultima также называется Dvommadvol . ^{[ 4 ]} Ultima-это производное третьего порядка значения опции до волатильности.

Греки для вариантов многоуровневых

Если значение производной зависит от двух или более базовых , его греки расширяются, чтобы включить перекрестные эффекты между базовыми.

Дельта корреляции измеряет чувствительность значения производной к изменению корреляции между базовыми. ^{[ 20 ]} Это также широко известно как CEGA . ^{[ 21 ]}^{[ 22 ]}

Cross Gamma измеряет скорость смены дельты в одном базовом изменении уровня другого базового. ^{[ 23 ]}

Cross Vanna измеряет скорость изменения VEGA в одном базовом из -за изменения уровня другого базового. Эквивалентно, он измеряет скорость изменения дельты во второй базовой основе из -за изменения волатильности первого базового. ^{[ 20 ]}

Cross Volga измеряет скорость смены VEGA в одном базовом изменении волатильности другого базового. ^{[ 23 ]}

Формулы для европейских вариантов греков

Греки европейских опционов ( вызовы и поставки ) под моделью чернокожих -шолсов рассчитываются следующим образом, где $\varphi$ (PHI) - стандартная нормальная функция плотности вероятности и $\Phi$ является стандартной нормальной кумулятивной функцией распределения . Обратите внимание, что формулы гамма и Вега одинаковы для вызовов и постановки.

Для данного:

Цена акций $S\,$ ,
Цена забастовки $K\,$ ,
Без риска ставка $r\,$ ,
Годовая дивидендная доходность $q\,$ ,
Время до зрелости $\tau =T-t\,$ (представлена как бездумная доля одного года), и
Волатильность $\sigma \,$ .

	Вызовы	Поставки
справедливая стоимость ( $V$ )	$Se^{-q\tau }\Phi (d_{1})-e^{-r\tau }K\Phi (d_{2})\,$	$e^{-r\tau }K\Phi (-d_{2})-Se^{-q\tau }\Phi (-d_{1})\,$

Дельта ( $\Delta$ )	$e^{-q\tau }\Phi (d_{1})\,$	$-e^{-q\tau }\Phi (-d_{1})\,$
Вега ( ${\mathcal {V}}$ )	$Se^{-q\tau }\varphi (d_{1}){\sqrt {\tau }}=Ke^{-r\tau }\varphi (d_{2}){\sqrt {\tau }}\,$
Тета ( $\Theta$ )	$-e^{-q\tau }{\frac {S\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}-rKe^{-r\tau }\Phi (d_{2})+qSe^{-q\tau }\Phi (d_{1})\,$	$-e^{-q\tau }{\frac {S\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}+rKe^{-r\tau }\Phi (-d_{2})-qSe^{-q\tau }\Phi (-d_{1})\,$
Ро ( $\rho$ )	$K\tau e^{-r\tau }\Phi (d_{2})\,$	$-K\tau e^{-r\tau }\Phi (-d_{2})\,$
Эпсилон ( $\epsilon$ )	$-S\tau e^{-q\tau }\Phi (d_{1})$	$S\tau e^{-q\tau }\Phi (-d_{1})$
лямбда ( $\lambda$ )	$\Delta {\frac {S}{V}}\,$

Гамма ( $\Gamma$ )	$e^{-q\tau }{\frac {\varphi (d_{1})}{S\sigma {\sqrt {\tau }}}}=Ke^{-r\tau }{\frac {\varphi (d_{2})}{S^{2}\sigma {\sqrt {\tau }}}}\,$
ванна	$-e^{-q\tau }\varphi (d_{1}){\frac {d_{2}}{\sigma }}\,={\frac {\mathcal {V}}{S}}\left[1-{\frac {d_{1}}{\sigma {\sqrt {\tau }}}}\right]\,$
шарм	$qe^{-q\tau }\Phi (d_{1})-e^{-q\tau }\varphi (d_{1}){\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{2\tau \sigma {\sqrt {\tau }}}}\,$	$-qe^{-q\tau }\Phi (-d_{1})-e^{-q\tau }\varphi (d_{1}){\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{2\tau \sigma {\sqrt {\tau }}}}\,$

ром	$Se^{-q\tau }\varphi (d_{1}){\sqrt {\tau }}{\frac {d_{1}d_{2}}{\sigma }}={\mathcal {V}}{\frac {d_{1}d_{2}}{\sigma }}\,$
оставаться	$-K\tau e^{-r\tau }\varphi (d_{2}){\frac {d_{1}}{\sigma }}\,$
Знать	$-Se^{-q\tau }\varphi (d_{1}){\sqrt {\tau }}\left[q+{\frac {\left(r-q\right)d_{1}}{\sigma {\sqrt {\tau }}}}-{\frac {1+d_{1}d_{2}}{2\tau }}\right]\,$
$\varpi$	$Se^{-q\tau }\varphi (d_{1}){\frac {1}{K^{2}\sigma {\sqrt {\tau }}}}=\left({\frac {S}{K}}\right)^{2}\Gamma \,$

скорость	$-e^{-q\tau }{\frac {\varphi (d_{1})}{S^{2}\sigma {\sqrt {\tau }}}}\left({\frac {d_{1}}{\sigma {\sqrt {\tau }}}}+1\right)=-{\frac {\Gamma }{S}}\left({\frac {d_{1}}{\sigma {\sqrt {\tau }}}}+1\right)\,$
Зомма	$e^{-q\tau }{\frac {\varphi (d_{1})\left(d_{1}d_{2}-1\right)}{S\sigma ^{2}{\sqrt {\tau }}}}=\Gamma {\frac {d_{1}d_{2}-1}{\sigma }}\,$
цвет	$-e^{-q\tau }{\frac {\varphi (d_{1})}{2S\tau \sigma {\sqrt {\tau }}}}\left[2q\tau +1+{\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{\sigma {\sqrt {\tau }}}}d_{1}\right]\,$

последний	${\frac {-{\mathcal {V}}}{\sigma ^{2}}}\left[d_{1}d_{2}(1-d_{1}d_{2})+d_{1}^{2}+d_{2}^{2}\right]$

Двойная дельта	$-e^{-r\tau }\Phi (d_{2})\,$	$e^{-r\tau }\Phi (-d_{2})\,$
двойная гамма	$e^{-r\tau }{\frac {\varphi (d_{2})}{K\sigma {\sqrt {\tau }}}}\,$

где

{\begin{aligned}d_{1}&={\frac {\ln(S/K)+\left(r-q+{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(S/K)+\left(r-q-{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\\\varphi (x)&={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}\\\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-{\frac {1}{2}}y^{2}}\,dy=1-{\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {1}{2}}y^{2}}\,dy\end{aligned}}

Под черной моделью (обычно используется для товаров и опций на фьючерсы), греки могут быть рассчитаны следующим образом:

	Вызовы	Поставки
справедливая стоимость ( $V$ )	$e^{-r\tau }[F\Phi (d_{1})-K\Phi (d_{2})]\$	$e^{-r\tau }[K\Phi (-d_{2})-F\Phi (-d_{1})]\,$

Дельта ( $\Delta$ ) $=\partial V/\partial F$	$e^{-r\tau }\Phi (d_{1})\,$	$-e^{-r\tau }\Phi (-d_{1})\,$
Вега ( ${\mathcal {V}}$ )	$Fe^{-r\tau }\varphi (d_{1}){\sqrt {\tau }}=Ke^{-r\tau }\varphi (d_{2}){\sqrt {\tau }}\,$ (*)
Тета ( $\Theta$ )	$-{\frac {Fe^{-r\tau }\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}-rKe^{-r\tau }\Phi (d_{2})+rFe^{-r\tau }\Phi (d_{1})\,$	$-{\frac {Fe^{-r\tau }\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}+rKe^{-r\tau }\Phi (-d_{2})-rFe^{-r\tau }\Phi (-d_{1})\,$
Ро ( $\rho$ )	$-\tau e^{-r\tau }[F\Phi (d_{1})-K\Phi (d_{2})]\$	$-\tau e^{-r\tau }[K\Phi (-d_{2})-F\Phi (-d_{1})]\,$

Гамма ( $\Gamma$ ) $={\partial ^{2}V \over \partial F^{2}}$	$e^{-r\tau }{\frac {\varphi (d_{1})}{F\sigma {\sqrt {\tau }}}}=Ke^{-r\tau }{\frac {\varphi (d_{2})}{F^{2}\sigma {\sqrt {\tau }}}}\,$ (*)
ванна $={\frac {\partial ^{2}V}{\partial F\partial \sigma }}$	$-e^{-r\tau }\varphi (d_{1}){\frac {d_{2}}{\sigma }}\,={\frac {\mathcal {V}}{F}}\left[1-{\frac {d_{1}}{\sigma {\sqrt {\tau }}}}\right]\,$

ром	$Fe^{-r\tau }\varphi (d_{1}){\sqrt {\tau }}{\frac {d_{1}d_{2}}{\sigma }}={\mathcal {V}}{\frac {d_{1}d_{2}}{\sigma }}\,$

где

{\begin{aligned}d_{1}&={\frac {\ln(F/K)+{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(F/K)-{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\end{aligned}}

(*) Можно показать, что $F\varphi (d_{1})=K\varphi (d_{2})$

Микрорецветинг:

позволять $x=\sigma {\sqrt {\tau }}$
$d_{1}={\frac {\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}}{x}}$
$d_{1}\cdot x=\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}$
$\ln(F/K)=d_{1}\cdot x-{\frac {1}{2}}x^{2}$
${\frac {F}{K}}=e^{d_{1}\cdot x-{\frac {1}{2}}x^{2}}$
Тогда у нас есть: ${\frac {F}{K}}\cdot {\frac {\varphi (d_{1})}{\varphi (d_{2})}}={\frac {F}{K}}\cdot e^{{\frac {1}{2}}\cdot {d_{2}}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}$

$=e^{d_{1}x-{\frac {1}{2}}x^{2}}\cdot e^{{\frac {1}{2}}\cdot {(d_{1}-x)}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}=e^{d_{1}x-{\frac {1}{2}}x^{2}+{\frac {1}{2}}\cdot (2d_{1}-x)(-x)}=e^{0}=1.$
Так $F\varphi (d_{1})=K\varphi (d_{2})$

Связанные меры

Некоторые связанные с этим показатели риска финансовых инструментов перечислены ниже.

Продолжительность и выпуклость связи

В торговых облигациях и других ценных бумагах с фиксированным доходом различные показатели продолжительности облигаций используются аналогично дельте опциона. Ближайшим аналогом дельты является DV01 , который представляет собой снижение цены (в валютных единицах) для увеличения одной базисной точки (т. Е. 0,01% в год) в доходности , где доходность является основной переменной; См. Продолжительность облигаций § Риск - продолжительность как чувствительность процентной ставки . (Связанный CS01 , измерение чувствительности к кредитному распространению .)

Аналогично Lambda - это модифицированная продолжительность , которая представляет собой процентное изменение рыночной цены облигации (ы) для изменения единицы доходности (то есть он эквивалентен DV01, разделенной на рыночную цену). В отличие от Lambda, которая является эластичностью (процентное изменение вывода для процентного изменения входного входа), модифицированная продолжительность является полу -эластичностью -процентное изменение вывода для изменения единицы входного входа. См. Также длительность ключевой скорости .

Выпуклость облигации является мерой чувствительности продолжительности к изменениям процентных ставок , второй производной цены облигации по отношению к процентным ставкам (продолжительность является первой производной); Тогда это аналогично гамме. В целом, чем выше выпуклость, тем более чувствительна цена облигаций к изменению процентных ставок. Выпуклость связи является одной из самых основных и широко используемых форм выпуклости в финансах .

Для облигации с встроенным опцией , стандартные вычисления на основе погашения здесь не учитывают, как изменения процентных ставок изменят денежные потоки из -за опционов. Чтобы решить эту проблему, эффективная продолжительность и эффективная выпуклость вводятся . Эти значения обычно рассчитываются с использованием модели на основе дерева, созданной для всей кривой доходности (в отличие от единого урожайности до зрелости), и, следовательно, захватывание поведения упражнений в каждой точке жизни опции как функции как времени, так и процентных ставок ; См. Модель решетки (финансы) § Производные процентные ставки .

Бета

Бета представляет собой число , (β) акций или портфеля описывающее волатильность актива в отношении волатильности теста, с которым сравнивается актив. Этот эталон, как правило, является общим финансовым рынком и часто оценивается в использовании репрезентативных индексов , таких как S & P 500 .

Актив имеет бета -версию нуля, если его доходность меняется независимо от изменений в доходности рынка. Позитивная бета -версия означает, что доходность актива обычно следуют доходности рынка, в том смысле, что они оба, как правило, превышают свои соответствующие средние значения, или оба, как правило, находятся ниже их соответствующих средних значений. Негативная бета -версия означает, что доходность актива, как правило, перемещается напротив доходности рынка: один будет, как правило, превышает среднее значение, когда другой ниже среднего.

Сбежал

Фугит - это ожидаемое время для использования американского или бермудского варианта. Fugit с пользой вычисляется для хеджирования - например, можно представлять потоки американского перекачивания , например, потоки обмена, начиная с Fugit, умноженного на Delta, а затем использовать их для вычисления других чувствительности.

Смотрите также

Ссылки

^ Бэнкс, Эрик; Зигель, Пол (2006). Руководство по приложениям опционов: методы хеджирования и спекуляции для профессиональных инвесторов . McGraw-Hill Professional . п. 263. ISBN 9780071453158 .
^ Jump up to: ^а ^{беременный} Macmillan, Lawrence G. (1993). Варианты как стратегические инвестиции (3 -е изд.). Нью -Йоркский институт финансов . ISBN 978-0-13-636002-5 .
^ Крисс, Нил (1996). Черные - Шоли и за его пределами: модели цены опциона . McGraw-Hill Professional . п. 308 . ISBN 9780786310258 .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж ^k ^л ^м ^не Haug, Espen Gaardner (2007). Полное руководство по опциональным ценообразованию . McGraw-Hill Professional . ISBN 9780071389976 .
^ Сума, Джон. «Варианты греки: риск дельта и вознаграждение» . Получено 7 января 2010 года .
^ Штайнер, Боб (2013). Освоение финансовых расчетов (3 -е изд.). Пирсон Великобритания. ISBN 9780273750604 .
^ Халл, Джон С. (1993). Опции, фьючерсы и другие производные ценные бумаги (2 -е изд.). Прентис-Холл . ISBN 9780136390145 .
^ Омега - инвесопедия
^ Де Спигелеер, Ян; Schoutens, Wim (2015). Справочник по конвертируемым облигациям: ценообразование, стратегии и управление рисками . Джон Уайли и сыновья . С. 255, 269–270. ISBN 9780470689684 .
^ Jump up to: ^а ^{беременный} Соклаков, (2023). «Информационная геометрия рисков и возвратов». Риск Июнь . Arxiv : 2206.08753 . SSRN 4134885 .
^ Уиллетт, Джефф (2014-05-28). «Понимание того, как гамма влияет на дельту» . www.traderbrains.com . Получено 2014-03-07 .
^ Уиллетт, Джефф (2014-05-28). «Почему длинный вариант гамма -положительный» . www.traderbrains.com . Получено 2014-03-07 .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин Haug, Espen Gaarder (2003), «Знай свое оружие, часть 1» (PDF) , журнал Wilmott (май 2003 г.): 49–57, doi : 10.1002/wilm.42820030313 (неактивный 2024-03-19) {{citation}}: CS1 Maint: doi неактивен с марта 2024 года ( ссылка )
^ Деривативы - дельта -распад - финансовая энциклопедия
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Haug, Espen Gaarder (2003), «Знай свое оружие, часть 2» , Журнал Уилмотта (июль 2003 г.): 43–57
^ Pierino ursone. Как рассчитать цены вариантов и их греков: изучение модели Black Scholes от Delta до Vega . Джон Уайли и сыновья. 2015.
^ Jump up to: ^а ^{беременный} Деривативы-греки второго порядка-финансовая энциклопедия
^ Breeden, Litzenberger, Цены на государственные претензии, подразумеваемые в опционных ценах [1]
^ «Деривативы - греки» . Инвестиции и финансы . Получено 2020-12-21 .
^ Jump up to: ^а ^{беременный} «Греки для вариантов с несколькими активами» . Получено 24 января 2017 года .
^ Корреляционный риск . Получено 22 марта 2018 года .
^ «Вращающиеся варианты горного хребта, оценка и риски / анализ производительности» . Получено 22 марта 2018 года .
^ Jump up to: ^а ^{беременный} Фенглер, Матиас; Schwendner, Peter (2003). «Премия риска корреляции для вариантов акционерного капитала» (PDF) . Университет Гумбольдта в Берлине, факультет экономики. Doi : 10.18452/3572 . {{cite journal}}: CITE Journal требует |journal= ( помощь )

Внешние ссылки

Теория

Delta, Gamma, Gammap, Gamma Symmetry, Vanna, Speed, Charm, Saddle Gamma: ванильные варианты - Espen Haug ,
Volga, Vanna, Speed, Charm, Color: варианты ванили - Uwe Wystup Archived 2007-09-28 в The Wayback Machine , Варианты ванили - Uwe Wystup

Онлайн -инструменты

Греки: Чувствительность цен на финансовые варианты , пакет R для вычисления греков для европейских, американских и азиатских вариантов

[1] Бэнкс, Эрик; Зигель, Пол (2006). Руководство по приложениям опционов: методы хеджирования и спекуляции для профессиональных инвесторов . McGraw-Hill Professional . п. 263. ISBN 9780071453158 .

[macmillan93-2] Jump up to: ^а ^{беременный} Macmillan, Lawrence G. (1993). Варианты как стратегические инвестиции (3 -е изд.). Нью -Йоркский институт финансов . ISBN 978-0-13-636002-5 .

[3] Крисс, Нил (1996). Черные - Шоли и за его пределами: модели цены опциона . McGraw-Hill Professional . п. 308 . ISBN 9780786310258 .

[autogenerated2007-4] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж ^k ^л ^м ^не Haug, Espen Gaardner (2007). Полное руководство по опциональным ценообразованию . McGraw-Hill Professional . ISBN 9780071389976 .

[5] Сума, Джон. «Варианты греки: риск дельта и вознаграждение» . Получено 7 января 2010 года .

[6] Штайнер, Боб (2013). Освоение финансовых расчетов (3 -е изд.). Пирсон Великобритания. ISBN 9780273750604 .

[Hull93-7] Халл, Джон С. (1993). Опции, фьючерсы и другие производные ценные бумаги (2 -е изд.). Прентис-Холл . ISBN 9780136390145 .

[8] Омега - инвесопедия

[9] Де Спигелеер, Ян; Schoutens, Wim (2015). Справочник по конвертируемым облигациям: ценообразование, стратегии и управление рисками . Джон Уайли и сыновья . С. 255, 269–270. ISBN 9780470689684 .

[autogenerated2023-10] Jump up to: ^а ^{беременный} Соклаков, (2023). «Информационная геометрия рисков и возвратов». Риск Июнь . Arxiv : 2206.08753 . SSRN 4134885 .

[11] Уиллетт, Джефф (2014-05-28). «Понимание того, как гамма влияет на дельту» . www.traderbrains.com . Получено 2014-03-07 .

[12] Уиллетт, Джефф (2014-05-28). «Почему длинный вариант гамма -положительный» . www.traderbrains.com . Получено 2014-03-07 .

[kyw1-13] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин Haug, Espen Gaarder (2003), «Знай свое оружие, часть 1» (PDF) , журнал Wilmott (май 2003 г.): 49–57, doi : 10.1002/wilm.42820030313 (неактивный 2024-03-19) {{citation}}: CS1 Maint: doi неактивен с марта 2024 года ( ссылка )

[14] Деривативы - дельта -распад - финансовая энциклопедия

[kyw2-15] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Haug, Espen Gaarder (2003), «Знай свое оружие, часть 2» , Журнал Уилмотта (июль 2003 г.): 43–57

[16] Pierino ursone. Как рассчитать цены вариантов и их греков: изучение модели Black Scholes от Delta до Vega . Джон Уайли и сыновья. 2015.

[FE-17] Jump up to: ^а ^{беременный} Деривативы-греки второго порядка-финансовая энциклопедия

[BL-18] Breeden, Litzenberger, Цены на государственные претензии, подразумеваемые в опционных ценах [1]

[19] «Деривативы - греки» . Инвестиции и финансы . Получено 2020-12-21 .

[greeksMulti-20] Jump up to: ^а ^{беременный} «Греки для вариантов с несколькими активами» . Получено 24 января 2017 года .

[21] Корреляционный риск . Получено 22 марта 2018 года .

[22] «Вращающиеся варианты горного хребта, оценка и риски / анализ производительности» . Получено 22 марта 2018 года .

[mao1-23] Jump up to: ^а ^{беременный} Фенглер, Матиас; Schwendner, Peter (2003). «Премия риска корреляции для вариантов акционерного капитала» (PDF) . Университет Гумбольдта в Берлине, факультет экономики. Doi : 10.18452/3572 . {{cite journal}}: CITE Journal требует |journal= ( помощь )

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]