Теория управления

Эта статья о теории управления в технике. Для теории управления в лингвистике см. управление (лингвистика) . Чтобы узнать о теории управления в психологии и социологии, см. теорию управления (социология) и теорию перцептивного контроля .

Теория управления — это область техники управления и прикладной математики , которая занимается управлением динамическими системами в инженерных процессах и машинах. Цель состоит в том, чтобы разработать модель или алгоритм, управляющий применением входных данных системы для приведения системы в желаемое состояние, минимизируя при этом любую задержку , перерегулирование или установившуюся ошибку и обеспечивая уровень стабильности управления ; часто с целью достижения определенной степени оптимальности .

Для этого контроллер необходим с необходимым корректирующим поведением. Этот контроллер контролирует контролируемую переменную процесса (PV) и сравнивает ее с опорным или заданным значением (SP). Разница между фактическим и желаемым значением переменной процесса, называемая сигналом ошибки или ошибкой SP-PV, применяется в качестве обратной связи для создания управляющего воздействия, приводящего контролируемую переменную процесса к тому же значению, что и заданное значение. Другими аспектами, которые также изучаются, являются управляемость и наблюдаемость . Теория управления используется в разработке систем управления для проектирования систем автоматизации, которые произвели революцию в производстве, авиации, связи и других отраслях, а также создали новые области, такие как робототехника .

Обычно широко используется схематический стиль, известный как блок-диаграмма . В нем передаточная функция , также известная как системная функция или сетевая функция, представляет собой математическую модель связи между входом и выходом, основанную на дифференциальных уравнениях, описывающих систему.

Теория контроля берет свое начало в 19 веке, когда теоретическая основа работы регуляторов была впервые описана Джеймсом Клерком Максвеллом . Теория управления была развита Эдвардом Раутом в 1874 году, Чарльзом Штурмом и в 1895 году Адольфом Гурвицем , которые внесли свой вклад в установление критериев устойчивости управления; и с 1922 года разработка ПИД-регулирования теории Николасом Минорским . Хотя основное применение математической теории управления находится в разработке систем управления , которая занимается проектированием систем управления технологическими процессами для промышленности, другие приложения выходят далеко за рамки этого. Как общая теория систем с обратной связью, теория управления полезна везде, где возникает обратная связь - таким образом, теория управления также имеет приложения в науках о жизни, компьютерной инженерии, социологии и исследовании операций .

История

Смотрите также: Техника управления § История

Центробежный регулятор в двигателе Boulton & Watt 1788 года.

Хотя системы управления различных типов восходят к античности, более формальный анализ этой области начался с анализа динамики центробежного регулятора , проведенного физиком Джеймсом Клерком Максвеллом в 1868 году под названием «О регуляторах» . Центробежный регулятор уже использовался для регулирования скорости ветряных мельниц. Максвелл описал и проанализировал явление автоколебаний , при котором лаги в системе могут привести к сверхкомпенсации и нестабильному поведению. Это вызвало шквал интереса к теме, в ходе которого одноклассник Максвелла Эдвард Джон Раут абстрагировал результаты Максвелла для общего класса линейных систем. Независимо, Адольф Гурвиц проанализировал устойчивость системы с помощью дифференциальных уравнений в 1877 году, что привело к тому, что сейчас известно как теорема Рауса-Гурвица .

Заметное применение динамического управления было в области полета с экипажем. Братья Райт совершили свои первые успешные испытательные полеты 17 декабря 1903 года и отличались способностью управлять полетом в течение длительного времени (в большей степени, чем известная способность создавать подъемную силу с помощью аэродинамического профиля). Непрерывное и надежное управление самолетом было необходимо для полетов длительностью более нескольких секунд.

Ко времени Второй мировой войны теория управления стала важной областью исследований. Ирмгард Флюгге-Лотц разработал теорию прерывистых систем автоматического управления и применил принцип «взрыв-взрыв» к разработке оборудования автоматического управления полетом самолетов. Другие области применения прерывистого управления включали системы управления огнем , системы наведения и электронику .

Иногда для повышения устойчивости систем используются механические методы. Например, корабельные стабилизаторы представляют собой плавники, установленные под ватерлинией и выступающие вбок. На современных судах это могут быть активные плавники с гироскопическим управлением, которые способны изменять угол атаки, чтобы противодействовать крену, вызванному ветром или волнами, действующими на корабль.

Космическая гонка также зависела от точного управления космическими кораблями, а теория управления также нашла все более широкое применение в таких областях, как экономика и искусственный интеллект. Здесь можно сказать, что цель состоит в том, чтобы найти внутреннюю модель , подчиняющуюся теореме о хорошем регуляторе . Так, например, в экономике, чем точнее торговая модель (акции или сырьевые товары) представляет действия рынка, тем легче ей контролировать этот рынок (и извлекать из него «полезную работу» (прибыль)). В области искусственного интеллекта примером может быть чат-бот, моделирующий дискурсивное состояние людей: чем точнее он может моделировать состояние человека (например, на горячей линии голосовой поддержки), тем лучше он может манипулировать человеком (например, заставляя его выполнять корректирующие действия). для решения проблемы, вызвавшей звонок в справочную службу). Эти последние два примера берут узкую историческую интерпретацию теории управления как набора дифференциальных уравнений, моделирующих и регулирующих кинетическое движение, и расширяют ее до обширного обобщения теории управления. регулятор, взаимодействующий с растением .

Управление с разомкнутым и замкнутым контуром (обратная связь)

Этот раздел представляет собой отрывок из книги «Контур управления § Разомкнутый и замкнутый контур» . [ редактировать ]

По сути, существует два типа контура управления: управление с разомкнутым контуром (прямая связь) и управление с обратной связью (обратная связь).

Электромеханический таймер, обычно используемый для управления с разомкнутым контуром, основанный исключительно на временной последовательности, без обратной связи с процессом.

При управлении с разомкнутым контуром управляющее действие контроллера не зависит от «выходного сигнала процесса» (или «управляемой переменной процесса»). Хорошим примером этого является котел центрального отопления, управляемый только таймером, поэтому тепло подается в течение постоянного времени, независимо от температуры в здании. Управляющим действием является включение/выключение котла, но регулируемой переменной должна быть температура здания, а не так, потому что это разомкнутое управление котлом, которое не дает замкнутого управления температурой.

При управлении с обратной связью управляющее действие контроллера зависит от выходного сигнала процесса. В случае аналогии с котлом это будет включать термостат для контроля температуры в здании и, таким образом, подавать обратный сигнал, чтобы гарантировать, что контроллер поддерживает в здании температуру, установленную на термостате. Таким образом, контроллер с замкнутым контуром имеет контур обратной связи, который гарантирует, что контроллер осуществляет управляющее воздействие, чтобы получить выходной сигнал процесса, такой же, как «заданный вход» или «заданное значение». По этой причине контроллеры с обратной связью также называют контроллерами с обратной связью.

Согласно определению Британского института стандартов, система управления с замкнутым контуром — это «система управления, имеющая контрольную обратную связь, при этом сигнал отклонения, формируемый в результате этой обратной связи, используется для управления действием конечного элемента управления таким образом, чтобы стремятся свести отклонение к нулю».

Так же; « Система управления с обратной связью — это система, которая имеет тенденцию поддерживать заданное соотношение одной системной переменной с другой путем сравнения функций этих переменных и использования разницы в качестве средства управления».

Классическая теория управления

Этот раздел представляет собой отрывок из книги «Контроллер с обратной связью» . [ редактировать ]

Пример одного контура промышленного управления; демонстрирующий непрерывно модулированное управление потоком процесса.

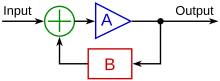
Контроллер с обратной связью или контроллер с обратной связью — это контур управления , который включает в себя обратную связь , в отличие от контроллера с разомкнутым контуром или контроллера без обратной связи .Контроллер с обратной связью использует обратную связь для управления состояниями или выходами динамической системы . Его название происходит от информационного пути в системе: входные данные процесса (например, напряжение, подаваемое на электродвигатель ) влияют на выходные данные процесса (например, скорость или крутящий момент двигателя), которые измеряются датчиками и обрабатываются контроллер; результат (управляющий сигнал) «подается обратно» в качестве входных данных в процесс, замыкая цикл.

В случае с линейной обратной связью систем контур управления , включающий датчики , алгоритмы управления и исполнительные механизмы, организуется для регулирования переменной в заданном значении (SP). Повседневным примером является круиз-контроль на дорожном транспортном средстве; где внешние воздействия, такие как холмы, могут вызвать изменение скорости, и водитель имеет возможность изменить желаемую заданную скорость. в ПИД-алгоритм контроллере восстанавливает фактическую скорость до желаемой оптимальным образом, с минимальной задержкой или превышением , путем управления выходной мощностью двигателя автомобиля.Системы контроля, которые включают в себя определенное определение результатов, которых они пытаются достичь, используют обратную связь и могут в некоторой степени адаптироваться к изменяющимся обстоятельствам. Системы управления с разомкнутым контуром не используют обратную связь и работают только заранее установленным образом.

Контроллеры с обратной связью имеют следующие преимущества перед контроллерами с разомкнутым контуром:

• подавление помех (например, холмы в примере с круиз-контролем выше)
• гарантированная производительность даже при неопределенностях модели , когда структура модели не полностью соответствует реальному процессу и параметры модели неточны
• нестабильные процессы можно стабилизировать
• пониженная чувствительность к изменениям параметров
• улучшена производительность отслеживания ссылок
• улучшенное исправление случайных колебаний

В некоторых системах одновременно используются замкнутый и разомкнутый контур управления. В таких системах управление с разомкнутым контуром называется упреждающим и служит для дальнейшего улучшения характеристик отслеживания задания.

Распространенной архитектурой контроллера с обратной связью является ПИД-регулятор .

Базовый цикл обратной связи

Линейная и нелинейная теория управления

Область теории управления можно разделить на две ветви:

• Теория линейного управления . Это применимо к системам, состоящим из устройств, которые подчиняются принципу суперпозиции , что примерно означает, что выходной сигнал пропорционален входному. Они управляются линейными дифференциальными уравнениями . Основным подклассом являются системы, которые, кроме того, имеют параметры, которые не меняются со временем, называемые линейными инвариантными во времени (LTI) системами. Эти системы поддаются мощным математическим методам частотной области большой общности, таким как преобразование Лапласа , преобразование Фурье , Z-преобразование , график Боде , корневой годограф и критерий устойчивости Найквиста . Это приводит к описанию системы с использованием таких терминов, как полоса пропускания , частотная характеристика , собственные значения , усиление , резонансные частоты , нули и полюса , которые дают решения для реакции системы и методы проектирования для большинства представляющих интерес систем.
• Теория нелинейного управления . Она охватывает более широкий класс систем, которые не подчиняются принципу суперпозиции, и применима к более реальным системам, поскольку все реальные системы управления нелинейны. Эти системы часто управляются нелинейными дифференциальными уравнениями . Те немногие математические методы, которые были разработаны для их решения, более сложны и гораздо менее универсальны и часто применимы только к узким категориям систем. К ним относятся предельного цикла теория , отображения Пуанкаре , теорема устойчивости Ляпунова и описывающие функции . Нелинейные системы часто анализируются с использованием численных методов на компьютерах, например, путем моделирования их работы с использованием языка моделирования . Если интерес представляют только решения вблизи устойчивой точки, нелинейные системы часто можно линеаризовать , аппроксимируя их линейной системой с использованием теории возмущений , и можно использовать линейные методы.

анализа – частотная и

Математические методы анализа и проектирования систем управления делятся на две разные категории:

• Частотная область . В этом типе значения переменных состояния , математических переменных, представляющих вход, выход и обратную связь системы, представлены как функции частоты . системы Входной сигнал и передаточная функция преобразуются из функций времени в функции частоты с помощью такого преобразования , как преобразование Фурье , преобразование Лапласа или Z-преобразование . Преимущество этого метода в том, что он приводит к упрощению математики; дифференциальные уравнения , представляющие систему, заменяются алгебраическими уравнениями в частотной области, которые гораздо проще решить. Однако, как упоминалось выше, методы частотной области можно использовать только с линейными системами.
• Представление пространства состояний во временной области . В этом типе значения переменных состояния представлены как функции времени. В этой модели анализируемая система представляется одним или несколькими дифференциальными уравнениями . Поскольку методы частотной области ограничены линейными системами, временная область широко используется для анализа реальных нелинейных систем. Хотя их сложнее решить, современные методы компьютерного моделирования, такие как языки моделирования, сделали их анализ рутинным.

В отличие от анализа частотной области классической теории управления, современная теория управления использует представление пространства состояний во временной области : математическая модель физической системы как набора входных, выходных переменных и переменных состояния, связанных дифференциальными уравнениями первого порядка. Чтобы абстрагироваться от количества входов, выходов и состояний, переменные выражаются в виде векторов, а дифференциальные и алгебраические уравнения записываются в матричной форме (последнее возможно только в том случае, если динамическая система является линейной). Представление в пространстве состояний (также известное как «подход во временной области») обеспечивает удобный и компактный способ моделирования и анализа систем с множеством входов и выходов. Что касается входов и выходов, в противном случае нам пришлось бы записывать преобразования Лапласа, чтобы закодировать всю информацию о системе. В отличие от подхода в частотной области, использование представления в пространстве состояний не ограничивается системами с линейными компонентами и нулевыми начальными условиями. «Пространство состояний» относится к пространству, оси которого являются переменными состояния. Состояние системы можно представить как точку внутри этого пространства.

Системный интерфейс — SISO и MIMO

Системы управления можно разделить на разные категории в зависимости от количества входов и выходов.

• Один вход и один выход (SISO). Это самый простой и распространенный тип, в котором один выход управляется одним управляющим сигналом. Примерами являются приведенный выше пример круиз-контроля или аудиосистема , в которой входным сигналом управления является входной аудиосигнал, а выходным сигналом — звуковые волны из динамика.
• Несколько входов и несколько выходов (MIMO). Они встречаются в более сложных системах. Например, современные большие телескопы, такие как Кек и ММТ, имеют зеркала, состоящие из множества отдельных сегментов, каждый из которых управляется приводом . Форма всего зеркала постоянно корректируется системой управления активной оптикой MIMO , используя данные от нескольких датчиков в фокальной плоскости, чтобы компенсировать изменения формы зеркала из-за теплового расширения, сжатия, напряжений при его вращении и искажения формы. волновой фронт из-за турбулентности в атмосфере. Сложные системы, такие как ядерные реакторы и человеческие клетки , моделируются компьютером как большие системы управления MIMO.

системы

Область применения классической теории управления ограничена проектированием систем с одним входом и одним выходом (SISO), за исключением анализа подавления помех с использованием второго входа. Анализ системы выполняется во временной области с использованием дифференциальных уравнений , в комплексной области с помощью преобразования Лапласа или в частотной области путем преобразования из комплексной области. Можно предположить, что многие системы имеют отклик системы второго порядка и одну переменную во временной области. Контроллер, спроектированный с использованием классической теории, часто требует настройки на месте из-за неправильных расчетных приближений. Тем не менее, из-за более простой физической реализации классических конструкций контроллеров по сравнению с системами, разработанными с использованием современной теории управления, эти контроллеры предпочтительнее в большинстве промышленных приложений. Наиболее распространенными регуляторами, разработанными с использованием классической теории управления, являются ПИД-регуляторы . Менее распространенная реализация может включать в себя один или оба фильтра опережения или задержки. Конечной целью является удовлетворение требований, обычно предоставляемых во временной области, называемой переходной характеристикой, или иногда в частотной области, называемой откликом разомкнутого контура. Характеристики переходного процесса, применяемые в спецификации, обычно включают процентное перерегулирование, время установления и т. д. Характеристики отклика разомкнутого контура, применяемые в спецификации, обычно представляют собой запас по усилению, фазе и полосу пропускания. Эти характеристики могут быть оценены посредством моделирования, включающего динамическую модель управляемой системы в сочетании с компенсационной моделью.

системы

Современная теория управления реализуется в пространстве состояний и может иметь дело с системами с множественным входом и множественным выходом (MIMO). Это преодолевает ограничения классической теории управления в более сложных задачах проектирования, таких как управление истребителем, с тем ограничением, что анализ частотной области невозможен. В современном проектировании система представляется в наибольшем преимуществе как набор несвязанных дифференциальных уравнений первого порядка, определенных с использованием переменных состояния . нелинейные , многопараметрические , адаптивные и робастные теории управления К этому разделу относятся . Матричные методы существенно ограничены для систем MIMO, где нельзя гарантировать линейную независимость во взаимосвязи между входами и выходами. Будучи достаточно новой, современная теория управления имеет множество областей, которые еще предстоит изучить. Такие ученые, как Рудольф Э. Кальман и Александр Ляпунов, хорошо известны среди людей, которые сформировали современную теорию управления.

теории

Стабильность

Устойчивость критериями устойчивости общей динамической системы без входных данных можно описать Ляпунова .

• Линейная система называется стабильной с ограниченным входом и ограниченным выходом (BIBO), если ее выход будет оставаться ограниченным для любого ограниченного входа.
• Стабильность нелинейных систем , принимающих входные данные, — это стабильность входного состояния (ISS), которая сочетает в себе устойчивость по Ляпунову и понятие, подобное устойчивости BIBO.

с непрерывным и дискретным временем Для простоты следующие описания сосредоточены на линейных системах .

Математически это означает, что для того, чтобы причинно-линейная система была стабильной, все полюса ее передаточной функции должны иметь отрицательно-действительные значения, т. е. действительная часть каждого полюса должна быть меньше нуля. Практически, устойчивость требует, чтобы комплексные полюса передаточной функции находились

• в открытой левой половине комплексной плоскости для непрерывного времени, когда преобразование Лапласа . для получения передаточной функции используется
• внутри единичного круга для дискретного времени, когда Z-преобразование . используется

Разница между этими двумя случаями обусловлена ​​традиционным методом построения передаточных функций непрерывного и дискретного времени. Непрерывное преобразование Лапласа находится в декартовых координатах , где $x$ ось — это действительная ось, а дискретное Z-преобразование находится в круговых координатах , где $\rho$ ось — это реальная ось.

Когда соответствующие условия, указанные выше, выполняются, система называется асимптотически устойчивой ; переменные асимптотически устойчивой системы управления всегда уменьшаются от своего начального значения и не демонстрируют постоянных колебаний. Постоянные колебания возникают, когда полюс имеет действительную часть, точно равную нулю (в случае непрерывного времени) или модуль, равный единице (в случае дискретного времени). Если просто стабильный отклик системы не затухает и не растет с течением времени и не имеет колебаний, он является маргинально устойчивым ; в этом случае передаточная функция системы имеет неповторяющиеся полюсы в начале комплексной плоскости (т.е. их действительная и комплексная компоненты равны нулю в случае непрерывного времени). Колебания возникают тогда, когда полюса, у которых действительная часть равна нулю, имеют мнимую часть, не равную нулю.

Если рассматриваемая система имеет импульсную характеристику

$\ x[n]=0.5^{n}u[n]$

тогда Z-преобразование (см. этот пример ) определяется выражением

$\ X(z)={\frac {1}{1-0.5z^{-1}}}$

в котором есть полюс $z=0.5$ (нулевая мнимая часть ). Эта система BIBO (асимптотически) устойчива, поскольку полюс находится внутри единичного круга.

Однако если импульсная характеристика была

$\ x[n]=1.5^{n}u[n]$

тогда Z-преобразование

$\ X(z)={\frac {1}{1-1.5z^{-1}}}$

у которого есть полюс $z=1.5$ и не является BIBO-стабильным, поскольку полюс имеет модуль строго больше единицы.

Существует множество инструментов для анализа полюсов системы. К ним относятся графические системы, такие как корневой годограф , графики Боде или графики Найквиста .

Механические изменения могут сделать оборудование (и системы управления) более стабильными. Моряки добавляют балласт, чтобы улучшить остойчивость корабля. На круизных лайнерах используются стабилизаторы крена , которые простираются в поперечном направлении от борта корабля примерно на 30 футов (10 м) и постоянно вращаются вокруг своей оси, создавая силы, противодействующие крену.

Управляемость и наблюдаемость

Основные статьи: Управляемость и наблюдаемость

Управляемость и наблюдаемость являются основными вопросами анализа системы перед принятием решения о том, какую стратегию управления лучше применить, или о том, возможно ли вообще контролировать или стабилизировать систему. Управляемость связана с возможностью перевода системы в определенное состояние с помощью соответствующего управляющего сигнала. Если состояние неуправляемо, то никакой сигнал никогда не сможет управлять этим состоянием. Если состояние неуправляемо, но его динамика стабильна, то такое состояние называют стабилизируемым . Вместо этого наблюдаемость связана с возможностью наблюдения посредством выходных измерений состояния системы. Если состояние не наблюдаемо, контроллер никогда не сможет определить поведение ненаблюдаемого состояния и, следовательно, не сможет использовать его для стабилизации системы. Однако, как и в случае с приведенным выше условием стабилизации, если состояние невозможно наблюдать, его все равно можно обнаружить.

С геометрической точки зрения, если рассматривать состояния каждой переменной управляемой системы, каждое «плохое» состояние этих переменных должно быть контролируемым и наблюдаемым, чтобы обеспечить хорошее поведение в замкнутой системе. То есть, если одно из собственных значений системы не является одновременно управляемым и наблюдаемым, эта часть динамики останется нетронутой в замкнутой системе. Если такое собственное значение не является стабильным, динамика этого собственного значения будет присутствовать в замкнутой системе, которая, следовательно, будет неустойчивой. Ненаблюдаемые полюса не присутствуют в реализации передаточной функции представления в пространстве состояний, поэтому иногда последнее отдается предпочтение в анализе динамических систем.

Решение проблем неконтролируемой или ненаблюдаемой системы включает добавление исполнительных механизмов и датчиков.

Спецификация управления

В последние годы было разработано несколько различных стратегий контроля. Они варьируются от очень общих (ПИД-регулятор) до других, посвященных очень конкретным классам систем (особенно робототехнике или круиз-контролю самолета).

Задача управления может иметь несколько спецификаций. Стабильность, конечно, всегда присутствует. Контроллер должен обеспечить стабильность системы с обратной связью, независимо от устойчивости системы с разомкнутым контуром. Неправильный выбор контроллера может даже ухудшить стабильность разомкнутой системы, чего обычно следует избегать. Иногда было бы желательно получить особую динамику в замкнутом контуре: т.е. чтобы полюса имели $Re[\lambda ]<-{\overline {\lambda }}$, где ${\overline {\lambda }}$ является фиксированным значением, строго большим нуля, вместо того, чтобы просто спрашивать об этом $Re[\lambda ]<0$.

Другая типичная спецификация — отказ от ступенчатого возмущения; включение интегратора в разомкнутую цепь (т.е. непосредственно перед управляемой системой) легко позволяет добиться этого. Другие классы помех требуют включения различных типов подсистем.

Другие «классические» спецификации теории управления касаются временной реакции системы с обратной связью. К ним относятся время нарастания (время, необходимое системе управления для достижения желаемого значения после возмущения), пиковое перерегулирование (наивысшее значение, достигнутое откликом до достижения желаемого значения) и другие ( время установления , четверть затухания). Характеристики частотной области обычно связаны с надежностью (см. далее).

Современные оценки производительности используют некоторые варианты интегрированной ошибки отслеживания (IAE, ISA, CQI).

и

Система управления всегда должна обладать некоторым свойством устойчивости. таков Робастный регулятор , что его свойства не сильно изменяются, если применить его к системе, несколько отличающейся от математической, использованной для его синтеза. Это требование важно, поскольку ни одна реальная физическая система не ведет себя так, как серия дифференциальных уравнений, используемых для ее математического представления. Обычно для упрощения расчетов выбирается более простая математическая модель, в противном случае истинная динамика системы может оказаться настолько сложной, что полная модель будет невозможна.

Идентификация системы

Дополнительная информация: Идентификация системы.

Процесс определения уравнений, управляющих динамикой модели, называется идентификацией системы . Это можно сделать в автономном режиме: например, выполнив ряд измерений, на основе которых можно рассчитать аппроксимированную математическую модель, обычно ее передаточную функцию или матрицу. Однако такая идентификация по выходным данным не может учитывать ненаблюдаемую динамику. Иногда модель строится непосредственно исходя из известных физических уравнений, например, в случае системы масса-пружина-демпфер мы знаем, что $m{\ddot {x}}(t)=-Kx(t)-\mathrm {B} {\dot {x}}(t)$. Даже если предположить, что при проектировании контроллера используется «полная» модель, все параметры, включенные в эти уравнения (называемые «номинальными параметрами») никогда не известны с абсолютной точностью; система управления должна будет вести себя правильно даже при подключении к физической системе с истинными значениями параметров, отличными от номинальных.

Некоторые продвинутые методы контроля включают процесс идентификации «онлайн» (см. ниже). Параметры модели рассчитываются («идентифицируются») во время работы самого контроллера. Таким образом, если произойдет резкое изменение параметров, например, если рука робота снимет вес, контроллер соответствующим образом отрегулирует себя, чтобы обеспечить правильную работу.

Анализ

Анализ устойчивости системы управления SISO (один вход и один выход) можно выполнить в частотной области, учитывая передаточную функцию системы и используя диаграммы Найквиста и Боде . Темы включают запас по усилению, фазе и запас по амплитуде. Для MIMO (многовходов и нескольких выходов) и, в целом, более сложных систем управления необходимо учитывать теоретические результаты, полученные для каждого метода управления (см. следующий раздел). То есть, если необходимы определенные качества устойчивости, инженер должен переключить свое внимание на метод управления, включив эти качества в его свойства.

Ограничения

Особой проблемой надежности является требование к системе управления работать должным образом при наличии ограничений ввода и состояния. В физическом мире каждый сигнал ограничен. Может случиться так, что контроллер отправит управляющие сигналы, которым не может следовать физическая система, например, попытается повернуть клапан на чрезмерной скорости. Это может привести к нежелательному поведению системы с обратной связью или даже к повреждению или поломке приводов или других подсистем. Для решения этой проблемы доступны специальные методы управления: управление с прогнозированием модели (см. ниже) и системы предотвращения срыва . Последний состоит из дополнительного блока управления, который гарантирует, что сигнал управления никогда не превысит заданный порог.

Системные классификации

Управление линейными системами

Основная статья: Государственное пространство (элементы управления)

Для систем MIMO размещение полюсов может быть выполнено математически с использованием представления в пространстве состояний разомкнутой системы и расчета матрицы обратной связи, назначающей полюса в желаемых положениях. В сложных системах это может потребовать возможности компьютерных вычислений и не всегда может обеспечить надежность. Более того, все состояния системы, как правило, не измеряются, поэтому наблюдатели должны быть включены и включены в проект размещения опор.

Управление нелинейными системами

Основная статья: Нелинейное управление

Процессы в таких отраслях, как робототехника и аэрокосмическая промышленность, обычно имеют сильную нелинейную динамику. В теории управления иногда возможно линеаризовать такие классы систем и применить линейные методы, но во многих случаях может оказаться необходимым разработать с нуля теории, позволяющие управлять нелинейными системами. Они, например, линеаризация с обратной связью , обратный шаг , управление скользящим режимом , управление линеаризацией траектории, обычно используют результаты, основанные на теории Ляпунова . Дифференциальная геометрия широко использовалась как инструмент для обобщения известных концепций линейного управления на нелинейный случай, а также для демонстрации тонкостей, которые делают эту проблему более сложной. Теория контроля также использовалась для расшифровки нейронного механизма, управляющего когнитивными состояниями.

Управление децентрализованными системами

Основная статья: Распределенная система управления

Когда системой управляют несколько контроллеров, проблема заключается в децентрализации управления. Децентрализация полезна во многих отношениях, например, она помогает системам управления работать на более обширной географической территории. Агенты в децентрализованных системах управления могут взаимодействовать по каналам связи и координировать свои действия.

Управление детерминированными и стохастическими системами

Основная статья: Стохастический контроль

Задача стохастического управления — это задача, в которой эволюция переменных состояния подвергается случайным воздействиям извне системы. Задача детерминированного управления не подвержена внешним случайным потрясениям.

Основные стратегии контроля

Каждая система управления должна, прежде всего, гарантировать стабильность поведения в замкнутом контуре. Для линейных систем этого можно добиться путем непосредственного размещения полюсов. Нелинейные системы управления используют специальные теории (обычно основанные на теории Александра Ляпунова ) для обеспечения устойчивости без учета внутренней динамики системы. Возможность выполнения различных спецификаций зависит от рассматриваемой модели и выбранной стратегии управления.

Перечень основных методов контроля

• Оптимальное управление — это особый метод управления, при котором управляющий сигнал оптимизирует определенный «показатель стоимости»: например, в случае со спутником реактивные тяги, необходимые для вывода его на желаемую траекторию, потребляют наименьшее количество топлива. Два метода проектирования оптимального управления широко используются в промышленных приложениях, поскольку было показано, что они могут гарантировать стабильность замкнутого контура. Это модельное прогнозирующее управление (MPC) и линейно-квадратично-гауссовское управление (LQG). Первый может более явно учитывать ограничения на сигналы в системе, что является важной особенностью многих промышленных процессов. Однако структура «оптимального управления» в MPC является лишь средством достижения такого результата, поскольку она не оптимизирует истинный показатель эффективности системы управления с обратной связью. Вместе с ПИД-регуляторами системы MPC являются наиболее широко используемым методом управления технологическими процессами .
• Робастное управление явно связано с неопределенностью в подходе к проектированию контроллера. Контроллеры, разработанные с использованием надежных методов управления, как правило, способны справляться с небольшими различиями между реальной системой и номинальной моделью, использованной для проектирования. Ранние методы Боде и других были довольно надежными; методы пространства состояний, изобретенные в 1960-х и 1970-х годах, иногда оказывались недостаточно надежными. Примеры современных надежных методов управления включают формирование контура H-бесконечности, разработанное Дунканом Макфарлейном и Китом Гловером , управление скользящим режимом (SMC), разработанное Вадимом Уткиным , и безопасные протоколы, разработанные для управления большими гетерогенными группами электрических нагрузок в приложениях Smart Power Grid. . Робастные методы направлены на достижение надежной производительности и/или стабильности при наличии небольших ошибок моделирования.
• Стохастическое управление связано с разработкой управления с неопределенностью в модели. В типичных задачах стохастического управления предполагается, что в модели и контроллере существуют случайный шум и возмущения, и при проектировании управления необходимо учитывать эти случайные отклонения.
• Адаптивное управление использует оперативную идентификацию параметров процесса или изменение коэффициентов усиления контроллера, тем самым обеспечивая высокие характеристики надежности. Адаптивное управление было впервые применено в аэрокосмической промышленности в 1950-х годах и добилось в этой области особого успеха.
• Иерархическая система управления — это тип системы управления , в которой набор устройств и управляющего программного обеспечения организован в виде иерархического дерева . Когда связи в дереве реализованы компьютерной сетью , то эта иерархическая система управления также является формой сетевой системы управления .
• Интеллектуальное управление использует различные вычислительные подходы искусственного интеллекта, такие как искусственные нейронные сети , байесовская вероятность , нечеткая логика , машинное обучение , эволюционные вычисления и генетические алгоритмы или комбинация этих методов, таких как нейро-нечеткие алгоритмы, для управления динамической системой .
• Самоорганизованный контроль критичности можно определить как попытку вмешательства в процессы, посредством которых самоорганизующаяся система рассеивает энергию.

Люди в системах и управлении

Основная статья: Люди в системах и управлении

Многие активные и исторические деятели внесли значительный вклад в теорию управления, в том числе

• Пьер-Симон Лаплас изобрел Z-преобразование в своей работе по теории вероятностей , которое теперь используется для решения задач теории управления в дискретном времени. Z-преобразование является эквивалентом преобразования Лапласа в дискретном времени , названного в его честь.
• Ирмгард Флюгге-Лотц разработал теорию прерывистого автоматического управления и применил ее к системам автоматического управления самолетами .
• Александр Ляпунов в 1890-е годы положил начало теории устойчивости .
• Гарольд С. Блэк изобрел концепцию усилителей с отрицательной обратной связью в 1927 году. Ему удалось разработать стабильные усилители с отрицательной обратной связью в 1930-х годах.
• Гарри Найквист разработал критерий устойчивости Найквиста для систем с обратной связью в 1930-х годах.
• Ричард Беллман разработал динамическое программирование в 1940-х годах.
• Уоррен Э. Диксон , теоретик управления и профессор
• Кириакос Г. Вамвудакис разработал алгоритмы синхронного обучения с подкреплением для решения задач оптимального управления и теории игр.
• Андрей Колмогоров был соавтором фильтра Винера-Колмогорова в 1941 году.
• Норберт Винер был соавтором фильтра Винера-Колмогорова и ввел термин «кибернетика» в 1940-х годах.
• Джон Р. Рагаццини представил цифровое управление и использование Z-преобразования в теории управления (изобретенной Лапласом) в 1950-х годах.
• Лев Понтрягин ввел принцип максимума и принцип «взрыва» .
• Пьер-Луи Лионс разработал решения по вязкости для методов стохастического управления и оптимального управления .
• Рудольф Э. Кальман был пионером подхода к системам и управлению в пространстве состояний . Введены понятия управляемости и наблюдаемости . Разработал фильтр Калмана для линейной оценки.
• Али Х. Найфе , который внес один из основных авторов в теорию нелинейного управления и опубликовал множество книг по методам возмущений.
• Ян К. Виллемс ввел концепцию диссипативности как обобщение функции Ляпунова на системы ввода/состояния/вывода. Построение функции накопления, как называют аналог функции Ляпунова, привело к изучению линейного матричного неравенства (ЛМИ) в теории управления. Он был пионером поведенческого подхода к теории математических систем.

См. также

Примеры систем управления

• Автоматизация
• Контроллер бездействия
• Системы с распределенными параметрами
• Управление дробного порядка
• Формирование петли H-бесконечности
• Иерархическая система управления
• Модель прогнозирующего управления
• Оптимальное управление
• Управление процессом
• Надежное управление
• Сервомеханизм
• Пространство состояний (управление)
• Векторное управление

Темы теории управления

• Метод диаграммы коэффициентов
• Реконфигурация управления
• Обратная связь
• Ч бесконечность
• Единственное значение Ганкеля
• Теорема Кренера
• Компенсатор опережения-запаздывания
• Незначительная обратная связь цикла
• Многоконтурная обратная связь
• Позитивные системы
• Радиальная базисная функция
• Корневой локус
• Графики потока сигналов
• Стабильный полином
• Государственное космическое представительство
• Устойчивое состояние
• Переходный процесс
• Переходное состояние
• Недоработка
• Параметризация Юлы – Кучеры
• Метод аппроксимации цепей Маркова

Другие связанные темы

• Адаптивная система
• Автоматизация и дистанционное управление
• График облигаций
• Техника управления
• Цикл управление-обратная связь-отмена
• Контроллер (теория управления)
• Кибернетика
• Интеллектуальное управление
• Математическая теория систем
• Усилитель с отрицательной обратной связью
• Схема управления
• Люди в системах и управлении
• Теория перцептивного контроля
• Теория систем

Дальнейшее чтение

• Левин, Уильям С., изд. (1996). Справочник по контролю . Нью-Йорк: CRC Press. ISBN  978-0-8493-8570-4 .
• Карл Дж. Острем; Ричард М. Мюррей (2008). Системы обратной связи: введение для ученых и инженеров (PDF) . Издательство Принстонского университета. ISBN  978-0-691-13576-2 .
• Кристофер Килиан (2005). Современные технологии управления . Томпсон Дельмар Обучение. ISBN  978-1-4018-5806-3 .
• Ванневар Буш (1929). Анализ оперативных цепей . Джон Уайли и сыновья, Inc.
• Роберт Ф. Стенгель (1994). Оптимальное управление и оценка . Дуврские публикации. ISBN  978-0-486-68200-6 .
• Франклин; и др. (2002). Управление динамическими системами с обратной связью (4-е изд.). Нью-Джерси: Прентис Холл. ISBN  978-0-13-032393-4 .
• Джозеф Л. Хеллерштейн; Дон М. Тилбери ; Суджай Парех (2004). Управление вычислительными системами с обратной связью . Джон Уайли и сыновья. ISBN  978-0-471-26637-2 .
• Дидерих Хинрихсен и Энтони Дж. Притчард (2005). Теория математических систем I – моделирование, анализ пространства состояний, устойчивость и устойчивость . Спрингер. ISBN  978-3-540-44125-0 .
• Зонтаг, Эдуардо (1998). Математическая теория управления: детерминированные конечномерные системы. Второе издание (PDF) . Спрингер. ISBN  978-0-387-98489-6 .
• Гудвин, Грэм (2001). Проектирование системы управления . Прентис Холл. ISBN  978-0-13-958653-8 .
• Кристоф Бассо (2012). Проектирование контуров управления для линейных и импульсных источников питания: Учебное пособие . Артех Хаус. ISBN  978-1608075577 .
• Борис Дж. Лурье; Пол Дж. Энрайт (2019). Классическое управление с обратной связью в нелинейных многоконтурных системах (3-е изд.). ЦРК Пресс. ISBN  978-1-1385-4114-6 .

Для химического машиностроения

• Луйбен, Уильям (1989). Моделирование процессов, моделирование и управление для инженеров-химиков . МакГроу Хилл. ISBN  978-0-07-039159-8 .

Внешние ссылки

• Учебные пособия по управлению для Matlab — набор проработанных примеров управления, решенных несколькими различными методами.
• Настройка управления и лучшие практики
• Расширенные структуры управления, бесплатные онлайн-симуляторы, объясняющие теорию управления.