Греки (финансы)

В математических финансах греки — это величины (известные в исчислении как частные производные ; первого порядка или выше), представляющие чувствительность цены производного инструмента, такого как опцион, к изменениям одного или нескольких базовых параметров , от которых зависит стоимость инструмент или портфель финансовых инструментов является зависимым. Это название используется потому, что наиболее распространенные из этих видов чувствительности обозначаются греческими буквами (как и некоторые другие финансовые меры). В совокупности их также называют чувствительностью к риску . ^[1] меры риска ^[2]^: 742 или параметры хеджирования . ^[3]

Использование греков

Базовый параметр	Параметр опции
Базовый параметр	Спотовая цена С	Волатильность $\sigma$	Прохождение время
Значение (В)	$\Delta$ Дельта	${\mathcal {V}}$ Вега	$\Theta$ Тета
Дельта ( $\Delta$ )	$\Gamma$ Гамма	Ванна	Очарование
Вега ( ${\mathcal {V}}$ )	Ванна	Животик	Знать
Тета ( $\Theta$ )	Очарование	Знать
Гамма ( $\Gamma$ )	Скорость	Увеличить	Цвет
Животик		Последний

Определение греков как чувствительности цены и риска опциона (в первой строке) к базовому параметру (в первом столбце).
Греки первого порядка выделены синим цветом, греки второго порядка - зеленым, а греки третьего порядка - желтым.
Ванна, очарование и вета появляются дважды, поскольку частные перекрестные производные равны по теореме Шварца . Ро, лямбда, эпсилон и вера не учитываются, поскольку они не так важны, как остальные. Три места в таблице не заняты, поскольку соответствующие величины еще не определены в финансовой литературе.

Греки являются жизненно важными инструментами в управлении рисками . Каждый грек измеряет чувствительность стоимости портфеля к небольшому изменению данного базового параметра, так что риски компонентов можно рассматривать изолированно, а портфель соответствующим образом перебалансировать для достижения желаемого риска; см., например, дельта-хеджирование .

Греки в модели Блэка-Шоулза (относительно простая идеализированная модель некоторых финансовых рынков) относительно легко поддаются расчету (желательное свойство финансовых моделей ) и очень полезны для трейдеров деривативов, особенно для тех, кто стремится застраховать свои портфели от неблагоприятных воздействий. изменения рыночных условий. По этой причине те греческие индексы, которые особенно полезны для хеджирования, такие как дельта, тета и вега, хорошо подходят для измерения изменений параметров спотовой цены, времени и волатильности. Хотя rho (частная производная по безрисковой процентной ставке ) является основным входным параметром модели Блэка-Шоулза, общее влияние на стоимость краткосрочного опциона, соответствующего изменениям безрисковой процентной ставки, равно в целом незначительны и поэтому производные финансовые инструменты более высокого порядка, включающие безрисковую процентную ставку, встречаются нечасто.

Наиболее распространены у греков производные первого порядка: дельта , вега , тета и ро ; а также гамма , производная второго порядка функции ценности. Остальные уязвимости в этом списке достаточно распространены и имеют общие названия, но этот список ни в коем случае не является исчерпывающим.

Игроки на рынке совершают конкурентные сделки с использованием многих миллиардов (долларов США, фунтов стерлингов или евро) базового актива каждый день, поэтому важно правильно рассчитать суммы. На практике они будут использовать более сложные модели, выходящие за рамки упрощающих предположений, использованных в модели Блэка-Шоулза и, следовательно, в греческой модели.

Имена

Использование названий греческих букв, по-видимому, является продолжением общих финансовых терминов «альфа» и «бета» , а также использования сигмы (стандартное отклонение логарифмической доходности) и тау (время до истечения срока действия) в модели ценообразования опционов Блэка-Шоулза . Несколько названий, таких как «вега» (символ которого похож на строчную греческую букву « ню» ; использование этого имени могло привести к путанице) и «зомма» придуманы, но звучат похоже на греческие буквы. Названия «цвет» и «очарование», предположительно, происходят от использования этих терминов для обозначения экзотических свойств кварков в физике элементарных частиц .

Греки первого порядка

Дельта

Дельта , ^[4] $\Delta$ , измеряет скорость изменения теоретической стоимости опциона относительно изменений цены базового актива. Дельта — это первая производная значения $V$ опциона по отношению к цене базового инструмента $S$ .

\Delta ={\frac {\partial V}{\partial S}}

Практическое использование

Для ванильного опциона дельта будет числом от 0,0 до 1,0 для длинного колл-опциона (или короткого пут-опциона) и от 0,0 до -1,0 для длинного пут-опциона (или короткого колл-опциона); В зависимости от цены опцион колл ведет себя так, как будто кто-то владеет 1 акцией базовой акции (если глубоко в деньгах), или не владеет ничем (если далеко от денег), или что-то среднее, и наоборот для опциона пут. Разница между дельтой колла и дельтой пута того же страйка равна единице. Согласно четности пут-колл , длинный колл и короткий пут эквивалентны форвардному опциону F , который является линейным в споте S, с единичным коэффициентом, поэтому производная dF/dS равна 1. См. формулы ниже.

Эти цифры обычно представляются в процентах от общего количества акций, представленных опционным контрактом(ами). Это удобно, поскольку опцион (мгновенно) будет вести себя так же, как количество акций, указанное дельтой. Например, если каждый портфель из 100 американских колл-опционов на XYZ имеет дельту 0,25 (= 25%), он будет увеличивать или уменьшать стоимость так же, как 2500 акций XYZ, поскольку цена изменяется при небольших ценовых движениях (100 опционных контрактов покрывают 10 000 акций). Знак и процент часто опускаются – знак неявно заложен в типе опциона (отрицательный для пут, положительный для колл), и процент понимается. Наиболее часто котируются 25-дельта-пут, 50-дельта-пут/50-дельта-колл и 25-дельта-колл. 50-дельта-пут и 50-дельта-колл не совсем идентичны, поскольку спот и форвард различаются коэффициентом дисконтирования, но их часто объединяют.

Дельта всегда положительна для длинных коллов и отрицательна для длинных путов (если только она не равна нулю). Общую дельту сложного портфеля позиций по одному и тому же базовому активу можно рассчитать, просто взяв сумму дельт для каждой отдельной позиции – дельта портфеля линейна по составляющим. Поскольку дельта базового актива всегда равна 1,0, трейдер может дельта-хеджировать всю свою позицию в базовом активе, покупая или шортя количество акций, указанное общей дельтой. Например, если дельта портфеля опционов в XYZ (выраженная в долях базового актива) равна +2,75, трейдер сможет дельта-хеджировать портфель, продав без покрытия 2,75 акций базового актива. Тогда этот портфель сохранит свою общую стоимость независимо от того, в каком направлении движется цена XYZ. (Хотя это происходит лишь при небольших изменениях базового актива, в течение короткого промежутка времени и несмотря на изменения других рыночных условий, таких как волатильность и норма прибыли для безрисковых инвестиций).

Как показатель вероятности

(Абсолютное значение) Дельта близка, но не идентична процентной денежности опциона, т.е. подразумеваемой вероятности того, что опцион истечет в деньгах (если рынок движется в соответствии с броуновским движением в риске). нейтральная мера ). ^[5] По этой причине некоторые опционные трейдеры используют абсолютное значение дельты в качестве приблизительного показателя процентной денежности. Например, если дельта опциона колл «вне денег» равна 0,15, трейдер может оценить, что вероятность истечения срока действия опциона «в деньгах» составляет примерно 15%. Аналогичным образом, если дельта пут-контракта равна -0,25, трейдер может ожидать, что опцион с вероятностью 25% истечет в деньгах. Коллы и пут-опционы при деньгах имеют дельту примерно 0,5 и -0,5 соответственно с небольшим уклоном в сторону более высоких дельт для коллов банкоматов, поскольку безрисковая ставка вносит некоторый сдвиг в дельту. Фактическая вероятность того, что опцион закончится в деньгах, равна его двойной дельте , которая является первой производной цены опциона относительно страйка. ^[6]

Связь между дельтой колла и пута

Учитывая европейский опцион колл и пут с одним и тем же базовым активом, ценой исполнения и временем до погашения, а также без дивидендной доходности, сумма абсолютных значений дельты каждого опциона будет равна 1 – точнее, дельта колл ( положительный) минус дельта пут-опциона (отрицательный) равен 1. Это связано с паритетом пут-колл : длинный колл плюс короткий пут (колл минус пут) копирует форвард, дельта которого равна 1.

Если значение дельты для опциона известно, можно рассчитать значение дельты опциона с той же ценой исполнения, базовым активом и сроком погашения, но в противоположном направлении, вычитая 1 из известной дельты колл или прибавляя 1 к известной дельте пут-опциона. .

\Delta ({\text{call}})-\Delta ({\text{put}})=1,{\text{ therefore: }}\Delta ({\text{call}})=\Delta ({\text{put}})+1{\text{ and }}\Delta ({\text{put}})=\Delta ({\text{call}})-1.

Например, если дельта колл-опциона равна 0,42, то можно вычислить дельту соответствующего пут-опциона при той же цене исполнения по формуле 0,42 – 1 = –0,58. Чтобы получить дельту колла из пут-опциона, можно аналогичным образом взять -0,58 и прибавить 1, чтобы получить 0,42.

Вега

Вега ^[4] измеряет чувствительность к волатильности . Вега — это производная стоимости опциона по отношению к волатильности базового актива.

{\mathcal {V}}={\frac {\partial V}{\partial \sigma }}

Вега — это не название какой-либо греческой буквы. Используемый глиф представляет собой нестандартную маюскульную версию греческой буквы ню ( ${\textstyle \nu }$ ), записанный как ${\mathcal {V}}$ . Предположительно, название «вега» было принято потому, что греческая буква «nu» была похожа на латинскую «vee» , а «vega» произошла от «vee» по аналогии с тем, как «beta» , «eta » и «theta» в американском английском произносятся .

Символ каппа , $\kappa$ , иногда используется (учеными) вместо вега (как и тау ( $\tau$ )или заглавная лямбда ( $\Lambda$ ), ^[7]^: 315хотя это редкость).

Вега обычно выражается как сумма денег на базовую акцию, которую стоимость опциона вырастет или потеряет при повышении или понижении волатильности на 1 процентный пункт . Все опционы (как колл, так и пут) будут расти в цене с ростом волатильности.

Вега может быть важным индикатором для опционного трейдера, особенно на волатильных рынках, поскольку стоимость некоторых опционных стратегий может быть особенно чувствительной к изменениям волатильности. стоимость опциона Например, «при деньгах» чрезвычайно зависит от изменений волатильности.См. Риск волатильности .

Тета

Тета , ^[4] $\Theta$ , измеряет чувствительность значения производной к течению времени (см. Вариант временного значения ): «время затухания».

\Theta =-{\frac {\partial V}{\partial \tau }}

С течением времени, с уменьшением времени до истечения срока действия и при прочих равных условиях, внешняя стоимость опциона уменьшается. Обычно (но см. ниже) это означает, что опцион со временем теряет ценность, что обычно называют длинными опционами, обычно имеющими короткую (отрицательную) тету. Фактически, как правило, буквальная первая производная по времени стоимости опциона представляет собой положительное число. Изменение стоимости опциона обычно отрицательное, поскольку течение времени число ( уменьшение представляет собой отрицательное $\tau \,$ , время истечения срока действия). Однако по соглашению практики обычно предпочитают относиться к тета-воздействию («распаду») долгосрочного опциона как к отрицательному (вместо течения времени как к отрицательному), и поэтому тэта обычно указывается как -1, умноженная на первую производную, как выше.

Хотя внешняя стоимость с течением времени уменьшается, иногда уравновешивающим фактором является дисконтирование. Для некоторых типов опционов «глубоко в деньгах» (для опционов Блэка-Шоулза, путов и коллов в опционах Блэка), поскольку коэффициенты дисконтирования увеличиваются до 1 с течением времени, это является элементом увеличения стоимости длинного опциона. . Иногда опционы «глубоко в деньгах» выиграют больше от увеличения коэффициентов дисконтирования, чем потеряют от уменьшения внешней стоимости, и сообщаемый тета будет положительным значением для длинного опциона вместо более типичного отрицательного значения (и опцион будет кандидат на досрочное исполнение, если он осуществим, и стоимость европейского опциона может оказаться ниже паритета).

По соглашению в формулах оценки опционов $\tau \,$ , срок истечения, определяется в годах. Практики обычно предпочитают рассматривать тэту с точки зрения изменения количества дней до истечения срока действия, а не количества лет до истечения срока действия. Поэтому сообщаемая тэта обычно делится на количество дней в году. (Считать ли календарные или рабочие дни зависит от личного выбора, и в пользу обоих есть аргументы.)

Ро

Ро , ^[4] $\rho$ , измеряет чувствительность к процентной ставке: это производная стоимости опциона относительно безрисковой процентной ставки (для соответствующего срока погашения).

\rho ={\frac {\partial V}{\partial r}}

За исключением чрезвычайных обстоятельств, стоимость опциона менее чувствительна к изменениям безрисковой процентной ставки, чем к изменениям других параметров. По этой причине ро у греков первого порядка употребляется реже всего.

Rho обычно выражается как сумма денег на акцию базового актива, которую стоимость опциона выиграет или потеряет при повышении или падении безрисковой процентной ставки на 1,0% в год (100 базисных пунктов).

Лямбда

Лямбда , ^[4] $\lambda$ , омега , ^[8] $\Omega$ , или эластичность ^[4] — это процентное изменение стоимости опциона на процентное изменение базовой цены, мера кредитного плеча , иногда называемая рычагом.

\lambda =\Omega ={\frac {\partial V}{\partial S}}\times {\frac {S}{V}}

Он утверждает, что $\lambda =\Omega =\Delta \times {\frac {S}{V}}$ .

Оно похоже на концепцию дельты, но выражается в процентах, а не в абсолютных величинах.

Эпсилон

Эпсилон , ^[9] $\varepsilon$ (также известный как пси, $\psi$ ), — это процентное изменение стоимости опциона на процентное изменение базовой дивидендной доходности, мера дивидендного риска. Влияние дивидендной доходности на практике определяется увеличением этой доходности на 10%. Очевидно, что такая чувствительность может применяться только к производным инструментам долевых инструментов.

\varepsilon =\psi ={\frac {\partial V}{\partial q}}

Численно все чувствительности первого порядка можно интерпретировать как разброс ожидаемой доходности. ^[10] Информационная геометрия предлагает другую (тригонометрическую) интерпретацию. ^[10]

Греки второго порядка

Гамма

Гамма , ^[4] $\Gamma$ , измеряет скорость изменения дельты по отношению к изменениям базовой цены. Гамма — это вторая производная функции стоимости по базовой цене.

\Gamma ={\frac {\partial \Delta }{\partial S}}={\frac {\partial ^{2}V}{\partial S^{2}}}

Большинство длинных опционов имеют положительную гамму, а большинство коротких опционов имеют отрицательную гамму. Длинные опционы имеют положительную взаимосвязь с гаммой, поскольку с ростом цены увеличивается и гамма, в результате чего дельта приближается к 1 от 0 (длинный опцион колл) и к 0 от −1 (длинный опцион пут). Обратное верно для коротких опционов. ^[11]

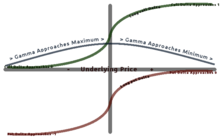
Гамма максимальна примерно при деньгах (ATM) и уменьшается по мере того, как вы уходите от денег (ITM) или вне денег (OTM). Гамма важна, поскольку она корректирует выпуклость значения.

Когда трейдер стремится установить эффективное дельта-хеджирование для портфеля, он также может попытаться нейтрализовать гамму портфеля, поскольку это гарантирует, что хеджирование будет эффективным в более широком диапазоне движений базовой цены.

Ванна

ванна , ^[4] также называется ДвегаДспот ^[13] и ДдельтаДвол , ^[13] является производной второго порядка от стоимости опциона, один раз от базовой спотовой цены и один раз от волатильности. Это математически эквивалентно DdeltaDvol , чувствительности дельты опциона к изменению волатильности; или, альтернативно, частичная вега по отношению к цене базового инструмента. Ванна может быть полезной чувствительностью для мониторинга при ведении портфеля с дельта- или вега-хеджированием, поскольку ванна поможет трейдеру предвидеть изменения в эффективности дельта-хеджирования при изменении волатильности или эффективности вега-хеджирования против изменений базовая спотовая цена.

Если базовое значение имеет непрерывные вторые частные производные, то ${\text{Vanna}}={\frac {\partial \Delta }{\partial \sigma }}={\frac {\partial {\mathcal {V}}}{\partial S}}={\frac {\partial ^{2}V}{\partial S\,\partial \sigma }}.$

Очарование

Очарование ^[4] или дельта-распад ^[14] измеряет мгновенную скорость изменения дельты с течением времени.

{\text{Charm}}=-{\frac {\partial \Delta }{\partial \tau }}={\frac {\partial \Theta }{\partial S}}=-{\frac {\partial ^{2}V}{\partial \tau \,\partial S}}

Charm также назывался DdeltaDtime . ^[13] Очарование может быть важным фактором для измерения/мониторинга при дельта-хеджировании позиции на выходных. Очарование — это производная второго порядка от стоимости опциона, зависящая от цены и от времени. В таком случае это также производная теты по отношению к цене базового актива.

Математический результат формулы очарования (см. ниже) выражается в дельта/год. Часто бывает полезно разделить это значение на количество дней в году, чтобы получить дельта-распад в день. Такое использование является достаточно точным, когда количество дней, оставшихся до истечения срока действия опциона, велико. Когда срок действия опциона приближается, само очарование может быстро измениться, что приведет к неточным оценкам затухания дельты за весь день.

Животик

Животик , ^[4] Волга , ^[15] вега-выпуклость , ^[15] или ДвегаДвол ^[15] измеряет чувствительность второго порядка к волатильности . Вомма — это вторая производная стоимости опциона по волатильности, или, другими словами, вомма измеряет скорость изменения веги при изменении волатильности.

{\text{Vomma}}={\frac {\partial {\mathcal {V}}}{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma ^{2}}}

При положительной вомме позиция становится длинной вегой по мере увеличения подразумеваемой волатильности и короткой вегой по мере ее уменьшения, что можно скальпировать аналогично длинной гамме. И изначально вега-нейтральная, лонг-вомма-позиция может быть построена на основе соотношений опционов при разных страйках. Вомма положительна для длинных опционов вдали от денег и первоначально увеличивается по мере удаления от денег (но падает по мере снижения веги). (В частности, vomma положительна, если обычные члены d ₁ и d ₂ имеют один и тот же знак, что верно, когда d ₁ < 0 или d ₂ > 0.)

Знать

Знать , ^[16] вега-распад или ДвегаДтайм ^[15] измеряет скорость изменения веги с течением времени. Вета — вторая производная функции ценности; один раз по волатильности и один раз по времени.

{\text{Veta}}={\frac {\partial {\mathcal {V}}}{\partial \tau }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial \tau }}

Обычной практикой является деление математического результата веты на 100-кратное количество дней в году, чтобы уменьшить значение до процентного изменения веты за один день.

Существование

Существование ^[17] (иногда рова ) ^[17] измеряет скорость изменения ро по отношению к волатильности. Вера — вторая производная функции ценности; один раз к волатильности и один раз к процентной ставке.

{\text{Vera}}={\frac {\partial \rho }{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial r}}

Слово «Вера» было придумано Р. Нарышкиным в начале 2012 года, когда эту чувствительность нужно было использовать на практике для оценки влияния изменений волатильности на ро-хеджирование, но в доступной литературе такого названия еще не существовало. Слово «Вера» было выбрано так, чтобы оно звучало похоже на комбинацию слов Вега и Ро, соответствующих греков первого порядка. Это имя теперь используется более широко, включая, например, программное обеспечение компьютерной алгебры Maple (в пакете Finance которого есть функция «BlackScholesVera»).

Частная производная второго порядка по страйку K

Эта частная производная играет фундаментальную роль в формуле Бридена – Литценбергера: ^[18] который использует котируемые цены опционов колл для оценки нейтральных к риску вероятностей, подразумеваемых такими ценами.

\varpi ={\frac {\partial ^{2}V}{\partial K^{2}}}

Для опционов колл его можно аппроксимировать, используя бесконечно малые портфели стратегий «бабочка» .

Греки третьего порядка

Скорость

Скорость ^[4] измеряет скорость изменения гаммы относительно изменений базовой цены.

{\text{Speed}}={\frac {\partial \Gamma }{\partial S}}={\frac {\partial ^{3}V}{\partial S^{3}}}

Это также иногда называют гаммой гаммы. ^[2]^: 799 или DgammaDspot . ^[13] Скорость — это третья производная функции стоимости по отношению к базовой спотовой цене. Скорость может быть важна для отслеживания при дельта-хеджировании или гамма-хеджировании портфеля.

Увеличить

Увеличить ^[4] измеряет скорость изменения гаммы по отношению к изменениям волатильности.

{\text{Zomma}}={\frac {\partial \Gamma }{\partial \sigma }}={\frac {\partial {\text{vanna}}}{\partial S}}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \sigma }}

Zomma также упоминается как DgammaDvol . ^[13] Зомма — это третья производная стоимости опциона: дважды от цены базового актива и один раз от волатильности. Zomma может быть полезной чувствительностью для мониторинга при ведении гамма-хеджированного портфеля, поскольку zomma поможет трейдеру предвидеть изменения в эффективности хеджирования по мере изменения волатильности.

Цвет

Цвет , ^[13] гамма-распад ^[19] или DgammaDtime ^[13] измеряет скорость изменения гаммы с течением времени.

{\text{Color}}={\frac {\partial \Gamma }{\partial \tau }}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \tau }}

Цвет — это производная третьего порядка от стоимости опциона, дважды от цены базового актива и один раз от времени. Цвет может быть важной чувствительностью, которую следует отслеживать при ведении портфеля с гамма-хеджированием, поскольку он может помочь трейдеру предвидеть эффективность хеджирования с течением времени.

Математический результат формулы цвета (см. ниже) выражается в гаммах в год. Часто бывает полезно разделить это значение на количество дней в году, чтобы получить изменение гаммы в день. Такое использование является достаточно точным, когда количество дней, оставшихся до истечения срока действия опциона, велико. Когда срок действия опциона приближается, сам цвет может быстро измениться, что делает оценку изменения гаммы за весь день неточной.

Последний

Последний ^[4] измеряет чувствительность опциона вомма к изменению волатильности.

{\text{Ultima}}={\frac {\partial {\text{vomma}}}{\partial \sigma }}={\frac {\partial ^{3}V}{\partial \sigma ^{3}}}

Ultima также упоминается как DvommaDvol . ^[4] Ultima — это производная третьего порядка от стоимости опциона по волатильности.

Греки за опционы с несколькими активами

Если стоимость дериватива зависит от двух или более базовых активов , его греки расширяются, чтобы включить перекрестные эффекты между базовыми активами.

Дельта корреляции измеряет чувствительность стоимости производного инструмента к изменению корреляции между базовыми активами. ^[20] Он также широко известен как сега . ^[21]^[22]

Перекрестная гамма измеряет скорость изменения дельты одного базового актива к изменению уровня другого базового актива. ^[23]

Кросс-ванна измеряет скорость изменения веги одного базового актива из-за изменения уровня другого базового актива. Аналогично, он измеряет скорость изменения дельты второго базового актива из-за изменения волатильности первого базового актива. ^[20]

Cross Volga измеряет скорость изменения веги одного базового актива по отношению к изменению волатильности другого базового актива. ^[23]

Формулы для европейского опциона греков

Греки европейских опционов ( коллов и путов ) по модели Блэка–Шоулза рассчитываются следующим образом, где $\varphi$ (phi) — стандартная нормальная функция плотности вероятности , а $\Phi$ — стандартная нормальная кумулятивная функция распределения . Обратите внимание, что формулы гаммы и веги одинаковы для коллов и путов.

Для данного:

Цена акции $S\,$ ,
Страйк-цена $K\,$ ,
Безрисковая ставка $r\,$ ,
Годовая дивидендная доходность $q\,$ ,
Время до зрелости $\tau =T-t\,$ (представленный как безразмерная доля одного года), и
Волатильность $\sigma \,$ .

	Звонки	Путы
справедливая стоимость ( $V$ )	$Se^{-q\tau }\Phi (d_{1})-e^{-r\tau }K\Phi (d_{2})\,$	$e^{-r\tau }K\Phi (-d_{2})-Se^{-q\tau }\Phi (-d_{1})\,$

дельта ( $\Delta$ )	$e^{-q\tau }\Phi (d_{1})\,$	$-e^{-q\tau }\Phi (-d_{1})\,$
вега ( ${\mathcal {V}}$ )	$Se^{-q\tau }\varphi (d_{1}){\sqrt {\tau }}=Ke^{-r\tau }\varphi (d_{2}){\sqrt {\tau }}\,$
тета ( $\Theta$ )	$-e^{-q\tau }{\frac {S\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}-rKe^{-r\tau }\Phi (d_{2})+qSe^{-q\tau }\Phi (d_{1})\,$	$-e^{-q\tau }{\frac {S\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}+rKe^{-r\tau }\Phi (-d_{2})-qSe^{-q\tau }\Phi (-d_{1})\,$
ро ( $\rho$ )	$K\tau e^{-r\tau }\Phi (d_{2})\,$	$-K\tau e^{-r\tau }\Phi (-d_{2})\,$
эпсилон ( $\epsilon$ )	$-S\tau e^{-q\tau }\Phi (d_{1})$	$S\tau e^{-q\tau }\Phi (-d_{1})$
лямбда ( $\lambda$ )	$\Delta {\frac {S}{V}}\,$

гамма ( $\Gamma$ )	$e^{-q\tau }{\frac {\varphi (d_{1})}{S\sigma {\sqrt {\tau }}}}=Ke^{-r\tau }{\frac {\varphi (d_{2})}{S^{2}\sigma {\sqrt {\tau }}}}\,$
ванна	$-e^{-q\tau }\varphi (d_{1}){\frac {d_{2}}{\sigma }}\,={\frac {\mathcal {V}}{S}}\left[1-{\frac {d_{1}}{\sigma {\sqrt {\tau }}}}\right]\,$
очарование	$qe^{-q\tau }\Phi (d_{1})-e^{-q\tau }\varphi (d_{1}){\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{2\tau \sigma {\sqrt {\tau }}}}\,$	$-qe^{-q\tau }\Phi (-d_{1})-e^{-q\tau }\varphi (d_{1}){\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{2\tau \sigma {\sqrt {\tau }}}}\,$

рубец	$Se^{-q\tau }\varphi (d_{1}){\sqrt {\tau }}{\frac {d_{1}d_{2}}{\sigma }}={\mathcal {V}}{\frac {d_{1}d_{2}}{\sigma }}\,$
существование	$-K\tau e^{-r\tau }\varphi (d_{2}){\frac {d_{1}}{\sigma }}\,$
Знать	$-Se^{-q\tau }\varphi (d_{1}){\sqrt {\tau }}\left[q+{\frac {\left(r-q\right)d_{1}}{\sigma {\sqrt {\tau }}}}-{\frac {1+d_{1}d_{2}}{2\tau }}\right]\,$
$\varpi$	$Se^{-q\tau }\varphi (d_{1}){\frac {1}{K^{2}\sigma {\sqrt {\tau }}}}=\left({\frac {S}{K}}\right)^{2}\Gamma \,$

скорость	$-e^{-q\tau }{\frac {\varphi (d_{1})}{S^{2}\sigma {\sqrt {\tau }}}}\left({\frac {d_{1}}{\sigma {\sqrt {\tau }}}}+1\right)=-{\frac {\Gamma }{S}}\left({\frac {d_{1}}{\sigma {\sqrt {\tau }}}}+1\right)\,$
зомма	$e^{-q\tau }{\frac {\varphi (d_{1})\left(d_{1}d_{2}-1\right)}{S\sigma ^{2}{\sqrt {\tau }}}}=\Gamma {\frac {d_{1}d_{2}-1}{\sigma }}\,$
цвет	$-e^{-q\tau }{\frac {\varphi (d_{1})}{2S\tau \sigma {\sqrt {\tau }}}}\left[2q\tau +1+{\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{\sigma {\sqrt {\tau }}}}d_{1}\right]\,$

последний	${\frac {-{\mathcal {V}}}{\sigma ^{2}}}\left[d_{1}d_{2}(1-d_{1}d_{2})+d_{1}^{2}+d_{2}^{2}\right]$

двойная дельта	$-e^{-r\tau }\Phi (d_{2})\,$	$e^{-r\tau }\Phi (-d_{2})\,$
двойная гамма	$e^{-r\tau }{\frac {\varphi (d_{2})}{K\sigma {\sqrt {\tau }}}}\,$

где

{\begin{aligned}d_{1}&={\frac {\ln(S/K)+\left(r-q+{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(S/K)+\left(r-q-{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\\\varphi (x)&={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}\\\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-{\frac {1}{2}}y^{2}}\,dy=1-{\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {1}{2}}y^{2}}\,dy\end{aligned}}

Согласно модели Блэка (обычно используемой для товаров и опционов на фьючерсы) греки можно рассчитать следующим образом:

	Звонки	Путы
справедливая стоимость ( $V$ )	$e^{-r\tau }[F\Phi (d_{1})-K\Phi (d_{2})]\$	$e^{-r\tau }[K\Phi (-d_{2})-F\Phi (-d_{1})]\,$

дельта ( $\Delta$ ) $=\partial V/\partial F$	$e^{-r\tau }\Phi (d_{1})\,$	$-e^{-r\tau }\Phi (-d_{1})\,$
вега ( ${\mathcal {V}}$ )	$Fe^{-r\tau }\varphi (d_{1}){\sqrt {\tau }}=Ke^{-r\tau }\varphi (d_{2}){\sqrt {\tau }}\,$ (*)
тета ( $\Theta$ )	$-{\frac {Fe^{-r\tau }\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}-rKe^{-r\tau }\Phi (d_{2})+rFe^{-r\tau }\Phi (d_{1})\,$	$-{\frac {Fe^{-r\tau }\varphi (d_{1})\sigma }{2{\sqrt {\tau }}}}+rKe^{-r\tau }\Phi (-d_{2})-rFe^{-r\tau }\Phi (-d_{1})\,$
ро ( $\rho$ )	$-\tau e^{-r\tau }[F\Phi (d_{1})-K\Phi (d_{2})]\$	$-\tau e^{-r\tau }[K\Phi (-d_{2})-F\Phi (-d_{1})]\,$

гамма ( $\Gamma$ ) $={\partial ^{2}V \over \partial F^{2}}$	$e^{-r\tau }{\frac {\varphi (d_{1})}{F\sigma {\sqrt {\tau }}}}=Ke^{-r\tau }{\frac {\varphi (d_{2})}{F^{2}\sigma {\sqrt {\tau }}}}\,$ (*)
ванна $={\frac {\partial ^{2}V}{\partial F\partial \sigma }}$	$-e^{-r\tau }\varphi (d_{1}){\frac {d_{2}}{\sigma }}\,={\frac {\mathcal {V}}{F}}\left[1-{\frac {d_{1}}{\sigma {\sqrt {\tau }}}}\right]\,$

рубец	$Fe^{-r\tau }\varphi (d_{1}){\sqrt {\tau }}{\frac {d_{1}d_{2}}{\sigma }}={\mathcal {V}}{\frac {d_{1}d_{2}}{\sigma }}\,$

где

{\begin{aligned}d_{1}&={\frac {\ln(F/K)+{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(F/K)-{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\end{aligned}}

(*) Можно показать, что $F\varphi (d_{1})=K\varphi (d_{2})$

Микродоказательство:

позволять $x=\sigma {\sqrt {\tau }}$
$d_{1}={\frac {\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}}{x}}$
$d_{1}\cdot x=\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}$
$\ln(F/K)=d_{1}\cdot x-{\frac {1}{2}}x^{2}$
${\frac {F}{K}}=e^{d_{1}\cdot x-{\frac {1}{2}}x^{2}}$
Тогда у нас есть: ${\frac {F}{K}}\cdot {\frac {\varphi (d_{1})}{\varphi (d_{2})}}={\frac {F}{K}}\cdot e^{{\frac {1}{2}}\cdot {d_{2}}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}$
$=e^{d_{1}x-{\frac {1}{2}}x^{2}}\cdot e^{{\frac {1}{2}}\cdot {(d_{1}-x)}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}=e^{d_{1}x-{\frac {1}{2}}x^{2}+{\frac {1}{2}}\cdot (2d_{1}-x)(-x)}=e^{0}=1.$
Так $F\varphi (d_{1})=K\varphi (d_{2})$

Сопутствующие меры

Некоторые соответствующие меры риска финансовых инструментов перечислены ниже.

Продолжительность связи и выпуклость

В торговле облигациями и другими ценными бумагами с фиксированным доходом различные меры дюрации облигаций используются аналогично дельте опциона. Ближайшим аналогом дельты является DV01 , который представляет собой снижение цены (в денежных единицах) при увеличении доходности на один базисный пункт (т. е. 0,01% в год) , где доходность является базовой переменной;см. Дюрация облигаций § Риск – дюрация как чувствительность процентной ставки .(Связан с CS01 , измеряющим чувствительность к кредитному спреду .)

Аналогом лямбды является модифицированная дюрация , которая представляет собой процентное изменение рыночной цены облигации (облигаций) на единицу изменения доходности (т. е. она эквивалентна DV01, деленному на рыночную цену). В отличие от лямбды, которая представляет собой эластичность (процентное изменение выпуска при процентном изменении затрат), модифицированная продолжительность вместо этого представляет собой — полуэластичность процентное изменение выпуска при единичном изменении затрат.См. также Длительность ключевой ставки .

Выпуклость облигации — это мера чувствительности дюрации к изменениям процентных ставок , вторая производная цены облигации по отношению к процентным ставкам (дюрация — первая производная); тогда это аналогично гамма. В целом, чем выше выпуклость, тем более чувствительна цена облигации к изменению процентных ставок. Выпуклость облигаций — одна из самых основных и широко используемых форм выпуклости в финансах .

Для облигации со встроенным опционом стандартные расчеты доходности к погашению здесь не учитывают, как изменения процентных ставок изменят денежные потоки в результате исполнения опциона. Для решения этой проблемы эффективная длительность и эффективная выпуклость вводятся . Эти значения обычно рассчитываются с использованием древовидной модели, построенной для всей кривой доходности (в отличие от одной доходности к погашению) и, следовательно, фиксирующей поведение исполнения в каждый момент срока действия опциона как функцию как времени, так и процентных ставок. ; см. Решетчатую модель (финансы) § Производные процентные ставки .

Бета

Бета это число , (β) акции или портфеля — описывающее волатильность актива по отношению к волатильности эталонного показателя, с которым сравнивается указанный актив. Этот ориентир обычно представляет собой общий финансовый рынок и часто оценивается с помощью репрезентативных индексов , таких как S&P 500 .

Актив имеет нулевую бета-коэффициент, если его доходность меняется независимо от изменений доходности рынка. Положительная бета означает, что доходность актива обычно соответствует доходности рынка в том смысле, что они оба имеют тенденцию быть выше своих соответствующих средних значений вместе или оба имеют тенденцию быть ниже своих соответствующих средних значений вместе. Отрицательное значение бета означает, что доходность актива обычно колеблется в противоположном направлении от доходности рынка: один будет иметь тенденцию быть выше среднего, тогда как другой будет ниже среднего.

бежал

Фуджит – это ожидаемое время для исполнения американского или бермудского опциона. Fugit удобно вычислять в целях хеджирования — например, можно представить потоки американского свопа как потоки свопа, начиная с fugit, умноженного на дельту, а затем использовать их для расчета других показателей чувствительности.

См. также

Ссылки

^ Бэнкс, Эрик; Сигел, Пол (2006). Справочник по применению опционов: методы хеджирования и спекуляций для профессиональных инвесторов . МакГроу-Хилл Профессионал . п. 263. ИСБН 9780071453158 .
^ Перейти обратно: ^а ^б Макмиллан, Лоуренс Г. (1993). Опционы как стратегические инвестиции (3-е изд.). Нью-Йоркский институт финансов . ISBN 978-0-13-636002-5 .
^ Крисс, Нил (1996). Блэк-Шоулз и другие: модели ценообразования опционов . МакГроу-Хилл Профессионал . п. 308 . ISBN 9780786310258 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н Хауг, Эспен Горднер (2007). Полное руководство по формулам ценообразования опционов . МакГроу-Хилл Профессионал . ISBN 9780071389976 .
^ Сума, Джон. «Греческие опционы: дельта-риск и вознаграждение» . Проверено 7 января 2010 г.
^ Штайнер, Боб (2013). Освоение финансовых расчетов (3-е изд.). Пирсон Великобритания. ISBN 9780273750604 .
^ Халл, Джон К. (1993). Опционы, фьючерсы и другие производные ценные бумаги (2-е изд.). Прентис-Холл . ISBN 9780136390145 .
^ Омега - Инвестопедия
^ Де Шпигелер, Ян; Схоутенс, Вим (2015). Справочник по конвертируемым облигациям: ценообразование, стратегии и управление рисками . Джон Уайли и сыновья . стр. 255, 269–270. ISBN 9780470689684 .
^ Перейти обратно: ^а ^б Соклаков, АН (2023). «Информационная геометрия рисков и доходности». Риск . Июнь . arXiv : 2206.08753 . ССНН 4134885 .
^ Уиллетт, Джефф (28 мая 2014 г.). «Понимание того, как гамма влияет на дельту» . www.traderbrains.com . Проверено 7 марта 2014 г.
^ Уиллетт, Джефф (28 мая 2014 г.). «Почему гамма-положительная длинная опция» . www.traderbrains.com . Проверено 7 марта 2014 г.
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Хауг, Эспен Гордер (2003), «Знай свое оружие, часть 1» (PDF) , Wilmott Magazine (май 2003 г.): 49–57, doi : 10.1002/wilm.42820030313 (неактивно 19 марта 2024 г.) {{citation}}: CS1 maint: DOI неактивен по состоянию на март 2024 г. ( ссылка )
^ Производные финансовые инструменты - Дельта-распад - Финансовая энциклопедия
^ Перейти обратно: ^а ^б ^с ^д Хауг, Эспен Гордер (2003), «Знай свое оружие, часть 2» , журнал Wilmott (июль 2003 г.): 43–57.
^ Пьерино Урсоне. Как рассчитать цены опционов и их греки: исследование модели Блэка-Шоулза от дельты до веги . Джон Уайли и сыновья. 2015.
^ Перейти обратно: ^а ^б Деривативы – греки второго порядка – Финансовая энциклопедия
^ Бриден, Литценбергер, Цены на требования, обусловленные государством, подразумеваемые в ценах опционов [1]
^ «Деривативы – греки» . Инвестиции и финансы . Проверено 21 декабря 2020 г.
^ Перейти обратно: ^а ^б «Греки за опционы с несколькими активами» . Проверено 24 января 2017 г.
^ Корреляционный риск . Проверено 22 марта 2018 г.
^ «Варианты вращающихся горных хребтов, оценка и риски / анализ эффективности» . Проверено 22 марта 2018 г.
^ Перейти обратно: ^а ^б Фенглер, Матиас; Швенднер, Питер (2003). «Премии за риск корреляции для опционов на акции с несколькими активами» (PDF) . Берлинский университет имени Гумбольдта, экономический факультет. дои : 10.18452/3572 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

Внешние ссылки

Теория

Дельта, Гамма, ГаммаП, Гамма-симметрия, Ванна, Скорость, Очарование, Седло Гамма: Ванильные варианты — Эспен Хауг ,
Волга, Ванна, Скорость, Очарование, Цвет: Ванильные опции — Уве Виступ. Архивировано 28 сентября 2007 г. в Wayback Machine , Ванильные опции — Уве Виступ.

Онлайн-инструменты

греки: чувствительность цен финансовых опционов , пакет R для расчета греков для европейских, американских и азиатских опционов

[1] Бэнкс, Эрик; Сигел, Пол (2006). Справочник по применению опционов: методы хеджирования и спекуляций для профессиональных инвесторов . МакГроу-Хилл Профессионал . п. 263. ИСБН 9780071453158 .

[macmillan93-2] Перейти обратно: ^а ^б Макмиллан, Лоуренс Г. (1993). Опционы как стратегические инвестиции (3-е изд.). Нью-Йоркский институт финансов . ISBN 978-0-13-636002-5 .

[3] Крисс, Нил (1996). Блэк-Шоулз и другие: модели ценообразования опционов . МакГроу-Хилл Профессионал . п. 308 . ISBN 9780786310258 .

[autogenerated2007-4] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н Хауг, Эспен Горднер (2007). Полное руководство по формулам ценообразования опционов . МакГроу-Хилл Профессионал . ISBN 9780071389976 .

[5] Сума, Джон. «Греческие опционы: дельта-риск и вознаграждение» . Проверено 7 января 2010 г.

[6] Штайнер, Боб (2013). Освоение финансовых расчетов (3-е изд.). Пирсон Великобритания. ISBN 9780273750604 .

[Hull93-7] Халл, Джон К. (1993). Опционы, фьючерсы и другие производные ценные бумаги (2-е изд.). Прентис-Холл . ISBN 9780136390145 .

[8] Омега - Инвестопедия

[9] Де Шпигелер, Ян; Схоутенс, Вим (2015). Справочник по конвертируемым облигациям: ценообразование, стратегии и управление рисками . Джон Уайли и сыновья . стр. 255, 269–270. ISBN 9780470689684 .

[autogenerated2023-10] Перейти обратно: ^а ^б Соклаков, АН (2023). «Информационная геометрия рисков и доходности». Риск . Июнь . arXiv : 2206.08753 . ССНН 4134885 .

[11] Уиллетт, Джефф (28 мая 2014 г.). «Понимание того, как гамма влияет на дельту» . www.traderbrains.com . Проверено 7 марта 2014 г.

[12] Уиллетт, Джефф (28 мая 2014 г.). «Почему гамма-положительная длинная опция» . www.traderbrains.com . Проверено 7 марта 2014 г.

[kyw1-13] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Хауг, Эспен Гордер (2003), «Знай свое оружие, часть 1» (PDF) , Wilmott Magazine (май 2003 г.): 49–57, doi : 10.1002/wilm.42820030313 (неактивно 19 марта 2024 г.) {{citation}}: CS1 maint: DOI неактивен по состоянию на март 2024 г. ( ссылка )

[14] Производные финансовые инструменты - Дельта-распад - Финансовая энциклопедия

[kyw2-15] Перейти обратно: ^а ^б ^с ^д Хауг, Эспен Гордер (2003), «Знай свое оружие, часть 2» , журнал Wilmott (июль 2003 г.): 43–57.

[16] Пьерино Урсоне. Как рассчитать цены опционов и их греки: исследование модели Блэка-Шоулза от дельты до веги . Джон Уайли и сыновья. 2015.

[FE-17] Перейти обратно: ^а ^б Деривативы – греки второго порядка – Финансовая энциклопедия

[BL-18] Бриден, Литценбергер, Цены на требования, обусловленные государством, подразумеваемые в ценах опционов [1]

[19] «Деривативы – греки» . Инвестиции и финансы . Проверено 21 декабря 2020 г.

[greeksMulti-20] Перейти обратно: ^а ^б «Греки за опционы с несколькими активами» . Проверено 24 января 2017 г.

[21] Корреляционный риск . Проверено 22 марта 2018 г.

[22] «Варианты вращающихся горных хребтов, оценка и риски / анализ эффективности» . Проверено 22 марта 2018 г.

[mao1-23] Перейти обратно: ^а ^б Фенглер, Матиас; Швенднер, Питер (2003). «Премии за риск корреляции для опционов на акции с несколькими активами» (PDF) . Берлинский университет имени Гумбольдта, экономический факультет. дои : 10.18452/3572 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]