Обобщенная теорема Стокса

Эта статья об обобщенной теореме. Для классической теоремы см. теорему Стокса . Чтобы узнать об уравнении вязкого сопротивления в жидкостях, см. закон Стокса .

В векторном исчислении и дифференциальной геометрии обобщенная теорема Стокса (иногда с апострофом в виде теоремы Стокса или теоремы Стокса ), также называемая теоремой Стокса-Картана , Это утверждение об интегрировании дифференциальных форм на многообразиях , которое одновременно упрощает и обобщает некоторые теоремы векторного исчисления . В частности, фундаментальная теорема исчисления — это частный случай, когда многообразие представляет собой отрезок прямой , теорема Грина и теорема Стокса — это случаи поверхности в $\mathbb {R} ^{2}$ или $\mathbb {R} ^{3},$ а теорема о дивергенции относится к случаю объема в $\mathbb {R} ^{3}.$ Следовательно, эту теорему иногда называют Фундаментальной теоремой многомерного исчисления .

Теорема Стокса гласит, что интеграл дифференциальной формы $\omega$ за границей $\partial \Omega$ некоторого ориентируемого многообразия $\Omega$ равен интегралу от своей внешней производной $d\omega$ на протяжении всего $\Omega$, то есть, $$\int _{\partial \Omega }\omega =\int _{\Omega }\operatorname {d} \omega \,.$$

Теорема Стокса была сформулирована в современной форме Эли Картаном в 1945 году: после более ранних работ по обобщению теорем векторного исчисления Вито Вольтерры , Эдуарда Гурса и Анри Пуанкаре .

Эта современная форма теоремы Стокса представляет собой обширное обобщение классического результата , который лорд Кельвин сообщил Джорджу Стоксу в письме от 2 июля 1850 года. Стоукс задал эту теорему в качестве вопроса на экзамене на премию Смита в 1854 году , в результате чего результат был назван его именем. Впервые оно было опубликовано Германом Ханкелем в 1861 году. классический случай связывает поверхностный интеграл ротора поля векторного Этот ${\textbf {F}}$ (т.е. поток по поверхности ${\text{curl}}\,{\textbf {F}}$) в евклидовом трехмерном пространстве к линейному интегралу векторного поля по границе поверхности.

Введение

Вторая фундаментальная теорема исчисления гласит, что интеграл от функции $f$ за интервал $[a,b]$ можно вычислить, найдя первообразную $F$ из $f$: $$\int _{a}^{b}f(x)\,dx=F(b)-F(a)\,.$$

Теорема Стокса является обширным обобщением этой теоремы в следующем смысле.

• По выбору $F$, ${\frac {dF}{dx}}=f(x)$. На языке дифференциальных форм это означает, что $f(x)\,dx$ — внешняя производная 0-формы, т. е. функция, $F$: другими словами, это $dF=f\,dx$. Общая теорема Стокса применима к более высокой степени . дифференциальным формам $\omega$ вместо просто 0-форм, таких как $F$.
• Закрытый интервал $[a,b]$ является простым примером одномерного многообразия с краем . Его границей является множество, состоящее из двух точек $a$ и $b$. Интеграция $f$ на интервале может быть обобщено до интегрирования форм на многомерном многообразии. Необходимы два технических условия: многообразие должно быть ориентируемым , а форма должна иметь компактный носитель , чтобы давать четко определенный интеграл.
• Две точки $a$ и $b$ образуют границу замкнутого интервала. В более общем смысле теорема Стокса применима к ориентированным многообразиям. $M$ с границей. Граница $\partial M$ из $M$ само является многообразием и наследует естественную ориентацию от ориентации $M$. Например, естественная ориентация интервала дает ориентацию двух граничных точек. Интуитивно, $a$ наследует противоположную ориентацию, поскольку $b$, поскольку они находятся на противоположных концах интервала. Итак, «интеграция» $F$ над двумя граничными точками $a$, $b$ берет на себя разницу $F(b)-F(a)$.

Еще проще, точки можно рассматривать как границы кривых, то есть как 0-мерные границы 1-мерных многообразий. Итак, так же, как можно найти значение интеграла ( $f\,dx=dF$) над одномерным многообразием ( $[a,b]$), рассматривая первообразную ( $F$) на 0-мерных границах ( $\{a,b\}$), можно обобщить фундаментальную теорему исчисления с несколькими дополнительными оговорками, чтобы иметь дело со значением интегралов ( $d\omega$) над $n$-мерные многообразия ( $\Omega$), рассматривая первообразную ( $\omega$) в $(n-1)$-мерные границы ( $\partial \Omega$) многообразия.

Итак, основная теорема гласит: $$\int _{[a,b]}f(x)\,dx=\int _{[a,b]}\,dF=\int _{\partial [a,b]}\,F=\int _{\{a\}^{-}\cup \{b\}^{+}}F=F(b)-F(a)\,.$$

Формулировка для гладких многообразий с краем

Позволять $\Omega$ — ориентированное гладкое размерности многообразие $n$ с границей и пусть $\alpha$ быть гладким $n$- дифференциальная форма , компактно опирающаяся на $\Omega$. Во-первых, предположим, что $\alpha$ компактно поддерживается в области одной ориентированной координатной карты $\{U,\varphi \}$. В этом случае мы определяем интеграл от $\alpha$ над $\Omega$ как $$\int _{\Omega }\alpha =\int _{\varphi (U)}(\varphi ^{-1})^{*}\alpha \,,$$ через откат то есть $\alpha$ к $\mathbb {R} ^{n}$.

В более общем смысле интеграл $\alpha$ над $\Omega$ определяется следующим образом: Пусть $\{\psi _{i}\}$ — разбиение единицы, связанное с локально конечным покрытием $\{U_{i},\varphi _{i}\}$ (последовательно ориентированных) координатных карт, затем определите интеграл $$\int _{\Omega }\alpha \equiv \sum _{i}\int _{U_{i}}\psi _{i}\alpha \,,$$где каждый член суммы оценивается путем возврата к $\mathbb {R} ^{n}$ как описано выше. Эта величина четко определена; то есть не зависит ни от выбора координатных карт, ни от разделения единицы.

Обобщенная теорема Стокса гласит:

Теорема   ( Стокса – Картана ) — Пусть $\omega$ быть гладким $(n-1)$- форма с компактной опорой на ориентированную , $n$-мерное многообразие с краем $\Omega$, где $\partial \Omega$ задана индуцированная ориентация. Тогда $$\int _{\Omega }d\omega =\int _{\partial \Omega }\omega .$$

Здесь $d$ — внешняя производная , которая определяется только с использованием структуры многообразия. Правая часть иногда записывается как ${\textstyle \oint _{\partial \Omega }\omega }$ подчеркнуть тот факт, что $(n-1)$-многообразие $\partial \Omega$ не имеет границы. (Этот факт также является следствием теоремы Стокса, поскольку для заданной гладкой $n$-мерное многообразие $\Omega$, двукратное применение теоремы дает ${\textstyle \int _{\partial (\partial \Omega )}\omega =\int _{\Omega }d(d\omega )=0}$ для любого $(n-2)$-форма $\omega$, что означает, что $\partial (\partial \Omega )=\emptyset$.) Правая часть уравнения часто используется для формулирования интегральных законов; тогда левая часть приводит к эквивалентным дифференциальным формулировкам (см. ниже).

Теорема часто используется в ситуациях, когда $\Omega$ является вложенным ориентированным подмногообразием некоторого большего многообразия, часто $\mathbb {R} ^{k}$, на котором форма $\omega$ определяется.

Топологические предварительные сведения; интеграция по цепочкам

Пусть M — гладкое многообразие . (Гладкий) сингулярный k -симплекс в M определяется как гладкое отображение стандартного симплекса в R ^к к М. ​Группа Ck _k ( M , Z ) особых k - цепей на M определяется как свободная абелева группа на множестве особых - в M. симплексов Эти группы вместе с граничным отображением ∂ определяют цепной комплекс . Соответствующая группа гомологий (соответственно когомологий) изоморфна обычной гомологий сингулярной группе H _k ( M , Z ) (соответственно сингулярных когомологий группе H ^к ( M , Z ) ), определенный с использованием непрерывных, а не гладких симплексов в M .

С другой стороны, дифференциальные формы с внешней производной d в качестве связующего отображения образуют коцепный комплекс, который определяет когомологий де Рама. группы $H_{dR}^{k}(M,\mathbf {R} )$.

Дифференциальные k -формы можно интегрировать по k -симплексу естественным путем, возвращаясь к R ^к . Расширение за счет линейности позволяет интегрировать по цепочкам. Это дает линейное отображение пространства k -форм в k -ю группу особых коцепей C ^к ( M , Z ) , линейные функционалы на C _k ( M , Z ) . Другими словами, k -форма ω определяет функционал $$I(\omega )(c)=\oint _{c}\omega .$$на k -цепях. Теорема Стокса утверждает, что это цепное отображение когомологий де Рама в сингулярные когомологии с действительными коэффициентами; внешняя производная d ведет себя как двойственная к ∂ на формах. Это дает гомоморфизм когомологий де Рама в сингулярные когомологии. На уровне форм это означает:

1. замкнутые формы, т. е. dω = 0 , имеют нулевой интеграл по границам , т. е. по многообразиям, которые можно записать как ∂Σ _c M _c , и
2. точные формы, т. е. ω = dσ , имеют нулевой интеграл по циклам , т. е. если сумма границ равна пустому множеству: ∂Σ _c M _c = ∅ .

Теорема Де Рама показывает, что этот гомоморфизм на самом деле является изоморфизмом . Таким образом, обратное к пунктам 1 и 2 выше справедливо. Другими словами, если { c _i } — циклы, порождающие k -ю группу гомологий, то для любых соответствующих действительных чисел { a _i } существует замкнутая форма ω такая, что $$\oint _{c_{i}}\omega =a_{i}\,,$$и эта форма уникальна с точностью до точных форм.

Теорему Стокса о гладких многообразиях можно вывести из теоремы Стокса для цепей в гладких многообразиях, и наоборот. Формально последнее гласит:

Теорема   ( теорема Стокса для цепей ) — Если c — гладкая k -цепь в гладком многообразии M , а ω — гладкая ( k − 1) -форма на M , то $$\int _{\partial c}\omega =\int _{c}d\omega .$$

Основной принцип

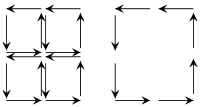
Чтобы упростить эти топологические аргументы, стоит изучить основополагающий принцип, рассмотрев пример для измерений d = 2 . Основную идею можно понять с помощью диаграммы слева, которая показывает, что в ориентированном замощении многообразия внутренние пути проходят в противоположных направлениях; таким образом, их вклады в интеграл по путям попарно компенсируют друг друга. В результате остается только вклад границы. Таким образом, достаточно доказать теорему Стокса для достаточно тонких мозаик (или, что то же самое, симплексов ), что обычно не составляет труда.

Пример классического векторного анализа

Позволять $\gamma :[a,b]\to \mathbb {R} ^{2}$ — кусочно- гладкая плоская жорданова кривая . Теорема Жордана о кривой означает, что $\gamma$ делит $\mathbb {R} ^{2}$ на две компоненты: компактную и некомпактную. Позволять $D$ обозначим компактную часть, ограниченную $\gamma$ и предположим $\psi :D\to \mathbb {R} ^{3}$ гладкая, с $S=\psi (D)$. Если $\Gamma$ - пространственная кривая, определяемая формулой $\Gamma (t)=\psi (\gamma (t))$ и ${\textbf {F}}$ представляет собой гладкое векторное поле на $\mathbb {R} ^{3}$, затем: $$\oint _{\Gamma }\mathbf {F} \,\cdot \,d{\mathbf {\Gamma } }=\iint _{S}\left(\nabla \times \mathbf {F} \right)\cdot \,d\mathbf {S}$$

Это классическое утверждение является частным случаем общей формулировки после отождествления векторного поля с 1-формой, а его ротора с двойной формой через $${\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\\\end{pmatrix}}\cdot d\Gamma \to F_{x}\,dx+F_{y}\,dy+F_{z}\,dz$$$${\begin{aligned}&\nabla \times {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\end{pmatrix}}\cdot d\mathbf {S} ={\begin{pmatrix}\partial _{y}F_{z}-\partial _{z}F_{y}\\\partial _{z}F_{x}-\partial _{x}F_{z}\\\partial _{x}F_{y}-\partial _{y}F_{x}\\\end{pmatrix}}\cdot d\mathbf {S} \to \\[1.4ex]&d(F_{x}\,dx+F_{y}\,dy+F_{z}\,dz)=\left(\partial _{y}F_{z}-\partial _{z}F_{y}\right)dy\wedge dz+\left(\partial _{z}F_{x}-\partial _{x}F_{z}\right)dz\wedge dx+\left(\partial _{x}F_{y}-\partial _{y}F_{x}\right)dx\wedge dy.\end{aligned}}$$

Обобщение на грубые множества

Область (здесь она называется D вместо Ω ) с кусочно-гладкой границей. Это многообразие с углами , поэтому его граница не является гладким многообразием.

Приведенная выше формулировка, в которой $\Omega$ является гладким многообразием с краем, во многих приложениях недостаточно. Например, если область интегрирования определяется как плоская область между двумя $x$-координаты и графики двух функций, часто бывает, что область имеет углы. В таком случае угловые точки означают, что $\Omega$ не является гладким многообразием с краем, поэтому приведенное выше утверждение теоремы Стокса неприменимо. Тем не менее, можно проверить, что заключение теоремы Стокса по-прежнему верно. Это потому, что $\Omega$ и его граница хорошо ведут себя вдали от небольшого набора точек ( множества нулевой меры ).

Версия теоремы Стокса, допускающая шероховатость, была доказана Уитни. Предположим, что $D$ является связным ограниченным открытым подмножеством $\mathbb {R} ^{n}$. Вызов $D$ , стандартный домен если он удовлетворяет следующему свойству: существует подмножество $P$ из $\partial D$, открыть в $\partial D$, дополнение которого в $\partial D$ есть Хаусдорф $(n-1)$-измерить ноль; и такой, что каждая точка $P$ имеет обобщенный вектор нормали . Это вектор ${\textbf {v}}(x)$ такое, что если система координат выбрана так, что ${\textbf {v}}(x)$ является первым базисным вектором, то в открытой окрестности вокруг $x$, существует гладкая функция $f(x_{2},\dots ,x_{n})$ такой, что $P$ это график $\{x_{1}=f(x_{2},\dots ,x_{n})\}$ и $D$ это регион $\{x_{1}:x_{1}<f(x_{2},\dots ,x_{n})\}$. Уитни отмечает, что граница стандартной области представляет собой объединение множества нулевых хаусдорфовых $(n-1)$-мера и конечное или счетное объединение гладких $(n-1)$-многообразия, каждое из которых имеет область определения только на одной стороне. Затем он доказывает, что если $D$ это стандартный домен в $\mathbb {R} ^{n}$, $\omega$ это $(n-1)$-форма, определенная, непрерывная и ограниченная на $D\cup P$, плавно $D$, интегрируемый на $P$, и такой, что $d\omega$ интегрируемо на $D$, то справедлива теорема Стокса, т. е. $$\int _{P}\omega =\int _{D}d\omega \,.$$

Изучение теоретико-мерных свойств грубых множеств приводит к геометрической теории меры . Еще более общие версии теоремы Стокса были доказаны Федерером и Харрисоном.

Особые случаи

Общая форма теоремы Стокса с использованием дифференциальных форм более мощна и проста в использовании, чем частные случаи. Традиционные версии могут быть сформулированы с использованием декартовых координат без применения дифференциальной геометрии и, следовательно, более доступны. Кроме того, они старше, и в результате их имена более знакомы. Традиционные формы часто считаются более удобными для практикующих ученых и инженеров, но неестественность традиционной формулировки становится очевидной при использовании других систем координат, даже таких привычных, как сферические или цилиндрические координаты. Существует вероятность путаницы в применении названий и использовании двойных формулировок.

Классический (векторное исчисление) случай

Основная статья: теорема Стокса

Иллюстрация теоремы Стокса о векторном исчислении с поверхностью $\Sigma$, его граница $\partial \Sigma$ и «нормальный» вектор n .

Это (дуализированный) (1 + 1)-мерный случай для 1-формы (дуализированной, поскольку это утверждение о векторных полях ). Этот особый случай во многих вводных университетских курсах векторного исчисления часто называют просто теоремой Стокса и используется в физике и технике. Ее также иногда называют теоремой о роторе .

теорема Стокса связывает поверхностный интеграл ротора поля векторного Классическая по поверхности $\Sigma$ в евклидовом трехмерном пространстве к линейному интегралу векторного поля по его границе. Это частный случай общей теоремы Стокса (с $n=2$) как только мы отождествляем векторное поле с 1-формой, используя метрику в евклидовом 3-пространстве. Кривая линейного интеграла, $\partial \Sigma$, должен иметь положительную направленность , то есть $\partial \Sigma$ указывает против часовой стрелки, когда поверхность нормальная , $n$, указывает на зрителя.

Одним из следствий этой теоремы является то, что силовые линии векторного поля с нулевым ротором не могут быть замкнутыми контурами. Формулу можно переписать так:

Теорема . Предположим , ${\textbf {F}}={\big (}P(x,y,z),Q(x,y,z),R(x,y,z){\big )}$ определяется в области с гладкой поверхностью $\Sigma$ первого порядка и имеет непрерывные частные производные . Затем $$\iint _{\Sigma }{\Biggl (}\left({\frac {\partial R}{\partial y}}-{\frac {\partial Q}{\partial z}}\right)dy\,dz+\left({\frac {\partial P}{\partial z}}-{\frac {\partial R}{\partial x}}\right)dz\,dx+\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)dx\,dy{\Biggr )}=\oint _{\partial \Sigma }{\Big (}P\,dx+Q\,dy+R\,dz{\Big )}\,,$$где $P,Q$ и $R$ являются компонентами ${\textbf {F}}$, и $\partial \Sigma$ это граница региона $\Sigma$.

Теорема Грина

Теорема Грина сразу узнаваема как третий подынтегральный знак обеих частей интеграла в терминах P , Q и R , упомянутых выше.

В электромагнетизме

Два из четырех уравнений Максвелла включают роторы трехмерных векторных полей, а их дифференциальная и интегральная формы связаны специальным трехмерным (векторным исчислением) случаем теоремы Стокса . Необходимо проявлять осторожность, чтобы избежать случаев с подвижными границами: частные производные по времени предназначены для исключения таких случаев. Если включены движущиеся границы, то замена интегрирования и дифференцирования приводит к появлению членов, связанных с движением границ, не включенных в приведенные ниже результаты (см. Дифференцирование под знаком интеграла ):

Имя	Дифференциальная форма	Интегральная форма (с использованием трехмерной теоремы Стокса плюс релятивистская инвариантность, $\textstyle \int {\tfrac {\partial }{\partial t}}\dots \to {\tfrac {d}{dt}}\textstyle \int \cdots$)
Уравнение Максвелла – Фарадея Закон индукции Фарадея :	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	${\begin{aligned}\oint _{C}\mathbf {E} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {E} \cdot d\mathbf {A} \\&=-\iint _{S}{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}$ (при этом C и S не обязательно стационарны)
Закон Ампера (с расширением Максвелла):	$\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}$	${\begin{aligned}\oint _{C}\mathbf {H} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {H} \cdot d\mathbf {A} \\&=\iint _{S}\mathbf {J} \cdot d\mathbf {A} +\iint _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}$ (при этом C и S не обязательно стационарны)

Перечисленная выше подгруппа уравнений Максвелла справедлива для электромагнитных полей, выраженных в единицах СИ . В других системах единиц, таких как СГС или гауссовы единицы , коэффициенты масштабирования для терминов различаются. Например, в гауссовых единицах закон индукции Фарадея и закон Ампера принимают формы: $${\begin{aligned}\nabla \times \mathbf {E} &=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}\,,\\\nabla \times \mathbf {H} &={\frac {1}{c}}{\frac {\partial \mathbf {D} }{\partial t}}+{\frac {4\pi }{c}}\mathbf {J} \,,\end{aligned}}$$соответственно, где c — скорость света в вакууме.

Теорема о дивергенции

Аналогично, теорема о расходимости $$\int _{\mathrm {Vol} }\nabla \cdot \mathbf {F} \,d_{\mathrm {Vol} }=\oint _{\partial \operatorname {Vol} }\mathbf {F} \cdot d{\boldsymbol {\Sigma }}$$является особым случаем, если мы отождествляем векторное поле с $(n-1)$-форма, полученная сжатием векторного поля с евклидовой формой объема. Применение этого случая ${\textbf {F}}=f{\vec {c}}$ где ${\vec {c}}$ — произвольный постоянный вектор. Вычисление расхождения произведения дает $${\vec {c}}\cdot \int _{\mathrm {Vol} }\nabla f\,d_{\mathrm {Vol} }={\vec {c}}\cdot \oint _{\partial \mathrm {Vol} }f\,d{\boldsymbol {\Sigma }}\,.$$Поскольку это справедливо для всех ${\vec {c}}$ мы находим $$\int _{\mathrm {Vol} }\nabla f\,d_{\mathrm {Vol} }=\oint _{\partial \mathrm {Vol} }f\,d{\boldsymbol {\Sigma }}\,.$$

Объемный интеграл градиента скалярного поля

Позволять $f:\Omega \to \mathbb {R}$ быть скалярным полем . Затем $$\int _{\Omega }{\vec {\nabla }}f=\int _{\partial \Omega }{\vec {n}}f$$где ${\vec {n}}$ вектор нормали к поверхности $\partial \Omega$ в данный момент.

Доказательство:Позволять ${\vec {c}}$ быть вектором. Затем $${\begin{aligned}0&=\int _{\Omega }{\vec {\nabla }}\cdot {\vec {c}}f-\int _{\partial \Omega }{\vec {n}}\cdot {\vec {c}}f&{\text{by the divergence theorem}}\\&=\int _{\Omega }{\vec {c}}\cdot {\vec {\nabla }}f-\int _{\partial \Omega }{\vec {c}}\cdot {\vec {n}}f\\&={\vec {c}}\cdot \int _{\Omega }{\vec {\nabla }}f-{\vec {c}}\cdot \int _{\partial \Omega }{\vec {n}}f\\&={\vec {c}}\cdot \left(\int _{\Omega }{\vec {\nabla }}f-\int _{\partial \Omega }{\vec {n}}f\right)\end{aligned}}$$Поскольку это справедливо для любого ${\vec {c}}$ (в частности, для каждого базисного вектора ) результат следующий.

См. также

• Лемма Чандрасекара – Вентцеля

Дальнейшее чтение

• Грунский, Гельмут (1983). Общая теорема Стокса . Бостон: Питман. ISBN  0-273-08510-7 .
• Кац, Виктор Дж. (май 1979 г.). «История теоремы Стокса». Журнал «Математика» . 52 (3): 146–156. дои : 10.2307/2690275 . JSTOR   2690275 .
• Лумис, Линн Гарольд ; Штернберг, Шломо (2014). Продвинутое исчисление . Хакенсак, Нью-Джерси: World Scientific. ISBN  978-981-4583-93-0 .
• Мэдсен, Иб ; Торнехаве, Йорген (1997). От исчисления к когомологиям: когомологии Де Рама и характеристические классы . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-58956-8 .
• Марсден, Джерролд Э .; Энтони, Тромба (2003). Векторное исчисление (5-е изд.). У. Х. Фриман.
• Ли, Джон (2003). Введение в гладкие многообразия . Спрингер-Верлаг. ISBN  978-0-387-95448-6 .
• Рудин, Уолтер (1976). Принципы математического анализа . Нью-Йорк, штат Нью-Йорк: МакГроу – Хилл. ISBN  0-07-054235-Х .
• Спивак, Михаил (1965). Исчисление на многообразиях: современный подход к классическим теоремам расширенного исчисления . Сан-Франциско: Бенджамин Каммингс. ISBN  0-8053-9021-9 .
• Стюарт, Джеймс (2009). Исчисление: концепции и контексты . Cengage Обучение. стр. 960–967. ISBN  978-0-495-55742-5 .
• Стюарт, Джеймс (2003). Исчисление: ранние трансцендентные функции (5-е изд.). Брукс/Коул.
• Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Нью-Йорк: Спрингер. ISBN  978-1-4419-7399-3 .

Внешние ссылки

• «Формула Стокса» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Доказательство теоремы о расходимости и теоремы Стокса.
• Исчисление 3 – Теорема Стокса от lamar.edu – поясняющее объяснение