Дата Пасхи

Как подвижный праздник , ^{[ 1 ]}^{[ 2 ]} Дата Пасхи определяется в каждом году посредством расчета, известного как компьютер ( латинская для «вычисления»). ^{[ 3 ]} Пасха отмечается в первое воскресенье после пасхальной полной луны (математическое приближение первой астрономической полнолуния , 21 марта или после или после этого - само по себе фиксированное приближение мартовского равноденствия ). Определение этой даты заранее требует корреляции между лунными месяцами и солнечным годом , а также учет месяца, даты и будта в календаре Юлиан или Григориан . ^{[ 4 ]} Сложность алгоритма возникает из -за желания связать дату Пасхи с датой еврейского праздника Пасхи , который, как считают христианами, заключается в том, что Иисус был распят. ^{[ 5 ]}

Первоначально для всей христианской церкви было выполнено ежегодно получать дату Пасхи через ежегодное объявление Папой . Однако к началу третьего века общения в Римской империи ухудшились до такой степени, что церковь придает большую ценность в системе, которая позволила бы духовенству определить дату для себя, независимо, но последовательно. ^{[ 6 ]} Кроме того, церковь хотела устранить зависимости от еврейского календаря , получая дату Пасхи непосредственно от мартовского равноденствия. ^{[ 7 ]}

В расчете времени (725) Беде использует Computus в качестве общего термина для любого вида расчетов, хотя он называет пасхальные циклы Феофила как «пасхальный компьютер ». К концу 8 -го века Computus стал конкретно относиться к расчету времени. ^{[ 8 ]} Расчеты дают разные результаты в зависимости от того, используется ли юлианский календарь или григорианский календарь. По этой причине католическая церковь и протестантские церкви (которые следуют за григорианским календарем) празднуют Пасху на другую дату, от восточной и восточной ортодоксальности (которая следует за календарем Юлиана). Это был дрейф 21 марта от наблюдаемого равноденствия, который привел к григорианской реформе календаря , чтобы вернуть их в линию.

Фон

Пасха отмечает воскресение Иисуса , которое, по мнению христиан, произошло на третий день (включительно) после начала Пасхи . В еврейском лун -календаре Пасха начинается в Сумерках на 14 -й день Нисана . ^{[ 9 ]}^{[ 10 ]} Нисан - первый месяц весны в северном полушарии , а 14 -й, соответствующий полнолуние. К 2 веку многие христиане решили соблюдать Пасху только в воскресенье. ^{[ 11 ]} Еврейский календарь не имеет простых отношений с христианскими календарями : он респинхронизируется с солнечным годом, интеркалируя прыжок в месяц каждые два или три года, до Лунного Нового года на 1 Нисане . Более поздние евреи приняли цикл мотонического цикла для прогнозирования будущих интеркаляций .

Возможным следствием этой интеркаляции является то, что 14 Нисан может произойти до равноденствия, которое некоторые христиане третьего века считали неприемлемым (это не может произойти в фиксированном календаре, используемом сегодня). ^{[ 12 ]} Следовательно, было решено отделить датировку Пасхи от еврейского календаря, идентифицируя первую полнолуние после мартовского равноденствия. К моменту Первого Совета Никей (325 г. н.э.) Церковь Александрии назвала 21 марта церковной датой для равноденствия, независимо от фактического астрономического наблюдения. В 395 году Феофил опубликовал таблицу дат будущего для Пасхи, подтвердив александрийские критерии. ^{[ 13 ]} После этого компьютер будет процедурой определения первого воскресенья после первого церковного полнолуния, падающего 21 марта или после этого.

История

Самые ранние известные римские таблицы были разработаны в 222 году Ипполитом Рима на основе восьмилетних циклов. Затем в Риме были введены 84-летние столы в Риме в конце 3-го века. ^{[ А ]} Несмотря на то, что процесс, основанный на 19-летнем цикле мотинического цикла, был впервые предложен епископом Анатолиусом Лаодичеи около 277, эта концепция не полностью охватила до тех пор, пока александрийский метод не стал авторитетным в конце 4-го века. ^{[ B ]}

Александрийский компьютер был преобразован из александрийского календаря в джулианский календарь в Александрии около 440, в результате чего пасхальная таблица (приписываемой Папе Сирилу из Александрии ), охватывающей 437 до 531 года. ^{[ 16 ]} Эта пасхальная таблица была источником, который вдохновил Дионисиус Эксигус , который работал в Риме с 500 до 540, ^{[ 17 ]} чтобы построить его продолжение в форме его знаменитого пасхального стола, охватывающего годы с 532 по 616. ^{[ 18 ]} Дионисий представил христианскую эру (подсчитывая годы из воплощения Христа), опубликовав эту новую пасхальную таблицу в 525. ^{[ 19 ]}^{[ C ]}

Модифицированный 84-летний цикл был принят в Риме в первой половине 4-го века. Викториус Аквитейн попытался адаптировать александрийский метод к римским правилам в 457 году в виде 532-летней таблицы, но он внес серьезные ошибки. ^{[ 20 ]} Эти викторианские таблицы использовались в Галлии (ныне Франция) и Испании до тех пор, пока они не были вытеснены дионисийскими таблицами в конце 8 -го века.

Столы Дионисия и Викториуса противоречат тем, которые традиционно используются на Британских островах. Британские таблицы использовали 84-летний цикл, но ошибка заставила полные луны падать слишком рано. ^{[ 21 ]} Расхождение привело к сообщению о том, что королева Эанфлд в системе Диониса - постилась в ее пальмовое воскресенье, в то время как ее муж Освуу , король Нортумбрии, пировал в его пасхальное воскресенье. ^{[ 22 ]}

В результате ирландского синода Маг-Ллен в 630 году южный ирландский стал использовать таблицы Дионисиан, ^{[ 23 ]} и северный английский последовал его примеру после Синода Уитби в 664 году. ^{[ 24 ]}

Расчет Дионисиан был полностью описан Беде в 725 году. ^{[ 25 ]} Возможно, он был принят Карл Великим для французской церкви еще в 782 годах от Alcuin , последователя Беде. Dionysian/Bedan Компьюс оставался в использовании в Западной Европе до реформы григорианского календаря, и остается в использовании в большинстве восточных церквей, включая подавляющее большинство восточных православных церквей и не-хальцедонских церквей . ^{[ 26 ]} Единственная восточная ортодоксальная церковь, которая не следует за системой, - это финская православная церковь, которая использует григорианскую.

Отклонившись от александрийцев в 6 -м веке, церкви за восточной границей бывшей Византийской империи, включая ассирийскую церковь Востока , ^{[ 27 ]} Теперь празднуйте Пасху в разные даты из восточных православных церквей четыре раза каждые 532 года. ^{[ Цитация необходима ]}

Помимо этих церквей на восточных полосах Римской империи, к десятым веку приняли Александрийскую Пасху, которая по -прежнему разместила весеннее равноденствие 21 марта, хотя Беде уже отметил свой дрейф в 725 16 -й век. ^{[ D ]} Хуже того, отплаченная луна, которая использовалась для вычисления Пасхи, была зафиксирована в Джулианском году 19-летним циклом. Это приближение создавало ошибку в один день каждые 310 лет, поэтому к 16 -м веку лунный календарь вышел из фазы с настоящей луной на четыре дня. Грегорианская Пасха использовалась с 1583 года Римско -католической церковью и была принята большинством протестантских церквей между 1753 и 1845 годами.

Немецкие протестантские государства использовали астрономическую Пасху между 1700 и 1776 годами, основанные на рудольфиновых таблицах Йоханнеса Кеплера , которые, в свою очередь, основывались на астрономических позициях Солнца и Луны, наблюдаемых Тихо Брахе на его Ураниборгской обсерватории на острове Вен , в то время как Шведен Использовал его с 1739 по 1844 год. Эта астрономическая Пасха была воскресеньем после мгновения полной луны, который был после весеннего равноденствия Мгновенное использование времени Uraniborg ( TT + 51 ^м) Тем не менее, это было отложено на одну неделю, если это воскресенье было еврейской датой Nisan 15, первого дня пасхальной недели, рассчитанной в соответствии с современными еврейскими методами. ^{[ 29 ]}

Это правило Nisan 15 повлияло на два шведских года, 1778 и 1798 гг., На то, что вместо недели до Грегорианской Пасхи было отложено на одну неделю, поэтому они были в то же воскресенье, что и Григорианская Пасха. Астрономическая Пасха Германии была за неделю до Григорианской Пасхи в 1724 и 1744 годах. ^{[ 29 ]} Астрономическая Пасха Швеции была за неделю до Григорианской Пасхи в 1744 году, но через неделю после этого в 1805, 1811, 1818, 1825 и 1829 годах. ^{[ 29 ]}

Две современные астрономические пасхи были предложены, но никогда не использовались ни одной церковью. Первый был предложен в рамках пересмотренного календаря Джулиана в Синоде в Константинополе в 1923 году, а второй был предложен Всемирным советом церквей 1997 года в 1997 году в 1997 году. Оба использовали то же правило, что и немецкие и шведские версии, но использовались современные астрономические расчеты и Иерусалима время ( TT + 2 ^час 21 ^м) без правила Нисана 15. Версия 1923 года поставила бы астрономическую Пасху за месяц до Григорианской Пасхи в 1924, 1943 и 1962 годах, но через неделю после этого в 1927, 1954 и 1967 годах. ^{[ 30 ]} Версия 1997 года поместила бы астрономическую Пасху в то же воскресенье, что и Грегорианская Пасха на 2000–2025 гг. За исключением 2019 года, когда это было бы месяцем ранее. ^{[ 31 ]}

Теория

Пасхальные циклы группируются дни в лунные месяцы, которые длится 29 или 30 дней. Есть исключение. Месяц, заканчивающийся в марте, обычно составляет 30 дней, но если 29 февраля висотного года попадает в него, он содержит 31. Поскольку эти группы основаны на лунном цикле , в течение длительного времени средний месяц в лунном календаре - очень Хорошее приближение синодического месяца , который составляет 29,530 59 дней. ^{[ 32 ]}

В лунный год существует 12 синодических месяцев, на общей сложности 354 или 355 дней. Лунный год примерно на 11 дней короче календарного года, который составляет 365 или 366 дней. В эти дни, когда солнечный год превышает лунный год, называются epacts ( греческий : ἐπακταὶ ἡμέραι , Transit. Épaktai Hēmérai , Lit. «Интеркальные дни»). ^{[ 33 ]}^{[ 34 ]}

Необходимо добавить их в день солнечного года, чтобы получить правильный день в лунном году. Всякий раз, когда Epact достигает или превышает 30, в лунный календарь должен быть выведен дополнительный интеркальный месяц (или эмболистский месяц) 30 дней: тогда 30 должны быть вычтены из Epact. Charles Wheatly предоставляет подробную информацию:

"Таким образом, начиная с года с марта (потому что это был древний обычай), они разрешили тридцать дней для Луны [окончания] в марте, и двадцать девять для этого [окончания] в апреле; и тридцать в мае и двадцать девять Для июня и т. Д. Согласно старым стихам:

Я разделяю Луну Пари, они, кажется, являются членом Императора;
В котором заканчивается ежемесячный понедельник.

«В течение первого, третьего, пятого, седьмого, девятого и одиннадцатого месяцев, которые называются менструациями Impares или неравными месяцами, имеют свои луны в соответствии с расчета по тридцать дней каждый, которые, следовательно, называются Pares Lunae , или равные луны: но Второй, четвертый, шестой, восьмой, десятый и двенадцатый месяц, которые называются менструациями Pares , или равны месяцам, имеют свои луны, но двадцать девять дней каждый, которые называются Имплектрирует Луна , или неравные луны ».
- пшеничный 1871 , с. 44

Таким образом, лунный месяц принял имя Джулианского месяца, в котором он закончился. Девятнадцатилетний цикл мотонического цикла предполагает, что 19 тропических лет составляют 235 синодических месяцев. Таким образом, через 19 лет лунные должны падать так же в солнечные годы, и ePacts должны повторяться. В течение 19 лет EPACT увеличивается на 19 × 11 = 209 ≡ 29 ( мод 30) , а не 0 (мод 30) . То есть 209, разделенные на 30 листьев оставшихся из 29 вместо того, чтобы быть кратным 30. Это проблема, если компенсация выполняется только путем добавления месяцев 30 дней. ^{[ E ]} Таким образом, через 19 лет EPACT должен быть исправлен на один день, чтобы цикл повторил. Это так называемый Saltus Lunae («прыжок луны»). Джулианский календарь обрабатывает его путем сокращения продолжительности лунного месяца, который начинается 1 июля за последний год цикла до 29 дней. Это делает три последовательных 29-дневных месяца. ^{[ f ]}

Сальтус . и семь дополнительных 30-дневных месяцев были в значительной степени скрыты, находясь в точках, где джулианские и лунные месяцы начинаются примерно в то же время Дополнительные месяцы начались 1 января (3 года), 2 сентября (5), 6 марта (8), 3 января (11), 31 декабря (13), 1 сентября (16) и 5 марта (19). ^{[ 35 ]}^{[ 36 ]} Номер последовательности года в 19-летнем цикле называется « Золотое число » и дается формулой

GN = ( Y MOD 19) + 1

То есть год y в христианской эпохе разделен на 19, а остальная часть плюс 1 - золотое число. (В некоторых источниках указывается, что вы добавляете 1, прежде чем взять остаток; в этом случае вам необходимо рассматривать результат 0 как золотой номер 19. В формуле выше мы сначала взяли остаток, а затем добавим 1, поэтому такая корректировка не требуется .) ^{[ G ]}

Циклы 19 лет не столько же, как и у них четыре или пять прыжков. Но период в четырех циклах, 76 лет ( каллиппический цикл ), имеет длину 76 × 365 + 19 = 27 759 дней (если он не пересекает дивизию столетия). В этот период 235 × 4 = 940 лунных месяцев, поэтому средняя длина составляет 27759 / 940 или около 29,530851 дня. Существует 76 × 6 = 456 обычных номинальных 30-дневных лунных месяцев и одинаковое количество обычных номинальных 29-дневных месяцев, но с 19 из них удлинено на день в дни прыжков, плюс 24 интеркалированных месяца 30 дней и четырех интеркалированных месяцев 29 дней. Поскольку это длиннее истинной длины синодического месяца, около 29,53059 дней, рассчитанная полная луна Пасхаля станет позже и позже по сравнению с астрономическим полнолунием, если только исправление не сделано, как в григорианской системе (см. Ниже).

Пасхальный или пасхальный месяц-первый в году, который проведет свой четырнадцатый день (его формальный полнолуние ) 21 марта или после. Пасха - это воскресенье после 14 -го дня (или, говоря то же самое, воскресенье в течение третьей недели). Пасхальный лунный месяц всегда начинается с даты в 29-дневный период с 8 марта по 5 апреля включительно. Следовательно, его четырнадцатый день всегда падает на дату с 21 марта по 18 апреля, включительно (в григорианском или юлианском календаре, для западной и восточной системы, соответственно), а затем в следующее воскресенье обязательно падает на дату в диапазоне 22 марта по 25 апреля включительно. Однако в западной системе Пасха не может упасть 22 марта в течение 300-летнего периода 1900-2199 (см. Ниже). В солнечном календаре Пасха называется подвижным праздником , поскольку его дата варьируется в пределах 35-дневного диапазона. Но в лунном календаре Пасха всегда является третьим воскресеньем в пасхальном лунном месяце, и она не более «подвижна», чем любой праздник, который зафиксирован в определенный день недели и недели в течение месяца, например, как День Благодарения .

Табличные методы

Григорианская реформа компьютера

Поскольку реформирование компьютера была основной мотивацией для введения григорианского календаря соответствующая компьютерная методология. в 1582 году, наряду с новым календарем была введена ^{[ H ]} Общий метод работы был дан Клавием в шести канонах (1582), и в его объяснении последовало полное объяснение (1603). ^{[ 37 ]}

Пасхальное воскресенье - воскресенье после даты полной луны Пасхаля. Дата полной луны Пасхаля - это церковная дата полнолуния 21 марта или после или после этого. Грегорианский метод получает даты полной луны пасхальной полной луны, определяя epact для каждого года. ^{[ 38 ]} EPACT может иметь значение от * (0 или 30) до 29 дней. Это возраст луны в дни (то есть лунная дата) 1 января, сокращенного на один день. В своей книге «Пасхальный компьютер и происхождение христианской эры» неверно ^{[ Согласно кому? ]} утверждает: «Теоретически, epact 30 = 0 представляет собой новолуние в ее соединении с солнцем. Эпакт 1 представляет собой теоретическую первую видимость первого полумесяца Луны. Это с этого момента, как первый день, когда четырнадцатый день Луна считается ». ^{[ 39 ]}

Четырнадцатый день лунного месяца считается днем полнолуния . ^{[ 40 ]} Это день лунного месяца, когда момент оппозиции («Полнолуние»), скорее всего, упадет. «Новолуние», скорее всего, станет видимым (как стройный полумесяц на западном небе после захода солнца) в первый день лунного месяца. Соединение Солнца и Луны («Новолуние»), скорее всего, упадет в предыдущий день, который является 29-м днем «пустого» (29-дневного) месяца и 30 «Полный» (30 дней) месяц.

Исторически из -за того, что дата полной луны пасхальной полной луны была обнаружена из его номера последовательности в цикле мотинического цикла, называемого золотым номером , которое повторяет лунную фазу 1 января каждые 19 лет. ^{[ 41 ]} Этот метод был изменен в григорианской реформе, потому что табличные даты проходят синхронизации с реальностью примерно через два столетия, но из метода EPACT можно построить упрощенную таблицу, которая имеет достоверность от одного до трех веков. ^{[ 42 ]}^{[ 43 ]}

Epacts для текущего велосипедного цикла, который начался в 2014 году, являются:

Год	2014	2015	2016	2017	2018	2019	2020	2021	2022	2023	2024	2025	2026	2027	2028	2029	2030	2031	2032
Золотой число	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
Эпакта ^{[ я ]}	29	10	21	2	13	24	5	16	27	8	19	*	11	22	3	14	25	6	17
Пасхал полная луна дата ^{[ 44 ]}	14 Апрель	3 Апрель	23 Маршировать	11 Апрель	31 Маршировать	18 Апрель	8 Апрель	28 Маршировать	16 Апрель	5 Апрель	25 Маршировать	13 Апрель	2 Апрель	22 Маршировать	10 Апрель	30 Маршировать	17 Апрель	7 Апрель	27 Маршировать

Как видно, дата полной луны Пасхала в определенном году обычно на 11 дней раньше, чем в предыдущем году, либо 19 дней спустя. Исключения состоит в том, что в 1, 6 и 17 годах цикла дата - всего через 18 дней, а в 7 и 18 годах - всего на 10 днях раньше, чем в предыдущем году. В восточной системе (см. Ниже) пасхальная полнолуние обычно через четыре дня. Прошло 34 дня спустя, за пять из 19 лет и 5 дней спустя в 6 и 17 годах, потому что в те годы григорианская система ставит пасхальную полнолуние на день раньше, чем обычно, чтобы сохранить Пасху перед 26 апреля, как объяснено ниже. В 2100 году разница увеличится на один день.

Epacts используются для поиска дат новолуния следующим образом: Запишите таблицу всех 365 дней в году (дневной день игнорируется). Затем пометьте все даты римским цифровым подсчетом вниз, от «*» (0 или 30), «xxix» (29), вплоть до «i» (1), начиная с 1 января, и повторите это до конца год. Однако во время каждой секунды такого периода подсчитывается всего 29 дней и помешайте дату XXV (25) также XXIV (24). Поэтому обращайтесь к 13 -м периоду (последние одиннадцать дней) и назначайте этикетки «XXV» и «XXIV» на последовательные даты (26 и 27 декабря соответственно). ^{[ 45 ]}

Добавьте этикетку «25» в даты, которые имеют «XXV» в 30-дневные периоды; Но в 29-дневные периоды (которые имеют «xxiv» вместе с «XXV») добавьте метку «25» к дате с «XXVI». Распределение продолжительности месяцев и длины циклов ePACT таково, что каждый гражданский календарный месяц начинается и заканчивается тем же ярлыком ePACT, за исключением февраля, и, можно сказать, для августа, которая начинается с двойной метки » xxv "/" xxiv ", но заканчивается единственной меткой" xxiv ". Эта таблица называется календарием . Церковные новые луны для любого года - это те даты, когда введен epact за год. ^{[ 45 ]}

Если Epact для года, например, 27, то в каждую дату этого года есть церковная новая луна , на которой есть этикетка epact «XXVII» (27). Если epact составляет 25, то есть осложнение, введенное так, чтобы церковное новолуние не упало в одну и ту же дату дважды во время цикла мотонического цикла. Если в силе Epact в силе включает EPACT 24 (как и цикл, используемый с 1900 года и до 2199), то 4 апреля Epact из 25 ставит церковную новую луну (имея этикетку «25»), в противном случае это в апреле 5 (с меткой «XXV»). ^{[ 45 ]}

Эпакт 25, дающий 4 апреля, может произойти только в том случае, если золотое число превышает 11. В этом случае это будет 11 лет после года с epact 24. Так, например, в 1954 году золотое число было 17, epact было 25 Церковное новолуние было рассчитано 4 апреля, полная луна 17 апреля. Пасха была 18 апреля, а не 25 апреля, как и в противном случае, например, в 1886 году, когда золотое число было 6. Эта система автоматически интеркалирует семь месяцы на велосипед.

Забегайте все даты в таблице буквами «A» для «G», начиная с 1 января и повторите до конца года. Если, например, первое воскресенье года состоится 5 января, у которого есть письмо «E», то каждая дата с письмом «E» - это воскресенье в этом году. Затем «E» называется доминительным письмом за этот год - от Dies Dominica (латынь на «День Господень»). Доминическая буква циклов в одну позицию каждый год. Через годы после 24 февраля воскресенье падают на предыдущее письмо цикла, так что в лепешках было два доминических буквах: первые для ранее, второй для дня прыжков.

На практике, с целью расчета Пасхи, это не должно быть сделано в течение всех 365 дней в году. Для Epacts март выходит точно так же, как январь, поэтому не нужно рассчитать январь или февраль. Чтобы избежать необходимости рассчитать доминические письма за январь и февраль, начните с D на 1 марта. Вам нужны epacts только с 8 марта по 5 апреля. Это приводит к следующей таблице:

Таблица из Швеции, чтобы найти дату Пасхи 1140–1671 в соответствии с календарем Юлиана . Каждый столбец соответствует периоду 28 лет. Обратите внимание на руны, используемые в качестве произвольных символов.

Этикетка	Маршировать	Дл	Апрель	Дл
*	1	Дюймовый
xxix	2	И	1	Глин
XXVIII	3	Фон	2	А
XXVII	4	Глин	3	Беременный
XXVI	5	А	4	В
25	6	Беременный	4	В
XXV	6	Беременный	5	Дюймовый
XXIV	7	В	5	Дюймовый
XXIII	8	Дюймовый	6	И
XXII	9	И	7	Фон
XXI	10	Фон	8	Глин
XX	11	Глин	9	А
xix	12	А	10	Беременный
XVIII	13	Беременный	11	В
XVII	14	В	12	Дюймовый
XVI	15	Дюймовый	13	И
XV	16	И	14	Фон
XIV	17	Фон	15	Глин
xiii	18	Глин	16	А
xii	19	А	17	Беременный
xi	20	Беременный	18	В
х	21	В	19	Дюймовый
IX	22	Дюймовый	20	И
VIII	23	И	21	Фон
VII	24	Фон	22	Глин
мы	25	Глин	23	А
v	26	А	24	Беременный
IV	27	Беременный	25	В
iii	28	В	26	Дюймовый
II	29	Дюймовый	27	И
я	30	И	28	Фон
*	31	Фон	29	Глин
xxix			30	А

В качестве примера, если ePACT составляет 27 (xxvii), церковная новая луна падает на каждую дату, помеченную XXVII . Церковная полнолуние падает 13 дней спустя. Из таблицы выше, это дает новолуние 4 марта и 3 апреля, и поэтому полнолуние 17 марта и 16 апреля. Затем Пасхальный день - первое воскресенье после первой церковной полной луны 21 марта или после или после этого. (Это определение использует «21 марта или после или после этого, чтобы избежать двусмысленности с историческим значением слова« после ». На современном языке эта фраза просто означает« после 20 марта ». Определение« на или после или после или после или после этого часто бывает Неправильно сокращено до «после 21 марта» в опубликованных и веб-статьях, что приводит к неправильным пасхальным датам.) В примере эта пасхальная полная луна - 16 апреля. Если доминическое письмо E, то пасхальный день - 20 апреля.

Метка « 25 » (в отличие от «XXV») используется следующим образом: В рамках цикла мотонического цикла годы, которые находятся в 11 лет, имеют эпакты, которые различаются на один день. Месяц, начиная с даты, с надписью XXIV и XXV, написанные бок о бок, составляет 29 или 30 дней. Если Epacts 24 и 25 происходят в пределах одного мотонического цикла, то новые (и полные) луны будут падать на одни и те же даты в течение этих двух лет. Это возможно для настоящей луны ^{[ J ]} но неэлеган в схематическом лунном календаре; Даты должны повторяться только через 19 лет. Чтобы избежать этого, в годы, которые имеют epacts 25 и с золотым номером, превышающим 11, присвоованная новолуние падает на дату с меткой 25, а не XXV . Там, где этикетки 25 и XXV вместе, нет проблем, так как они одинаковы. Это не переносит проблему к паре «25» и «XXVI», потому что самый ранний Epact 26 может появиться в 23 -м году, который длится всего 19 лет: существует салтус -лун между ними Луны падают на отдельные даты.

Грегорианский календарь имеет коррекцию в тропический год, отбросив три вировых дня за 400 лет (всегда за вековой год). Это коррекция к длине тропического года, но не должно влиять на мотиническую связь между годами и лунными. Следовательно, EPACT компенсируется этому (частично - см. Epact ), вычитая один в эти столетия. Это так называемая солнечная коррекция или «солнечное уравнение» («уравнение», используемое в его средневековом смысле «коррекции»).

Тем не менее, 19 некорректированных юлианских лет чуть больше 235 Лун. Разница накапливается до одного дня примерно через 308 лет, или 0,00324 дня в году. В одном цикле EPACT уменьшается из -за солнечной коррекции на 19 × 0,0075 = 0,1425 в среднем, поэтому цикл эквивалентен 235–0,1425 / 30 = 234,99525 месяца, тогда как существует 19 × 365,2425 / 29,5305889 ≈ 234,97261 месяцев. Разница в 0,002011 синодических месяцев в 19-летний цикл, или 0,003126 дней в году, требует случайной лунной коррекции в EPACT. В григорианском календаре это делается путем добавления 1 восемь раз за 2500 (григорианских) лет (чуть более 2500 × 0,003126, или около 7,8), всегда за столетие года: это так называемая лунная коррекция (исторически называемая » лунное уравнение »). Первый был применен в 1800 году, следующий в 2100 году и будет применяться каждые 300 лет, за исключением интервала 400 лет между 3900 и 4300, что запускает новый цикл. Во время реформы эпакты были изменены на 7, хотя 10 дней были пропущены, чтобы сделать трехдневную коррекцию в сроки новых лун. ^{[ 45 ]}

Солнечные и лунные коррекции работают в противоположных направлениях, а в течение некоторых веков (например, 1800 и 2100) они отменяют друг друга. Результатом является то, что григорианский лунный календарь использует таблицу EPACT, которая действительна в течение периода от 100 до 300 лет. Таблица EPACT, перечисленная выше, действительна для периода с 1900 по 2199.

Как объяснено ниже, даты пасхального повторения через 5 700 000 лет, и в течение этого периода средняя продолжительность церковного месяца составляет 2 081 882 250/70 499,183 ≈ 29,5305869 дней,, ^{[ 46 ]} что отличается от текущей фактической средней длины лунного лун (29 5305889 D: см. Лунный месяц#Синодический месяц ) на 6 -й цифре после десятичной точки. Это соответствует ошибке менее чем за день в фазе Луны более 40000 лет, но на самом деле изменяется продолжительность дня (как и длина синодического месяца), поэтому система не является точной в течение таких периодов Полем См. Статью ΔT (хронометрирование) для получения информации о кумулятивном изменении длины дня.

Подробности

Этот метод вычисления имеет несколько тонкостей:

У любого остального лунного месяца всего 29 дней, поэтому в один день должно быть два (из 30) этикетки EPACT. Причиной перемещения этикетки epact «XXV/25», а не любой другой, представляется следующим: согласно Дионисиусу (в его вступительном письме Петронеусу), Никейский совет, на власти Евсевия , установил, что первый месяц Церковного лунного года (Пасхальный месяц) должен начаться с 8 марта по 5 апреля включительно, а 14 -й день падает с 21 марта и 18 апреля включительно, таким образом, охватывая период (только) 29 дней. Новолуние 7 марта, у которого есть лейбл Epact «XXIV», имеет свой 14 -й день (полнолуние) 20 марта, что слишком рано (не 20 марта). Итак, годы с эпактом "xxiv", если бы лунный месяц, начиная с 7 марта Еще в 26 апреля. В юлианском календаре последняя дата Пасхи была 25 апреля, и григорианская реформа сохранила этот предел. Таким образом, Paschal Full Moon должна упасть не позднее 18 апреля и новолуние 5 апреля, у которой есть этикетка Epact «XXV». Поэтому 5 апреля должны иметь свои двойные этикетки ePACT «XXIV» и «XXV». Тогда Epact "XXV" должен рассматриваться по -разному, как объяснено в параграфе выше.

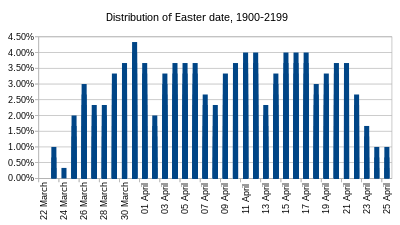
Распределение частот на дату Пасхи плохо определено, потому что каждые 100-300 лет отображение от золотого числа к изменению EPACT и долгосрочное распределение частот действительнее только в течение миллионов лет (см. Ниже),), тогда как система, безусловно, не будет использоваться так долго. Нынешнее картирование, действительное с 1900 по 2199, дает пасхальные даты с очень различными частотами. 22 марта никогда не может произойти, тогда как 31 марта происходит 13 раз за этот 300-летний промежуток.

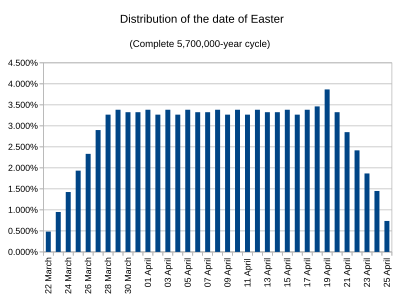
Если кто-то задает вопрос о том, каким будет распределение в долгосрочной перспективе, то есть за весь 5,7 миллиона лет, после чего даты повторяются, это распределение можно найти довольно просто и сильно отличается от распределения В период с 1900 по 2199 или даже распределение за период до реформы до сих пор. Дата Пасхи в данный год зависит только от эпакта в течение года, его золотого числа и его доминического письма , которое сообщает нам, какие дни являются воскресеньями (точнее, доминическое письмо за часть года после февраля, какое отличается в лечебных годах из письма за январь и февраль). (Золотое число имеет значение только тогда, когда ePact составляет 25 лет, как объяснялось ранее.) Если мы пойдем вперед на 3230 000 лет с определенного года, мы обнаружим год в той же точке в 400-летнем григорианском цикле и с тем же золотым числом, но с эпактом, дополненным 1. Следовательно, в долгосрочной перспективе все тридцать эпактов одинаково вероятны. С другой стороны, доминические буквы не все имеют одинаковую частоту - годы с буквами A и C (в конце года) встречаются 14% времени каждый, E и F встречаются в 14,25% случаев, и и B, D и G встречаются в 14,5% случаев. Принимая во внимание осложнение, связанное с Epact 25, это дает распределение, показанное на втором графике. 19 апреля является наиболее распространенным, потому что, когда epact - 25, церковная полнолуние падает 17 или 18 апреля (в зависимости от золотого числа), и он также подпадает на эти даты, когда epact составляет 26 или 24, соответственно. Есть семь дней, на которые может упасть полная луна, в том числе 17 апреля и 18 апреля, чтобы Пасха была 19 апреля (это также последняя возможная пасхальная дата, когда церковная полнолуние может упасть в субботу, как апрель 18 - последняя дата церковного полнолуния, в которой Пасха на следующий день, если церковная полнолуние в субботу). ^{[ 45 ]} Как следствие, 19 апреля - это дата, когда Пасха чаще всего попадает в григорианский календарь, примерно в 3,87% лет. 22 марта наименее частые, с 0,48%. ^{[ 47 ]}^{[ 45 ]}

Связь между лунным и солнечным календарным датом становятся независимыми от схемы Дня скачка за солнечный год. В основном григорианский календарь все еще использует календарь Джулиана с височным днем каждые четыре года, поэтому в мотиническом цикле 19 лет 6 940 или 6939 дней с пятью или четырьмя видальными днями. Теперь лунный цикл имеет только 19 × 354 + 19 × 11 = 6935 дней . Не маркируя и подсчитывая прыжок с номером epact, но, имея следующую новолуние на ту же дату календаря, что и без дневного дня, нынешнее лунное продливается на один день, ^{[ k ]} И 235 Лунных охватывают столько дней, сколько 19 лет (до тех пор, пока 19 лет не включают «солнечную коррекцию», как в 1900 году). Таким образом, бремя синхронизации календаря с луной (точность средней скорости) смещается в солнечный календарь, который может использовать любую подходящую схему интеркаляции, все это при предположении, что 19 солнечных лет = 235 Лун (создание долгосрочной неточности, если не исправлено «лунной коррекцией»). Следствием этого является то, что уплаченный век Луны может быть отключен к дню, а также что луны, которые содержат прыжковой день, могут длиться 31 день, что никогда не произойдет, если будет соблюдать реальную луну (краткосрочные неточности). Это цена регулярного соответствия солнечному календарю.

С точки зрения тех, кто, возможно, захочет использовать григорианский пасхальный цикл в качестве календаря на весь год, в григорианском лунном календаре есть некоторые недостатки ^{[ 48 ]} (Хотя они не влияют на пасхальный месяц и дату Пасхи):

Лунные 31 (а иногда и 28) дней происходят.
Если год с Golden Number 19 происходит EPACT 19, то последнее церковное новолуние выпадает 2 декабря; Следующее будет должно быть должно быть сделано 1 января. Однако в начале Нового года салтус -лун увеличивает ePact другим подразделением, а новолуние должно было произойти в предыдущий день. Так что новолуние пропускается. Календарий учитывает это , Missale Romanum назначив Epact Label «19» вместо «XX» до 31 декабря такого года, что делает эту дату новолуние. Это происходило каждые 19 лет, когда вступил в силу первоначальную таблицу григорианского эпакта (в последний раз в 1690 году), а затем происходит в 8511.
Если epact года составляет 20 лет, церковная новая луна падает 31 декабря. Если этот год падает до года в столетие, то в большинстве случаев, солнечная коррекция уменьшает эпакт на новый год на один: полученный epact «*» означает, что еще одна церковная новая луна считается 1 января. Таким образом, формально, Лунное однодневное прошло. Следующее происходит в 4199–4200.
Другие пограничные случаи происходят (много) позже, и если правила соблюдаются строго, и эти случаи не рассматриваются специально, они генерируют последовательные даты новолуния, которые составляют 1, 28, 59 или (очень редко) с интервалом 58 дней.

Тщательный анализ показывает, что благодаря тому, как они используются и исправлены в григорианском календаре, эпакты на самом деле ⁠ 1/30 ⁠ дней . лунного, а не полных Смотрите Epact для обсуждения.

Солнечные и лунные коррекции повторяются после 4 × 25 = 100 веков. В этот период EPACT для данного золотого числа изменяется в общей сложности на -1 × ⁠ 3 / 4 ⁠ × 100 + 1 × ⁠ 8/25 . × 100 = −43 ⁠ ≡ 17 мод 30 требуется 100 × 30 = 3000 веков Это является ярким для 30 возможных epacts, поэтому до повторения отображений ePACT ; и 3000 × 19 = 57 000 веков до того, как они повторяются на том же золотом номере. Не очевидно, сколько церковных лун в этом 5,7 млн. Человек подсчитываются. Мотинические циклы составляют (5 700 000/19) × 235 = 70 500 000 лун. Но есть чистые коррекции -43 × (5 700 000/10 000) поправки к ePacts, которые делятся на 30, что составляет на коррекцию -817 лунных, в общей сложности 70 499 183 лун. Это число, по -видимому, было впервые получено Магнусом Георгом Паукером в 1837 году. ^{[ 49 ]} Это также упоминается в главе о календарях (стр. 744) в морском альманаке 1931 года. ^{[ 50 ]} и в объяснительном дополнении 1992 года (стр. 582). ^{[ 51 ]}^{[ L ]} Таким образом, григорианские пасхальные даты повторяются в том же порядке только после 5 700 000 лет, 70 499 183 лун или 2 081 882 250 дней; Средняя длина лунна составляет 2 081 882 250/70 499,183 = 29,53058690 дней. Конечно, календарь должен быть скорректирован через несколько тысячелетий из -за изменений в длине тропического года, синодического месяца и дня.

Это поднимает вопрос, почему григорианский лунный календарь имеет отдельные солнечные и лунные исправления, которые иногда отменяют друг друга. Первоначальная работа Лилиуса не была сохранена, но его предложение было описано в Compendium novae rationis restituendi Kalendarium , распространяемое в 1577 году, в котором объясняется, что созданная им система коррекции должна была стать совершенно гибким инструментом в руках будущих календарных реформаторов,, реформировщики календаря,, реформировщики календаря,, он была совершенно гибким инструментом в руках будущих календарных реформаторов, Поскольку солнечный и лунный календарь может быть исправлен без взаимного вмешательства. ^{[ 52 ]} Пример этой гибкости был предоставлен посредством альтернативной интеркаляционной последовательности, полученной из теорий Коперника, наряду с соответствующими поправками этаксирования. ^{[ 53 ]}

«Солнечные коррекции» приблизительно отменили влияние григорианских модификаций на прыжковые дни солнечного календаря на лунный календарь: они (частично) возвращают цикл Epact обратно к первоначальному мотоническому отношению между юлианским годом и лунным месяцем. Неоплачиваемое несоответствие между солнцем и луной в этом основном 19-летнем цикле затем корректируется каждые три или четыре столетия с помощью «лунной коррекции» к epacts. Тем не менее, коррекции эпакта возникают в начале григорианских веков, а не Джулиана столетия, и, следовательно, оригинальный цикл Джулиана Мантонического цикла не полностью восстановлен.

В то время как чистый 4 × 8 - 3 × 25 = 43 вычитания эпакта могут быть распределены равномерно более 10 000 лет (как было предложено, например, Lichtenberg 2003 , стр. 45–76), если коррекции объединяются, то неточности двух Циклы также добавлены и не могут быть исправлены отдельно.

Соотношения (средних солнечных) дней в год и дни на лунное изменяются как из-за внутренних долгосрочных изменений в орбитах, так и из-за того, что вращение Земли замедляется из-за приливного замедления , поэтому параметры григорианцев становятся все более устаревшими.

Это влияет на дату равноденствия, но выяснилось, что интервал между равноденствий между северным полушарием) был довольно стабильным в течение исторических времен, особенно если они измеряются в среднем солнечном времени. ^{[ 54 ]}^{[ 55 ]}

Кроме того, дрейф в церковных лунах, рассчитанных по григорианским методам, по сравнению с истинными полными лунами, меньше, чем можно было бы ожидать, потому что увеличение длины дня почти точно компенсируется увеличением длины месяца, Поскольку приливное торможение передает угловой импульс вращения земли в орбитальный угловой импульс луны.

Значение Птолемея длины среднего синодического месяца, установленного вавилонянами в 4 -м веке, составляет 29 дней 12 часов 44 мин. ⁠3 + 1/3 ⁠ ( ; s см. Кидинну ) Текущее значение на 0,46 с меньше (см. Новолуние ). В тот же исторический промежуток времени длина среднего тропического года уменьшилась примерно на 10 с (все значения среднее время солнечно).

Британский календарный акт и книга общей молитвы

Часть раздела табличных методов выше описывает исторические аргументы и методы, с помощью которых католическая церковь была определена в нынешних датах пасхального воскресенья в конце 16 -го века. В Британии, где джулианский календарь тогда все еще использовался, было определено пасхальное воскресенье, с 1662 по 1752 год (в соответствии с предыдущей практикой), простым таблицей дат в англиканской книге общей молитвы (представленной актом единообразия 1662 ). Таблица была проиндексирована непосредственно золотым номером и воскресным письмом , которое (в пасхальной части книги) предполагалось, что уже известно.

Для Британской империи и колоний новая решимость даты пасхального воскресенья была определена тем, что сейчас называется Законом о календаре (новый стиль) 1750 года с его приложением. Метод был выбран для того, чтобы дать даты согласования с григорианским правилом, уже используемым в другом месте. Закон требовал, чтобы он был введен в книгу общей молитвы , и поэтому это общее англиканское правление. Первоначальный акт можно увидеть в британских законах в целом в 1765 году . ^{[ 56 ]} Приложение к закону включает определение: « Пасхальный день (от которого зависят остальные)-это всегда первое воскресенье после полной луны , на которой произойдет, или в следующем после двадцати первого дня марта . И если полная луна В воскресенье в воскресенье после воскресенья . » Впоследствии в Приложении используются термины «Пасхальная полнолуние» и «церковное полное луну», что дает понять, что они приближаются к настоящему полнолуние.

Метод весьма отличается от описанного выше в § Грегорианской реформе компьютера . В течение общего года один сначала определяет золотое число , а затем использует три таблицы, чтобы определить воскресную букву , «цифр» и дату полной луны Пасхаля, с которой следует дата пасхального воскресенья. Epact явно не появляется. Проще -простые таблицы могут использоваться в течение ограниченных периодов (например, 1900–2199), в течение которых Cypher (который представляет эффект солнечной и лунной коррекции) не меняется. Детали Клавиуса были использованы при строительстве метода, но они не играют последующей части его использования. ^{[ 57 ]}^{[ 58 ]}

JR Stockton показывает свой вывод эффективного компьютерного алгоритма, прослеживаемого таблицами в молитвенном книге и Законе о календаре (при условии, что описание того, как использовать таблицы, под рукой) и проверяет его процессы, вычисливая соответствующие таблицы. ^{[ 59 ]}

Джулианский календарь

Метод вычисления даты церковного полнолуния, который был стандартным для западной церкви до реформы григорианского календаря и до сих пор используется сегодня большинством восточных христиан , использовал некорректированное повторение 19-летнего целостного цикла в сочетании с Джулианский календарь. С точки зрения метода эпактов, обсуждаемых выше, он эффективно использовал одну таблицу epact, начиная с эпакта 0, который никогда не был исправлен. В этом случае EPACT был рассчитан на 22 марта, самую раннюю дату Пасхи. Это повторяется каждые 19 лет, поэтому с 21 марта по 18 апреля есть только 19 возможных дат.

Поскольку нет никаких исправлений, как и для григорианского календаря, церковная полная луна уходит от истинного полнолуния более чем на три дня в каждом тысячелетии. Это уже несколько дней спустя. В результате восточные церкви отмечают Пасху на неделю позже, чем западные церкви примерно в 44% случаев, и в тот же день около 30% случаев. (Восточная Паровая иногда происходит четыре или пять недель спустя, потому что календарь Юлиана находится на 13 дней позади григорианского в 1900–2099 годах, и поэтому григорианский пасхальный полнолуние иногда находится до Джулиана 21 марта.)

Номер последовательности года в 19-летнем цикле называется его золотым номером . Этот термин был впервые использован в компьютерной поэме Massa Compoti Александром де Вилла деи в 1200 году. Поздний писец добавил золотое число в таблицы, первоначально составленные Аббо Флери в 988 году.

Претензия католической церкви в Papal Bull Intersisimas 1582 года , которая обнародовала григорианский календарь, что он восстановил «Празднование Пасхи в соответствии с правилами, установленными ... Великим экуменическим советом Никей» ^{[ 60 ]} был основан на ложном требовании Дионисиуса Эстигуса (525), что «мы определяем дату Пасхального дня ... в соответствии с предложением, согласованным 318 отцами церкви в Совете в Никей». ^{[ 61 ]}

Первый Совет Никей (325), однако, не предоставил каких -либо явных правил для определения этой даты, а написал только «все наши братья на Востоке, которые ранее следили за обычаем евреев, отныне, чтобы отпраздновать упомянутый самый священный праздник Пасха в то же время с римлянами и самими собой [Церковью Александрии] и всеми, кто наблюдал Пасху с самого начала ». ^{[ 62 ]} Средневековый компьютер был основан на александрийском компьютере , которая была разработана Церковью Александрии в течение первого десятилетия 4 -го века с использованием александрийского календаря . ^{[ 63 ]}

Восточная Римская империя приняла его вскоре после 380 после конвертации компьютерного календаря. ^{[ 64 ]} Рим принял его где -то между шестым и девятым веками. Британские острова приняли его в восьмом веке, за исключением нескольких монастырей. ^{[ Цитация необходима ]} Франсия (вся Западная Европа, кроме Скандинавии (язычника), Британских островов, иберийского полуострова и южной Италии) приняла его в течение последней четверти восьмого века. ^{[ Цитация необходима ]}

Последний кельтский монастырь , чтобы принять его, Иона , сделал это в 716 году. ^{[ Цитация необходима ]} Последний английский монастырь, чтобы принять это, сделал это в 931 году. ^{[ Цитация необходима ]} Перед этими датами другие методы дали даты пасхального воскресенья, которые могут отличаться до пяти недель. ^{[ Цитация необходима ]}

Это таблица пасхальной полнолуние даты для всех юлианских лет с 931:

Золотой число	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
Пасхал полная луна Дата (Джулиан)	5 Апрель	25 Маршировать	13 Апрель	2 Апрель	22 Маршировать	10 Апрель	30 Маршировать	18 Апрель	7 Апрель	27 Маршировать	15 Апрель	4 Апрель	24 Маршировать	12 Апрель	1 Апрель	21 Маршировать	9 Апрель	29 Маршировать	17 Апрель
Пасхал полная луна Дата, 1900–2099, Григорианский календарь	18 Апрель	7 Апрель	26 Апрель	15 Апрель	4 Апрель	23 Апрель	12 Апрель	1 Может	20 Апрель	9 Апрель	28 Апрель	17 Апрель	6 Апрель	25 Апрель	14 Апрель	3 Апрель	22 Апрель	11 Апрель	30 Апрель
Пасхал полная луна Дата, Западный, 1900-2199 (Грегориан)	14 Апрель	3 Апрель	23 Маршировать	11 Апрель	31 Маршировать	18 Апрель	8 Апрель	28 Маршировать	16 Апрель	5 Апрель	25 Маршировать	13 Апрель	2 Апрель	22 Маршировать	10 Апрель	30 Маршировать	17 Апрель	7 Апрель	27 Маршировать

Как упоминалось ранее, эти пасхальные полные луны составляют 4, 5 или 34 дня позже, чем в западной системе, и примерно на три дня позже, чем астрономическая полнолуние. (Например, лунное затмение в апреле 2015 года было 4 апреля в григорианском календаре, или 22 марта в календаре Джулиана, но пасхальная полнолуние на этот год (Золотое число 2) было 25 марта в календаре Юлиана.) Всякий раз, когда там был Является ли лунная коррекция, различия между западным и восточным церковным лун 35 дней. Диапазон дат в григорианском календаре восточного пасхального полнолуния движется один день спустя каждый раз, когда будет коррекция солнечной энергии, поэтому с 2100 по 2199 годы он будет 5 апреля по 9 мая. В настоящее время существует пять лет за цикл, когда Восточный Пагает на несколько недель позже, чем западный, на золотых числах 3, 8, 11, 14 и 19. Это увеличится до шести раз за цикл в 2200 (добавление золотого числа 6) , до семи в 2300 (добавление золотого числа 17), затем вернитесь к шести в 2400 (лунная коррекция и без солнечная коррекция), вернемся к семи в 2500 и перейдите к восемью только в 2900 (добавление золотого числа 9). ^{[ Цитация необходима ]}

Пример расчета с использованием этой таблицы:

Золотое число для 1573 года составляет 16 ( 1573 + 1 = 1574 ; 1574 ÷ 19 = 82 остаток 16 ). Из таблицы Paschal Full Moon для Golden Number 16 - 21 марта. Из недели Таблица 21 марта - суббота. Пасхальное воскресенье - следующее воскресенье, 22 марта.

Таким образом, на дату церковного полнолуния церковного луна есть семь возможных пасхальных дат. Цикл воскресных букв, не повторяется через семь лет: из -за перерывов висотного дня каждые четыре года, полный цикл, в котором в будние дни повторяются в календаре одинаково, составляет 4 × 7 = 28 лет, солнечная батара цикл . Таким образом, пасхальные даты повторялись в том же порядке после 4 × 7 × 19 = 532 года. Этот пасхальный цикл также называется викторианским циклом после Викториуса Аквитайн, который представил его в Риме в 457 году.

Сначала известно, что он использовался Аннианом Александрии в начале 5 -го века. Это также иногда ошибочно называлось циклом Дионисиа , после того, как Дионисий Эмигюс , который подготовил пасхальные столы, которые начались в 532 году. Он, очевидно, не осознавал, что описанный он александрийский компьютер, который он описал, имел 532-летний цикл, хотя он понял, что его 95- Годовой таблица не была настоящим циклом. Почетный Бед (7 -й век), по -видимому, был первым, кто идентифицировал солнечный цикл и объяснил пасхальный цикл из цикла мотонического цикла и солнечного цикла.

В средневековой Западной Европе даты пасхальной полнолуния (14 нисан), указанных выше, можно было запомнить с помощью аллитеративного стихотворения на 19 строк на латыни: ^{[ 65 ]}^{[ 66 ]}

Девятый апрель Они знают, кто V

Octonae Calender Ассим дезами. я

В апреле Даже шесть МЫ

Девятый кватернал Для Pumpondio. II

Предмет Undene Они будут V

Четыре IDE поймать три раза. Iii

Первый из первого старый старый, МЫ

Четыре Дене Переплет на квадрате. IIII

Сепенас Идес Семь выберите VII

Старый старый календарь Сортуть три Iii

Денис Септенис Донант, как это. я

За день до Нонеса Кроме того, четыре IIII

девятый месяц календа отмечен на семи. VII

На IDES Пандитур пять V

Первый апреля выразить один. я

Для двенадцати преподавал четыре раза IIII

сформировать пятую Мы надеемся увидеть два. II

Кватерна календенды Пять этажей: V

Квинден постоянная Племя из вас присутствовало. Iii

Первая половина линии каждой строки дает дату пасхальной полнолуния из таблицы выше для каждого года в 19-летнем цикле. Вторая половина линии дает регулярное или буднее перемещение в будние дни дня Paschal Full Moon от одного года из параллельного или буднего дня 24 марта. ^{[ 67 ]} Регулярное регулярное количество повторяется в римских цифрах в третьей колонке.

«Парадоксальные» пасхальные даты

Из -за несоответствий между приближениями компьютерных расчетов времени среднего (северного полушария) словесного равноденствия и лунных фаз, а также истинных значений, рассчитанных в соответствии с астрономическими принципами, различия иногда возникают между датой пасхи в соответствии с расчетами и расплаты и расплаты и расчеты Гипотетическая дата Пасхи рассчитывается по астрономическим методам с использованием принципов, приписываемых отцам церкви. Эти расхождения называются «парадоксальными» пасхальными датами. ^{[ 68 ]}

В своем календариуме 1474 года Regiomontanus вычислил точное время всех соединений Солнца и Луны для долготы Нюрнберга в соответствии с таблицами Alfonsine в течение периода с 1475 по 1531 год. В своей работе он таблицы 30 случаев, где Пасха Юлиан Computus не согласен с Пасхой, вычисленной с использованием астрономического новолуния . В восемнадцати случаях дата отличалась на неделю, в семи случаях на 35 дней и в пяти случаях к 28 дням. ^{[ 68 ]}

Людвиг Ланге исследовал и классифицировал различные типы парадоксальных пасхальных дат, используя григорианский компьютер . ^{[ 69 ]} В тех случаях, когда первая весенняя полная луна в соответствии с астрономическим расчетом происходит в воскресенье, и компьютер дает то же воскресенье, что и Пасха, знаменитая Пасха происходит за неделю заранее по сравнению с гипотетическим «астрономически» правильной Пасхой. Ланге назвал этот случай негативным еженедельным (евребдодом) парадокс (парадокс H-). Если астрономический расчет дает субботу для первой весенней полнолуния, а Пасха не отмечается в ближайшее время после воскресенья, но через неделю Пасха отмечается в соответствии с Computus на одну неделю слишком поздно по сравнению с астрономическим результатом. Он классифицировал такие случаи положительный еженедельный (Hebdomadal) парадокс (парадокс H+). ^{[ 69 ]}

Расхождения еще больше, если существует разница в соответствии с весенним равноденствием в отношении астрономической теории и приближения компьютера . Если астрономическая равная луна в экстраноктом находится перед компьютерным равномерным полнолуние, Пасха будет отмечаться четыре или даже пять недель опоздание. Такие случаи называются положительным равномерным парадоксом (парадокс A+) в соответствии с Ланге. В обратном случае, когда компьютерная равная полнолуние падает за месяц до астрономической равной полной луны, Пасха отмечается четыре или пять недель слишком рано. Такие случаи называются отрицательным равномерным парадоксом (парадокс A-). ^{[ 69 ]}

Равноктические парадоксы всегда действительны во всем мире для всей Земли, потому что последовательность равноденствия и полнолуния не зависит от географической долготы. Напротив, еженедельные парадоксы являются местными в большинстве случаев и действительны только для части земли, потому что изменение дня между субботой и воскресеньем зависит от географической долготы. Компьютистические расчеты основаны на астрономических таблицах, действительных для долготы Венеции, которую Ланге назвал григорианскую долготу. ^{[ 69 ]}

В 21 и 22 -м веках ^{[ 69 ]}^{[ 70 ]} Отрицательные еженедельные парадоксальные пасхальные даты возникают в 2049, 2076, 2106, 2119 (глобальный), 2133, 2147, 2150, 2170 и 2174. Положительные еженедельные парадоксальные даты встречаются в 2045, 2069, 2089 (глобальный) и 2096. Положительные равноксичные парадозгические Даты в 2019, 2038, 2057, 2076, 2095, 2114, 2133, 2152, 2171 и 2190. ^{[ 70 ]}

В 2076 и 2133 годах возникают двойные парадоксы (положительные равноценные и отрицательные еженедельные). Отрицательные равноценные парадоксы чрезвычайно редки. Они происходят только дважды до 4000 года в 2353, когда Пасха на пять недель слишком рано и в 2372, когда Пасха на четыре недели слишком рано. ^{[ 70 ]}

Алгоритмы

Примечание об операциях

При выражении пасхальных алгоритмов без использования таблиц было обычным образом использовать только добавление , вычитание , умножение, умножение , разделение , модуло и назначение в соответствии с использованием простых механических или электронных калькуляторов. Это ограничение нежелательно для компьютерного программирования, где доступны условные операторы и операторы, а также таблицы поиска. Можно легко увидеть, как может быть сделано обращение с дня марта (от 22 до 56) в день и месяц (22 марта по 25 апреля) if (DoM > 31) {Day=DoM-31, Month=Apr} else {Day=DoM, Month=Mar}Полем Что еще более важно, использование таких условий также упрощает ядро григорианского расчета.

Пасхальный алгоритм Гаусса

В 1800 году математик Карл Фридрих Гаусс представил этот алгоритм для расчета даты Джулианской или Григорианской Пасхи. ^{[ 71 ]}^{[ 72 ]} Он исправил выражение для расчета переменной P в 1816 году. ^{[ 73 ]} В 1800 году он неправильно заявил p = пол ( ⁠ k / 3 ⁠ ) = ⌊ ⁠ K / 3 ⁠ ⌋ . В 1807 году он заменил условие (11 м + 11) мод 30 <19 на более простой A > 10 . В 1811 году он ограничил свой алгоритм только 18 -м и 19 -м веками и заявил, что 26 апреля всегда заменяется с 19 и 25 апреля к 18 апреля в изложенных обстоятельствах. В 1816 году он поблагодарил своего ученика Питера Пола Титтела за то, что P. P был неправ в оригинальной версии. ^{[ 74 ]}

Переменная	Выражение	Год = 1777	2024	2025
a =	Год мод 19	10	10	11
b =	Год мод 4	1	0	1
c =	Год мод 7	6	1	2
k =	год div 100 = ⌊ ⁠ year / 100 ⁠ ⌋	17	20	20
p =	(13 + 8 K ) Div 25 = ⌊ ⁠ 13 + 8 K / 25 ⁠ ⌋	5	6	6
Q =	k div 4 = ⌊ ⁠ k / 4 ⁠ ⌋	4	5	5
M =	(15 - p + k - q ) мод 30	23	24	24
N =	(4 + k - q ) Мод 7	3	5	5
Для Пасхи Джулиана в календаре Джулиана m = 15 и n = 6 ( K , P и Q не нужны)
d =	(19 а + м ) мод 30	3	4	23
E =	(2 B + 4 C + 6 D + N ) Мод 7	5	5	6
Март Пасхальный день =	22 + d + e	30	31	51
Апрель Пасхальный день =	d + e - 9	−1	0	20
	(11 м + 11) против 30	24	5	5
Если d = 28, e = 6 и (11 м + 11) мод 30 <19, замените 25 апреля на 18 апреля
Если d = 29 и e = 6, замените 26 апреля на 19 апреля

Анализ пасхального алгоритма Гаусса разделен на две части. Первая часть - это приблизительное отслеживание лунного орбита, а вторая часть - точное детерминированное смещение, чтобы получить воскресенье после полной луны.

Первая часть состоит в определении переменной D , количество дней (подсчетов с 22 марта) до дня после полной луны. Формула для D содержит термины 19 a и постоянный m . А является позицией года в 19-летнем лунном фазовом цикле, в котором путем предположения о движении Луны относительно Земли повторяется каждые 19 календарных лет. В более старшие времена 19 календарных лет были приравнивались к 235 лунным месяцам (монеттоническому циклу), что удивительно близок с 235 лунных месяцев составляет приблизительно 6939,6813 дней, а 19 лет - в среднем 6939,6075 дней.

Выражение (19 A + M ) MOD 30 повторяется каждые 19 лет в течение каждого века, как M определяется на веке. 19-летний цикл не имеет ничего общего с «19» в 19 A ; Это просто совпадение, что появляется еще один «19». «19» в 19 A происходит от исправления несоответствия между календарным годом и целым числом лунных месяцев.

Календарный год (без летательного года) имеет 365 дней, а ближайший из них может быть с целым числом лунных месяцев- 12 × 29,5 = 354 дня. Разница составляет 11 дней, которые должны быть исправлены при перемещении в следующем году на полную луну 11 дней назад. Но в арифметике Modulo 30 вычитание 11 - это то же самое, что добавление 19, следовательно, добавление 19 за каждый год добавленного, т.е. 19 a .

M A в 19 + M . служит для правильной отправной точки в начале каждого века Он определяется расчетом, который занимает количество прыжков до того столетия, когда K ингибирует прыжок каждые 100 лет и переустанавливает его каждые 400 лет, что дает ( k - q ) в качестве общего числа ингибирования схемы Прыжок каждые четыре года. Таким образом, мы добавляем ( k - q ) , чтобы исправить в течение дни, которые никогда не происходили. P корректирует, чтобы лунная орбита не была полностью описана в целочисленных терминах.

Диапазон дней, рассмотренных для полной луны для определения Пасхи,-21 марта (день церковного равноденствия весны) до 18 апреля-29-дневный диапазон. Однако в арифметике мод 30 переменной d и константы m , оба из которых могут иметь целочисленные значения в диапазоне от 0 до 29, диапазон составляет 30. Следовательно, корректировки вносятся в критических случаях. Как только D определяется, это количество дней, чтобы добавить к 22 марта (на следующий день после самой ранней возможной полной луны, что совпадает с церковным равноденствием весны), чтобы получить дату дня после полнолуния.

Таким образом, первая допустимая дата Пасхи - 22 марта + D + 0 , так как Пасха должна отпраздновать воскресенье после церковного полнолуния; То есть, если полнолуние падает в воскресенье 21 марта, Пасха будет отмечаться через 7 дней, а если полнолуние падает в субботу 21 марта, Пасха - следующие 22 марта.

Вторая часть - это нахождение E , дополнительные дни смещения, которые должны быть добавлены в смещение даты D , чтобы он прибыл в воскресенье. Поскольку неделя имеет 7 дней, смещение должно быть в диапазоне от 0 до 6 и определяется арифметикой Modulo 7. E определяется путем расчета 2 B + 4 C + 6 D + N MOD 7 . Сначала эти константы могут показаться странными, но они довольно легко объяснимы, если мы помним, что мы работаем под арифметикой MOD 7. Для начала 2 B + 4 C гарантирует, что мы заботимся о том, что будние дни скользят на каждый год.

Нормальный год имеет 365 дней, но 52 × 7 = 364 , так что 52 полных недель составляют слишком мало. Следовательно, каждый год подряд, будний день «Слайды на один день вперед», то есть, если 6 мая был средней один год, это четверг в следующем году (игнорируя лечебные годы). Как B , так и C увеличиваются на один для достижения одного года (игнорирование модульных эффектов). Выражение 2 B + 4 C, таким образом, увеличивается на 6, но помните, что это то же самое, что вычитание 1 мод 7.

Вычесть 1 - это именно то, что требуется в течение обычного года - так как один день в будние дни мы должны компенсировать за один день меньше, чтобы прибыть в подходящий будний день (т.е. воскресенье). В течение височного года B становится 0 и 2 B , таким образом, составляет 0 вместо 8, что при мод 7, является еще одним вычитанием на 1 - то есть, полное вычитание на 2, так как в будние дни после прыжкового дня в тот год проскользнул вперед на два дни

Выражение 6 D работает так же. Увеличение D на некоторое количество Y указывает на то, что полная луна происходит в течение нескольких дней в этом году, и, следовательно, мы должны компенсировать y дни меньше. Добавление 6 D является мод 7, так же, как вычитание D , что является желаемой операцией. Таким образом, опять же, мы делаем вычитание, добавляя под арифметику Modulo. В общей сложности переменная E содержит шаг с дня после дня полной луны до ближайшего воскресенья, между 0 и 6 днями вперед. Постоянная N обеспечивает отправную точку для расчетов для каждого века и зависит от того, где 1 января 1, год был неявно расположен, когда был построен григорианский календарь.

Выражение D + E может дать смещения в диапазоне от 0 до 35, указывающих на возможные пасхальные воскресенья 22 марта по 26 апреля. По соображениям исторической совместимости все смещения 35 и некоторые из 34 вычитаются 7, прыгая одно воскресенье в день полнолуния (фактически с использованием отрицательного E -1). Это означает, что 26 апреля никогда не бывает пасхального воскресенья, и что 19 апреля перепредставлено. Эти последние исправления связаны только с историческими причинами и не имеют ничего общего с математическим алгоритмом. Смещение 34 корректируется, если (и только если) d = 28 и d = 29 в другом месте в 19-летнем цикле.

Использование пасхального алгоритма Гаусса в течение многих лет до 1583 года исторически бессмысленно, поскольку григорианский календарь не использовался для определения Пасхи до этого года. Использование алгоритма далеко в будущее сомнительно, поскольку мы ничего не знаем о том, как разные церкви будут определять Пасху далеко вперед. Пасхальные расчеты основаны на соглашениях и соглашениях, а не на фактических небесных движениях, ни на неоспоримых фактах истории.

Анонимный григорианский алгоритм

Оригинальный формат 1876 *года* .
Дивиденд	Делитель	Коэффициент	Остаток
год	19	—	а
год	100	беременный	в
беременный	4	дюймовый	и
B + 8	25	фон	—
b - f + 1	3	глин	—
19 a + b - d - g + 15	30	—	час
в	4	я	k
32 + 2 e + 2 i - h - k	7	—	л
A + 11 H + 22 L	451	м	—
H + L - 7 м + 114	31	не	а

«Нью -Йоркский корреспондент» представил этот алгоритм для определения Григорианской Пасхи в журнале Nature в 1876 году. ^{[ 74 ]}^{[ 75 ]} Он был переиздан много раз, например, В 1877 году Сэмюэль Балчер в церковном календаре , ^{[ 76 ]} В 1916 году Артур Даунинг в обсерватории , ^{[ 77 ]} В 1922 году Х. Спенсер Джонс в общей астрономии , ^{[ 78 ]} В 1977 году журналом Британской астрономической ассоциации , ^{[ 79 ]} В 1977 году старым фермером Альманаком , В 1988 году Питер Дафетт-Смит в практической астрономии с вашим калькулятором , а в 1991 году Жан Мией в астрономических алгоритмах . ^{[ 80 ]} Из -за цитирования книги Мией это также называется алгоритм «Мией/Джонс/Мясник»:

Переменная	Выражение	Y = 1961	2024	2025
a =	Y Мод 19	4	10	11
b =	⌊ ⁠ Y / 100 ⁠ ⌋	19	20	20
c =	Y мод 100	61	24	25
d =	⌊ ⁠ b / 4 ⁠ ⌋	4	5	5
E =	B против 4	3	0	0
f =	⌊ ⁠ b + 8 / 25 ⁠ ⌋	1	1	1
g =	⌊ ⁠ B - F + 1/3 ⁠ ⌋	6	6	6
H =	(19 a + b - d - g + 15) мод 30	10	4	23
i =	⌊ ⁠ c / 4 ⁠ ⌋	15	6	6
k =	C против 4	1	0	1
l =	(32 + 2 e + 2 i - h - k ) мод 7	1	5	6
m =	⌊ ⁠ A + 11 H + 22 L / 451 ⁠ ⌋	0	0	0
	h + l − 7m + 114	125	123	143
n =	⌊ ⁠ H + L - 7 м + 114 / 31 ⁠ ⌋ ⌋	4	3	4
o =	( H + L - 7 м + 114) Мод 31	1	30	19
Григорианская Пасха		2 апреля 1961 года	31 марта 2024 года	20 апреля 2025 года

В этом алгоритме переменная N указывает на месяц года (либо март для n = 3, либо апрель для n = 4), в то время как день месяца получается как ( O + 1). В 1961 году новый ученый опубликовал версию алгоритма природы , включающую несколько изменений. ^{[ 81 ]} Переменная G была рассчитана с использованием коррекции Гаусса 1816 года, что привело к устранению переменной f . Некоторые приводит к замене переменной O (к которой нужно добавить, чтобы получить дату Пасхи) с переменной p , которая дает дату напрямую.

Переменная	Выражение	Y = 1961	2024	2025
фон	—	—	—
g =	⌊ ⁠ 8 b + 13 / 25 ⁠ ⌋	6	6	6
m =	⌊ ⁠ A + 11 H + 19 L / 433 ⁠ ⌋	0	0	0
n =	⌊ ⁠ H + L 7 м + 90/25 ⁠ ⌋ -	4	3	4
а	—	—	—	—
p =	( H + L - 7 м + 33 N + 19) Мод 32	2	31	20
Григорианская Пасха		2 апреля 1961 года	31 марта 2024 года	20 апреля 2025 года

Джулианский алгоритм Маюуса

Жан Мией, в своей книге «Астрономические алгоритмы» (1991, стр. 69), представляет следующий алгоритм для расчета Пасхи Джулиана на джулианском календаре, который не является григорианским календарем, используемым в качестве гражданского календаря во всем современном мире. Чтобы получить дату Восточной Православной Пасхи в последнем календаре, в джулианские даты должны быть добавлены 13 дней (по состоянию на 1900 по 2099 год), создавая даты ниже, в последнем ряду. (До 2099 года, 21 марта Джулиан приравнивается к 3 апреля Григориан.)

Православная (восточная) пасхальная дата
Переменная	Выражение	Y = 2008	2009	2010	2011	2016	2024	2025
a =	Y Мод 4	0	1	2	3	0	0	1
b =	Y Мод 7	6	0	1	2	0	1	2
c =	Y Мод 19	13	14	15	16	2	10	11
d =	(19 C + 15) против 30	22	11	0	19	23	25	14
E =	(2 a + 4 b - d + 34) мод 7	1	4	0	1	4	6	2
	D + E + 114	137	129	114	134	141	145	130
месяц =	⌊ ⁠ D + E + 114 / 31 ⁠ ⌋ ⌋	4	4	3	4	4	4	4
день =	(( D + E + 114) против 31) + 1	14	6	22	11	18	22	7
Пасхальный день (джулианский календарь)		14 апреля 2008 г.	6 апреля 2009 г.	22 марта 2010	11 апреля 2011 года	18 апреля 2016 года	22 апреля 2024 года	7 апреля 2025 года
Григорианский календарь эквивалент		27 апреля 2008 г.	19 апреля 2009 г.	4 апреля 2010 года	24 апреля 2011 года	1 мая 2016 года	5 мая 2024 года	20 апреля 2025 года

Смотрите также

Кристиан Зеллер - немецкий математик
Распятие тьма - Эпизод христианского евангелия темного неба
Реформа даты Пасхи - предложения по изменению даты фестиваля

Ссылки

Примечания

^ Хотя это датирование Августалиса Бруно Круша , см. Аргументы за дату 5 -го века в Моссхаммере 2008 , с. 217, 227–228.
^ Лунный цикл Анатолия, согласно таблицам в De Ratione Paschali , включал только два биссекстильных (прыжковых) лет каждые 19 лет, поэтому никто не мог использоваться любым, использующим юлианский календарь, у которого было четыре или пять летательных лет на лунный цикл Полем ^{[ 14 ]}^{[ 15 ]}
^ Для подтверждения роли Дионисиуса см. Blackburn & Holford-Strevens 1999 , p. 794.
^ Например, в юлианском календаре, в Риме в 1550 году, мартовское равноденствие произошло 11 марта в 6:51 в местном среднем . ^{[ 28 ]}
^ Хотя до замены юлианского календаря в 1752 году некоторые принтеры Книги общей молитвы правильно поместили салтус , начиная с следующего месяца 30 июля, ни один из них не продолжал последовательность правильно до конца года.
^ Хотя до замены юлианского календаря в 1752 году некоторые принтеры Книги общей молитвы правильно поместили салтус , начиная с следующего месяца 30 июля, ни один из них не продолжал последовательность правильно до конца года.
^ «[Золотое число] года объявления обнаружено путем добавления одного, разделения на 19 и взяв остаток (лечение 0 как 19)» ( Blackburn & Holford-Strevens 1999 , стр. 810).
^ См. Особенно первое , второй , Четвертый , и шестой канон и календарий
^ Можно проверить с помощью Blackburn & Holford-Strevens 1999 , p. 825, Таблица 7.
^ В 2004 году и снова в 2015 году 2 и 31 июля имеются полные луны.
^ Традиционно на Христианском Западе, эта ситуация была обработана путем продления первого 29-дневного лунного месяца года на 30 дней, и начнут следующий лунный месяц на один день позже, чем иначе, если это должно было начаться до первого дня (( Blackburn & Holford-Strevens 1999 , p.
^ Expl.suppl. 2013 года на стр. 599 вместо этого указаны 70 499 175 лунков без объяснения или ссылки. Это число, по -видимому, является усеченным значением деления 2 081 882 250 дней на 29,53059, что является округлым значением для длины луна, обнаруженной в таблице в верхней части с.587. Таким образом, число 70,499 175 было бы оценкой фактического числа лун в период 5,7 млн., И не число новых лун, фактически подсчитанных григорианским лунным календарем в течение полного цикла.

Цитаты

^ Ayto 2009 , p. 123.
^ Петерсон 2015 , с. 468.
^ Bede 1999 , p. 18
^ Bede 1999 , стр. 18-20.
^ Иоанна 19:14
^ Bede 1999 , p. XX.
^ Bede 1999 , p. XXXVI.
^ Bede 1999 , pp. 425–426, Приложение 4: Примечание на термин Computus.
^ Исход 12:18
^ Левит 23: 5
^ Bede 1999 , стр. 35-37.
^ Анатолий , Книга 7, Глава 33.
^ Bede 1999 , стр. 38-40.
^ Тернер 1895 , с. 699–710.
^ McCarthy 1996 , pp. 285–320.
^ Declercq 2000 , p. 80
^ Declercq 2000 , p. 97
^ Declercq 2000 , p. 99
^ Аутет, Родольф (9 декабря 2007 г.). «Дионисий Экгюс - Либер де Пасхат» . Архивировано из оригинала 15 апреля 2021 года . Получено 26 июня 2021 года .
^ Блэкберн 1999 , с. 793.
^ McCarthy 1993 , pp. 204–224.
^ Бед 1907 , с. 193, Книга III, Глава XXV.
^ Bede 1943 , p. 90: Письмо [о Cummian] одновременно является отчетом и извинениями или оправданием аббату Сегину в Ионе синода, проводимого в кампусе Ленис (Маг-Лене), где был рассмотрен пасхальный вопрос. Прямым результатом синода было изменение соблюдения южных ирландцев и принятия александрийского расчета.
^ Бед 1907 , с. 27
^ Bede 1999 , стр. 59-63.
^ Кекис, Теохарис. «Православный церковный календарь» (PDF) . Кипрская сеть Америки. Архивировано из оригинала (PDF) 26 ноября 2012 года . Получено 11 марта 2012 года .
^ Revision Radio's Tower of Song. «Многие пасхи и эостро для многих: выбор аллилуйя» . Архивировано из оригинала 16 апреля 2021 года . Получено 26 июня 2021 года .
^ «Калькулятор сезонов» . Время и дата как . 2014. Архивировано с оригинала 23 марта 2019 года . Получено 23 марта 2019 года .
^ Jump up to: ^а ^{беременный} ^в от Ghent 2019 .
^ Шилдс 1924 , с. 407–411.
^ На пути к общей дате Пасхи Алеппо, Сирия: Всемирный совет церквей/Совет по Ближнему Востоку Церквей, 10 марта 1997 года, архивируется с оригинала 30 марта 2018 года .
^ Ричардс 2013 , с. 587: день состоит из 86 400 секунд SI , и то же значение дается для 500, 1000, 1500 и 2000.
^ ἐπακτός . Лидделл, Генри Джордж ; Скотт, Роберт ; Грек -английский лексикон в проекте Персея .
^ Харпер, Дуглас. "Эпакт" . Онлайн этимологический словарь .
^ HM Nautical Almanac Office (1974). Пояснительное дополнение к астрономическим эфемерисам . Лондон п. 422. {{cite book}}: CS1 Maint: местоположение отсутствует издатель ( ссылка )
^ Молитесь 1999 , с. Xlvi.
^ Клавий 1603 .
^ Dershowitz & Reingold 2008 , с. 113–117.
^ Mosshammer 2008 , p. 76
^ Dershowitz & Reingold 2008 , с. 114–115.
^ Derswowitz & Reingold 2008 , p. 114
^ Великий 1891 .
^ Гинзель 1914 .
^ Weisstein (c. 2006) "Paschal Full Moon" соглашается с этой линией таблицы до 2009 года.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон Дэвисон, Майкл Э. (1980). «Распределение частот дат Пасхи» . Ирландский астрономический журнал . 14 : 156–164. Bibcode : 1980iraj ... 14..156d . Архивировано из оригинала 9 апреля 2023 года . Получено 17 мая 2022 года .
^ Derswowitz & Reingold 2008 , p. 117
^ Уокер, Джордж В. (1944). «Редкие даты на Пасху» . Популярная астрономия . № 52. С. 139–142. Bibcode : 1944pa ..... 52..139W . Архивировано из оригинала 9 апреля 2023 года . Получено 17 мая 2022 года .
^ Рогель, Денис (24 ноября 2004 г.). «Пропавшая новолуние в 16399 году и другие аномалии григорианского календаря» (PDF) . Архивировано (PDF) из оригинала 25 февраля 2021 года . Получено 26 июня 2021 года .
^ Паукер, Георг (1837). «Пасхальный законопроект или предложение о введении церковного календаря и Пасхального канона» . Рига: книжный магазин Эдуарда Францена. п. 59. Архивировано из оригинала 9 апреля 2023 года . Получено 6 сентября 2022 года .
^ «Альманак и астрономические эфемериды за 1931 год» . Лондон: офис его величества. 1929.
^ Доггетт, Ле (1992). Seidelmann, P.Kenneth (ред.). Пояснительное дополнение к астрономическому Альманаку . Вашингтон: военно -морская обсерватория США. п. 582. ISBN 0-935702-68-7 .
^ De short 1949 , pp. 109–116.
^ Sverdlow 1986 , стр. 109-118.
^ «Длина сезонов» . У. Торонто . Канада. Архивировано с оригинала 20 января 2018 года . Получено 31 января 2018 года .
^ «Средняя продолжительность равенства на север» (PDF) . У. Торонто . Канада. Архивировано (PDF) из оригинала 5 марта 2016 года . Получено 31 января 2018 года .
^ Закон о регулировании начала года; и для коррекции календаря, который сейчас используется в целом 1765, с пасхальными таблицами
^ Книга общей молитвы и управление таинствами и другими обрядами и церемониями церкви . Джозеф Бентам. 9 августа 1765 года . Получено 9 августа 2017 года - через интернет -архив.
^ Книга общей молитвы. «Таблицы и правила» . Архивировано из оригинала 27 мая 2021 года . Получено 26 июня 2021 года .
^ Стоктон, младший «Расчет пасхального воскресенья после книги общей молитвы» . Архивировано из оригинала 7 сентября 2015 года . Получено 9 августа 2017 года .
^ Папа Григорий XIII (24 февраля 1582 г.). "Inter Gravissimas" . Архивировано из оригинала 13 февраля 2006 года . Получено 9 августа 2017 года .
^ Teres 1984 , p.
^ Шафф, Филипп; Wace, Генри, ред. (1890), Синодальная буква , Никна и отцы пост-никена: вторая серия, вып. 14, Семь экуменических советов, Гранд -Рапидс, Мичиган , США: Eerdmans Pub Co., с. 112–114, ISBN 0-8028-8129-7 , архивировано с оригинала 28 сентября 2020 года , получено 4 июля 2020 года.
^ Truel 1958 , p. 36
^ Truel 1958 , p. 48
^ Byrhtferth of Ramsey 1995 , с. 136–7, 320–322.
^ Некоторый старый 2009 , с. 151.
^ Bede 1999 , pp. Xlvii.
^ Jump up to: ^а ^{беременный} Nothaft 2018 , с. 275–277.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и Long 1928 .
^ Jump up to: ^а ^{беременный} ^в Zeyer 2020 , с. 5–10.
^ "Гаус-CD" . webdoc.sub.gwdg.de . Архивировано с оригинала 6 декабря 2016 года . Получено 9 августа 2017 года .
^ Коте, Джохен. «Расчет Пасхи» . Астрономические трактаты [ астрономические трактаты ] (на немецком языке). Архивировано из оригинала 9 июля 2012 года . Получено 9 августа 2017 года .
^ Коте, Джохен. «Исправление эссе» . Астрономические трактаты [ астрономические трактаты ] (на немецком языке). Архивировано из оригинала 12 июля 2012 года . Получено 9 августа 2017 года .
^ Jump up to: ^а ^{беременный} Хорошо 2004 , с. 439–452.
^ Нью -Йоркский корреспондент (20 апреля 1876 г.). «Чтобы найти Пасху» . Природа : 487. {{cite journal}}: |author= имеет общее имя ( справка )
^ Мясник 1877 , с. 225
^ Даунинг 1916 , с. 215–219.
^ Спенсер Джонс 1922 , с. 73.
^ «Письма в редактор». Журнал Британской астрономической ассоциации . 88 : 91. Декабрь 1977 г. Бибкод : 1977Jbaa ... 88 ... 87.
^ Meeus 1991 , pp. 67–68.
^ О'Бейрн 1961 , с. 828.

Источники

Анатолий Лаодичеи , « Пасхальские каноны, цитируемые Евсевием» , церковная история Евсевия , архивировав из оригинала 14 апреля 2021 года , извлеченной 13 апреля 2021 года .
Айто, Джон, изд. (2009). Оксфордский словарь английских идиомов (3 -е изд.). УП Оксфорд. п. 123. ISBN 978-0-19-954378-6 .
Беде (1907) [731]. Церковная история Беде . Перевод Селлара, AM; Джайлс, JA London: Джордж Белл и сыновья. Архивировано из оригинала 12 мая 2019 года . Получено 23 марта 2019 года - через проект Гутенберг .
Беде (1943). Чарльз Уильямс Джонс (ред.). Bedae Opera de Timembus . Средневековая академия Америки. Архивировано из оригинала 9 апреля 2023 года . Получено 9 июня 2021 года .
Беде (1999). Расчет времени . Перевод веры Уоллиса. Ливерпульский университет издательство. ISBN 978-0-85323-693-1 Полем Архивировано из оригинала 9 апреля 2023 года . Получено 11 марта 2016 года .
Bien, Reinhold (июль 2004 г.). «Гаус и за его пределами: создание пасхальных алгоритмов». Архив для истории точных наук . 58 (5): 439–452. Bibcode : 2004ahes ... 58..439b . doi : 10.1007/s00407-004-0078-5 . S2CID 121657716 .
Блэкберн, Бонни Дж.; Holford-Strevens, Leofranc (1999). Оксфордский компаньон до года . Издательство Оксфордского университета. ISBN 978-0-19-214231-3 .
Мясник, Самуил (1877). Церковный календарь: его теория и конструкция . Дублин: Ходжес, Фостер и Фиггис. Архивировано из оригинала 9 апреля 2023 года . Получено 11 марта 2016 года .
Byrhtferth of Ramsey (1995). Лапидж, Майкл; Питер Стюарт Бейкер (ред.). Энчиридион Бирхтферта . Раннее английское текстовое общество. ISBN 978-0-19-722416-8 Полем Архивировано из оригинала 9 апреля 2023 года . Получено 9 июня 2021 года .
Клавий, Кристофер (1603). Romani Calendarij à Gregorio XIII. PM Restuti Exprongitio Архивировано апреля с оригинала 9 Получено 16 ноября В пятом томе Opera Mathematica, Mainz, 1612. Opera Mathematica of Christophy Clavius включает в себя изображения шести канонов и Explicatio (перейдите на страницу: римский календарь Грегория XII).
Константин Великий, Император (325): письмо епископам, которые не посещали первый Никейский совет; от Евсевия Вита Константини . Переводы на английский: документы Первого Совета Никеи , «о сохранении Пасхи» (близко) архивировали 27 января 2013 года на машине Wayback и Евсевия, жизнь Константина , Книга III, Главы XVIII - XIX Архивировано 16 сентября 2009 г. Wayback Machine
Корт, JJMA (Septetember 1949). «Эквансономическая оценка григанского календаря». Астрономические исследования . 2 (6): 109–116. Bibcode : 19499ra …… 2..109d .
Declercq, Georges (2000). Anno Domini: происхождение христианской эры Isd. ISBN 978-2-503-51050-7 Полем Архивировано из оригинала 9 апреля 2023 года . Получено 14 декабря 2020 года .
Дершовиц, Начум ; Рейнгольд, Эдвард М. (2008). Календрические расчеты . Издательство Кембриджского университета. ISBN 978-0-521-88540-9 Полем Архивировано из оригинала 9 апреля 2023 года . Получено 14 декабря 2020 года .
Dionysius Exiguus (525): Liber de Paschate . Он-лайн: (Полный латинский текст) Архивировал 3 июня 2008 года на машине Wayback и (таблица с аргументацией на латыни, с английским переводом)
Некоторые старые (июль 2009 г.). Кармина средневековья Индита . Библиобазар. ISBN 978-1-110-75828-9 .
Даунинг, AMW (май 1916). «Дата Пасхи». Обсерватория . 39 : 215–219. Bibcode : 1916obs .... 39..215d .
Евсевий Цезария, история церкви , перевод Га -Уильямсона. Пересмотренный и отредактирован с новым введением Эндрю Лаута. Penguin Books, Лондон, 1989.
ГРЕГОРИЙ XIII (Папа) и Комитет по реформе календаря (1581): папский бык -междиссимс и шесть канонов. Он-лайн под: Les Textes Fondateurs du Calendier Gregorien » Архивировал 29 апреля 2012 года на машине Wayback Clavius , с некоторыми частями .
Van Gent, Robert (2019), Аномальное пасхальное воскресенье датируется 18 -го и началом 19 -го века Утрехт Университет, архивировав с оригинала 1 августа 2020 года , извлеченные 23 июля 2019 года .
Гинзель, Фридрих Карл (1914). Справочник по математической и технической хронологии, том III . Лейпциг, Германия: Хинрихс.
Grotefend, Hermann (1891). Расчет времени немецкого среднего века и современного времени . Кран. Архивировано из оригинала 9 апреля 2023 года . Получено 27 ноября 2020 года .
Grumel, V. (1958). Хронология (на французском языке). ПАРИЖ: прессает Университет -де -Франс. OCLC 4260118 .
Ланге, Людвиг (1928). «Парадокс» пасхальные данные в григорианском календаре и его значение для современной реформы календаря Людвига Ланге. Представлено Эдуардом Шварцем 7 июля 1928 года . Байер. Акад. Науки. Архивировано из оригинала 9 апреля 2023 года . Получено 27 ноября 2020 года .
Лихтенберг, Хейнер (2003). «Адаптируемая циклическая, растворительная система подсчета времени григорианского календаря». Отчеты по математическому семестру . 50 : 45–76. Doi : 10.1007/s00591-003-0063-0 . S2CID 120639320 .
Маккарти, Даниэль (август 1993 г.). «Пасхальные принципы и лунный цикл пятого века, используемые на Британских островах». Журнал «История астрономии» . 24 (3): 204–224. Bibcode : 1993jha .... 24..204M . doi : 10.1177/002182869302400304 . S2CID 115765809 .
Маккарти, Даниэль (1996). «Лунные и пасхальные таблицы De Ratione Paschali приписывают Анатолий Лаодичеи». Архив для истории точных наук . 49 (4): 285–320. Bibcode : 1996ahes ... 49..285m . doi : 10.1007/bf00374701 . S2CID 120081352 .
Мией, Джин (1991). Астрономические алгоритмы . Ричмонд, Вирджиния: Уиллманн-Белл.
Мосхаммер, Олден А. (2008). Пасхальный компьютер и происхождение христианской эры . Оксфорд: Университетская издательство. ISBN 978-0-19-954312-0 Полем Архивировано из оригинала 9 апреля 2023 года . Получено 9 июня 2021 года .
Nothaft, C. Philipp E. (2018). Скандальная ошибка: календарная реформа и календарная астрономия в средневековой Европе . Издательство Оксфордского университета. ISBN 978-0-19-879955-9 Полем Архивировано из оригинала 9 апреля 2023 года . Получено 27 ноября 2020 года .
О'Бейрн, Т. Т. (30 марта 1961 г.). «Как десять дивизий приводят к Пасхе» . Новый ученый . 9 (228): 828. Архивировано с оригинала 9 апреля 2023 года . Получено 7 июня 2021 года .
Петерсон, Майкл Д. (2015). «Пост: восточный христианин». В Джонстоне, Уильям М.; Кляйнхенц, Кристофер (ред.). Энциклопедия монашеской . Routledge. п. 468. ISBN 978-1-57958-090-2 Полем Архивировано из оригинала 9 апреля 2023 года . Получено 21 марта 2023 года .
Ричардс, например (2013). "Календари". В SE Urban; PK Seidelmann (ред.). Пояснительное дополнение к астрономическому Альманаку (3 -е изд.). Милл -Вэлли, Калифорния: Univ Science Books.
Swerdlow, Noel M. (1986). «Продолжительность года в первоначальном предложении для григорианского календаря». Журнал «История астрономии» . 17 (49): 109–118. Bibcode : 1986jha .... 17..109s . doi : 10.1177/002182868601700204 . S2CID 118491152 .
Шилдс, Мириам Нэнси (1924). «Новый календарь восточных церквей». Популярная астрономия . 32 : 407–411. Bibcode : 1924pa ..... 32..407s .
Спенсер Джонс, Х. (1922). Общая астрономия . Лондон: Лонгсман, зеленый.
Терс, Густав (1984). "Расчеты времени и Dionysius exiguus" истории Jogoral для 15 (3): 177–188. Bibcode : 1984jha ... 15 ... 177t doi 10.1177/002182868401500302: 117094612S2CID
Тернер, Ch (1895). «Пасхальный канон Анатолия Лаодичеи». Английский исторический обзор . 10 : 699–710. doi : 10.1093/ehr/x.xl.699 .
Пшеница, Чарльз (1871) [1710]. Рациональная иллюстрация Книги общей молитвы Англии . Лондон: Белл и Далди.
Зейер, Клаус Питер (2020). «Частота пасхальных парадоксов: отрицательные равноценные парадоксы годов 2353 и 2372 как самый редкий вариант». Regiomontanus Messenger . 33 : 5-10.

Дальнейшее чтение

Борст, Арно (1993). Заказ времени: от древнего компьютера до современного компьютерного транса. Эндрю Виннард. Кембридж: Polity Press; Чикаго: Univ. Чикагской прессы.
Coyne, GV, Ma Hoskin, MA, и Pedersen, O. (ed.) реформа календаря: Материалы Ватиканской конференции, чтобы отметить его 400 -летие, гг . Грегорианская 1582–1982 : Папская академия наук, Specolo Vaticano, 1983).
Гибсон, Маргарет Данлоп, Didascalia Apostolorum в Сирийском , издательство Кембриджского университета, Лондон, 1903.
Шварц Э., Христианские и еврейские пасхальные таблетки (Трактаты Королевского общества наук в Геттингене. Пилологический исторический класс. Новый эпизод, том VIII.) Книжный магазин Вейдмана , Берлин, 1905.
Филипп Шафф (ред.) Теодорет, Джером, Геннадиус и Руфиния: исторические сочинения, архивные 15 мая 2019 года на машине Wayback
Стерн, Сача, Календарь и Сообщество: История еврейского календаря второго века до н.э. - десятого века н.э. , издательство Оксфордского университета, Оксфорд, 2001.
Уокер, Джордж У, Пасхальные интервалы архивировали 17 мая 2022 года на машине Wayback , Популярная астрономия, апрель 1945 г., вып. 53, с. 162–179.
Уокер, Джордж У, пасхальные интервалы архивировали 17 мая 2022 года на машине Wayback (продолжение), популярная астрономия, май 1945 г., вып. 53, с. 218–232.
Вейсштейн, Эрик. (ок. 2006) « Пасхальная полнолуние » в мире астрономии .

Внешние ссылки

Excel электронные таблицы и функции для расчета Пасхи
Полные работы почтенных Bede Vol. 6. (содержит период времени и сезона .)
Запись на epacts в католической энциклопедии 1911 года.
Первоначальные тексты реформы григорианского календаря (на латыни) с переводами на французский от Родольфа Аутета
Пасхальный калькулятор с обширной библиографией и с полезными ссылками
Ephemeris site Бюро продоки с пасхальным калькулятором (действительный между 325 и 2500)
Страница календаря и калькулятор от Holger Oertel
Страница от Клайва Петер с кратким объяснением, еще некоторыми столами и другим алгоритмом
(на немецком языке) Обширный календарный сайт и календарь и пасхальный калькулятор от Николауса А. Бэра Архивировали 6 сентября 2003 года на машине Wayback
Объяснение григорианского солнечного и лунного календаря с улучшенными процедурами по сравнению с табличным методом, Дэвид Мадоре
Дионисий маленький пасхальный стол
Мнемонические компьютерные диаграммы рук из рукописи в Британской библиотеке
Св. Сент -Галлен, Стифтсбиблиотек, Кодекс Сангалленсис 378 (11 век) с. 28. Содержит стихотворение, девятое апрель, знает это .
Упрощенный метод определения даты Пасхи за все годы с 326 до 4099 Рональда В. Маллена
Текст календаря (Новый стиль) Закон 1750 года, Британский акт парламента, внедряющий григорианский календарь с поправками на сегодняшний день. Содержит таблицы для расчета Пасхи вплоть до 8599 года. В отличие от принятого действия.
ComputusLat А. База данных средневековых рукописей, содержащих латинские компьютерные алгоритмы, тексты, таблицы, диаграммы и календари.

[14] Хотя это датирование Августалиса Бруно Круша , см. Аргументы за дату 5 -го века в Моссхаммере 2008 , с. 217, 227–228.

[17] Лунный цикл Анатолия, согласно таблицам в De Ratione Paschali , включал только два биссекстильных (прыжковых) лет каждые 19 лет, поэтому никто не мог использоваться любым, использующим юлианский календарь, у которого было четыре или пять летательных лет на лунный цикл Полем ^{[ 14 ]}^{[ 15 ]}

[22] Для подтверждения роли Дионисиуса см. Blackburn & Holford-Strevens 1999 , p. 794.

[32] Например, в юлианском календаре, в Риме в 1550 году, мартовское равноденствие произошло 11 марта в 6:51 в местном среднем . ^{[ 28 ]}

[39] Хотя до замены юлианского календаря в 1752 году некоторые принтеры Книги общей молитвы правильно поместили салтус , начиная с следующего месяца 30 июля, ни один из них не продолжал последовательность правильно до конца года.

[40] Хотя до замены юлианского календаря в 1752 году некоторые принтеры Книги общей молитвы правильно поместили салтус , начиная с следующего месяца 30 июля, ни один из них не продолжал последовательность правильно до конца года.

[43] «[Золотое число] года объявления обнаружено путем добавления одного, разделения на 19 и взяв остаток (лечение 0 как 19)» ( Blackburn & Holford-Strevens 1999 , стр. 810).

[44] См. Особенно первое , второй , Четвертый , и шестой канон и календарий

[52] Можно проверить с помощью Blackburn & Holford-Strevens 1999 , p. 825, Таблица 7.

[55] В 2004 году и снова в 2015 году 2 и 31 июля имеются полные луны.

[58] Традиционно на Христианском Западе, эта ситуация была обработана путем продления первого 29-дневного лунного месяца года на 30 дней, и начнут следующий лунный месяц на один день позже, чем иначе, если это должно было начаться до первого дня (( Blackburn & Holford-Strevens 1999 , p.

[63] Expl.suppl. 2013 года на стр. 599 вместо этого указаны 70 499 175 лунков без объяснения или ссылки. Это число, по -видимому, является усеченным значением деления 2 081 882 250 дней на 29,53059, что является округлым значением для длины луна, обнаруженной в таблице в верхней части с.587. Таким образом, число 70,499 175 было бы оценкой фактического числа лун в период 5,7 млн., И не число новых лун, фактически подсчитанных григорианским лунным календарем в течение полного цикла.

[FOOTNOTEAyto2009123-1] Ayto 2009 , p. 123.

[FOOTNOTEPeterson2015468-2] Петерсон 2015 , с. 468.

[FOOTNOTEBede1999xviii-3] Bede 1999 , p. 18

[FOOTNOTEBede1999xviii–xx-4] Bede 1999 , стр. 18-20.

[5] Иоанна 19:14

[FOOTNOTEBede1999xx-6] Bede 1999 , p. XX.

[FOOTNOTEBede1999xxxvi-7] Bede 1999 , p. XXXVI.

[FOOTNOTEBede1999425–426Appendix_4:_A_Note_on_the_Term_Computus-8] Bede 1999 , pp. 425–426, Приложение 4: Примечание на термин Computus.

[9] Исход 12:18

[10] Левит 23: 5

[FOOTNOTEBede1999xxxv–xxxvii-11] Bede 1999 , стр. 35-37.

[FOOTNOTEAnatoliusBook_7,_Chapter_33-12] Анатолий , Книга 7, Глава 33.

[FOOTNOTEBede1999xxxviii–xl-13] Bede 1999 , стр. 38-40.

[FOOTNOTETurner1895699–710-15] Тернер 1895 , с. 699–710.

[FOOTNOTEMcCarthy1996285–320-16] McCarthy 1996 , pp. 285–320.

[FOOTNOTEDeclercq200080-18] Declercq 2000 , p. 80

[FOOTNOTEDeclercq200097-19] Declercq 2000 , p. 97

[FOOTNOTEDeclercq200099-20] Declercq 2000 , p. 99

[audette-21] Аутет, Родольф (9 декабря 2007 г.). «Дионисий Экгюс - Либер де Пасхат» . Архивировано из оригинала 15 апреля 2021 года . Получено 26 июня 2021 года .

[FOOTNOTEBlackburnHolford-Strevens1999793-23] Блэкберн 1999 , с. 793.

[FOOTNOTEMcCarthy1993204–224-24] McCarthy 1993 , pp. 204–224.

[FOOTNOTEBede1907193Book_III,_Chapter_XXV-25] Бед 1907 , с. 193, Книга III, Глава XXV.

[FOOTNOTEBede194390-26] Bede 1943 , p. 90: Письмо [о Cummian] одновременно является отчетом и извинениями или оправданием аббату Сегину в Ионе синода, проводимого в кампусе Ленис (Маг-Лене), где был рассмотрен пасхальный вопрос. Прямым результатом синода было изменение соблюдения южных ирландцев и принятия александрийского расчета.

[FOOTNOTEBede1907xxvii-27] Бед 1907 , с. 27

[FOOTNOTEBede1999lix–lxiii-28] Bede 1999 , стр. 59-63.

[Kekis-29] Кекис, Теохарис. «Православный церковный календарь» (PDF) . Кипрская сеть Америки. Архивировано из оригинала (PDF) 26 ноября 2012 года . Получено 11 марта 2012 года .

[revradiotowerofsong-30] Revision Radio's Tower of Song. «Многие пасхи и эостро для многих: выбор аллилуйя» . Архивировано из оригинала 16 апреля 2021 года . Получено 26 июня 2021 года .

[31] «Калькулятор сезонов» . Время и дата как . 2014. Архивировано с оригинала 23 марта 2019 года . Получено 23 марта 2019 года .

[FOOTNOTEvan_Gent2019-33] Jump up to: ^а ^{беременный} ^в от Ghent 2019 .

[FOOTNOTEShields1924407–411-34] Шилдс 1924 , с. 407–411.

[WCC-35] На пути к общей дате Пасхи Алеппо, Сирия: Всемирный совет церквей/Совет по Ближнему Востоку Церквей, 10 марта 1997 года, архивируется с оригинала 30 марта 2018 года .

[FOOTNOTERichards2013587-36] Ричардс 2013 , с. 587: день состоит из 86 400 секунд SI , и то же значение дается для 500, 1000, 1500 и 2000.

[37] ἐπακτός . Лидделл, Генри Джордж ; Скотт, Роберт ; Грек -английский лексикон в проекте Персея .

[38] Харпер, Дуглас. "Эпакт" . Онлайн этимологический словарь .

[41] HM Nautical Almanac Office (1974). Пояснительное дополнение к астрономическим эфемерисам . Лондон п. 422. {{cite book}}: CS1 Maint: местоположение отсутствует издатель ( ссылка )

[FOOTNOTEBede1999xlvi-42] Молитесь 1999 , с. Xlvi.

[FOOTNOTEClavius1603-45] Клавий 1603 .

[FOOTNOTEDershowitzReingold2008113–117-46] Dershowitz & Reingold 2008 , с. 113–117.

[FOOTNOTEMosshammer200876-47] Mosshammer 2008 , p. 76

[FOOTNOTEDershowitzReingold2008114–115-48] Dershowitz & Reingold 2008 , с. 114–115.

[FOOTNOTEDershowitzReingold2008114-49] Derswowitz & Reingold 2008 , p. 114

[FOOTNOTEGrotefend1891-50] Великий 1891 .

[FOOTNOTEGinzel1914-51] Гинзель 1914 .

[53] Weisstein (c. 2006) "Paschal Full Moon" соглашается с этой линией таблицы до 2009 года.

[Davison-54] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон Дэвисон, Майкл Э. (1980). «Распределение частот дат Пасхи» . Ирландский астрономический журнал . 14 : 156–164. Bibcode : 1980iraj ... 14..156d . Архивировано из оригинала 9 апреля 2023 года . Получено 17 мая 2022 года .

[FOOTNOTEDershowitzReingold2008117-56] Derswowitz & Reingold 2008 , p. 117

[57] Уокер, Джордж В. (1944). «Редкие даты на Пасху» . Популярная астрономия . № 52. С. 139–142. Bibcode : 1944pa ..... 52..139W . Архивировано из оригинала 9 апреля 2023 года . Получено 17 мая 2022 года .

[59] Рогель, Денис (24 ноября 2004 г.). «Пропавшая новолуние в 16399 году и другие аномалии григорианского календаря» (PDF) . Архивировано (PDF) из оригинала 25 февраля 2021 года . Получено 26 июня 2021 года .

[60] Паукер, Георг (1837). «Пасхальный законопроект или предложение о введении церковного календаря и Пасхального канона» . Рига: книжный магазин Эдуарда Францена. п. 59. Архивировано из оригинала 9 апреля 2023 года . Получено 6 сентября 2022 года .

[61] «Альманак и астрономические эфемериды за 1931 год» . Лондон: офис его величества. 1929.

[62] Доггетт, Ле (1992). Seidelmann, P.Kenneth (ред.). Пояснительное дополнение к астрономическому Альманаку . Вашингтон: военно -морская обсерватория США. п. 582. ISBN 0-935702-68-7 .

[FOOTNOTEde_Kort1949109–116-64] De short 1949 , pp. 109–116.

[FOOTNOTESwerdlow1986109–118-65] Sverdlow 1986 , стр. 109-118.

[66] «Длина сезонов» . У. Торонто . Канада. Архивировано с оригинала 20 января 2018 года . Получено 31 января 2018 года .

[67] «Средняя продолжительность равенства на север» (PDF) . У. Торонто . Канада. Архивировано (PDF) из оригинала 5 марта 2016 года . Получено 31 января 2018 года .

[68] Закон о регулировании начала года; и для коррекции календаря, который сейчас используется в целом 1765, с пасхальными таблицами

[69] Книга общей молитвы и управление таинствами и другими обрядами и церемониями церкви . Джозеф Бентам. 9 августа 1765 года . Получено 9 августа 2017 года - через интернет -архив.

[70] Книга общей молитвы. «Таблицы и правила» . Архивировано из оригинала 27 мая 2021 года . Получено 26 июня 2021 года .

[71] Стоктон, младший «Расчет пасхального воскресенья после книги общей молитвы» . Архивировано из оригинала 7 сентября 2015 года . Получено 9 августа 2017 года .

[72] Папа Григорий XIII (24 февраля 1582 г.). "Inter Gravissimas" . Архивировано из оригинала 13 февраля 2006 года . Получено 9 августа 2017 года .

[FOOTNOTETeres1984178-73] Teres 1984 , p.

[74] Шафф, Филипп; Wace, Генри, ред. (1890), Синодальная буква , Никна и отцы пост-никена: вторая серия, вып. 14, Семь экуменических советов, Гранд -Рапидс, Мичиган , США: Eerdmans Pub Co., с. 112–114, ISBN 0-8028-8129-7 , архивировано с оригинала 28 сентября 2020 года , получено 4 июля 2020 года.

[FOOTNOTEGrumel195836-75] Truel 1958 , p. 36

[FOOTNOTEGrumel195848-76] Truel 1958 , p. 48

[FOOTNOTEByrhtferth_of_Ramsey1995136–7,_320–322-77] Byrhtferth of Ramsey 1995 , с. 136–7, 320–322.

[FOOTNOTEDomus_Quaedam_Vetus2009151-78] Некоторый старый 2009 , с. 151.

[FOOTNOTEBede1999xlvii-79] Bede 1999 , pp. Xlvii.

[FOOTNOTENothaft2018275–277-80] Jump up to: ^а ^{беременный} Nothaft 2018 , с. 275–277.

[FOOTNOTELange1928-81] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и Long 1928 .

[FOOTNOTEZeyer20205–10-82] Jump up to: ^а ^{беременный} ^в Zeyer 2020 , с. 5–10.

[Gauß-CD-83] "Гаус-CD" . webdoc.sub.gwdg.de . Архивировано с оригинала 6 декабря 2016 года . Получено 9 августа 2017 года .

[Kothe1-84] Коте, Джохен. «Расчет Пасхи» . Астрономические трактаты [ астрономические трактаты ] (на немецком языке). Архивировано из оригинала 9 июля 2012 года . Получено 9 августа 2017 года .

[Kothe2-85] Коте, Джохен. «Исправление эссе» . Астрономические трактаты [ астрономические трактаты ] (на немецком языке). Архивировано из оригинала 12 июля 2012 года . Получено 9 августа 2017 года .

[FOOTNOTEBien2004439–452-86] Jump up to: ^а ^{беременный} Хорошо 2004 , с. 439–452.

[87] Нью -Йоркский корреспондент (20 апреля 1876 г.). «Чтобы найти Пасху» . Природа : 487. {{cite journal}}: |author= имеет общее имя ( справка )

[FOOTNOTEButcher1877225-88] Мясник 1877 , с. 225

[FOOTNOTEDowning1916215–219-89] Даунинг 1916 , с. 215–219.

[FOOTNOTESpencer_Jones192273-90] Спенсер Джонс 1922 , с. 73.

[91] «Письма в редактор». Журнал Британской астрономической ассоциации . 88 : 91. Декабрь 1977 г. Бибкод : 1977Jbaa ... 88 ... 87.

[FOOTNOTEMeeus199167–68-92] Meeus 1991 , pp. 67–68.

[FOOTNOTEO'Beirne1961828-93] О'Бейрн 1961 , с. 828.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ А ]

[ B ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ C ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ D ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ E ]

[ f ]

[ 35 ]

[ 36 ]

[ G ]

[ H ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ я ]

[ 44 ]

[ 45 ]

[ J ]

[ 46 ]

[ 47 ]

[ k ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ L ]

[ 52 ]

[ 53 ]

[ 54 ]

[ 55 ]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

[ 68 ]

[ 69 ]

[ 70 ]

[ 71 ]

[ 72 ]

[ 73 ]

[ 74 ]

[ 75 ]

[ 76 ]

[ 77 ]

[ 78 ]

[ 79 ]

[ 80 ]

[ 81 ]

[ 14 ]

[ 15 ]

[ 28 ]