Арифметика

Чтобы узнать о песне Брук Фрейзер 2004 года, см. «Арифметика» (песня) . О русском учебнике 1703 года см. Арифметика (книга) .

Основными арифметическими действиями являются сложение, вычитание, умножение и деление.

Арифметика – это элементарный раздел математики , изучающий числовые операции , такие как сложение , вычитание , умножение и деление . В более широком смысле сюда также входят возведение в степень , извлечение корней и логарифмирование .

Арифметические системы можно различать по типу чисел, с которыми они оперируют. Целочисленная арифметика – это вычисления с положительными и отрицательными целыми числами . Арифметика рациональных чисел включает в себя операции с дробями целых чисел. Арифметика действительных чисел занимается вычислениями с действительными числами , которые включают в себя как рациональные , так и иррациональные числа .

Другое различие основано на системе счисления, используемой для выполнения вычислений. Десятичная арифметика является наиболее распространенной. используются основные цифры от 0 до 9 и их комбинации Для выражения чисел . Двоичная арифметика, напротив, используется большинством компьютеров и представляет числа в виде комбинаций основных цифр 0 и 1. Компьютерная арифметика занимается особенностями реализации двоичной арифметики на компьютерах . Некоторые арифметические системы работают с математическими объектами , отличными от чисел, например, интервальная арифметика и матричная арифметика.

Арифметические операции составляют основу многих разделов математики, таких как алгебра , исчисление и статистика . Они играют аналогичную роль в таких науках , как физика и экономика . Арифметика присутствует во многих аспектах повседневной жизни , например, для расчета сдачи во время покупок или для управления личными финансами . Это одна из самых ранних форм математического образования , с которой сталкиваются студенты. Его когнитивные и концептуальные основы изучаются психологией и философией .

Практике арифметики насчитывает по меньшей мере тысячи, а возможно, и десятки тысяч лет. Древние цивилизации, такие как египтяне и шумеры, изобрели системы счисления для решения практических арифметических задач примерно в 3000 году до нашей эры. Начиная с VII и VI веков до нашей эры, древние греки начали более абстрактное изучение чисел и ввели метод строгих математических доказательств . Древние индийцы разработали концепцию нуля и десятичной системы , которую арабские математики в дальнейшем усовершенствовали и распространили на западный мир в средневековый период. Первые механические калькуляторы были изобретены в 17 веке. В XVIII и XIX веках развивается современная теория чисел и формулируются аксиоматические основы арифметики. В 20 веке появление электронных калькуляторов и компьютеров произвело революцию в точности и скорости выполнения арифметических вычислений.

Определение, этимология и смежные области

Арифметика – это фундаментальный раздел математики , изучающий числа и операции с ними. В частности, он занимается численными вычислениями с использованием арифметических операций сложения , вычитания , умножения и деления . В более широком смысле сюда также входят возведение в степень , извлечение корней и логарифмирование . Корень термина «арифметика» происходит от латинского термина « arithmetica », который происходит от древнегреческих слов ἀριθμός (арифмос), означающих «число», и ἀριθμητική τέχνη (arithmetike tekhne), означающих «искусство счета».

Существуют разногласия относительно его точного определения. Согласно узкой характеристике, арифметика имеет дело только с натуральными числами . Однако более распространенная точка зрения состоит в том, чтобы включать в свою область действия операции с целыми , рациональными числами , действительными числами , а иногда и с комплексными числами . Некоторые определения ограничивают арифметику областью числовых вычислений. В более широком смысле оно включает также изучение того, как развивалось понятие числа , анализ свойств и отношений между числами, а также рассмотрение аксиоматической структуры арифметических операций.

Арифметика тесно связана с теорией чисел , и некоторые авторы используют эти термины как синонимы. Однако в более конкретном смысле теория чисел ограничивается изучением целых чисел и фокусируется на их свойствах и отношениях, таких как делимость , факторизация и простота . Традиционно это известно как высшая арифметика.

Числа

Числа — это математические объекты, используемые для подсчета величин и измерения величин. Они являются фундаментальными элементами арифметики, поскольку все арифметические операции выполняются над числами. Существуют разные виды чисел и разные системы счисления для их представления.

Виды

Различные типы чисел на числовой прямой . Целые числа окрашены в черный цвет, рациональные числа — в синий, а иррациональные числа — в зеленый.

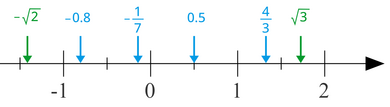
Основными видами чисел, используемых в арифметике, являются натуральные числа , целые числа, целые числа , рациональные числа и действительные числа . Натуральные числа – это целые числа, начинающиеся с 1 и идущие до бесконечности. Они исключают 0 и отрицательные числа. Они также известны как счетные числа и могут быть выражены как $\{1,2,3,4,...\}$. Символом натуральных чисел является $\mathbb {N}$. Целые числа идентичны натуральным числам с той лишь разницей, что они включают 0. Их можно представить как $\{0,1,2,3,4,...\}$ и иметь символ $\mathbb {N} _{0}$. Некоторые математики не проводят различия между натуральными и целыми числами, включая 0 в набор натуральных чисел. Набор целых чисел включает в себя как положительные, так и отрицательные целые числа. Он имеет символ $\mathbb {Z}$ и может быть выражено как $\{...,-2,-1,0,1,2,...\}$.

В зависимости от того, как используются натуральные и целые числа, их можно разделить на кардинальные и порядковые числа . Кардинальные числа, такие как один, два и три, — это числа, выражающие количество объектов. Они отвечают на вопрос «сколько?». Порядковые номера, такие как первый, второй и третий, указывают порядок или размещение в серии. Они отвечают на вопрос «какая должность?».

Число является рациональным, если его можно представить как отношение двух целых чисел. Например, рациональное число ${\tfrac {1}{2}}$ образуется путем деления целого числа 1, называемого числителем, на целое число 2, называемое знаменателем. Другими примерами являются ${\tfrac {3}{4}}$ и ${\tfrac {281}{3}}$. В множество рациональных чисел входят все целые числа, являющиеся дробями со знаменателем 1. Символом рациональных чисел является $\mathbb {Q}$. Десятичные дроби , такие как 0,3 и 25,12, представляют собой особый тип рациональных чисел, поскольку их знаменатель представляет собой степень 10. Например, 0,3 равно ${\tfrac {3}{10}}$, а 25,12 равно ${\tfrac {2512}{100}}$. Каждое рациональное число соответствует конечной или повторяющейся десятичной дроби .

Иррациональные числа иногда требуются для описания величин в геометрии . Например, длина гипотенузы прямоугольного треугольника иррациональна , если длина его катетов равна 1.

Иррациональные числа – это числа, которые невозможно выразить через отношение двух целых чисел. Они часто требуются для описания геометрических величин. Например, если катет прямоугольного треугольника равен 1, то длина его гипотенузы определяется иррациональным числом. ${\sqrt {2}}$. π отношение окружности длины – еще одно иррациональное число, описывающее к ее диаметру . Десятичное представление иррационального числа бесконечно без повторяющихся десятичных знаков. Множество рациональных чисел вместе с множеством иррациональных чисел составляют множество действительных чисел. Символ действительных чисел $\mathbb {R}$. Еще более широкие классы чисел включают комплексные числа и кватернионы .

Системы счисления

Основная статья: Система счисления

Цифра — это символ , обозначающий число, а системы счисления — это системы представления. Обычно они имеют ограниченное количество основных цифр, которые напрямую относятся к определенным числам. Система определяет, как эти основные цифры могут быть объединены для выражения любого числа. Системы счисления бывают позиционными и непозиционными. Все ранние системы счисления были непозиционными. Для непозиционных систем счисления значение цифры не зависит от ее положения в числительном.

В метках и некоторых метках используется непозиционная унарная система счисления .

Простейшей непозиционной системой счисления является унарная система счисления . Он основан на одном символе числа 1. Все более высокие числа записываются путем повторения этого символа. Например, число 7 можно представить, повторив символ 1 семь раз. Эта система затрудняет запись больших чисел, поэтому многие непозиционные системы включают дополнительные символы для непосредственного представления больших чисел. Вариации унарной системы счисления используются в счетных палочках с вмятинами и в счетных метках .

Иероглифические цифры от 1 до 10 000.

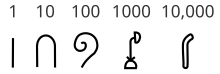
Египетские иероглифы имели более сложную непозиционную систему счисления . У них есть дополнительные символы для чисел, таких как 10, 100, 1000 и 10 000. Эти символы можно объединить в сумму для более удобного выражения больших чисел. Например, в цифре 10 405 один раз используется символ 10 000, четыре раза — символ 100 и пять раз — символ 1. Аналогичной хорошо известной структурой является римская система счисления . В качестве основных цифр для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются символы I, V, X, L, C, D, M.

Система счисления является позиционной, если положение основного числительного в сложном выражении определяет его значение. Позиционные системы счисления имеют систему счисления , которая действует как множимое различных позиций. Для каждой последующей позиции основание системы счисления возводится в более высокую степень. В общей десятичной системе счисления, также называемой индуистско-арабской системой счисления , основание системы счисления равно 10. Это означает, что первая цифра умножается на $10^{0}$, следующая цифра умножается на $10^{1}$, и так далее. Например, десятичная цифра 532 означает $5\cdot 10^{2}+3\cdot 10^{1}+2\cdot 10^{0}$. Из-за влияния положения цифр цифра 532 отличается от цифр 325 и 253, хотя цифры у них одинаковые.

Другая позиционная система счисления, широко используемая в компьютерной арифметике, — это двоичная система счисления , имеющая основание 2. Это означает, что первая цифра умножается на $2^{0}$, следующая цифра через $2^{1}$, и так далее. Например, число 13 в двоичной системе записи записывается как 1101, что означает $1\cdot 2^{3}+1\cdot 2^{2}+0\cdot 2^{1}+1\cdot 2^{0}$. В вычислительной технике каждая цифра в двоичной системе счисления соответствует одному биту . Самая ранняя позиционная система была разработана древними вавилонянами и имела систему счисления 60.

Операции

Арифметические операции лежат в основе многих повседневных явлений, например, когда складываются четыре яблока из одного мешка вместе с тремя яблоками из другого мешка (верхнее изображение) или когда поровну распределяются девять яблок между тремя детьми (нижнее изображение).

Арифметические операции — это способы объединения, преобразования или манипулирования числами. Это функции , которые имеют числа как на входе, так и на выходе. Важнейшими операциями арифметики являются сложение , вычитание , умножение и деление . Дальнейшие операции включают возведение в степень , извлечение корней и логарифмирование . Если эти операции выполняются над переменными, а не над числами, их иногда называют алгебраическими операциями .

Двумя важными понятиями, связанными с арифметическими операциями, являются тождественные элементы и обратные элементы . Элемент идентификации или нейтральный элемент операции не вызывает никаких изменений, если он применяется к другому элементу. Например, единичным элементом сложения является 0, поскольку любая сумма числа и 0 дает одно и то же число. Инверсный элемент — это элемент, который в результате объединения с другим элементом образует идентификационный элемент. Например, аддитивное число , обратное числу 6, равно -6, поскольку их сумма равна 0.

Существуют не только обратные элементы, но и обратные операции . В неформальном смысле одна операция является обратной другой операции, если она отменяет первую операцию. Например, вычитание является обратным сложению, поскольку число возвращается к исходному значению, если второе число сначала добавляется, а затем вычитается, как в $13+4-4=13$. Если определить более формально, то операция " $\star$" является обратной операцией " $\circ$", если оно удовлетворяет следующему условию: $t\star s=r$ тогда и только тогда, когда $r\circ s=t$.

Коммутативность и ассоциативность — это законы, определяющие порядок выполнения некоторых арифметических операций. Операция является коммутативной, если порядок аргументов можно изменить, не влияя на результат. Так обстоит дело, например, с добавлением $7+9$ то же самое, что $9+7$. Ассоциативность — это правило, влияющее на порядок выполнения ряда операций. Операция называется ассоциативной, если в серии из двух операций не имеет значения, какая операция выполняется первой. Так обстоит дело, например, с умножением, поскольку $(5\times 4)\times 2$ то же самое, что $5\times (4\times 2)$.

Сложение и вычитание

Основные статьи: Сложение и вычитание

Сложение и вычитание

Сложение — это арифметическая операция, при которой два числа, называемые слагаемыми, объединяются в одно число, называемое суммой. Символом сложения является $+$. Примеры: $2+2=4$ и $6.3+1.26=7.56$. Термин суммирование используется, если подряд выполняется несколько сложений. Счет — это тип повторяющегося сложения, при котором непрерывно прибавляется число 1.

Вычитание является обратным действием сложения. В нем одно число, называемое вычитаемым, вычитается из другого, называемого вычитаемым. Результат этой операции называется разницей. Символ вычитания $-$. Примеры: $14-8=6$ и $45-1.7=43.3$. Вычитание часто рассматривают как частный случай сложения: вместо вычитания положительного числа можно прибавить и отрицательное число. Например $14-8=14+(-8)$. Это помогает упростить математические вычисления за счет уменьшения количества основных арифметических операций, необходимых для выполнения вычислений.

Аддитивный единичный элемент равен 0, а аддитивное обратное число является отрицательным для этого числа. Например, $13+0=13$ и $13+(-13)=0$. Сложение бывает как коммутативным, так и ассоциативным.

Умножение и деление

Основные статьи: Умножение и деление (математика)

Умножение и деление

Умножение — это арифметическая операция, при которой два числа, называемые множителем и множимым, объединяются в одно число, называемое произведением . Символами умножения являются $\times$, $\cdot$, и *. Примеры: $2\times 3=6$ и $0.3\cdot 5=1.5$. Если множимое является натуральным числом, то умножение аналогично многократному сложению, как в $2\times 3=2+2+2$.

Деление является обратным действием умножения. В нем одно число, известное как делимое, разбивается на несколько равных частей другим числом, называемым делителем. Результат этой операции называется фактором . Символами деления являются $\div$ и $/$. Примеры: $48\div 8=6$ и $29.4/1.4=21$. Деление часто рассматривается как частный случай умножения: вместо деления на число можно также умножить на обратное ему число . Обратное число равно 1, разделенному на это число. Например, $48\div 8=48\times {\tfrac {1}{8}}$.

Мультипликативный единичный элемент равен 1, а мультипликативное обратное число является обратным этому числу. Например, $13\times 1=13$ и $13\times {\tfrac {1}{13}}=1$. Умножение бывает коммутативным и ассоциативным.

Возведение в степень и логарифм

Основные статьи: Возведение в степень и логарифм

Возведение в степень и логарифм

Возведение в степень — это арифметическая операция, при которой число, известное как основание, возводится в степень другого числа, известного как показатель степени. Результат этой операции называется мощностью. Возведение в степень иногда выражается с помощью символа ^, но более распространенным способом является запись показателя степени в верхнем индексе сразу после основания. Примеры: $2^{4}=16$ и $3$^ $3=27$. Если показатель степени является натуральным числом, то возведение в степень аналогично многократному умножению, как в $2^{4}=2\times 2\times 2\times 2$.

Корни — это особый тип возведения в степень с использованием дробного показателя. Например, извлечение квадратного корня из числа — это то же самое, что возведение числа в степень. ${\tfrac {1}{2}}$ а кубический корень из числа — это то же самое, что возведение числа в степень ${\tfrac {1}{3}}$. Примеры: ${\sqrt {4}}=4^{\frac {1}{2}}=2$ и ${\sqrt[{3}]{27}}=27^{\frac {1}{3}}=3$.

Логарифм является обратным возведению в степень. Логарифм числа $x$ на базу $b$ является показателем , которому $b$ необходимо поднять, чтобы произвести $x$. Например, поскольку $1000=10^{3}$, логарифм по основанию 10 от 1000 равен 3. Логарифм $x$ базировать $b$ обозначается как $\log _{b}(x)$, или без скобок, $\log _{b}x$, или даже без явной базы, $\log x$, когда основу можно понять из контекста. Итак, предыдущий пример можно записать $\log _{10}1000=3$.

Возведение в степень и логарифм не имеют общих элементов тождества и обратных элементов, таких как сложение и умножение. Нейтральный элемент возведения в степень по отношению к показателю равен 1, как в $14^{1}=14$. Однако возведение в степень не имеет общего единичного элемента, поскольку 1 не является нейтральным элементом для основания. Возведение в степень и логарифм не являются ни коммутативными, ни ассоциативными.

Типы

В научной литературе обсуждаются различные типы арифметических систем. Они отличаются друг от друга в зависимости от того, с каким типом чисел они работают, какую систему счисления они используют для их представления и работают ли они с математическими объектами, отличными от чисел.

Целочисленная арифметика

Используя метод числовых линий, вычисляем $5+2$ выполняется, начиная с начала числовой прямой, а затем перемещая пять единиц вправо для первого сложения. Результат достигается перемещением еще двух единиц вправо для второго слагаемого.

Целочисленная арифметика — это раздел арифметики, который занимается операцией с положительными и отрицательными целыми числами. Простые операции с одной цифрой можно выполнять, следуя или запоминая таблицу, в которой представлены результаты всех возможных комбинаций, например таблицу сложения или таблицу умножения . Другими распространенными методами являются устный счет и подсчет пальцев .

Таблица сложения

+	0	1	2	3	4	...
0	0	1	2	3	4	...
1	1	2	3	4	5	...
2	2	3	4	5	6	...
3	3	4	5	6	7	...
4	4	5	6	7	8	...
...	...	...	...	...	...	...

Таблица умножения

×	0	1	2	3	4	...
0	0	0	0	0	0	...
1	0	1	2	3	4	...
2	0	2	4	6	8	...
3	0	3	6	9	12	...
4	0	4	8	12	16	...
...	...	...	...	...	...	...

Пример сложения с переносом . Черные числа — это сложение, зеленое число — перенос, а синее число — сумма.

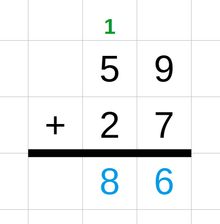
Для операций с числами, состоящими более чем из одной цифры, можно использовать различные методы для вычисления результата, используя несколько операций с одной цифрой подряд. Например, в методе сложения с переносами два числа пишутся одно над другим. Каждая пара цифр суммируется, начиная с самой правой цифры. Под ними пишется самая правая цифра суммы. Если сумма представляет собой двузначное число, то самая левая цифра, называемая «переносом», добавляется к следующей паре цифр слева. Этот процесс повторяется до тех пор, пока не будут добавлены все цифры. Другими методами, используемыми для сложения целых чисел, являются метод числовой прямой , метод частичной суммы и метод компенсации. Аналогичный метод используется для вычитания: он также начинается с самой правой цифры и использует «заимствование» или отрицательный перенос для столбца слева, если результат вычитания одной цифры отрицательный.

Пример длинного умножения . Черные числа — это множитель и множимое. Зеленые числа — это промежуточные продукты, полученные путем умножения множителя только на одну цифру множимого. Синее число — это общий продукт, рассчитанный путем сложения промежуточных продуктов.

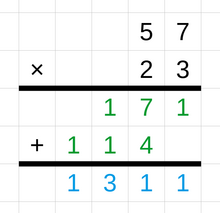
Базовый метод целочисленного умножения предполагает многократное сложение. Например, продукт $3\times 4$ можно рассчитать как $3+3+3+3$. Распространенный метод умножения больших чисел называется длинным умножением . Этот метод начинается с записи множителя над множимым. Расчет начинается с умножения множителя только на самую правую цифру множимого и записи результата ниже, начиная с крайнего правого столбца. То же самое проделывается с каждой цифрой множимого и результат в каждом случае сдвигается на одну позицию влево. На последнем этапе все отдельные продукты складываются, чтобы получить общий продукт двух многозначных чисел. Другими методами, используемыми для умножения, являются метод сетки и метод решетки . Информатика заинтересована в алгоритмах умножения с низкой вычислительной сложностью , позволяющих эффективно умножать очень большие целые числа, таких как алгоритм Карацубы , алгоритм Шенхаге-Штрассена и алгоритм Тума-Кука . Распространенный метод деления называется длинным делением . Другие методы включают короткое деление и фрагментирование .

Целочисленная арифметика не является замкнутой при делении. Это означает, что при делении одного целого числа на другое результат не всегда является целым числом. Например, 7 разделить на 2 — это не целое число, а 3,5. Один из способов гарантировать, что результат является целым числом, — округлить результат до целого числа. Однако этот метод приводит к неточностям, поскольку исходное значение изменяется. Другой метод — выполнить деление только частично и сохранить остаток . Например, 7 разделить на 2 — это 3 с остатком 1. Этих трудностей можно избежать с помощью арифметики рациональных чисел, которая позволяет точно представлять дроби.

Простой метод вычисления возведения в степень — многократное умножение. Например, возведение в степень $3^{4}$ можно рассчитать как $3\times 3\times 3\times 3$. Более эффективный метод, используемый для больших показателей, — это возведение в степень возведением в квадрат . Он разбивает вычисление на ряд операций возведения в квадрат. Например, возведение в степень $3^{65}$ можно записать как $(((((3^{2})^{2})^{2})^{2})^{2})^{2}\times 3$. Используя преимущества повторяющихся операций возведения в квадрат, потребуется всего 7 отдельных операций, а не 64 операции, необходимые для обычного повторного умножения. Методы вычисления логарифмов включают ряд Тейлора и цепные дроби . Целочисленная арифметика не замкнута при логарифме и при возведении в степень с отрицательными показателями, а это означает, что результат этих операций не всегда является целым числом.

Теория чисел

Основная статья: Теория чисел

Теория чисел изучает структуру и свойства целых чисел, а также отношения и законы между ними. Некоторые из основных разделов современной теории чисел включают элементарную теорию чисел , аналитическую теорию чисел , алгебраическую теорию чисел и геометрическую теорию чисел . Элементарная теория чисел изучает аспекты целых чисел, которые можно исследовать с помощью элементарных методов. Его темы включают делимость , факторизацию и простоту . Аналитическая теория чисел, напротив, опирается на методы анализа и исчисления. В нем рассматриваются такие проблемы, как распределение простых чисел и утверждение, что каждое четное число является суммой двух простых чисел . Алгебраическая теория чисел использует алгебраические структуры для анализа свойств и отношений между числами. Примерами являются использование полей и колец , например, в полях алгебраических чисел, таких как кольцо целых чисел . Геометрическая теория чисел использует понятия геометрии для изучения чисел. Например, он исследует, как точки решетки с целочисленными координатами ведут себя на плоскости. Дальнейшие разделы теории чисел — вероятностная теория чисел , в которой используются методы теории вероятностей . комбинаторная теория чисел , которая опирается на область комбинаторики , вычислительная теория чисел , которая подходит к теоретико-числовым задачам с помощью вычислительных методов, и прикладная теория чисел, которая исследует применение теории чисел в таких областях, как физика , биология и криптография .

Важнейшие теоремы в теории чисел включают фундаментальную теорему арифметики , теорему Евклида и последнюю теорему Ферма . Согласно фундаментальной теореме арифметики, каждое целое число больше 1 является либо простым числом, либо может быть представлено в виде уникального произведения простых чисел. Например, число 18 не является простым числом и его можно представить как $2\times 3\times 3$, все из которых являются простыми числами. Число 19 , напротив, является простым числом, не имеющим другой простой факторизации. Теорема Евклида утверждает, что существует бесконечно много простых чисел. Последняя теорема Ферма — это утверждение, что для $a$, $b$, и $c$, чтобы решить уравнение $a^{n}+b^{n}=c^{n}$ если $n$ больше, чем $2$.

Арифметика рациональных чисел

Арифметика рациональных чисел — это раздел арифметики, который занимается манипулированием числами, которые можно выразить как отношение двух целых чисел. Большинство арифметических операций над рациональными числами можно вычислить, выполнив серию целочисленных арифметических операций над числителями и знаменателями участвующих чисел. Если два рациональных числа имеют одинаковый знаменатель, то их можно сложить, сложив числители и сохранив общий знаменатель. Например, ${\tfrac {2}{7}}+{\tfrac {3}{7}}={\tfrac {5}{7}}$. Аналогичная процедура используется и для вычитания. Если у двух чисел разные знаменатели, их необходимо преобразовать, чтобы найти общий знаменатель. Этого можно достичь путем масштабирования первого числа со знаменателем второго числа и масштабирования второго числа со знаменателем первого числа. Например, ${\tfrac {1}{3}}+{\tfrac {1}{2}}={\tfrac {1\cdot 2}{3\cdot 2}}+{\tfrac {1\cdot 3}{2\cdot 3}}={\tfrac {2}{6}}+{\tfrac {3}{6}}={\tfrac {5}{6}}$.

Два рациональных числа умножаются путем умножения их числителей и знаменателей соответственно, как в ${\tfrac {2}{3}}\cdot {\tfrac {2}{5}}={\tfrac {2\cdot 2}{3\cdot 5}}={\tfrac {4}{15}}$. Разделить одно рациональное число на другое можно, умножив первое число на обратное второму числу. Это означает, что числитель и знаменатель второго числа меняют положение. Например, ${\tfrac {3}{5}}:{\tfrac {2}{7}}={\tfrac {3}{5}}\cdot {\tfrac {7}{2}}={\tfrac {21}{10}}$. В отличие от целочисленной арифметики, арифметика рациональных чисел замкнута относительно деления до тех пор, пока делитель не равен 0.

И целочисленная арифметика, и арифметика рациональных чисел не замкнуты при возведении в степень и логарифме. Один из способов вычисления возведения в степень с дробным показателем - выполнить два отдельных вычисления: одно возведение в степень с использованием числителя показателя, а затем извлечь корень n-й степени из результата на основе знаменателя показателя. Например, $5^{\frac {2}{3}}={\sqrt[{3}]{5^{2}}}$. Первую операцию можно выполнить, используя такие методы, как повторное умножение или возведение в степень возведением в квадрат. Один из способов получить приблизительный результат для второй операции — использовать метод Ньютона , который использует ряд шагов для постепенного уточнения первоначального предположения, пока оно не достигнет желаемого уровня точности. Ряд Тейлора или метод цепных дробей можно использовать для вычисления логарифмов.

Обозначение десятичной дроби — это особый способ представления рациональных чисел, знаменатель которых равен степени 10. Например, рациональные числа ${\tfrac {1}{10}}$, ${\tfrac {371}{100}}$, и ${\tfrac {44}{10000}}$ записываются как 0,1, 3,71 и 0,0044 в формате десятичной дроби. Модифицированные версии методов вычисления целых чисел, такие как сложение с переносом и длинное умножение, можно применять к вычислениям с десятичными дробями. Не все рациональные числа имеют конечное представление в десятичной системе счисления. Например, рациональное число ${\tfrac {1}{3}}$ соответствует 0,333... с бесконечным числом троек. Сокращенное обозначение этого типа повторяющейся десятичной дроби — 0.3 . Каждая повторяющаяся десятичная дробь выражает рациональное число.

Арифметика действительных чисел

Арифметика действительных чисел — это раздел арифметики, который занимается манипулированием как рациональными, так и иррациональными числами. Иррациональные числа — это числа, которые нельзя выразить через дроби или повторяющиеся десятичные дроби, например, корень из 2 и π . В отличие от арифметики рациональных чисел, арифметика действительных чисел замкнута при возведении в степень, если в качестве основы используется положительное число. То же самое верно и для логарифма положительных действительных чисел, если основание логарифма положительное, а не 1.

Иррациональные числа представляют собой бесконечный неповторяющийся ряд десятичных цифр. Из-за этого часто не существует простого и точного способа выразить результаты арифметических операций, таких как ${\sqrt {2}}+\pi$ или $e\cdot {\sqrt {3}}$. В тех случаях, когда абсолютная точность не требуется, проблему вычисления арифметических операций над действительными числами обычно решают путем усечения или округления . При усечении определенное количество крайних левых цифр сохраняется, а оставшиеся цифры отбрасываются или заменяются нулями. Например, число π имеет бесконечное количество цифр, начиная с 3,14159.... Если это число усечь до 4 десятичных знаков, результат будет 3,141. Округление — это аналогичный процесс, в котором последняя сохраненная цифра увеличивается на единицу, если следующая цифра равна 5 или больше, но остается той же, если следующая цифра меньше 5, так что округленное число является лучшим приближением заданной точности для исходный номер. Например, если число π округлить до 4 десятичных знаков, результат будет 3,142, поскольку следующая цифра — 5, поэтому 3,142 ближе к π, чем 3,141. Эти методы позволяют компьютерам эффективно выполнять приблизительные вычисления с действительными числами.

Приближения и ошибки

В науке и технике числа представляют собой оценки физических величин, полученные в результате измерений или моделирования. В отличие от математически точных чисел, таких как π или ⁠ ${\sqrt {2}}$⁠ научно значимые числовые данные по своей сути неточны, что приводит к некоторой неопределенности измерений . Один из основных способов выразить степень уверенности в значении каждого числа и избежать ложной точности — округлить каждое измерение до определенного количества цифр, называемых значащими цифрами , которые считаются точными. Например, рост человека, измеренный рулеткой , может быть известен только с точностью до сантиметра, поэтому его следует представлять как 1,62 метра, а не 1,6217 метра. При преобразовании в британские единицы эту величину следует округлить до 64 дюймов или 63,8 дюйма, а не до 63,7795 дюйма, чтобы четко передать точность измерения. Когда число записано с использованием обычной десятичной записи, ведущие нули не имеют значения, а конечные нули чисел, не записанных с десятичной точкой, неявно считаются незначащими. Например, числа 0,056 и 1200 имеют только по 2 значащие цифры, а число 40,00 имеет 4 значащие цифры. Представление неопределенности с использованием только значащих цифр — относительно грубый метод с некоторыми неинтуитивными тонкостями; явное отслеживание оценки или верхней границы ошибки аппроксимации является более сложным подходом. В этом примере рост человека может быть представлен как 1,62 ± 0,005 метра или 63,8 ± 0,2 дюйма .

При выполнении расчетов с неопределенными величинами неопределенность должна распространяться на рассчитанные величины. При сложении или вычитании двух или более величин сложите абсолютные неопределенности каждого слагаемого, чтобы получить абсолютную неопределенность суммы. При умножении или делении двух или более величин сложите относительные неопределенности каждого фактора, чтобы получить относительную неопределенность продукта. При представлении неопределенности значащими цифрами неопределенность может быть грубо распространена путем округления результата сложения или вычитания двух или более величин до крайнего левого последнего значащего десятичного знака среди слагаемых, а также путем округления результата умножения или деления двух или более величин до наименьшее количество значащих цифр среди факторов. (См. «Значительные цифры § Арифметика ».)

Более сложные методы работы с неопределенными значениями включают интервальную арифметику и аффинную арифметику . Интервальная арифметика описывает операции с интервалами . Интервалы можно использовать для представления диапазона значений, если неизвестна точная величина, например, из-за ошибок измерения . Интервальная арифметика включает в себя такие операции, как сложение и умножение интервалов, например $[1,2]+[3,4]=[4,6]$ и $[1,2]\times [3,4]=[3,8]$. Она тесно связана с аффинной арифметикой, целью которой является получение более точных результатов путем выполнения вычислений над аффинными формами, а не над интервалами. Аффинная форма — это число вместе с погрешностями, которые описывают, как число может отклоняться от фактической величины.

Точность числовых величин можно выразить единообразно, используя нормализованную экспоненциальную запись , которая также удобна для краткого представления чисел, которые намного больше или меньше 1. Используя экспоненциальную запись, число разлагается на произведение числа от 1 до 10, называется мантиссой , а 10 возводится в некоторую целочисленную степень, называемую экспонентой . Мантисса состоит из значащих цифр числа и записывается в виде первой цифры 1–9, за которой следует десятичная точка и последовательность цифр 0–9. Например, нормализованное научное обозначение числа 8276000 имеет вид $8.276\times 10^{6}$ с мантиссой 8,276 и показателем 6, а нормализованное научное обозначение числа 0,00735 равно $7.35\times 10^{-3}$ с мантиссой 7,35 и показателем -3. В отличие от обычной десятичной записи, где конечные нули больших чисел неявно считаются несущественными, в научной записи каждая цифра мантиссы считается значимой, а добавление конечных нулей указывает на более высокую точность. Например, хотя число 1200 неявно имеет только 2 значащие цифры, число ⁠ $1.20\times 10^{3}$⁠ явно имеет 3.

Распространенный метод, используемый компьютерами для аппроксимации арифметики действительных чисел, называется арифметикой с плавающей запятой . Он представляет действительные числа, аналогичные научным обозначениям, через три числа: мантиссу, основание и показатель степени. Точность мантиссы ограничена количеством битов, выделенных для ее представления. Если в результате арифметической операции получается число, для которого требуется больше бит, чем доступно, компьютер округляет результат до ближайшего представимого числа. Это приводит к ошибкам округления . Следствием такого поведения является то, что некоторые законы арифметики нарушаются арифметикой с плавающей запятой. Например, сложение чисел с плавающей запятой не является ассоциативным, поскольку вносимые ошибки округления могут зависеть от порядка сложения. Это означает, что результат $(a+b)+c$ иногда отличается от результата $a+(b+c)$. Самый распространенный технический стандарт, используемый для арифметики с плавающей запятой, называется IEEE 754 . Помимо прочего, он определяет, как представляются числа, как выполняются арифметические операции и округления, а также как обрабатываются ошибки и исключения. В случаях, когда скорость вычислений не является ограничивающим фактором, можно использовать арифметику произвольной точности , для которой точность вычислений ограничивается только памятью компьютера.

Использование инструмента

Вычисления в ментальной арифметике производятся исключительно в уме, не опираясь на внешние средства.

Формы арифметики также можно отличить по инструментам, используемым для выполнения вычислений, и включают в себя множество подходов, помимо регулярного использования ручки и бумаги. Ментальная арифметика опирается исключительно на разум без внешних инструментов. Вместо этого он использует визуализацию, запоминание и определенные методы вычислений для решения арифметических задач. Одним из таких методов является метод компенсации, который заключается в изменении чисел, чтобы облегчить расчет, а затем в корректировке результата. Например, вместо расчета $85-47$, рассчитывается $85-50$ что проще, поскольку используется круглое число. На следующем этапе добавляется $3$ к результату, чтобы компенсировать предыдущую настройку. Ментальную арифметику часто преподают в начальной школе для тренировки числовых способностей учащихся.

Человеческое тело также можно использовать в качестве арифметического инструмента. с использованием рук при счете пальцев, Маленьких детей часто знакомят чтобы научить их цифрам и простым вычислениям. В самой базовой форме количество вытянутых пальцев соответствует представленному количеству, а арифметические операции, такие как сложение и вычитание, выполняются путем вытягивания или втягивания пальцев. Эта система ограничена небольшими числами, в то время как более продвинутые системы используют другие подходы и для представления больших количеств. Человеческий голос используется в качестве арифметического средства при словесном счете.

Счеты – это инструменты для выполнения арифметических операций путем перемещения бусинок.

Метки представляют собой простую систему, основанную на внешних инструментах, отличных от тела. Он основан на штрихах, нарисованных на поверхности, или насечках на деревянной палочке, чтобы отслеживать количество. В некоторых формах меток штрихи располагаются группами по пять, чтобы их было легче читать. Счеты — это более совершенный инструмент для представления чисел и выполнения вычислений. Счеты обычно состоят из ряда стержней, на каждой из которых находится несколько бусин . Каждая бусина представляет собой количество, которое засчитывается, если бусину переместить от одного конца стержня к другому. Расчеты происходят путем изменения положения бусинок до тех пор, пока окончательный рисунок бусинок не покажет результат. Сопутствующие вспомогательные средства включают в себя счетные доски , на которых используются жетоны, ценность которых зависит от области на доске, на которой они размещены. и счетные стержни , которые расположены горизонтально и вертикально для обозначения разных чисел. Секторы и логарифмические линейки — это более совершенные вычислительные инструменты, которые основаны на геометрических отношениях между различными масштабами для выполнения как основных, так и сложных арифметических операций. Печатные таблицы были особенно полезны для поиска результатов таких операций, как логарифмирование и тригонометрические функции .

Механические калькуляторы автоматизируют процессы ручных вычислений. Они предоставляют пользователю некое устройство ввода для ввода чисел, поворачивая циферблаты или нажимая клавиши. Они включают в себя внутренний механизм, обычно состоящий из шестерен , рычагов и колес для выполнения вычислений и отображения результатов. Для электронных калькуляторов и компьютеров эта процедура дополнительно уточняется путем замены механических компонентов электронными схемами, такими как микропроцессоры , которые объединяют и преобразуют электрические сигналы для выполнения вычислений.

Другие

Пример модульной арифметики с использованием часов: после прибавления 4 часов к 9 часам стрелка снова начинается сначала и указывает на 1 час.

Есть много других видов арифметики. Модульная арифметика оперирует конечным набором чисел. Если в результате операции получается число, выходящее за пределы этого конечного набора, то это число возвращается обратно в набор, подобно тому, как стрелки часов снова начинают сначала после завершения одного цикла. Число, при котором происходит эта регулировка, называется модулем. Например, обычные часы имеют модуль 12. В случае прибавления 4 к 9 это означает, что результатом будет не 13, а 1. Тот же принцип применим и к другим операциям, таким как вычитание, умножение и деление.

Некоторые формы арифметики связаны с операциями, выполняемыми над математическими объектами, отличными от чисел. Интервальная арифметика описывает операции с интервалами. Векторная арифметика и матричная арифметика описывают арифметические операции над векторами и матрицами , такие как сложение векторов и умножение матриц .

Арифметические системы можно классифицировать в зависимости от системы счисления, на которой они основаны. Например, десятичная арифметика описывает арифметические операции в десятичной системе. Другими примерами являются двоичная арифметика, восьмеричная арифметика и шестнадцатеричная арифметика.

Арифметика составных единиц описывает арифметические операции, выполняемые над величинами с составными единицами. Он включает в себя дополнительные операции для управления преобразованием между количествами отдельных единиц и составных единиц. Например, операция редукции используется для преобразования составного количества 1 час 90 минут в единичное количество 150 минут.

Недиофантова арифметика — это арифметические системы, которые нарушают традиционную арифметическую интуицию и включают такие уравнения, как $1+1=1$ и $2+2=5$. Их можно использовать для представления некоторых реальных ситуаций в современной физике и повседневной жизни. Например, уравнение $1+1=1$ может использоваться для описания наблюдения о том, что если одну каплю дождя добавить к другой капле дождя, они не останутся двумя отдельными сущностями, а станут одним целым.

Аксиоматические основы

Аксиоматические основы арифметики пытаются обеспечить небольшой набор законов, называемых аксиомами , из которых могут быть выведены все фундаментальные свойства чисел и операции над числами. Они представляют собой логически последовательные и систематические основы, которые можно использовать для формулировки математических доказательств строгой . Двумя хорошо известными подходами являются аксиомы Дедекинда – Пеано и теоретико-множественные конструкции.

Аксиомы Дедекинда – Пеано обеспечивают аксиоматизацию арифметики натуральных чисел. Их основные принципы были впервые сформулированы Рихардом Дедекиндом , а позднее уточнены Джузеппе Пеано . Они полагаются лишь на небольшое количество примитивных математических понятий, таких как 0, натуральное число и преемник . Аксиомы Пеано определяют, как эти понятия связаны друг с другом. Все остальные арифметические понятия затем могут быть определены в терминах этих примитивных понятий.

1. 0 – натуральное число.
2. У каждого натурального числа есть преемник, который также является натуральным числом.
3. Последователи двух разных натуральных чисел никогда не бывают идентичными.
4. 0 не является преемником натурального числа.
5. Если набор содержит 0 и всех его преемников, то он содержит все натуральные числа.

Числа больше 0 выражаются повторным применением функции-преемника. $s$. Например, $1$ является $s(0)$ и $3$ является $s(s(s(0)))$. Арифметические операции можно определить как механизмы, влияющие на применение функции-преемника. Например, чтобы добавить $2$ к любому числу — это то же самое, что дважды применить функцию-преемник к этому числу.

Различные аксиоматизации арифметики опираются на теорию множеств. Они охватывают натуральные числа, но также могут быть распространены на целые, рациональные и действительные числа. Каждое натуральное число представлено уникальным набором. 0 обычно определяется как пустой набор $\varnothing$. Каждое последующее число можно определить как объединение предыдущего числа с множеством, содержащим предыдущее число. Например, $1=0\cup \{0\}=\{0\}$, $2=1\cup \{1\}=\{0,1\}$, и $3=2\cup \{2\}=\{0,1,2\}$. Целые числа можно определить как упорядоченные пары натуральных чисел, в которых второе число вычитается из первого. Например, пара (9, 0) представляет число 9, а пара (0, 9) представляет число -9. Рациональные числа определяются как пары целых чисел, где первое число представляет собой числитель, а второе число представляет собой знаменатель. Например, пара (3, 7) представляет рациональное число ${\tfrac {3}{7}}$. Один из способов построения действительных чисел основан на концепции дедекиндовых сокращений . Согласно этому подходу, каждое действительное число представляется разделением всех рациональных чисел на два набора: один для всех чисел ниже представленного действительного числа, а другой для остальных. Арифметические операции определяются как функции, которые выполняют различные теоретико-множественные преобразования над множествами, представляющими входные числа, для получения набора, представляющего результат.

История

Некоторые историки интерпретируют кость Ишанго как один из самых ранних арифметических артефактов.

Самые ранние формы арифметики иногда восходят к счету и счетным меткам, используемым для учета количества. Некоторые историки предполагают, что кость Лебомбо (датированная примерно 43 000 лет назад) и кость Ишанго (датированная примерно 22 000–30 000 лет назад) являются древнейшими арифметическими артефактами, но эта интерпретация оспаривается. Однако базовое чувство чисел могло предшествовать этим открытиям и могло даже существовать до развития языка.

Лишь с появлением древних цивилизаций , начиная примерно с 3000 г. до н. э., начал развиваться более сложный и структурированный подход к арифметике. Это стало необходимым из-за возросшей необходимости отслеживать хранящиеся предметы, управлять землевладением и организовывать обмены. Все основные древние цивилизации разработали непозиционные системы счисления для облегчения представления чисел. У них также были символы для таких операций, как сложение и вычитание, и они знали дроби. Примерами являются египетские иероглифы , а также системы счисления, изобретенные в Шумере , Китае и Индии . Первая позиционная система счисления была разработана вавилонянами примерно в 1800 году до нашей эры. Это было значительным улучшением по сравнению с более ранними системами счисления, поскольку делало представление больших чисел и вычисления над ними более эффективными. Счеты использовались как ручные вычислительные инструменты с древних времен как эффективное средство для выполнения сложных вычислений.

Ранние цивилизации в основном использовали числа для конкретных практических целей, таких как коммерческая деятельность и налоговый учет, но у них не было абстрактной концепции самого числа. Ситуация изменилась с появлением древнегреческих математиков , которые начали исследовать абстрактную природу чисел, а не изучать, как они применяются к конкретным задачам. Еще одной новой особенностью было использование доказательств для установления математических истин и подтверждения теорий. Еще одним вкладом стало различие различных классов чисел, таких как четные , нечетные и простые числа . Это включало открытие того, что числа для определенных геометрических длин иррациональны и поэтому не могут быть выражены в виде дроби. Работы Фалеса Милетского и Пифагора VII и VI веков до нашей эры часто считаются началом греческой математики. Диофант был влиятельной фигурой в греческой арифметике в III веке до нашей эры благодаря его многочисленным вкладам в теорию чисел и исследованию применения арифметических операций к алгебраическим уравнениям .

Древние индийцы были первыми, кто разработал концепцию нуля как числа, используемого в вычислениях. Точные правила его работы были записаны Брахмагуптой примерно в 628 году нашей эры. Понятие «ноль или ничего» существовало задолго до этого, но оно не считалось объектом арифметических операций. Брахмагупта далее подробно обсудил вычисления с отрицательными числами и их применение к таким проблемам, как кредит и долг. Сама концепция отрицательных чисел значительно старше и впервые была исследована в китайской математике в первом тысячелетии до нашей эры.

Индийские математики также разработали позиционную десятичную систему, используемую сегодня, в частности концепцию нулевой цифры вместо пустых или недостающих позиций. Например, подробное описание его деятельности было предоставлено Арьябхатой примерно на рубеже VI века нашей эры. Индийская десятичная система была дополнительно усовершенствована и расширена до нецелых чисел во время Золотого века ислама арабскими математиками, такими как Аль-Хорезми . Его работа оказала влияние на внедрение десятичной системы счисления в западный мир, который в то время опирался на римскую систему счисления . Там ее популяризировали такие математики, как Леонардо Фибоначчи , который жил в 12 и 13 веках и также разработал последовательность Фибоначчи . В средние века и эпоху Возрождения было опубликовано множество популярных учебников, посвященных практическим расчетам в торговле. В этот период также стало широко распространено использование счетов. В 16 веке математик Джероламо Кардано придумал концепцию комплексных чисел как способ решения кубических уравнений .

Лейбница Ступенчатый счетчик был первым калькулятором, который мог выполнять все четыре арифметических действия.

Первые механические калькуляторы были разработаны в 17 веке и значительно облегчили сложные математические вычисления, такие как Блеза Паскаля и калькулятор ступенчатый Готфрида Вильгельма Лейбница счётчик . открыл логарифм Непер В 17 веке Джон .

В XVIII и XIX веках такие математики, как Леонард Эйлер и Карл Фридрих Гаусс, заложили основы современной теории чисел. Еще одно событие этого периода касалось работ по формализации и основам арифметики, таких как Георга Кантора и теория множеств аксиомы Дедекинда-Пеано, используемые в качестве аксиоматизации арифметики натуральных чисел. Компьютеры и электронные калькуляторы были впервые разработаны в 20 веке. Их широкое использование произвело революцию как в точности, так и в скорости, с которой могут быть выполнены даже сложные арифметические вычисления.

В различных областях

Образование

Основная статья: Математическое образование

Обучение арифметике является частью начального образования . Это одна из первых форм математического образования , с которой сталкиваются дети. Цель элементарной арифметики — дать учащимся базовое представление о числах и познакомить их с фундаментальными числовыми операциями, такими как сложение, вычитание, умножение и деление. Обычно его вводят в отношении конкретных сценариев, таких как подсчет бусин , разделение класса на группы детей одинакового размера и расчет сдачи при покупке товаров. Обычными инструментами раннего арифметического обучения являются числовые линии , таблицы сложения и умножения, счетные кубики и счеты.

На более поздних этапах основное внимание уделяется более абстрактному пониманию и знакомству учащихся с различными типами чисел, такими как отрицательные числа, дроби, действительные числа и комплексные числа. Кроме того, они охватывают более сложные числовые операции, такие как возведение в степень, извлечение корней и логарифм. Они также показывают, как арифметические операции используются в других разделах математики, например, их применение для описания геометрических фигур и использование переменных в алгебре. Другой аспект — научить учащихся использовать алгоритмы и калькуляторы для решения сложных арифметических задач.

Психология

Психология . арифметики интересуется тем, как люди и животные изучают числа, представляют их и используют для вычислений Он исследует, как понимаются и решаются математические задачи и как арифметические способности связаны с восприятием , памятью , суждением и принятием решений . Например, он исследует, как наборы конкретных предметов сначала встречаются в восприятии, а затем связываются с числами. Дальнейшая область исследований касается связи между числовыми вычислениями и использованием языка для формирования представлений. Психология также исследует биологическое происхождение арифметики как врожденной способности. Это касается довербальных и досимволических когнитивных процессов, реализующих арифметические операции, необходимые для успешного представления мира и выполнения таких задач, как пространственная навигация.

Одним из понятий, изучаемых психологией, является умение считать , то есть способность понимать числовые понятия, применять их к конкретным ситуациям и рассуждать с их помощью. Оно включает в себя фундаментальное чувство чисел, а также способность оценивать и сравнивать количества. Кроме того, он включает в себя способности символически представлять числа в системах счисления, интерпретировать числовые данные и оценивать арифметические вычисления. Умение считать является ключевым навыком во многих академических областях. Отсутствие навыков счета может препятствовать успеху в учебе и привести к принятию плохих экономических решений в повседневной жизни, например, из-за неправильного понимания планов ипотеки и страховых полисов .

Философия

Основная статья: Философия математики

Философия арифметики изучает фундаментальные концепции и принципы, лежащие в основе чисел и арифметических операций. Он исследует природу и онтологический статус чисел, связь арифметики с языком и логикой , а также способы приобретения арифметических знаний .

Согласно платонизму , числа существуют независимо от разума: они существуют как абстрактные объекты вне пространства-времени и без причинных сил. Эта точка зрения отвергается интуиционистами , которые утверждают, что математические объекты являются мысленными конструкциями. Дальнейшими теориями являются логицизм , который утверждает, что математические истины сводимы к логическим истинам . и формализм , который утверждает, что математические принципы — это правила манипулирования символами, не утверждая, что они соответствуют сущностям вне деятельности, управляемой правилами.

Традиционно доминирующая точка зрения в эпистемологии арифметики состоит в том, что арифметические истины познаваемы априорно . Это означает, что их можно познать только путем мышления, без необходимости полагаться на чувственный опыт . Некоторые сторонники этой точки зрения утверждают, что арифметические знания являются врожденными, в то время как другие утверждают, что существует некая форма рациональной интуиции, с помощью которой можно постичь математические истины. Более поздняя альтернативная точка зрения была предложена философами -натуралистами, такими как Уиллард Ван Орман Куайн , которые утверждают, что математические принципы являются обобщениями высокого уровня, которые в конечном итоге основаны на чувственном мире, описанном эмпирическими науками.

Другие

Арифметика актуальна для многих областей. В повседневной жизни требуется рассчитывать сдачу при покупках, управлять личными финансами , корректировать рецепт приготовления на разное количество порций. Предприятия используют арифметику для расчета прибылей и убытков и анализа рыночных тенденций . В области машиностроения он используется для измерения величин, расчета нагрузок и сил, а также проектирования конструкций. Криптография опирается на арифметические операции для защиты конфиденциальной информации путем шифрования данных и сообщений.

Арифметика тесно связана со многими разделами математики, которые зависят от числовых операций. Алгебра опирается на арифметические принципы для решения уравнений с использованием переменных. Эти принципы также играют ключевую роль в исчислении в попытках определить скорость изменений и площади под кривыми . Геометрия использует арифметические операции для измерения свойств фигур, а статистика использует их для анализа числовых данных. Из-за актуальности арифметических операций в математике влияние арифметики распространяется на большинство наук, таких как физика , информатика и экономика . Эти операции используются в расчетах, решении проблем , анализе данных и алгоритмах, что делает их неотъемлемой частью научных исследований, технологических разработок и экономического моделирования.

См. также

• Алгоризм
• Арифметика конечных полей
• Краткое описание арифметики
• Растительная арифметика

Ссылки

Источники

• Ахац, Томас; Андерсон, Джон Г. (2005). Технический цех Математика . Industrial Press Inc. ISBN  978-0-8311-3086-2 .
• Адамович, Зофия (1994). «Сила возведения в степень в арифметике». У Джозефа, Энтони; Миньо, Фульбер; Мюрат, Франсуа; Прум, Бернар; Рентшлер, Рудольф (ред.). Первый европейский математический конгресс: Париж, 6–10 июля 1992 г. Том I, приглашенные лекции (Часть 1) . Биркхойзер. стр. 299–320. дои : 10.1007/978-3-0348-9110-3_9 . ISBN  978-3-0348-9110-3 .
• Адхами, Реза; Минен, Питер М.; Минен, Питер; Хайт, Денис (2007). Фундаментальные концепции электротехники и вычислительной техники с практическими задачами проектирования . Универсал-Издательство. ISBN  978-1-58112-971-7 .
• Али Рахман, Эрна Сукинна; Шахрилл, Масита; Аббас, Нор Арифахвати; Тан, Эбби (2017). «Развитие математических навыков учащихся с учетом порядка действий». Международный журнал исследований в области образования и науки : 373. doi : 10.21890/ijres.327896 .
• Анг, Тянь Се; Лам, Лэй Йонг (2004). Мимолетные шаги: прослеживание концепции арифметики и алгебры в древнем Китае (пересмотренное издание). Всемирная научная. ISBN  978-981-4483-60-5 .
• Асано, Акихито (2013). Введение в математику для экономики . Издательство Кембриджского университета. ISBN  978-1-107-00760-4 .
• Аскью, Майк (2010). «Это не (просто) то, что вы делаете: эффективные учителя счета» . В Яне, Томпсоне (ред.). Проблемы преподавания счета в начальной школе . McGraw-Hill Education (Великобритания). ISBN  978-0-335-24153-8 .
• Обри, Кэрол (1999). Развивающий подход к раннему чтению: помощь в повышении достижений детей и преодолении трудностей в обучении . А&С Черный. ISBN  978-1-4411-9164-9 .
• Багария, Джоан (2023). «Теория множеств» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета . Проверено 19 ноября 2023 г.
• Барнс, Эндрю Дж.; Райс, Томас; Ханох, Янив (2017). «Использование поведенческой экономики для улучшения решений людей о покупке медицинской страховки» . В Ханохе Янив; Барнс, Эндрю; Райс, Томас (ред.). Поведенческая экономика и здоровое поведение: ключевые концепции и текущие исследования . Тейлор и Фрэнсис. ISBN  978-1-317-26952-6 .
• Берч, Дэниел Б.; Гири, Дэвид С.; Кепке, Кэтлин Манн (2015). Развитие математического познания: нейронные субстраты и генетические влияния . Академическая пресса. ISBN  978-0-12-801909-2 .
• Берд, Джон (2021). Инженерная математика Берда . Тейлор и Фрэнсис. ISBN  978-0-367-64378-2 .
• Блох, Итан Д. (2011). Реальные цифры и реальный анализ . Springer Science & Business Media. ISBN  978-0-387-72177-4 .
• Бохачек, Питер (2009). «Введение в измерения» . Обучение количественным навыкам в области наук о Земле . Ресурсный центр научного образования Карлтонского колледжа; Американская ассоциация учителей физики . Проверено 6 марта 2024 г.
• Букер, Джордж; Бонд, Дениз; Воробей, Лен; Лебедь, Пол (2015). Преподавание начальной математики . Пирсон Высшее образование, Австралия. ISBN  978-1-4860-0488-1 .
• Брэдли, Майкл Дж. (2006). Рождение математики: от древности до 1300 года . Издательство информационной базы. ISBN  978-0-7910-9723-6 .
• Брент, Ричард П.; Циммерманн, Пол (2010). Современная компьютерная арифметика . Издательство Кембриджского университета. ISBN  978-1-139-49228-7 .
• Бронштейн И.Н.; Семендяев К.А.; Мусиоль, Герхард; Мюлиг, Хайнер (2015). Справочник по математике . Спрингер. ISBN  978-3-662-46221-8 .
• Браун, Дэвид (2010). «Измерение времени и расстояния на небесах над Месопотамией с краткими ссылками на другие древние астральные науки» . В Морли, Иэн; Ренфрю, Колин (ред.). Археология измерения: понимание неба, земли и времени в древних обществах . Издательство Кембриджского университета. ISBN  978-0-521-11990-0 .
• Брюдерер, Герберт (2021). Вехи развития аналоговых и цифровых вычислений . Спрингер Природа. ISBN  978-3-030-40974-6 .
• Бадд, Кристофер Дж.; Сангвин, Кристофер (2001). Математика в изобилии!: Мастер-классы, семинары и командные проекты по математике и ее приложениям . ОУП Оксфорд. ISBN  978-0-19-850770-3 .
• Бухштаб А.А.; Нечаев, В.И. (2014). «Элементарная теория чисел» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Бухштаб А.А.; Нечаев, В.И. (2016). «Натуральное число» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Бухштаб А.А.; Печаев, В.И. (2020). «Арифметика» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Бургин, Марк (2022). Трилогия чисел и арифметики — Книга 1: История чисел и арифметики: информационная перспектива . Всемирная научная. ISBN  978-981-12-3685-3 .
• Кафаро, Массимо; Эпикоко, Итало; Пулимено, Марко (2018). «Методы разработки алгоритмов биоинформатики» . Энциклопедия биоинформатики и вычислительной биологии: Азбука биоинформатики . Эльзевир. ISBN  978-0-12-811432-2 .
• Цай, Тяньсинь (2023 г.). Краткая история математики: прогулка по цивилизациям нашего мира . Спрингер Природа. ISBN  978-3-031-26841-0 .
• Кэмпбелл, Стивен Р. (2012). «Понимание элементарной теории чисел применительно к арифметике и алгебре» . В Зазкисе, Рина; Кэмпбелл, Стивен Р. (ред.). Теория чисел в математическом образовании: перспективы и перспективы . Рутледж. ISBN  978-1-136-50143-2 .
• Кэмпбелл-Келли, Мартин; Кроаркен, Мэри; Флуд, Рэймонд; Робсон, Элеонора (2007). История математических таблиц: от Шумера к электронным таблицам . ОУП. ISBN  978-0-19-850841-0 .
• Каприо, Микеле; Авени, Андреа; Мукерджи, Саян (2022). «О трех классах недиофантовой арифметики». Involve, Математический журнал . 15 (5): 763–774. arXiv : 2102.04197 . дои : 10.2140/involve.2022.15.763 . S2CID   231847291 .
• Каррахер, Дэвид В.; Шлиман, Аналюсия Д. (2015). «Мощные идеи по математике в начальной школе» . На английском языке: Лин Д .; Киршнер, Дэвид (ред.). Справочник международных исследований в области математического образования . Рутледж. ISBN  978-1-134-62664-9 .
• Кавана, Джозеф (2017). «6. Умножение с фиксированной точкой» . Основы компьютерной арифметики и Verilog HDL . ЦРК Пресс. ISBN  978-1-351-83411-7 .
• Чакраверти, Снехашиш; Рут, Саудамини (2022). Решение неопределенных статических и динамических задач на основе аффинной арифметики . Спрингер Природа. ISBN  978-3-031-02424-5 .
• Чемла, Карин; Келлер, Агата; Пруст, Кристина (2023). Культуры вычислений и количественной оценки в древнем мире: числа, измерения и операции в документах из Месопотамии, Китая и Южной Азии . Спрингер Природа. ISBN  978-3-030-98361-1 .
• Чиньони, Джоанни А.; Коссу, Джованни А. (2016). «Глобальный виртуальный музей информатики и технологий, идея проекта» . В Татналле, Артур; Лесли, Кристофер (ред.). Международные сообщества изобретателей и инноваций: Международная конференция IFIP WG 9.7 по истории вычислений, ХК 2016, Бруклин, Нью-Йорк, США, 25–29 мая 2016 г., Пересмотренные избранные статьи . Спрингер. ISBN  978-3-319-49463-0 .
• Коэн, Джоэл С. (2003). Компьютерная алгебра и символьные вычисления: математические методы . ЦРК Пресс. ISBN  978-1-4398-6370-1 .
• Коливан, Марк (2023). «Аргументы незаменимости в философии математики» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета . Проверено 20 марта 2024 г.
• Конфри, Джер (1994). «Расщепление, сходство и скорость изменения: новый подход к умножению и экспоненциальным функциям». В Хареле, Гершон; Конфри, Джер (ред.). Развитие мультипликативного мышления при изучении математики . Издательство Государственного университета Нью-Йорка. ISBN  978-1-4384-0580-3 .
• Конради, Уиллем; Горанко, Валентин (2015). Логика и дискретная математика: краткое введение . Джон Уайли и сыновья. ISBN  978-1-118-76109-0 .
• Крайер, CW (2014). Математический учебник для инженеров . ИОС Пресс. ISBN  978-1-61499-299-8 .
• Каннингем, Дэниел В. (2016). Теория множеств: первый курс . Издательство Кембриджского университета. ISBN  978-1-316-68204-3 .
• Керли, Роберт (2011). Вычисления: от счетов к iPad . Образовательное издательство Британника. ISBN  978-1-61530-707-4 .
• Кайт, Энни AM ; Петерсен, Вигдис; Вердонк, Бриджит; Вааделанд, Хокон; Джонс, Уильям Б. (2008). Справочник цепных дробей для специальных функций . Springer Science & Business Media. ISBN  978-1-4020-6949-9 .
• Дэвис, Эндрю; Гулдинг, Мария; Саггейт, Дженнифер (2017). Математические знания для учителей начальных классов . Тейлор и Фрэнсис. ISBN  978-1-317-21901-9 .
• Де Круз, Хелен; Нет, Хансйорг; Шлимм, Дирк (2010). «Когнитивные основы арифметики». В Лёве, Бенедикт; Мюллер, Томас (ред.). PhiMSAMP: Философия математики: социологические аспекты и математическая практика . Публикации колледжа. ISBN  978-1-904987-95-6 .
• Даукер, Энн (2019). Индивидуальные различия в арифметике: значение для психологии, нейронауки и образования . Рутледж. ISBN  978-1-317-62743-2 .
• Дребен-Иримия, Ольга (2010). Обучение пациентов в области реабилитации . Издательство Джонс и Бартлетт. ISBN  978-1-4496-1775-2 .
• Дросг, Манфред (2007). Работа с неопределенностями . Спрингер. ISBN  978-3-540-29606-5 .
• Даффи, Дэниел Дж. (2018). Оценка финансовых инструментов с использованием C++ . Джон Уайли и сыновья. ISBN  978-1-119-17048-8 .
• Дюверни, Дэниел (2010). Теория чисел: элементарное введение через диофантовые проблемы . Всемирная научная. ISBN  978-981-4307-46-8 .
• Эбби, Кэролайн Б.; Халберт, Элизабет Т.; Бродхед, Рэйчел М. (2020). Акцент на сложении и вычитании: проведение исследований в области математического образования в классе . Рутледж. ISBN  978-1-000-22087-2 .
• Эмерсон, Джейн; Бэбти, Патрисия (2014). Решение проблемы дискалькулии: обучение чувству числа . Издательство Блумсбери. ISBN  978-1-4729-2099-7 .
• Эрикссон, Кеннет; Эстеп, Дональд; Джонсон, Клаас (2013). Прикладная математика: Тело и душа: Том 2: Интегралы и геометрия в IRn . Springer Science & Business Media. ISBN  978-3-662-05798-8 .
• Фармер, Уильям М. (2023). Простая теория типов: практическая логика для выражения и рассуждения математических идей . Спрингер Природа. ISBN  978-3-031-21112-6 .
• Феррейрос, Хосе (2013). Лабиринт мысли: история теории множеств и ее роль в современной математике . Биркхойзер. ISBN  978-3-0348-5049-0 .
• Галлистел, Чехия; Гельман, Р. (2005). «Математическое познание». В Холиоке, Кей Джей; Моррисон, Р.Г. (ред.). Кембриджский справочник по мышлению и рассуждению . Издательство Кембриджского университета. ISBN  978-0-521-53101-6 .
• Гири, Дэвид К. (2006). «Развитие математического понимания» . В Дэймоне, Уильям; Лернер, Ричард М.; Кун, Дина; Зиглер, Роберт С. (ред.). Справочник по детской психологии, познанию, восприятию и языку . Джон Уайли и сыновья. ISBN  978-0-470-05054-5 .
• Геллерт, В.; Хеллвич, М.; Кестнер, Х.; Кюстнер, Х. (2012). Краткая математическая энциклопедия ВНР . Springer Science & Business Media. ISBN  978-94-011-6982-0 .
• Джерарди, Кристофер; Гетте, Лоренц; Мейер, Стефан (2013). «Числовая способность предсказывает дефолт по ипотеке» . Труды Национальной академии наук . 110 (28): 11267–11271. Бибкод : 2013PNAS..11011267G . дои : 10.1073/pnas.1220568110 . ПМЦ   3710828 . ПМИД   23798401 .
• Гудштейн, Р.Л. (2014). Основные понятия математики . Эльзевир. ISBN  978-1-4831-5405-3 .
• Грайс, Мэтт; Кемп, Саймон; Мортон, Никола Дж.; Грейс, Рэндольф К. (2023). «Психологический каркас арифметики» . Психологический обзор . 131 (2): 494–522. дои : 10.1037/rev0000431 . ПМИД   37358523 . S2CID   259251163 .
• Григорьева, Эллина (2018). Методы решения задач теории чисел . Биркхойзер. ISBN  978-3-319-90915-8 .
• Гриффин, Кэрролл В. (1935). «Важные цифры». Национальный математический журнал . 10 (1): 20–24. дои : 10.2307/3028249 . JSTOR   3028249 .
• Гупта, Раджеш Кумар (2019). Численные методы: основы и приложения . Издательство Кембриджского университета. ISBN  978-1-108-68660-0 .
• Хафстром, Джон Эдвард (2013). Основные понятия современной математики . Курьерская корпорация. ISBN  978-0-486-31627-7 .
• Гамильтон, Норман Т.; Ландин, Джозеф (2018). Теория множеств: структура арифметики . Публикации Курьера Дувра. ISBN  978-0-486-83047-6 .
• Харт, Роджер (2011). Китайские корни линейной алгебры . Джу Пресс. ISBN  978-0-8018-9958-4 .
• Хейлок, Дерек; Кокберн, Энн Д. (2008). Понимание математики для детей младшего возраста: Руководство для учителей начальных классов и младших классов начальной школы . МУДРЕЦ. ISBN  978-1-4462-0497-9 .
• Сотрудники ХК (2022 г.). «Цифра» . Словарь американского наследия . ХарперКоллинз . Проверено 11 ноября 2023 г.
• Сотрудники ХК (2022а). «Система счисления» . Словарь американского наследия . ХарперКоллинз . Проверено 11 ноября 2023 г.
• Сотрудники ХК (2022б). «Арифметика» . Словарь американского наследия . ХарперКоллинз . Проверено 19 октября 2023 г.
• Хайэм, Николас (2002). Точность и стабильность численных алгоритмов (PDF) (2-е изд.). СИАМ. дои : 10.1137/1.9780898718027 . ISBN  978-0-89871-521-7 .
• Хиндри, Марк (2011). Арифметика . Университеттекст. Спрингер. дои : 10.1007/978-1-4471-2131-2 . ISBN  978-1-4471-2130-5 .
• Ходжкин, Люк (2013). История математики: от Месопотамии до современности . ОУП Оксфорд. ISBN  978-0-19-166436-6 .
• Хоффман, Джо Д.; Франкель, Стивен (2018). Численные методы для инженеров и ученых . ЦРК Пресс. ISBN  978-1-4822-7060-0 .
• Хофвебер, Томас (2016). «Философия арифметики». Онтология и амбиции метафизики . Издательство Оксфордского университета. ISBN  978-0-19-876983-5 .
• Хорстен, Леон (2023). «Философия математики» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета . Проверено 22 ноября 2023 г.
• Хуа, Цзюэмин; Фэн, Лишэн (2020). Тридцать великих изобретений Китая: от земледелия до артемизинина . Спрингер Природа. ISBN  978-981-15-6525-0 .
• Гуссерль, Эдмунд; Уиллард, Даллас (2012). «Введение переводчика» . Философия арифметики: психологические и логические исследования с дополнительными текстами 1887–1901 гг . Springer Science & Business Media. ISBN  978-94-010-0060-4 .
• Игараси, Ёсихидэ; Альтман, Том; Фунада, Марико; Камияма, Барбара (2014). Вычисления: историческая и техническая перспектива . ЦРК Пресс. ISBN  978-1-4822-2741-3 .
• Международная организация по стандартизации (2019). ISO 80000-2: 2019 Величины и единицы. Часть 2. Математика (PDF) . Международная организация по стандартизации.
• ITL Education Solutions Limited (2011 г.). Введение в информатику . Пирсон Образовательная Индия. ISBN  978-81-317-6030-7 .
• Джексон, Жанна М. (2008). «Чтение/запись соединения» . Во Флиппо, Рона Ф. (ред.). Справочник по чтению в колледже и исследованию стратегии обучения . Рутледж. ISBN  978-1-135-70373-8 .
• Йена, Сисир Кумар (2021). Программирование на C: научитесь программировать . ЦРК Пресс. ISBN  978-1-000-46056-8 .
• Кайзер, Сара С.; Гранад, Кристофер (2021). Изучите квантовые вычисления с помощью Python и Q#: практический подход . Саймон и Шустер. ISBN  978-1-61729-613-0 .
• Карацуба, А.А. (2014). «Аналитическая теория чисел» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Карацуба, А.А. (2020). «Теория чисел» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Кей, Энтони (2021). Системы счисления: путь к строгой математике . ЦРК Пресс. ISBN  978-0-429-60776-9 .
• Хан, Халид; Грэм, Тони Ли (2018). Инженерная математика с приложениями к пожарной технике . ЦРК Пресс. ISBN  978-1-351-59761-6 .
• Хаттар, Динеш (2010). Руководство Пирсона по объективной арифметике для конкурсных экзаменов, 3/E . Пирсон Образовательная Индия. ISBN  978-81-317-2673-0 .
• Хури, Джозеф; Ламот, Жиль (2016). Математика, которая питает наш мир: как она устроена? . Всемирная научная. ISBN  978-981-4730-86-0 .
• Клаф, А. Альберт (2011). Курс повышения квалификации по тригонометрии . Курьерская корпорация. ISBN  978-0-486-15104-5 .
• Кляйн, Элиза; Мёллер, Корбиниан; Дрессел, Катарина; Домас, Фрэнк; Вуд, Гильерме; Уиллмс, Клаус; Нуерк, Ханс-Кристоф (2010). «Нести или не нести — в этом вопрос? Распутывание эффекта переноса при сложении многозначных чисел» . Акта Психологика . 135 (1): 67–76. дои : 10.1016/j.actpsy.2010.06.002 . ПМИД   20580340 .
• Кляйн, Андреас (2013). Потоковые шифры . Springer Science & Business Media. ISBN  978-1-4471-5079-4 .
• Кляйн, Джейкоб (2013a). Греческая математическая мысль и происхождение алгебры . Курьерская корпорация. ISBN  978-0-486-31981-0 .
• Кляйнер, Израиль (2012). Экскурсии в историю математики . Springer Science & Business Media. ISBN  978-0-8176-8268-2 .
• Клозе, Орвал М. (2014). Системы счисления и арифметические операции: объяснение основных принципов математики, лежащих в основе понимания и использования арифметики, предназначено для повышения квалификации кандидатов в учителя начальной школы. Сервисная подготовка кандидатов в учителя начальной школы . Эльзевир. ISBN  978-1-4831-3709-4 .
• Кноблох, Эберхард; Комацу, Хикосабуро; Лю, Дун (2013). Секи, основатель современной математики в Японии: память о его трехсотлетии . Springer Science & Business Media. ISBN  978-4-431-54273-5 .
• Кепф, Вольфрам (2021). Компьютерная алгебра: алгоритмоориентированное введение . Спрингер Природа. ISBN  978-3-030-78017-3 .
• Коэтсьер, Теун (2018). Восхождение GIM, глобальной интеллектуальной машины: история производства и информационных машин . Спрингер. ISBN  978-3-319-96547-5 .
• Корен, Израиль (2018). Компьютерные арифметические алгоритмы . ЦРК Пресс. ISBN  978-1-4398-6371-8 .
• Кернер, Т.В. (2019). Откуда берутся цифры? . Издательство Кембриджского университета. ISBN  978-1-108-77594-6 .
• Кренн, Стефан; Лорюнсер, Томас (2023). Введение в обмен секретами: систематический обзор и руководство по выбору протокола . Спрингер Природа. ISBN  978-3-031-28161-7 .
• Кубилюс, ИП (2018). «Теория чисел, вероятностные методы в» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Кудрявцев, Л.Д. (2020). «Реальное число» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Купферман, Раз (2015). Математика начальной школы для родителей и учителей - Том 1 . Мировое научное издательство. ISBN  978-981-4699-93-8 .
• Кржижек, Михал; Сомер, Лоуренс; Солцова, Алена (2021). От великих открытий в теории чисел к приложениям . Спрингер Природа. ISBN  978-3-030-83899-7 .
• Ланг, Серж (2002). «Формула Тейлора» . Краткое исчисление: оригинальное издание «Первого курса исчисления» . Тексты для бакалавриата по математике. Спрингер. стр. 195–210. дои : 10.1007/978-1-4613-0077-9_14 . ISBN  978-1-4613-0077-9 .
• Ланг, Филиппа (2015). Наука: Древность и ее наследие . Издательство Блумсбери. ISBN  978-0-85773-955-1 .
• Ланге, Кеннет (2010). Численный анализ для статистиков . Springer Science & Business Media. ISBN  978-1-4419-5944-7 .
• Ласки, Элида В.; Джордан, Джамила Р.; Дауст, Кэролайн; Мюррей, Анджела К. (2015). «Что делает математические манипуляции эффективными? Уроки когнитивной науки и образования Монтессори» . СЕЙДЖ Открыть . 5 (2). дои : 10.1177/2158244015589588 . hdl : 1808/20642 . S2CID   11722953 .
• Лернер, Бренда Уилмот; Лернер, К. Ли, ред. (2008). «Модульная арифметика». Научная энциклопедия Гейла (4-е изд.). Томпсон Гейл. ISBN  978-1-4144-2877-2 .
• Ли, Йепин; Шенфельд, Алан Х. (2019). «Проблематизация преподавания и изучения математики как данности в STEM-образовании» . Международный журнал STEM-образования . 6 (1). дои : 10.1186/s40594-019-0197-9 .
• Либлер, Роберт А. (2018). Базовая матричная алгебра с алгоритмами и приложениями . ЦРК Пресс. ISBN  978-0-429-85287-9 .
• Локхарт, Пол (2017). Арифметика . Издательство Belknap Press издательства Гарвардского университета. ISBN  978-0-674-97223-0 .
• Лосано-Робледо, Альваро (2019). Теория чисел и геометрия: введение в арифметическую геометрию . Американское математическое соц. ISBN  978-1-4704-5016-8 .
• Людерер, Бернд; Ноллау, Волкер; Веттерс, Клаус (2013). Математические формулы для экономистов . Springer Science & Business Media. ISBN  978-3-662-12431-4 .
• Лютцен, Йеспер (2023). История математической невозможности . Издательство Оксфордского университета. ISBN  978-0-19-286739-1 .
• Лустик, Дэвид (1997). «Игра чисел: подчеркивание важности значащих цифр и научных обозначений». Учитель естественных наук . 64 (5): 16–18. JSTOR   24152064 .
• Ма, Липинг (2020). Знание и преподавание элементарной математики: понимание учителями фундаментальной математики в Китае и США . Рутледж. ISBN  978-1-000-02734-1 .
• Мэдден, Дэниел Дж.; Обри, Джейсон А. (2017). Введение в доказательство посредством реального анализа . Джон Уайли и сыновья. ISBN  978-1-119-31472-1 .
• Махаджан, Санджой (2010). Математика уличных боев: искусство обоснованного угадывания и оппортунистического решения проблем . МТИ Пресс. ISBN  978-0-262-26559-1 .
• Маркус, Рассел; МакЭвой, Марк (2016). Историческое введение в философию математики: читатель . Издательство Блумсбери. ISBN  978-1-4725-3291-6 .
• Мазумдер, Пинаки; Эбонг, Идонгесит Э. (2023). Лекции по принципам цифрового дизайна . ЦРК Пресс. ISBN  978-1-000-92194-6 .
• Маццола, Гуэрино; Мильмейстер, Жерар; Вайсманн, Джоди (2004). Комплексная математика для специалистов по информатике 1: множества и числа, графики и алгебра, логика и машины, линейная геометрия . Springer Science & Business Media. ISBN  978-3-540-20835-8 .
• Мейер, Карл Д. (2023). Матричный анализ и прикладная линейная алгебра: второе издание . СИАМ. ISBN  978-1-61197-744-8 .
• Монахан, Джон Ф. (2012). «2. Основные вычислительные алгоритмы» . В «Нежности», Джеймс Э.; Хердле, Вольфганг Карл; Мори, Юичи (ред.). Справочник по вычислительной статистике: концепции и методы . Springer Science & Business Media. ISBN  978-3-642-21551-3 .
• Монкайо, Рауль (2018). Лаланг, Sinthome, Jouissance и номинация: помощник по чтению и комментарий к XXIII семинару Лакана о Sinthome . Рутледж. ISBN  978-0-429-91554-3 .
• Муни, Клэр; Бриггс, Мэри; Хансен, Алиса; Маккаллуш, Джудит; Флетчер, Майк (2014). Начальная математика: теория и практика преподавания . Обучение имеет значение. ISBN  978-1-4739-0707-2 .
• Мур, Рамон Э.; Кирфотт, Р. Бейкер; Клауд, Майкл Дж. (2009). Введение в интервальный анализ . СИАМ. ISBN  978-0-89871-669-6 .
• Мюллер, Жан-Мишель; Бризебар, Николя; Динешен, Флоран де; Жаннерод, Клод-Пьер; Лефевр, Винсент; Мелькионд, Гийом; Револь, Натали ; Штеле, Дэмиен; Торрес, Серж (2009). Справочник по арифметике с плавающей запятой . Springer Science & Business Media. ISBN  978-0-8176-4705-6 .
• Мюллер, Жан-Мишель; Бруни, Николас; Динешен, Флоран де; Жаннерод, Клод-Пьер; Джолдес, Миоара; Лефевр, Винсент; Мелькионд, Гийом; Револь, Натали ; Торрес, Серж (2018). Справочник по арифметике с плавающей запятой . Биркгаузер. ISBN  978-3-319-76526-6 .
• Массер, Гэри Л.; Петерсон, Блейк Э.; Бургер, Уильям Ф. (2013). Математика для учителей начальных классов: современный подход . Джон Уайли и сыновья. ISBN  978-1-118-48700-6 .
• Сотрудники МВ (2023 г.). «Определение арифметики» . www.merriam-webster.com . Проверено 19 октября 2023 г.
• Нагель, Роб (2002). Научная энциклопедия UXL . УХЛ. ISBN  978-0-7876-5440-5 .
• Нагель, Эрнест; Ньюман, Джеймс Рой (2008). Доказательство Геделя . Нью-Йорк Пресс. ISBN  978-0-8147-5837-3 .
• Наков, Светлин; Колев, Веселин (2013). Основы компьютерного программирования на C#: Болгарская книга по C# . Издательство Фабер. ISBN  978-954-400-773-7 .
• Сотрудники НКТМ. «Числа и действия» . www.nctm.org . Национальный совет учителей математики . Проверено 21 ноября 2023 г.
• Нельсон, Джеральд (2019). Английский: Основная грамматика . Рутледж. ISBN  978-1-351-12273-3 .
• Налл, Линда; Лобур, Юлия (2006). Основы компьютерной организации и архитектуры . Джонс и Бартлетт Обучение. ISBN  978-0-7637-3769-6 .
• Нюрнбергер-Хааг, Джули (2017). «Одолжить, обменять, перегруппировать или распаковать? Выясняем, как учебные метафоры отображают десятичное число» . В Джао, Лимин; Радакович, Ненад (ред.). Трансдисциплинарность в математическом образовании: стирание дисциплинарных границ . Спрингер. ISBN  978-3-319-63624-5 .
• О'Лири, Майкл Л. (2015). Первый курс математической логики и теории множеств . Джон Уайли и сыновья. ISBN  978-0-470-90588-3 .
• О'Риган, Джерард (2012). Краткая история вычислений . Springer Science & Business Media. ISBN  978-1-4471-2359-0 .
• Оукс, Элизабет (2020). Энциклопедия ученых мира, обновленное издание . Издательство информационной базы. ISBN  978-1-4381-9545-2 .
• Одом, Сэмюэл Л.; Барбарин, Оскар А.; Васик, Барбара Ханна (2009). «Применение уроков науки о развитии к раннему образованию» . В Барбарине, Оскар А.; Васик, Барбара Ханна (ред.). Справочник по развитию детей и раннему образованию: исследования на практике . Гилфорд Пресс. ISBN  978-1-60623-302-3 .
• Оливер, Александр Д. (2005). «Арифметика. Основы». В Хондерихе, Тед (ред.). Оксфордский справочник по философии . Издательство Оксфордского университета. ISBN  978-0-19-926479-7 .
• Омонди, Амос Р. (2020). Криптографическая арифметика: алгоритмы и аппаратные архитектуры . Спрингер Природа. ISBN  978-3-030-34142-8 .
• Онгли, Джон; Кэри, Розалинда (2013). Рассел: Путеводитель для растерянных . Издательство Блумсбери. ISBN  978-1-4411-9123-6 .
• Оре, Эйстейн (1948). Теория чисел и ее история . МакГроу-Хилл. ISBN  978-0-486-65620-5 . OCLC   1397541 .
• Орр, Дэвид Б. (1995). Основы прикладной статистики и исследований . ЦРК Пресс. ISBN  978-0-412-98821-9 .
• Отис, Джессика Мари (2024). В цифрах: умение считать, религия и количественная трансформация Англии раннего Нового времени . Издательство Оксфордского университета. ISBN  978-0-19-760877-7 .
• Паар, Кристоф; Пельцль, Ян (2009). Понимание криптографии: Учебник для студентов и практиков . Springer Science & Business Media. ISBN  978-3-642-04101-3 .
• Пейдж, Роберт Л. (2003). «Теория чисел, элементарная» . Энциклопедия физических наук и технологий (Третье изд.). Академическая пресса. ISBN  978-0-12-227410-7 .
• Пейн, Эндрю (2017). Телеология действия в «Государстве» Платона . Издательство Оксфордского университета. ISBN  978-0-19-879902-3 .
• Пирс, Чарльз С. (2015). Арифметика . Вальтер де Грюйтер ГмбХ & Ко КГ. ISBN  978-3-11-086970-5 .
• Фарр, Мэтт; Якоб, Венцель; Хамфрис, Грег (2023). Физически обоснованный рендеринг: от теории к реализации (4-е изд.). МТИ Пресс. ISBN  978-0-262-37403-3 .
• Померанс, Карл (2010). «IV.3 Вычислительная теория чисел» (PDF) . В Гауэрсе, Тимоти ; Барроу-Грин, июнь ; Лидер, Имре (ред.). Принстонский спутник математики . Издательство Принстонского университета. стр. 348–362. ISBN  978-1-4008-3039-8 .
• Померанс, К.; Саркози, А. (1995). «Комбинаторная теория чисел» . В Грэме, Р.Л. (ред.). Справочник по комбинаторике . Эльзевир. ISBN  978-0-08-093384-9 .
• Понтикорво, Микела; Шмбри, Массимилиано; Миглино, Орацио (2019). «Как улучшить пространственное и числовое познание с помощью игрового и технологического подхода к обучению» . В Висенте — Хосе Мануэль Феррандес; Альварес-Санчес, Хосе Рамон; Лопес, Феликс де ла Пас; Морео, Хавьер Толедо; Адели, Ходжат (ред.). Понимание функции мозга и эмоций: 8-я Международная рабочая конференция по взаимодействию естественных и искусственных вычислений, IWINAC 2019, Альмерия, Испания, 3–7 июня 2019 г., Материалы, Часть I. Спрингер. ISBN  978-3-030-19591-5 .
• Прата, Стивен (2002). С Праймер Плюс . Издательство Самс. ISBN  978-0-672-32222-8 .
• Кинтеро, Ана Хельвиа; Розарио, Гектор (2016). Математика имеет смысл!: конструктивистский подход к преподаванию и изучению математики . Всемирная научная. ISBN  978-1-78326-866-5 .
• Раджан, Хридеш (2022). Экспериментальное введение в принципы языков программирования . МТИ Пресс. ISBN  978-0-262-36243-6 .
• Рейли, Норман Р. (2009). Введение в прикладные алгебраические системы . Издательство Оксфордского университета. ISBN  978-0-19-970992-2 .
• Рейтано, Роберт Р. (2010). Введение в количественные финансы: набор математических инструментов . МТИ Пресс. ISBN  978-0-262-01369-7 .
• Резник, Л.Б.; Форд, WW (2012). Психология математики для обучения . Рутледж. ISBN  978-1-136-55759-0 .
• Рейнольдс, Барбара Э. (2008). "Счеты". В Селин, Хелейн (ред.). Энциклопедия истории науки, техники и медицины в незападных культурах . Springer Science & Business Media. ISBN  978-1-4020-4559-2 .
• Ризель, Ганс (2012). Простые числа и компьютерные методы факторизации . Springer Science & Business Media. ISBN  978-1-4612-0251-6 .
• Рост, Джеральд Р.; Мэтьюз, Джеймс Р.; Шоафф, Эйлин; Мэтью, Джудит (2021). О математике . Линус Обучение. ISBN  978-1-60797-892-3 .
• Роббинс, Невилл (2006). Начало теории чисел . Джонс и Бартлетт Обучение. ISBN  978-0-7637-3768-9 .
• Родда, Харви Дж. Э.; Литтл, Макс А. (2015). Понимание математических и статистических методов в гидрологии: подход, основанный на примерах . Джон Уайли и сыновья. ISBN  978-1-119-07659-9 .
• Роу, Джон; деФорест, Расс; Джамшиди, Сара (2018). Математика для устойчивого развития . Спрингер. ISBN  978-3-319-76660-7 .
• Романовский, Перри (2008). «Арифметика». В Лернере – Бренда Уилмот; Лернер, К. Ли (ред.). Научная энциклопедия Гейла (4-е изд.). Томпсон Гейл. ISBN  978-1-4144-2877-2 .
• Руни, Энн (2021). Думайте как математик . Издательская группа Розен. ISBN  978-1-4994-7092-5 .
• Росси, Ричард Дж. (2011). Теоремы, следствия, леммы и методы доказательства . Джон Уайли и сыновья. ISBN  978-1-118-03057-8 .
• Рутвен, Кеннет (2012). «12. Калькуляторы в учебной программе по математике: область применения персональных вычислительных технологий» . В Бишопе, Алан; Клементс, Массачусетс (Кен); Кейтель-Крейдт, Кристина; Килпатрик, Джереми; Лаборд, Колетт (ред.). Международный справочник по математическому образованию . Springer Science & Business Media. ISBN  978-94-009-1465-0 .
• Салли, Джудит Д.; Салли (младшая), Пол Дж. (2012). Целые числа, дроби и арифметика: Руководство для учителей . Американское математическое соц. ISBN  978-0-8218-8798-1 .
• Моряк, Уильям; Росслер, Отто Э.; Бургин, Марк (2023). Хаос, информация и будущее физики: диалог Симана-Росслера с информационными перспективами Бергина и Симана . Всемирная научная. ISBN  978-981-12-7138-0 .
• Шива, Саджан Г. (2018). Введение в логический дизайн . ЦРК Пресс. ISBN  978-1-351-98983-1 .
• Серпинская, Анна; Лерман, Стивен (1996). «Эпистемологии математики и математического образования». У Алана Дж. Бишопа; Кен Клементс; Кристин Кейтель; Джереми Килпатрик; Колетт Лаборд (ред.). Международный справочник по математическому образованию: Часть 1 . Международные справочники по образованию Kluwer, том. 4. Спрингер Нидерланды. стр. 827–876. дои : 10.1007/978-94-009-1465-0_23 . ISBN  978-94-009-1465-0 .
• Смит, Дэвид Э. (1958). История математики . Курьерская корпорация. ISBN  978-0-486-20430-7 .
• Смит, Уильям (1864). Элементарная алгебра: для школ и академий . Бэйли и Нойес. OCLC   3901163143 .
• Софиан, Кэтрин (2017). Истоки математических знаний в детстве . Рутледж. ISBN  978-1-351-54175-6 .
• Сперлинг, Авраам; Стюарт, Монро (1981). Математика . Эльзевир Наука. ISBN  978-0-7506-0405-5 .
• Стахов, Алексей (2020). Математика гармонии как новое междисциплинарное направление и «золотая» парадигма современной науки - Том 2: Алгоритмическая теория измерения, Фибоначчи, золотая арифметика и троичная зеркально-симметричная арифметика . Всемирная научная. ISBN  978-981-12-1348-9 .
• Штернберг, Роберт Дж.; Бен-Зеев, Талия (2012). Природа математического мышления . Рутледж. ISBN  978-1-136-48750-7 .
• Стивенсон, Ангус; Уэйт, Морис (2011). Краткий Оксфордский словарь английского языка: роскошное издание . ОУП Оксфорд. ISBN  978-0-19-960111-0 .
• Стюарт, Дэвид Э. (2022). Численный анализ: аспирантура . Спрингер Природа. ISBN  978-3-031-08121-7 .
• Стратерн, Пол (2012). Тьюринг и компьютер . Случайный дом. ISBN  978-1-4481-0656-1 .
• Суонсон, Ирена (2021). Введение в анализ комплексных чисел . Всемирная научная. ISBN  978-981-12-2587-1 .
• Шварцландер, Эрл Э. (2017). «Высокоскоростная компьютерная арифметика» . В Оклобдзе, Вожин Г. (ред.). Цифровой дизайн и производство . ЦРК Пресс. ISBN  978-0-8493-8604-6 .
• Тарасов, Василий (2008). Квантовая механика негамильтоновых и диссипативных систем . Эльзевир. ISBN  978-0-08-055971-1 .
• Тейлор, Джозеф Л. (2012). Основы анализа . Американское математическое соц. ISBN  978-0-8218-8984-8 .
• Тиам, Тьерно; Рошон, Гилберт (2019). Устойчивое развитие, новые технологии и панафриканизм . Спрингер Природа. ISBN  978-3-030-22180-5 .
• Плитка, Мэри (2009). «Кантианский взгляд на философию математики» . В Ирвине, Эндрю Д. (ред.). Философия математики . Эльзевир. ISBN  978-0-08-093058-9 .
• Успенский, В.А.; Семенов А.Л. (2001). «Решаемые и нерешаемые алгоритмические задачи» . Табачников, Серж (ред.). Квант Селекта: Комбинаторика, И: Комбинаторика, И . Американское математическое соц. ISBN  978-0-8218-2171-8 .
• Ваккаро, Альфредо; Пепичелло, Антонио (2022). Методы аффинной арифметики для анализа неопределенной энергосистемы . Эльзевир. ISBN  978-0-323-90503-9 .
• Вершаффель, Ливен; Торбейнс, Шутка; Де Смедт, Берт (2011). «Ментальная арифметика» . В Силе, Норберт М. (ред.). Энциклопедия наук об обучении . Springer Science & Business Media. ISBN  978-1-4419-1427-9 .
• Сотрудники Департамента образования штата Виктория (2023 г.). «Счет для всех учащихся» . www.education.vic.gov.au . Проверено 22 ноября 2023 г.
• Виноградов, А.И. (2019). «Алгебраическая теория чисел» . Энциклопедия математики . Спрингер . Проверено 23 октября 2023 г.
• Вулло, Винченцо (2020). Gears: Том 3: Краткая история . Спрингер Природа. ISBN  978-3-030-40164-1 .
• Уэйт, Морис (2013). Карманный Оксфордский словарь английского языка . ОУП Оксфорд. ISBN  978-0-19-966615-7 .
• Уоллис, WD (2011). Руководство для начинающих по дискретной математике . Springer Science & Business Media. ISBN  978-0-8176-8286-6 .
• Уоллис, WD (2013). Руководство для начинающих по дискретной математике . Springer Science & Business Media. ISBN  978-1-4757-3826-1 .
• Ван, Хао (1997). Логическое путешествие: от Гёделя к философии . МТИ Пресс. ISBN  978-0-262-26125-8 .
• Уорд, JP (2012). Кватернионы и числа Кэли: алгебра и приложения . Springer Science & Business Media. ISBN  978-94-011-5768-1 .
• Веделл, Мориц (2015). «Цифры» . В Классене, Альбрехт (ред.). Справочник средневековой культуры. Том 2 . Вальтер де Грюйтер ГмбХ & Ко КГ. ISBN  978-3-11-037763-7 .
• Вейль, Андре (2009). Теория чисел: подход через историю от Хаммурапи до Лежандра . Springer Science & Business Media. ISBN  978-0-8176-4571-7 .
• Вейр, Алан (2022). «Формализм в философии математики» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета . Проверено 22 ноября 2023 г.
• Уитер, Кэролайн (2015). Алгебра I. Дорлинг Киндерсли Лимитед. ISBN  978-0-241-88779-0 .
• Уилсон, Робин (2020). Теория чисел: очень краткое введение . Издательство Оксфордского университета. ISBN  978-0-19-879809-5 .
• Райт, Роберт Дж.; Эллемор-Коллинз, Дэвид; Табор, Памела Д. (2011). Развитие знаний о числах: оценка, обучение и вмешательство с детьми 7–11 лет . МУДРЕЦ. ISBN  978-1-4462-8927-3 .
• Сюй, Живэй; Чжан, Цзялин (2022). Вычислительное мышление: взгляд на информатику . Спрингер Природа. ISBN  978-981-16-3848-0 .
• Ядин, Аарон (2016). Архитектура компьютерных систем . ЦРК Пресс. ISBN  978-1-315-35592-4 .
• Ян, Сун Ю. (2002). Теория чисел для вычислений . Springer Science & Business Media. ISBN  978-3-642-07710-4 .
• Ян, Сун Ю. (2013a). Вычислительная теория чисел и современная криптография . Джон Уайли и сыновья. ISBN  978-1-118-18858-3 .
• Янг, Синтия Ю. (2010). Предварительный расчет . Джон Уайли и сыновья. ISBN  978-0-471-75684-2 .
• Янг, Синтия Ю. (2021). Алгебра и тригонометрия . Джон Уайли и сыновья. ISBN  978-1-119-77830-1 .
• Чжан, Г. (2012). Логика доменов . Springer Science & Business Media. ISBN  978-1-4612-0445-9 .