Теория хаоса

Чтобы узнать о других значениях, см. Теорию хаоса (значения) .

График аттрактора Лоренца для значений r = 28 , σ = 10 , b = ⁠ 8 / 3 ⁠

An animation of a double-rod pendulum at an intermediate energy showing chaotic behavior. Starting the pendulum from a slightly different initial condition would result in a vastly different trajectory. The double-rod pendulum is one of the simplest dynamical systems with chaotic solutions.

Теория хаоса — междисциплинарная область научных исследований и раздел математики . Основное внимание уделяется основным закономерностям и детерминированным законам динамических систем , которые очень чувствительны к начальным условиям . Когда-то считалось, что они имеют совершенно случайные состояния беспорядка и нарушений. Теория хаоса утверждает, что внутри кажущейся случайности хаотических сложных систем существуют основные закономерности, взаимосвязи, постоянные петли обратной связи , повторение, самоподобие , фракталы и самоорганизация . Эффект бабочки , основополагающий принцип хаоса, описывает, как небольшое изменение в одном состоянии детерминированной нелинейной системы может привести к большим различиям в более позднем состоянии (это означает, что существует чувствительная зависимость от начальных условий). Метафорой такого поведения является то, что взмах крыльев бабочки в Бразилии может вызвать торнадо в Техасе .

Небольшие различия в начальных условиях, например, из-за ошибок в измерениях или из-за ошибок округления в числовых вычислениях , могут привести к сильно различающимся результатам для таких динамических систем, что в целом делает долгосрочное прогнозирование их поведения невозможным. This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution and is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:

Chaos: When the present determines the future but the approximate present does not approximately determine the future.

Chaotic behavior exists in many natural systems, including fluid flow, heartbeat irregularities, weather and climate. It also occurs spontaneously in some systems with artificial components, such as road traffic. This behavior can be studied through the analysis of a chaotic mathematical model or through analytical techniques such as recurrence plots and Poincaré maps. Chaos theory has applications in a variety of disciplines, including meteorology, anthropology, sociology, environmental science, computer science, engineering, economics, ecology, and pandemic crisis management. The theory formed the basis for such fields of study as complex dynamical systems, edge of chaos theory and self-assembly processes.

Introduction

Chaos theory concerns deterministic systems whose behavior can, in principle, be predicted. Chaotic systems are predictable for a while and then 'appear' to become random. The amount of time for which the behavior of a chaotic system can be effectively predicted depends on three things: how much uncertainty can be tolerated in the forecast, how accurately its current state can be measured, and a time scale depending on the dynamics of the system, called the Lyapunov time. Some examples of Lyapunov times are: chaotic electrical circuits, about 1 millisecond; weather systems, a few days (unproven); the inner solar system, 4 to 5 million years. In chaotic systems, the uncertainty in a forecast increases exponentially with elapsed time. Hence, mathematically, doubling the forecast time more than squares the proportional uncertainty in the forecast. This means, in practice, a meaningful prediction cannot be made over an interval of more than two or three times the Lyapunov time. When meaningful predictions cannot be made, the system appears random.

Chaos theory is a method of qualitative and quantitative analysis to investigate the behavior of dynamic systems that cannot be explained and predicted by single data relationships, but must be explained and predicted by whole, continuous data relationships.

Chaotic dynamics

The map defined by x → 4 x (1 – x) and y → (x + y) mod 1 displays sensitivity to initial x positions. Here, two series of x and y values diverge markedly over time from a tiny initial difference.

In common usage, "chaos" means "a state of disorder". However, in chaos theory, the term is defined more precisely. Although no universally accepted mathematical definition of chaos exists, a commonly used definition, originally formulated by Robert L. Devaney, says that to classify a dynamical system as chaotic, it must have these properties:

1. it must be sensitive to initial conditions,
2. it must be topologically transitive,
3. it must have dense periodic orbits.

In some cases, the last two properties above have been shown to actually imply sensitivity to initial conditions. In the discrete-time case, this is true for all continuous maps on metric spaces. In these cases, while it is often the most practically significant property, "sensitivity to initial conditions" need not be stated in the definition.

If attention is restricted to intervals, the second property implies the other two. An alternative and a generally weaker definition of chaos uses only the first two properties in the above list.

Sensitivity to initial conditions

Main article: Butterfly effect

Lorenz equations used to generate plots for the y variable. The initial conditions for x and z were kept the same but those for y were changed between 1.001, 1.0001 and 1.00001. The values for $\rho$, $\sigma$ and $\beta$ were 45.91, 16 and 4 respectively. As can be seen from the graph, even the slightest difference in initial values causes significant changes after about 12 seconds of evolution in the three cases. This is an example of sensitive dependence on initial conditions.

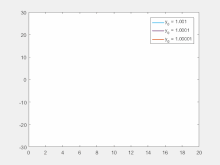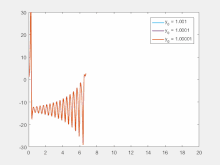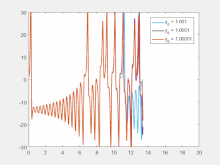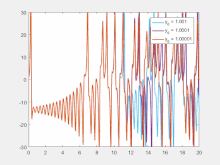
Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points that have significantly different future paths or trajectories. Thus, an arbitrarily small change or perturbation of the current trajectory may lead to significantly different future behavior.

Sensitivity to initial conditions is popularly known as the "butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science in Washington, D.C., entitled Predictability: Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas?. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events that prevents the predictability of large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the overall system could have been vastly different.

As suggested in Lorenz's book entitled The Essence of Chaos, published in 1993, "sensitive dependence can serve as an acceptable definition of chaos". In the same book, Lorenz defined the butterfly effect as: "The phenomenon that a small alteration in the state of a dynamical system will cause subsequent states to differ greatly from the states that would have followed without the alteration." The above definition is consistent with the sensitive dependence of solutions on initial conditions (SDIC). An idealized skiing model was developed to illustrate the sensitivity of time-varying paths to initial positions. A predictability horizon can be determined before the onset of SDIC (i.e., prior to significant separations of initial nearby trajectories).

A consequence of sensitivity to initial conditions is that if we start with a limited amount of information about the system (as is usually the case in practice), then beyond a certain time, the system would no longer be predictable. This is most prevalent in the case of weather, which is generally predictable only about a week ahead. This does not mean that one cannot assert anything about events far in the future—only that some restrictions on the system are present. For example, we know that the temperature of the surface of the earth will not naturally reach 100 °C (212 °F) or fall below −130 °C (−202 °F) on earth (during the current geologic era), but we cannot predict exactly which day will have the hottest temperature of the year.

In more mathematical terms, the Lyapunov exponent measures the sensitivity to initial conditions, in the form of rate of exponential divergence from the perturbed initial conditions. More specifically, given two starting trajectories in the phase space that are infinitesimally close, with initial separation $\delta \mathbf {Z} _{0}$, the two trajectories end up diverging at a rate given by

$|\delta \mathbf {Z} (t)|\approx e^{\lambda t}|\delta \mathbf {Z} _{0}|,$

where $t$ is the time and $\lambda$ is the Lyapunov exponent. The rate of separation depends on the orientation of the initial separation vector, so a whole spectrum of Lyapunov exponents can exist. The number of Lyapunov exponents is equal to the number of dimensions of the phase space, though it is common to just refer to the largest one. For example, the maximal Lyapunov exponent (MLE) is most often used, because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.

In addition to the above property, other properties related to sensitivity of initial conditions also exist. These include, for example, measure-theoretical mixing (as discussed in ergodic theory) and properties of a K-system.

Non-periodicity

A chaotic system may have sequences of values for the evolving variable that exactly repeat themselves, giving periodic behavior starting from any point in that sequence. However, such periodic sequences are repelling rather than attracting, meaning that if the evolving variable is outside the sequence, however close, it will not enter the sequence and in fact, will diverge from it. Thus for almost all initial conditions, the variable evolves chaotically with non-periodic behavior.

Topological mixing

Six iterations of a set of states $[x,y]$ passed through the logistic map. The first iterate (blue) is the initial condition, which essentially forms a circle. Animation shows the first to the sixth iteration of the circular initial conditions. It can be seen that mixing occurs as we progress in iterations. The sixth iteration shows that the points are almost completely scattered in the phase space. Had we progressed further in iterations, the mixing would have been homogeneous and irreversible. The logistic map has equation $x_{k+1}=4x_{k}(1-x_{k})$. To expand the state-space of the logistic map into two dimensions, a second state, $y$, was created as $y_{k+1}=x_{k}+y_{k}$, if $x_{k}+y_{k}<1$ and $y_{k+1}=x_{k}+y_{k}-1$ otherwise.

The map defined by x → 4 x (1 – x) and y → (x + y) mod 1 also displays topological mixing. Here, the blue region is transformed by the dynamics first to the purple region, then to the pink and red regions, and eventually to a cloud of vertical lines scattered across the space.

Topological mixing (or the weaker condition of topological transitivity) means that the system evolves over time so that any given region or open set of its phase space eventually overlaps with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.

Topological mixing is often omitted from popular accounts of chaos, which equate chaos with only sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points eventually becomes widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behavior: all points except 0 tend to positive or negative infinity.

Topological transitivity

A map $f:X\to X$ is said to be topologically transitive if for any pair of non-empty open sets $U,V\subset X$, there exists $k>0$ such that $f^{k}(U)\cap V\neq \emptyset$. Topological transitivity is a weaker version of topological mixing. Intuitively, if a map is topologically transitive then given a point x and a region V, there exists a point y near x whose orbit passes through V. This implies that it is impossible to decompose the system into two open sets.

An important related theorem is the Birkhoff Transitivity Theorem. It is easy to see that the existence of a dense orbit implies topological transitivity. The Birkhoff Transitivity Theorem states that if X is a second countable, complete metric space, then topological transitivity implies the existence of a dense set of points in X that have dense orbits.

Density of periodic orbits

For a chaotic system to have dense periodic orbits means that every point in the space is approached arbitrarily closely by periodic orbits. The one-dimensional logistic map defined by x → 4 x (1 – x) is one of the simplest systems with density of periodic orbits. For example, ${\tfrac {5-{\sqrt {5}}}{8}}$ → ${\tfrac {5+{\sqrt {5}}}{8}}$ → ${\tfrac {5-{\sqrt {5}}}{8}}$ (or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).

Sharkovskii's theorem is the basis of the Li and Yorke (1975) proof that any continuous one-dimensional system that exhibits a regular cycle of period three will also display regular cycles of every other length, as well as completely chaotic orbits.

Strange attractors

The Lorenz attractor displays chaotic behavior. These two plots demonstrate sensitive dependence on initial conditions within the region of phase space occupied by the attractor.

Some dynamical systems, like the one-dimensional logistic map defined by x → 4 x (1 – x), are chaotic everywhere, but in many cases chaotic behavior is found only in a subset of phase space. The cases of most interest arise when the chaotic behavior takes place on an attractor, since then a large set of initial conditions leads to orbits that converge to this chaotic region.

An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it is not only one of the first, but it is also one of the most complex, and as such gives rise to a very interesting pattern that, with a little imagination, looks like the wings of a butterfly.

Unlike fixed-point attractors and limit cycles, the attractors that arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set, which forms at the boundary between basins of attraction of fixed points. Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and the fractal dimension can be calculated for them.

Coexisting attractors

Coexisting chaotic and non-chaotic attractors within the generalized Lorenz model. There are 128 orbits in different colors, beginning with different initial conditions for dimensionless time between 0.625 and 5 and a heating parameter r = 680. Chaotic orbits recurrently return close to the saddle point at the origin. Nonchaotic orbits eventually approach one of two stable critical points, as shown with large blue dots. Chaotic and nonchaotic orbits occupy different regions of attraction within the phase space.

In contrast to single type chaotic solutions, recent studies using Lorenz models have emphasized the importance of considering various types of solutions. For example, coexisting chaotic and non-chaotic may appear within the same model (e.g., the double pendulum system) using the same modeling configurations but different initial conditions. The findings of attractor coexistence, obtained from classical and generalized Lorenz models, suggested a revised view that "the entirety of weather possesses a dual nature of chaos and order with distinct predictability", in contrast to the conventional view of "weather is chaotic".

Minimum complexity of a chaotic system

Bifurcation diagram of the logistic map x → r x (1 – x). Each vertical slice shows the attractor for a specific value of r. The diagram displays period-doubling as r increases, eventually producing chaos. Darker points are visited more frequently.

Discrete chaotic systems, such as the logistic map, can exhibit strange attractors whatever their dimensionality. In contrast, for continuous dynamical systems, the Poincaré–Bendixson theorem shows that a strange attractor can only arise in three or more dimensions. Finite-dimensional linear systems are never chaotic; for a dynamical system to display chaotic behavior, it must be either nonlinear or infinite-dimensional.

The Poincaré–Bendixson theorem states that a two-dimensional differential equation has very regular behavior. The Lorenz attractor discussed below is generated by a system of three differential equations such as:

${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma y-\sigma x,\\{\frac {\mathrm {d} y}{\mathrm {d} t}}&=\rho x-xz-y,\\{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}$

where $x$, $y$, and $z$ make up the system state, $t$ is time, and $\sigma$, $\rho$, $\beta$ are the system parameters. Five of the terms on the right hand side are linear, while two are quadratic; a total of seven terms. Another well-known chaotic attractor is generated by the Rössler equations, which have only one nonlinear term out of seven. Sprott found a three-dimensional system with just five terms, that had only one nonlinear term, which exhibits chaos for certain parameter values. Zhang and Heidel showed that, at least for dissipative and conservative quadratic systems, three-dimensional quadratic systems with only three or four terms on the right-hand side cannot exhibit chaotic behavior. The reason is, simply put, that solutions to such systems are asymptotic to a two-dimensional surface and therefore solutions are well behaved.

While the Poincaré–Bendixson theorem shows that a continuous dynamical system on the Euclidean plane cannot be chaotic, two-dimensional continuous systems with non-Euclidean geometry can still exhibit some chaotic properties. Perhaps surprisingly, chaos may occur also in linear systems, provided they are infinite dimensional. A theory of linear chaos is being developed in a branch of mathematical analysis known as functional analysis.

The above set of three ordinary differential equations has been referred to as the three-dimensional Lorenz model. Since 1963, higher-dimensional Lorenz models have been developed in numerous studies for examining the impact of an increased degree of nonlinearity, as well as its collective effect with heating and dissipations, on solution stability.

Infinite dimensional maps

The straightforward generalization of coupled discrete maps is based upon convolution integral which mediates interaction between spatially distributed maps:$\psi _{n+1}({\vec {r}},t)=\int K({\vec {r}}-{\vec {r}}^{,},t)f[\psi _{n}({\vec {r}}^{,},t)]d{\vec {r}}^{,}$,

where kernel $K({\vec {r}}-{\vec {r}}^{,},t)$ is propagator derived as Green function of a relevant physical system,$f[\psi _{n}({\vec {r}},t)]$ might be logistic map alike $\psi \rightarrow G\psi [1-\tanh(\psi )]$ or complex map. For examples of complex maps the Julia set $f[\psi ]=\psi ^{2}$ or Ikeda map$\psi _{n+1}=A+B\psi _{n}e^{i(|\psi _{n}|^{2}+C)}$ may serve. When wave propagation problems at distance $L=ct$ with wavelength $\lambda =2\pi /k$ are considered the kernel $K$ may have a form of Green function for Schrödinger equation:.

$K({\vec {r}}-{\vec {r}}^{,},L)={\frac {ik\exp[ikL]}{2\pi L}}\exp[{\frac {ik|{\vec {r}}-{\vec {r}}^{,}|^{2}}{2L}}]$.

Jerk systems

In physics, jerk is the third derivative of position, with respect to time. As such, differential equations of the form

$J\left({\overset {...}{x}},{\ddot {x}},{\dot {x}},x\right)=0$

are sometimes called jerk equations. It has been shown that a jerk equation, which is equivalent to a system of three first order, ordinary, non-linear differential equations, is in a certain sense the minimal setting for solutions showing chaotic behavior. This motivates mathematical interest in jerk systems. Systems involving a fourth or higher derivative are called accordingly hyperjerk systems.

A jerk system's behavior is described by a jerk equation, and for certain jerk equations, simple electronic circuits can model solutions. These circuits are known as jerk circuits.

One of the most interesting properties of jerk circuits is the possibility of chaotic behavior. In fact, certain well-known chaotic systems, such as the Lorenz attractor and the Rössler map, are conventionally described as a system of three first-order differential equations that can combine into a single (although rather complicated) jerk equation. Another example of a jerk equation with nonlinearity in the magnitude of $x$ is:

${\frac {\mathrm {d} ^{3}x}{\mathrm {d} t^{3}}}+A{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+{\frac {\mathrm {d} x}{\mathrm {d} t}}-|x|+1=0.$

Here, A is an adjustable parameter. This equation has a chaotic solution for A=3/5 and can be implemented with the following jerk circuit; the required nonlinearity is brought about by the two diodes:

In the above circuit, all resistors are of equal value, except $R_{A}=R/A=5R/3$, and all capacitors are of equal size. The dominant frequency is $1/2\pi RC$. The output of op amp 0 will correspond to the x variable, the output of 1 corresponds to the first derivative of x and the output of 2 corresponds to the second derivative.

Similar circuits only require one diode or no diodes at all.

See also the well-known Chua's circuit, one basis for chaotic true random number generators. The ease of construction of the circuit has made it a ubiquitous real-world example of a chaotic system.

Spontaneous order

Under the right conditions, chaos spontaneously evolves into a lockstep pattern. In the Kuramoto model, four conditions suffice to produce synchronization in a chaotic system.Examples include the coupled oscillation of Christiaan Huygens' pendulums, fireflies, neurons, the London Millennium Bridge resonance, and large arrays of Josephson junctions.

Moreover, from the theoretical physics standpoint, dynamical chaos itself, in its most general manifestation, is a spontaneous order. The essence here is that most orders in nature arise from the spontaneous breakdown of various symmetries. This large family of phenomena includes elasticity, superconductivity, ferromagnetism, and many others. According to the supersymmetric theory of stochastic dynamics, chaos, or more precisely, its stochastic generalization, is also part of this family. The corresponding symmetry being broken is the topological supersymmetry which is hidden in all stochastic (partial) differential equations, and the corresponding order parameter is a field-theoretic embodiment of the butterfly effect.

History

Barnsley fern created using the chaos game. Natural forms (ferns, clouds, mountains, etc.) may be recreated through an iterated function system (IFS).

James Clerk Maxwell first emphasized the "butterfly effect", and is seen as being one of the earliest to discuss chaos theory, with work in the 1860s and 1870s. An early proponent of chaos theory was Henri Poincaré. In the 1880s, while studying the three-body problem, he found that there can be orbits that are nonperiodic, and yet not forever increasing nor approaching a fixed point. In 1898, Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature, called "Hadamard's billiards". Hadamard was able to show that all trajectories are unstable, in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent.

Chaos theory began in the field of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out by George David Birkhoff, Andrey Nikolaevich Kolmogorov, Mary Lucy Cartwright and John Edensor Littlewood, and Stephen Smale. Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.

Despite initial insights in the first half of the twentieth century, chaos theory became formalized as such only after mid-century, when it first became evident to some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behavior of certain experiments like that of the logistic map. What had been attributed to measure imprecision and simple "noise" was considered by chaos theorists as a full component of the studied systems. In 1959 Boris Valerianovich Chirikov proposed a criterion for the emergence of classical chaos in Hamiltonian systems (Chirikov criterion). He applied this criterion to explain some experimental results on plasma confinement in open mirror traps. This is regarded as the very first physical theory of chaos, which succeeded in explaining a concrete experiment. And Boris Chirikov himself is considered as a pioneer in classical and quantum chaos.

The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical, while figures and images made it possible to visualize these systems. As a graduate student in Chihiro Hayashi's laboratory at Kyoto University, Yoshisuke Ueda was experimenting with analog computers and noticed, on November 27, 1961, what he called "randomly transitional phenomena". Yet his advisor did not agree with his conclusions at the time, and did not allow him to report his findings until 1970.

Turbulence in the tip vortex from an airplane wing. Studies of the critical point beyond which a system creates turbulence were important for chaos theory, analyzed for example by the Soviet physicist Lev Landau, who developed the Landau-Hopf theory of turbulence. David Ruelle and Floris Takens later predicted, against Landau, that fluid turbulence could develop through a strange attractor, a main concept of chaos theory.

Edward Lorenz was an early pioneer of the theory. His interest in chaos came about accidentally through his work on weather prediction in 1961. Lorenz and his collaborator Ellen Fetter and Margaret Hamilton were using a simple digital computer, a Royal McBee LGP-30, to run weather simulations. They wanted to see a sequence of data again, and to save time they started the simulation in the middle of its course. They did this by entering a printout of the data that corresponded to conditions in the middle of the original simulation. To their surprise, the weather the machine began to predict was completely different from the previous calculation. They tracked this down to the computer printout. The computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.506127 printed as 0.506. This difference is tiny, and the consensus at the time would have been that it should have no practical effect. However, Lorenz discovered that small changes in initial conditions produced large changes in long-term outcome. Lorenz's discovery, which gave its name to Lorenz attractors, showed that even detailed atmospheric modeling cannot, in general, make precise long-term weather predictions.

In 1963, Benoit Mandelbrot, studying information theory, discovered that noise in many phenomena (including stock prices and telephone circuits) was patterned like a Cantor set, a set of points with infinite roughness and detail Mandelbrot described both the "Noah effect" (in which sudden discontinuous changes can occur) and the "Joseph effect" (in which persistence of a value can occur for a while, yet suddenly change afterwards). In 1967, he published "How long is the coast of Britain? Statistical self-similarity and fractional dimension", showing that a coastline's length varies with the scale of the measuring instrument, resembles itself at all scales, and is infinite in length for an infinitesimally small measuring device. Arguing that a ball of twine appears as a point when viewed from far away (0-dimensional), a ball when viewed from fairly near (3-dimensional), or a curved strand (1-dimensional), he argued that the dimensions of an object are relative to the observer and may be fractional. An object whose irregularity is constant over different scales ("self-similarity") is a fractal (examples include the Menger sponge, the Sierpiński gasket, and the Koch curve or snowflake, which is infinitely long yet encloses a finite space and has a fractal dimension of circa 1.2619). In 1982, Mandelbrot published The Fractal Geometry of Nature, which became a classic of chaos theory.

In December 1977, the New York Academy of Sciences organized the first symposium on chaos, attended by David Ruelle, Robert May, James A. Yorke (coiner of the term "chaos" as used in mathematics), Robert Shaw, and the meteorologist Edward Lorenz. The following year Pierre Coullet and Charles Tresser published "Itérations d'endomorphismes et groupe de renormalisation", and Mitchell Feigenbaum's article "Quantitative Universality for a Class of Nonlinear Transformations" finally appeared in a journal, after 3 years of referee rejections. Thus Feigenbaum (1975) and Coullet & Tresser (1978) discovered the universality in chaos, permitting the application of chaos theory to many different phenomena.

In 1979, Albert J. Libchaber, during a symposium organized in Aspen by Pierre Hohenberg, presented his experimental observation of the bifurcation cascade that leads to chaos and turbulence in Rayleigh–Bénard convection systems. He was awarded the Wolf Prize in Physics in 1986 along with Mitchell J. Feigenbaum for their inspiring achievements.

In 1986, the New York Academy of Sciences co-organized with the National Institute of Mental Health and the Office of Naval Research the first important conference on chaos in biology and medicine. There, Bernardo Huberman presented a mathematical model of the eye tracking dysfunction among people with schizophrenia. This led to a renewal of physiology in the 1980s through the application of chaos theory, for example, in the study of pathological cardiac cycles.

In 1987, Per Bak, Chao Tang and Kurt Wiesenfeld published a paper in Physical Review Letters describing for the first time self-organized criticality (SOC), considered one of the mechanisms by which complexity arises in nature.

Alongside largely lab-based approaches such as the Bak–Tang–Wiesenfeld sandpile, many other investigations have focused on large-scale natural or social systems that are known (or suspected) to display scale-invariant behavior. Although these approaches were not always welcomed (at least initially) by specialists in the subjects examined, SOC has nevertheless become established as a strong candidate for explaining a number of natural phenomena, including earthquakes, (which, long before SOC was discovered, were known as a source of scale-invariant behavior such as the Gutenberg–Richter law describing the statistical distribution of earthquake sizes, and the Omori law describing the frequency of aftershocks), solar flares, fluctuations in economic systems such as financial markets (references to SOC are common in econophysics), landscape formation, forest fires, landslides, epidemics, and biological evolution (where SOC has been invoked, for example, as the dynamical mechanism behind the theory of "punctuated equilibria" put forward by Niles Eldredge and Stephen Jay Gould). Given the implications of a scale-free distribution of event sizes, some researchers have suggested that another phenomenon that should be considered an example of SOC is the occurrence of wars. These investigations of SOC have included both attempts at modelling (either developing new models or adapting existing ones to the specifics of a given natural system), and extensive data analysis to determine the existence and/or characteristics of natural scaling laws.

Also in 1987 James Gleick published Chaos: Making a New Science, which became a best-seller and introduced the general principles of chaos theory as well as its history to the broad public. Initially the domain of a few, isolated individuals, chaos theory progressively emerged as a transdisciplinary and institutional discipline, mainly under the name of nonlinear systems analysis. Alluding to Thomas Kuhn's concept of a paradigm shift exposed in The Structure of Scientific Revolutions (1962), many "chaologists" (as some described themselves) claimed that this new theory was an example of such a shift, a thesis upheld by Gleick.

The availability of cheaper, more powerful computers broadens the applicability of chaos theory. Currently, chaos theory remains an active area of research, involving many different disciplines such as mathematics, topology, physics, social systems, population modeling, biology, meteorology, astrophysics, information theory, computational neuroscience, pandemic crisis management, etc.

Lorenz's pioneering contributions to chaotic modeling

Throughout his career, Professor Lorenz authored a total of 61 research papers, out of which 58 were solely authored by him. Commencing with the 1960 conference in Japan, Lorenz embarked on a journey of developing diverse models aimed at uncovering the SDIC and chaotic features. A recent review of Lorenz's model progression spanning from 1960 to 2008 revealed his adeptness at employing varied physical systems to illustrate chaotic phenomena. These systems encompassed Quasi-geostrophic systems, the Conservative Vorticity Equation, the Rayleigh-Bénard Convection Equations, and the Shallow Water Equations. Moreover, Lorenz can be credited with the early application of the logistic map to explore chaotic solutions, a milestone he achieved ahead of his colleagues (e.g. Lorenz 1964).

In 1972, Lorenz coined the term "butterfly effect" as a metaphor to discuss whether a small perturbation could eventually create a tornado with a three-dimensional, organized, and coherent structure. While connected to the original butterfly effect based on sensitive dependence on initial conditions, its metaphorical variant carries distinct nuances. To commemorate this milestone, a reprint book containing invited papers that deepen our understanding of both butterfly effects was officially published to celebrate the 50th anniversary of the metaphorical butterfly effect.

A popular but inaccurate analogy for chaos

The sensitive dependence on initial conditions (i.e., butterfly effect) has been illustrated using the following folklore:

For want of a nail, the shoe was lost.

For want of a shoe, the horse was lost.

For want of a horse, the rider was lost.

For want of a rider, the battle was lost.

For want of a battle, the kingdom was lost.

And all for the want of a horseshoe nail.

Based on the above, many people mistakenly believe that the impact of a tiny initial perturbation monotonically increases with time and that any tiny perturbation can eventually produce a large impact on numerical integrations. However, in 2008, Lorenz stated that he did not feel that this verse described true chaos but that it better illustrated the simpler phenomenon of instability and that the verse implicitly suggests that subsequent small events will not reverse the outcome. Based on the analysis, the verse only indicates divergence, not boundedness. Boundedness is important for the finite size of a butterfly pattern. In a recent study, the characteristic of the aforementioned verse was recently denoted as "finite-time sensitive dependence".

Applications

A conus textile shell, similar in appearance to Rule 30, a cellular automaton with chaotic behaviour.

Although chaos theory was born from observing weather patterns, it has become applicable to a variety of other situations. Some areas benefiting from chaos theory today are geology, mathematics, biology, computer science, economics, engineering, finance, meteorology, philosophy, anthropology, physics, politics, population dynamics, and robotics. A few categories are listed below with examples, but this is by no means a comprehensive list as new applications are appearing.

Cryptography

Chaos theory has been used for many years in cryptography. In the past few decades, chaos and nonlinear dynamics have been used in the design of hundreds of cryptographic primitives. These algorithms include image encryption algorithms, hash functions, secure pseudo-random number generators, stream ciphers, watermarking, and steganography. The majority of these algorithms are based on uni-modal chaotic maps and a big portion of these algorithms use the control parameters and the initial condition of the chaotic maps as their keys. From a wider perspective, without loss of generality, the similarities between the chaotic maps and the cryptographic systems is the main motivation for the design of chaos based cryptographic algorithms. One type of encryption, secret key or symmetric key, relies on diffusion and confusion, which is modeled well by chaos theory. Another type of computing, DNA computing, when paired with chaos theory, offers a way to encrypt images and other information. Many of the DNA-Chaos cryptographic algorithms are proven to be either not secure, or the technique applied is suggested to be not efficient.

Robotics

Robotics is another area that has recently benefited from chaos theory. Instead of robots acting in a trial-and-error type of refinement to interact with their environment, chaos theory has been used to build a predictive model.Chaotic dynamics have been exhibited by passive walking biped robots.

Biology

For over a hundred years, biologists have been keeping track of populations of different species with population models. Most models are continuous, but recently scientists have been able to implement chaotic models in certain populations. For example, a study on models of Canadian lynx showed there was chaotic behavior in the population growth. Chaos can also be found in ecological systems, such as hydrology. While a chaotic model for hydrology has its shortcomings, there is still much to learn from looking at the data through the lens of chaos theory. Another biological application is found in cardiotocography. Fetal surveillance is a delicate balance of obtaining accurate information while being as noninvasive as possible. Better models of warning signs of fetal hypoxia can be obtained through chaotic modeling.

As Perry points out, modeling of chaotic time series in ecology is helped by constraint. There is always potential difficulty in distinguishing real chaos from chaos that is only in the model. Hence both constraint in the model and or duplicate time series data for comparison will be helpful in constraining the model to something close to the reality, for example Perry & Wall 1984. Gene-for-gene co-evolution sometimes shows chaotic dynamics in allele frequencies. Adding variables exaggerates this: Chaos is more common in models incorporating additional variables to reflect additional facets of real populations. Robert M. May himself did some of these foundational crop co-evolution studies, and this in turn helped shape the entire field. Even for a steady environment, merely combining one crop and one pathogen may result in quasi-periodic- or chaotic- oscillations in pathogen population.

Economics

It is possible that economic models can also be improved through an application of chaos theory, but predicting the health of an economic system and what factors influence it most is an extremely complex task. Economic and financial systems are fundamentally different from those in the classical natural sciences since the former are inherently stochastic in nature, as they result from the interactions of people, and thus pure deterministic models are unlikely to provide accurate representations of the data. The empirical literature that tests for chaos in economics and finance presents very mixed results, in part due to confusion between specific tests for chaos and more general tests for non-linear relationships.

Chaos could be found in economics by the means of recurrence quantification analysis. In fact, Orlando et al. by the means of the so-called recurrence quantification correlation index were able detect hidden changes in time series. Then, the same technique was employed to detect transitions from laminar (regular) to turbulent (chaotic) phases as well as differences between macroeconomic variables and highlight hidden features of economic dynamics. Finally, chaos theory could help in modeling how an economy operates as well as in embedding shocks due to external events such as COVID-19.

Finite Predictability in Weather and Climate

Due to the sensitive dependence of solutions on initial conditions (SDIC), also known as the butterfly effect, chaotic systems like the Lorenz 1963 model imply a finite predictability horizon. This means that while accurate predictions are possible over a finite time period, they are not feasible over an infinite time span. Considering the nature of Lorenz's chaotic solutions, the committee led by Charney et al. in 1966 extrapolated a doubling time of five days from a general circulation model, suggesting a predictability limit of two weeks. This connection between the five-day doubling time and the two-week predictability limit was also recorded in a 1969 report by the Global Atmospheric Research Program (GARP). To acknowledge the combined direct and indirect influences from the Mintz and Arakawa model and Lorenz's models, as well as the leadership of Charney et al., Shen et al. refer to the two-week predictability limit as the "Predictability Limit Hypothesis," drawing an analogy to Moore's Law.

AI-Extended Modeling Framework

В моделях большого языка, управляемых искусственным интеллектом, ответы могут проявлять чувствительность к таким факторам, как изменения в форматировании и вариации подсказок. Эта чувствительность подобна эффекту бабочки. Хотя классификация больших языковых моделей, основанных на искусственном интеллекте, как классических детерминированных хаотических систем, создает проблемы, подходы и методы, основанные на хаосе (такие как ансамблевое моделирование), могут использоваться для извлечения достоверной информации из этих обширных языковых моделей (см. также « Эффект бабочки в популярной культуре »). ).

Другие области

В химии прогнозирование растворимости газов имеет важное значение для производства полимеров , но модели, использующие оптимизацию роя частиц (PSO), имеют тенденцию сходиться к неверным точкам. Улучшенная версия PSO была создана за счет введения хаоса, который предотвращает застревание моделирования. В небесной механике , особенно при наблюдении астероидов, применение теории хаоса позволяет лучше предсказывать, когда эти объекты достигнут Земли и других планет. Четыре из пяти спутников Плутона вращаются хаотично. В квантовой физике и электротехнике изучение больших массивов джозефсоновских переходов значительно выиграло от теории хаоса. Ближе к дому угольные шахты всегда были опасными местами, где частые утечки природного газа приводят к множеству смертей. До недавнего времени не было надежного способа предсказать, когда они произойдут. Но эти утечки газа имеют хаотическую тенденцию, которую при правильном моделировании можно предсказать довольно точно.

Теория хаоса может применяться за пределами естественных наук, но исторически почти все подобные исследования страдали от отсутствия воспроизводимости; плохая внешняя валидность; и/или невнимание к перекрестной проверке, что приводит к низкой точности прогнозирования (если даже была предпринята попытка прогнозирования за пределами выборки). Стекло и Манделл и Зельц обнаружили, что ни одно исследование ЭЭГ до сих пор не выявило наличие странных аттракторов или других признаков хаотического поведения.

Исследователи продолжают применять теорию хаоса в психологии. Например, моделируя групповое поведение, в котором разнородные члены могут вести себя так, как будто в разной степени разделяют то, что в теории Уилфреда Биона является основным предположением, исследователи обнаружили, что групповая динамика является результатом индивидуальной динамики членов: каждый индивид воспроизводит групповую динамику в разном масштабе, и хаотичное поведение группы отражается на каждом ее члене.

Редингтон и Рейдборд (1992) попытались продемонстрировать, что человеческое сердце может проявлять хаотичные черты. Они отслеживали изменения интервалов между ударами сердца у одной психотерапевтической пациентки, когда она проходила через периоды различной эмоциональной интенсивности во время терапевтического сеанса. Результаты были, по общему признанию, неубедительными. Двусмысленность присутствовала не только в различных графиках, которые авторы создали, якобы чтобы продемонстрировать доказательства хаотической динамики (спектральный анализ, фазовые траектории и графики автокорреляции), но и когда они попытались вычислить показатель Ляпунова как более определенное подтверждение хаотического поведения, авторы обнаружили, что они не могут сделать это надежно.

В своей статье 1995 года Меткалф и Аллен утверждали, что они обнаружили в поведении животных закономерность удвоения периода, ведущую к хаосу. Авторы исследовали хорошо известную реакцию, называемую полидипсией, вызванной графиком, при которой животное, лишенное еды в течение определенного периода времени, пьет необычное количество воды, когда еда наконец-то ему представлена. Действующим здесь управляющим параметром (r) была продолжительность интервала между кормлениями после возобновления. Авторы постарались протестировать большое количество животных и включить множество повторений, и спланировали свой эксперимент так, чтобы исключить вероятность того, что изменения в паттернах реакции были вызваны разными стартовыми местами для r.

Временные ряды и графики первой задержки лучше всего подтверждают сделанные утверждения, демонстрируя довольно четкий переход от периодичности к нерегулярности по мере увеличения времени кормления. С другой стороны, различные графики фазовых траекторий и спектральный анализ недостаточно хорошо согласуются с другими графиками или с общей теорией, чтобы неумолимо привести к хаотическому диагнозу. Например, фазовые траектории не демонстрируют определенного прогресса в сторону все большей и большей сложности (и от периодичности); процесс кажется довольно запутанным. Кроме того, там, где Меткалф и Аллен видели на своих спектральных графиках периоды два и шесть, есть место для альтернативных интерпретаций. Вся эта двусмысленность требует некоторых извилистых, апостериорных объяснений, чтобы показать, что результаты соответствуют хаотичной модели.

Адаптировав модель карьерного консультирования, включив в нее хаотичную интерпретацию взаимоотношений между работниками и рынком труда, Амундсон и Брайт обнаружили, что людям, которые сталкиваются с трудностями при выборе карьеры, можно дать более эффективные рекомендации. Современные организации все чаще рассматриваются как открытые сложные адаптивные системы с фундаментальными естественными нелинейными структурами, подверженные внутренним и внешним силам, которые могут способствовать хаосу. Например, построение команды и развитие группы все чаще исследуются как по своей сути непредсказуемая система, поскольку неопределенность при первой встрече разных людей делает траекторию движения команды непознаваемой.

Некоторые говорят, что метафора хаоса, используемая в вербальных теориях, основана на математических моделях и психологических аспектах человеческого поведения.дает полезную информацию для описания сложности небольших рабочих групп, выходящую за рамки самой метафоры.

The red cars and blue cars take turns to move; the red ones only move upwards, and the blue ones move rightwards. Every time, all the cars of the same colour try to move one step if there is no car in front of it. Here, the model has self-organized in a somewhat geometric pattern where there are some traffic jams and some areas where cars can move at top speed.

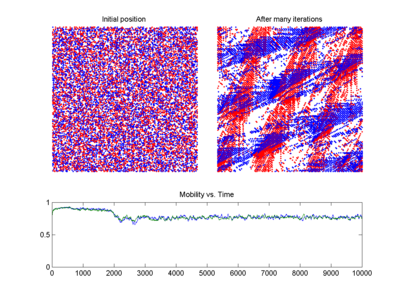
Прогнозирование дорожного движения может выиграть от применения теории хаоса. Более точный прогноз того, когда произойдет затор, позволит принять меры по его разгону до того, как он возникнет. Сочетание принципов теории хаоса с несколькими другими методами привело к созданию более точной модели краткосрочного прогнозирования (см. график модели трафика BML справа).

Теория хаоса применялась к данным о водном цикле окружающей среды (также к гидрологическим данным), таким как количество осадков и речной сток. Эти исследования дали противоречивые результаты, поскольку методы обнаружения хаотичной сигнатуры зачастую относительно субъективны. Ранние исследования, как правило, «преуспевали» в обнаружении хаоса, тогда как последующие исследования и метаанализы ставили эти исследования под сомнение и давали объяснения, почему эти наборы данных вряд ли будут иметь низкоразмерную хаотическую динамику.

См. также

Примеры хаотических систем

• Адвектируемые контуры
• Карта кошек Арнольда
• Теория бифуркации
• Динамика прыгающего мяча
• Схема Чуа
• Клиодинамика
• Решетка связанных карт
• Двойной маятник
• Уравнение Даффинга
• Динамический бильярд
• Экономический пузырь
• Система Гаспара-Райса
• Карта Энона
• Карта подковы
• Список хаотичных карт
• Аттрактор Ресслера
• Стандартная карта
• Качающаяся машина Этвуда
• Наклонить вихрь

Другие связанные темы

• Амплитудная смерть
• Аносовский диффеоморфизм
• Теория катастроф
• Причинность
• Хаос как нарушение топологической суперсимметрии
• Машина хаоса
• Хаотическое смешивание
• Хаотическое рассеяние
• Контроль над хаосом
• Детерминизм
• Грань хаоса
• Появление
• Набор Мандельброта
• Теорема Колмогорова–Арнольда–Мозера.
• Плохое кондиционирование
• некорректность
• Нелинейная система
• Узоры в природе
• Предсказуемость
• Квантовый хаос
• Институт Санта-Фе
• Лемма о затенении
• Синхронизация хаоса
• Непредвиденное последствие

Люди

• Ральф Абрахам
• Майкл Берри
• Леон О. Чуа
• Ивар Экеланд
• Дойн Фармер
• Мартин Гуцвиллер
• Бросль Хасслахер
• Мишель Энон
• Aleksandr Lyapunov
• Норман Паккард
• Отто Рёсслер
• Дэвид Рюэль
• Александр Николаевич Шарковский
• Роберт Шоу
• Флорис Такенс
• Джеймс А. Йорк
• Георгий Михайлович Заславский

Дальнейшее чтение

Статьи

• Шарковский А. Н. (1964). «Сосуществование циклов непрерывного отображения прямой в себя». Украинская математика. Дж . 16 : 61–71.
• Ли, Тайвань ; Йорк, Дж.А. (1975). «Третий период подразумевает хаос» (PDF) . Американский математический ежемесячник . 82 (10): 985–92. Бибкод : 1975AmMM...82..985L . CiteSeerX   10.1.1.329.5038 . дои : 10.2307/2318254 . JSTOR   2318254 . Архивировано из оригинала (PDF) 29 декабря 2009 г. Проверено 12 августа 2009 г.
• Алемансур, Хамед; Миандоаб, Эхсан Маани; Пишкенари, Хосейн Неджат (март 2017 г.). «Влияние размера на хаотическое поведение нанорезонаторов». Коммуникации в нелинейной науке и численном моделировании . 44 : 495–505. Бибкод : 2017CNSNS..44..495A . дои : 10.1016/j.cnsns.2016.09.010 .
• Кратчфилд ; Такер; Моррисон; Джей Ди Фармер ; Паккард ; Нью-Хэмпшир; Шоу ; РС (декабрь 1986 г.). "Хаос". Научный американец . 255 (6): 38–49 (библиография стр. 136). Бибкод : 1986SciAm.255d..38T . дои : 10.1038/scientificamerican1286-46 . Онлайн-версия (Примечание: объем и цитирование страниц онлайн-текста отличаются от цитируемых здесь. Цитата здесь взята из фотокопии, которая соответствует другим цитатам, найденным в Интернете, без просмотра статей. Онлайн-контент идентичен к печатному тексту. Варианты цитирования зависят от страны публикации).
• Коляда, С.Ф. (2004). «Чувствительность Ли-Йорка и другие концепции хаоса». Украинская математика. Дж . 56 (8): 1242–57. дои : 10.1007/s11253-005-0055-4 . S2CID   207251437 .
• Дэй, Р.Х.; Павлов О.В. (2004). «Вычисление экономического хаоса». Вычислительная экономика . 23 (4): 289–301. arXiv : 2211.02441 . doi : 10.1023/B:CSEM.0000026787.81469.1f . S2CID   119972392 . ССНР   806124 .
• Стрельев, К.; Хюблер, А. (2006). «Среднесрочное предсказание хаоса» (PDF) . Физ. Преподобный Летт . 96 (4): 044101. Бибкод : 2006PhRvL..96d4101S . doi : 10.1103/PhysRevLett.96.044101 . ПМИД   16486826 . 044101. Архивировано из оригинала (PDF) 26 апреля 2013 г.
• Хюблер, А.; Фостер, Г.; Фелпс, К. (2007). «Управление хаосом: нестандартное мышление» (PDF) . Сложность . 12 (3): 10–13. Бибкод : 2007Cmplx..12c..10H . дои : 10.1002/cplx.20159 . Архивировано из оригинала (PDF) 30 октября 2012 г. Проверено 17 июля 2011 г.
• Моттер, Адилсон Э.; Кэмпбелл, Дэвид К. (2013). «Хаос в 50». Физика сегодня . 66 (5): 27. arXiv : 1306.5777 . Бибкод : 2013ФТ....66е..27М . дои : 10.1063/PT.3.1977 . S2CID   54005470 .

Учебники

• Аллигуд, Коннектикут; Зауэр, Т.; Йорк, Дж.А. (1997). Хаос: введение в динамические системы . Спрингер-Верлаг. ISBN  978-0-387-94677-1 .
• Бейкер, Г.Л. (1996). Хаос, рассеяние и статистическая механика . Издательство Кембриджского университета. ISBN  978-0-521-39511-3 .
• Бадии, Р.; Полити А. (1997). Сложность: иерархические структуры и масштабирование в физике . Издательство Кембриджского университета. ISBN  978-0-521-66385-4 .
• Колле, Пьер; Экманн, Жан-Пьер (1980). Итерированные карты на интервале как динамические системы . Биркгаузер. ISBN  978-0-8176-4926-5 .
• Девани, Роберт Л. (2003). Введение в хаотические динамические системы (2-е изд.). Вествью Пресс. ISBN  978-0-8133-4085-2 .
• Робинсон, Кларк (1995). Динамические системы: стабильность, символическая динамика и хаос . ЦРК Пресс. ISBN  0-8493-8493-1 .
• Фельдман, Д.П. (2012). Хаос и фракталы: элементарное введение . Издательство Оксфордского университета. ISBN  978-0-19-956644-0 . Архивировано из оригинала 31 декабря 2019 г. Проверено 29 декабря 2016 г.
• Голлуб, JP; Бейкер, Г.Л. (1996). Хаотическая динамика . Издательство Кембриджского университета. ISBN  978-0-521-47685-0 .
• Гукенхаймер, Джон ; Холмс, Филип (1983). Нелинейные колебания, динамические системы и бифуркации векторных полей . Спрингер-Верлаг. ISBN  978-0-387-90819-9 .
• Гулик, Денни (1992). Встречи с Хаосом . МакГроу-Хилл. ISBN  978-0-07-025203-5 .
• Гуцвиллер, Мартин (1990). Хаос в классической и квантовой механике . Спрингер-Верлаг. ISBN  978-0-387-97173-5 .
• Гувер, Уильям Грэм (2001) [1999]. Обратимость времени, компьютерное моделирование и хаос . Всемирная научная. ISBN  978-981-02-4073-8 .
• Каутц, Ричард (2011). Хаос: наука о предсказуемом случайном движении . Издательство Оксфордского университета. ISBN  978-0-19-959458-0 .
• Киль, Л. Дуглас; Эллиотт, Юэл В. (1997). Теория хаоса в социальных науках . Издательство Персей. ISBN  978-0-472-08472-2 .
• Мун, Фрэнсис (1990). Хаотическая и фрактальная динамика . Спрингер-Верлаг. ISBN  978-0-471-54571-2 .
• Орландо, Джузеппе ; Писарчик, Александр; Ступ, Руди (2021). Нелинейности в экономике . Динамическое моделирование и эконометрика в экономике и финансах. Том. 29. дои : 10.1007/978-3-030-70982-2 . ISBN  978-3-030-70981-5 . S2CID   239756912 .
• Отт, Эдвард (2002). Хаос в динамических системах . Издательство Кембриджского университета. ISBN  978-0-521-01084-9 .
• Строгац, Стивен (2000). Нелинейная динамика и хаос . Издательство Персей. ISBN  978-0-7382-0453-6 .
• Спротт, Жюльен Клинтон (2003). Хаос и анализ временных рядов . Издательство Оксфордского университета. ISBN  978-0-19-850840-3 .
• Зима, Тамаш; Груис, Мартон (2006). Хаотическая динамика: Введение на основе классической механики . Издательство Кембриджского университета. ISBN  978-0-521-83912-9 .
• Тешль, Джеральд (2012). Обыкновенные дифференциальные уравнения и динамические системы . Провиденс : Американское математическое общество . ISBN  978-0-8218-8328-0 .
• Томпсон Дж. М., Стюарт Х. Б. (2001). Нелинейная динамика и хаос . Джона Вили и Сыновей Лтд. ISBN  978-0-471-87645-8 .
• Туфилларо ; Рейли (1992). Экспериментальный подход к нелинейной динамике и хаосу . Американский журнал физики. Том. 61. Аддисон-Уэсли. п. 958. Бибкод : 1993AmJPh..61..958T . дои : 10.1119/1.17380 . ISBN  978-0-201-55441-0 .
• Виггинс, Стивен (2003). Введение в прикладные динамические системы и хаос . Спрингер. ISBN  978-0-387-00177-7 .
• Заславский, Джордж М. (2005). Гамильтонов хаос и дробная динамика . Издательство Оксфордского университета. ISBN  978-0-19-852604-9 .

Полутехнические и популярные произведения

• Кристоф Летелье , Хаос в природе , World Scientific Publishing Company, 2012, ISBN   978-981-4374-42-2 .
• Авраам, Ральф Х.; Уэда, Ёсисуке, ред. (2000). Авангард хаоса: воспоминания о первых днях теории хаоса . Всемирная научная серия по нелинейной науке. Серия A. Vol. 39. Всемирный научный. Бибкод : 2000cagm.book.....A . дои : 10.1142/4510 . ISBN  978-981-238-647-2 .
• Барнсли, Майкл Ф. (2000). Фракталы повсюду . Морган Кауфманн. ISBN  978-0-12-079069-2 .
• Берд, Ричард Дж. (2003). Хаос и жизнь: сложность и порядок в эволюции и мышлении . Издательство Колумбийского университета. ISBN  978-0-231-12662-5 .
• Джон Бриггс и Дэвид Пит, Турбулентное зеркало: Иллюстрированное руководство по теории хаоса и науке о целостности , Harper Perennial 1990, 224 стр.
• Джон Бриггс и Дэвид Пит, Семь жизненных уроков хаоса: духовная мудрость науки перемен , Harper Perennial 2000, 224 стр.
• Каннингем, Лоуренс А. (1994). «От случайных блужданий к хаотическим крахам: линейная генеалогия гипотезы эффективного рынка капитала». Обзор права Джорджа Вашингтона . 62 : 546.
• Предраг Цвитанович , Универсальность в хаосе , Адам Хилгер, 1989, 648 стр.
• Леон Гласс и Майкл К. Макки, От часов к хаосу: ритмы жизни, Princeton University Press, 1988, 272 стр.
• Джеймс Глейк , Хаос: Создание новой науки , Нью-Йорк: Penguin, 1988. 368 стр.
• Джон Гриббин. Глубокая простота . Пингвин Пресс Сайенс. Книги о пингвинах.
• Л. Дуглас Киль, Юэл В. Эллиотт (редактор), Теория хаоса в социальных науках: основы и приложения , University of Michigan Press, 1997, 360 стр.
• Арвинд Кумар, Хаос, фракталы и самоорганизация; Новые взгляды на сложность природы , Национальный книжный фонд, 2003.
• Ханс Лауверье, Фракталы , Princeton University Press, 1991.
• Эдвард Лоренц , Сущность хаоса , Вашингтонский университет Press, 1996.
• Маршалл, Алан (2002). Единство природы – целостность и дезинтеграция в экологии и науке . дои : 10.1142/9781860949548 . ISBN  9781860949548 .
• Дэвид Пик и Майкл Фрейм, Хаос под контролем: искусство и наука о сложности , Фриман, 1994.
• Хайнц-Отто Пейтген и Дитмар Саупе (ред.), «Наука фрактальных изображений» , Springer 1988, 312 стр.
• Нурия Перпинья , Хаос, вирус, спокойствие. Теория хаоса в применении к художественным, социальным и политическим беспорядкам , Páginas de Espuma, 2021.
• Клиффорд А. Пиковер , Компьютеры, узор, хаос и красота: графика из невидимого мира , Сент-Мартинс, 1991.
• Клиффорд А. Пиковер , Хаос в стране чудес: визуальные приключения во фрактальном мире , Сент-Мартинс, 1994.
• Илья Пригожин и Изабель Стенгерс , «Порядок из хаоса» , Bantam, 1984.
• Пейтген, Хайнц-Отто; Рихтер, Питер Х. (1986). Красота фракталов . дои : 10.1007/978-3-642-61717-1 . ISBN  978-3-642-61719-5 .
• Дэвид Рюэль , Случайность и хаос , Princeton University Press, 1993.
• Иварс Петерсон , Часы Ньютона: Хаос в Солнечной системе , Фриман, 1993.
• Ян Роулстон; Джон Норбери (2013). Невидимый во время шторма: роль математики в понимании погоды . Издательство Принстонского университета. ISBN  978-0691152721 .
• Рюэль, Д. (1989). Хаотическая эволюция и странные аттракторы . дои : 10.1017/CBO9780511608773 . ISBN  9780521362726 .
• Манфред Шредер, Фракталы, хаос и степенные законы , Фриман, 1991.
• Смит, Питер (1998). Объяснение хаоса . дои : 10.1017/CBO9780511554544 . ISBN  9780511554544 .
• Ян Стюарт , Играет ли Бог в кости?: Математика хаоса , Blackwell Publishers, 1990.
• Стивен Строгац , Синхронизация: новая наука о спонтанном порядке , Гиперион, 2003.
• Ёсисуке Уэда, Дорога к хаосу , Aerial Pr, 1993.
• М. Митчелл Уолдроп, Сложность: новая наука на грани порядка и хаоса , Simon & Schuster, 1992.
• Антонио Савайя, Анализ финансовых временных рядов: подход хаоса и нейродинамики , Ламберт, 2012.

Внешние ссылки

• «Хаос» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Группа исследования нелинейной динамики с анимацией во Flash
• Группа Хаос в Университете Мэриленда
• Гиперучебник Хаоса . Вводный курс по хаосу и фракталам
• ChaosBook.org Продвинутый учебник по хаосу (без фракталов) для выпускников.
• Общество теории хаоса в психологии и науках о жизни
• Группа исследования нелинейной динамики CSDC , Флоренция , Италия
• Нелинейная динамика: как наука постигает хаос , доклад Санни Ауян, 1998.
• Нелинейная динамика . Модели бифуркации и хаоса Элмера Г. Винса
• Глейка Хаос (отрывок). Архивировано 2 февраля 2007 г. в Wayback Machine.
• Группа системного анализа, моделирования и прогнозирования Оксфордского университета
• Страница об уравнении Макки-Гласса
• Высокие тревоги - Математика хаоса (2008), документальный фильм BBC, режиссер Дэвид Мэлоун
• Теория эволюции хаоса - статья, опубликованная в журнале Newscientist, показывающая сходство эволюции и нелинейных систем, включая фрактальную природу жизни и хаоса.
• Хос Лейс, Этьен Гис и Орельен Альварес, Хаос, математическое приключение . Девять фильмов о динамических системах, эффекте бабочки и теории хаоса, рассчитанные на широкую аудиторию.
• «Теория хаоса» , дискуссия на BBC Radio 4 со Сьюзен Гринфилд, Дэвидом Папино и Нилом Джонсоном ( «В наше время» , 16 мая 2002 г.)
• Хаос: наука об эффекте бабочки (2019), объяснение, представленное Дереком Мюллером

Примечание об авторских правах

• В эту статью включен текст из бесплатного контента . Лицензия CC-BY ( лицензионное заявление/разрешение ). Текст взят из книги «Три вида эффектов бабочки в моделях Лоренца» , Бо-Вэнь Шен, Роджер А. Пилке-старший, Сюбин Цзэн, Цзялин Цуй, Сара Фаги-Наини, Вэй Паксон и Роберт Атлас, MDPI. Энциклопедия.