Кластерный анализ

Результат кластерного анализа представлен раскраской квадратов на три кластера.

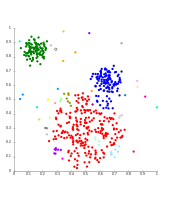
Кластерный анализ или кластеризация — это задача группировки набора объектов таким образом, чтобы объекты в одной группе (называемой кластером ) были более похожи (в некотором конкретном смысле, определенном аналитиком) друг на друга, чем на объекты в других группах. (кластеры). Это основная задача исследовательского анализа данных и общий метод статистического анализа данных , используемый во многих областях, включая распознавание образов , анализ изображений , поиск информации , биоинформатику , сжатие данных , компьютерную графику и машинное обучение .

Кластерный анализ относится к семейству алгоритмов и задач, а не к одному конкретному алгоритму . Этого можно достичь с помощью различных алгоритмов, которые существенно различаются в понимании того, что представляет собой кластер и как его эффективно найти. Популярные понятия кластеров включают группы с небольшими расстояниями между членами кластера, плотные области пространства данных, интервалы или определенные статистические распределения . Таким образом, кластеризацию можно сформулировать как задачу многокритериальной оптимизации . Соответствующий алгоритм кластеризации и настройки параметров (включая такие параметры, как используемая функция расстояния , порог плотности или количество ожидаемых кластеров) зависят от индивидуального набора данных и предполагаемого использования результатов. Кластерный анализ как таковой — это не автоматическая задача, а итеративный процесс открытия знаний или интерактивная многокритериальная оптимизация, включающая пробы и неудачи. Часто необходимо изменить параметры предварительной обработки данных и модели, пока результат не достигнет желаемых свойств.

Помимо термина «кластеризация» , существует ряд терминов со схожим значением, включая автоматическую классификацию , числовую таксономию , ботриологию (от греческого : βότρυς « виноград » ), типологический анализ и обнаружение сообществ . Тонкие различия часто заключаются в использовании результатов: если при интеллектуальном анализе данных представляют интерес полученные группы, то при автоматической классификации интерес представляет результирующая дискриминационная способность.

Кластерный анализ зародился в антропологии Драйвером и Крёбером в 1932 году. и введен в психологию Джозефом Зубиным в 1938 году. и Роберт Трайон в 1939 году и широко использовался Кеттеллом с 1943 года. для классификации теории черт в психологии личности .

Определение

Понятие «кластер» не может быть точно определено, и это одна из причин, почему существует так много алгоритмов кластеризации. Есть общий знаменатель: группа объектов данных. Однако разные исследователи используют разные кластерные модели, и для каждой из этих кластерных моделей опять-таки могут быть предложены разные алгоритмы. Понятие кластера, найденное разными алгоритмами, существенно различается по своим свойствам. Понимание этих «кластерных моделей» является ключом к пониманию различий между различными алгоритмами. Типичные кластерные модели включают в себя:

• связности Модели : например, иерархическая кластеризация строит модели на основе удаленной связи.
• Модель центроида s : например, алгоритм k-средних представляет каждый кластер одним средним вектором.
• распределения Модели : кластеры моделируются с использованием статистических распределений, таких как многомерные нормальные распределения, используемые алгоритмом максимизации ожидания .
• плотности Модель : например, DBSCAN и OPTICS определяют кластеры как связанные плотные области в пространстве данных.
• подпространства Модели : при бикластеризации (также известной как совместная кластеризация или двухрежимная кластеризация) кластеры моделируются как с использованием членов кластера, так и с соответствующими атрибутами.
• Групповые модели : некоторые алгоритмы не предоставляют уточненную модель своих результатов, а просто предоставляют информацию о группировке.
• на основе графов Модель : клика , то есть подмножество узлов в графе , в котором каждые два узла в подмножестве соединены ребром, может рассматриваться как прототипическая форма кластера. Ослабление требований полной связности (часть ребер может отсутствовать) известны как квазиклики, как в алгоритме кластеризации HCS .
• Модели знаковых графов . Каждый путь в подписанном графе имеет знак, полученный из произведения знаков на ребрах. Согласно предположениям теории баланса , ребра могут изменить знак и привести к раздвоению графа. Более слабая «аксиома кластеризации» (ни один цикл не имеет ровно одного отрицательного ребра) дает результаты с более чем двумя кластерами или подграфами только с положительными ребрами.
• Нейронные модели : наиболее известной неконтролируемой нейронной сетью является самоорганизующаяся карта , и эти модели обычно можно охарактеризовать как аналогичные одной или нескольким из вышеперечисленных моделей, включая модели подпространства, когда нейронные сети реализуют форму анализа главных компонентов. или Независимый анализ компонентов .

«Кластеризация» — это, по сути, набор таких кластеров, обычно содержащий все объекты в наборе данных. Дополнительно может указываться взаимосвязь кластеров друг с другом, например, иерархия кластеров, встроенных друг в друга. Кластеризации можно условно разделить на:

• Жесткая кластеризация : каждый объект принадлежит кластеру или нет.
• Мягкая кластеризация (также: нечеткая кластеризация : каждый объект в определенной степени принадлежит каждому кластеру (например, вероятность принадлежности к кластеру)

Возможны и более тонкие различия, например:

• Строгая кластеризация с разделением : каждый объект принадлежит ровно одному кластеру.
• Строгая кластеризация с выбросами : объекты также могут не принадлежать ни одному кластеру; в этом случае они считаются выбросами
• Перекрывающаяся кластеризация (также: альтернативная кластеризация , многопредставленная кластеризация ): объекты могут принадлежать более чем одному кластеру; обычно с участием жестких кластеров
• Иерархическая кластеризация : объекты, принадлежащие дочернему кластеру, также принадлежат родительскому кластеру.
• Кластеризация подпространств : при перекрывающейся кластеризации в пределах однозначно определенного подпространства кластеры не должны перекрываться.

Алгоритмы

Основная категория: Алгоритмы кластерного анализа

Как указано выше, алгоритмы кластеризации можно разделить на категории в зависимости от их кластерной модели. В следующем обзоре будут перечислены только наиболее известные примеры алгоритмов кластеризации, поскольку, возможно, существует более 100 опубликованных алгоритмов кластеризации. Не все предоставляют модели для своих кластеров, и поэтому их нелегко классифицировать. Обзор алгоритмов, объясненных в Википедии, можно найти в списке алгоритмов статистики .

Объективно «правильного» алгоритма кластеризации не существует, но, как было отмечено, «кластеризация — в глазах смотрящего». Наиболее подходящий алгоритм кластеризации для конкретной задачи часто приходится выбирать экспериментально, если только нет математической причины предпочитать одну модель кластера другой. Алгоритм, разработанный для модели одного типа, обычно не работает с набором данных, содержащим модель совершенно другого типа. Например, k-средние не могут найти невыпуклые кластеры. Большинство традиционных методов кластеризации предполагают, что кластеры имеют сферическую, эллиптическую или выпуклую форму.

Кластеризация на основе связности (иерархическая кластеризация)

Основная статья: Иерархическая кластеризация

Кластеризация на основе связности, также известная как иерархическая кластеризация , основана на основной идее, согласно которой объекты больше связаны с близлежащими объектами, чем с объектами, расположенными дальше. Эти алгоритмы соединяют «объекты» в «кластеры» в зависимости от их расстояния. Кластер можно в основном описать максимальным расстоянием, необходимым для соединения частей кластера. На разных расстояниях будут образовываться разные кластеры, которые можно представить с помощью дендрограммы , что объясняет происхождение общего названия « иерархическая кластеризация »: эти алгоритмы не обеспечивают единого разбиения набора данных, а вместо этого предоставляют обширную иерархию кластеры, которые сливаются друг с другом на определенных расстояниях. На дендрограмме ось Y отмечает расстояние, на котором кластеры сливаются, а объекты располагаются вдоль оси X так, чтобы кластеры не смешивались.

Кластеризация на основе связности — это целое семейство методов, которые различаются способом вычисления расстояний. Помимо обычного выбора функций расстояния , пользователю также необходимо определиться с критерием связи (поскольку кластер состоит из нескольких объектов, существует несколько кандидатов для вычисления расстояния), которые он будет использовать. Популярные варианты известны как кластеризация с одной связью (минимальное расстояние до объекта), кластеризация с полной связью (максимальное расстояние до объекта) и UPGMA или WPGMA («Метод невзвешенной или взвешенной пары пар со средним арифметическим», также известный как средняя связь). кластеризация). Кроме того, иерархическая кластеризация может быть агломеративной (начиная с отдельных элементов и объединяя их в кластеры) или разделительной (начиная с полного набора данных и разделяя его на разделы).

Эти методы не создают уникального разделения набора данных, а создают иерархию, из которой пользователю все равно необходимо выбирать соответствующие кластеры. Они не очень устойчивы к выбросам, которые либо проявляются как дополнительные кластеры, либо даже вызывают слияние других кластеров (известное как «феномен цепочки», в частности, при кластеризации с одной связью ). В общем случае сложность ${\mathcal {O}}(n^{3})$ для агломеративной кластеризации и ${\mathcal {O}}(2^{n-1})$ для разделительной кластеризации , что делает их слишком медленными для больших наборов данных. Для некоторых частных случаев оптимально эффективные методы (сложности ${\mathcal {O}}(n^{2})$) известны: SLINK для однорычажного и CLINK для кластеризации с полной связью.

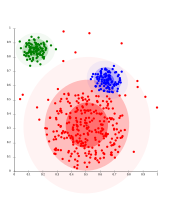
• Примеры кластеризации связей
• 
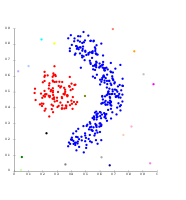
  Одинарная связь с гауссовскими данными. При 35 кластерах самый большой кластер начинает фрагментироваться на более мелкие части, тогда как раньше он еще был связан со вторым по величине из-за эффекта одноканального соединения.
• 
  Одинарная связь в кластерах на основе плотности. Извлечено 20 кластеров, большинство из которых содержат одиночные элементы, поскольку в связной кластеризации нет понятия «шум».

Центроидная кластеризация

Основная статья: кластеризация k-средних

При кластеризации на основе центроидов каждый кластер представлен центральным вектором, который не обязательно является членом набора данных. Когда количество кластеров равно k , кластеризация k -mean дает формальное определение как задача оптимизации: найти k центров кластеров и назначить объекты ближайшему центру кластера так, чтобы квадраты расстояний от кластера были минимизированы.

Сама задача оптимизации, как известно, является NP-трудной , поэтому общепринятым подходом является поиск только приближенных решений. Особенно известным приближенным методом является алгоритм Ллойда , часто называют просто « алгоритмом k-средних » (хотя это название введено другим алгоритмом ). Однако он находит только локальный оптимум и обычно запускается несколько раз с разными случайными инициализациями. Вариации k -средних часто включают в себя такие оптимизации, как выбор лучшего из нескольких прогонов, а также ограничение центроидов членами набора данных ( k -medoids ), выбор медиан ( k кластеризация -медианов ), менее случайный выбор начальных центров (k-medoids). k -means++ ) или разрешить нечеткое назначение кластера ( fuzzy c-means ).

Большинство алгоритмов типа k -средних требуют заранее указать количество кластеров k , что считается одним из самых больших недостатков этих алгоритмов. Более того, алгоритмы предпочитают кластеры примерно одинакового размера, поскольку они всегда присваивают объект ближайшему центроиду. Это часто приводит к неправильному обрезанию границ кластеров (что неудивительно, поскольку алгоритм оптимизирует центры кластеров, а не границы кластеров).

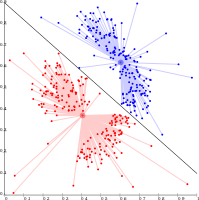
K-средние обладают рядом интересных теоретических свойств. Во-первых, он разбивает пространство данных на структуру, известную как диаграмма Вороного . Во-вторых, она концептуально близка к классификации ближайших соседей и поэтому популярна в машинном обучении . В-третьих, его можно рассматривать как вариант кластеризации на основе модели, а алгоритм Ллойда — как вариант алгоритма максимизации ожидания для этой модели, обсуждаемого ниже.

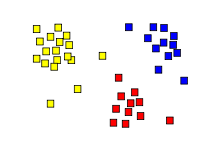
• k -средние примеры кластеризации
• 
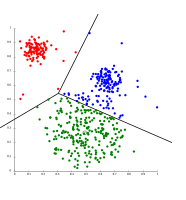
  k -means разделяет данные на ячейки Вороного, что предполагает кластеры одинакового размера (здесь это не подходит).
• 
  k -means не может представлять кластеры на основе плотности.

Проблемы кластеризации на основе центроидов, такие как k -means и k -medoids, являются частными случаями недееспособной метрической проблемы размещения объектов , канонической проблемы в сообществах исследования операций и вычислительной геометрии. В базовой задаче размещения объектов (существует множество вариантов, моделирующих более сложные условия) задача состоит в том, чтобы найти лучшие места складов для оптимального обслуживания заданного набора потребителей. Можно рассматривать «склады» как центроиды кластера, а «местоположения потребителей» как данные, подлежащие кластеризации. Это позволяет применить хорошо разработанные алгоритмические решения из литературы по размещению объектов к рассматриваемой в настоящее время задаче кластеризации на основе центроидов.

Кластеризация на основе модели

Структура кластеризации, наиболее тесно связанная со статистикой, — это кластеризация на основе моделей , основанная на моделях распределения . Этот подход моделирует данные как результат смеси распределений вероятностей. Его преимущество заключается в том, что он дает принципиальные статистические ответы на такие вопросы, как количество кластеров, какой метод или модель кластеризации использовать, а также как обнаруживать выбросы и справляться с ними.

Хотя теоретическая основа этих методов превосходна, они страдают от переобучения, если не наложены ограничения на сложность модели. Более сложная модель обычно способна лучше объяснить данные, что существенно затрудняет выбор модели подходящей сложности. Стандартные методы кластеризации на основе моделей включают более экономные модели, основанные на разложении по собственным значениям ковариационных матриц, которые обеспечивают баланс между переоснащением и точностью данных.

Один из известных методов известен как модели гауссовой смеси (с использованием алгоритма максимизации ожидания ). Здесь набор данных обычно моделируется с фиксированным (во избежание переобучения) количеством гауссовских распределений , которые инициализируются случайным образом и чьи параметры итеративно оптимизируются для лучшего соответствия набору данных. Это приведет к локальному оптимуму , поэтому несколько прогонов могут дать разные результаты. Чтобы получить жесткую кластеризацию, объектам часто присваивают распределение Гаусса, которому они, скорее всего, принадлежат; для мягкой кластеризации в этом нет необходимости.

Кластеризация на основе распределения создает сложные модели кластеров, которые могут отражать корреляцию и зависимость между атрибутами. Однако эти алгоритмы налагают дополнительную нагрузку на пользователя: для многих реальных наборов данных может не быть четко определенной математической модели (например, если предположить, что распределение Гаусса является довольно сильным предположением о данных).

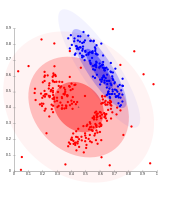
• Примеры кластеризации модели гауссовой смеси
• 
  С данными, распределенными по гауссу, EM работает хорошо, поскольку использует гауссово распределение для моделирования кластеров.
• 
  Кластеры на основе плотности нельзя моделировать с использованием гауссовых распределений.

Кластеризация на основе плотности

При кластеризации на основе плотности кластеры определяются как области более высокой плотности, чем остальная часть набора данных. Объекты в разреженных областях, необходимые для разделения кластеров, обычно считаются шумом и граничными точками.

Самый популярный Метод кластеризации на основе плотности — DBSCAN . В отличие от многих более новых методов, он имеет четко определенную кластерную модель, называемую «плотность достижимости». Подобно кластеризации на основе связей, она основана на соединении точек в пределах определенных пороговых значений расстояния. Однако он соединяет только точки, которые удовлетворяют критерию плотности, в исходном варианте определяемому как минимальное количество других объектов в пределах этого радиуса. Кластер состоит из всех связанных по плотности объектов (которые могут образовывать кластер произвольной формы, в отличие от многих других методов) плюс всех объектов, находящихся в радиусе действия этих объектов. Еще одним интересным свойством DBSCAN является то, что его сложность довольно низка – он требует линейного числа запросов к базе данных – и что он обнаруживает по существу одни и те же результаты (он детерминирован для основных и шумовых точек, но не для граничных точек). при каждом запуске, поэтому нет необходимости запускать его несколько раз. ОПТИКА является обобщением DBSCAN, которое устраняет необходимость выбирать подходящее значение для параметра диапазона. $\varepsilon$и дает иерархический результат, аналогичный результату кластеризации связей . ДеЛи-Клю, Density-Link-Clustering сочетает в себе идеи односвязной кластеризации и ОПТИКИ, устраняя $\varepsilon$ параметр полностью и предлагает повышение производительности по сравнению с ОПТИКОЙ за счет использования индекса R-дерева .

Ключевой недостаток DBSCAN и OPTICS заключается в том, что они ожидают некоторого падения плотности для обнаружения границ кластера. В наборах данных, например, с перекрывающимися распределениями Гаусса (обычный случай использования искусственных данных) границы кластеров, создаваемые этими алгоритмами, часто будут выглядеть произвольными, поскольку плотность кластеров постоянно уменьшается. В наборе данных, состоящем из смеси гауссиан, эти алгоритмы почти всегда уступают по производительности таким методам, как EM-кластеризация , которые способны точно моделировать данные такого типа.

Сдвиг среднего значения — это подход к кластеризации, при котором каждый объект перемещается в самую плотную область в его окрестностях на основе оценки плотности ядра . В конце концов, объекты сходятся к локальным максимумам плотности. Подобно кластеризации k-средних, эти «аттракторы плотности» могут служить представителями набора данных, но сдвиг среднего может обнаруживать кластеры произвольной формы, аналогично DBSCAN. Из-за дорогостоящей итеративной процедуры и оценки плотности сдвиг среднего значения обычно происходит медленнее, чем DBSCAN или k-Means. Кроме того, применимости алгоритма среднего сдвига к многомерным данным препятствует негладкое поведение оценки плотности ядра, что приводит к чрезмерной фрагментации хвостов кластеров.

• Примеры кластеризации на основе плотности
• 
  Кластеризация на основе плотности с помощью DBSCAN
• 
  DBSCAN предполагает, что кластеры имеют одинаковую плотность, и могут возникнуть проблемы с разделением соседних кластеров.
• 
  ОПТИКА — это вариант DBSCAN, улучшающий обработку кластеров различной плотности.

Кластеризация на основе сетки

Метод сетки используется для многомерного набора данных. В этом методе мы создаем структуру сетки, и сравнение выполняется в сетках (также известных как ячейки). Метод, основанный на сетке, является быстрым и имеет низкую вычислительную сложность. Существует два типа методов кластеризации на основе сетки: STING и CLIQUE. кластеризации на основе сетки Шаги алгоритма :

1. Разделите пространство данных на конечное число ячеек.
2. Случайным образом выберите ячейку «c», где c не следует заранее проходить.
3. Вычислите плотность «c»
4. Если плотность «c» превышает пороговую плотность
   1. Отметить ячейку «c» как новый кластер
   2. Вычислить плотность всех соседей точки «c»
   3. Если плотность соседней ячейки превышает пороговую плотность, добавьте ячейку в кластер и повторяйте шаги 4.2 и 4.3, пока не останется соседа с плотностью, превышающей пороговую плотность.
5. Повторяйте шаги 2,3 и 4, пока не будут пройдены все ячейки.
6. Останавливаться.

Последние события

В последние годы значительные усилия были направлены на улучшение производительности существующих алгоритмов. Среди них КЛАРАНС , и БЕРЕЗКА . В связи с недавней необходимостью обрабатывать все большие и большие наборы данных (также известные как большие данные ), готовность обменивать семантическое значение генерируемых кластеров на производительность растет. Это привело к разработке методов предварительной кластеризации, таких как Canopy Clustering , которые могут эффективно обрабатывать огромные наборы данных, но полученные «кластеры» представляют собой просто грубое предварительное разделение набора данных для последующего анализа разделов с помощью существующих более медленных методов, таких как как k-средства кластеризации .

Для многомерных данных многие из существующих методов терпят неудачу из-за проклятия размерности , которое делает определенные функции расстояния проблематичными в многомерных пространствах. Это привело к появлению новых алгоритмов кластеризации для многомерных данных , которые фокусируются на кластеризации подпространств (где используются только некоторые атрибуты, а модели кластеров включают соответствующие атрибуты для кластера) и корреляционной кластеризации , которая также ищет произвольно повернутое («коррелированное») подпространство. кластеры, которые можно смоделировать, задав корреляцию их атрибутов. Примерами таких алгоритмов кластеризации являются CLIQUE. и СУБКЛ .

Идеи методов кластеризации на основе плотности (в частности, семейства алгоритмов DBSCAN / OPTICS ) были адаптированы для подпространственной кластеризации (HiSC, иерархическая кластеризация подпространств и DiSH ) и корреляционная кластеризация (HiCO, иерархическая корреляционная кластеризация, 4C с использованием «корреляционной связи» и ERiC изучение иерархических корреляционных кластеров на основе плотности).

несколько различных систем кластеризации, основанных на взаимной информации Было предложено метрики Марины Мейлэ . Одним из них является вариант информационной ; другой обеспечивает иерархическую кластеризацию. Используя генетические алгоритмы, можно оптимизировать широкий спектр различных функций подгонки, включая взаимную информацию. Кроме того , распространение убеждений — недавнее достижение в области информатики и статистической физики — привело к созданию новых типов алгоритмов кластеризации.

Оценка и оценка

Оценка (или «проверка») результатов кластеризации так же сложна, как и сама кластеризация. Популярные подходы включают « внутреннюю » оценку, при которой кластеризация сводится к единому показателю качества, « внешнюю » оценку, при которой кластеризация сравнивается с существующей классификацией «основных данных», « ручную » оценку, проводимую экспертом-человеком, и « косвенную» оценку. «оценка путем оценки полезности кластеризации в ее предполагаемом применении.

Меры внутренней оценки страдают от той проблемы, что они представляют собой функции, которые сами по себе могут рассматриваться как цель кластеризации. Например, можно кластеризовать набор данных по коэффициенту Силуэта; за исключением того, что для этого не существует известного эффективного алгоритма. Используя такую ​​внутреннюю меру для оценки, скорее сравнивают сходство задач оптимизации: и не обязательно, насколько полезна кластеризация.

Внешняя оценка имеет схожие проблемы: если бы у нас были такие ярлыки «основной истины», нам не нужно было бы проводить кластеризацию; а в практических приложениях таких меток обычно нет. С другой стороны, метки отражают только одно возможное разделение набора данных, что не означает, что не существует другой, и, возможно, даже лучшей кластеризации.

Таким образом, ни один из этих подходов не может в конечном итоге судить о фактическом качестве кластеризации, но для этого требуется человеческая оценка. что очень субъективно. Тем не менее, такая статистика может быть весьма информативной при выявлении плохих кластеризаций. но не следует сбрасывать со счетов субъективную человеческую оценку.

Внутренняя оценка

См. также: Определение количества кластеров в наборе данных.

Когда результат кластеризации оценивается на основе данных, которые были кластеризованы сами, это называется внутренней оценкой. Эти методы обычно присваивают лучшую оценку алгоритму, который создает кластеры с высоким сходством внутри кластера и низким сходством между кластерами. Одним из недостатков использования внутренних критериев при оценке кластера является то, что высокие баллы по внутреннему показателю не обязательно приводят к эффективным приложениям для поиска информации. Кроме того, эта оценка смещена в сторону алгоритмов, использующих одну и ту же модель кластера. Например, кластеризация k-средних естественным образом оптимизирует расстояния до объектов, а внутренний критерий, основанный на расстоянии, скорее всего, переоценит результирующую кластеризацию.

Таким образом, меры внутренней оценки лучше всего подходят для получения некоторого понимания ситуаций, когда один алгоритм работает лучше, чем другой, но это не означает, что один алгоритм дает более достоверные результаты, чем другой. Валидность, измеряемая таким индексом, зависит от утверждения о том, что такая структура существует в наборе данных. Алгоритм, разработанный для некоторых моделей, не имеет шансов, если набор данных содержит радикально другой набор моделей или если оценка измеряет радикально другой критерий. Например, кластеризация k-средних позволяет найти только выпуклые кластеры, а многие индексы оценки предполагают наличие выпуклых кластеров. В наборе данных с невыпуклыми кластерами нецелесообразно использовать k -средние или критерий оценки, предполагающий выпуклость.

Существует более дюжины мер внутренней оценки, обычно основанных на интуитивном понимании того, что элементы в одном кластере должны быть более похожими, чем элементы в разных кластерах. Например, для оценки качества алгоритмов кластеризации по внутреннему критерию можно использовать следующие методы:

• Индекс Дэвиса-Булдина

Индекс Дэвиса-Булдина можно рассчитать по следующей формуле:

$DB={\frac {1}{n}}\sum _{i=1}^{n}\max _{j\neq i}\left({\frac {\sigma _{i}+\sigma _{j}}{d(c_{i},c_{j})}}\right)$

где n — количество кластеров, $c_{i}$ является центроидом кластера $i$, $\sigma _{i}$ среднее расстояние всех элементов в кластере $i$ к центроиду $c_{i}$, и $d(c_{i},c_{j})$ расстояние между центроидами $c_{i}$ и $c_{j}$. Поскольку алгоритмы, создающие кластеры с низкими внутрикластерными расстояниями (высокое внутрикластерное сходство) и высокими межкластерными расстояниями (низкое межкластерное сходство), будут иметь низкий индекс Дэвиса-Булдина, алгоритм кластеризации, создающий набор кластеров с наименьший индекс Дэвиса-Булдина считается лучшим алгоритмом, основанным на этом критерии.

• Индекс Данна

Индекс Данна направлен на выявление плотных и хорошо разделенных кластеров. Оно определяется как отношение минимального межкластерного расстояния к максимальному внутрикластерному расстоянию. Для каждого раздела кластера индекс Данна можно рассчитать по следующей формуле:

$D={\frac {\min _{1\leq i<j\leq n}d(i,j)}{\max _{1\leq k\leq n}d^{\prime }(k)}}\,,$

где d ( i , j ) представляет расстояние между кластерами i и j , а d '( k ) измеряет расстояние внутри кластера кластера k . Межкластерное расстояние d ( i , j ) между двумя кластерами может быть любым количеством мер расстояния, например, расстоянием между центроидами кластеров. Аналогично, внутрикластерное расстояние d '( k ) может быть измерено различными способами, например, как максимальное расстояние между любой парой элементов в кластере k . Поскольку внутренний критерий ищет кластеры с высоким внутрикластерным сходством и низким межкластерным сходством, более желательны алгоритмы, создающие кластеры с высоким индексом Данна.

• Коэффициент силуэта

Коэффициент силуэта сравнивает среднее расстояние до элементов в одном кластере со средним расстоянием до элементов в других кластерах. Объекты с высоким значением силуэта считаются хорошо кластеризованными, объекты с низким значением могут быть выбросами. Этот индекс хорошо работает с кластеризацией k -средних, а также используется для определения оптимального количества кластеров.

Внешняя оценка

При внешней оценке результаты кластеризации оцениваются на основе данных, которые не использовались для кластеризации, таких как известные метки классов и внешние тесты. Такие тесты состоят из набора предварительно классифицированных элементов, и эти наборы часто создаются (экспертами) людьми. Таким образом, наборы эталонов можно рассматривать как золотой стандарт оценки. Эти типы методов оценки измеряют, насколько близка кластеризация к заранее определенным контрольным классам. Однако недавно обсуждалось, подходит ли это для реальных данных или только для синтетических наборов данных с фактической основой, поскольку классы могут содержать внутреннюю структуру, имеющиеся атрибуты могут не позволять разделение кластеров или классы могут содержать аномалии . Кроме того, с точки зрения открытия знаний воспроизведение известных знаний не обязательно может быть запланированным результатом. В специальном сценарии ограниченной кластеризации , где метаинформация (например, метки классов) используется уже в процессе кластеризации, сохранение информации для целей оценки является нетривиальной задачей.

Ряд показателей адаптирован из вариантов, используемых для оценки задач классификации. Вместо подсчета количества раз, когда класс был правильно присвоен одной точке данных (известный как истинные положительные результаты ), такие метрики подсчета пар оценивают, прогнозируется ли, что каждая пара точек данных, которая действительно находится в одном и том же кластере, будет находиться в одном и том же кластере. кластер.

Как и в случае внутренней оценки, существует несколько мер внешней оценки: например:

• Чистота . Чистота — это мера того, насколько кластеры содержат один класс. Его расчет можно представить следующим образом: для каждого кластера подсчитайте количество точек данных из наиболее распространенного класса в указанном кластере. Теперь возьмите сумму по всем кластерам и разделите на общее количество точек данных. Формально, учитывая некоторый набор кластеров $M$ и некоторый набор классов $D$, оба разделения $N$ точки данных, чистота может быть определена как:

${\frac {1}{N}}\sum _{m\in M}\max _{d\in D}{|m\cap d|}$

Эта мера не ограничивает наличие большого количества кластеров, а большее количество кластеров облегчит получение высокой чистоты. Оценка чистоты 1 всегда возможна, если поместить каждую точку данных в отдельный кластер. Кроме того, чистота неэффективна для несбалансированных данных, где даже плохо работающие алгоритмы кластеризации дают высокое значение чистоты. Например, если набор данных размером 1000 состоит из двух классов, один из которых содержит 999 точек, а другой — 1 точку, то каждый возможный раздел будет иметь чистоту не менее 99,9%.

• Индекс Рэнда

Индекс Рэнда вычисляет, насколько кластеры (возвращаемые алгоритмом кластеризации) похожи на эталонные классификации. Его можно рассчитать по следующей формуле:

$RI={\frac {TP+TN}{TP+FP+FN+TN}}$

где $TP$ количество истинных положительных результатов, $TN$ количество истинных негативов , $FP$ - количество ложных срабатываний , и $FN$ это количество ложноотрицательных результатов . Здесь подсчитываются экземпляры — это количество правильных парных присваиваний. То есть, $TP$ - это количество пар точек, которые сгруппированы вместе в предсказанном разделе и в разделе основной истины, $FP$ - это количество пар точек, которые сгруппированы вместе в прогнозируемом разделе, но не в разделе основной истины и т. д. Если набор данных имеет размер N, то $TP+TN+FP+FN={\binom {N}{2}}$.

Одна из проблем индекса Рэнда заключается в том, что ложноположительные и ложноотрицательные результаты имеют одинаковый вес. Это может быть нежелательной характеристикой для некоторых приложений кластеризации. F-мера решает эту проблему: как и скорректированный на случайность скорректированный индекс Рэнда .

• F-мера

F-меру можно использовать для балансировки доли ложноотрицательных результатов путем взвешивания отзыва по параметру. $\beta \geq 0$. Пусть точность и полнота (обе внешние меры оценки сами по себе) определяются следующим образом:

$P={\frac {TP}{TP+FP}}$

$R={\frac {TP}{TP+FN}}$

где $P$ это уровень точности и $R$ это скорость отзыва . Мы можем рассчитать F-меру, используя следующую формулу:

$F_{\beta }={\frac {(\beta ^{2}+1)\cdot P\cdot R}{\beta ^{2}\cdot P+R}}$

Когда $\beta =0$, $F_{0}=P$. Другими словами, припоминание не влияет на F-меру, когда $\beta =0$и увеличение $\beta$ выделяет увеличивающийся вес для отзыва в финальной F-мере.

Также $TN$ не учитывается и может неограниченно меняться от 0 и выше.

• Индекс Жаккара

Индекс Жаккара используется для количественной оценки сходства между двумя наборами данных. Индекс Жаккара принимает значение от 0 до 1. Индекс 1 означает, что два набора данных идентичны, а индекс 0 указывает, что наборы данных не имеют общих элементов. Индекс Жаккара определяется по следующей формуле:

$J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {TP}{TP+FP+FN}}$

Это просто количество уникальных элементов, общих для обоих наборов, разделенное на общее количество уникальных элементов в обоих наборах.

Обратите внимание, что $TN$ не учитывается.

• Индекс кубика

Симметричная мера Дайса удваивает вес $TP$ все еще игнорируя $TN$:

$DSC={\frac {2TP}{2TP+FP+FN}}$

• Индекс Фаулкса-Мэллоуза

Индекс Фаулкса-Мэллоуза вычисляет сходство между кластерами, возвращаемыми алгоритмом кластеризации, и эталонными классификациями. Чем выше значение индекса Фаулкса-Мэллоуза, тем более схожими являются кластеры и эталонные классификации. Его можно рассчитать по следующей формуле:

$FM={\sqrt {{\frac {TP}{TP+FP}}\cdot {\frac {TP}{TP+FN}}}}$

где $TP$ количество истинных положительных результатов , $FP$ - количество ложных срабатываний , и $FN$ это количество ложноотрицательных результатов . $FM$ индекс — это среднее геометрическое точности и полноты $P$ и $R$, и поэтому также известен как G-мера , а F-мера является их средним гармоническим значением. Более того, точность и полнота также известны как индексы Уоллеса. $B^{I}$ и $B^{II}$. Случайные нормализованные версии отзыва, точности и G-меры соответствуют информированности , маркированности и корреляции Мэтьюза и тесно связаны с каппа .

• Индекс Чи — это внешний индекс проверки, который измеряет результаты кластеризации с помощью статистики хи-квадрат . Этот индекс положительно оценивает тот факт, что метки в кластерах максимально разрежены, т. е. каждый кластер имеет как можно меньше разных меток. Чем выше значение индекса Хи, тем больше связь между полученными кластерами и используемой меткой.
• Взаимная информация — это теоретико-информационная мера того, сколько информации разделяется между кластеризацией и истинной классификацией, которая может обнаружить нелинейное сходство между двумя кластеризациями. Нормализованная взаимная информация представляет собой семейство ее вариантов с поправкой на случайность, которые имеют уменьшенную погрешность при изменении числа кластеров.
• Матрица путаницы

Матрицу путаницы можно использовать для быстрой визуализации результатов алгоритма классификации (или кластеризации). Он показывает, насколько кластер отличается от кластера золотого стандарта.

Кластерная тенденция

Измерение тенденции к кластеризации означает измерение степени присутствия кластеров в данных, подлежащих кластеризации, и может быть выполнено в качестве первоначального теста перед попыткой кластеризации. Один из способов сделать это — сравнить данные со случайными данными. В среднем случайные данные не должны иметь кластеров.

• Статистика Хопкинса

Существует несколько формулировок статистики Хопкинса . Типичный вариант заключается в следующем. Позволять $X$ быть набором $n$ точки данных в $d$ мерное пространство. Рассмотрим случайную выборку (без замены) $m\ll n$ точки данных с членами $x_{i}$. Также создайте набор $Y$ из $m$ равномерно случайным образом распределенные точки данных. Теперь определим две меры расстояния, $u_{i}$ быть расстоянием $y_{i}\in Y$ от своего ближайшего соседа в X и $w_{i}$ быть расстоянием $x_{i}\in X$ от своего ближайшего соседа в X. Затем мы определяем статистику Хопкинса как:

$H={\frac {\sum _{i=1}^{m}{u_{i}^{d}}}{\sum _{i=1}^{m}{u_{i}^{d}}+\sum _{i=1}^{m}{w_{i}^{d}}}}\,,$

Согласно этому определению, однородные случайные данные должны иметь тенденцию иметь значения, близкие к 0,5, а кластерные данные должны иметь тенденцию иметь значения, близкие к 1.

Однако данные, содержащие только один гауссиан, также будут иметь оценку, близкую к 1, поскольку эта статистика измеряет отклонение от равномерного распределения, а не мультимодальность , что делает эту статистику в значительной степени бесполезной в применении (поскольку реальные данные никогда не бывают даже отдаленно однородными).

Приложения

Биология, вычислительная биология и биоинформатика

См. Также: Матрицы расстояний в филогении.

растений и животных Экология

Кластерный анализ используется для описания и проведения пространственных и временных сравнений сообществ (комплексов) организмов в гетерогенных средах. Он также используется в систематике растений для создания искусственных филогений или групп организмов (особей) на уровне вида, рода или более высокого уровня, которые имеют ряд общих признаков.

Транскриптомика

Кластеризация используется для создания групп генов со связанными паттернами экспрессии (также известными как коэкспрессируемые гены), как в алгоритме кластеризации HCS . Часто такие группы содержат функционально связанные белки, такие как ферменты определенного пути или гены, которые совместно регулируются. Высокопроизводительные эксперименты с использованием меток экспрессируемых последовательностей (EST) или микрочипов ДНК могут стать мощным инструментом для аннотации генома – общего аспекта геномики .

Анализ последовательности

Кластеризация последовательностей используется для группировки гомологичных последовательностей в семейства генов . Это очень важная концепция в биоинформатике и эволюционной биологии в целом. См. эволюцию путем дупликации генов .

Высокопроизводительные генотипирования платформы

Алгоритмы кластеризации используются для автоматического назначения генотипов.

Генетическая кластеризация человека

Сходство генетических данных используется при кластеризации для определения структуры популяции.

Лекарство

Медицинская визуализация

При ПЭТ-сканировании кластерный анализ можно использовать для различения разных типов тканей на трехмерном изображении для самых разных целей.

Анализ противомикробной активности

Кластерный анализ можно использовать для анализа закономерностей устойчивости к антибиотикам, для классификации противомикробных соединений по механизму действия, для классификации антибиотиков по их антибактериальной активности.

Сегментация IMRT

Кластеризация может использоваться для разделения карты флюенса на отдельные области для преобразования в поля результатов в лучевой терапии на основе MLC.

Бизнес и маркетинг

Исследование рынка

Кластерный анализ широко используется в исследованиях рынка при работе с многомерными данными опросов и тестовых панелей. Исследователи рынка используют кластерный анализ, чтобы разделить общую совокупность потребителей сегментации на сегменты рынка и лучше понять отношения между различными группами потребителей/потенциальных клиентов , а также использовать его при рынка , позиционировании продукта , разработке нового продукта и выборе тестовых рынков.

Группировка товаров для покупок

Кластеризацию можно использовать для группировки всех товаров, доступных в Интернете, в набор уникальных продуктов. Например, все товары на eBay можно сгруппировать в уникальные товары (на eBay нет понятия SKU ).

Всемирная паутина

Анализ социальных сетей

При исследовании социальных сетей кластеризация может использоваться для распознавания сообществ внутри больших групп людей.

Группировка результатов поиска

В процессе интеллектуальной группировки файлов и веб-сайтов кластеризация может использоваться для создания более релевантного набора результатов поиска по сравнению с обычными поисковыми системами, такими как Google. . В настоящее время существует ряд веб-инструментов кластеризации, таких как Clusty . Его также можно использовать для возврата более полного набора результатов в тех случаях, когда поисковый запрос может относиться к совершенно разным вещам. Каждое отдельное использование термина соответствует уникальному кластеру результатов, что позволяет алгоритму ранжирования возвращать комплексные результаты, выбирая лучший результат из каждого кластера.

Скользкая оптимизация карты

Карта фотографий Flickr и другие картографические сайты используют кластеризацию для уменьшения количества маркеров на карте. Это ускоряет работу и уменьшает количество визуального беспорядка.

Информатика

Эволюция программного обеспечения

Кластеризация полезна в развитии программного обеспечения, поскольку помогает уменьшить устаревшие свойства кода за счет реформирования рассредоточенной функциональности. Это форма реструктуризации и, следовательно, способ прямого профилактического обслуживания.

Сегментация изображений

Кластеризация может использоваться для разделения цифрового изображения на отдельные области для обнаружения границ или распознавания объектов .

Эволюционные алгоритмы

Кластеризация может использоваться для определения различных ниш в популяции эволюционного алгоритма, чтобы репродуктивные возможности могли быть более равномерно распределены между развивающимися видами или подвидами.

Рекомендательные системы

Рекомендательные системы предназначены для рекомендации новых товаров на основе вкусов пользователя. Иногда они используют алгоритмы кластеризации для прогнозирования предпочтений пользователя на основе предпочтений других пользователей в кластере пользователя.

Цепь Маркова, методы Монте-Карло

Кластеризация часто используется для обнаружения и характеристики экстремумов в целевом распределении.

Обнаружение аномалий

Аномалии/выбросы обычно (явно или неявно) определяются относительно структуры кластеризации данных.

Обработка естественного языка

Кластеризация может использоваться для разрешения лексической неоднозначности .

DevOps

Кластеризация использовалась для анализа эффективности команд DevOps.

Социальные науки

Анализ последовательности в социальных науках

Кластерный анализ используется, например, для выявления закономерностей траекторий семейной жизни, профессиональной карьеры и ежедневного или еженедельного использования времени.

Анализ преступности

Кластерный анализ можно использовать для выявления областей, где наблюдается больше случаев определенных видов преступлений. Выявив эти отдельные области или «горячие точки», где в течение определенного периода времени произошло аналогичное преступление, можно более эффективно управлять ресурсами правоохранительных органов.

Интеллектуальный анализ образовательных данных

Кластерный анализ, например, используется для выявления групп школ или учащихся со схожими свойствами.

Типологии

На основе данных опросов в проектах, подобных тем, которые реализует Исследовательский центр Pew, кластерный анализ используется для выявления типологий мнений, привычек и демографии, которые могут быть полезны в политике и маркетинге.

Другие

Полевая робототехника

Алгоритмы кластеризации используются для роботизированной ситуационной осведомленности, позволяющей отслеживать объекты и обнаруживать выбросы в данных датчиков.

Математическая химия

Для нахождения структурного сходства и т. д., например, 3000 химических соединений группировались в пространстве 90 топологических индексов .

Климатология

Чтобы найти погодные режимы или предпочтительные атмосферные характеристики давления на уровне моря.

Финансы

Кластерный анализ использовался для кластеризации акций по секторам.

Нефтяная геология

Кластерный анализ используется для восстановления отсутствующих данных керна забоя скважины или отсутствующих кривых каротажа с целью оценки свойств коллектора.

Геохимия

Кластеризация химических свойств в разных местах образца.

См. также

Специализированные виды кластерного анализа

• Алгоритмы автоматической кластеризации
• Сбалансированная кластеризация
• Кластеризация многомерных данных
• Концептуальная кластеризация
• Консенсусная кластеризация
• Ограниченная кластеризация
• Обнаружение сообщества
• Кластеризация потоков данных
• HCS-кластеризация
• Кластеризация последовательностей
• Спектральная кластеризация

Методы, используемые в кластерном анализе

• Искусственная нейронная сеть (ИНС)
• Поиск ближайшего соседа
• Анализ компонентов соседства
• Скрытый классовый анализ
• Распространение сходства

Проекция и предварительная обработка данных

• Уменьшение размеров
• Анализ главных компонентов
• Многомерное масштабирование

Другой

• Кластерно-взвешенное моделирование
• Проклятие размерности
• Определение количества кластеров в наборе данных
• Параллельные координаты
• Структурированный анализ данных
• Линейная разделимость