Импульс

Эта статья о линейном импульсе. Не путать с угловым моментом или моментом (физика) .

Эта статья об импульсе в физике. Чтобы узнать о других значениях, см. Импульс (значения) .

Импульс
После столкновения импульс битка передается на установленные шары.
Общие символы	п , п
И объединились	кг⋅м/с
Другие подразделения	пуля ⋅ фут/с
Сохранено ?	Да
Измерение	${\mathsf {M}}{\mathsf {L}}{\mathsf {T}}^{-1}$

В ньютоновской механике импульс ( мн.ч .: импульсы или импульсы ; , линейный импульс или поступательный импульс ) является произведением массы точнее и скорости объекта. Это векторная величина, обладающая величиной и направлением. Если m — масса объекта, а v — его скорость (также векторная величина), то импульс объекта p (от латинского pellere «толкать, двигать») равен: $\mathbf {p} =m\mathbf {v} .$

В Международной системе единиц (СИ) единицей измерения импульса является килограмм- метр в секунду (кг⋅м/с), что по размерности эквивалентно ньютон -секунде .

Второй закон движения Ньютона гласит, что скорость изменения импульса тела равна результирующей силе, действующей на него. Импульс зависит от системы отсчета , но в любой инерциальной системе отсчета он является сохраняющейся величиной, а это означает, что если на закрытую систему не действуют внешние силы, ее полный линейный импульс не изменится. Импульс также сохраняется в специальной теории относительности (с измененной формулой) и, в модифицированной форме, в электродинамике , квантовой механике , квантовой теории поля и общей теории относительности . Это выражение одной из фундаментальных симметрий пространства и времени: трансляционной симметрии .

Расширенные формулировки классической механики, лагранжевой и гамильтоновой механики , позволяют выбирать системы координат, включающие симметрии и ограничения. В этих системах сохраняющейся величиной является обобщенный импульс , и в целом он отличается от кинетического импульса, определенного выше. Понятие обобщенного импульса переносится в квантовую механику, где оно становится оператором волновой функции . Операторы импульса и положения связаны принципом неопределенности Гейзенберга .

В непрерывных системах, таких как электромагнитные поля , гидродинамика и деформируемые тела , может быть определена плотность импульса, а непрерывная версия сохранения импульса приводит к таким уравнениям, как уравнения Навье-Стокса для жидкостей или уравнение импульса Коши для деформируемых твердых тел. или жидкости.

Определение в классической механике

Импульс — векторная величина : он имеет как величину, так и направление. Поскольку импульс имеет направление, его можно использовать для прогнозирования результирующего направления и скорости движения объектов после их столкновения. Ниже основные свойства импульса описаны в одном измерении. Векторные уравнения почти идентичны скалярным уравнениям (см. множественные измерения ).

Одна частица

Импульс частицы условно обозначается буквой р . частицы Это произведение двух величин: массы (обозначенной буквой m ) и ее скорости ( v ): $$p=mv.$$

Единица импульса — это произведение единиц массы и скорости. В единицах СИ , если масса в килограммах, а скорость в метрах в секунду, то импульс измеряется в килограммах-метрах в секунду (кг⋅м/с). В единицах СГС , если масса в граммах, а скорость в сантиметрах в секунду, то импульс измеряется в граммах-сантиметрах в секунду (г⋅см/с).

Будучи вектором, импульс имеет величину и направление. Например, модель самолета массой 1 кг, движущаяся на север со скоростью 1 м/с в прямолинейном и горизонтальном полете, имеет импульс 1 кг⋅м/с на север, измеренный относительно земли.

Многие частицы

Импульс системы частиц есть векторная сумма их импульсов. Если две частицы имеют соответствующие массы m ₁ и m ₂ и скорости v ₁ и v ₂ , общий импульс равен $${\begin{aligned}p&=p_{1}+p_{2}\\&=m_{1}v_{1}+m_{2}v_{2}\,.\end{aligned}}$$Импульсы более чем двух частиц можно сложить в более общем плане следующим образом: $$p=\sum _{i}m_{i}v_{i}.$$

Система частиц имеет центр масс — точку, определяемую взвешенной суммой их положений: $$r_{\text{cm}}={\frac {m_{1}r_{1}+m_{2}r_{2}+\cdots }{m_{1}+m_{2}+\cdots }}={\frac {\sum _{i}m_{i}r_{i}}{\sum _{i}m_{i}}}.$$

Если одна или несколько частиц движутся, центр масс системы, как правило, также будет двигаться (если только система не находится в чистом вращении вокруг него). Если общая масса частиц равна $m$, а центр масс движется со скоростью v _см , импульс системы равен:

$$p=mv_{\text{cm}}.$$

Это известно как первый закон Эйлера .

Отношение к силе

Если результирующая сила F, приложенная к частице, постоянна и применяется в течение интервала времени Δt , импульс частицы изменяется на величину $$\Delta p=F\Delta t\,.$$

В дифференциальной форме это второй закон Ньютона ; скорость изменения импульса частицы равна мгновенной силе F, действующей на нее, $$F={\frac {{\text{d}}p}{{\text{d}}t}}.$$

Если результирующая сила, действующая на частицу, изменяется как функция времени F ( t ) , изменение импульса (или импульса J ) между моментами времени t ₁ и t ₂ равно $$\Delta p=J=\int _{t_{1}}^{t_{2}}F(t)\,{\text{d}}t\,.$$

Импульс измеряется в производных единицах ньютон- секунды (1 Н⋅с = 1 кг⋅м/с) или дина- секунды (1 дин⋅с = 1 г⋅см/с).

В предположении постоянной массы m это эквивалентно записи

$$F={\frac {{\text{d}}(mv)}{{\text{d}}t}}=m{\frac {{\text{d}}v}{{\text{d}}t}}=ma,$$

следовательно, результирующая сила равна массе частицы, умноженной на ее ускорение .

Пример : Модель самолета массой 1 кг разгоняется из состояния покоя до скорости 6 м/с в направлении на север за 2 с. Чистая сила, необходимая для создания этого ускорения, равна 3 ньютонам на севере. Изменение импульса составляет 6 кг⋅м/с на севере. Скорость изменения импульса составляет 3 (кг⋅м/с)/с на севере, что численно эквивалентно 3 ньютонам.

Сохранение

В закрытой системе (которая не обменивается веществом с окружающей средой и на которую не действуют внешние силы) общий импульс остается постоянным. Этот факт, известный как закон сохранения импульса , следует из законов движения Ньютона . Предположим, например, что две частицы взаимодействуют. Как объясняется третьим законом, силы между ними равны по величине, но противоположны по направлению. Если частицы пронумерованы 1 и 2, второй закон гласит, что F ₁ = ⁠ d p ₁ / d t ⁠ и F ₂ = ⁠ d п ₂ / d т ⁠ . Поэтому,

$${\frac {{\text{d}}p_{1}}{{\text{d}}t}}=-{\frac {{\text{d}}p_{2}}{{\text{d}}t}},$$со знаком минус, указывающим на то, что силы противостоят друг другу. Эквивалентно,

$${\frac {\text{d}}{{\text{d}}t}}\left(p_{1}+p_{2}\right)=0.$$

Если скорости частиц v _A1 и v _B1 до взаимодействия , а после — v _A2 и v _B2 , то

$$m_{A}v_{A1}+m_{B}v_{B1}=m_{A}v_{A2}+m_{B}v_{B2}.$$

Этот закон сохраняется независимо от того, насколько сложна сила взаимодействия между частицами. Аналогично, если частиц несколько, импульс, которым обмениваются между каждой парой частиц, равен нулю, поэтому общее изменение импульса равно нулю. Сохранение полного импульса ряда взаимодействующих частиц можно выразить как $$m_{A}v_{A}+m_{B}v_{B}+m_{C}v_{C}+...=constant.$$

Этот закон сохранения применим ко всем взаимодействиям, включая столкновения (как упругие , так и неупругие ) и разъединения, вызванные взрывными силами. Его также можно обобщить на ситуации, когда законы Ньютона не выполняются, например, в теории относительности и электродинамике .

Зависимость от системы отсчета

Импульс — измеримая величина, и его измерение зависит от системы отсчета . Например: если самолет массой 1000 кг летит по воздуху со скоростью 50 м/с, его импульс можно рассчитать равным 50 000 кг·м/с. Если самолет летит при встречном ветре 5 м/с, его скорость относительно поверхности Земли составит всего 45 м/с, а его импульс можно рассчитать как 45 000 кг·м/с. Оба расчета одинаково верны. В обеих системах отсчета любое изменение импульса будет соответствовать соответствующим законам физики.

Предположим, x — положение в инерциальной системе отсчета. С точки зрения другой системы отсчета, движущейся с постоянной скоростью u относительно другой, положение (представленное координатой со штрихом) меняется со временем как

$$x'=x-ut\,.$$

Это называется преобразованием Галилея .

Если частица движется со скоростью ⁠ d x / d t ⁠ = v в первой системе отсчета, во второй она движется со скоростью

$$v'={\frac {{\text{d}}x'}{{\text{d}}t}}=v-u\,.$$

Поскольку u не меняется, вторая система отсчета также является инерциальной и ускорения такие же:

$$a'={\frac {{\text{d}}v'}{{\text{d}}t}}=a\,.$$

Таким образом, импульс сохраняется в обеих системах отсчета. Более того, пока сила имеет одинаковую форму в обеих системах отсчёта, второй закон Ньютона остаётся неизменным. Этому критерию удовлетворяют такие силы, как ньютоновская гравитация, которая зависит только от скалярного расстояния между объектами. Эта независимость системы отсчета называется теорией относительности Ньютона или инвариантностью Галилея .

Изменение системы отсчета часто может упростить расчеты движения. Например, при столкновении двух частиц можно выбрать систему отсчета, в которой одна частица начинается в покое. Другая, часто используемая система отсчета — это система центра масс , которая движется вместе с центром масс. В этой системе общий импульс равен нулю.

Применение к столкновениям

Если две частицы, каждая из которых имеет известный импульс, сталкиваются и сливаются, закон сохранения импульса можно использовать для определения импульса слившегося тела. Если в результате столкновения две частицы разделяются, закона недостаточно для определения импульса каждой частицы. Если известен импульс одной частицы после столкновения, закон можно использовать для определения импульса другой частицы. объединенная кинетическая энергия после столкновения, закон можно использовать для определения импульса каждой частицы после столкновения. В качестве альтернативы, если известна Кинетическая энергия обычно не сохраняется. Если оно сохраняется, столкновение называется упругим столкновением ; если нет, то это неупругое столкновение .

Упругие столкновения

Основная статья: Упругое столкновение

Упругое столкновение равных масс

Упругое столкновение неравных масс.

Упругое столкновение — это столкновение, при котором кинетическая энергия не преобразуется в тепло или какую-либо другую форму энергии. Совершенно упругие столкновения могут происходить, когда объекты не касаются друг друга, как, например, при атомном или ядерном рассеянии, когда электрическое отталкивание удерживает объекты друг от друга. Стремительный маневр спутника вокруг планеты также можно рассматривать как идеально упругое столкновение. Столкновение двух бильярдных шаров является хорошим примером почти полностью упругого столкновения из-за их высокой жесткости , но когда тела вступают в контакт, всегда происходит некоторая диссипация .

Лобовое упругое столкновение двух тел можно представить скоростями в одном измерении вдоль линии, проходящей через тела. Если скорости равны v _A1 и v _B1 до столкновения и v _A2 и v _B2 после, уравнения, выражающие сохранение импульса и кинетической энергии, будут следующими:

$${\begin{aligned}m_{A}v_{A1}+m_{B}v_{B1}&=m_{A}v_{A2}+m_{B}v_{B2}\\{\tfrac {1}{2}}m_{A}v_{A1}^{2}+{\tfrac {1}{2}}m_{B}v_{B1}^{2}&={\tfrac {1}{2}}m_{A}v_{A2}^{2}+{\tfrac {1}{2}}m_{B}v_{B2}^{2}\,.\end{aligned}}$$

Изменение системы отсчета может упростить анализ столкновения. Например, предположим, что есть два тела одинаковой массы m , одно неподвижное, а другое приближающееся к другому со скоростью v (как показано на рисунке). Центр масс движется со скоростью ⁠ v / 2 ⁠ и оба тела движутся к нему со скоростью ⁠ v / 2 ⁠ . Из-за симметрии после столкновения оба должны удаляться от центра масс с одинаковой скоростью. Прибавив к обеим скорости центра масс, мы получим, что тело, которое двигалось, теперь остановилось, а другое движется прочь со скоростью v . Тела поменялись скоростями. Независимо от скоростей тел переход к системе центра масс приводит нас к одному и тому же выводу. Следовательно, конечные скорости определяются выражением

$${\begin{aligned}v_{A2}&=v_{B1}\\v_{B2}&=v_{A1}\,.\end{aligned}}$$

В общем случае, когда известны начальные скорости, конечные скорости определяются выражением

$${\begin{aligned}v_{A2}&=\left({\frac {m_{A}-m_{B}}{m_{A}+m_{B}}}\right)v_{A1}+\left({\frac {2m_{B}}{m_{A}+m_{B}}}\right)v_{B1}\\v_{B2}&=\left({\frac {m_{B}-m_{A}}{m_{A}+m_{B}}}\right)v_{B1}+\left({\frac {2m_{A}}{m_{A}+m_{B}}}\right)v_{A1}\,.\end{aligned}}$$

Если одно тело имеет гораздо большую массу, чем другое, столкновение мало повлияет на его скорость, в то время как другое тело претерпит большие изменения.

Неупругие столкновения

Основная статья: Неупругое столкновение

совершенно неупругое столкновение между равными массами

При неупругом столкновении часть кинетической энергии сталкивающихся тел преобразуется в другие формы энергии (например, тепло или звук ). Примеры включают дорожно-транспортные происшествия , в которых эффект потери кинетической энергии можно увидеть в повреждении транспортных средств; электроны теряют часть своей энергии атомам (как в эксперименте Франка-Герца ); и ускорители частиц , в которых кинетическая энергия преобразуется в массу в виде новых частиц.

При совершенно неупругом столкновении (например, при ударе жука о лобовое стекло) оба тела впоследствии совершают одинаковое движение. Лобовое неупругое столкновение двух тел можно представить скоростями в одном измерении вдоль линии, проходящей через тела. Если до столкновения скорости равны v _A1 и v _B1, будут двигаться со скоростью v ₂ то при совершенно неупругом столкновении оба тела после столкновения . Уравнение, выражающее сохранение импульса:

$${\begin{aligned}m_{A}v_{A1}+m_{B}v_{B1}&=\left(m_{A}+m_{B}\right)v_{2}\,.\end{aligned}}$$

Если одно тело изначально неподвижно (например, $u_{2}=0$), уравнение сохранения импульса имеет вид

$$m_{A}v_{A1}=\left(m_{A}+m_{B}\right)v_{2}\,,$$

так

$$v_{2}={\frac {m_{A}}{m_{A}+m_{B}}}v_{A1}\,.$$

В другой ситуации, если система отсчета движется с конечной скоростью такой, что $v_{2}=0$, объекты остановятся в результате совершенно неупругого столкновения, и 100% кинетической энергии преобразуется в другие формы энергии. В этом случае начальные скорости тел были бы отличны от нуля, или тела должны были бы быть безмассовыми.

Одной из мер неупругости столкновения является коэффициент восстановления C _R , определяемый как отношение относительной скорости отделения к относительной скорости сближения. Применяя эту меру к мячу, отскакивающему от твердой поверхности, ее можно легко измерить по следующей формуле:

$$C_{\text{R}}={\sqrt {\frac {\text{bounce height}}{\text{drop height}}}}\,.$$

Уравнения импульса и энергии также применимы к движениям объектов, которые начинаются вместе, а затем расходятся. Например, взрыв является результатом цепной реакции, которая преобразует потенциальную энергию, запасенную в химической, механической или ядерной форме, в кинетическую энергию, акустическую энергию и электромагнитное излучение. В ракетах также используется принцип сохранения импульса: топливо выбрасывается наружу, набирая импульс, и ракете сообщается равный и противоположный импульс.

Несколько измерений

Двумерное упругое столкновение. Движения, перпендикулярного изображению, нет, поэтому для представления скоростей и импульсов необходимы только два компонента. Два синих вектора представляют скорости после столкновения и векторно суммируются, чтобы получить начальную (красную) скорость.

Реальное движение имеет как направление, так и скорость и должно быть представлено вектором . В системе координат с осями x , y , z скорость имеет компоненты v _x в направлении x , v _y в направлении y , v _z в направлении z . Вектор представлен жирным шрифтом:

$$\mathbf {v} =\left(v_{x},v_{y},v_{z}\right).$$

Аналогично, импульс является векторной величиной и обозначается жирным шрифтом:

$$\mathbf {p} =\left(p_{x},p_{y},p_{z}\right).$$

Уравнения в предыдущих разделах работают в векторной форме, если скаляры p и v заменены векторами p и v . Каждое векторное уравнение представляет собой три скалярных уравнения. Например,

$$\mathbf {p} =m\mathbf {v}$$

представляет собой три уравнения:

$${\begin{aligned}p_{x}&=mv_{x}\\p_{y}&=mv_{y}\\p_{z}&=mv_{z}.\end{aligned}}$$

Уравнения кинетической энергии являются исключением из приведенного выше правила замены. Уравнения по-прежнему одномерны, но каждый скаляр представляет величину вектора , например,

$$v^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\,.$$

Каждое векторное уравнение представляет собой три скалярных уравнения. Часто координаты можно выбрать так, что понадобятся только две компоненты, как на рисунке. Каждый компонент можно получить отдельно, а результаты объединить для получения векторного результата.

Простую конструкцию, включающую систему центра масс, можно использовать, чтобы показать, что если неподвижную упругую сферу ударит движущаяся сфера, после столкновения они разойдутся под прямым углом (как показано на рисунке).

Объекты переменной массы

См. Также: Система переменной массы.

Концепция импульса играет фундаментальную роль в объяснении поведения объектов переменной массы, таких как ракета, выбрасывающая топливо, или звезду газ, аккумулирующий . При анализе такого объекта мы рассматриваем массу объекта как функцию, которая меняется со временем: m ( t ) . Таким образом, импульс объекта в момент времени t равен p ( t ) = m ( t ) v ( t ) . Тогда можно было бы попытаться применить второй закон движения Ньютона, сказав, что внешняя сила F, действующая на объект, связана с его импульсом p ( t ) соотношением F = ⁠ d p / d t ⁠ , но это неверно, как и связанное выражение, полученное путем применения правила произведения к ⁠ d ( м v ) / d т ⁠ :

$$F=m(t){\frac {{\text{d}}v}{{\text{d}}t}}+v(t){\frac {{\text{d}}m}{{\text{d}}t}}.{\text{(incorrect)}}$$

Это уравнение неправильно описывает движение объектов переменной массы. Правильное уравнение

$$F=m(t){\frac {{\text{d}}v}{{\text{d}}t}}-u{\frac {{\text{d}}m}{{\text{d}}t}},$$

где u — скорость выброшенной/присоединившейся массы , видимая в системе покоя объекта . Это отличается от v , который представляет собой скорость самого объекта, видимого в инерциальной системе отсчета.

Это уравнение получается путем отслеживания как импульса объекта, так и импульса выброшенной/аккрецированной массы ( d m ). Если рассматривать вместе, объект и масса ( d m ) составляют замкнутую систему, в которой сохраняется полный импульс.

$$P(t+{\text{d}}t)=(m-{\text{d}}m)(v+{\text{d}}v)+{\text{d}}m(v-u)=mv+m{\text{d}}v-u{\text{d}}m=P(t)+m{\text{d}}v-u{\text{d}}m$$

релятивистский

См. Также: Масса в специальной теории относительности и Тесты релятивистской энергии и импульса.

Лоренц-инвариантность

Ньютоновская физика предполагает, что абсолютное время и пространство существуют вне какого-либо наблюдателя; это приводит к инвариантности Галилея . Это также приводит к предсказанию, что скорость света может варьироваться от одной системы отсчета к другой. Это противоречит тому, что наблюдалось. В специальной теории относительности Эйнштейн придерживается постулата о том, что уравнения движения не зависят от системы отсчета, но предполагает, что скорость света c инвариантна. В результате положение и время в двух системах отсчета связаны преобразованием Лоренца вместо преобразования Галилея .

Рассмотрим, например, одну систему отсчета, движущуюся относительно другой со скоростью v в направлении x . Преобразование Галилея дает координаты движущейся системы отсчета как

$${\begin{aligned}t'&=t\\x'&=x-vt\end{aligned}}$$

а преобразование Лоренца дает

$${\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x-vt\right)\,\end{aligned}}$$

где γ — фактор Лоренца :

$$\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}.$$

Второй закон Ньютона при фиксированной массе не инвариантен относительно преобразований Лоренца. Однако его можно сделать инвариантным, сделав инерционную массу m объекта функцией скорости:

$$m=\gamma m_{0}\,;$$

m ₀ объекта — инвариантная масса .

Модифицированный импульс,

$$\mathbf {p} =\gamma m_{0}\mathbf {v} \,,$$

подчиняется второму закону Ньютона:

$$\mathbf {F} ={\frac {d\mathbf {p} }{dt}}\,.$$

В области классической механики релятивистский импульс близко приближается к ньютоновскому импульсу: при низкой скорости γ m ₀ v примерно равен m ₀ v , ньютоновскому выражению импульса.

Четырехвекторная формулировка

Основная статья: Четыре импульса

В специальной теории относительности физические величины выражаются через четыре вектора , которые включают время в качестве четвертой координаты наряду с тремя пространственными координатами. Эти векторы обычно обозначаются заглавными буквами, например R для обозначения позиции. Выражение для четырехимпульса зависит от того, как выражены координаты. Время может быть задано в обычных единицах или умножено на скорость света, так что все компоненты четырехвектора имеют измерения длины. Если используется последнее масштабирование, интервал собственного времени τ , определяемый формулой

$$c^{2}{\text{d}}\tau ^{2}=c^{2}{\text{d}}t^{2}-{\text{d}}x^{2}-{\text{d}}y^{2}-{\text{d}}z^{2}\,,$$

инвариантен относительно преобразований Лоренца (в этом выражении и далее (+ − − −) сигнатура метрики используется , разные авторы используют разные соглашения). Математически эту инвариантность можно обеспечить одним из двух способов: рассматривая четыре вектора как евклидовы векторы и умножая время на √ −1 ; или сохраняя время реальной величиной и встраивая векторы в пространство Минковского . В пространстве Минковского скалярное произведение двух четырехвекторов U = ( U ₀ , U ₁ , U ₂ , U ₃ ) и V = ( V ₀ , V ₁ , V ₂ , V ₃ ) определяется как

$$\mathbf {U} \cdot \mathbf {V} =U_{0}V_{0}-U_{1}V_{1}-U_{2}V_{2}-U_{3}V_{3}\,.$$

Во всех системах координат ( контравариантная ) релятивистская четырехскорость определяется выражением

$$\mathbf {U} \equiv {\frac {{\text{d}}\mathbf {R} }{{\text{d}}\tau }}=\gamma {\frac {{\text{d}}\mathbf {R} }{{\text{d}}t}}\,,$$

а (контравариантный) четырехимпульс равен

$$\mathbf {P} =m_{0}\mathbf {U} \,,$$

где m ₀ — инвариантная масса. Если R = ( c t , x , y , z ) (в пространстве Минковского), то

$$\mathbf {P} =\gamma m_{0}\left(c,\mathbf {v} \right)=(mc,\mathbf {p} )\,.$$

Эйнштейна Используя эквивалентность массы и энергии , E = m c ² , это можно переписать как

$$\mathbf {P} =\left({\frac {E}{c}},\mathbf {p} \right)\,.$$

Таким образом, сохранение четырехимпульса является лоренц-инвариантным и предполагает сохранение как массы, так и энергии.

Величина четырехвекторного импульса равна m ₀ c :

$$\|\mathbf {P} \|^{2}=\mathbf {P} \cdot \mathbf {P} =\gamma ^{2}m_{0}^{2}\left(c^{2}-v^{2}\right)=(m_{0}c)^{2}\,,$$

и инвариантен во всех системах отсчета.

Релятивистское соотношение энергии и импульса справедливо даже для безмассовых частиц, таких как фотоны; полагая m ₀ = 0, следует, что

$$E=pc\,.$$

В игре в релятивистский «бильярд», если неподвижная частица сталкивается с движущейся частицей при упругом столкновении, траектории, образованные этими двумя частицами впоследствии, образуют острый угол. Это отличается от нерелятивистского случая, когда они движутся под прямым углом.

Четырехимпульс плоской волны можно связать с волновым четырехвектором

$$\mathbf {P} =\left({\frac {E}{c}},{\vec {\mathbf {p} }}\right)=\hbar \mathbf {K} =\hbar \left({\frac {\omega }{c}},{\vec {\mathbf {k} }}\right)$$

Для частицы соотношение между временными компонентами E = ħ ω является соотношением Планка–Эйнштейна , а соотношение между пространственными компонентами p = ħ k описывает де Бройля волну материи .

Обобщенный

Смотрите также: Аналитическая механика

Законы Ньютона может быть трудно применить ко многим видам движения, поскольку движение ограничено ограничениями . Например, бусина на счетах вынуждена двигаться вдоль своей проволоки, а качающийся маятник вынужден качаться на фиксированном расстоянии от оси. Многие такие ограничения могут быть включены путем замены обычных декартовых координат на набор обобщенных координат , которых может быть меньше. Разработаны усовершенствованные математические методы решения задач механики в обобщенных координатах. Они вводят обобщенный импульс , также известный как канонический или сопряженный импульс , который расширяет концепции как линейного момента, так и углового момента . Чтобы отличить его от обобщенного импульса, произведение массы и скорости также называют механическим , кинетическим или кинематическим импульсом . Ниже описаны два основных метода.

Лагранжева механика

В лагранжевой механике лагранжиан определяется как разность между кинетической энергией T и потенциальной энергией V :

$${\mathcal {L}}=T-V\,.$$

Если обобщенные координаты представлены в виде вектора q = ( q ₁ , q ₂ , ... , q _N ) , а дифференцирование по времени представлено точкой над переменной, то уравнения движения (известные как уравнения Лагранжа или Эйлера–Эйлера) Уравнения Лагранжа ) представляют собой совокупность N уравнений:

$${\frac {\text{d}}{{\text{d}}t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial {\mathcal {L}}}{\partial q_{j}}}=0\,.$$

Если координата q _i не является декартовой координатой, соответствующая компонента обобщенного импульса p _i не обязательно имеет размеры линейного импульса. Даже если q _i является декартовой координатой, p _i не будет таким же, как механический импульс, если потенциал зависит от скорости. В некоторых источниках кинематический импульс обозначается символом Π .

В этой математической структуре обобщенный импульс связан с обобщенными координатами. Его компоненты определяются как

$$p_{j}={\frac {\partial {\mathcal {L}}}{\partial {\dot {q}}_{j}}}\,.$$

Каждый компонент p _j называется сопряженным импульсом координаты q _j .

Теперь, если данная координата q _i не появляется в лагранжиане (хотя ее производная по времени может появиться), то p _j является постоянным. Это обобщение закона сохранения импульса.

Даже если обобщенные координаты — это просто обычные пространственные координаты, сопряженные импульсы не обязательно являются обычными координатами импульса. Пример можно найти в разделе электромагнетизма.

гамильтонова механика

В гамильтоновой механике лагранжиан (функция обобщенных координат и их производных) заменяется гамильтонианом, который является функцией обобщенных координат и импульса. Гамильтониан определяется как

$${\mathcal {H}}\left(\mathbf {q} ,\mathbf {p} ,t\right)=\mathbf {p} \cdot {\dot {\mathbf {q} }}-{\mathcal {L}}\left(\mathbf {q} ,{\dot {\mathbf {q} }},t\right)\,,$$

где импульс получается путем дифференцирования лагранжиана, как указано выше. Гамильтоновы уравнения движения имеют вид

$${\begin{aligned}{\dot {q}}_{i}&={\frac {\partial {\mathcal {H}}}{\partial p_{i}}}\\-{\dot {p}}_{i}&={\frac {\partial {\mathcal {H}}}{\partial q_{i}}}\\-{\frac {\partial {\mathcal {L}}}{\partial t}}&={\frac {{\text{d}}{\mathcal {H}}}{{\text{d}}t}}\,.\end{aligned}}$$

Как и в лагранжевой механике, если обобщенная координата не появляется в гамильтониане, ее сопряженная компонента импульса сохраняется.

Симметрия и сохранение

Сохранение импульса — математическое следствие однородности ( симметрии сдвига ) пространства (положение в пространстве — каноническая величина, сопряженная с импульсом). То есть сохранение импульса является следствием того, что законы физики не зависят от положения; это частный случай теоремы Нётер . Для систем, не обладающих этой симметрией, может быть невозможно определить сохранение импульса. Примеры, когда сохранение импульса неприменимо, включают искривленное пространство-время в общей теории относительности. или кристаллы времени в физике конденсированного состояния .

Электромагнитный

Частица в поле

В уравнениях Максвелла силы между частицами передаются электрическими и магнитными полями. Электромагнитная сила ( сила Лоренца ) на частицу с зарядом q, возникающая вследствие комбинации электрического поля E и магнитного поля B, равна

$$\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ).$$

(в единицах СИ ). Он имеет электрический потенциал φ ( r , t ) и магнитный векторный потенциал A ( r , t ) . В нерелятивистском режиме его обобщенный импульс равен

$$\mathbf {P} =m\mathbf {\mathbf {v} } +q\mathbf {A} ,$$

тогда как в релятивистской механике это становится

$$\mathbf {P} =\gamma m\mathbf {\mathbf {v} } +q\mathbf {A} .$$

Величину V = q A иногда называют потенциальным импульсом . Это импульс, возникающий в результате взаимодействия частицы с электромагнитными полями. Название представляет собой аналогию с потенциальной энергией U = q φ , которая представляет собой энергию взаимодействия частицы с электромагнитными полями. Эти величины образуют четырехвектор, поэтому аналогия непротиворечива; кроме того, понятие потенциального импульса важно для объяснения так называемого скрытого импульса электромагнитных полей.

Сохранение

В ньютоновской механике закон сохранения импульса можно вывести из закона действия и противодействия , который гласит, что каждая сила имеет возвратно-поступательно равную и противоположную силу. При некоторых обстоятельствах движущиеся заряженные частицы могут оказывать друг на друга силы в непротивоположных направлениях. Тем не менее, совокупный импульс частиц и электромагнитного поля сохраняется.

Вакуум

Сила Лоренца сообщает импульс частице, поэтому по второму закону Ньютона частица должна сообщать импульс электромагнитным полям.

В вакууме импульс единицы объема равен

$$\mathbf {g} ={\frac {1}{\mu _{0}c^{2}}}\mathbf {E} \times \mathbf {B} \,,$$

где µ ₀ — проницаемость вакуума , а c — скорость света . Плотность импульса пропорциональна вектору Пойнтинга S , который определяет направленную скорость передачи энергии на единицу площади:

$$\mathbf {g} ={\frac {\mathbf {S} }{c^{2}}}\,.$$

Если импульс должен сохраняться в объеме V в области Q , изменения импульса материи за счет силы Лоренца должны быть уравновешены изменениями импульса электромагнитного поля и оттоком импульса. Если P _mech — это импульс всех частиц в Q и частицы рассматриваются как континуум, то второй закон Ньютона дает

$${\frac {{\text{d}}\mathbf {P} _{\text{mech}}}{{\text{d}}t}}=\iiint \limits _{Q}\left(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} \right){\text{d}}V\,.$$

Электромагнитный импульс

$$\mathbf {P} _{\text{field}}={\frac {1}{\mu _{0}c^{2}}}\iiint \limits _{Q}\mathbf {E} \times \mathbf {B} \,dV\,,$$

и уравнение сохранения каждой компоненты i импульса имеет вид

$${\frac {\text{d}}{{\text{d}}t}}\left(\mathbf {P} _{\text{mech}}+\mathbf {P} _{\text{field}}\right)_{i}=\iint \limits _{\sigma }\left(\sum \limits _{j}T_{ij}n_{j}\right){\text{d}}\Sigma \,.$$

Член справа представляет собой интеграл по площади Σ поверхности σ, представляющий поток импульса в объем и из него, а n _j является компонентом нормали к поверхности S . Величина T _{i j} называется тензором напряжений Максвелла и определяется как

$$T_{ij}\equiv \epsilon _{0}\left(E_{i}E_{j}-{\frac {1}{2}}\delta _{ij}E^{2}\right)+{\frac {1}{\mu _{0}}}\left(B_{i}B_{j}-{\frac {1}{2}}\delta _{ij}B^{2}\right)\,.$$

СМИ

Приведенные выше результаты относятся к микроскопическим уравнениям Максвелла, применимым к электромагнитным силам в вакууме (или в очень малых масштабах в средах). В средах определить плотность импульса сложнее, поскольку разделение на электромагнитные и механические условно. Определение плотности электромагнитного импульса изменено на

$$\mathbf {g} ={\frac {1}{c^{2}}}\mathbf {E} \times \mathbf {H} ={\frac {\mathbf {S} }{c^{2}}}\,,$$

где H-поле H связано с B-полем и намагниченностью M соотношением

$$\mathbf {B} =\mu _{0}\left(\mathbf {H} +\mathbf {M} \right)\,.$$

Тензор электромагнитных напряжений зависит от свойств среды.

Квантово-механический

Дополнительная информация: Оператор импульса.

В квантовой механике импульс определяется как самосопряженный оператор волновой функции . Принцип Гейзенберга неопределенности определяет пределы того, насколько точно можно одновременно знать импульс и положение одной наблюдаемой системы. В квантовой механике положение и импульс являются сопряженными переменными .

Для отдельной частицы, описанной в базисе позиций, оператор импульса можно записать как

$$\mathbf {p} ={\hbar \over i}\nabla =-i\hbar \nabla \,,$$

где ∇ — оператор градиента , ħ — приведенная постоянная Планка , а i — мнимая единица . Это часто встречающаяся форма оператора импульса, хотя оператор импульса в других базисах может принимать и другие формы. Например, в импульсном пространстве оператор импульса представлен собственных значений уравнением

$$\mathbf {p} \psi (p)=p\psi (p)\,,$$

где оператор p, действующий на собственную волновую функцию ψ ( p ), дает эту волновую функцию, умноженную на собственное значение p , аналогично тому, как оператор положения, действующий на волновую функцию ψ ( x ), дает эту волновую функцию, умноженную на собственное значение х .

Как для массивных, так и для безмассовых объектов релятивистский импульс связан с фазовой постоянной β соотношением

$$p=\hbar \beta$$

Электромагнитное излучение (включая видимый свет , ультрафиолетовый свет и радиоволны ) переносится фотонами . Хотя фотоны (частичный аспект света) не имеют массы, они все равно несут импульс. Это приводит к появлению таких приложений, как солнечный парус . Расчет импульса света в диэлектрических средах несколько спорен (см. Споры Абрахама-Минковского ).

В деформируемых телах и жидкостях

Сохранение в континууме

Основная статья: уравнение импульса Коши

Движение материального тела

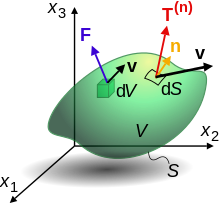
В таких областях, как гидродинамика и механика твердого тела , невозможно проследить за движением отдельных атомов или молекул. Вместо этого материалы должны быть аппроксимированы континуумом , в каждой точке которого имеется частица или жидкий пакет , которому присвоено среднее значение свойств атомов в небольшой области поблизости. В частности, он имеет плотность ρ и скорость v , которые зависят от времени t и положения r . Импульс единицы объема равен ρ v .

Рассмотрим столб воды, находящийся в гидростатическом равновесии . Все силы, действующие на воду, уравновешены, и вода неподвижна. В любой капле воды две силы уравновешиваются. Первый — гравитация, которая действует непосредственно на каждый атом и молекулу внутри. Сила гравитации на единицу объема равна ρg g , где — ускорение свободного падения . Вторая сила представляет собой сумму всех сил, действующих на его поверхность со стороны окружающей воды. Сила снизу больше силы сверху ровно на величину, необходимую для уравновешивания гравитации. Нормальная сила на единицу площади — это давление p . Средняя сила на единицу объема внутри капли представляет собой градиент давления, поэтому уравнение баланса сил имеет вид

$$-\nabla p+\rho \mathbf {g} =0\,.$$

Если силы не уравновешены, капля ускоряется. Это ускорение не является просто частной производной ⁠ ∂ v / ∂ t ⁠ потому что жидкость в данном объёме изменяется со временем. Вместо этого материальная производная : необходима

$${\frac {D}{Dt}}\equiv {\frac {\partial }{\partial t}}+\mathbf {v} \cdot {\boldsymbol {\nabla }}\,.$$

Применительно к любой физической величине производная материала включает в себя скорость изменения в точке и изменения, вызванные адвекцией , когда жидкость переносится мимо этой точки. В единице объема скорость изменения импульса равна ρ ⁠ D v / D т ⁠ . Это равно чистой силе, действующей на каплю.

Силы, которые могут изменить импульс капли, включают градиент давления и гравитацию, как указано выше. Кроме того, поверхностные силы могут деформировать каплю. В простейшем случае сдвиговое напряжение τ , действующее под действием силы, параллельной поверхности капли, пропорционально скорости деформации или скорости деформации . Такое напряжение сдвига возникает, если жидкость имеет градиент скорости, поскольку жидкость движется с одной стороны быстрее, чем с другой. Если скорость в направлении x изменяется в зависимости от z , касательная сила в направлении x на единицу площади, нормальная к направлению z , равна

$$\sigma _{zx}=-\mu {\frac {\partial v_{x}}{\partial z}}\,,$$

где ц — вязкость . Это также поток , или поток на единицу площади . x -импульса через поверхность

С учетом влияния вязкости уравнения баланса импульса для течения несжимаемой ньютоновской жидкости имеют вид

$$\rho {\frac {D\mathbf {v} }{Dt}}=-{\boldsymbol {\nabla }}p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {g} .\,$$

Они известны как уравнения Навье – Стокса .

Уравнения баланса импульса можно распространить на более общие материалы, включая твердые тела. Для каждой поверхности с нормалью в направлении i и силой в направлении j существует составляющая напряжения σ _{i j} . Девять компонентов составляют тензор напряжений Коши σ , который включает в себя как давление, так и сдвиг. Локальное сохранение импульса выражается уравнением импульса Коши :

$$\rho {\frac {D\mathbf {v} }{Dt}}={\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}+\mathbf {f} \,,$$

где f — объемная сила .

Уравнение количества движения Коши широко применимо к деформациям твердых тел и жидкостей. Связь между напряжениями и скоростью деформации зависит от свойств материала (см. Виды вязкости ).

Акустические волны

Возмущение в среде вызывает колебания или волны , которые распространяются от своего источника. В жидкости небольшие изменения давления p часто можно описать уравнением акустической волны :

$${\frac {\partial ^{2}p}{\partial t^{2}}}=c^{2}\nabla ^{2}p\,,$$

где с — скорость звука . В твердом теле аналогичные уравнения можно получить для распространения давления ( P-волны ) и сдвига ( S-волны ).

Поток или перенос на единицу площади компонента импульса v j _со скоростью vi _ρ равен ρ v _j v _j . В линейном приближении, которое приводит к приведенному выше акустическому уравнению, среднее время этого потока равно нулю. Однако нелинейные эффекты могут привести к ненулевому среднему значению. Поток импульса может возникнуть, даже если сама волна не имеет среднего импульса.

История концепции

Импульс

Основная статья: Теория импульса

Иоанн Филопон

Примерно в 530 году нашей эры Иоанн Филопон разработал концепцию импульса в «О физике» , комментарии к Аристотеля » «Физике . Аристотель утверждал, что все, что движется, должно чем-то поддерживаться в движении. Например, брошенный мяч должен двигаться за счет движения воздуха. Филопон указал на абсурдность утверждения Аристотеля о том, что движению объекта способствует тот же воздух, который препятствует его прохождению. Вместо этого он предположил, что толчок придавался объекту в процессе его броска.

У Ибн Сины

У Ибн Сины
(980–1037)

В 1020 году Ибн Сина (также известный под своим латинизированным именем Авиценна) прочитал Филопона и опубликовал свою собственную теорию движения в «Книге исцеления» . Он согласился с тем, что метатель сообщает снаряду импульс; но в отличие от Филопона, который считал, что это временная добродетель, которая будет уменьшаться даже в вакууме, он рассматривал ее как постоянную, требующую внешних сил, таких как сопротивление воздуха, чтобы рассеять ее.

Питер Оливи, Жан Буридан

В 13 и 14 веках Питер Оливи и Жан Буридан читали и уточняли работы Филопона и, возможно, Ибн Сины. Буридан, который примерно в 1350 году стал ректором Парижского университета, говорил, что импульс пропорционален произведению веса на скорость. Более того, теория Буридана отличалась от теории его предшественника тем, что он не считал импульс саморассеяющимся, утверждая, что тело будет остановлено силами сопротивления воздуха и гравитации, которые могут противодействовать его импульсу.

Количество движения

Рене Декарт

В «Принципах философии» ( Principia Philosophiae ) 1644 года французский философ Рене Декарт определил «количество движения» ( лат . quantitas motus ) как произведение размера и скорости. и утверждал, что общее количество движения во Вселенной сохраняется.

Рене Декарт
(1596–1650)

Если x в два раза больше y и движется вдвое быстрее, то в каждом из них наблюдается одинаковое количество движения.

[Бог] создал материю вместе с ее движением… просто позволяя вещам идти своим чередом, он сохраняет то же количество движения… которое он заложил вначале.

Это не следует воспринимать как утверждение современного закона сохранения импульса , поскольку у Декарта не было понятия массы, отличного от веса и размера. (Понятие массы, в отличие от веса, было введено Ньютоном в 1686 году.) Что еще более важно, он считал, что сохраняется именно скорость, а не скорость. Так, по Декарту, если бы движущийся объект отскакивал от поверхности, изменяя свое направление, но не скорость, то количество его движения не изменилось бы. Галилей в своей книге «Две новые науки» (опубликованной в 1638 году) использовал итальянское слово impeto, чтобы аналогичным образом описать количество движения Декарта.

Кристиан Гюйгенс

Кристиан Гюйгенс
(1629–1695)

В 1600-х годах Христиан Гюйгенс довольно рано пришел к выводу, что законы Декарта об упругом столкновении двух тел неверны, и сформулировал правильные законы. Важным шагом стало признание им галилеевой инвариантности задач. На распространение его взглядов потребовалось много лет. Он лично передал их Уильяму Браункеру и Кристоферу Рену в Лондоне в 1661 году. То, что Спиноза писал Генриху Ольденбургу о них в 1666 году во время Второй англо-голландской войны , было скрыто. Гюйгенс фактически разработал их в рукописи De motu corporum ex percussione в период 1652–1656 годов. Война закончилась в 1667 году, и Гюйгенс объявил свои результаты Королевскому обществу в 1668 году. Он опубликовал их в Journal des sçavans в 1669 году.

Импульс

Джон Уоллис

В 1670 году Джон Уоллис в Mechanica sive De Motu, Tractatus Geometricus , сформулировал закон сохранения количества движения: «начальное состояние тела, либо покоя, либо движения, будет сохраняться» и «Если сила больше, чем сопротивление, результатом будет движение». Уоллис использовал импульс для количества движения, а силу — для силы.

Готфрид Лейбниц

В 1686 году Готфрид Вильгельм Лейбниц в «Рассуждениях о метафизике » привел аргумент против конструкции Декарта о сохранении «количества движения», используя пример отбрасывания блоков разного размера на разные расстояния. Он указывает, что сила сохраняется, но количество движения, рассматриваемое как произведение размера и скорости объекта, не сохраняется.

Исаак Ньютон

Исаак Ньютон
(1642–1727)

В 1687 году Исаак Ньютон в «Philosophiæ Naturalis Principia Mathematica» , как и Уоллис, продемонстрировал аналогичный подбор слов для обозначения математического импульса. Его Определение II определяет quantitas motus , «количество движения», как «возникающее одновременно из скорости и количества материи», что идентифицирует его как импульс. Таким образом, когда в Законе II он говорит о mutatio motus , «изменении движения», пропорциональном приложенной силе, его обычно понимают под импульсом, а не движением.

Джон Дженнингс

В 1721 году Джон Дженнингс опубликовал «Разное» Ньютона , где засвидетельствован импульс в его нынешнем математическом смысле, за пять лет до окончательного издания «Начал математики» . Импульс M или «количество движения» определялся для студентов как «прямоугольник», произведение Q и V , где Q — «количество материала», а V — «скорость». ⁠ s / t ⁠ .

В 1728 году в «Циклопедии» говорится:

Импульс [т. е , импульс или количество движения любого тела — это факт . произведение] его скорости (или пространства, в котором оно движется в данное время, см. Движение ) умножается на его Массу.

См. также

• Угловой момент
• Кристаллический импульс
• Галилейская пушка
• Импульсное уплотнение
• Передача импульса
• колыбель Ньютона
• Пространство положения и импульса

Библиография

• Холлидей, Дэвид; Резник, Роберт (13 августа 2013 г.). Основы физики . Джон Уайли и сыновья. Глава 9. ISBN  978-1-118-23071-8 .
• Дюга, Рене (1988). История механики . Переведено на английский Дж. Р. Мэддоксом (изд. Дувра). Нью-Йорк: Dover Publications. ISBN  978-0-486-65632-8 .
• Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (2005). Лекции Фейнмана по физике, Том 1: В основном механика, излучение и тепло (Окончательное издание). Сан-Франциско: Пирсон Аддисон-Уэсли. ISBN  978-0-8053-9046-9 .
• Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (2006). Лекции Фейнмана по физике (Окончательное издание). Сан-Франциско: Пирсон Аддисон-Уэсли. ISBN  978-0-8053-9047-6 .
• Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (2005). Лекции Фейнмана по физике, Том III: Квантовая механика (Окончательное издание). Нью-Йорк: BasicBooks. ISBN  978-0-8053-9049-0 .
• Гольдштейн, Герберт (1980). Классическая механика (2-е изд.). Ридинг, Массачусетс: Паб Addison-Wesley. компании ISBN  978-0-201-02918-5 .
• Хэнд, Луи Н.; Финч, Джанет Д. Аналитическая механика . Издательство Кембриджского университета. Глава 4.
• Джексон, Джон Дэвид (1975). Классическая электродинамика (2-е изд.). Нью-Йорк: Уайли. ISBN  978-0-471-43132-9 .
• Джаммер, Макс (1999). Концепции силы: исследование основ динамики (изд. Факсима). Минеола, Нью-Йорк: Dover Publications. ISBN  978-0-486-40689-3 .
• Ландау, Л.Д.; Лифшиц, Э.М. (2000). Классическая теория полей . Английское издание, перепечатанное с исправлениями; перевод с русского Мортона Хамермеша (4-е изд.). Оксфорд: Баттерворт Хайнеманн. ISBN  978-0-7506-2768-9 .
• Риндлер, Вольфганг (1986). Основная теория относительности: специальная, общая и космологическая (2-е изд.). Нью-Йорк: Спрингер. ISBN  978-0-387-10090-6 .
• Сервей, Раймонд; Джуэтт, Джон (2003). Физика для ученых и инженеров (6-е изд.). Брукс Коул. ISBN  978-0-534-40842-8 .
• Стенджер, Виктор Дж. (2000). Вневременная реальность: симметрия, простота и множественные вселенные . Книги Прометея. стр. Главу 12 в частности.
• Типлер, Пол (1998). Физика для ученых и инженеров: Vol. 1: Механика, колебания и волны, термодинамика (4-е изд.). У. Х. Фриман. ISBN  978-1-57259-492-0 .
• Триттон, диджей (2006). Физическая гидродинамика (2-е изд.). Оксфорд: Кларендон Пресс. п. 58. ИСБН  978-0-19-854493-7 .

Внешние ссылки

• СМИ, связанные с Momentum, на Викискладе?
• Сохранение импульса – Глава из онлайн-учебника