Гамма-распределение

Гамма

Функция плотности вероятности
Кумулятивная функция распределения
Параметры	к > 0 форма θ > 0 масштаб	форма > 0 β > 0 скорость
Поддерживать	$x\in (0,\infty )$	$x\in (0,\infty )$
PDF	$f(x)={\frac {1}{\Gamma (k)\theta ^{k}}}x^{k-1}e^{-x/\theta }$	$f(x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{\alpha -1}e^{-\beta x}$
CDF	$F(x)={\frac {1}{\Gamma (k)}}\gamma \left(k,{\frac {x}{\theta }}\right)$	$F(x)={\frac {1}{\Gamma (\alpha )}}\gamma (\alpha ,\beta x)$
Иметь в виду	$k\theta$	${\frac {\alpha }{\beta }}$
медиана	Нет простой закрытой формы	Нет простой закрытой формы
Режим	$(k-1)\theta {\text{ for }}k\geq 1$, $0{\text{ for }}k<1$	${\frac {\alpha -1}{\beta }}{\text{ for }}\alpha \geq 1{\text{, }}0{\text{ for }}\alpha <1$
Дисперсия	$k\theta ^{2}$	${\frac {\alpha }{\beta ^{2}}}$
асимметрия	${\frac {2}{\sqrt {k}}}$	${\frac {2}{\sqrt {\alpha }}}$
Избыточный эксцесс	${\frac {6}{k}}$	${\frac {6}{\alpha }}$
Энтропия	${\begin{aligned}k&+\ln \theta +\ln \Gamma (k)\\&+(1-k)\psi (k)\end{aligned}}$	${\begin{aligned}\alpha &-\ln \beta +\ln \Gamma (\alpha )\\&+(1-\alpha )\psi (\alpha )\end{aligned}}$
МГФ	$(1-\theta t)^{-k}{\text{ for }}t<{\frac {1}{\theta }}$	$\left(1-{\frac {t}{\beta }}\right)^{-\alpha }{\text{ for }}t<\beta$
CF	$(1-\theta it)^{-k}$	$\left(1-{\frac {it}{\beta }}\right)^{-\alpha }$
Информация о Фишере	$I(k,\theta )={\begin{pmatrix}\psi ^{(1)}(k)&\theta ^{-1}\\\theta ^{-1}&k\theta ^{-2}\end{pmatrix}}$	$I(\alpha ,\beta )={\begin{pmatrix}\psi ^{(1)}(\alpha )&-\beta ^{-1}\\-\beta ^{-1}&\alpha \beta ^{-2}\end{pmatrix}}$
Метод моментов	$k={\frac {E[X]^{2}}{V[X]}}\quad \quad$ $\theta ={\frac {V[X]}{E[X]}}\quad \quad$	$\alpha ={\frac {E[X]^{2}}{V[X]}}$ $\beta ={\frac {E[X]}{V[X]}}$

В теории вероятностей и статистике гамма -распределение представляет собой универсальное двухпараметрическое семейство непрерывных распределений вероятностей . Экспоненциальное распределение , распределение Эрланга и распределение хи-квадрат являются частными случаями гамма-распределения. Обычно используются две эквивалентные параметризации:

1. С параметром формы k и параметром масштаба θ
2. С параметром формы $\alpha =k$ и обратный масштабный параметр $\beta =1/\theta$ , называемый параметром скорости .

В каждой из этих форм оба параметра являются положительными действительными числами.

Распределение имеет важные приложения в различных областях, включая эконометрику , байесовскую статистику , тестирование жизни. В эконометрике параметризация (k, θ) распространена для моделирования времени ожидания, например времени до смерти, где она часто принимает форму распределения Эрланга для целочисленных значений k. Байесовская статистика предпочитает параметризацию (α, β), используя гамма-распределение в качестве сопряженного априорного значения для нескольких параметров обратного масштаба, что облегчает аналитическую управляемость в вычислениях апостериорного распределения. Плотность вероятности и кумулятивные функции распределения гамма-распределения варьируются в зависимости от выбранной параметризации, что дает представление о поведении гамма-распределенных случайных величин. Гамма-распределение является неотъемлемой частью моделирования ряда явлений благодаря своей гибкой форме, которая может отражать различные статистические распределения, включая экспоненциальное распределение и распределение хи-квадрат при определенных условиях. Его математические свойства, такие как среднее значение, дисперсия, асимметрия и более высокие моменты, предоставляют набор инструментов для статистического анализа и выводов. Практическое применение распределения охватывает несколько дисциплин, что подчеркивает его важность в теоретической и прикладной статистике.

Гамма-распределение — это распределение вероятностей максимальной энтропии (как по отношению к единой базовой мере, так и по отношению к $1/x$ базовая мера) для случайной величины , для которой E [ X ] = kθ = α / β фиксировано и больше нуля, а E [ln X ] = ψ ( k ) + ln θ = ψ ( α ) − ln β X фиксированный ( ψ — дигамма-функция ).

Определения

Параметризация с помощью k и θ , по-видимому, более распространена в эконометрике и других прикладных областях, где гамма-распределение часто используется для моделирования времени ожидания. Например, при тестировании жизни время ожидания до смерти является случайной величиной , которую часто моделируют с помощью гамма-распределения. Увидеть Хогга и Крейга. для явной мотивации.

Параметризация с помощью α и β более распространена в байесовской статистике , где гамма-распределение используется в качестве сопряженного априорного распределения для различных типов параметров обратного масштаба (скорости), таких как λ экспоненциального распределения или распределения Пуассона. – или, если уж на то пошло, β самого гамма-распределения. Тесно связанное обратное гамма-распределение используется в качестве априорного сопряжения для параметров масштаба, таких как дисперсия нормального распределения .

Если k — положительное целое число , то распределение представляет собой распределение Эрланга ; т.е. сумма k независимых экспоненциально распределенных случайных величин , каждая из которых имеет среднее значение θ .

Характеристика с использованием формы α и скорости β

Гамма-распределение можно параметризовать с помощью параметра формы α = k и обратного параметра масштаба β = 1/ θ , называемого параметром скорости . Случайная величина X , которая имеет гамма-распределение с формой α и скоростью β, обозначается

$X\sim \Gamma (\alpha ,\beta )\equiv \operatorname {Gamma} (\alpha ,\beta )$

Соответствующая функция плотности вероятности в параметризации скорости формирования равна

${\begin{aligned}f(x;\alpha ,\beta )&={\frac {x^{\alpha -1}e^{-\beta x}\beta ^{\alpha }}{\Gamma (\alpha )}}\quad {\text{ for }}x>0\quad \alpha ,\beta >0,\\[6pt]\end{aligned}}$

где $\Gamma (\alpha )$ это гамма-функция .Для всех положительных целых чисел $\Gamma (\alpha )=(\alpha -1)!$.

Кумулятивная функция распределения представляет собой регуляризованную гамма-функцию:

$F(x;\alpha ,\beta )=\int _{0}^{x}f(u;\alpha ,\beta )\,du={\frac {\gamma (\alpha ,\beta x)}{\Gamma (\alpha )}},$

где $\gamma (\alpha ,\beta x)$ — нижняя неполная гамма-функция .

Если α — положительное целое число (т. е. распределение является распределением Эрланга ), кумулятивная функция распределения имеет следующее разложение в ряд:

$F(x;\alpha ,\beta )=1-\sum _{i=0}^{\alpha -1}{\frac {(\beta x)^{i}}{i!}}e^{-\beta x}=e^{-\beta x}\sum _{i=\alpha }^{\infty }{\frac {(\beta x)^{i}}{i!}}.$

Примечание о GAMMA.DIST( $x$, альфа , бета ,...) функция в Microsoft Excel: Параметры в Microsoft Excel на самом деле являются параметрами формы и скорости соответственно, т. е. правильной интерпретацией функции Microsoft Excel является ГАММА.РАСП( $x,k,\theta$,...).

Характеристика с использованием формы k и масштаба θ

Случайная величина X , гамма-распределенная с формой k и масштабом θ, обозначается через

$X\sim \Gamma (k,\theta )\equiv \operatorname {Gamma} (k,\theta )$

Иллюстрация гамма-PDF для значений параметров по k и x с θ, установленным на 1, 2, 3, 4, 5 и 6 . Здесь можно увидеть каждый слой θ отдельно [2], а также по k [3] и x . [4] .

Функция плотности вероятности с использованием параметризации масштаба формы равна

$f(x;k,\theta )={\frac {x^{k-1}e^{-x/\theta }}{\theta ^{k}\Gamma (k)}}\quad {\text{ for }}x>0{\text{ and }}k,\theta >0.$

Здесь Γ( k ) — гамма-функция , оцененная при k .

Кумулятивная функция распределения представляет собой регуляризованную гамма-функцию:

$F(x;k,\theta )=\int _{0}^{x}f(u;k,\theta )\,du={\frac {\gamma \left(k,{\frac {x}{\theta }}\right)}{\Gamma (k)}},$

где $\gamma \left(k,{\frac {x}{\theta }}\right)$ — нижняя неполная гамма-функция .

Это также можно выразить следующим образом, если k — положительное целое число (т. е. распределение является распределением Эрланга ):

$F(x;k,\theta )=1-\sum _{i=0}^{k-1}{\frac {1}{i!}}\left({\frac {x}{\theta }}\right)^{i}e^{-x/\theta }=e^{-x/\theta }\sum _{i=k}^{\infty }{\frac {1}{i!}}\left({\frac {x}{\theta }}\right)^{i}.$

Обе параметризации являются общими, поскольку любая из них может быть более удобной в зависимости от ситуации.

Характеристики

Среднее и дисперсия

Среднее значение гамма-распределения определяется как произведение его формы и масштабных параметров:

$\mu =k\theta =\alpha /\beta$

Разница составляет:

$\sigma ^{2}=k\theta ^{2}=\alpha /\beta ^{2}$

Квадратный корень из обратного параметра формы дает коэффициент вариации :

$\sigma /\mu =k^{-0.5}=1/{\sqrt {\alpha }}$

асимметрия

Асимметрия гамма - распределения зависит только от его параметра формы k и равна $2/{\sqrt {k}}.$

Высшие моменты

n -ый необработанный момент определяется выражением:

$\mathrm {E} [X^{n}]=\theta ^{n}{\frac {\Gamma (k+n)}{\Gamma (k)}}=\theta ^{n}\prod _{i=1}^{n}(k+i-1)\;{\text{ for }}n=1,2,\ldots .$

Медианные приближения и границы

Границы и асимптотические приближения медианы гамма-распределения. Область голубого цвета указывает на большой разрыв между опубликованными нижними и верхними границами до 2021 года.

В отличие от моды и среднего значения, формулы которых легко вычисляются на основе параметров, медиана не имеет уравнения в замкнутой форме. Медианой для этого распределения является значение ν такое, что

${\frac {1}{\Gamma (k)\theta ^{k}}}\int _{0}^{\nu }x^{k-1}e^{-x/\theta }dx={\frac {1}{2}}.$

Строгой трактовкой проблемы определения асимптотического разложения и границ медианы гамма-распределения впервые занимались Чен и Рубин, доказавшие, что (при $\theta =1$)

$k-{\frac {1}{3}}<\nu (k)<k,$

где $\mu (k)=k$ это среднее и $\nu (k)$ является медианой ${\text{Gamma}}(k,1)$ распределение. Для других значений параметра масштаба среднее значение масштабируется до $\mu =k\theta$, а медианные границы и аппроксимации будут аналогичным образом масштабироваться по θ .

К. П. Чой нашел первые пять членов в асимптотической аппроксимации медианы рядом Лорана , сравнив медиану с формулой Рамануджана. $\theta$ функция . Берг и Педерсен нашли еще термины:

$\nu (k)=k-{\frac {1}{3}}+{\frac {8}{405k}}+{\frac {184}{25515k^{2}}}+{\frac {2248}{3444525k^{3}}}-{\frac {19006408}{15345358875k^{4}}}-O\left({\frac {1}{k^{5}}}\right)+\cdots$

Две медианные асимптоты гамма-распределения, границы которых были доказаны в 2023 году (верхний сплошной красный и нижний пунктирный красный), из $\nu (k)\approx 2^{-1/k}(A+k)$и интерполяцию между ними, которая дает аппроксимацию (красный пунктир), точную при k = 1 и имеющую максимальную относительную ошибку около 0,6%. Область, заштрихованная голубым цветом, представляет собой оставшийся разрыв между верхней и нижней границами (или предполагаемыми границами), включая эти новые границы и границы на предыдущем рисунке.

Логарифмический график верхней (сплошной) и нижней (пунктирной) границ медианы гамма-распределения и промежутков между ними. Зеленая, желтая и голубая области обозначают разрыв до документа Лиона 2021 года. Зеленый и желтый сокращают этот разрыв с нижними границами, которые доказал Лион. Границы Лиона в 2023 году еще больше сузили желтую зону. В основном внутри желтого цвета в замкнутой форме, интерполированной рациональной функцией, предполагаемые границы наносятся на графики вместе с численно рассчитанным медианным (пунктирным) значением. Существуют более точные интерполированные границы, но они не наносятся на график, поскольку их невозможно разрешить в этом масштабе.

Частичные суммы этих рядов являются хорошими приближениями для достаточно высоких k ; они не показаны на рисунке, который сосредоточен на области low -k , которая менее хорошо аппроксимирована.

Берг и Педерсен также доказали многие свойства медианы, показав, что она является выпуклой функцией от k : и что асимптотическое поведение вблизи $k=0$ является $\nu (k)\approx e^{-\gamma }2^{-1/k}$ (где γ — постоянная Эйлера–Машерони ), и что для всех $k>0$ медиана ограничена $k2^{-1/k}<\nu (k)<ke^{-1/3k}$.

Более близкая линейная верхняя граница для $k\geq 1$ только было предоставлено в 2021 году Гонтом и Меркле, полагаясь на результат Берга и Педерсена, наклон $\nu (k)$ везде меньше 1:

$\nu (k)\leq k-1+\log 2~~$ для $k\geq 1$ (с равенством при $k=1$)

которое можно расширить до границы для всех $k>0$ взяв максимум с хордой, показанной на рисунке, поскольку медиана оказалась выпуклой.

Аппроксимация медианы, асимптотически точная при высоких k и разумная вплоть до $k=0.5$ или немного ниже следует из преобразования Вильсона–Хилферти :

$\nu (k)=k\left(1-{\frac {1}{9k}}\right)^{3}$

что становится отрицательным для $k<1/9$.

В 2021 году Лион предложил несколько аппроксимаций вида $\nu (k)\approx 2^{-1/k}(A+Bk)$. Он выдвинул гипотезу о значениях A и B, для которых это приближение является асимптотически точной верхней или нижней границей для всех $k>0$. В частности, он предложил эти оценки в замкнутой форме, которые доказал в 2023 году:

$\nu _{L\infty }(k)=2^{-1/k}(\log 2-{\frac {1}{3}}+k)\quad$ является нижней границей, асимптотически точной, поскольку $k\to \infty$

$\nu _{U}(k)=2^{-1/k}(e^{-\gamma }+k)\quad$ является верхней границей, асимптотически точной, поскольку $k\to 0$

Лион также показал (неформально в 2021 году, строго в 2023 году) две другие нижние границы, которые не являются выражениями в замкнутой форме , включая эту, включающую гамма-функцию , основанную на решении интегрального выражения, заменяющего 1 вместо $e^{-x}$:

$\nu (k)>\left({\frac {2}{\Gamma (k+1)}}\right)^{-1/k}\quad$ (приближаясь к равенству как $k\to 0$)

и касательная линия в $k=1$ где была найдена производная $\nu ^{\prime }(1)\approx 0.9680448$:

$\nu (k)\geq \nu (1)+(k-1)\nu ^{\prime }(1)\quad$ (с равенством при $k=1$)

$\nu (k)\geq \log 2+(k-1)(\gamma -2\operatorname {Ei} (-\log 2)-\log \log 2)$

где Ei – экспоненциальный интеграл .

Кроме того, он показал, что интерполяция между границами может обеспечить превосходные аппроксимации или более точные границы медианы, включая аппроксимацию с точностью до $k=1$ (где $\nu (1)=\log 2$) и имеет максимальную относительную погрешность менее 0,6%. Интерполированные приближения и границы имеют вид

$\nu (k)\approx {\tilde {g}}(k)\nu _{L\infty }(k)+(1-{\tilde {g}}(k))\nu _{U}(k)$

где ${\tilde {g}}$ — это интерполирующая функция, монотонно работающая от 0 при низком k до 1 при высоком k , аппроксимирующая идеальный или точный интерполятор. $g(k)$:

$g(k)={\frac {\nu _{U}(k)-\nu (k)}{\nu _{U}(k)-\nu _{L\infty }(k)}}$

Для простейшей рассматриваемой интерполяционной функции — рациональная функция первого порядка

${\tilde {g}}_{1}(k)={\frac {k}{b_{0}+k}}$

самая точная нижняя граница имеет

$b_{0}={\frac {{\frac {8}{405}}+e^{-\gamma }\log 2-{\frac {\log ^{2}2}{2}}}{e^{-\gamma }-\log 2+{\frac {1}{3}}}}-\log 2\approx 0.143472$

и самая точная верхняя граница имеет

$b_{0}={\frac {e^{-\gamma }-\log 2+{\frac {1}{3}}}{1-{\frac {e^{-\gamma }\pi ^{2}}{12}}}}\approx 0.374654$

Интерполированные границы нанесены (в основном внутри желтой области) на показанном логарифмическом графике . Еще более точные границы доступны с использованием различных интерполирующих функций, но обычно не с такими параметрами закрытой формы.

Суммирование

Если X _i имеет распределение Gamma( k _i , θ ) для i = 1, 2, ..., N (т. е. все распределения имеют одинаковый масштабный параметр θ ), то

$\sum _{i=1}^{N}X_{i}\sim \mathrm {Gamma} \left(\sum _{i=1}^{N}k_{i},\theta \right)$

все X _i независимы при условии, что .

Для случаев, когда X _i независимы , но имеют разные параметры масштаба, см. Mathai. или Мосхопулос.

Гамма-распределение демонстрирует бесконечную делимость .

Масштабирование

Если

$X\sim \mathrm {Gamma} (k,\theta ),$

тогда для любого c > 0

$cX\sim \mathrm {Gamma} (k,c\,\theta ),$ по моментным производящим функциям,

или эквивалентно, если

$X\sim \mathrm {Gamma} \left(\alpha ,\beta \right)$ (параметризация скорости формы)

$cX\sim \mathrm {Gamma} \left(\alpha ,{\frac {\beta }{c}}\right),$

Действительно, мы знаем, что если X — экспоненциальная с.в. со скоростью λ , то cX — экспоненциальная с.в. со скоростью λ / c ; то же самое справедливо и с переменными Гаммы (и это можно проверить с помощью производящей момент функции , см., например, эти примечания , 10.4-(ii)): умножение на положительную константу c делит скорость (или, что то же самое, умножает масштаб).

Экспоненциальное семейство

Гамма-распределение представляет собой двухпараметрическое экспоненциальное семейство с натуральными параметрами k − 1 и −1/ θ (эквивалентно α − 1 и − β ) и натуральной статистикой X и ln X .

Если параметр формы k остается фиксированным, результирующее однопараметрическое семейство распределений представляет собой естественное экспоненциальное семейство .

Логарифмическое ожидание и дисперсия

Можно показать, что

$\operatorname {E} [\ln X]=\psi (\alpha )-\ln \beta$

или эквивалентно,

$\operatorname {E} [\ln X]=\psi (k)+\ln \theta$

где ψ – дигамма-функция . Так же,

$\operatorname {var} [\ln X]=\psi ^{(1)}(\alpha )=\psi ^{(1)}(k)$

где $\psi ^{(1)}$ это тригамма-функция .

Это можно получить, используя формулу экспоненциального семейства для производящей функции момента достаточной статистики , поскольку одной из достаточных статистик гамма-распределения является ln x .

Информационная энтропия

Информационная энтропия – это

${\begin{aligned}\operatorname {H} (X)&=\operatorname {E} [-\ln p(X)]\\[4pt]&=\operatorname {E} [-\alpha \ln \beta +\ln \Gamma (\alpha )-(\alpha -1)\ln X+\beta X]\\[4pt]&=\alpha -\ln \beta +\ln \Gamma (\alpha )+(1-\alpha )\psi (\alpha ).\end{aligned}}$

В k , θ параметризации информационная энтропия определяется выражением

$\operatorname {H} (X)=k+\ln \theta +\ln \Gamma (k)+(1-k)\psi (k).$

Расхождение Кульбака – Лейблера

Иллюстрация расходимости Кульбака – Лейблера (КЛ) для двух гамма-PDF. Здесь β = β ₀ + 1, которые установлены на 1, 2, 3, 4, 5 и 6 . Отчетливо видна типичная асимметрия КЛ-дивергенции.

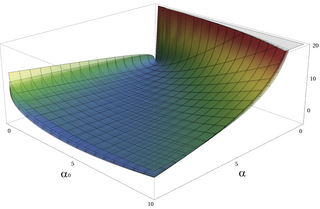
Дивергенция Кульбака-Лейблера (KL-дивергенция) Gamma( α _p , β _p ) («истинное» распределение) от Gamma ( α _q , β _q ) («аппроксимирующее» распределение) определяется выражением

${\begin{aligned}D_{\mathrm {KL} }(\alpha _{p},\beta _{p};\alpha _{q},\beta _{q})={}&(\alpha _{p}-\alpha _{q})\psi (\alpha _{p})-\log \Gamma (\alpha _{p})+\log \Gamma (\alpha _{q})\\&{}+\alpha _{q}(\log \beta _{p}-\log \beta _{q})+\alpha _{p}{\frac {\beta _{q}-\beta _{p}}{\beta _{p}}}.\end{aligned}}$

Записанное с использованием параметризации k , θ , KL-расхождение Gamma( k _p , θ _p ) от Gamma ( k _q , θ _q ) определяется выражением

${\begin{aligned}D_{\mathrm {KL} }(k_{p},\theta _{p};k_{q},\theta _{q})={}&(k_{p}-k_{q})\psi (k_{p})-\log \Gamma (k_{p})+\log \Gamma (k_{q})\\&{}+k_{q}(\log \theta _{q}-\log \theta _{p})+k_{p}{\frac {\theta _{p}-\theta _{q}}{\theta _{q}}}.\end{aligned}}$

Преобразование Лапласа

Преобразование Лапласа гамма-PDF:

$F(s)=(1+\theta s)^{-k}={\frac {\beta ^{\alpha }}{(s+\beta )^{\alpha }}}.$

Связанные дистрибутивы

Общий

• Позволять $X_{1},X_{2},\ldots ,X_{n}$ быть $n$ независимые и одинаково распределенные случайные величины, следующие экспоненциальному распределению с параметром скорости λ, тогда $\sum _{i}X_{i}$ ~ Gamma(n, λ), где n — параметр формы, λ — скорость, и ${\textstyle {\bar {X}}={\frac {1}{n}}\sum _{i}X_{i}\sim \operatorname {Gamma} (n,n*\lambda )}$.
• Если X ~ Gamma(1, λ ) (в параметризации скорости формы), то X имеет экспоненциальное распределение с параметром скорости λ . В параметризации масштаба формы X ~ Gamma(1, λ ) имеет экспоненциальное распределение с параметром скорости 1/ λ .
• Если X ~ Gamma( ν /2, 2) (в формомасштабной параметризации), то X тождественен χ ² ( ν ) , распределение хи-квадрат с ν степенями свободы. Обратно, если Q ~ х ² ( ν ) и c — положительная константа, то cQ ~ Gamma( ν /2, 2 c ) .
• Если θ = 1/ k , получается распределение Шульца-Цимма , которое наиболее часто используется для моделирования длин полимерных цепей.
• Если k целое число , гамма-распределение является распределением Эрланга и представляет собой распределение вероятностей времени ожидания до k -го «прихода» в одномерном пуассоновском процессе с интенсивностью 1/ θ . Если

$X\sim \Gamma (k\in \mathbf {Z} ,\theta ),\qquad Y\sim \operatorname {Pois} \left({\frac {x}{\theta }}\right),$

затем

$P(X>x)=P(Y<k).$

• Если X имеет распределение Максвелла – Больцмана с параметром a , то

$X^{2}\sim \Gamma \left({\frac {3}{2}},2a^{2}\right).$

• Если X ~ Gamma( k , θ ) , то ${\textstyle \log X}$ следует экспоненциальному гамма-распределению (сокращенно экспоненциальное гамма). Его иногда называют логарифмическим гамма-распределением. Формулы для его среднего и дисперсии находятся в разделе #Логарифмическое ожидание и дисперсия .
• Если X ~ Gamma( k , θ ) , то ${\sqrt {X}}$ следует обобщенному гамма-распределению с параметрами p = 2 , d = 2 k и $a={\sqrt {\theta }}$ .
• В более общем смысле, если X ~ Gamma( k , θ ) , то $X^{q}$ для $q>0$ следует обобщенному гамма-распределению с параметрами p = 1/ q , d = k / q и $a=\theta ^{q}$.
• Если X ~ Gamma( k , θ ) с формой k и масштабом θ , то 1/ X ~ Inv-Gamma( k , θ ⁻¹ ) (см. вывод обратного гамма-распределения ).
• Параметризация 1: Если $X_{k}\sim \Gamma (\alpha _{k},\theta _{k})\,$ независимы, то ${\frac {\alpha _{2}\theta _{2}X_{1}}{\alpha _{1}\theta _{1}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})$или, что то же самое, ${\frac {X_{1}}{X_{2}}}\sim \beta '\left(\alpha _{1},\alpha _{2},1,{\frac {\theta _{1}}{\theta _{2}}}\right)$
• Параметризация 2: Если $X_{k}\sim \Gamma (\alpha _{k},\beta _{k})\,$ независимы, то ${\frac {\alpha _{2}\beta _{1}X_{1}}{\alpha _{1}\beta _{2}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})$или, что то же самое, ${\frac {X_{1}}{X_{2}}}\sim \beta '\left(\alpha _{1},\alpha _{2},1,{\frac {\beta _{2}}{\beta _{1}}}\right)$
• Если X ~ Gamma( α , θ ) и Y ~ Gamma( β , θ ) независимо распределены, то X /( X + Y ) имеет бета-распределение с параметрами α и β , а X /( X + Y ) является независимым X + + Y , который является Gamma( α θ β , -распределенным ) .
• Если X _i ~ Gamma( α _i , 1) независимо распределены, то вектор ( X ₁ / S , ..., X _n / S ) , где S = X ₁ + ... + X _n , следует правилу Дирихле. распределение с параметрами α ₁ , ..., α _n .
• При больших k гамма-распределение сходится к нормальному распределению со средним значением µ = kθ и дисперсией σ. ² = к-й ² .
• Гамма-распределение является априорным для точности нормального распределения с известным средним значением .
• Матричное гамма-распределение и распределение Уишарта представляют собой многомерное обобщение гамма-распределения (выборки представляют собой положительно определенные матрицы, а не положительные действительные числа).
• Гамма-распределение является частным случаем обобщенного гамма-распределения , обобщенного целочисленного гамма-распределения и обобщенного обратного распределения Гаусса .
• Среди дискретных распределений отрицательное биномиальное распределение иногда считают дискретным аналогом гамма-распределения.
• Распределения Твиди – гамма-распределение является членом семейства моделей экспоненциальной дисперсии Твиди .
• Модифицированное полунормальное распределение . Гамма-распределение является членом семейства модифицированного полунормального распределения . Соответствующая плотность равна $f(x\mid \alpha ,\beta ,\gamma )={\frac {2\beta ^{\frac {\alpha }{2}}x^{\alpha -1}\exp(-\beta x^{2}+\gamma x)}{\Psi {\left({\frac {\alpha }{2}},{\frac {\gamma }{\sqrt {\beta }}}\right)}}}$, где $\Psi (\alpha ,z)={}_{1}\Psi _{1}\left({\begin{matrix}\left(\alpha ,{\frac {1}{2}}\right)\\(1,0)\end{matrix}};z\right)$ обозначает Пси-функцию Фокса–Райта .
• Для параметризации масштаба формы $x|\theta \sim \Gamma (k,\theta )$, если параметр масштаба $\theta \sim IG(b,1)$ где $IG$ обозначает обратное гамма-распределение , затем предельное распределение $x\sim \beta '(k,b)$ где $\beta '$ обозначает бета-распределение простых чисел .

Сложная гамма

Если параметр формы гамма-распределения известен, но параметр обратного масштаба неизвестен, то гамма-распределение для обратного масштаба образует сопряженное априорное значение. Составное распределение , полученное в результате интегрирования обратной шкалы, имеет решение в замкнутой форме, известное как составное гамма-распределение .

Если вместо этого параметр формы известен, но среднее значение неизвестно, а априорное значение среднего значения задается другим гамма-распределением, то это приводит к K-распределению .

Вейбулл и стабильный счет

Гамма-распределение $f(x;k)\,(k>1)$ может быть выражено как распределение продуктов распределения Вейбулла и вариантная форма распределения стабильного количества .Его параметр формы $k$ можно рассматривать как обратную величину параметра устойчивости Леви в стабильном распределении количества: $$f(x;k)=\displaystyle \int _{0}^{\infty }{\frac {1}{u}}\,W_{k}\left({\frac {x}{u}}\right)\left[ku^{k-1}\,{\mathfrak {N}}_{\frac {1}{k}}\left(u^{k}\right)\right]\,du,$$где ${\mathfrak {N}}_{\alpha }(\nu )$ представляет собой стандартное стабильное распределение чисел формы $\alpha =1/k$, и $W_{k}(x)$ представляет собой стандартное распределение Вейбулла формы $k$.

Статистический вывод

Оценка параметров

Оценка максимального правдоподобия

Функция правдоподобия для N iid наблюдений ( x ₁ , ..., x _N ) равна

$L(k,\theta )=\prod _{i=1}^{N}f(x_{i};k,\theta )$

из которого мы вычисляем функцию логарифмического правдоподобия

$\ell (k,\theta )=(k-1)\sum _{i=1}^{N}\ln x_{i}-\sum _{i=1}^{N}{\frac {x_{i}}{\theta }}-Nk\ln \theta -N\ln \Gamma (k)$

Нахождение максимума по θ путем взятия производной и установки ее равной нулю дает максимального правдоподобия оценку параметра θ , которая равна выборочному среднему значению. ${\bar {x}}$ разделенное на параметр формы k :

${\hat {\theta }}={\frac {1}{kN}}\sum _{i=1}^{N}x_{i}={\frac {\bar {x}}{k}}$

Подстановка этого в функцию логарифмического правдоподобия дает

$\ell (k)=(k-1)\sum _{i=1}^{N}\ln x_{i}-Nk-Nk\ln \left({\frac {\sum x_{i}}{kN}}\right)-N\ln \Gamma (k)$

Нам нужно как минимум два образца: $N\geq 2$, потому что для $N=1$, функция $\ell (k)$ неограниченно возрастает, так как $k\to \infty$. Для $k>0$, можно убедиться, что $\ell (k)$ является строго вогнутой , используя свойства неравенства полигамма-функции . Нахождение максимума по k, взяв производную и приравняв ее нулю, дает

$\ln k-\psi (k)=\ln \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)-{\frac {1}{N}}\sum _{i=1}^{N}\ln x_{i}=\ln {\bar {x}}-{\overline {\ln x}}$

где ψ — дигамма-функция и ${\overline {\ln x}}$ — выборочное среднее ln x . не существует решения в замкнутой форме Для k . В численном отношении функция очень хорошо себя ведет, поэтому, если требуется численное решение, его можно найти, например, с помощью метода Ньютона . Начальное значение k можно найти либо методом моментов , либо с помощью приближения

$\ln k-\psi (k)\approx {\frac {1}{2k}}\left(1+{\frac {1}{6k+1}}\right)$

Если мы позволим

$s=\ln \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)-{\frac {1}{N}}\sum _{i=1}^{N}\ln x_{i}=\ln {\bar {x}}-{\overline {\ln x}}$

тогда k примерно

$k\approx {\frac {3-s+{\sqrt {(s-3)^{2}+24s}}}{12s}}$

что находится в пределах 1,5% от правильного значения. Явная форма обновления Ньютона-Рафсона этого первоначального предположения такова:

$k\leftarrow k-{\frac {\ln k-\psi (k)-s}{{\frac {1}{k}}-\psi ^{\prime }(k)}}.$

По оценке максимального правдоподобия $({\hat {k}},{\hat {\theta }})$, ожидаемые значения x и $\ln x$ согласен с эмпирическими средними значениями:

${\begin{aligned}{\hat {k}}{\hat {\theta }}&={\bar {x}}&&{\text{and}}&\psi ({\hat {k}})+\ln {\hat {\theta }}&={\overline {\ln x}}.\end{aligned}}$

Предостережение относительно небольшого параметра формы

Для данных, $(x_{1},\ldots ,x_{N})$, представленный в формате с плавающей запятой , который принимает значение 0 для значений, меньших, чем $\varepsilon$, логарифмы, необходимые для оценки максимального правдоподобия, приведут к сбою, если возникнут какие-либо потери. Если предположить, что данные были сгенерированы гамма-распределением с помощью cdf $F(x;k,\theta )$, то вероятность того, что произойдет хотя бы одно опустошение, равна:

$P({\text{underflow}})=1-(1-F(\varepsilon ;k,\theta ))^{N}$

Эта вероятность будет приближаться к 1 для малых и больших N. k Например, в $k=10^{-2}$, $N=10^{4}$ и $\varepsilon =2.25\times 10^{-308}$, $P({\text{underflow}})\approx 0.9998$. Обходной путь — вместо этого иметь данные в логарифмическом формате.

Чтобы протестировать реализацию средства оценки максимального правдоподобия, которое принимает логарифмические данные в качестве входных данных, полезно иметь возможность генерировать не выпадающие логарифмы случайных гамма-переменных, когда $k<1$. После внедрения в scipy.stats.loggamma, это можно сделать следующим образом: образец $Y\sim {\text{Gamma}}(k+1,\theta )$ и $U\sim {\text{Uniform}}$ независимо. Тогда требуемая логарифмическая выборка равна $Z=\ln(Y)+\ln(U)/k$, так что $\exp(Z)\sim {\text{Gamma}}(k,\theta )$.

Оценщики закрытой формы

Существуют непротиворечивые оценки k и θ в замкнутой форме , которые получены на основе вероятности обобщенного гамма-распределения .

Оценка формы k равна

${\hat {k}}={\frac {N\sum _{i=1}^{N}x_{i}}{N\sum _{i=1}^{N}x_{i}\ln x_{i}-\sum _{i=1}^{N}x_{i}\sum _{i=1}^{N}\ln x_{i}}}$

а оценка масштаба θ равна

${\hat {\theta }}={\frac {1}{N^{2}}}\left(N\sum _{i=1}^{N}x_{i}\ln x_{i}-\sum _{i=1}^{N}x_{i}\sum _{i=1}^{N}\ln x_{i}\right)$

Использование выборочного среднего значения x , выборочного среднего ln x и выборочного среднего произведения x ·ln x упрощает выражения до:

${\hat {k}}={\bar {x}}/{\hat {\theta }}$

${\hat {\theta }}={\overline {x\ln {x}}}-{\bar {x}}{\overline {\ln {x}}}.$

Если используется параметризация скорости, оценка ${\hat {\beta }}=1/{\hat {\theta }}$.

Эти оценки не являются строго оценками максимального правдоподобия, а вместо этого называются оценками логарифмического момента смешанного типа. Однако они имеют такую ​​же эффективность, как и оценки максимального правдоподобия.

Хотя эти оценки последовательны, они имеют небольшую погрешность. Вариант оценки шкалы θ с коррекцией смещения :

${\tilde {\theta }}={\frac {N}{N-1}}{\hat {\theta }}$

Поправка смещения для параметра формы k определяется как

${\tilde {k}}={\hat {k}}-{\frac {1}{N}}\left(3{\hat {k}}-{\frac {2}{3}}\left({\frac {\hat {k}}{1+{\hat {k}}}}\right)-{\frac {4}{5}}{\frac {\hat {k}}{(1+{\hat {k}})^{2}}}\right)$

Байесовская минимальная среднеквадратическая ошибка

При известном k и неизвестном θ апостериорная функция плотности для теты (с использованием стандартного масштабно-инвариантного априора для θ ) равна

$P(\theta \mid k,x_{1},\dots ,x_{N})\propto {\frac {1}{\theta }}\prod _{i=1}^{N}f(x_{i};k,\theta )$

Обозначая

$y\equiv \sum _{i=1}^{N}x_{i},\qquad P(\theta \mid k,x_{1},\dots ,x_{N})=C(x_{i})\theta ^{-Nk-1}e^{-y/\theta }$

Интегрирование по θ можно выполнить с помощью замены переменных, обнаруживая, что 1/ θ имеет гамма-распределение с параметрами α = Nk , β = y .

$\int _{0}^{\infty }\theta ^{-Nk-1+m}e^{-y/\theta }\,d\theta =\int _{0}^{\infty }x^{Nk-1-m}e^{-xy}\,dx=y^{-(Nk-m)}\Gamma (Nk-m)\!$

Моменты можно вычислить, взяв соотношение ( m на m = 0 )

$\operatorname {E} [x^{m}]={\frac {\Gamma (Nk-m)}{\Gamma (Nk)}}y^{m}$

который показывает, что оценка среднего ± стандартного отклонения апостериорного распределения для θ равна

${\frac {y}{Nk-1}}\pm {\sqrt {\frac {y^{2}}{(Nk-1)^{2}(Nk-2)}}}.$

Байесовский вывод

Сопряжение до

В байесовском выводе является гамма-распределение сопряженным перед многими распределениями правдоподобия: Пуассона , экспоненциальное , нормальное (с известным средним), Парето , гамма с известной формой σ , обратная гамма с известным параметром формы и Гомпертца с известным параметром масштаба.

гамма-распределения Сопряженный априор :

$p(k,\theta \mid p,q,r,s)={\frac {1}{Z}}{\frac {p^{k-1}e^{-\theta ^{-1}q}}{\Gamma (k)^{r}\theta ^{ks}}},$

где Z — нормировочная константа, не имеющая решения в замкнутой форме.Апостериорное распределение можно найти, обновив параметры следующим образом:

${\begin{aligned}p'&=p\prod \nolimits _{i}x_{i},\\q'&=q+\sum \nolimits _{i}x_{i},\\r'&=r+n,\\s'&=s+n,\end{aligned}}$

где n — количество наблюдений, а x _i — i -е наблюдение.

Возникновение и применение

Рассмотрим последовательность событий, где время ожидания каждого события представляет собой экспоненциальное распределение со скоростью β . Тогда время ожидания возникновения n -го события представляет собой гамма-распределение целочисленной формы. $\alpha =n$. Такая конструкция гамма-распределения позволяет моделировать широкий спектр явлений, при которых несколько дополнительных событий, каждое из которых занимает время с экспоненциальным распределением, должны произойти последовательно, чтобы произошло главное событие. Примеры включают время ожидания событий деления клеток , количество компенсаторных мутаций для данной мутации, время ожидания ремонта гидросистемы, и так далее.

В биофизике время пребывания между этапами молекулярного мотора, такого как АТФ-синтаза , почти экспоненциально при постоянной концентрации АТФ, показывая, что каждый этап мотора требует одного гидролиза АТФ. Если бы было n событий гидролиза АТФ, то это было бы гамма-распределение со степенью n.

Гамма-распределение использовалось для моделирования размера страховых выплат. и дожди. Это означает, что совокупные страховые выплаты и количество осадков, накопленных в водохранилище, моделируются гамма-процессом – так же, как экспоненциальное распределение генерирует процесс Пуассона .

Гамма-распределение также используется для моделирования ошибок в многоуровневых регрессии Пуассона, моделях поскольку смесь распределений Пуассона с коэффициентами, распределенными по гамма-распределению, имеет известное распределение закрытой формы, называемое отрицательным биномиальным .

В беспроводной связи гамма-распределение используется для моделирования многолучевого замирания мощности сигнала; см. также распределение Рэлея и распределение Райса .

В онкологии возрастное распределение раком заболеваемости часто повторяет гамма-распределение, при этом параметры формы и масштаба предсказывают соответственно количество драйверных событий и временной интервал между ними.

В нейробиологии гамма-распределение часто используется для описания распределения интервалов между спайками .

При экспрессии бактериальных генов число копий конститутивно экспрессируемого белка часто соответствует гамма-распределению, где параметр масштаба и формы представляют собой соответственно среднее количество всплесков за клеточный цикл и среднее количество молекул белка, продуцируемых одной мРНК в течение срок его службы.

В геномике гамма-распределение применялось на этапе вызова пика (т. е. при распознавании сигнала) в ChIP-чипе. и ЧИП-сек. анализ данных.

В байесовской статистике гамма-распределение широко используется как сопряженное априорное значение . Это априорное значение точности ( т.е. обратной дисперсии) нормального распределения . Это также сопряженное априорное значение для экспоненциального распределения .

В филогенетике гамма-распределение является наиболее часто используемым подходом для моделирования вариаций скорости между участками. когда методы максимального правдоподобия , байесовского метода или матрицы расстояний для оценки филогенетических деревьев используются . Филогенетический анализ, который использует гамма-распределение для моделирования изменения скорости, оценивает один параметр на основе данных, поскольку ограничивает рассмотрение распределениями, где α = β . Эта параметризация означает, что среднее значение этого распределения равно 1, а дисперсия равна 1/ α . Методы максимального правдоподобия и байесовские методы обычно используют дискретную аппроксимацию непрерывного гамма-распределения.

Генерация случайной переменной

Учитывая указанное выше свойство масштабирования, достаточно сгенерировать гамма-переменные с θ = 1 , поскольку позже мы сможем преобразовать их в любое значение β с помощью простого деления.

Предположим, мы хотим сгенерировать случайные величины из Gamma( n + δ , 1) , где n — неотрицательное целое число и 0 < δ < 1 . Используя тот факт, что распределение Gamma(1, 1) совпадает с распределением Exp(1) , и учитывая метод генерации экспоненциальных переменных , мы заключаем, что если U на равномерно распределено (0, 1], то −ln U — это распределенная гамма(1, 1) (т.е. выборка с обратным преобразованием ). Теперь, используя свойство « α -сложения» гамма-распределения, мы расширяем этот результат:

$-\sum _{k=1}^{n}\ln U_{k}\sim \Gamma (n,1)$

где все U _k равномерно распределены на (0, 1] и независимы . Все, что теперь осталось, — это сгенерировать переменную, распределенную как Gamma( δ , 1) для 0 < δ < 1 , и один раз применить свойство « α -сложения» больше. Это самая сложная часть.

Случайная генерация гамма-вариантов подробно обсуждается Деврой. отметив, что ни один из них не является одинаково быстрым для всех параметров формы. Для малых значений параметра формы алгоритмы часто не работают. Для произвольных значений параметра формы можно применить формулы Аренса и Дитера. модифицированный метод принятия-брака Алгоритм GD (форма k ≥ 1 ), или метод преобразования когда 0 < к <1 . См. также Алгоритм Ченга и Пира GKM 3. или метод сжатия Марсальи.

Ниже приводится версия метода принятия-отвержения Аренса-Дитера :

1. Сгенерируйте U , V и W как iid (0, 1). переменные
2. Если $U\leq {\frac {e}{e+\delta }}$ затем $\xi =V^{1/\delta }$ и $\eta =W\xi ^{\delta -1}$. В противном случае, $\xi =1-\ln V$ и $\eta =We^{-\xi }$.
3. Если $\eta >\xi ^{\delta -1}e^{-\xi }$ затем перейдите к шагу 1.
4. ξ распределяется как Γ( δ , 1) .

Краткое изложение этого

$\theta \left(\xi -\sum _{i=1}^{\lfloor k\rfloor }\ln U_{i}\right)\sim \Gamma (k,\theta )$

где $\scriptstyle \lfloor k\rfloor$ — целая часть k , ξ генерируется с помощью описанного выше алгоритма с δ = { k } (дробная часть k ), и все U _k независимы.

Хотя описанный выше подход технически верен, Деврой отмечает, что он линеен по значению k и в целом не является хорошим выбором. Вместо этого он рекомендует использовать либо методы, основанные на отклонении, либо табличные методы, в зависимости от контекста.

Например, простой метод преобразования-отклонения Марсальи, основанный на одной нормальной переменной X и одной однородной переменной U :

1. Набор $d=a-{\frac {1}{3}}$ и $c={\frac {1}{\sqrt {9d}}}$.
2. Набор $v=(1+cX)^{3}$.
3. Если $v>0$ и $\ln U<{\frac {X^{2}}{2}}+d-dv+d\ln v$ возвращаться $dv$, иначе вернитесь к шагу 2.

С $1\leq a=\alpha =k$ генерирует гамма-распределенное случайное число во времени, которое приблизительно постоянно с k . Скорость принятия зависит от k : скорость принятия составляет 0,95, 0,98 и 0,99 для k=1, 2 и 4. Для k < 1 можно использовать $\gamma _{\alpha }=\gamma _{1+\alpha }U^{1/\alpha }$ чтобы повысить k , чтобы его можно было использовать с этим методом.

Внешние ссылки

• «Гамма-распределение» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Гамма-распределение» . Математический мир .
• ModelAssist (2017). Использование гамма-распределения в моделировании рисков, включая прикладные примеры в Excel. Архивировано 9 мая 2017 г. на Wayback Machine .
• Справочник по инженерной статистике