Вот номер

Иллюстрация беззнаковых чисел Лаха для n и k от 1 до 4.

В математике числа Лаха (знаковые и беззнаковые) представляют собой коэффициенты, выражающие возрастающие факториалы через падающие факториалы и наоборот. Их обнаружил Иво Ла в 1954 году. Явно, беззнаковые числа Лаха $L(n,k)$ задаются формулой с биномиальным коэффициентом

$$L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$$

для $n\geq k\geq 1$.

Беззнаковые числа Лаха имеют интересное значение в комбинаторике : они подсчитывают количество способов, можно которыми ${\textstyle n}$ элементы можно разделить на ${\textstyle k}$ непустые линейно упорядоченные подмножества . Числа Лаха связаны с числами Стирлинга .

Для ${\textstyle n\geq 1}$, число Лаха ${\textstyle L(n,1)}$ равен факториалу ${\textstyle n!}$ в приведенной выше интерпретации единственный раздел ${\textstyle \{1,2,3\}}$ в 1 набор можно упорядочить свой набор 6 способами: $$\{(1,2,3)\},\{(1,3,2)\},\{(2,1,3)\},\{(2,3,1)\},\{(3,1,2)\},\{(3,2,1)\}$$${\textstyle L(3,2)}$ равно 6, поскольку имеется шесть разделов ${\textstyle \{1,2,3\}}$ на две упорядоченные части: $$\{1,(2,3)\},\{1,(3,2)\},\{2,(1,3)\},\{2,(3,1)\},\{3,(1,2)\},\{3,(2,1)\}$$${\textstyle L(n,n)}$ всегда равно 1, потому что единственный способ разделить ${\textstyle \{1,2,\ldots ,n\}}$ в $n$ непустые подмножества приводят к образованию подмножеств размера 1, которые можно переставлять только одним способом.В более поздней литературе Карамата – Кнута появились обозначения в стиле . Числа Ла теперь часто записываются как $$L(n,k)=\left\lfloor {n \atop k}\right\rfloor$$

Таблица значений

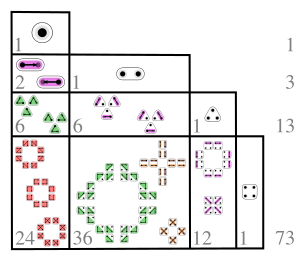
Ниже приведена таблица значений чисел Лаха:

к н	0	1	2	3	4	5	6	7	8	9	10
0	1
1	0	1
2	0	2	1
3	0	6	6	1
4	0	24	36	12	1
5	0	120	240	120	20	1
6	0	720	1800	1200	300	30	1
7	0	5040	15120	12600	4200	630	42	1
8	0	40320	141120	141120	58800	11760	1176	56	1
9	0	362880	1451520	1693440	846720	211680	28224	2016	72	1
10	0	3628800	16329600	21772800	12700800	3810240	635040	60480	3240	90	1

Суммы строк равны ${\textstyle 1,1,3,13,73,501,4051,37633,\dots }$ (последовательность A000262 в OEIS ).

Рост и падение факториалов

Позволять ${\textstyle x^{(n)}}$ представляют собой растущий факториал ${\textstyle x(x+1)(x+2)\cdots (x+n-1)}$ и пусть ${\textstyle (x)_{n}}$ представляют собой падающий факториал ${\textstyle x(x-1)(x-2)\cdots (x-n+1)}$. Числа Лаха — это коэффициенты, которые выражают каждое из этих семейств полиномов через другое. Явно, $$x^{(n)}=\sum _{k=0}^{n}L(n,k)(x)_{k}$$и $$(x)_{n}=\sum _{k=0}^{n}(-1)^{n-k}L(n,k)x^{(k)}.$$Например, $$x(x+1)(x+2)={\color {red}6}x+{\color {red}6}x(x-1)+{\color {red}1}x(x-1)(x-2)$$и $$x(x-1)(x-2)={\color {red}6}x-{\color {red}6}x(x+1)+{\color {red}1}x(x+1)(x+2),$$

где коэффициенты 6, 6 и 1 — это в точности числа Лаха. $L(3,1)$, $L(3,2)$, и $L(3,3)$.

Личности и отношения

Числа Лаха удовлетворяют множеству тождеств и отношений.

В Карамате – обозначение Кнута для чисел Стирлинга. $$L(n,k)=\sum _{j=k}^{n}\left[{n \atop j}\right]\left\{{j \atop k}\right\}$$где ${\textstyle \left[{n \atop j}\right]}$ – числа Стирлинга первого рода и ${\textstyle \left\{{j \atop k}\right\}}$ — числа Стирлинга второго рода .

$L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}={n \choose k}{\frac {(n-1)!}{(k-1)!}}={n \choose k}{n-1 \choose k-1}(n-k)!$

$L(n,k)={\frac {n!(n-1)!}{k!(k-1)!}}\cdot {\frac {1}{(n-k)!}}=\left({\frac {n!}{k!}}\right)^{2}{\frac {k}{n(n-k)!}}$

$k(k+1)L(n,k+1)=(n-k)L(n,k)$, для $k>0$.

Рекуррентные отношения

Числа Лаха удовлетворяют рекуррентным соотношениям $${\begin{aligned}L(n+1,k)&=(n+k)L(n,k)+L(n,k-1)\\&=k(k+1)L(n,k+1)+2kL(n,k)+L(n,k-1)\end{aligned}}$$где $L(n,0)=\delta _{n}$, дельта Кронекера и $L(n,k)=0$ для всех $k>n$.

Экспоненциальная производящая функция

$\sum _{n\geq k}L(n,k){\frac {x^{n}}{n!}}={\frac {1}{k!}}\left({\frac {x}{1-x}}\right)^{k}$

Производная exp(1/ x )

n -я ​ производная функции $e^{\frac {1}{x}}$ может быть выражено с помощью чисел Лаха следующим образом $${\frac {{\textrm {d}}^{n}}{{\textrm {d}}x^{n}}}e^{\frac {1}{x}}=(-1)^{n}\sum _{k=1}^{n}{\frac {L(n,k)}{x^{n+k}}}\cdot e^{\frac {1}{x}}.$$Например,

${\frac {\textrm {d}}{{\textrm {d}}x}}e^{\frac {1}{x}}=-{\frac {1}{x^{2}}}\cdot e^{\frac {1}{x}}$

${\frac {{\textrm {d}}^{2}}{{\textrm {d}}x^{2}}}e^{\frac {1}{x}}={\frac {\textrm {d}}{{\textrm {d}}x}}\left(-{\frac {1}{x^{2}}}e^{\frac {1}{x}}\right)=-{\frac {-2}{x^{3}}}\cdot e^{\frac {1}{x}}-{\frac {1}{x^{2}}}\cdot {\frac {-1}{x^{2}}}\cdot e^{\frac {1}{x}}=\left({\frac {2}{x^{3}}}+{\frac {1}{x^{4}}}\right)\cdot e^{\frac {1}{x}}$

${\frac {{\textrm {d}}^{3}}{{\textrm {d}}x^{3}}}e^{\frac {1}{x}}={\frac {\textrm {d}}{{\textrm {d}}x}}\left(\left({\frac {2}{x^{3}}}+{\frac {1}{x^{4}}}\right)\cdot e^{\frac {1}{x}}\right)=\left({\frac {-6}{x^{4}}}+{\frac {-4}{x^{5}}}\right)\cdot e^{\frac {1}{x}}+\left({\frac {2}{x^{3}}}+{\frac {1}{x^{4}}}\right)\cdot {\frac {-1}{x^{2}}}\cdot e^{\frac {1}{x}}=-\left({\frac {6}{x^{4}}}+{\frac {6}{x^{5}}}+{\frac {1}{x^{6}}}\right)\cdot e^{\frac {1}{x}}$

Ссылка на полиномы Лагерра

Обобщенные полиномы Лагерра $L_{n}^{(\alpha )}(x)$ привязаны к числам Ла при установке $\alpha =-1$$$n!L_{n}^{(-1)}(x)=\sum _{k=0}^{n}L(n,k)(-x)^{k}$$Эта формула является полиномом Лагерра по умолчанию в соглашении об исчислении Умбрала .

Практическое применение

В последние годы числа Лаха используются в стеганографии для сокрытия данных на изображениях. По сравнению с такими альтернативами, как DCT , DFT и DWT , он имеет меньшую сложность расчета. $O(n\log n)$— их целых коэффициентов. Преобразования Лаха и Лагерра естественным образом возникают при пертурбативном описании хроматической дисперсии . В оптике Ла-Лагера такой подход чрезвычайно ускоряет задачи оптимизации.

См. также

• Числа Стирлинга
• Матрица Паскаля

Внешние ссылки

• Числа Лаха со знаком и без знака соответственно (последовательность A008297 в OEIS ) и (последовательность A105278 в OEIS )