Число Стирлинга

В математике . числа Стирлинга возникают в различных аналитических и комбинаторных задачах Они названы в честь Джеймса Стирлинга , который представил их в чисто алгебраической форме в своей книге «Methodus Differentialis» (1730). Они были заново открыты и им придан комбинаторный смысл Масанобу Сака в 1782 году.

Это название носят два разных набора чисел: числа Стирлинга первого рода и числа Стирлинга второго рода . Кроме того, числа Лаха иногда называют числами Стирлинга третьего рода. Каждый вид подробно описан в соответствующей статье, которая служит описанием отношений между ними.

Общим свойством всех трех видов является то, что они описывают коэффициенты, относящиеся к трем различным последовательностям многочленов, которые часто возникают в комбинаторике. Более того, все три можно определить как количество разбиений n элементов на k непустые подмножества, где каждое подмножество наделено определенным порядком (без порядка, циклическим или линейным).

Обозначения

Основные статьи: числа Стирлинга первого рода и числа Стирлинга второго рода.

Используются несколько различных обозначений чисел Стирлинга. Обыкновенные (знаковые) числа Стирлинга первого рода принято обозначать:

$s(n,k)\,.$

Беззнаковые числа Стирлинга первого рода , подсчитывающие количество перестановок элементов n с k непересекающимися циклами , обозначаются:

${\biggl [}{n \atop k}{\biggr ]}=c(n,k)=|s(n,k)|=(-1)^{n-k}s(n,k)\,$

Числа Стирлинга второго рода , подсчитывающие количество способов разбить набор из n элементов на k непустые подмножества:

${\biggl \{}{\!n\! \atop \!k\!}{\biggr \}}=S(n,k)=S_{n}^{(k)}\,$

Абрамовиц и Стегун используют заглавные буквы $S$ и черное письмо ${\mathfrak {S}}$соответствен- но для первого и второго рода чисел Стирлинга. Обозначение скобок и фигурных скобок, по аналогии с биномиальными коэффициентами , было введено в 1935 году Йованом Караматой и развито позже Дональдом Кнутом . (Обозначение скобок противоречит общепринятому обозначению гауссовских коэффициентов . ) Математическое обоснование этого типа обозначений, а также дополнительные формулы чисел Стирлинга можно найти на странице Числа Стирлинга и экспоненциальные производящие функции .

Еще одно нечастое обозначение: $s_{1}(n,k)$ и $s_{2}(n,k)$.

Разложения падающих и возрастающих факториалов

Числа Стирлинга выражают коэффициенты в разложениях падающих и возрастающих факториалов (также известных как символ Поххаммера) в виде многочленов.

То есть падающий факториал , определяемый как $\ (x)_{n}=x(x-1)\ \cdots (x-n+1)\ ,$ — многочлен от x степени n, разложение которого есть

$(x)_{n}\ =\ \sum _{k=0}^{n}\ s(n,k)\ x^{k}\$

с (со знаком) числами Стирлинга первого рода в качестве коэффициентов.

Обратите внимание, что $\ (x)_{0}\equiv 1\ ,$ по соглашению, потому что это пустой продукт . Обозначения $\ x^{\underline {n}}\$ для падающего факториала и $\ x^{\overline {n}}\$ для восходящего факториала также часто используются. (Как ни странно, символ Поххаммера, который многие используют для обозначения падающих факториалов, используется в специальных функциях для возрастающих факториалов.)

Аналогично, восходящий факториал , определяемый как $\ x^{(n)}\ =\ x(x+1)\ \cdots (x+n-1)\ ,$ — многочлен от x степени n, разложение которого есть

$x^{(n)}\ =\ \sum _{k=0}^{n}\ {\biggl [}{n \atop k}{\biggr ]}\ x^{k}\ =\ \sum _{k=0}^{n}\ (-1)^{n-k}\ s(n,k)\ x^{k}\ ,$

с беззнаковыми числами Стирлинга первого рода в качестве коэффициентов.Одно из этих разложений можно вывести из другого, заметив, что $\ x^{(n)}=(-1)^{n}(-x)_{n}~.$

Числа Стирлинга второго рода выражают обратные соотношения:

$\ x^{n}\ =\ \sum _{k=0}^{n}\ S(n,k)\ (x)_{k}\$

и

$\ x^{n}\ =\ \sum _{k=0}^{n}\ (-1)^{n-k}\ S(n,k)\ x^{(k)}~.$

По мере изменения базисных коэффициентов

Рассматривая набор полиномов от (неопределённой) переменной x как векторное пространство,каждая из трех последовательностей

$x^{0},x^{1},x^{2},x^{3},\dots \quad (x)_{0},(x)_{1},(x)_{2},\dots \quad x^{(0)},x^{(1)},x^{(2)},\dots$

является основой .То есть каждый многочлен от x можно записать в виде суммы $a_{0}x^{(0)}+a_{1}x^{(1)}+\dots +a_{n}x^{(n)}$ для некоторых уникальных коэффициентов $a_{i}$ (аналогично для двух других баз).Вышеупомянутые отношения затем выражают изменение базиса между ними, что суммировано в следующей коммутативной диаграмме :

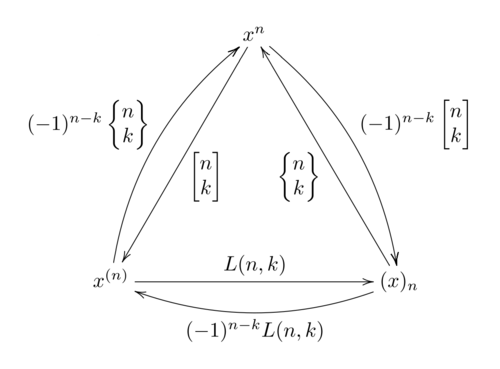
A diagram of how different Stirling numbers give coefficients for changing one basis of polynomials to another

Коэффициенты для двух нижних изменений описываются числами Лаха ниже.Поскольку коэффициенты в любом базисе уникальны, таким образом можно определить числа Стирлинга как коэффициенты, выражающие многочлены одного базиса через другой, то есть уникальные числа, связывающие $x^{n}$ с падающими и возрастающими факториалами, как указано выше.

Падающие факториалы определяют с точностью до масштабирования те же полиномы, что и биномиальные коэффициенты : ${\textstyle {\binom {x}{k}}=(x)_{k}/k!}$. Изменения между стандартной базой $\textstyle x^{0},x^{1},x^{2},\dots$ и основа ${\textstyle {\binom {x}{0}},{\binom {x}{1}},{\binom {x}{2}},\dots }$ описываются аналогичными формулами:

$x^{n}=\sum _{k=0}^{n}{\biggl \{}{\!n\! \atop \!k\!}{\biggr \}}k!{\binom {x}{k}}\quad {\text{and}}\quad {\binom {x}{n}}=\sum _{k=0}^{n}{\frac {s(n,k)}{n!}}x^{k}$.

Пример

Выражение многочлена на основе падающих факториалов полезно для вычисления сумм многочлена, вычисляемого по последовательным целым числам.Действительно, сумма падающих факториалов при фиксированном k может быть выражена как еще один падающий факториал (для $k\neq -1$)

$\sum _{0\leq i<n}(i)_{k}={\frac {(n)_{k+1}}{k+1}}$

Это можно доказать по индукции .

Например, сумма четвертых степеней целых чисел до n (на этот раз с включением n ):

${\begin{aligned}\sum _{i=0}^{n}i^{4}&=\sum _{i=0}^{n}\sum _{k=0}^{4}{\biggl \{}{\!4\! \atop \!k\!}{\biggr \}}(i)_{k}=\sum _{k=0}^{4}{\biggl \{}{\!4\! \atop \!k\!}{\biggr \}}\sum _{i=0}^{n}(i)_{k}=\sum _{k=0}^{4}{\biggl \{}{\!4\! \atop \!k\!}{\biggr \}}{\frac {(n{+}1)_{k+1}}{k{+}1}}\\[10mu]&={\biggl \{}{\!4\! \atop \!1\!}{\biggr \}}{\frac {(n{+}1)_{2}}{2}}+{\biggl \{}{\!4\! \atop \!2\!}{\biggr \}}{\frac {(n{+}1)_{3}}{3}}+{\biggl \{}{\!4\! \atop \!3\!}{\biggr \}}{\frac {(n{+}1)_{4}}{4}}+{\biggl \{}{\!4\! \atop \!4\!}{\biggr \}}{\frac {(n{+}1)_{5}}{5}}\\[8mu]&={\frac {1}{2}}(n{+}1)_{2}+{\frac {7}{3}}(n{+}1)_{3}+{\frac {6}{4}}(n{+}1)_{4}+{\frac {1}{5}}(n{+}1)_{5}\,.\end{aligned}}$

Здесь числа Стирлинга можно вычислить из их определения как количества разбиений четырех элементов на k непустые немаркированные подмножества.

Напротив, сумма ${\textstyle \sum _{i=0}^{n}i^{k}}$ в стандартном базисе задается формулой Фаульхабера , которая в общем случае более сложна.

Как обратные матрицы

Числа Стирлинга первого и второго рода можно считать обратными друг другу:

$\sum _{j=k}^{n}s(n,j)S(j,k)=\sum _{j=k}^{n}(-1)^{n-j}{\biggl [}{n \atop j}{\biggr ]}{\biggl \{}{\!j\! \atop \!k\!}{\biggr \}}=\delta _{n,k}$

и

$\sum _{j=k}^{n}S(n,j)s(j,k)=\sum _{j=k}^{n}(-1)^{j-k}{\biggl \{}{\!n\! \atop \!j\!}{\biggr \}}{\biggl [}{j \atop k}{\biggr ]}=\delta _{n,k},$

где $\delta _{nk}$ это дельта Кронекера . Эти два отношения можно понимать как матричные обратные отношения. То есть пусть s — нижняя треугольная матрица чисел Стирлинга первого рода, матричные элементы которой $s_{nk}=s(n,k).\,$Обратной S этой матрицей является , нижняя треугольная матрица чисел Стирлинга второго рода, элементы которой $S_{nk}=S(n,k).$ Символично это написано

$s^{-1}=S\,$

Хотя s и S бесконечны, поэтому вычисление записи продукта включает в себя бесконечную сумму, матричные умножения работают, поскольку эти матрицы имеют нижнюю треугольную форму, поэтому только конечное число членов в сумме не равно нулю.

числа Ла

Основная статья: Числа Лаха

Числа Лаха $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ иногда называют числами Стирлинга третьего рода. По соглашению, $L(0,0)=1$ и $L(n,k)=0$ если $n<k$ или $k=0<n$.

Эти числа являются коэффициентами, выражающими падающие факториалы через возрастающие факториалы и наоборот:

$x^{(n)}=\sum _{k=0}^{n}L(n,k)(x)_{k}\quad$ и $\quad (x)_{n}=\sum _{k=0}^{n}(-1)^{n-k}L(n,k)x^{(k)}.$

Как указано выше, это означает, что они выражают изменение базиса между базисами. $(x)_{0},(x)_{1},(x)_{2},\cdots$ и $x^{(0)},x^{(1)},x^{(2)},\cdots$, завершая схему.В частности, одна формула является обратной другой, поэтому:

$\sum _{j=k}^{n}(-1)^{j-k}L(n,j)L(j,k)=\delta _{n,k}.$

Аналогично, составляя замену базиса из $x^{(n)}$ к $x^{n}$ с изменением основы с $x^{n}$ к $(x)_{n}$ дает замену базиса непосредственно из $x^{(n)}$ к $(x)_{n}$:

$L(n,k)=\sum _{j=k}^{n}{\biggl [}{n \atop j}{\biggr ]}{\biggl \{}{\!j\! \atop \!k\!}{\biggr \}},$

и аналогично для других композиций. С точки зрения матриц, если $L$ обозначает матрицу с элементами $L_{nk}=L(n,k)$ и $L^{-}$ обозначает матрицу с элементами $L_{nk}^{-}=(-1)^{n-k}L(n,k)$, то одно является обратным другому: $L^{-}=L^{-1}$.Составление матрицы беззнаковых чисел Стирлинга первого рода с матрицей чисел Стирлинга второго рода дает числа Лаха: $L=|s|\cdot S$.

Перечислительно , ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ может быть определен как количество разбиений n элементов на k непустые немаркированные подмножества, где каждое подмножество наделено отсутствием порядка, циклическим порядком или линейным порядком соответственно. В частности, отсюда следуют неравенства:

${\biggl \{}{\!n\! \atop \!k\!}{\biggr \}}\leq {\biggl [}{n \atop k}{\biggr ]}\leq L(n,k).$

Соотношения инверсии и преобразование Стирлинга

Для любой пары последовательностей $\{f_{n}\}$ и $\{g_{n}\}$, связанные формулой числа Стирлинга конечной суммы, заданной формулой

$g_{n}=\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}f_{k},$

для всех целых чисел $n\geq 0$, мы имеем соответствующую формулу обращения для $f_{n}$ данный

$f_{n}=\sum _{k=0}^{n}\left[{\begin{matrix}n\\k\end{matrix}}\right](-1)^{n-k}g_{k}.$

Нижние индексы могут быть любым целым числом между ${\textstyle 0}$ и ${\textstyle n}$.

последовательности, Эти отношения инверсии между двумя последовательностями преобразуются в функциональные уравнения между экспоненциальными производящими функциями заданными преобразованием Стирлинга (производящая функция) как

${\widehat {G}}(z)={\widehat {F}}\left(e^{z}-1\right)$

и

${\widehat {F}}(z)={\widehat {G}}\left(\log(1+z)\right).$

Для $D=d/dx$, дифференциальные операторы $x^{n}D^{n}$ и $(xD)^{n}$ связаны следующими формулами для всех целых чисел $n\geq 0$:

${\begin{aligned}(xD)^{n}&=\sum _{k=0}^{n}S(n,k)x^{k}D^{k}\\x^{n}D^{n}&=\sum _{k=0}^{n}s(n,k)(xD)^{k}=(xD)_{n}=xD(xD-1)\ldots (xD-n+1)\end{aligned}}$

Другая пара « инверсионных » соотношений, включающих числа Стирлинга, связана с прямыми разностями и обычными числами. $n^{th}$ производные функции, $f(x)$, который является аналитическим для всех $x$ по формулам

${\frac {1}{k!}}{\frac {d^{k}}{dx^{k}}}f(x)=\sum _{n=k}^{\infty }{\frac {s(n,k)}{n!}}\Delta ^{n}f(x)$

${\frac {1}{k!}}\Delta ^{k}f(x)=\sum _{n=k}^{\infty }{\frac {S(n,k)}{n!}}{\frac {d^{n}}{dx^{n}}}f(x).$

Похожие объекты

Таблица сходства

Числа Стирлинга первого рода	Числа Стирлинга второго рода
$\left[{n+1 \atop k}\right]=n\left[{n \atop k}\right]+\left[{n \atop k-1}\right]$	$\left\{{n+1 \atop k}\right\}=k\left\{{n \atop k}\right\}+\left\{{n \atop k-1}\right\}$
$\sum _{k=0}^{n}\left[{n \atop k}\right]=n!$	$\sum _{k=0}^{n}\left\{{n \atop k}\right\}=B_{n}$, где $B_{n}$ - n-е число Белла
$\sum _{k=0}^{n}\left[{n \atop k}\right]x^{k}=x^{(n)}$, где $\{x^{(n)}\}_{n\in \mathbb {N} }$ это растущие факториалы	$\sum _{k=0}^{n}\left\{{n \atop k}\right\}x^{k}=T_{n}(x)$, где $\{T_{n}\}_{n\in \mathbb {N} }$ – полиномы Тушара
$\left[{n \atop 0}\right]=\delta _{n},\ \left[{n \atop n-1}\right]={\binom {n}{2}},\ \left[{n \atop n}\right]=1$	$\left\{{n \atop 0}\right\}=\delta _{n},\ \left\{{n \atop n-1}\right\}={\binom {n}{2}},\ \left\{{n \atop n}\right\}=1$
$\left[{n+1 \atop k+1}\right]=\sum _{j=k}^{n}\left[{n \atop j}\right]{\binom {j}{k}}$	$\left\{{n+1 \atop k+1}\right\}=\sum _{j=k}^{n}{\binom {n}{j}}\left\{{j \atop k}\right\}$
$\left[{\begin{matrix}n+1\\k+1\end{matrix}}\right]=\sum _{j=k}^{n}{\frac {n!}{j!}}\left[{j \atop k}\right]$	$\left\{{n+1 \atop k+1}\right\}=\sum _{j=k}^{n}(k+1)^{n-j}\left\{{j \atop k}\right\}$
$\left[{n+k+1 \atop n}\right]=\sum _{j=0}^{k}(n+j)\left[{n+j \atop j}\right]$	$\left\{{n+k+1 \atop k}\right\}=\sum _{j=0}^{k}j\left\{{n+j \atop j}\right\}$
$\left[{n \atop l+m}\right]{\binom {l+m}{l}}=\sum _{k}\left[{k \atop l}\right]\left[{n-k \atop m}\right]{\binom {n}{k}}$	$\left\{{n \atop l+m}\right\}{\binom {l+m}{l}}=\sum _{k}\left\{{k \atop l}\right\}\left\{{n-k \atop m}\right\}{\binom {n}{k}}$
$\left[{n+k \atop n}\right]{\underset {n\to \infty }{\sim }}{\frac {n^{2k}}{2^{k}k!}}.$	$\left\{{n+k \atop n}\right\}{\underset {n\to \infty }{\sim }}{\frac {n^{2k}}{2^{k}k!}}.$
$\sum _{n=k}^{\infty }\left[{n \atop k}\right]{\frac {x^{n}}{n!}}={\frac {(-\log(1-x))^{k}}{k!}}.$	$\sum _{n=k}^{\infty }\left\{{n \atop k}\right\}{\frac {x^{n}}{n!}}={\frac {(e^{x}-1)^{k}}{k!}}.$
$\left[{n \atop k}\right]=\sum _{0\leq i_{1}<\ldots <i_{n-k}<n}i_{1}i_{2}\cdots i_{n-k}.$	$\left\{{n \atop k}\right\}=\sum _{\begin{array}{c}c_{1}+\ldots +c_{k}=n-k\\c_{1},\ldots ,\ c_{k}\ \geq \ 0\end{array}}1^{c_{1}}2^{c_{2}}\cdots k^{c_{k}}$

Подробности смотрите в конкретных статьях.

Симметричные формулы

Абрамовиц и Стегун приводят следующие симметричные формулы, связывающие числа Стирлинга первого и второго рода.

$\left[{n \atop k}\right]=\sum _{j=n}^{2n-k}(-1)^{j-k}{\binom {j-1}{k-1}}{\binom {2n-k}{j}}\left\{{j-k \atop j-n}\right\}$

и

$\left\{{n \atop k}\right\}=\sum _{j=n}^{2n-k}(-1)^{j-k}{\binom {j-1}{k-1}}{\binom {2n-k}{j}}\left[{j-k \atop j-n}\right]$

Числа Стирлинга с отрицательными целыми значениями

Числа Стирлинга можно расширить до отрицательных целых значений, но не все авторы делают это одинаково. Независимо от выбранного подхода стоит отметить, что числа Стирлинга первого и второго рода связаны соотношениями:

${\biggl [}{n \atop k}{\biggr ]}={\biggl \{}{\!-k\! \atop \!-n\!}{\biggr \}}\quad {\text{and}}\quad {\biggl \{}{\!n\! \atop \!k\!}{\biggr \}}={\biggl [}{-k \atop -n}{\biggr ]}$

когда n и k — целые неотрицательные числа. Итак, у нас есть следующая таблица для $\left[{-n \atop -k}\right]$:

к н	−1	−2	−3	−4	−5
−1	1	1	1	1	1
−2	0	1	3	7	15
−3	0	0	1	6	25
−4	0	0	0	1	10
−5	0	0	0	0	1

Дональд Кнут определил более общие числа Стирлинга, распространив рекуррентное отношение на все целые числа. В этом подходе ${\textstyle \left[{n \atop k}\right]}$ и ${\textstyle \left\{{\!n\! \atop \!k\!}\right\}}$ равны нулю, если n отрицательно и k неотрицательно, или если n неотрицательно и k отрицательно, и поэтому мы имеем для любых целых чисел n и k ,

${\biggl [}{n \atop k}{\biggr ]}={\biggl \{}{\!-k\! \atop \!-n\!}{\biggr \}}\quad {\text{and}}\quad {\biggl \{}{\!n\! \atop \!k\!}{\biggr \}}={\biggl [}{-k \atop -n}{\biggr ]}.$

С другой стороны, для натуральных чисел n и k Дэвид Брэнсон определенный ${\textstyle \left[{-n \atop -k}\right]\!,}$ ${\textstyle \left\{{\!-n\! \atop \!-k\!}\right\}\!,}$ ${\textstyle \left[{-n \atop k}\right]\!,}$ и ${\textstyle \left\{{\!-n\! \atop \!k\!}\right\}}$ (но не ${\textstyle \left[{n \atop -k}\right]}$ или ${\textstyle \left\{{\!n\! \atop \!-k\!}\right\}}$). В этом подходе имеется следующее расширение рекуррентного соотношения чисел Стирлинга первого рода:

${\biggl [}{-n \atop k}{\biggr ]}={\frac {(-1)^{n+1}}{n!}}\sum _{i=1}^{n}{\frac {(-1)^{i+1}}{i^{k}}}{\binom {n}{i}}$,

Например, ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ Это приводит к следующей таблице значений ${\textstyle \left[{n \atop k}\right]}$ для отрицательного целого n .

к н	0	1	2	3	4
−1	1	1	1	1	1
−2	${\tfrac {-1}{2}}$	${\tfrac {-3}{4}}$	${\tfrac {-7}{8}}$	${\tfrac {-15}{16}}$	${\tfrac {-31}{32}}$
−3	${\tfrac {1}{6}}$	${\tfrac {11}{36}}$	${\tfrac {85}{216}}$	${\tfrac {575}{1296}}$	${\tfrac {3661}{7776}}$
−4	${\tfrac {-1}{24}}$	${\tfrac {-25}{288}}$	${\tfrac {-415}{3456}}$	${\tfrac {-5845}{41472}}$	${\tfrac {-76111}{497664}}$
−5	${\tfrac {1}{120}}$	${\tfrac {137}{7200}}$	${\tfrac {12019}{432000}}$	${\tfrac {874853}{25920000}}$	${\tfrac {58067611}{1555200000}}$

В этом случае ${\textstyle \sum _{n=1}^{\infty }\left[{-n \atop -k}\right]=B_{k}}$ где $B_{k}$ является числом Белла , и поэтому отрицательные числа Белла можно определить как ${\textstyle \sum _{n=1}^{\infty }\left[{-n \atop k}\right]=:B_{-k}}$.

Например, это производит ${\textstyle \sum _{n=1}^{\infty }\left[{-n \atop 1}\right]=B_{-1}={\frac {1}{e}}\sum _{j=1}^{\infty }{\frac {1}{j\cdot j!}}={\frac {1}{e}}\int _{0}^{1}{\frac {e^{t}-1}{t}}dt=0.4848291\dots }$, в целом ${\textstyle B_{-k}={\frac {1}{e}}\sum _{j=1}^{\infty }{\frac {1}{j^{k}j!}}}$.

См. также

• Полиномы Белла
• Каталонский номер
• Циклы и фиксированные точки
• Символ Поххаммера
• Полиномиальная последовательность
• Полиномы
• Перестановка Стирлинга

Ссылки

• Розен, Кеннет Х., изд. (2018), Справочник по дискретной и комбинаторной математике , CRC Press, ISBN  978-1-5848-8780-5
• Мансур, Туфик; Шорк, Матиас (2015), Коммутационные отношения, нормальный порядок и числа Стирлинга , CRC Press, ISBN  978-1-4665-7989-7

Дальнейшее чтение

• Адамчик, Виктор (1997). «О числах Стирлинга и суммах Эйлера» (PDF) . Журнал вычислительной и прикладной математики . 79 : 119–130. дои : 10.1016/s0377-0427(96)00167-7 . Архивировано (PDF) из оригинала 14 декабря 2004 г.
• Бенджамин, Артур Т.; Престон, Грегори О.; Куинн, Дженнифер Дж. (2002). «Встреча Стерлинга с гармоническими числами» (PDF) . Журнал «Математика» . 75 (2): 95–103. CiteSeerX   10.1.1.383.722 . дои : 10.2307/3219141 . JSTOR   3219141 . Архивировано (PDF) из оригинала 10 сентября 2020 г.
• Бояджиев, Христо Н. (2012). «Близкие встречи с числами Стирлинга второго рода» (PDF) . Журнал «Математика» . 85 (4): 252–266. arXiv : 1806.09468 . дои : 10.4169/math.mag.85.4.252 . S2CID   115176876 . Архивировано (PDF) из оригинала 5 сентября 2015 г.
• Конте, Луи (1970). «Значение s ( n , k ) » . Комбинаторный анализ, том второй (на французском языке): 51.
• Конте, Луи (1974). Продвинутая комбинаторика: искусство конечных и бесконечных расширений . Дордрехт-Голландия/Бостон-США: Издательская компания Reidel. ISBN  9789027703804 .
• Сянь-Куэй Хван (1995). «Асимптотические разложения чисел Стирлинга первого рода» . Журнал комбинаторной теории, серия А. 71 (2): 343–351. дои : 10.1016/0097-3165(95)90010-1 .
• Кнут, DE (1992), «Два примечания к обозначениям», Amer. Математика. Ежемесячно , 99 (5): 403–422, arXiv : math/9205211 , doi : 10.2307/2325085 , JSTOR   2325085 , S2CID   119584305
• Микса, Фрэнсис Л. (январь 1956 г.). «Числа Стирлинга первого рода: 27 листов воспроизведены из машинописной рукописи, хранящейся в файле UMT». Математические таблицы и другие средства вычислений: обзоры и описания таблиц и книг . 10 (53): 37–38. JSTOR   2002617 .
• Микса, Фрэнсис Л. (1972) [1964]. «Комбинаторный анализ, таблица 24.4, числа Стирлинга второго рода» . В Абрамовице, Милтон; Стегун, Ирен А. (ред.). Справочник по математическим функциям (с формулами, графиками и математическими таблицами) . 55. Министерство торговли США, Национальное бюро стандартов, Прикладная математика. п. 835.
• Митринович, Драгослав С. (1959). «О числах Стирлинга первого рода и полиномах Стирлинга» (PDF) . Публикации электротехнического факультета Белградского университета, серия «Математика и физика» (на французском языке) (23): 1–20. ISSN   0522-8441 . Архивировано (PDF) из оригинала 17 июня 2009 г.
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (сентябрь 1998 г.). «Джеймс Стирлинг (1692–1770)» .
• Сикденье, Ж.М.; Пенсон, Калифорния; Соломон, А.И. (2001). «Расширенные числа Белла и Стирлинга из гипергеометрического возведения в степень» (PDF) . Журнал целочисленных последовательностей . 4 : 01.1.4. arXiv : math/0106123 . Бибкод : 2001JIntS...4...14S .
• Спайви, Майкл З. (2007). «Комбинаторные суммы и конечные разности» . Дискретная математика . 307 (24): 3130–3146. CiteSeerX   10.1.1.134.8665 . дои : 10.1016/j.disc.2007.03.052 .
• Слоан, Нью-Джерси (ред.). «Последовательность A008275 (Числа Стирлинга первого рода)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.
• Слоан, Нью-Джерси (ред.). «Последовательность A008277 (Числа Стирлинга 2-го рода)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.