Дилемма заключенного

Чтобы узнать о других значениях, см. Дилемма узника (значения) .

Не путать с проблемой трех заключенных , парадоксом неожиданного повешения , проблемой 100 заключенных или дилеммой невиновного заключенного .

— Дилемма заключенного это теории игр мысленный эксперимент , в котором участвуют два рациональных агента , каждый из которых может сотрудничать ради взаимной выгоды или предать своего партнера («дефект») за индивидуальное вознаграждение. Эта дилемма была первоначально сформулирована Меррилом Флудом и Мелвином Дрешером в 1950 году, когда они работали в корпорации RAND . Позже Альберт В. Такер формализовал игру, структурировав вознаграждение в виде тюремного заключения, и назвал ее «дилеммой заключенного».

Дилемма заключенного моделирует множество реальных ситуаций, связанных со стратегическим поведением. В повседневном использовании термин «дилемма заключенного» можно применять к любой ситуации, в которой две организации могут получить важные выгоды от сотрудничества или пострадать от неспособности сделать это, но считают, что координировать свою деятельность сложно или дорого.

Помещение

Пример матрицы выигрышей дилеммы заключенного

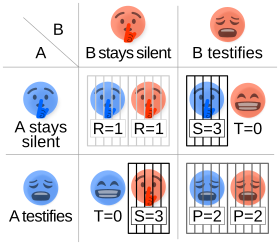
Уильям Паундстоун описал эту «типичную современную версию» игры в своей книге « Дилемма узника» 1993 года :

Двое членов преступной группировки арестованы и заключены в тюрьму. Каждый заключенный находится в одиночной камере без возможности разговаривать или обмениваться сообщениями с другим. Полиция признает, что у нее недостаточно доказательств, чтобы осудить пару по основному обвинению. Оба планируют приговорить к году тюремного заключения по менее строгому обвинению. Одновременно полиция предлагает каждому заключенному фаустовскую сделку . Если он даст показания против своего партнера, он выйдет на свободу, а партнер получит три года лишения свободы по основному обвинению. Ах, да, есть подвох... Если оба заключенных дадут показания друг против друга, оба будут приговорены к двум годам лишения свободы. Заключенным дается немного времени на обдумывание, но ни в коем случае нельзя узнать, что решил другой, пока он не примет окончательного решения. Каждому сообщают, что другому заключенному предлагают ту же самую сделку. Каждый заключенный озабочен только своим благополучием — минимизацией своего тюремного срока.

Это приводит к четырем различным возможным последствиям для заключенных А и Б:

1. Если А и Б промолчат, каждый из них будет приговорен к одному году тюремного заключения.
2. Если А дает показания против Б, но Б хранит молчание, А будет освобожден, а Б отсидит три года в тюрьме.
3. Если А будет хранить молчание, а Б даст показания против А, то А отсидит три года в тюрьме, а Б будет освобожден.
4. Если А и Б дадут показания друг против друга, каждый из них будет отбывать наказание по два года.

Стратегия решения дилеммы заключенного

Двое заключенных помещены в отдельные комнаты и не могут общаться друг с другом. Предполагается, что оба заключенных понимают суть игры, не лояльны друг к другу и не имеют возможности возмездия или вознаграждения вне игры. Обычная игра показана ниже:

Заключенный Б Заключенный А	Заключенный Б хранит молчание ( сотрудничает )	Заключенный Б дает показания ( дефекты )
Заключенный А молчит ( сотрудничает )	Каждый служит 1 год	Заключенный А: 3 года Заключенный Б: выходит на свободу
Заключенный А дает показания ( дефекты )	Заключенный А: выходит на свободу Заключенный Б: 3 года	Каждый служит по 2 года

Независимо от того, что решит другой, каждый заключенный получает более высокую награду, предав другого («дезертирство»). Рассуждения включают в себя анализ лучших ответов обоих игроков : B либо будет сотрудничать, либо откажется. Если B будет сотрудничать, A должен дезертировать, потому что выйти на свободу лучше, чем отсидеть один год. Если B дезертирует, A тоже должен дезертировать, потому что отсидеть 2 года лучше, чем отсидеть 3. Таким образом, в любом случае A должен дезертировать, поскольку дезертирство — лучший ответ для A, независимо от стратегии B. Параллельные рассуждения покажут, что B должен отказаться.

Бегство всегда приводит к более выгодному результату, чем сотрудничество, поэтому это строго доминирующая стратегия для обоих игроков. Взаимное отступничество — единственное сильное равновесие Нэша в игре. Поскольку коллективный идеальный результат взаимного сотрудничества иррационален с точки зрения корыстных интересов, это равновесие Нэша не является эффективным по Парето .

Обобщенная форма

Структуру традиционной дилеммы заключенного можно обобщить, исходя из ее исходной ситуации с заключенным. Предположим, что два игрока представлены красным и синим цветами и каждый игрок выбирает либо «сотрудничать», либо «отступать».

Если оба игрока сотрудничают, они оба получают награду. $R$ за сотрудничество. Если оба игрока отказываются от участия, они оба получают наказание. $P$. Если Синий откажется, а Красный сотрудничает, то Синий получит вознаграждение за искушение. $T$, а Красный получает выигрыш «лоха», $S$. Аналогично, если Синий сотрудничает, а Красный отступает, то Синий получает выигрыш неудачника. $S$, в то время как Красный получает вознаграждение за искушение $T$.

Это можно выразить в нормальной форме :

Каноническая матрица выигрышей дилеммы заключенного

Красный Синий	Сотрудничать	Дефект
Сотрудничать	Р Р	Т С
Дефект	С Т	П П

и чтобы игра была «дилеммой заключенного» в строгом смысле слова, для выигрышей должно выполняться следующее условие:

⁠ $T>R>P>S$⁠

Отношения выигрыша ⁠ $R>P$⁠ подразумевает, что взаимное сотрудничество превосходит взаимное предательство, а отношения вознаграждения ⁠ $T>R$⁠ и ⁠ $P>S$⁠ подразумевают, что бегство является доминирующей стратегией для обоих агентов.

Повторяющаяся дилемма заключенного

Если два игрока разыгрывают дилемму заключенного более одного раза подряд, помнят предыдущие действия своего противника и могут соответствующим образом изменить свою стратегию, игра называется повторяющейся дилеммой заключенного.

В дополнение к общей форме, приведенной выше, итеративная версия также требует, чтобы ⁠ $2R>T+S$⁠ , чтобы предотвратить попеременное сотрудничество и предательство, приносящее большую награду, чем взаимное сотрудничество.

Повторяющаяся дилемма заключенного является фундаментальной для некоторых теорий человеческого сотрудничества и доверия. Если предположить, что игра эффективно моделирует транзакции между двумя людьми, требующие доверия, совместное поведение в популяциях можно смоделировать с помощью многопользовательской итерированной версии игры. В 1975 году Грофман и Пул оценили количество посвященных ему научных статей более чем в 2000. Повторяющуюся дилемму заключенного также называют « игрой мир-война ».

Общая стратегия

Если повторяющаяся дилемма заключенного разыгрывается конечное число раз и оба игрока знают об этом, то доминирующая стратегия и равновесие Нэша заключаются в отказе от игры во всех раундах. Доказательство носит индуктивный характер : с таким же успехом можно отступить на последнем ходу, поскольку у противника не будет возможности позже нанести ответный удар. Следовательно, оба откажутся в последнюю очередь. Таким образом, игрок может с таким же успехом сбежать на предпоследнем ходу, поскольку противник сбежит на последнем, независимо от того, что будет сделано, и так далее. То же самое применимо, если продолжительность игры неизвестна, но имеет известный верхний предел.

Чтобы между рациональными игроками возникло сотрудничество , количество раундов должно быть неизвестным или бесконечным. В этом случае принцип «всегда отказываться» может перестать быть доминирующей стратегией. Как показал Роберт Ауманн в статье 1959 года, рациональные игроки, неоднократно взаимодействующие в течение неопределенно долгих игр, могут поддерживать сотрудничество. В частности, игрок может быть менее склонен к сотрудничеству, если его коллега не сотрудничал много раз, что вызывает разочарование. И наоборот, с течением времени вероятность сотрудничества имеет тенденцию возрастать благодаря установлению «молчаливого соглашения» между участвующими игроками. В экспериментальных ситуациях сотрудничество может иметь место, даже если оба участника знают, сколько итераций будет сыграно.

Согласно экспериментальному исследованию 2019 года, опубликованному в American Economic Review , в котором проверялось, какие стратегии реальные испытуемые использовали в повторяющихся ситуациях «дилеммы заключенного» с идеальным мониторингом, большинство выбранных стратегий всегда заключались в отступничестве, ответной реакции и мрачном триггере . Какую стратегию выбирали испытуемые, зависело от параметров игры.

Турнир Аксельрода и условия успешной стратегии

Интерес к повторяющейся дилемме заключенного был разожжен Робертом Аксельродом в его книге 1984 года «Эволюция сотрудничества» , в которой он сообщает об организованном им турнире по N -шаговой дилемме заключенного (с фиксированным N ), в котором участники должны выбрать свою стратегию. неоднократно и вспоминать свои предыдущие встречи. Аксельрод пригласил коллег-ученых со всего мира разработать компьютерные стратегии для участия в повторяющемся турнире по дилемме заключенного. Введенные программы сильно различались по алгоритмической сложности, начальной враждебности, способности к прощению и т. д.

Аксельрод обнаружил, что когда эти встречи повторялись в течение длительного периода времени со многими игроками, каждый из которых использовал разные стратегии, жадные стратегии имели тенденцию приносить очень плохие результаты в долгосрочной перспективе, в то время как более альтруистические стратегии давали лучшие результаты, если судить исключительно по личным интересам. Он использовал это, чтобы показать возможный механизм эволюции альтруистического поведения из изначально чисто эгоистичных механизмов путем естественного отбора .

Победившая детерминистская стратегия была разработана и введена в турнир Анатолем Рапопортом . Это была самая простая из всех представленных программ, содержащая всего четыре строки БЕЙСИКА . и выиграл конкурс. Стратегия состоит в том, чтобы просто сотрудничать на первой итерации игры; после этого игрок делает то же, что его противник сделал на предыдущем ходу. В зависимости от ситуации, чуть лучшей стратегией может быть «око за око с прощением»: когда противник отступает, на следующем ходу игрок иногда все равно сотрудничает с небольшой вероятностью (около 1–5%, в зависимости от состава). противников). Это позволяет время от времени восстанавливаться после попадания в цикл дезертирства.

Проанализировав наиболее результативные стратегии, Аксельрод сформулировал несколько условий, необходимых для успеха стратегии:

• Приятно : стратегия не будет первой, кто откажется (иногда это называют «оптимистическим» алгоритмом). ), т. е. он не будет «обманывать» своего противника в первую очередь из чисто корыстных соображений. Почти все самые результативные стратегии были хороши.
• Ответные меры : стратегия иногда должна принимать ответные меры. Примером стратегии отсутствия ответных мер является «Всегда сотрудничать» — очень плохой выбор, который часто будет использоваться «неприятными» стратегиями.
• Прощение . Успешные стратегии должны быть прощающими. Хотя игроки будут принимать ответные меры, они снова будут сотрудничать, если противник не продолжит отступать. Это может остановить длительные серии мести и контр-мести, максимизируя очки.
• Независтливость : стратегия не должна стремиться набрать больше очков, чем противник.

В отличие от игры с дилеммой бывшего заключенного, оптимальная стратегия в повторяющейся дилемме заключенного зависит от стратегий вероятных противников и от того, как они отреагируют на предательство и сотрудничество. Например, если популяция полностью состоит из игроков, которые всегда отказываются от игры, за исключением одного, который следует стратегии «око за око», этот человек находится в небольшом невыгодном положении из-за поражения на первом ходу. В такой популяции оптимальная стратегия — каждый раз дезертировать. В более общем плане, учитывая популяцию с определенным процентом всегда перебежчиков, а остальные — игроками, играющими «око за око», оптимальная стратегия зависит от процента и количества сыгранных итераций.

Другие стратегии

Выработка оптимальной стратегии обычно осуществляется двумя способами:

• Байесовское равновесие Нэша : если можно определить статистическое распределение противоположных стратегий, оптимальную контрстратегию можно вывести аналитически.
• Монте-Карло Было проведено моделирование популяций методом , при котором особи с низкими показателями вымирают, а особи с высокими показателями размножаются ( генетический алгоритм поиска оптимальной стратегии). Состав алгоритмов в конечной популяции обычно зависит от состава в исходной популяции. Введение мутации (случайной изменчивости при размножении) уменьшает зависимость от исходной популяции; эмпирические эксперименты с такими системами, как правило, приводят к появлению игроков, работающих по принципу «око за око», но не существует аналитического доказательства того, что это будет происходить всегда.

В стратегии, называемой «выигрыш-останье-проигрыш-переключение» , столкнувшись с неспособностью сотрудничать, игрок меняет стратегию на следующем ходу. В определенных обстоятельствах Павлов превосходит все другие стратегии, предоставляя преимущество товарищам по игре, использующим аналогичную стратегию.

Хотя «око за око» считается самой надежной базовой стратегией, команда из Саутгемптонского университета в Англии представила более успешную стратегию на конкурсе повторяющихся дилемм заключенного, посвященном 20-летнему юбилею. Он полагался на сговор между программами для получения наибольшего количества баллов за одну программу. Университет представил на конкурс 60 программ, которые были рассчитаны на узнавание друг друга через серию из пяти-десяти ходов на старте. Как только это признание было сделано, одна программа всегда будет сотрудничать, а другая всегда отказываться, гарантируя максимальное количество баллов перебежчику. Если бы программа поняла, что играет с игроком, не принадлежащим Саутгемптону, она бы постоянно отступала, пытаясь минимизировать счет конкурирующей программы. В результате результаты турнира «Дилемма заключенных» 2004 года показывают, что стратегии Университета Саутгемптона занимают первые три места (и ряд позиций ближе к концу), несмотря на то, что у них меньше побед и гораздо больше поражений, чем у стратегии GRIM. Стратегия Саутгемптона использует тот факт, что в этом конкретном соревновании было разрешено несколько заявок и что результативность команды измерялась по результатам игрока, набравшего наибольшее количество очков (это означает, что использование самоотверженных игроков было формой минимаксинга ).

Из-за этого нового правила это соревнование также не имеет теоретического значения при анализе стратегий одного агента по сравнению с плодотворным турниром Аксельрода. Но это обеспечило основу для анализа того, как реализовать стратегии сотрудничества в многоагентных структурах, особенно в присутствии шума.

Задолго до того, как был сыгран этот турнир по новым правилам, Докинз в своей книге «Эгоистичный ген » указал на возможность победы таких стратегий, если было разрешено несколько заявок, но заметил, что Аксельрод, скорее всего, не допустил бы их, если бы они были поданы. Он также основан на обходе правила, запрещающего общение между игроками, что, возможно, и сделали программы «Саутгемптона» с заранее запрограммированным «танцем из десяти движений», чтобы узнавать друг друга, что еще раз подчеркивает, насколько ценным может быть общение для изменения баланса в игре.

Даже без неявного сговора между программными стратегиями , игра «око за око» не всегда является абсолютным победителем любого турнира; точнее, ее долгосрочные результаты в серии турниров превосходят конкурентов, но это не значит, что она самая успешная в краткосрочной перспективе. То же самое относится и к взаимодействию с прощением и другими оптимальными стратегиями.

Это также можно проиллюстрировать с помощью дарвиновского моделирования ESS . В таком моделировании принцип «око за око» почти всегда будет доминировать, хотя неприятные стратегии будут проникать в популяцию и исчезать из нее, поскольку в популяцию «око за око» можно проникнуть с помощью нерепрессивных хороших стратегий, которые, в свою очередь, легко жертва неприятных стратегий. Докинз показал, что здесь никакое статическое сочетание стратегий не образует устойчивого равновесия, и система всегда будет колебаться между границами.

Стохастическая повторяющаяся дилемма заключенного

В стохастической повторяющейся игре «Дилемма заключенного» стратегии определяются с точки зрения «вероятностей сотрудничества». В столкновении между игроком X и игроком стратегия определяется X P набором вероятностей сотрудничества с Y. Y P является функцией результатов их предыдущих встреч или некоторого их подмножества. Если P является функцией только их последних n встреч, это называется стратегией «память-n». Стратегия памяти-1 затем определяется четырьмя вероятностями сотрудничества: $P=\{P_{cc},P_{cd},P_{dc},P_{dd}\}$, где P _cd — вероятность того, что X будет сотрудничать в нынешней встрече, учитывая, что предыдущая встреча характеризовалась сотрудничеством X и Y. отказом Если каждая из вероятностей равна 1 или 0, стратегия называется детерминированной. Примером детерминированной стратегии является стратегия «око за око», записанная как $P=\{1,0,1,0\}$, в котором X реагирует так же, как Y в предыдущей встрече. Другой вариант — стратегия «выиграл-остался-проиграл», записанная как $P=\{1,0,0,1\}$. Было показано, что для любой стратегии памяти n существует соответствующая стратегия памяти 1, которая дает те же статистические результаты, так что необходимо рассматривать только стратегии памяти 1.

Если $P$ определяется как указанный выше вектор стратегии из 4 элементов X и $Q=\{Q_{cc},Q_{cd},Q_{dc},Q_{dd}\}$ В качестве 4-элементного вектора стратегии Y (где индексы указаны с M точки зрения Y), матрица перехода может быть определена для X -я запись которой , ij представляет собой вероятность того, что результат конкретной встречи между X и Y будет j, учитывая, что предыдущая встреча была i , где i и j — один из четырех индексов результата: cc , cd , dc или dd . Например, с точки зрения X учитывая , , вероятность того, что исход текущего столкновения будет cd, что предыдущее столкновение было cd, равна $M_{cd,cd}=P_{cd}(1-Q_{dc})$. Согласно этим определениям, повторяющаяся дилемма заключённого квалифицируется как случайный процесс , а M — стохастическая матрица , позволяющая применять всю теорию случайных процессов.

Одним из результатов стохастической теории является то, что существует стационарный вектор v для матрицы v такой, что $v\cdot M=v$. Без ограничения общности можно указать, что v нормировано так, что сумма его четырех компонентов равна единице. ij -я запись в $M^{n}$ даст вероятность того, что исход встречи между X и Y будет j, учитывая, что встреча на n предыдущих шагах равна i . В пределе, когда n приближается к бесконечности, M будет сходиться к матрице с фиксированными значениями, давая долгосрочные вероятности встречи, производящей j, независимо от i . Другими словами, строки $M^{\infty }$ будут идентичны, что дает долгосрочные равновесные вероятности результата повторяющейся дилеммы заключенного без необходимости явно оценивать большое количество взаимодействий. Видно, что v — стационарный вектор для $M^{n}$ и особенно $M^{\infty }$, так что каждая строка $M^{\infty }$ будет равен v . стационарный вектор определяет вероятности равновесного результата для X. Таким образом , Определение $S_{x}=\{R,S,T,P\}$ и $S_{y}=\{R,T,S,P\}$ в качестве векторов краткосрочных выигрышей для результатов { cc,cd,dc,dd } (с и X точки зрения X), равновесные выигрыши для Y теперь можно определить как $s_{x}=v\cdot S_{x}$ и $s_{y}=v\cdot S_{y}$, что позволяет сравнить две стратегии P и Q на предмет их долгосрочных выигрышей.

Стратегии нулевого детерминанта

Взаимосвязь между нулевой детерминантой (ZD), стратегиями сотрудничества и отказа в повторяющейся дилемме заключённого (повторяемая дилемма заключённого)

В 2012 году Уильям Х. Пресс и Фримен Дайсон опубликовали новый класс стратегий для решения стохастической повторяющейся дилеммы заключенного, названный стратегиями «нулевой детерминант» (ZD). Долгосрочные выигрыши от встреч между X и Y можно выразить как определитель матрицы, которая является функцией двух стратегий и векторов краткосрочных выигрышей: $s_{x}=D(P,Q,S_{x})$ и $s_{y}=D(P,Q,S_{y})$, которые не включают стационарный вектор v . Поскольку определительная функция $s_{y}=D(P,Q,f)$ линейна по $f$, отсюда следует, что $\alpha s_{x}+\beta s_{y}+\gamma =D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)$ (где $U=\{1,1,1,1\}$). Любые стратегии, для которых $D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)=0$ по определению являются стратегией ZD, а долгосрочные выигрыши подчиняются соотношению $\alpha s_{x}+\beta s_{y}+\gamma =0$.

«Око за око» — это стратегия ZD, которая является «справедливой» в том смысле, что не дает преимущества над другим игроком. Но пространство ZD также содержит стратегии, которые в случае двух игроков могут позволить одному игроку в одностороннем порядке установить счет другого игрока или, альтернативно, заставить эволюционного игрока получить выигрыш, на несколько процентов меньший, чем его собственный. Игрок, у которого вымогают деньги, может отказаться от участия, но тем самым нанесет себе вред, получив меньший выигрыш. Таким образом, решения, связанные с вымогательством, превращают повторяющуюся дилемму заключенного в своего рода игру-ультиматум . В частности, X может выбрать стратегию, для которой $D(P,Q,\beta S_{y}+\gamma U)=0$, в одностороннем порядке устанавливающий y ₍ определенное значение в определенном диапазоне значений, независимо от Y стратегии возможность , предлагая X «вымогать» у игрока Y и наоборот). Но если X попытается присвоить s _x определенное значение, диапазон возможностей будет намного меньше и состоит только из полного сотрудничества или полного предательства.

Расширением повторяющейся дилеммы заключённого является эволюционная стохастическая повторяющаяся дилемма заключённого, в которой относительное изобилие конкретных стратегий может меняться, при этом более успешные стратегии относительно увеличиваются. Этот процесс можно осуществить, заставив менее успешных игроков подражать более успешным стратегиям или исключив из игры менее успешных игроков, одновременно умножая более успешных. Было показано, что несправедливые стратегии ZD не являются эволюционно стабильными . Основная интуиция заключается в том, что эволюционно стабильная стратегия должна не только иметь возможность вторгнуться в другую популяцию (что могут сделать грабительские стратегии ZD), но также должна хорошо работать против других игроков того же типа (что вымогательские игроки ZD делают плохо, потому что они уменьшают влияние друг друга). излишек).

Теория и моделирование подтверждают, что за пределами критического размера популяции вымогательство ZD проигрывает в эволюционной конкуренции более кооперативным стратегиям, и в результате средний выигрыш в популяции увеличивается, когда популяция больше. Кроме того, в некоторых случаях вымогатели могут даже стимулировать сотрудничество, помогая вырваться из противостояния между перебежчиками в униформе и агентами «выиграл-остался-проиграл-поменялся» .

Хотя вымогательские стратегии ZD не стабильны в больших группах населения, другой класс ZD, называемый «щедрыми» стратегиями, является одновременно стабильным и надежным. Когда популяция не слишком мала, эти стратегии могут вытеснить любую другую стратегию ZD и даже хорошо работать против широкого спектра общих стратегий для повторяющейся дилеммы заключенного, включая победу-остаться, проиграть-переключиться. Это было доказано специально на донорской игре Александром Стюартом и Джошуа Плоткиным в 2013 году. Щедрые стратегии будут сотрудничать с другими кооперативными игроками, и в случае отказа щедрый игрок теряет больше полезности, чем его соперник. Щедрые стратегии представляют собой пересечение стратегий ZD и так называемых «хороших» стратегий, которые Итан Акин определил как те, в которых игрок отвечает на прошлое взаимное сотрудничество будущим сотрудничеством и распределяет ожидаемые выигрыши поровну, если он получает хотя бы кооперативную сумму. ожидаемая выплата. Среди хороших стратегий щедрая (ZD) подгруппа хорошо работает, когда популяция не слишком мала. Если население очень мало, стратегии дезертирства имеют тенденцию доминировать.

Непрерывная повторяющаяся дилемма заключенного

Большая часть работ по повторной дилемме заключенного сосредоточена на дискретном случае, когда игроки либо сотрудничают, либо отступают, поскольку эту модель относительно легко анализировать. Однако некоторые исследователи рассмотрели модели непрерывно повторяющейся дилеммы заключенного, в которой игроки могут вносить переменный вклад в жизнь другого игрока. Ле и Бойд обнаружили, что в таких ситуациях развивать сотрудничество гораздо труднее, чем в дискретно повторяющейся дилемме заключенного. В постоянной дилемме заключенного, если популяция изначально находится в состоянии некооперативного равновесия, игроки, которые лишь незначительно более склонны к сотрудничеству, чем те, кто не сотрудничает, получают мало пользы от сортировки друг с другом. Напротив, в дилемме дискретного заключенного участники, сотрудничающие по принципу «око за око», получают большую выгоду от сортировки друг с другом в условиях некооперативного равновесия по сравнению с теми, кто не сотрудничает. Поскольку природа, возможно, предлагает больше возможностей для разнообразного сотрудничества, а не строгую дихотомию сотрудничества или предательства, дилемма постоянного заключенного может помочь объяснить, почему реальные примеры сотрудничества по принципу «око за око» крайне редки. даже несмотря на то, что в теоретических моделях соотношение «око за око» кажется надежным.

Примеры из реальной жизни

Многие примеры человеческого взаимодействия и естественных процессов имеют матрицы выигрышей, подобные дилемме заключенного. Поэтому он представляет интерес для социальных наук , таких как экономика , политика и социология , а также для биологических наук, таких как этология и эволюционная биология . Многие естественные процессы были абстрагированы в модели, в которых живые существа участвуют в бесконечных играх с дилеммой заключенного.

Экологические исследования

В экологических исследованиях дилемма очевидна в таких кризисах, как глобальное изменение климата . Утверждается, что все страны выиграют от стабильного климата, но каждая отдельная страна часто не решается ограничить выбросы CO ₂ . Непосредственная выгода для любой страны от сохранения текущего поведения воспринимается как более значительная, чем предполагаемая конечная выгода для этой страны в случае изменения поведения всех стран, что объясняет тупиковую ситуацию с изменением климата в 2007 году.

Важным различием между политикой изменения климата и дилеммой заключенного является неопределенность; степень и скорость, с которой загрязнение может изменить климат, неизвестны. Таким образом, дилемма, с которой сталкиваются правительства, отличается от дилеммы заключенного тем, что выгоды от сотрудничества неизвестны. Эта разница предполагает, что государства будут сотрудничать гораздо меньше, чем в реальной повторяющейся дилемме заключённого, так что вероятность избежать возможной климатической катастрофы намного меньше, чем предполагает теоретико-игровой анализ ситуации с использованием реальной повторяющейся дилеммы заключённого.

Томас Осанг и Арундати Нэнди дают теоретическое объяснение с доказательствами беспроигрышной ситуации, основанной на регулировании, в соответствии с гипотезой Майкла Портера , в которой государственное регулирование конкурирующих фирм является существенным.

Животные

Кооперативное поведение многих животных можно рассматривать как пример повторяющейся дилеммы заключенного. Часто животные вступают в долгосрочные партнерские отношения; например, гуппи совместно осматривают хищников группами и, как полагают, наказывают инспекторов, отказывающихся сотрудничать.

Летучие мыши-вампиры — социальные животные, которые участвуют во взаимном обмене пищей. Применение выигрышей от дилеммы заключенного может помочь объяснить такое поведение.

Психология

В зависимости исследованиях экономике и поведенческой Джордж Эйнсли указывает, что зависимость можно рассматривать как межвременную дилемму заключенного между настоящим и будущим «я» наркомана. В данном случае «дезертирство» означает рецидив, а отсутствие рецидива ни сегодня, ни в будущем, безусловно, является лучшим результатом. Случай, когда человек воздерживается сегодня, но в будущем у него случается рецидив, является наихудшим исходом: в каком-то смысле дисциплина и самопожертвование, необходимые для воздержания сегодня, были «растрачены впустую», потому что будущий рецидив означает, что наркоман возвращается к тому, с чего начал, и придется начинать заново. Рецидив сегодня и завтра — это немного «лучший» результат, потому что, хотя наркоман все еще является зависимым, он не приложил усилий, чтобы попытаться остановиться. В последнем случае, когда сегодня человек участвует в аддиктивном поведении, а завтра воздерживается от него, возникает проблема: (как и в других дилеммах заключенного) существует очевидная польза от побега «сегодня», но завтра он столкнется с той же дилеммой заключенного, и Тогда будет присутствовать та же очевидная выгода, что в конечном итоге приведет к бесконечной череде дезертирств.

В «Науке доверия » Джон Готтман определяет хорошие отношения как отношения, в которых партнеры знают, что им не следует вступать в поведение взаимного предательства или, по крайней мере, не застревать в этом цикле. В когнитивной нейробиологии быстрая передача сигналов мозгом, связанная с обработкой различных раундов, может указывать на выбор в следующем раунде. Результаты взаимного сотрудничества влекут за собой изменения в активности мозга, предсказывающие, насколько быстро человек будет сотрудничать в натуральной форме при следующей возможности; эта деятельность может быть связана с основными гомеостатическими и мотивационными процессами, что, возможно, увеличивает вероятность срыва взаимного сотрудничества.

Экономика

Дилемму заключенного назвали кишечной палочкой социальной психологии, и она широко использовалась для исследования различных тем, таких как олигополистическая конкуренция и коллективные действия для производства коллективного блага.

Рекламу иногда называют реальным примером дилеммы заключенного. Когда реклама сигарет была легальной в Соединенных Штатах, конкурирующим производителям сигарет приходилось решать, сколько денег тратить на рекламу. Эффективность рекламы фирмы А частично определялась рекламой, проводимой фирмой Б. Аналогичным образом, на прибыль, полученную от рекламы фирмы Б, влияет реклама, проводимая фирмой А. Если и фирма А, и фирма Б решили размещать рекламу в течение определенного периода времени, период, то реклама каждой фирмы сводит на нет рекламу другой, поступления остаются постоянными, а расходы увеличиваются за счет затрат на рекламу. Обе фирмы выиграют от сокращения рекламы. Однако если фирма Б решит не заниматься рекламой, фирма А может получить от рекламы большую выгоду. Тем не менее оптимальный объем рекламы одной фирмы зависит от того, какой объем рекламы берет на себя другая. Поскольку лучшая стратегия зависит от того, что выберет другая фирма, доминирующей стратегии не существует, что несколько отличает ее от дилеммы заключенного. Однако результат аналогичен: обеим фирмам было бы лучше, если бы они рекламировали меньше, чем в равновесии.

Иногда кооперативное поведение действительно возникает в деловых ситуациях. Например, производители сигарет поддержали принятие законов, запрещающих рекламу сигарет, понимая, что это позволит снизить затраты и увеличить прибыль во всей отрасли.

Без соглашений, имеющих обязательную силу, члены картеля также оказываются перед (многопользовательской) дилеммой заключенного. «Сотрудничество» обычно означает согласие на минимальную цену , а «отказ» означает продажу ниже этого минимального уровня, мгновенно отбирая бизнес у других членов картеля. Антимонопольные органы хотят, чтобы потенциальные члены картеля перешли на сторону друг друга, обеспечивая потребителям максимально низкие цены.

Спорт

Допинг в спорте приводится в качестве примера дилеммы заключенного. Два соревнующихся спортсмена имеют возможность использовать запрещенный и/или опасный препарат для повышения своих результатов. Если ни один из спортсменов не принимает препарат, то ни один из спортсменов не получает преимущества. Если это сделает только один спортсмен, то этот спортсмен получает значительное преимущество перед конкурентом, уменьшенное за счет юридических и/или медицинских рисков, связанных с приемом препарата. Но если оба спортсмена принимают препарат, польза сводится на нет, и остается только опасность, ставя их обоих в худшее положение, чем если бы ни один из них не принимал допинг.

Международная политика

В теории международных отношений дилемма заключенного часто используется, чтобы продемонстрировать, почему сотрудничество терпит неудачу в ситуациях, когда сотрудничество между государствами коллективно оптимально, но индивидуально неоптимально. Классическим примером является дилемма безопасности , когда повышение безопасности одного государства (например, увеличение его военной мощи) приводит к тому, что другие государства опасаются за свою собственную безопасность из-за страха перед наступательными действиями. Следовательно, меры по повышению безопасности могут привести к напряженности, эскалации или конфликту с одной или несколькими другими сторонами, приводя к результату, которого на самом деле не желает ни одна из сторон. Дилемма безопасности становится особенно острой в ситуациях, когда трудно отличить наступательное оружие от оборонительного, а нападение имеет преимущество в любом конфликте перед обороной.

Дилемма заключенного часто использовалась реалистическими теоретиками международных отношений, чтобы продемонстрировать, почему всем государствам (независимо от их внутренней политики или исповедуемой идеологии) в условиях международной анархии будет трудно сотрудничать друг с другом, даже если все выигрывают от такого сотрудничества.

Критики реализма утверждают, что итерация и расширение тени будущего являются решением дилеммы заключенного. Когда актеры разыгрывают дилемму заключенного один раз, у них появляются стимулы к отказу, но когда они рассчитывают повторить ее неоднократно, у них появляется больше стимулов к сотрудничеству.

Многопользовательские дилеммы

Многие дилеммы реальной жизни требуют участия нескольких игроков. Несмотря на метафоричность, Хардина Гаррета трагедию общин можно рассматривать как пример многопользовательского обобщения дилеммы заключенного: каждый житель деревни делает выбор в пользу личной выгоды или ограничения. Коллективной наградой за единодушное или частое отступничество являются очень низкие выплаты и разрушение общественного достояния.

Общественное достояние не всегда эксплуатируется: Уильям Паундстоун в книге о дилемме заключенного описывает ситуацию в Новой Зеландии, когда ящики с газетами остаются незапертыми. Люди могут взять бумагу, не заплатив (перебежав), но очень немногие это делают, чувствуя, что если они не заплатят, то и другие не заплатят, что разрушает систему. Последующее исследование Элинор Остром , лауреата Нобелевской премии по экономике 2009 года , выдвинуло гипотезу, что трагедия общего пользования слишком упрощена, а на негативный результат влияют внешние влияния. Не усложняя давление, группы общаются и управляют общими ресурсами между собой ради взаимной выгоды, обеспечивая соблюдение социальных норм для сохранения ресурсов и достижения максимального блага для группы, что является примером достижения наилучшего результата для дилеммы заключенного.

Академические настройки

Дилемма заключенного использовалась в различных академических кругах, чтобы проиллюстрировать сложности сотрудничества и конкуренции. Ярким примером является классный эксперимент, проведенный профессором социологии Дэном Чемблиссом в Гамильтон-колледже в 1980-х годах. Начиная с 1981 года Чамблисс предлагал, что, если ни один студент не сдаст выпускной экзамен, все получат пятерку, но если хотя бы один студент сдаст его, те, кто не сдаст, получат ноль. В 1988 году Джон Вернер , студент первого курса, успешно организовал своих одноклассников бойкотировать экзамен, продемонстрировав практическое применение теории игр и концепции дилеммы заключенного.

Почти 25 лет спустя аналогичный инцидент произошел в Университете Джонса Хопкинса в 2013 году. Политика профессора Питера Фрелиха оценивала выпускные экзамены по наивысшему баллу, а это означает, что, если бы все получили одинаковый балл, все они получили бы пятерку. Студенты в классах Фрелиха организовал бойкот выпускного экзамена, гарантируя, что его никто не сдаст. В результате каждый студент получил пятерку, успешно решив дилемму заключенного взаимооптимальным способом без итераций. Эти примеры показывают, как дилемма заключенного может быть использована для изучения совместного поведения и принятия стратегических решений в образовательном контексте.

Похожие игры

Обмен закрытых сумок

Дилемма заключенного как обмен портфеля

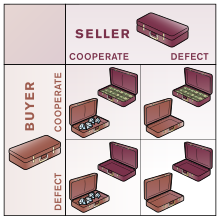
Дуглас Хофштадтер предположил, что людям часто легче понять такие проблемы, как дилемма заключенного, когда они проиллюстрированы в форме простой игры или компромисса. Одним из нескольких примеров, которые он использовал, был «закрытый обмен сумками»:

Два человека встречаются и обмениваются закрытыми сумками, понимая, что в одном из них деньги, а в другом покупка. Любой игрок может выполнить сделку, положив в свою сумку то, о чем он договорился, или он или она может отказаться, отдав пустую сумку.

Друг или враг?

Друг или враг? — игровое шоу, которое транслировалось с 2002 по 2003 год на Game Show Network в США. В игровом шоу соревнуются три пары людей. Когда пара выбывает, они играют в игру, похожую на дилемму заключенного, чтобы определить, как будет разделен выигрыш. Если они оба сотрудничают (Друг), они делят выигрыш 50 на 50. Если один сотрудничает, а другой отказывается (Враг), перебежчик получает весь выигрыш, а сотрудничающий не получает ничего. Если оба откажутся, оба уйдут ни с чем. Обратите внимание, что матрица вознаграждений немного отличается от стандартной, приведенной выше, поскольку награды для случаев «оба дезертируют» и «сотрудничать, пока противник дезертирует» идентичны. Это делает случай «оба дефекта» слабым равновесием по сравнению со строгим равновесием в стандартной дилемме заключенного. Если участник знает, что его оппонент проголосует за «Противника», то его собственный выбор не повлияет на его собственный выигрыш. В определенном смысле в «Друге или враге» есть модель вознаграждения между дилеммой заключенного и дилеммой заключенного. игра «Цыпленок» .

Это матрица вознаграждений:

Пара 2 Пара 1	"Друг" (сотрудничать)	«Враг» (дефект)
"Друг" (сотрудничать)	1 1	2 0
«Враг» (дефект)	0 2	0 0

Эта матрица выигрышей также использовалась в британских телевизионных программах «Доверься мне» , «Shafted» , «Ограбление в банке» и «Золотые шары» , а также в американских игровых шоу « Take It All» , а также для пары-победителя в реалити-шоу «Холостяк Pad» и «Остров любви». . Данные игры из серии Golden Balls были проанализированы командой экономистов, которые обнаружили, что сотрудничество было «на удивление высоким» для сумм денег, которые могли бы показаться значимыми в реальном мире, но были сравнительно низкими в контексте игры.

Итерированный сугроб

Исследователи из Лозаннского и Эдинбургского университетов предположили, что «Итерированная игра в сугроб» может более точно отражать реальные социальные ситуации, хотя на самом деле эта модель представляет собой игру с курицей . В этой модели риск эксплуатации из-за дезертирства ниже, и люди всегда выигрывают, делая совместный выбор. В игре «Сугроб» представлены два водителя, застрявшие по разные стороны сугроба , каждому из которых предоставляется возможность расчищать снег, чтобы расчистить путь, или оставаться в своей машине. Наивысшая выгода игрока получается в том случае, если он позволяет противнику самостоятельно расчищать весь снег, но противник все равно номинально вознаграждается за свою работу.

Это может лучше отражать реальные сценарии: исследователи приводят пример двух ученых, сотрудничающих над отчетом, оба из которых выиграют, если другой будет работать усерднее. «Но когда ваш коллега не выполняет никакой работы, вам, вероятно, лучше сделать всю работу самому. В конечном итоге вы все равно получите завершенный проект».

Пример выплат по сугробу (A, B) Б А Сотрудничает Дефекты Сотрудничает 500, 500 200, 800 Дефекты 800, 200 0, 0

Пример выплат в случае дилеммы заключенного (A, B) Б А Сотрудничает Дефекты Сотрудничает 500, 500 −200, 1200 Дефекты 1200, −200 0, 0

Координационные игры

Основная статья: Координационная игра

В координационных играх игроки должны координировать свои стратегии для достижения хорошего результата. Пример — две машины, внезапно встретившиеся в метель; каждый должен выбрать, повернуть ли ему влево или вправо. Если оба свернут налево или оба направо, автомобили не столкнутся. Местные правила левостороннего и правостороннего движения помогают скоординировать их действия.

К симметричным координационным играм относятся «Охота на оленя» , «Бах» или «Стравинский» .

Асимметричные дилеммы заключенного

Более общий набор игр асимметричен. Как и в дилемме заключенного, лучшим результатом является сотрудничество, и существуют мотивы для дезертирства. Однако, в отличие от симметричной дилеммы заключенного, один игрок может больше потерять и/или больше получить, чем другой. Некоторые такие игры были описаны как дилемма заключенного, в которой у одного заключенного есть алиби , отсюда и термин «игра-алиби».

В экспериментах игроки, получающие неравные выигрыши в повторяющихся играх, могут стремиться максимизировать прибыль, но только при условии, что оба игрока получают равные выигрыши; это может привести к устойчивой равновесной стратегии, в которой игрок, находящийся в невыгодном положении, отказывается от каждой игры X, в то время как другой игрок всегда сотрудничает. Такое поведение может зависеть от социальных норм эксперимента, касающихся справедливости.

Программное обеспечение

Было создано несколько пакетов программного обеспечения для проведения симуляций и турниров по дилемме заключенного, исходный код некоторых из которых доступен:

• Исходный код второго турнира, проводимого Робертом Аксельродом (написанный Аксельродом и многими другими участниками на Фортране ), доступен в Интернете.
• Prison — библиотека, написанная на Java , последнее обновление в 1998 году.
• Аксельрод-Питон , написанный на Python
• Evoplex — программа быстрого агентного моделирования, выпущенная в 2018 году Маркосом Кардино.

В художественной литературе

Ханну Раджаниеми поместил первую сцену своей трилогии «Квантовый вор» в «тюрьму дилемм». Основная тема сериала была описана как «неадекватность бинарной вселенной», а главным антагонистом является персонаж по имени Всеперебежчик. Первая книга серии была опубликована в 2010 году, а два продолжения, «Фрактальный принц» и «Причинный ангел» , были опубликованы в 2012 и 2014 годах соответственно.

Игра, созданная по образцу повторяющейся дилеммы заключенного, занимает центральное место в видеоигре 2012 года Zero Escape: Virtue's Last Reward и второстепенную роль в ее продолжении 2016 года Zero Escape: Zero Time Dilemma .

В «Таинственное общество Бенедикта и дилемма узника книге Трентона Ли Стюарта » главные герои начинают с того, что играют в версию игры и вообще сбегают из «тюрьмы». Позже они становятся настоящими пленниками и снова сбегают.

В подарке «Зона приключений : Баланс во время игры Страдания » персонажи игроков дважды сталкиваются с дилеммой заключенного во время их пребывания в владениях двух личей: один раз они сотрудничают, а другой - дезертируют.

В восьмом романе автора Джеймса С.А. Кори Тиамат «Гнев Тиамата » Уинстон Дуарте объясняет дилемму заключенного своей 14-летней дочери Терезе, чтобы научить ее стратегическому мышлению.

В фильме 2008 года «Темный рыцарь» есть сцена, в общих чертах основанная на проблеме, в которой Джокер монтирует два парома, один с заключенными, а другой с гражданскими лицами, вооружая обе группы средствами для взрыва бомбы на паромах друг друга, угрожая взорвать их. оба, если они колеблются.

В моральной философии

Дилемма заключенного обычно используется в качестве инструмента мышления в философии морали как иллюстрация потенциального противоречия между пользой отдельного человека и пользой общества.

И однократная, и повторяющаяся дилемма заключенного имеют применение в моральной философии. Действительно, многие моральные ситуации, такие как геноцид , нелегко повторить более одного раза. Более того, во многих ситуациях исходы предыдущих раундов игрокам неизвестны, поскольку они не обязательно совпадают (например, взаимодействие с попрошайкой на улице).

Философ Давид Готье использует дилемму заключенного, чтобы показать, как мораль и рациональность могут конфликтовать.

Некоторые теоретики игр раскритиковали использование дилеммы заключенного как инструмента мышления в моральной философии. Кеннет Бинмор утверждал, что дилемма заключенного неточно описывает игру, в которую играет человечество, которая, по его мнению, ближе к координационной игре . Брайан Скирмс разделяет эту точку зрения.

Стивен Кун предполагает, что эти взгляды можно согласовать, если учесть, что моральное поведение может изменить матрицу выигрышей игры, превратив ее из дилеммы заключенного в другие игры.

Дилемма чистого и нечистого заключенного

Дилемма заключенного считается «нечистой», если смешанная стратегия может дать лучшие ожидаемые выигрыши, чем чистая стратегия. Это создает интересную возможность того, что моральное действие с утилитарной точки зрения (т. е. направленное на максимизацию пользы от действия) может потребовать рандомизации стратегии, например, сотрудничество с вероятностью 80% и отступление с вероятностью 20%.

См. также

• Парадокс Абилина
• игра многоножка
• Внешние эффекты
• Народная теорема (теория игр)
• Проблема безбилетника
• Игра-обмен подарками
• Гоббсова ловушка
• Дилемма невиновного заключенного
• Игра Лжец
• Метаигра
• Необязательная дилемма заключенного
• Дилемма заключенного и сотрудничество
• Игра «Общественные блага»
• Взаимный альтруизм
• Погоня за рентой
• Социальные предпочтения
• Сверхрациональность
• Теория доверия Свифта
• Трагедия общего пользования
• Дилемма путешественника
• Дилемма недобросовестного посетителя

Ссылки

Библиография

• Паундстоун, Уильям (1993). Дилемма заключенного (1-е изд. Anchor Books). Нью-Йорк: Якорь. ISBN  0-385-41580-Х .

Дальнейшее чтение

• Амадае, С. (2016). «Дилемма узника» , Узники разума . Издательство Кембриджского университета , Нью-Йорк, стр. 24–61.
• Ауманн, Роберт (1959). «Приемлемые баллы в общих кооперативных играх для n человек». В Люсе, РД; Такер, AW (ред.). Вклад в теорию 23 игр IV . Анналы изучения математики. Том. 40. Принстон, штат Нью-Джерси: Издательство Принстонского университета. стр. 287–324. МР   0104521 .
• Аксельрод, Роберт (2006). Эволюция сотрудничества (пересмотренная ред.). Основные книги. ISBN  0-465-00564-0 .
• Биккьери, Кристина (1993). Рациональность и координация. Издательство Кембриджского университета .
• Шахматы, Дэвид М. (декабрь 1988 г.). «Моделирование эволюции поведения: повторяющаяся проблема дилеммы заключенных» (PDF) . Сложные системы . 2 (6): 663–70. Архивировано (PDF) из оригинала 30 мая 2015 г.
• Коллинз, Рори В. (март 2022 г.). «Парадокс дилеммы заключенного: рациональность, мораль и взаимность» . Подумайте: Философия для всех . 21 (61): 45–55. дои : 10.1017/S1477175621000464 .
• Дрешер, М. (1961). Математика стратегических игр: теория и приложения Прентис-Холл , Энглвуд Клиффс, Нью-Джерси.
• Грейф, А. (2006). Институты и путь к современной экономике: уроки средневековой торговли. Издательство Кембриджского университета, Кембридж , Великобритания.
• Копельман, Ширли (февраль 2020 г.). «Око за око и не только: легендарное произведение Анатоля Рапопорта» . Исследования в области переговоров и управления конфликтами . 13 (1): 60–84. дои : 10.1111/ncmr.12172 . hdl : 2027.42/153763 .
• Рапопорт, Анатол и Альберт М. Чамма (1965). Дилемма заключенного . Издательство Мичиганского университета .
• Шнайдер, Марк; Шилдс, Тимоти В. (июнь 2022 г.). «Мотивы сотрудничества в дилемме одноразового заключенного» . Журнал поведенческих финансов . 23 (4): 438–456. дои : 10.1080/15427560.2022.2081974 . S2CID   249903572 .

Внешние ссылки

• СМИ, связанные с дилеммой заключенного, на Викискладе?
• Дилемма Шалашника Дилемма узника в орнитологии - математический мультфильм Ларри Гоника.
• Диксит, Авинаш ; Нейлебафф, Барри (2008). «Дилемма заключенного» . В Дэвиде Р. Хендерсоне (ред.). Краткая экономическая энциклопедия (2-е изд.). Индианаполис: Библиотека экономики и свободы . ISBN  978-0865976658 . OCLC   237794267 .
• Докинз: Хорошие парни финишируют первыми
• Аксельрода «Дилемма заключённого» Python Библиотека
• Сыграйте в «Дилемму заключенного» на oTree (нет данных 11-5-17)
• Ники Кейса «Эволюция доверия» , пример игры с пожертвованиями
• Онлайн-игра «Итерированная дилемма заключенного» Уэйна Дэвиса
• Что говорит «Дилемма узника» о жизни, Вселенной и остальном всем