Каталонский номер

В комбинаторной математике каталонские числа представляют собой последовательность натуральных чисел , которые встречаются в различных задачах счета , часто с участием рекурсивно определенных объектов. Они названы в честь французско-бельгийского математика Эжена Шарля Каталана , хотя ранее они были открыты в 1730-х годах Минггату .
n -е число Каталана может быть выражено непосредственно через центральные биномиальные коэффициенты :
Первые каталонские числа для n = 0, 1, 2, 3,... :
Характеристики
[ редактировать ]Альтернативное выражение для C n :
- для
что эквивалентно приведенному выше выражению, поскольку . Это выражение показывает, что C n — целое число , что не сразу очевидно из первой приведенной формулы. Это выражение составляет основу доказательства правильности формулы .
Другое альтернативное выражение:
что можно непосредственно интерпретировать в терминах леммы о цикле ; см. ниже.
Каталонские числа удовлетворяют рекуррентным соотношениям
и
Асимптотически каталонские числа растут как в том смысле, что частное n -го каталонского числа и выражения справа стремится к 1, когда n приближается к бесконечности.
Это можно доказать, используя асимптотический рост центральных биномиальных коэффициентов , аппроксимацию Стирлинга для или через производящие функции .
Нечетными каталонскими числами C n являются только те, у которых n = 2. к − 1 ; все остальные четные. Единственными простыми каталонскими числами являются C 2 = 2 и C 3 = 5 . [1]
Каталонские числа имеют целочисленное представление [2] [3]
что сразу дает .
Это имеет простую вероятностную интерпретацию. Рассмотрим случайное блуждание по целочисленной строке, начиная с 0. Пусть -1 будет состоянием «ловушки», так что если ходок достигнет -1, он останется там. Ходок может прийти в состояние ловушки за раз 1, 3, 5, 7..., а количество способов, которыми ходячий может прийти в состояние ловушки за раз является . Поскольку одномерное случайное блуждание является повторяющимся, вероятность того, что ходок в конечном итоге достигнет -1, равна .
Приложения в комбинаторике
[ редактировать ]существует множество задач о счете В комбинаторике , решение которых дают числа Каталана. Книга «Перечислительная комбинаторика: Том 2» комбинаториста Ричарда П. Стэнли содержит набор упражнений, которые описывают 66 различных интерпретаций каталонских чисел. Ниже приведены несколько примеров с иллюстрациями случаев C 3 = 5 и C 4 = 14 .

- C n — количество слов Дика . [4] длины 2 н . Слово Дайка — это строка , состоящая из n X и n Y, такая, что ни в одном начальном сегменте строки Y не превышает числа X. Например, ниже приведены слова Дика длиной до 6:
- Переинтерпретируя символ X как открывающую скобку , а Y как закрывающую скобку, C n подсчитывает количество выражений, содержащих n пар скобок, которые правильно сопоставлены:
- C n — это количество различных способов, которыми n + 1 фактор может быть полностью заключен в круглые скобки (или количество способов связать n применений бинарного оператора , как в задаче умножения цепочки матриц ). для n = 3 у нас есть следующие пять различных заключений четырех факторов в скобки: Например,
- Последовательные применения бинарного оператора можно представить в виде полного двоичного дерева , пометив каждый лист a,b,c,d . Отсюда следует, что C n — это количество полных бинарных деревьев с n + 1 листьями или, что то же самое, с n внутренними узлами:


- C n — количество неизоморфных упорядоченных (или плоских) деревьев с n + 1 вершиной. [5] См. кодирование общих деревьев как двоичных деревьев . Например, C n — это количество возможных деревьев синтаксического анализа предложения (при условии двоичного ветвления) при обработке естественного языка.
- C n — количество монотонных путей решетки по краям сетки с n × n квадратными ячейками, не выходящим за пределы диагонали. Монотонный путь — это путь, который начинается в левом нижнем углу, заканчивается в правом верхнем углу и полностью состоит из ребер, направленных вправо или вверх. Подсчет таких путей эквивалентен подсчету слов Дика: X означает «движение вправо», а Y означает «движение вверх».
На следующих диаграммах показан случай n = 4:

Это можно представить, перечислив каталонские элементы по высоте столбца: [6]

- с Выпуклый многоугольник n + 2 сторонами можно разрезать на треугольники , соединяя вершины непересекающимися отрезками линий (разновидность триангуляции многоугольника ). Число образованных треугольников равно n , а количество различных способов, которыми это можно сделать, равно C n . Следующие шестиугольники иллюстрируют случай n = 4:

- C n — количество по стеку сортируемых перестановок {1, ..., n }. Перестановка w называется сортируемой стеком, если S ( w ) = (1, ..., n ), где S ( w ) определяется рекурсивно следующим образом: напишите w = unv, где n — наибольший элемент в w и u , а v — более короткие последовательности, и установите S ( w ) = S ( u ) S ( v ) n , где S — тождество для одноэлементных последовательностей.
- C n — количество перестановок {1, ..., n }, которые избегают шаблона перестановки 123 (или, альтернативно, любого другого шаблона длины 3); то есть количество перестановок без трехчленной возрастающей подпоследовательности. Для n = 3 это 132, 213, 231, 312 и 321. Для n = 4 это 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312. и 4321.
- C n — количество непересекающихся разбиений множества {1, ..., n }. Тем более , C n никогда не превышает n -го числа Белла . C n — это также количество непересекающихся разделов набора {1, ..., 2 n }, в которых каждый блок имеет размер 2.
- C n — количество способов замостить ступеньку высоты n прямоугольниками n . Разрезание антидиагонали и просмотр только краев дает полные бинарные деревья. Следующий рисунок иллюстрирует случай n = 4:

- C n — это количество способов сформировать «горный хребет» с n движениями вверх и n движениями вниз, которые все остаются выше горизонтальной линии. Интерпретация горного хребта заключается в том, что горы никогда не уйдут за горизонт.
| * | 1 путь | |
| /\ | 1 путь | |
| /\ /\/\, / \ |
2 способа | |
| /\ /\ /\ /\/\ / \ /\/\/\, /\/ \, / \/\, / \, / \ |
5 способов |
- C n — количество стандартных таблиц Юнга , диаграмма которых представляет собой прямоугольник размером 2× n . Другими словами, это количество способов, которыми числа 1, 2, ..., 2 n можно расположить в прямоугольнике размером 2 на n так, чтобы каждая строка и каждый столбец увеличивались. Таким образом, формула может быть выведена как частный случай формулы длины крючка .
123 124 125 134 135 456 356 346 256 246
- — количество последовательностей длины n , начинающихся с , и может увеличиться либо или , или уменьшиться на любое число (хотя бы до ). Для это . По пути Дика начните счетчик с 0 . X увеличивает счетчик на 1 , а Y уменьшает его на 1 . Запишите значения только в точках X. По сравнению с аналогичным представлением чисел Белла , только отсутствует.
Доказательство формулы
[ редактировать ]Есть несколько способов объяснить, почему формула
решает комбинаторные задачи, перечисленные выше. Первое доказательство ниже использует производящую функцию . Остальные доказательства являются примерами биективных доказательств ; они включают в себя буквально подсчет совокупности каких-то объектов, чтобы прийти к правильной формуле.
Первое доказательство
[ редактировать ]Прежде всего заметим, что все перечисленные выше комбинаторные задачи удовлетворяют задаче Сегнера. [7] рекуррентное отношение
Например, каждое слово Дика w длины ≥ 2 можно единственным образом записать в виде
- ш = Х ш 1 Y ш 2
с (возможно, пустыми) словами Дика w 1 и w 2 .
каталонских Производящая функция чисел определяется формулой
Приведенное выше рекуррентное соотношение затем можно обобщить в виде производящей функции соотношением
другими словами, это уравнение следует из рекуррентного соотношения путем разложения обеих частей в степенные ряды . С одной стороны, рекуррентное соотношение однозначно определяет числа Каталана; с другой стороны, интерпретируя xc 2 − c + 1 = 0 как квадратное уравнение для c , и используя квадратичную формулу , соотношение производящей функции можно алгебраически решить, чтобы получить две возможности решения.
- или .
Из двух возможностей следует выбрать вторую, поскольку только вторая дает
- .
Член квадратного корня можно разложить в степенной ряд, используя биномиальный ряд.
Таким образом,
Второе доказательство
[ редактировать ]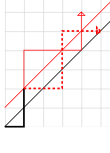
Мы подсчитываем количество путей, которые начинаются и заканчиваются на диагонали сетки n × n . Все такие пути имеют n ступеней вправо и n ступеней вверх. Поскольку мы можем выбирать, какой из 2n шагов верный или правильный, всего существует монотонные пути этого типа. Плохой путь пересекает главную диагональ и касается следующей , более высокой диагонали (красный на рисунке).
Часть пути после более высокой диагонали затем переворачивается вокруг этой диагонали, как показано красной пунктирной линией. Это поменяет местами все правильные шаги на шаги вверх и наоборот. На участке пути, который не отражен, имеется на один шаг вверх больше, чем шагов вправо, поэтому оставшийся участок плохого пути имеет на один шаг вправо больше, чем шаги вверх. Когда эта часть пути будет отражена, она будет иметь на один шаг вверх больше, чем шаги вправо.
Поскольку шагов по-прежнему 2n , теперь есть n + 1 шагов вверх и n − 1 шагов вправо. Таким образом, вместо того, чтобы достичь ( n , n ), все плохие пути после отражения заканчиваются в ( n − 1, n + 1). Поскольку каждый монотонный путь в сетке ( n − 1) × ( n + 1) соответствует более высокой диагонали, и поскольку процесс отражения обратим, отражение, следовательно, представляет собой биекцию между плохими путями в исходной сетке и монотонными путями в новой. сетка.
Таким образом, количество плохих путей равно:
а количество каталонских путей (т.е. хороших путей) получается путем исключения количества плохих путей из общего количества монотонных путей исходной сетки,
С точки зрения слов Дика, мы начинаем с (не-Дейка) последовательности из n X и n Y и меняем местами все X и Y после первого Y, который нарушает условие Дика. После этого Y заметьте, что Y ровно на один больше, чем X.
Третье доказательство
[ редактировать ]Это биективное доказательство дает естественное объяснение слагаемому n + 1, появляющемуся в знаменателе формулы для C n . Обобщенную версию этого доказательства можно найти в статье Рукавицкой Йозефа (2011). [8]

Учитывая монотонный путь, превышение пути определяется как количество вертикальных ребер над диагональю. Например, на рисунке 2 ребра над диагональю отмечены красным, поэтому превышение этого пути равно 5.
Учитывая монотонный путь, превышение которого не равно нулю, мы применяем следующий алгоритм для построения нового пути, превышение которого на 1 меньше того, с которого мы начали.
- Начиная с нижнего левого угла, следуйте по пути, пока он не пройдет выше диагонали.
- Продолжайте идти по пути, пока он снова не коснется диагонали. Обозначим через X первое достигнутое такое ребро.
- Поменяйте местами часть пути, происходящую до X на часть, происходящую после X. ,
На рисунке 3 черная точка указывает точку, где путь впервые пересекает диагональ. Черный край — это X , и мы помещаем последнюю точку решетки красной части в верхний правый угол, а первую точку решетки зеленой части в нижний левый угол и размещаем X соответственно, чтобы создать новый путь. , показанный на второй диаграмме.
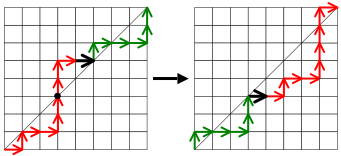
Превышение снизилось с 3 до 2 . Фактически, алгоритм заставляет превышение уменьшаться на 1 для любого пути, который мы ему подаем, потому что первый вертикальный шаг, начинающийся по диагонали (в точке, отмеченной черной точкой), является единственным вертикальным ребром, который не находится над диагональ ниже нее, когда мы применяем алгоритм - все остальные вертикальные ребра остаются на той же стороне диагонали.

Можно видеть, что этот процесс обратим : для любого пути P , превышение которого меньше n , существует ровно один путь, который дает P , когда к нему применяется алгоритм. Действительно, (черное) ребро X , которое изначально было первым горизонтальным шагом, заканчивающимся на диагонали, стало последним горизонтальным шагом, начинающимся на диагонали. Альтернативно, измените исходный алгоритм, чтобы найти первое ребро, проходящее ниже диагонали.
Это означает, что количество путей превышения n равно количеству путей превышения n - 1, которое равно количеству путей превышения n - 2, и так далее, вплоть до нуля. Другими словами, мы разделили набор всех монотонных путей на n + 1 класс одинакового размера, соответствующий возможным превышениям между 0 и n . Поскольку существуют монотонных путей, получаем искомую формулу
Рисунок 4 иллюстрирует ситуацию для n = 3. Каждый из 20 возможных монотонных путей появляется где-то в таблице. В первом столбце показаны все пути превышения три, которые полностью лежат выше диагонали. Столбцы справа показывают результат последовательных применений алгоритма, при этом превышение уменьшается на одну единицу за раз. Строок пять, то есть C 3 = 5, а в последнем столбце отображаются все пути не выше диагонали.
Используя слова Дика, начните с последовательности из . Позволять быть первым X , который приводит начальную подпоследовательность к равенству, и настройте последовательность как . Новая последовательность .
Четвертое доказательство
[ редактировать ]Это доказательство использует определение триангуляции каталонских чисел, чтобы установить связь между C n и C n +1 .
Дан многоугольник P с n + 2 сторонами и триангуляцией. Отметьте одну из его сторон как основание, а также сориентируйте одно из 2 n + 1 его ребер. существует (4 n + 2) C n Таких отмеченных триангуляций для данной базы .
Дан многоугольник Q с n + 3 сторонами и (разной) триангуляцией. Снова отметьте одну из его сторон как основу. Отметьте одну из сторон, кроме базовой стороны (а не внутреннего края треугольника). существует ( n + 2) C n + 1 Таких отмеченных триангуляций для данной базы .
Между этими двумя отмеченными триангуляциями существует простая биекция: мы можем либо свернуть треугольник в Q , сторона которого отмечена (двумя способами, и вычесть те два, которые не могут свернуть основание), либо, наоборот, расширить ориентированное ребро в P. к треугольнику и отметьте его новую сторону.
Таким образом
- .
Писать
Потому что
у нас есть
Применение рекурсии с дает результат.
Пятое доказательство
[ редактировать ]Это доказательство основано на словами Дейка , поэтому интерпретации каталонских чисел — количество способов правильно сопоставить n пар скобок. Мы обозначаем правильную строку (возможно, пустую) через c и обратную ей через c' . Поскольку любой c однозначно разлагается на , суммируя по возможным длинам сразу дает рекурсивное определение
- .
Пусть b — сбалансированная строка длины 2n , т. е. b содержит равное количество и , так . Сбалансированную строку также можно однозначно разложить на любую или , так
Любая неправильная (не каталанская) сбалансированная строка начинается с , а оставшаяся строка имеет еще один чем , так
Также из определений имеем:
Следовательно, поскольку это верно для всех n ,
Шестое доказательство
[ редактировать ]Это доказательство основано на словами Дейка интерпретации каталонских чисел и использует лемму о цикле Дворецкого и Моцкина. [9] [10]
Последовательность X и Y назовем доминирующей , если при чтении слева направо число X всегда строго больше числа Y. Лемма о цикле [11] утверждает, что любая последовательность Х и Да, где , имеет именно преобладают круговые сдвиги . Чтобы убедиться в этом, расположите данную последовательность X и Y в круге. Многократное удаление пар XY оставляет ровно Х. Каждый из этих крестиков был началом доминирующего кругового сдвига, прежде чем что-либо было удалено. Например, рассмотрим . Эта последовательность является доминирующей, но ни одного ее кругового смещения , , и являются.
Строка – это слово Дайка, состоящее из Х и Y является тогда и только тогда, когда добавление X к слову Дика дает доминирующую последовательность с Х и Y, поэтому мы можем посчитать первое, посчитав второе. В частности, когда , существует ровно один доминирующий круговой сдвиг. Есть последовательности с ровно Х и Да. Для каждого из них только один из преобладают круговые сдвиги. Поэтому существуют отдельные последовательности Х и Доминирующие буквы Y, каждая из которых соответствует ровно одному слову Дейка.
Матрица Ханкеля
[ редактировать ]Матрица размера n × n, Ганкеля элементом ( i , j ) которого является каталанское число C i + j −2, имеет определитель 1, независимо от значения n . Например, для n = 4 имеем
Более того, если индексация «сдвинута» так, что запись ( i , j ) заполнена каталонским числом C i + j −1, тогда определитель по-прежнему равен 1, независимо от значения n . Например, для n = 4 имеем
В совокупности эти два условия однозначно определяют каталонские числа.
Еще одна особенность, уникальная для матрицы Каталана – Ханкеля, заключается в том, что подматрица размера n × n, начинающаяся с 2, имеет определитель n + 1.
и так далее.
История
[ редактировать ]
Каталонская последовательность была описана в XVIII веке Леонардом Эйлером , которого интересовало количество различных способов деления многоугольника на треугольники. Последовательность названа в честь Эжена Шарля Каталана , который обнаружил связь с выражениями в скобках во время исследования загадки Ханойских башен . Трюк подсчета отражений (второе доказательство) для слов Дейка был найден Дезире Андре в 1887 году.
Название «каталонские числа» произошло от Джона Риордана . [12]
В 1988 году выяснилось, что каталонская последовательность чисел использовалась в Китае монгольским математиком Минганту к 1730 году. [13] [14] Именно тогда он начал писать свою книгу « Гэ Юань Ми Лу Цзе Фа» («Быстрый метод получения точного отношения деления круга») , которую завершил его ученик Чэнь Цзисинь в 1774 году, но опубликовал шестьдесят лет спустя. Питер Дж. Ларкомб (1999) обрисовал некоторые особенности творчества Минганту, в том числе стимул Пьера Жарту, который привез в Китай три бесконечные серии в начале 1700-х годов.
Например, Мин использовал каталонскую последовательность для выражения разложения ряда и с точки зрения .
Обобщения
[ редактировать ]Каталонские числа можно интерпретировать как частный случай теоремы Бертрана о голосовании . Конкретно, — это количество способов, которыми кандидат A с n+1 голосами может опередить кандидата B с n голосами.
Двухпараметрическая последовательность неотрицательных целых чисел является обобщением каталонских чисел. это так называемые суперкаталонские числа , По словам Иры Гессель . Их не следует путать с числами Шредера – Гиппарха , которые иногда также называют суперкаталонскими числами.
Для , это всего в два раза больше обычных каталонских цифр, и для , числа имеют простое комбинаторное описание. Однако другие комбинаторные описания известны только [15] для и , [16] и найти общую комбинаторную интерпретацию — открытая проблема.
Сергей Фомин и Натан Ридинг дали обобщенное число Каталана, связанное с любой конечной кристаллографической группой Кокстера , а именно количество полностью коммутативных элементов группы; с точки зрения связанной корневой системы это количество антицепей (или идеалов порядка) в частично упорядоченном множестве положительных корней. Классический каталонский номер соответствует корневой системе типа . Классическое рекуррентное соотношение обобщает: число Каталана диаграммы Кокстера равно сумме чисел Каталана всех ее максимальных собственных поддиаграмм. [17]
Числа Каталана являются решением проблемы моментов Хаусдорфа . [18]
Каталонская k -кратная свертка
[ редактировать ]Каталонская k -кратная свертка, где k=m , равна: [19]
См. также
[ редактировать ]- Ассоциэдр
- Теорема Бертрана о голосовании
- Биномиальное преобразование
- Каталонский треугольник
- Каталонское число – Мерсенна
- Число Деланной
- Фусс – каталонский номер
- Список факториальных и биномиальных тем
- числа Лобба
- число Моцкина
- Число Нараяны
- Полиномы Нараяны
- число Шредера
- Число Шредера – Гиппарха
- Полузаказ
- Тамари в латексе
- Число Уэддерберна – Этерингтона
- Закон полукруга Вигнера
Примечания
[ редактировать ]- ^ Коши, Томас; Салмасси, Мохаммед (2006). «Четность и простота каталонских чисел» (PDF) . Математический журнал колледжа . 37 (1): 52–53. дои : 10.2307/27646275 . JSTOR 27646275 .
- ^ Чхве, Хаёнг; Да, Ён-Нан; Ю, Сонгук (2020), «Каталонские числовые последовательности и последовательности моментов Хаусдорфа», Discrete Mathematics , 343 (5): 111808, 11, arXiv : 1809.07523 , doi : 10.1016/j.disc.2019.111808 , MR 4052255 , ID 214165563 , Пример 3.1
- ^ Фэн, Ци; Бай-Ни, Го (2017), «Интегральные представления каталонских чисел и их приложения», Математика , 5 (3): 40, doi : 10.3390/math5030040 , Теорема
- ^ Пути Дика
- ^ Стэнли, стр. 221, пример (д)
- ^ Черпиншек, Матей; Мерник, Лука (2009). «Эффективное представление для решения проблем, связанных с каталонскими числами» (PDF) . Международный журнал чистой и прикладной математики . 56 (4): 589–604.
- ^ А. де Сегнер, Перечисление способов разделения прямолинейных плоских фигур диагоналями на треугольники. Новые комментарии Петрополитической академии наук 7 (1758/59) 203–209.
- ^ Рукавицка Йозеф (2011), Об обобщенных путях Дика, Электронный журнал комбинаторики онлайн
- ^ Дершовиц, Нахум; Закс, Шмуэль (1980), «Перечисления упорядоченных деревьев», Дискретная математика , 31 : 9–28, doi : 10.1016/0012-365x(80)90168-5 , hdl : 2027/uiuo.ark:/13960/t3kw6z60d
- ^ Дворецкий, Арье; Моцкин, Теодор (1947), «Проблема расположения», Duke Mathematical Journal , 14 (2): 305–313, doi : 10.1215/s0012-7094-47-01423-3
- ^ Дершовиц, Нахум; Закс, Шмуэль (январь 1990 г.). «Лемма о цикле и некоторые приложения» (PDF) . Европейский журнал комбинаторики . 11 (1): 35–40. дои : 10.1016/S0195-6698(13)80053-4 .
- ^ Стэнли, Ричард П. (2021). «Исчислительная и алгебраическая комбинаторика в 1960-х и 1970-х годах». arXiv : 2105.07884 [ math.HO ].
- ^ Ларкомб, Питер Дж. «Китайское открытие каталонских чисел в XVIII веке» (PDF) .
- ^ «Минг Анту, первый в мире изобретатель каталонских чисел» . Архивировано из оригинала 31 января 2020 г. Проверено 24 июня 2014 г.
- ^ Чен, Синь; Ван, Джейн (2012). «Суперкаталонские числа S(m, m + s) для s ≤ 4». arXiv : 1208.4196 [ math.CO ].
- ^ Георгичук, Ирина; Ореловиц, Гидон (2020). «Суперкаталонские числа третьего и четвертого рода». arXiv : 2008.00133 [ math.CO ].
- ^ Сергей Фомин и Натан Ридинг, «Корневые системы и обобщенные ассоциэдры», Геометрическая комбинаторика, IAS/Park City Math. Сер. 13 , Американское математическое общество , Провиденс, Род-Айленд, 2007, стр. 63–131. arXiv : математика/0505518
- ^ Чхве, Хаёнг; Да, Ён-Нан; Ю, Сонгук (2020), «Каталонские числовые последовательности и последовательности моментов Хаусдорфа», Discrete Mathematics , 343 (5): 111808, 11, arXiv : 1809.07523 , doi : 10.1016/j.disc.2019.111808 , MR 4052255 , ID 214165563
- ^ Боуман, Д.; Регев, Алон (2014). «Счет симметрии: классы разрезов выпуклого правильного многоугольника» . Адв. Прил. Математика . 56 : 35–55. arXiv : 1209.6270 . дои : 10.1016/j.aam.2014.01.004 . S2CID 15430707 .
Ссылки
[ редактировать ]- Стэнли, Ричард П. (2015), Каталонские числа . Издательство Кембриджского университета, ISBN 978-1-107-42774-7 .
- Конвей и Гай (1996) Книга чисел . Нью-Йорк: Коперник, стр. 96–106.
- Гарднер, Мартин (1988), Путешествие во времени и другие математические недоумения , Нью-Йорк: WH Freeman and Company, стр. 253–266 (гл. 20) , Bibcode : 1988ttom.book.....G , ISBN 0-7167-1924-Х
- Коши, Томас (2008), Каталонские числа с приложениями , Oxford University Press, ISBN 978-0-19-533454-8
- Коши, Томас и Чжэньгуан Гао (2011) «Некоторые свойства делимости каталонских чисел», Mathematical Gazette 95:96–102.
- Ларкомб, П.Дж. (1999). «Китайское открытие каталонских чисел в XVIII веке» (PDF) . Математический спектр . 32 : 5–7.
- Стэнли, Ричард П. (1999), Перечислительная комбинаторика. Том. 2 , Кембриджские исследования по высшей математике, том. 62, Издательство Кембриджского университета , ISBN 978-0-521-56069-6 , МР 1676282
- Эгечиоглу, Омер (2009), Оценка детерминанта Каталонии – Ханкеля (PDF)
- Георгичук, Ирина; Ореловиц, Гидон (2020), Суперкаталонские числа третьего и четвертого рода , arXiv : 2008.00133
Внешние ссылки
[ редактировать ]- Стэнли, Ричард П. (1998), каталонское приложение к перечислительной комбинаторике, том 2 (PDF)
- Вайсштейн, Эрик В. «Каталонский номер» . Математический мир .
- Дэвис, Том: Каталонские числа . Еще примеры.
- «Эквивалентность трех интерпретаций каталонских чисел» из демонстрационного проекта Wolfram [1]
 Учебные материалы, связанные с числовыми треугольниками, связанными с разделами, в Викиверситете
Учебные материалы, связанные с числовыми треугольниками, связанными с разделами, в Викиверситете





























































































![{\displaystyle \sum _{i_{1}+\cdots +i_{m}=n \atop i_{1},\ldots,i_{m}\geq 0}C_{i_{1}}\cdots C_{ i_{m}}={\begin{cases}{\dfrac {m(n+1)(n+2)\cdots (n+m/2-1)}{2(n+m/2+2) (n+m/2+3)\cdots (n+m)}}C_{n+m/2},&m{\text{ четный,}}\\[5pt]{\dfrac {m(n+1) )(n+2)\cdots (n+(m-1)/2)}{(n+(m+3)/2)(n+(m+3)/2+1)\cdots (n+m)} }C_{n+(m-1)/2},&m{\text{ нечетный.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45120dc51e2755ca8b30b3ae9e3e6c8717b268f1)