Speed of light

"Lightspeed" redirects here. For other uses, see Speed of light (disambiguation) and Lightspeed (disambiguation).

Speed of light

On average, sunlight takes 8 minutes and 17 seconds to travel from the Sun to Earth.
Exact value
metres per second	299792458
Approximate values (to three significant digits)
kilometres per hour	1080000000
miles per second	186000
miles per hour	671000000
astronomical units per day	173
parsecs per year	0.307
Approximate light signal travel times
Distance	Time
one foot	1.0 ns
one metre	3.3 ns
from geostationary orbit to Earth	119 ms
the length of Earth's equator	134 ms
from Moon to Earth	1.3 s
from Sun to Earth (1 AU)	8.3 min
one light-year	1.0 year
one parsec	3.26 years
from the nearest star to Sun (1.3 pc)	4.2 years
from the nearest galaxy to Earth	70000 years
across the Milky Way	87400 years
from the Andromeda Galaxy to Earth	2.5 million years

The speed of light in vacuum, commonly denoted c, is a universal physical constant that is exactly equal to 299,792,458 metres per second (approximately 300,000 kilometres per second; 186,000 miles per second; 671 million miles per hour). According to the special theory of relativity, c is the upper limit for the speed at which conventional matter or energy (and thus any signal carrying information) can travel through space.

All forms of electromagnetic radiation, including visible light, travel at the speed of light. For many practical purposes, light and other electromagnetic waves will appear to propagate instantaneously, but for long distances and very sensitive measurements, their finite speed has noticeable effects. Any starlight viewed on Earth is from the distant past, allowing humans to study the history of the universe by viewing distant objects. When communicating with distant space probes, it can take minutes to hours for signals to travel. In computing, the speed of light fixes the ultimate minimum communication delay. The speed of light can be used in time of flight measurements to measure large distances to extremely high precision.

Ole Rømer first demonstrated in 1676 that light does not travel instantaneously by studying the apparent motion of Jupiter's moon Io. Progressively more accurate measurements of its speed came over the following centuries. In a paper published in 1865, James Clerk Maxwell proposed that light was an electromagnetic wave and, therefore, travelled at speed c. In 1905, Albert Einstein postulated that the speed of light c with respect to any inertial frame of reference is a constant and is independent of the motion of the light source. He explored the consequences of that postulate by deriving the theory of relativity and, in doing so, showed that the parameter c had relevance outside of the context of light and electromagnetism.

Massless particles and field perturbations, such as gravitational waves, also travel at speed c in vacuum. Such particles and waves travel at c regardless of the motion of the source or the inertial reference frame of the observer. Particles with nonzero rest mass can be accelerated to approach c but can never reach it, regardless of the frame of reference in which their speed is measured. In the theory of relativity, c interrelates space and time and appears in the famous mass–energy equivalence, E = mc².

In some cases, objects or waves may appear to travel faster than light (e.g., phase velocities of waves, the appearance of certain high-speed astronomical objects, and particular quantum effects). The expansion of the universe is understood to exceed the speed of light beyond a certain boundary.

The speed at which light propagates through transparent materials, such as glass or air, is less than c; similarly, the speed of electromagnetic waves in wire cables is slower than c. The ratio between c and the speed v at which light travels in a material is called the refractive index n of the material (n = c/v). For example, for visible light, the refractive index of glass is typically around 1.5, meaning that light in glass travels at c/1.5 ≈ 200000 km/s (124000 mi/s); the refractive index of air for visible light is about 1.0003, so the speed of light in air is about 90 km/s (56 mi/s) slower than c.

Numerical value, notation, and units

The speed of light in vacuum is usually denoted by a lowercase c, for "constant" or the Latin celeritas (meaning 'swiftness, celerity'). In 1856, Wilhelm Eduard Weber and Rudolf Kohlrausch had used c for a different constant that was later shown to equal √2 times the speed of light in vacuum. Historically, the symbol V was used as an alternative symbol for the speed of light, introduced by James Clerk Maxwell in 1865. In 1894, Paul Drude redefined c with its modern meaning. Einstein used V in his original German-language papers on special relativity in 1905, but in 1907 he switched to c, which by then had become the standard symbol for the speed of light.

Sometimes c is used for the speed of waves in any material medium, and c₀ for the speed of light in vacuum. This subscripted notation, which is endorsed in official SI literature, has the same form as related electromagnetic constants: namely, μ₀ for the vacuum permeability or magnetic constant, ε₀ for the vacuum permittivity or electric constant, and Z₀ for the impedance of free space. This article uses c exclusively for the speed of light in vacuum.

Use in unit systems

Further information: Metre § Speed of light definition

Since 1983, the constant c has been defined in the International System of Units (SI) as exactly 299792458 m/s; this relationship is used to define the metre as exactly the distance that light travels in vacuum in 1⁄299792458 of a second. By using the value of c, as well as an accurate measurement of the second, one can thus establish a standard for the metre. As a dimensional physical constant, the numerical value of c is different for different unit systems. For example, in imperial units, the speed of light is approximately 186282 miles per second, or roughly 1 foot per nanosecond.

In branches of physics in which c appears often, such as in relativity, it is common to use systems of natural units of measurement or the geometrized unit system where c = 1. Using these units, c does not appear explicitly because multiplication or division by 1 does not affect the result. Its unit of light-second per second is still relevant, even if omitted.

Fundamental role in physics

See also: Special relativity and One-way speed of light

The speed at which light waves propagate in vacuum is independent both of the motion of the wave source and of the inertial frame of reference of the observer. This invariance of the speed of light was postulated by Einstein in 1905, after being motivated by Maxwell's theory of electromagnetism and the lack of evidence for motion against the luminiferous aether. It has since been consistently confirmed by many experiments. It is only possible to verify experimentally that the two-way speed of light (for example, from a source to a mirror and back again) is frame-independent, because it is impossible to measure the one-way speed of light (for example, from a source to a distant detector) without some convention as to how clocks at the source and at the detector should be synchronized.

By adopting Einstein synchronization for the clocks, the one-way speed of light becomes equal to the two-way speed of light by definition. The special theory of relativity explores the consequences of this invariance of c with the assumption that the laws of physics are the same in all inertial frames of reference. One consequence is that c is the speed at which all massless particles and waves, including light, must travel in vacuum.

The Lorentz factor γ as a function of velocity. It starts at 1 and approaches infinity as v approaches c.

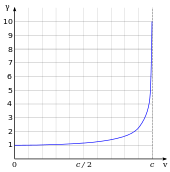
Special relativity has many counterintuitive and experimentally verified implications. These include the equivalence of mass and energy (E = mc²), length contraction (moving objects shorten), and time dilation (moving clocks run more slowly). The factor γ by which lengths contract and times dilate is known as the Lorentz factor and is given by γ = (1 − v²/c²)^−1/2, where v is the speed of the object. The difference of γ from 1 is negligible for speeds much slower than c, such as most everyday speeds – in which case special relativity is closely approximated by Galilean relativity – but it increases at relativistic speeds and diverges to infinity as v approaches c. For example, a time dilation factor of γ = 2 occurs at a relative velocity of 86.6% of the speed of light (v = 0.866 c). Similarly, a time dilation factor of γ = 10 occurs at 99.5% the speed of light (v = 0.995 c).

The results of special relativity can be summarized by treating space and time as a unified structure known as spacetime (with c relating the units of space and time), and requiring that physical theories satisfy a special symmetry called Lorentz invariance, whose mathematical formulation contains the parameter c. Lorentz invariance is an almost universal assumption for modern physical theories, such as quantum electrodynamics, quantum chromodynamics, the Standard Model of particle physics, and general relativity. As such, the parameter c is ubiquitous in modern physics, appearing in many contexts that are unrelated to light. For example, general relativity predicts that c is also the speed of gravity and of gravitational waves, and observations of gravitational waves have been consistent with this prediction. In non-inertial frames of reference (gravitationally curved spacetime or accelerated reference frames), the local speed of light is constant and equal to c, but the speed of light can differ from c when measured from a remote frame of reference, depending on how measurements are extrapolated to the region.

It is generally assumed that fundamental constants such as c have the same value throughout spacetime, meaning that they do not depend on location and do not vary with time. However, it has been suggested in various theories that the speed of light may have changed over time. No conclusive evidence for such changes has been found, but they remain the subject of ongoing research.

It is generally assumed that the two-way speed of light is isotropic, meaning that it has the same value regardless of the direction in which it is measured. Observations of the emissions from nuclear energy levels as a function of the orientation of the emitting nuclei in a magnetic field (see Hughes–Drever experiment), and of rotating optical resonators (see Resonator experiments) have put stringent limits on the possible two-way anisotropy.

Upper limit on speeds

According to special relativity, the energy of an object with rest mass m and speed v is given by γmc², where γ is the Lorentz factor defined above. When v is zero, γ is equal to one, giving rise to the famous E = mc² formula for mass–energy equivalence. The γ factor approaches infinity as v approaches c, and it would take an infinite amount of energy to accelerate an object with mass to the speed of light. The speed of light is the upper limit for the speeds of objects with positive rest mass, and individual photons cannot travel faster than the speed of light. This is experimentally established in many tests of relativistic energy and momentum.

Event A precedes B in the red frame, is simultaneous with B in the green frame, and follows B in the blue frame.

More generally, it is impossible for signals or energy to travel faster than c. One argument for this follows from the counter-intuitive implication of special relativity known as the relativity of simultaneity. If the spatial distance between two events A and B is greater than the time interval between them multiplied by c then there are frames of reference in which A precedes B, others in which B precedes A, and others in which they are simultaneous. As a result, if something were travelling faster than c relative to an inertial frame of reference, it would be travelling backwards in time relative to another frame, and causality would be violated. In such a frame of reference, an "effect" could be observed before its "cause". Such a violation of causality has never been recorded, and would lead to paradoxes such as the tachyonic antitelephone.

Faster-than-light observations and experiments

See also: Faster-than-light and Superluminal motion

There are situations in which it may seem that matter, energy, or information-carrying signal travels at speeds greater than c, but they do not. For example, as is discussed in the propagation of light in a medium section below, many wave velocities can exceed c. The phase velocity of X-rays through most glasses can routinely exceed c, but phase velocity does not determine the velocity at which waves convey information.

If a laser beam is swept quickly across a distant object, the spot of light can move faster than c, although the initial movement of the spot is delayed because of the time it takes light to get to the distant object at the speed c. However, the only physical entities that are moving are the laser and its emitted light, which travels at the speed c from the laser to the various positions of the spot. Similarly, a shadow projected onto a distant object can be made to move faster than c, after a delay in time. In neither case does any matter, energy, or information travel faster than light.

The rate of change in the distance between two objects in a frame of reference with respect to which both are moving (their closing speed) may have a value in excess of c. However, this does not represent the speed of any single object as measured in a single inertial frame.

Certain quantum effects appear to be transmitted instantaneously and therefore faster than c, as in the EPR paradox. An example involves the quantum states of two particles that can be entangled. Until either of the particles is observed, they exist in a superposition of two quantum states. If the particles are separated and one particle's quantum state is observed, the other particle's quantum state is determined instantaneously. However, it is impossible to control which quantum state the first particle will take on when it is observed, so information cannot be transmitted in this manner.

Another quantum effect that predicts the occurrence of faster-than-light speeds is called the Hartman effect: under certain conditions the time needed for a virtual particle to tunnel through a barrier is constant, regardless of the thickness of the barrier. This could result in a virtual particle crossing a large gap faster than light. However, no information can be sent using this effect.

So-called superluminal motion is seen in certain astronomical objects, such as the relativistic jets of radio galaxies and quasars. However, these jets are not moving at speeds in excess of the speed of light: the apparent superluminal motion is a projection effect caused by objects moving near the speed of light and approaching Earth at a small angle to the line of sight: since the light which was emitted when the jet was farther away took longer to reach the Earth, the time between two successive observations corresponds to a longer time between the instants at which the light rays were emitted.

A 2011 experiment where neutrinos were observed to travel faster than light turned out to be due to experimental error.

In models of the expanding universe, the farther galaxies are from each other, the faster they drift apart. For example, galaxies far away from Earth are inferred to be moving away from the Earth with speeds proportional to their distances. Beyond a boundary called the Hubble sphere, the rate at which their distance from Earth increases becomes greater than the speed of light.These recession rates, defined as the increase in proper distance per cosmological time, are not velocities in a relativistic sense. Faster-than-light cosmological recession speeds are only a coordinate artifact.

Propagation of light

In classical physics, light is described as a type of electromagnetic wave. The classical behaviour of the electromagnetic field is described by Maxwell's equations, which predict that the speed c with which electromagnetic waves (such as light) propagate in vacuum is related to the distributed capacitance and inductance of vacuum, otherwise respectively known as the electric constant ε₀ and the magnetic constant μ₀, by the equation

$c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}.$

In modern quantum physics, the electromagnetic field is described by the theory of quantum electrodynamics (QED). In this theory, light is described by the fundamental excitations (or quanta) of the electromagnetic field, called photons. In QED, photons are massless particles and thus, according to special relativity, they travel at the speed of light in vacuum.

Extensions of QED in which the photon has a mass have been considered. In such a theory, its speed would depend on its frequency, and the invariant speed c of special relativity would then be the upper limit of the speed of light in vacuum. No variation of the speed of light with frequency has been observed in rigorous testing, putting stringent limits on the mass of the photon. The limit obtained depends on the model used: if the massive photon is described by Proca theory, the experimental upper bound for its mass is about 10⁻⁵⁷ grams; if photon mass is generated by a Higgs mechanism, the experimental upper limit is less sharp, m ≤ 10⁻¹⁴ eV/c²  (roughly 2 × 10⁻⁴⁷ g).

Another reason for the speed of light to vary with its frequency would be the failure of special relativity to apply to arbitrarily small scales, as predicted by some proposed theories of quantum gravity. In 2009, the observation of gamma-ray burst GRB 090510 found no evidence for a dependence of photon speed on energy, supporting tight constraints in specific models of spacetime quantization on how this speed is affected by photon energy for energies approaching the Planck scale.

In a medium

See also: Refractive index

In a medium, light usually does not propagate at a speed equal to c; further, different types of light wave will travel at different speeds. The speed at which the individual crests and troughs of a plane wave (a wave filling the whole space, with only one frequency) propagate is called the phase velocity v_p. A physical signal with a finite extent (a pulse of light) travels at a different speed. The overall envelope of the pulse travels at the group velocity v_g, and its earliest part travels at the front velocity v_f.

The blue dot moves at the speed of the ripples, the phase velocity; the green dot moves with the speed of the envelope, the group velocity; and the red dot moves with the speed of the foremost part of the pulse, the front velocity.

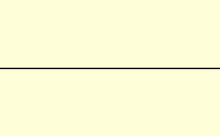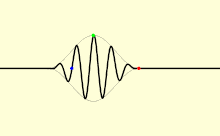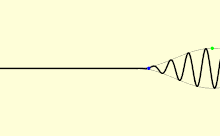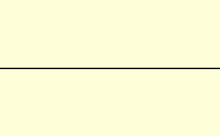
The phase velocity is important in determining how a light wave travels through a material or from one material to another. It is often represented in terms of a refractive index. The refractive index of a material is defined as the ratio of c to the phase velocity v_p in the material: larger indices of refraction indicate lower speeds. The refractive index of a material may depend on the light's frequency, intensity, polarization, or direction of propagation; in many cases, though, it can be treated as a material-dependent constant. The refractive index of air is approximately 1.0003. Denser media, such as water, glass, and diamond, have refractive indexes of around 1.3, 1.5 and 2.4, respectively, for visible light.

In exotic materials like Bose–Einstein condensates near absolute zero, the effective speed of light may be only a few metres per second. However, this represents absorption and re-radiation delay between atoms, as do all slower-than-c speeds in material substances. As an extreme example of light "slowing" in matter, two independent teams of physicists claimed to bring light to a "complete standstill" by passing it through a Bose–Einstein condensate of the element rubidium. The popular description of light being "stopped" in these experiments refers only to light being stored in the excited states of atoms, then re-emitted at an arbitrarily later time, as stimulated by a second laser pulse. During the time it had "stopped", it had ceased to be light. This type of behaviour is generally microscopically true of all transparent media which "slow" the speed of light.

In transparent materials, the refractive index generally is greater than 1, meaning that the phase velocity is less than c. In other materials, it is possible for the refractive index to become smaller than 1 for some frequencies; in some exotic materials it is even possible for the index of refraction to become negative. The requirement that causality is not violated implies that the real and imaginary parts of the dielectric constant of any material, corresponding respectively to the index of refraction and to the attenuation coefficient, are linked by the Kramers–Kronig relations. In practical terms, this means that in a material with refractive index less than 1, the wave will be absorbed quickly.

A pulse with different group and phase velocities (which occurs if the phase velocity is not the same for all the frequencies of the pulse) smears out over time, a process known as dispersion. Certain materials have an exceptionally low (or even zero) group velocity for light waves, a phenomenon called slow light.The opposite, group velocities exceeding c, was proposed theoretically in 1993 and achieved experimentally in 2000. It should even be possible for the group velocity to become infinite or negative, with pulses travelling instantaneously or backwards in time.

None of these options allow information to be transmitted faster than c. It is impossible to transmit information with a light pulse any faster than the speed of the earliest part of the pulse (the front velocity). It can be shown that this is (under certain assumptions) always equal to c.

It is possible for a particle to travel through a medium faster than the phase velocity of light in that medium (but still slower than c). When a charged particle does that in a dielectric material, the electromagnetic equivalent of a shock wave, known as Cherenkov radiation, is emitted.

Practical effects of finiteness

The speed of light is of relevance to communications: the one-way and round-trip delay time are greater than zero. This applies from small to astronomical scales. On the other hand, some techniques depend on the finite speed of light, for example in distance measurements.

Small scales

In computers, the speed of light imposes a limit on how quickly data can be sent between processors. If a processor operates at 1 gigahertz, a signal can travel only a maximum of about 30 centimetres (1 ft) in a single clock cycle – in practice, this distance is even shorter since the printed circuit board refracts and slows down signals. Processors must therefore be placed close to each other, as well as memory chips, to minimize communication latencies, and care must be exercised when routing wires between them to ensure signal integrity. If clock frequencies continue to increase, the speed of light may eventually become a limiting factor for the internal design of single chips.

Large distances on Earth

Duration: 4 seconds.0:04

Acoustic representation of the speed of light, at every beep the light makes a full circle around the equator

Given that the equatorial circumference of the Earth is about 40075 km and that c is about 300000 km/s, the theoretical shortest time for a piece of information to travel half the globe along the surface is about 67 milliseconds. When light is traveling in optical fibre (a transparent material) the actual transit time is longer, in part because the speed of light is slower by about 35% in optical fibre, depending on its refractive index n. Straight lines are rare in global communications and the travel time increases when signals pass through electronic switches or signal regenerators.

Although this distance is largely irrelevant for most applications, latency becomes important in fields such as high-frequency trading, where traders seek to gain minute advantages by delivering their trades to exchanges fractions of a second ahead of other traders. For example, traders have been switching to microwave communications between trading hubs, because of the advantage which radio waves travelling at near to the speed of light through air have over comparatively slower fibre optic signals.

Spaceflight and astronomy

A beam of light is depicted travelling between the Earth and the Moon in the time it takes a light pulse to move between them: 1.255 seconds at their mean orbital (surface-to-surface) distance. The relative sizes and separation of the Earth–Moon system are shown to scale.

Similarly, communications between the Earth and spacecraft are not instantaneous. There is a brief delay from the source to the receiver, which becomes more noticeable as distances increase. This delay was significant for communications between ground control and Apollo 8 when it became the first crewed spacecraft to orbit the Moon: for every question, the ground control station had to wait at least three seconds for the answer to arrive.

The communications delay between Earth and Mars can vary between five and twenty minutes depending upon the relative positions of the two planets. As a consequence of this, if a robot on the surface of Mars were to encounter a problem, its human controllers would not be aware of it until 5–20 minutes later. It would then take a further 5–20 minutes for commands to travel from Earth to Mars.

Receiving light and other signals from distant astronomical sources takes much longer. For example, it takes 13 billion (13×10⁹) years for light to travel to Earth from the faraway galaxies viewed in the Hubble Ultra-Deep Field images. Those photographs, taken today, capture images of the galaxies as they appeared 13 billion years ago, when the universe was less than a billion years old. The fact that more distant objects appear to be younger, due to the finite speed of light, allows astronomers to infer the evolution of stars, of galaxies, and of the universe itself.

Astronomical distances are sometimes expressed in light-years, especially in popular science publications and media. A light-year is the distance light travels in one Julian year, around 9461 billion kilometres, 5879 billion miles, or 0.3066 parsecs. In round figures, a light year is nearly 10 trillion kilometres or nearly 6 trillion miles. Proxima Centauri, the closest star to Earth after the Sun, is around 4.2 light-years away.

Distance measurement

Main article: Distance measurement

Radar systems measure the distance to a target by the time it takes a radio-wave pulse to return to the radar antenna after being reflected by the target: the distance to the target is half the round-trip transit time multiplied by the speed of light. A Global Positioning System (GPS) receiver measures its distance to GPS satellites based on how long it takes for a radio signal to arrive from each satellite, and from these distances calculates the receiver's position. Because light travels about 300000 kilometres (186000 mi) in one second, these measurements of small fractions of a second must be very precise. The Lunar Laser Ranging experiment, radar astronomy and the Deep Space Network determine distances to the Moon, planets and spacecraft, respectively, by measuring round-trip transit times.

Measurement

There are different ways to determine the value of c. One way is to measure the actual speed at which light waves propagate, which can be done in various astronomical and Earth-based setups. It is also possible to determine c from other physical laws where it appears, for example, by determining the values of the electromagnetic constants ε₀ and μ₀ and using their relation to c. Historically, the most accurate results have been obtained by separately determining the frequency and wavelength of a light beam, with their product equalling c. This is described in more detail in the "Interferometry" section below.

In 1983 the metre was defined as "the length of the path travelled by light in vacuum during a time interval of 1⁄299792458 of a second", fixing the value of the speed of light at 299792458 m/s by definition, as described below. Consequently, accurate measurements of the speed of light yield an accurate realization of the metre rather than an accurate value of c.

Astronomical measurements

Measurement of the speed of light from the time it takes Io to orbit Jupiter, using eclipses of Io by Jupiter's shadow to precisely measure its orbit.

Outer space is a convenient setting for measuring the speed of light because of its large scale and nearly perfect vacuum. Typically, one measures the time needed for light to traverse some reference distance in the Solar System, such as the radius of the Earth's orbit. Historically, such measurements could be made fairly accurately, compared to how accurately the length of the reference distance is known in Earth-based units.

Ole Christensen Rømer used an astronomical measurement to make the first quantitative estimate of the speed of light in the year 1676. When measured from Earth, the periods of moons orbiting a distant planet are shorter when the Earth is approaching the planet than when the Earth is receding from it. The difference is small, but the cumulative time becomes significant when measured over months. The distance travelled by light from the planet (or its moon) to Earth is shorter when the Earth is at the point in its orbit that is closest to its planet than when the Earth is at the farthest point in its orbit, the difference in distance being the diameter of the Earth's orbit around the Sun. The observed change in the moon's orbital period is caused by the difference in the time it takes light to traverse the shorter or longer distance. Rømer observed this effect for Jupiter's innermost major moon Io and deduced that light takes 22 minutes to cross the diameter of the Earth's orbit.

Aberration of light: light from a distant source appears to be from a different location for a moving telescope due to the finite speed of light.

Another method is to use the aberration of light, discovered and explained by James Bradley in the 18th century. This effect results from the vector addition of the velocity of light arriving from a distant source (such as a star) and the velocity of its observer (see diagram on the right). A moving observer thus sees the light coming from a slightly different direction and consequently sees the source at a position shifted from its original position. Since the direction of the Earth's velocity changes continuously as the Earth orbits the Sun, this effect causes the apparent position of stars to move around. From the angular difference in the position of stars (maximally 20.5 arcseconds) it is possible to express the speed of light in terms of the Earth's velocity around the Sun, which with the known length of a year can be converted to the time needed to travel from the Sun to the Earth. In 1729, Bradley used this method to derive that light travelled 10210 times faster than the Earth in its orbit (the modern figure is 10066 times faster) or, equivalently, that it would take light 8 minutes 12 seconds to travel from the Sun to the Earth.

Astronomical unit

An astronomical unit (AU) is approximately the average distance between the Earth and Sun. It was redefined in 2012 as exactly 149597870700 m. Previously the AU was not based on the International System of Units but in terms of the gravitational force exerted by the Sun in the framework of classical mechanics. The current definition uses the recommended value in metres for the previous definition of the astronomical unit, which was determined by measurement. This redefinition is analogous to that of the metre and likewise has the effect of fixing the speed of light to an exact value in astronomical units per second (via the exact speed of light in metres per second).

Previously, the inverse of c expressed in seconds per astronomical unit was measured by comparing the time for radio signals to reach different spacecraft in the Solar System, with their position calculated from the gravitational effects of the Sun and various planets. By combining many such measurements, a best fit value for the light time per unit distance could be obtained. For example, in 2009, the best estimate, as approved by the International Astronomical Union (IAU), was:

light time for unit distance: t_au = 499.004783836(10) s,

c = 0.00200398880410(4) AU/s = 173.144632674(3) AU/d.

The relative uncertainty in these measurements is 0.02 parts per billion (2×10⁻¹¹), equivalent to the uncertainty in Earth-based measurements of length by interferometry. Since the metre is defined to be the length travelled by light in a certain time interval, the measurement of the light time in terms of the previous definition of the astronomical unit can also be interpreted as measuring the length of an AU (old definition) in metres.

Time of flight techniques

One of the last and most accurate time of flight measurements, Michelson, Pease and Pearson's 1930–1935 experiment used a rotating mirror and a one-mile (1.6 km) long vacuum chamber which the light beam traversed 10 times. It achieved accuracy of ±11 km/s.

Diagram of the Fizeau apparatus:

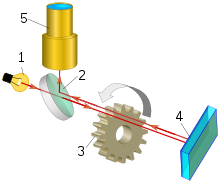
1. Light source
2. Beam-splitting semi-transparent mirror
3. Toothed wheel-breaker of the light beam
4. Remote mirror
5. Telescopic tube

A method of measuring the speed of light is to measure the time needed for light to travel to a mirror at a known distance and back. This is the working principle behind experiments by Hippolyte Fizeau and Léon Foucault.

The setup as used by Fizeau consists of a beam of light directed at a mirror 8 kilometres (5 mi) away. On the way from the source to the mirror, the beam passes through a rotating cogwheel. At a certain rate of rotation, the beam passes through one gap on the way out and another on the way back, but at slightly higher or lower rates, the beam strikes a tooth and does not pass through the wheel. Knowing the distance between the wheel and the mirror, the number of teeth on the wheel, and the rate of rotation, the speed of light can be calculated.

The method of Foucault replaces the cogwheel with a rotating mirror. Because the mirror keeps rotating while the light travels to the distant mirror and back, the light is reflected from the rotating mirror at a different angle on its way out than it is on its way back. From this difference in angle, the known speed of rotation and the distance to the distant mirror the speed of light may be calculated. Foucault used this apparatus to measure the speed of light in air versus water, based on a suggestion by François Arago.

Today, using oscilloscopes with time resolutions of less than one nanosecond, the speed of light can be directly measured by timing the delay of a light pulse from a laser or an LED reflected from a mirror. This method is less precise (with errors of the order of 1%) than other modern techniques, but it is sometimes used as a laboratory experiment in college physics classes.

Electromagnetic constants

An option for deriving c that does not directly depend on a measurement of the propagation of electromagnetic waves is to use the relation between c and the vacuum permittivity ε₀ and vacuum permeability μ₀ established by Maxwell's theory: c² = 1/(ε₀μ₀). The vacuum permittivity may be determined by measuring the capacitance and dimensions of a capacitor, whereas the value of the vacuum permeability was historically fixed at exactly 4π×10⁻⁷ H⋅m⁻¹ through the definition of the ampere. Rosa and Dorsey used this method in 1907 to find a value of 299710±22 km/s. Their method depended upon having a standard unit of electrical resistance, the "international ohm", and so its accuracy was limited by how this standard was defined.

Cavity resonance

Electromagnetic standing waves in a cavity

Another way to measure the speed of light is to independently measure the frequency f and wavelength λ of an electromagnetic wave in vacuum. The value of c can then be found by using the relation c = fλ. One option is to measure the resonance frequency of a cavity resonator. If the dimensions of the resonance cavity are also known, these can be used to determine the wavelength of the wave. In 1946, Louis Essen and A.C. Gordon-Smith established the frequency for a variety of normal modes of microwaves of a microwave cavity of precisely known dimensions. The dimensions were established to an accuracy of about ±0.8 μm using gauges calibrated by interferometry. As the wavelength of the modes was known from the geometry of the cavity and from electromagnetic theory, knowledge of the associated frequencies enabled a calculation of the speed of light.

The Essen–Gordon-Smith result, 299792±9 km/s, was substantially more precise than those found by optical techniques. By 1950, repeated measurements by Essen established a result of 299792.5±3.0 km/s.

A household demonstration of this technique is possible, using a microwave oven and food such as marshmallows or margarine: if the turntable is removed so that the food does not move, it will cook the fastest at the antinodes (the points at which the wave amplitude is the greatest), where it will begin to melt. The distance between two such spots is half the wavelength of the microwaves; by measuring this distance and multiplying the wavelength by the microwave frequency (usually displayed on the back of the oven, typically 2450 MHz), the value of c can be calculated, "often with less than 5% error".

Interferometry

An interferometric determination of length. Left: constructive interference; Right: destructive interference.

Interferometry is another method to find the wavelength of electromagnetic radiation for determining the speed of light. A coherent beam of light (e.g. from a laser), with a known frequency (f), is split to follow two paths and then recombined. By adjusting the path length while observing the interference pattern and carefully measuring the change in path length, the wavelength of the light (λ) can be determined. The speed of light is then calculated using the equation c = λf.

Before the advent of laser technology, coherent radio sources were used for interferometry measurements of the speed of light. Interferometric determination of wavelength becomes less precise with wavelength and the experiments were thus limited in precision by the long wavelength (~4 mm (0.16 in)) of the radiowaves. The precision can be improved by using light with a shorter wavelength, but then it becomes difficult to directly measure the frequency of the light.

One way around this problem is to start with a low frequency signal of which the frequency can be precisely measured, and from this signal progressively synthesize higher frequency signals whose frequency can then be linked to the original signal. A laser can then be locked to the frequency, and its wavelength can be determined using interferometry. This technique was due to a group at the National Bureau of Standards (which later became the National Institute of Standards and Technology). They used it in 1972 to measure the speed of light in vacuum with a fractional uncertainty of 3.5×10⁻⁹.

History

Until the early modern period, it was not known whether light travelled instantaneously or at a very fast finite speed. The first extant recorded examination of this subject was in ancient Greece. The ancient Greeks, Arabic scholars, and classical European scientists long debated this until Rømer provided the first calculation of the speed of light. Einstein's theory of special relativity postulates that the speed of light is constant regardless of one's frame of reference. Since then, scientists have provided increasingly accurate measurements.

History of measurements of c (in m/s)

<1638	Galileo, covered lanterns	inconclusive
<1667	Accademia del Cimento, covered lanterns	inconclusive
1675	Rømer and Huygens, moons of Jupiter	220000000	−27%
1729	James Bradley, aberration of light	301000000	+0.40%
1849	Hippolyte Fizeau, toothed wheel	315000000	+5.1%
1862	Léon Foucault, rotating mirror	298000000±500000	−0.60%
1875	Werner Siemens	260 000 000
1893	Heinrich Hertz	200 000 000
1907	Rosa and Dorsey, EM constants	299710000±30000	−280 ppm
1926	Albert A. Michelson, rotating mirror	299796000±4000	+12 ppm
1950	Essen and Gordon-Smith, cavity resonator	299792500±3000	+0.14 ppm
1958	K. D. Froome, radio interferometry	299792500±100	+0.14 ppm
1972	Evenson et al., laser interferometry	299792456.2±1.1	−0.006 ppm
1983	17th CGPM, definition of the metre	299792458 (exact)

Early history

Empedocles (c. 490–430 BCE) was the first to propose a theory of light and claimed that light has a finite speed. He maintained that light was something in motion, and therefore must take some time to travel. Aristotle argued, to the contrary, that "light is due to the presence of something, but it is not a movement". Euclid and Ptolemy advanced Empedocles' emission theory of vision, where light is emitted from the eye, thus enabling sight. Based on that theory, Heron of Alexandria argued that the speed of light must be infinite because distant objects such as stars appear immediately upon opening the eyes.

Early Islamic philosophers initially agreed with the Aristotelian view that light had no speed of travel. In 1021, Alhazen (Ibn al-Haytham) published the Book of Optics, in which he presented a series of arguments dismissing the emission theory of vision in favour of the now accepted intromission theory, in which light moves from an object into the eye. This led Alhazen to propose that light must have a finite speed, and that the speed of light is variable, decreasing in denser bodies. He argued that light is substantial matter, the propagation of which requires time, even if this is hidden from the senses. Also in the 11th century, Abū Rayhān al-Bīrūnī agreed that light has a finite speed, and observed that the speed of light is much faster than the speed of sound.

In the 13th century, Roger Bacon argued that the speed of light in air was not infinite, using philosophical arguments backed by the writing of Alhazen and Aristotle. In the 1270s, Witelo considered the possibility of light travelling at infinite speed in vacuum, but slowing down in denser bodies.

In the early 17th century, Johannes Kepler believed that the speed of light was infinite since empty space presents no obstacle to it. René Descartes argued that if the speed of light were to be finite, the Sun, Earth, and Moon would be noticeably out of alignment during a lunar eclipse. Although this argument fails when aberration of light is taken into account, the latter was not recognized until the following century. Since such misalignment had not been observed, Descartes concluded the speed of light was infinite. Descartes speculated that if the speed of light were found to be finite, his whole system of philosophy might be demolished. Despite this, in his derivation of Snell's law, Descartes assumed that some kind of motion associated with light was faster in denser media. Pierre de Fermat derived Snell's law using the opposing assumption, the denser the medium the slower light travelled. Fermat also argued in support of a finite speed of light.

First measurement attempts

In 1629, Isaac Beeckman proposed an experiment in which a person observes the flash of a cannon reflecting off a mirror about one mile (1.6 km) away. In 1638, Galileo Galilei proposed an experiment, with an apparent claim to having performed it some years earlier, to measure the speed of light by observing the delay between uncovering a lantern and its perception some distance away. He was unable to distinguish whether light travel was instantaneous or not, but concluded that if it were not, it must nevertheless be extraordinarily rapid. In 1667, the Accademia del Cimento of Florence reported that it had performed Galileo's experiment, with the lanterns separated by about one mile, but no delay was observed. The actual delay in this experiment would have been about 11 microseconds.

Наблюдения Рёмера затмений Ио с Земли

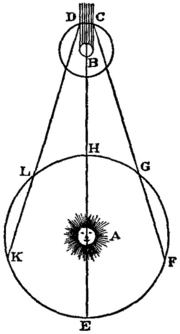
The first quantitative estimate of the speed of light was made in 1676 by Ole Rømer. From the observation that the periods of Jupiter's innermost moon Io appeared to be shorter when the Earth was approaching Jupiter than when receding from it, he concluded that light travels at a finite speed, and estimated that it takes light 22 minutes to cross the diameter of Earth's orbit. Christiaan Huygens combined this estimate with an estimate for the diameter of the Earth's orbit to obtain an estimate of speed of light of 220000 km/s, which is 27% lower than the actual value.

В своей книге «Оптика » 1704 года Исаак Ньютон сообщил о расчетах Рёмера конечной скорости света и дал значение «семь или восемь минут» для времени, необходимого свету для путешествия от Солнца до Земли (современное значение составляет 8 минут 19). секунды). Ньютон задался вопросом, были ли тени Рёмера цветными. Услышав, что это не так, он пришел к выводу, что разные цвета движутся с одинаковой скоростью. В 1729 году Джеймс Брэдли обнаружил звездную аберрацию . На основе этого эффекта он определил, что свет должен двигаться в 10 210 раз быстрее, чем Земля на ее орбите (современная цифра в 10 066 раз быстрее) или, что то же самое, что свету потребуется 8 минут 12 секунд, чтобы пройти путь от Солнца до Земли.

Связи с электромагнетизмом

Смотрите также: История электромагнитной теории и История специальной теории относительности.

В 19 веке Ипполит Физо разработал метод определения скорости света на основе измерений времени полета на Земле и сообщил о значении 315 000 км/с . Его метод был усовершенствован Леоном Фуко , который в 1862 году получил значение 298 000 км/с . В 1856 году Вильгельм Эдуард Вебер и Рудольф Кольрауш измерили соотношение электромагнитных и электростатических единиц заряда, 1/ √ ε ₀ μ ₀ , разрядив лейденскую банку , и обнаружили, что его численное значение очень близко к скорости свет, измеренный непосредственно Физо. В следующем году Густав Кирхгоф подсчитал, что электрический сигнал в проводе без сопротивления распространяется по проводу с такой скоростью.

В начале 1860-х годов Максвелл показал, что согласно теории электромагнетизма, над которой он работал, электромагнитные волны распространяются в пустом пространстве. со скоростью, равной указанному выше соотношению Вебера/Кольрауша, и обратив внимание на числовую близость этого значения к скорости света, измеренной Физо, он предположил, что свет на самом деле является электромагнитной волной. Максвелл подкрепил свое утверждение собственным экспериментом, опубликованным в «Философских трудах» 1868 года, который определил соотношение электростатических и электромагнитных единиц электричества.

«Светоносный эфир»

Основная статья: Светоносный эфир

Волновые свойства света были хорошо известны со времен Томаса Янга . В 19 веке физики считали, что свет распространяется в среде, называемой эфиром (или эфиром). Но электрическая сила больше похожа на силу гравитации в законе Ньютона. Передающая среда не требовалась. После того, как теория Максвелла объединила свет, электрические и магнитные волны, стало предпочтительным, чтобы и световые, и электрические магнитные волны распространялись в одной и той же эфирной среде (или называемой светоносным эфиром ).

Хендрик Лоренц (справа) с Альбертом Эйнштейном (1921 г.)

В то время считалось, что пустое пространство заполнено фоновой средой, называемой светоносным эфиром , в которой существует электромагнитное поле. Некоторые физики думали, что этот эфир действует как предпочтительная система отсчета для распространения света и, следовательно, должно быть возможно измерить движение Земли относительно этой среды, измеряя изотропию скорости света. Начиная с 1880-х годов было проведено несколько экспериментов с целью обнаружить это движение, самым известным из которых является эксперимент, проведенный Альбертом А. Майкельсоном и Эдвардом В. Морли в 1887 году. Обнаруженное движение всегда оказывалось нулевым (в пределах ошибки наблюдения). Современные эксперименты показывают, что двусторонняя скорость света изотропна ( одинакова во всех направлениях) с точностью до 6 нанометров в секунду.

Благодаря этому эксперименту Хендрик Лоренц предположил, что движение аппарата через эфир может привести к сжатию аппарата по его длине в направлении движения, и далее он предположил, что переменная времени для движущихся систем также должна быть изменена соответствующим образом («локальное время»), что привело к формулировке преобразования Лоренца . Основываясь на теории эфира Лоренца , Анри Пуанкаре (1900) показал, что это локальное время (в первом порядке по v / c ) обозначается часами, движущимися в эфире, которые синхронизированы в предположении постоянной скорости света. В 1904 году он предположил, что скорость света может быть предельной скоростью в динамике при условии, что все предположения теории Лоренца подтвердятся. В 1905 году Пуанкаре привел теорию эфира Лоренца в полное наблюдательное согласие с принципом относительности .

Специальная теория относительности

В 1905 году Эйнштейн с самого начала постулировал, что скорость света в вакууме, измеренная неускоряющимся наблюдателем, не зависит от движения источника или наблюдателя. Используя это и принцип относительности в качестве основы, он вывел специальную теорию относительности , в которой скорость света в вакууме c фигурирует как фундаментальная константа, также появляющаяся в контекстах, не связанных со светом. Это сделало концепцию стационарного эфира (которой все еще придерживались Лоренц и Пуанкаре) бесполезной и произвело революцию в концепциях пространства и времени.

Повышенная точность c и новое определение метра и секунды.

Смотрите также: История счетчика.

Во второй половине 20 века был достигнут большой прогресс в повышении точности измерений скорости света сначала с помощью методов резонаторного резонанса, а затем с помощью методов лазерного интерферометра. Этому способствовали новые, более точные определения метра и секунды. В 1950 году Эссен определил скорость как 299 792,5 Луи ± 3,0 км/с , используя резонанс полости. Это значение было принято 12-й Генеральной ассамблеей Радионаучного союза в 1957 году. В 1960 году метр был переопределен в терминах длины волны конкретной спектральной линии криптона-86 , а в 1967 году вторая была переопределена в термины частоты сверхтонкого перехода основного состояния цезия-133 .

В 1972 году, используя метод лазерного интерферометра и новые определения, группа Национального бюро стандартов США в Боулдере, штат Колорадо, определила скорость света в вакууме как c = 299 792 456,2 1,1 м ± /с . Это было в 100 раз менее неопределенным, чем ранее принятое значение. Оставшаяся неопределенность была в основном связана с определением метра. Поскольку аналогичные эксперименты показали сопоставимые результаты для c , 15-я Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать значение 299 792 458 м/с для скорости света.

Определяется как явная константа

В 1983 году 17-е заседание Генеральной конференции по мерам и весам (CGPM) установило, что длины волн, полученные из измерений частоты, и заданное значение скорости света более воспроизводимы , чем предыдущий стандарт. Они сохранили определение секунды 1967 года, поэтому цезия частота сверхтонкой теперь будет определять как секунду, так и метр. Для этого они переопределили метр как «длину пути, пройденного светом в вакууме за интервал времени 1/299 792 458 секунды ».

В результате этого определения значение скорости света в вакууме составляет ровно 299 792 458 м/с. и стал определенной константой в системе единиц СИ. Усовершенствованные экспериментальные методы, которые до 1983 года позволяли измерять скорость света, больше не влияют на известное значение скорости света в единицах СИ, а вместо этого позволяют более точно реализовать измеритель за счет более точного измерения длины волны криптона. 86 и другие источники света.

В 2011 году CGPM заявила о своем намерении переопределить все семь базовых единиц СИ, используя то, что она называет «формулировкой явной константы», где каждая «единица определяется косвенно путем явного указания точного значения общепризнанной фундаментальной константы», как было сделано для скорости света. Он предложил новую, но полностью эквивалентную формулировку определения метра: «Метр, обозначение м, является единицей длины; его величина устанавливается путем фиксации числового значения скорости света в вакууме, равного ровно 299». 792 458, если оно выражено в единицах СИ мс ⁻¹ ." Это было одно из изменений, которые были включены в переопределение базовых единиц СИ в 2019 году , также называемое Новой СИ .

См. также

• Световая секунда
• Скорость электричества
• Скорость гравитации
• Скорость звука
• Фактор скорости
• Фактор деформации (вымышленный)

Дальнейшее чтение

Исторические справки

• Рёмер, О. (1676 г.). «Демонстрация движения света, найденная М. Рёмером из Королевской академии наук» (PDF) . Journal des sçavans (на французском языке): 223–236. Архивировано из оригинала (PDF) 8 сентября 2022 года . Проверено 10 марта 2020 г.
  • Переведено как «Демонстрация движения света» . Философские труды Королевского общества . 12 (136): 893–894. 1677. Бибкод : 1677RSPT...12..893. . дои : 10.1098/rstl.1677.0024 . Архивировано из оригинала 29 июля 2007 года.
• Галлей, Э. (1694). «Месье Кассини, его Новые и точные таблицы затмений первого спутника Юпитера, сведенные к юлианскому Стайлу и лондонскому меридиану» . Философские труды Королевского общества . 18 (214): 237–256. Бибкод : 1694RSPT...18..237C . дои : 10.1098/rstl.1694.0048 .
• Физо, HL (1849). «Об эксперименте, касающемся скорости распространения света» (PDF) . Труды Академии наук (на французском языке). 29 :90–92, 132.
• Фуко, Ж.Л. (1862). «Экспериментальное определение скорости света: параллакс Солнца» . Труды Академии наук (на французском языке). 55 : 501–503, 792–796.
• Майкельсон, А.А. (1878). «Экспериментальное определение скорости света» . Труды Американской ассоциации содействия развитию науки . 27 : 71–77.
• Майкельсон, А.А.; Пиз, ФГ ; Пирсон, Ф. (1935). «Измерение скорости света в частичном вакууме». Астрофизический журнал . 82 (2091): 26–61. Бибкод : 1935ApJ....82...26M . дои : 10.1086/143655 . ПМИД   17816642 . S2CID   123010613 .
• Ньюкомб, С. (1886). «Скорость света» . Природа . 34 (863): 29–32. Бибкод : 1886Природа..34...29. . дои : 10.1038/034029c0 .
• Перротен, Дж. (1900). «О скорости света». Труды Академии наук (на французском языке). 131 :731–734.

Современные ссылки

• Бриллюэн, Л. (1960). Распространение волн и групповая скорость . Академическая пресса .
• Джексон, доктор юридических наук (1975). Классическая электродинамика (2-е изд.). Джон Уайли и сыновья. ISBN  978-0-471-30932-1 .
• Кайзер, Г. (2000). Оптоволоконная связь (3-е изд.). МакГроу-Хилл. п. 32 . ISBN  978-0-07-232101-2 .
• Нг, Ю.Дж. (2004). «Квантовая пена и феноменология квантовой гравитации» . В Амелино-Камелии Г; Ковальски-Гликман, Дж. (ред.). Эффекты планковского масштаба в астрофизике и космологии . Спрингер. стр. 321 и далее. ISBN  978-3-540-25263-4 .
• Хельмке, Дж.; Риле, Ф. (2001). «Физика, лежащая в основе определения метра» . В Куинне, Ти Джей; Лешютта, С.; Тавелла, П. (ред.). Последние достижения в метрологии и фундаментальные константы . IOS Пресс . п. 453. ИСБН  978-1-58603-167-1 .
• Дафф, MJ (2004). «Комментарий к изменению фундаментальных констант во времени». arXiv : hep-th/0208093 .

Внешние ссылки

• «Испытание скорости света в вакуумной трубке длиной в милю» . Popular Science Monthly , сентябрь 1930 г., стр. 17–18.
• Определение метра (Международное бюро мер и весов, BIPM)
• Скорость света в вакууме (Национальный институт стандартов и технологий, NIST)
• Галерея данных: Скорость света по Майкельсону (одномерная оценка местоположения) (загрузить данные, собранные Альбертом А. Майкельсоном )
• Subluminal (Java-апплет Грега Игана, демонстрирующий пределы информации о групповой скорости)
• Легкое обсуждение добавления скоростей
• Скорость света (Шестьдесят символов, физический факультет Ноттингемского университета [видео])
• Скорость света , обсуждение BBC Radio   4 ( В наше время , 30 ноября 2006 г.)
• Скорость света (Live-Counter – Иллюстрации)
• Скорость света – анимированные демонстрации
• « Скорость света », Альберт А. Николсон, Scientific American , 28 сентября 1878 г., стр. 193