Дисперсионный анализ

Дисперсионный анализ ( ANOVA ) представляет собой набор статистических моделей и связанных с ними процедур оценки (таких как «вариация» между группами), используемых для анализа различий между средними значениями. ANOVA был разработан статистиком Рональдом Фишером . ANOVA основан на законе общей дисперсии , согласно которому наблюдаемая дисперсия конкретной переменной разбивается на компоненты, относящиеся к различным источникам вариации. В своей простейшей форме ANOVA обеспечивает статистическую проверку равенства двух или более средних значений совокупности и, следовательно, обобщает t -критерий за пределы двух средних. Другими словами, ANOVA используется для проверки разницы между двумя или более средними значениями.

История

Хотя дисперсионный анализ достиг успеха в 20 веке, согласно Стиглеру , предшественники уходят в прошлое . К ним относятся проверка гипотез, разделение сумм квадратов, экспериментальные методы и аддитивная модель. Лаплас проводил проверку гипотез в 1770-х годах. Около 1800 года Лаплас и Гаусс разработали метод наименьших квадратов для объединения наблюдений, который усовершенствовал методы, использовавшиеся тогда в астрономии и геодезии . Он также положил начало тщательному изучению вкладов в суммы квадратов. Лаплас знал, как оценить дисперсию по остаточной (а не общей) сумме квадратов. К 1827 году Лаплас использовал методы наименьших квадратов для решения задач ANOVA, связанных с измерениями атмосферных приливов. До 1800 года астрономы имели отдельные ошибки наблюдений, приводившие к от времени реакции (« личное уравнение ») и разработал методы уменьшения ошибок. Экспериментальные методы, использованные при изучении личного уравнения, позже были приняты развивающейся областью психологии. которые разработали сильные (полные факториальные) экспериментальные методы, к которым вскоре были добавлены рандомизация и слепое исследование. Красноречивое нематематическое объяснение модели аддитивных эффектов было доступно в 1885 году.

Рональд Фишер ввел термин «дисперсия» и предложил его формальный анализ в статье 1918 года по теоретической популяционной генетике « Корреляция между родственниками на основании предположения о менделевском наследовании» . Его первое применение дисперсионного анализа к анализу данных было опубликовано в 1921 году « Исследования вариаций сельскохозяйственных культур I» . Это разделило вариацию временного ряда на компоненты, отражающие ежегодные причины и медленное ухудшение. В следующей статье Фишера « Исследования вариаций культур II» , написанной совместно с Уинифред Маккензи и опубликованной в 1923 году, изучались различия в урожайности на участках, засеянных разными сортами и подвергнутых различным обработкам удобрениями. Дисперсионный анализ стал широко известен после того, как был включен в книгу Фишера «Статистические методы для научных работников» 1925 года .

Модели рандомизации были разработаны несколькими исследователями. Первая была опубликована на польском языке Ежи Нейманом в 1923 году.

Пример

Не подходит: молодые против старых, короткошерстные против длинношерстных.

Достаточное соответствие: домашние животные против рабочих пород, менее спортивные против более спортивных.

Очень хорошо подходит: вес в зависимости от породы.

Дисперсионный анализ можно использовать для описания сложных отношений между переменными. Яркий пример – выставка собак. Выставка собак не является случайной выборкой породы: обычно она ограничивается взрослыми, чистопородными и образцовыми собаками. Гистограмма веса собак на выставке, вероятно, может быть довольно сложной, как желто-оранжевое распределение, показанное на иллюстрациях. Предположим, мы хотели предсказать вес собаки на основе определенного набора характеристик каждой собаки. Один из способов сделать это — объяснить распределение весов, разделив популяцию собак на группы на основе этих характеристик. Успешная группировка разделит собак так, что (а) каждая группа имеет низкую дисперсию веса собак (это означает, что группа относительно однородна) и (б) среднее значение каждой группы различно (если две группы имеют одинаковое среднее значение, то неразумно делать вывод, что эти группы фактически разделены каким-либо значимым образом).

На иллюстрациях справа группы обозначены как X ₁ , X ₂ и т. д. На первой иллюстрации собаки разделены в соответствии с произведением (взаимодействием) двух бинарных групп: молодые против старых и короткошерстные против длинных. -шерстные (например, 1 группа – молодые короткошерстные собаки, 2 группа – молодые длинношерстные собаки и т. д.). Поскольку распределение веса собаки внутри каждой группы (показано синим цветом) имеет относительно большую дисперсию и поскольку средние значения очень схожи в разных группах, группирование собак по этим характеристикам не дает эффективного способа объяснить различия в весе собак. : знание того, в какой группе находится собака, не позволяет нам предсказать ее вес намного лучше, чем просто знание того, что собака участвует в выставке. Таким образом, эта группировка не может объяснить изменение общего распределения (желто-оранжевое).

Попытка объяснить распределение веса путем группировки собак на домашние и рабочие породы и на менее спортивную и более спортивную породу, вероятно, была бы несколько более успешной (удовлетворительное соответствие). Самые тяжелые выставочные собаки, скорее всего, будут большими, сильными и рабочими породами, в то время как породы, содержащиеся в качестве домашних питомцев, как правило, меньше по размеру и, следовательно, легче. Как показывает вторая иллюстрация, распределения имеют дисперсии значительно меньшие, чем в первом случае, а средние более различимы. Однако значительное перекрытие распределений, например, означает, что мы не можем надежно различить X ₁ и X ₂ . Группирование собак по принципу подбрасывания монеты может привести к схожим распределениям.

Попытка объяснить вес породой, скорее всего, приведет к очень хорошему совпадению. Все чихуахуа легкие, а все сенбернары тяжелые. Разница в весе сеттеров и пойнтеров не является основанием для разделения пород. Дисперсионный анализ предоставляет формальные инструменты для обоснования этих интуитивных суждений. Обычно метод используется для анализа экспериментальных данных или разработки моделей. Этот метод имеет некоторые преимущества перед корреляцией: не все данные должны быть числовыми, и одним из результатов метода является суждение о достоверности объяснительной связи.

Классы моделей

Существует три класса моделей, используемых в дисперсионном анализе, и они описаны здесь.

Модели с фиксированными эффектами

Основная статья: Модель с фиксированными эффектами

Модель дисперсионного анализа с фиксированными эффектами (класс I) применяется к ситуациям, в которых экспериментатор применяет одно или несколько методов лечения к испытуемым эксперимента, чтобы увидеть, изменяются ли значения переменных ответа . Это позволяет экспериментатору оценить диапазоны значений переменных ответа, которые лечение будет генерировать в популяции в целом.

Фиксированные эффекты против случайных эффектов

Модели случайных эффектов

Основная статья: Модель случайных эффектов

Модель случайных эффектов (класс II) используется, когда методы лечения не фиксированы. Это происходит, когда различные уровни факторов выбираются из более крупной совокупности. Поскольку уровни сами по себе являются случайными переменными , некоторые предположения и метод сопоставления обработок (многопараметрическое обобщение простых различий) отличаются от модели с фиксированными эффектами.

Модели со смешанными эффектами

Основная статья: Смешанная модель

Модель смешанных эффектов (класс III) содержит экспериментальные факторы как с фиксированными, так и со случайными эффектами, с соответственно разными интерпретациями и анализом для двух типов.

Пример

Учебные эксперименты могут проводиться факультетом колледжа или университета, чтобы найти хороший вводный учебник, при этом каждый текст рассматривается как лечение. Модель с фиксированными эффектами будет сравнивать список текстов-кандидатов. Модель случайных эффектов позволит определить, существуют ли важные различия между списком случайно выбранных текстов. Модель смешанных эффектов будет сравнивать (фиксированные) действующие тексты со случайно выбранными альтернативами.

Определить фиксированные и случайные эффекты оказалось непросто, поскольку существует множество конкурирующих определений.

Предположения

Дисперсионный анализ изучался с использованием нескольких подходов, наиболее распространенный из которых использует линейную модель , которая связывает реакцию на лечение и блокировку. Обратите внимание, что модель линейна по параметрам, но может быть нелинейной по уровням факторов. Интерпретация проста, когда данные сбалансированы по факторам, но для несбалансированных данных требуется более глубокое понимание.

Анализ учебника с использованием нормального распределения

Дисперсионный анализ может быть представлен в виде линейной модели , которая делает следующие предположения о распределении вероятностей ответов:

• Независимость наблюдений – это допущение модели, упрощающее статистический анализ.
• Нормальность распределения остатков нормальные . –
• Равенство (или «однородность») дисперсий, называемое гомоскедастичностью — дисперсия данных в группах должна быть одинаковой.

Отдельные предположения модели учебника подразумевают, что ошибки независимы, одинаково и нормально распределяются для моделей с фиксированными эффектами, то есть, что ошибки ( $\varepsilon$) независимы и $$\varepsilon \thicksim N(0,\sigma ^{2}).$$

Анализ на основе рандомизации

См. Также: Случайное назначение и тест рандомизации.

В рандомизированном контролируемом эксперименте методы лечения случайным образом распределяются по экспериментальным единицам в соответствии с протоколом эксперимента. Эта рандомизация является объективной и объявляется до проведения эксперимента. Объективное случайное присвоение используется для проверки значимости нулевой гипотезы , следуя идеям К.С. Пирса и Рональда Фишера . Этот основанный на дизайне анализ обсуждался и разрабатывался Фрэнсисом Дж. Анскомбом на экспериментальной станции в Ротамстеде и Оскаром Кемпторном из Университета штата Айова . Кемпторн и его ученики делают предположение об аддитивности единичного лечения , которое обсуждается в книгах Кемпторна и Дэвида Р. Кокса .

Аддитивность единицы лечения

В своей простейшей форме предположение об аддитивности единичного лечения утверждает, что наблюдаемая реакция $y_{i,j}$ из экспериментальной части $i$ при получении лечения $j$ можно записать как сумму ответа устройства $y_{i}$ и эффект лечения $t_{j}$, то есть $$y_{i,j}=y_{i}+t_{j}.$$Предположение об аддитивности единичных процедур подразумевает, что для каждой обработки $j$, $j$лечение имеет точно такой же эффект $t_{j}$ на каждой экспериментальной единице.

предположение об аддитивности единичного лечения обычно не может быть напрямую опровергнуто По мнению Кокса и Кемпторна, . Однако многие последствия аддитивности лечебных единиц можно сфальсифицировать. Для рандомизированного эксперимента предположение об аддитивности единичного лечения подразумевает , что дисперсия постоянна для всех методов лечения. Следовательно, в противоположность этому , необходимым условием аддитивности единичного лечения является постоянство дисперсии.

Использование аддитивности и рандомизации единичного лечения аналогично умозаключению на основе дизайна, которое является стандартным для выборки при обследовании конечной совокупности .

Производная линейная модель

Кемпторн использует рандомизированное распределение и предположение об аддитивности единичного лечения для создания производной линейной модели , очень похожей на модель из учебника, обсуждавшуюся ранее. Статистика испытаний этой производной линейной модели близко аппроксимируется статистикой испытаний соответствующей нормальной линейной модели согласно теоремам аппроксимации и исследованиям моделирования. Однако есть различия. Например, анализ на основе рандомизации приводит к небольшой, но (строго) отрицательной корреляции между наблюдениями. В анализе, основанном на рандомизации, не делается предположений о нормальном распределении и, тем более , о независимости . Наоборот, наблюдения зависимы !

Анализ, основанный на рандомизации, имеет тот недостаток, что его изложение требует утомительной алгебры и требует много времени. Поскольку анализ на основе рандомизации сложен и близко приближен к подходу с использованием нормальной линейной модели, большинство учителей делают упор на подход обычной линейной модели. Лишь немногие статистики возражают против модельного анализа сбалансированных рандомизированных экспериментов.

Статистические модели для данных наблюдений

Однако применительно к данным нерандомизированных экспериментов или обсервационных исследований анализ на основе моделей не требует рандомизации. Для данных наблюдений при получении доверительных интервалов необходимо использовать субъективные модели, как подчеркивают Рональд Фишер и его последователи. На практике оценки эффектов лечения, полученные в ходе обсервационных исследований, как правило, часто противоречивы. На практике «статистические модели» и данные наблюдений полезны для выдвижения гипотез, к которым общественность должна относиться очень осторожно.

Краткое изложение предположений

См. также: тест Шапиро-Уилка , тест Бартлетта и тест Левена.

Анализ ANOVA на основе нормальной модели предполагает независимость, нормальность и однородность дисперсий остатков. Анализ на основе рандомизации предполагает только однородность дисперсий остатков (как следствие аддитивности единичного лечения) и использует процедуру рандомизации эксперимента. Оба этих анализа требуют гомоскедастичности как предположения для анализа нормальной модели и как следствие рандомизации и аддитивности для анализа на основе рандомизации.

Однако исследования процессов, которые меняют дисперсию, а не средние значения (так называемые эффекты дисперсии), были успешно проведены с использованием ANOVA. F - Для ANOVA в его полной общности нет необходимых предположений, но критерий , используемый для проверки гипотез ANOVA, содержит предположения и практические рекомендации. ограничения, которые представляют постоянный интерес.

Проблемы, которые не удовлетворяют предположениям ANOVA, часто можно преобразовать, чтобы удовлетворить этим предположениям. Свойство аддитивности единичного лечения не является инвариантным при «изменении масштаба», поэтому статистики часто используют преобразования для достижения аддитивности единичного лечения. Если ожидается, что переменная ответа будет следовать параметрическому семейству вероятностных распределений, то статистик может указать (в протоколе эксперимента или наблюдательного исследования), что ответы должны быть преобразованы для стабилизации дисперсии. Кроме того, статистик может указать, что к ответам, которые, как предполагается, соответствуют мультипликативной модели, следует применять логарифмические преобразования. Согласно теореме Коши о функциональном уравнении , логарифм — единственное непрерывное преобразование, которое превращает действительное умножение в сложение.

Характеристики

ANOVA используется при анализе сравнительных экспериментов, в которых интерес представляет только разница в результатах. Статистическая значимость эксперимента определяется соотношением двух дисперсий. Это соотношение не зависит от нескольких возможных изменений экспериментальных наблюдений: добавление константы ко всем наблюдениям не меняет значимости. Умножение всех наблюдений на константу не меняет значения. Таким образом, результат статистической значимости ANOVA не зависит от постоянной систематической ошибки и ошибок масштабирования, а также от единиц, используемых при выражении наблюдений. В эпоху механических вычислений было обычным вычитать константу из всех наблюдений (что эквивалентно отбрасыванию первых цифр), чтобы упростить ввод данных. Это пример кодирования данных .

Алгоритм

Расчеты ANOVA можно охарактеризовать как вычисление ряда средних и дисперсий, деление двух дисперсий и сравнение отношения со справочным значением для определения статистической значимости. В этом случае расчет эффекта лечения тривиален: «эффект любого лечения оценивается путем определения разницы между средним значением наблюдений, которые получают лечение, и общим средним значением».

text-middle

Разделение суммы квадратов

Основная статья: Разделение сумм квадратов

Таблица однофакторного дисперсионного анализа, показывающая пример выходных данных

См. Также: Несоответствующая сумма квадратов.

ANOVA использует традиционную стандартизированную терминологию. Определяющее уравнение выборочной дисперсии: ${\textstyle s^{2}={\frac {1}{n-1}}\sum _{i}(y_{i}-{\bar {y}})^{2}}$, где делитель называется степенями свободы (DF), суммирование называется сумма квадратов (SS), результат называется средним квадратом (MS), а квадратичные члены представляют собой отклонения от выборочного среднего. ANOVA оценивает три выборочные дисперсии: общую дисперсию, основанную на всех отклонениях наблюдения от общего среднего значения, дисперсию ошибок, основанную на всех отклонениях наблюдения от соответствующих средних значений лечения, и дисперсию лечения. Дисперсия лечения основана на отклонениях средних значений лечения от общего среднего, при этом результат умножается на количество наблюдений в каждом лечении, чтобы учесть разницу между дисперсией наблюдений и дисперсией средних значений.

Фундаментальным методом является разбиение общей суммы квадратов SS на компоненты, связанные с эффектами, используемыми в модели. Например, модель упрощенного дисперсионного анализа с одним типом обработки на разных уровнях.

$$SS_{\text{Total}}=SS_{\text{Error}}+SS_{\text{Treatments}}$$

Число степеней свободы DF можно разделить аналогичным образом: один из этих компонентов (то есть для ошибки) определяет распределение хи-квадрат , которое описывает соответствующую сумму квадратов, в то время как то же самое верно для «обработок», если существует никакого лечебного эффекта.

$$DF_{\text{Total}}=DF_{\text{Error}}+DF_{\text{Treatments}}$$

тест F -

Основная статья: F-тест

Чтобы проверить статистическую значимость одностороннего дисперсионного анализа, мы сверяемся с таблицей F-вероятности, используя степени свободы на уровне альфа 0,05 . После вычисления F-статистики мы сравниваем значение на пересечении каждой степени свободы, также известное как критическое значение. Если F-статистика по величине превышает их критическое значение, мы можем сказать, что статистическая значимость существует на уровне альфа 0,05 .

F - тест используется для сравнения коэффициентов общего отклонения. Например, в однофакторном или однофакторном дисперсионном анализе статистическая значимость проверяется путем сравнения статистики F-критерия.

$$F={\frac {\text{variance between treatments}}{\text{variance within treatments}}}$$$$F={\frac {MS_{\text{Treatments}}}{MS_{\text{Error}}}}={{SS_{\text{Treatments}}/(I-1)} \over {SS_{\text{Error}}/(n_{T}-I)}}$$

где MS — среднеквадратичный, $I$ количество процедур и $n_{T}$ общее количество случаев

к F -распределению с $I-1$ являющиеся числителем степеней свободы и $n_{T}-I$ знаменатель степеней свободы. Использование F -распределения является естественным кандидатом, поскольку тестовая статистика представляет собой соотношение двух масштабированных сумм квадратов, каждая из которых соответствует масштабированному распределению хи-квадрат .

Ожидаемое значение F равно $1+{n\sigma _{\text{Treatment}}^{2}}/{\sigma _{\text{Error}}^{2}}$ (где $n$ — размер выборки лечения), который равен 1 для отсутствия эффекта лечения. По мере того, как значения F превышают 1, доказательства становятся все более несовместимыми с нулевой гипотезой. Два очевидных экспериментальных метода увеличения F — это увеличение размера выборки и уменьшение дисперсии ошибок за счет жесткого экспериментального контроля.

Существует два метода завершения проверки гипотезы ANOVA, оба из которых дают один и тот же результат:

• Учебный метод заключается в сравнении наблюдаемого значения F с критическим значением F, определенным по таблицам. Критическое значение F является функцией степеней свободы числителя и знаменателя и уровня значимости ( α ). Если F ≥ F _Critical , нулевая гипотеза отклоняется.
• Компьютерный метод вычисляет вероятность (р-значение) значения F, большего или равного наблюдаемому значению. Нулевая гипотеза отклоняется, если эта вероятность меньше или равна уровню значимости ( α ).

-тест ANOVA Известно, что F почти оптимален в смысле минимизации ложноотрицательных ошибок при фиксированной частоте ложноположительных ошибок (т.е. максимизации мощности при фиксированном уровне значимости). Например, чтобы проверить гипотезу о том, что различные медицинские методы лечения имеют одинаковый эффект, F -теста близко значения p приближаются к перестановочного теста : значениям p аппроксимация особенно близка, когда план сбалансирован. Такие перестановочные тесты характеризуют тесты с максимальной мощностью против всех альтернативных гипотез , как заметил Розенбаум . -тест ANOVA F (нулевая гипотеза о том, что все методы лечения имеют одинаковый эффект) рекомендуется в качестве практического теста из-за его устойчивости ко многим альтернативным распределениям.

Расширенный алгоритм

ANOVA состоит из отдельных частей; Разделение источников дисперсии и проверка гипотез могут использоваться индивидуально. ANOVA используется для поддержки других статистических инструментов. Регрессия сначала используется для сопоставления более сложных моделей с данными, затем используется ANOVA для сравнения моделей с целью выбора простых моделей, которые адекватно описывают данные. «Такие модели могут быть подобраны без какой-либо ссылки на ANOVA, но затем инструменты ANOVA можно использовать, чтобы придать некоторый смысл подобранным моделям и проверить гипотезы о группах коэффициентов». «[Мы] думаем об дисперсионном анализе как о способе понимания и структурирования многоуровневых моделей — не как об альтернативе регрессии, а как об инструменте для обобщения сложных многомерных выводов…»

Для одного фактора

Основная статья: Односторонний дисперсионный анализ

Самый простой эксперимент, подходящий для анализа ANOVA, — это полностью рандомизированный эксперимент с одним фактором. Более сложные эксперименты с одним фактором предполагают ограничения на рандомизацию и включают полностью рандомизированные блоки и латинские квадраты (и варианты: греко-латинские квадраты и т. д.). Более сложные эксперименты разделяют многие сложности множества факторов. относительно полное обсуждение анализа (модели, сводки данных, таблица ANOVA) полностью рандомизированного эксперимента Доступно .

Существует несколько альтернатив традиционному одностороннему дисперсионному анализу, например: гетероскедастический F-критерий Уэлча, гетероскедастический F-критерий Уэлча с усеченными средними и дисперсиями Винзора, тест Брауна-Форсайта, тест Александера-Говерна, тест второго порядка Джеймса и тест Крускала-Уоллиса. , доступно в onewaytests R

Полезно представлять каждую точку данных в следующей форме, называемой статистической моделью: $$Y_{ij}=\mu +\tau _{j}+\varepsilon _{ij}$$где

• я = 1, 2, 3, ..., р
• j = 1, 2, 3, ..., С
• μ = общее среднее (среднее)
• τ _j = дифференциальный эффект (ответ), связанный с j -уровнем X;
  это предполагает, что в целом значения τ _j в сумме равны нулю (т. е. ${\textstyle \sum _{j=1}^{C}\tau _{j}=0}$)
• ε _ij = шум или ошибка, связанная с конкретным ij значением данных

То есть мы представляем себе аддитивную модель, которая утверждает, что каждая точка данных может быть представлена ​​путем суммирования трех величин: истинного среднего значения, усредненного по всем исследуемым уровням факторов, плюс приростной компонент, связанный с конкретным столбцом (уровень фактора), плюс окончательный результат. компонент, связанный со всем остальным, влияющим на это конкретное значение данных.

По нескольким факторам

Основная статья: Двусторонний дисперсионный анализ

ANOVA обобщает изучение воздействия множества факторов. Когда эксперимент включает наблюдения на всех комбинациях уровней каждого фактора, его называют факториалом . Факторные эксперименты более эффективны, чем серия однофакторных экспериментов, и эффективность растет с увеличением числа факторов. Следовательно, факторные планы широко используются.

Использование ANOVA для изучения влияния множества факторов имеет сложности. В трехфакторном дисперсионном анализе с факторами x, y и z модель ANOVA включает члены для основных эффектов (x, y, z) и условия для взаимодействий (xy, xz, yz, xyz). Все термины требуют проверки гипотез. Увеличение количества терминов взаимодействия увеличивает риск того, что некоторые проверки гипотез случайно дадут ложноположительный результат. К счастью, опыт показывает, что взаимодействия высокого порядка встречаются редко. Способность обнаруживать взаимодействия является основным преимуществом многофакторного дисперсионного анализа. Проверка одного фактора за раз скрывает взаимодействия, но дает явно противоречивые экспериментальные результаты.

При взаимодействии следует соблюдать осторожность; Сначала проверьте условия взаимодействия и расширьте анализ за пределы ANOVA, если взаимодействия обнаружены. Тексты различаются рекомендациями относительно продолжения процедуры ANOVA после обнаружения взаимодействия. Взаимодействия усложняют интерпретацию экспериментальных данных. Ни расчеты значимости, ни предполагаемые эффекты лечения не могут приниматься за чистую монету. «Значительное взаимодействие часто маскирует значимость основных эффектов». Для улучшения понимания рекомендуется использовать графические методы. Регрессия часто бывает полезна. Подробное обсуждение взаимодействий доступно у Кокса (1958). Некоторые взаимодействия можно удалить (с помощью преобразований), а другие — нет.

Для снижения затрат используются различные методы с многофакторным дисперсионным анализом. Одним из методов, используемых в факторных планах, является минимизация репликации (возможно, отсутствие репликации при поддержке аналитических ухищрений ) и объединение групп, когда эффекты оказываются статистически (или практически) незначительными. Эксперимент со многими незначительными факторами может развалиться в эксперимент с несколькими факторами, поддерживаемыми множеством повторений.

Сопутствующий анализ

Некоторый анализ необходим для обоснования плана эксперимента, в то время как другой анализ проводится после того, как формально установлено, что изменения факторов приводят к статистически значимым изменениям в ответах. Поскольку экспериментирование является итеративным, результаты одного эксперимента меняют планы последующих экспериментов.

Подготовительный анализ

Количество экспериментальных единиц

При планировании эксперимента количество экспериментальных единиц планируется удовлетворить целям эксперимента. Эксперименты часто носят последовательный характер.

Ранние эксперименты часто предназначены для получения несмещенных к среднему оценок эффектов лечения и экспериментальных ошибок. Более поздние эксперименты часто предназначены для проверки гипотезы о том, что эффект лечения имеет важную величину; в этом случае количество экспериментальных единиц выбирается таким образом, чтобы эксперимент, помимо прочего, соответствовал бюджету и имел достаточную мощность.

В психологии обычно требуется отчет об анализе размера выборки. «Предоставьте информацию о размере выборки и процессе, который привел к принятию решений о размере выборки». Анализ, который записывается в протокол эксперимента до его проведения, рассматривается в заявках на гранты и в административных наблюдательных комиссиях.

Помимо анализа мощности, существуют менее формальные методы выбора количества экспериментальных единиц. К ним относятся графические методы, основанные на ограничении вероятности ложноотрицательных ошибок, графические методы, основанные на ожидаемом увеличении вариации (выше остатков) и методы, основанные на достижении желаемого доверительного интервала.

Анализ мощности

Анализ мощности часто применяется в контексте ANOVA, чтобы оценить вероятность успешного отклонения нулевой гипотезы, если мы предполагаем определенный дизайн ANOVA, размер эффекта в популяции, размер выборки и уровень значимости. Анализ мощности может помочь в планировании исследования, определяя, какой размер выборки потребуется, чтобы иметь разумную вероятность отклонения нулевой гипотезы, когда альтернативная гипотеза верна.

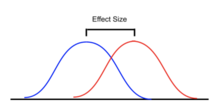
Размер эффекта

Размер эффекта

Основная статья: Размер эффекта

Для ANOVA было предложено несколько стандартизированных показателей эффекта, чтобы суммировать силу связи между предиктором(ами) и зависимой переменной или общую стандартизированную разницу полной модели. Стандартизированные оценки размера эффекта облегчают сравнение результатов исследований и дисциплин. Однако, хотя стандартизированные размеры эффекта обычно используются в большей части профессиональной литературы, для целей отчетности может быть предпочтительнее нестандартизированная мера размера эффекта, которая имеет непосредственно «значимые» единицы.

Подтверждение модели

Иногда проводятся тесты, чтобы определить, нарушены ли предположения ANOVA. Остатки исследуются или анализируются для подтверждения гомоскедастичности и общей нормальности. Остатки должны выглядеть как шум (нулевое среднее нормальное распределение), когда они отображаются как функция чего-либо, включая время и значения смоделированных данных. Тенденции намекают на взаимодействие между факторами или наблюдениями.

Последующие тесты

Статистически значимый эффект в ANOVA часто сопровождается дополнительными тестами. Это можно сделать для того, чтобы оценить, какие группы отличаются от других групп, или проверить различные другие целенаправленные гипотезы. Последующие тесты часто различают по тому, являются ли они «плановыми» ( априори ) или «постфактум ». Плановые тесты определяются до просмотра данных, а апостериорные тесты задуманы только после просмотра данных (хотя термин «апостериорный» используется непоследовательно).

Последующие тесты могут представлять собой «простые» попарные сравнения средних значений отдельных групп или могут быть «составными» сравнениями (например, сравнение объединенных средних значений групп A, B и C со средним значением группы D). При сравнении можно также использовать критерии тренда, такие как линейные и квадратичные зависимости, когда независимая переменная включает упорядоченные уровни. Часто последующие тесты включают метод корректировки проблемы множественных сравнений .

Последующие тесты для определения того, какие конкретные группы, переменные или факторы имеют статистически разные средние значения, включают тест диапазона Тьюки и новый тест множественных диапазонов Дункана . В свою очередь, эти тесты часто сопровождаются методологией компактного буквенного отображения (CLD) , чтобы сделать результаты упомянутых тестов более прозрачными для нестатистической аудитории.

Дизайн исследования

Существует несколько типов ANOVA. Многие статистики основывают ANOVA на дизайне эксперимента . особенно в протоколе, который определяет случайное назначение лечения субъектам; Описание механизма назначения в протоколе должно включать спецификацию структуры обработки и любой блокировки . Также принято применять ANOVA к данным наблюдений с использованием соответствующей статистической модели.

В некоторых популярных проектах используются следующие типы дисперсионного анализа:

• Однофакторный дисперсионный анализ используется для проверки различий между двумя или более независимыми группами (средними), например, разные уровни применения мочевины в культуре или разные уровни действия антибиотиков на несколько разных видов бактерий. или разные уровни воздействия того или иного лекарства на группы пациентов. Однако если эти группы не являются независимыми и существует порядок в группах (например, легкое, среднее и тяжелое заболевание) или в дозе препарата (например, 5 мг/мл, 10 мг/мл, 20 мг /мл) для одной и той же группы пациентов, то оценку линейного тренда следует использовать . Однако обычно однофакторный дисперсионный анализ используется для проверки различий как минимум между тремя группами, поскольку случай с двумя группами можно охватить с помощью t-критерия . Когда есть только два средства для сравнения, t-критерий ANOVA и F -критерий эквивалентны; связь между ANOVA и t определяется как F = t ² .
• Факторный дисперсионный анализ используется, когда имеется более одного фактора.
• ANOVA с повторными измерениями используется, когда для каждого фактора используются одни и те же субъекты (например, в продольном исследовании ).
• Многомерный дисперсионный анализ (MANOVA) используется, когда имеется более одной переменной отклика .

Предостережения

Сбалансированные эксперименты (с одинаковым размером выборки для каждого варианта лечения) относительно легко интерпретировать; несбалансированные эксперименты более сложны. Для однофакторного (одностороннего) ANOVA корректировка несбалансированных данных проста, но несбалансированному анализу не хватает как надежности, так и мощности. В более сложных конструкциях отсутствие баланса приводит к дальнейшим осложнениям. «Свойство ортогональности основных эффектов и взаимодействий, присутствующее в сбалансированных данных, не переносится на несбалансированный случай. Это означает, что обычные методы дисперсионного анализа не применимы. Следовательно, анализ несбалансированных факториалов гораздо сложнее, чем анализ сбалансированных. конструкции». В общем случае «дисперсионный анализ можно применять и к несбалансированным данным, но тогда суммы квадратов, средние квадраты и F -отношения будут зависеть от порядка, в котором рассматриваются источники вариаций».

ANOVA (частично) является тестом статистической значимости. Американская психологическая ассоциация (и многие другие организации) придерживается мнения, что простого сообщения о статистической значимости недостаточно и что предпочтительнее сообщать о доверительных границах.

Обобщения

ANOVA считается частным случаем линейной регрессии. что, в свою очередь, является частным случаем общей линейной модели . Все считают наблюдения суммой модели (подгонки) и невязки (ошибки), которую необходимо минимизировать.

Критерий Крускала -Уоллиса и критерий Фридмана являются непараметрическими тестами, которые не полагаются на предположение о нормальности.

Связь с линейной регрессией

Ниже мы поясним связь между многофакторным дисперсионным анализом и линейной регрессией.

Линейно переупорядочить данные так, чтобы $k$-е наблюдение связано с реакцией $y_{k}$ и факторы $Z_{k,b}$ где $b\in \{1,2,\ldots ,B\}$ обозначает различные факторы и $B$ это общее количество факторов. В одностороннем дисперсионном анализе $B=1$ и в двустороннем дисперсионном анализе $B=2$. Кроме того, мы предполагаем, что $b$-й фактор имеет $I_{b}$ уровни, а именно $\{1,2,\ldots ,I_{b}\}$. Теперь мы можем оперативно закодировать факторы в ${\textstyle \sum _{b=1}^{B}I_{b}}$ размерный вектор $v_{k}$.

Функция горячего кодирования $g_{b}:\{1,2,\ldots ,I_{b}\}\mapsto \{0,1\}^{I_{b}}$ определяется так, что $i$-я запись $g_{b}(Z_{k,b})$ является $$g_{b}(Z_{k,b})_{i}={\begin{cases}1&{\text{if }}i=Z_{k,b}\\0&{\text{otherwise}}\end{cases}}$$Вектор $v_{k}$ представляет собой конкатенацию всех вышеуказанных векторов для всех $b$. Таким образом, $v_{k}=[g_{1}(Z_{k,1}),g_{2}(Z_{k,2}),\ldots ,g_{B}(Z_{k,B})]$. Чтобы получить полностью общее $B$-способ взаимодействия ANOVA, мы также должны объединить каждый дополнительный член взаимодействия в векторе $v_{k}$ а затем добавьте термин перехвата. Пусть этот вектор будет $X_{k}$.

Имея эти обозначения, мы теперь имеем точную связь с линейной регрессией. Мы просто регрессируем реакцию $y_{k}$ против вектора $X_{k}$. Однако есть опасения по поводу идентифицируемости . Чтобы преодолеть такие проблемы, мы предполагаем, что сумма параметров внутри каждого набора взаимодействий равна нулю. Отсюда можно использовать F -статистику или другие методы для определения значимости отдельных факторов.

Пример

Мы можем рассмотреть пример двустороннего взаимодействия, где мы предполагаем, что первый фактор имеет 2 уровня, а второй фактор — 3 уровня.

Определять $a_{i}=1$ если $Z_{k,1}=i$ и $b_{i}=1$ если $Z_{k,2}=i$, то есть $a$ - это горячее кодирование первого фактора и $b$ — это горячее кодирование второго фактора.

При этом, $$X_{k}=[a_{1},a_{2},b_{1},b_{2},b_{3},a_{1}\times b_{1},a_{1}\times b_{2},a_{1}\times b_{3},a_{2}\times b_{1},a_{2}\times b_{2},a_{2}\times b_{3},1]$$где последний член является членом прерывания. Для более конкретного примера предположим, что $${\begin{aligned}Z_{k,1}&=2\\Z_{k,2}&=1\end{aligned}}$$Затем, $$X_{k}=[0,1,1,0,0,0,0,0,1,0,0,1]$$

См. также

• ANOVA по рангам
• ANOVA-одновременный компонентный анализ
• Ковариационный анализ ( ANCOVA )
• Анализ молекулярной дисперсии (AMOVA)
• Анализ ритмической дисперсии (ANORVA)
• Ожидаемые средние квадраты
• Объясненная вариация
• Оценка линейного тренда
• Дисперсионный анализ смешанного плана
• Многомерный ковариационный анализ ( MANCOVA )
• Перестановочный анализ дисперсии
• Разложение дисперсии

Ссылки

• Анскомб, Ф.Дж. (1948). «Достоверность сравнительных экспериментов». Журнал Королевского статистического общества. Серия А (Общая) . 111 (3): 181–211. дои : 10.2307/2984159 . JSTOR   2984159 . МР   0030181 .
• Бейли, РА (2008). План сравнительных экспериментов . Издательство Кембриджского университета. ISBN  978-0-521-68357-9 . Предварительные главы доступны в Интернете.
• Белль, Джеральд ван (2008). Статистические правила (2-е изд.). Хобокен, Нью-Джерси: Уайли. ISBN  978-0-470-14448-0 .
• Кокран, Уильям Г .; Кокс, Гертруда М. (1992). Экспериментальные конструкции (2-е изд.). Нью-Йорк: Уайли. ISBN  978-0-471-54567-5 .
• Коэн, Джейкоб (1988). Статистический анализ мощности для наук о поведении (2-е изд.). Рутледж ISBN   978-0-8058-0283-2
• Коэн, Джейкоб (1992). «Статистика – энергетический букварь». Психологический вестник . 112 (1): 155–159. дои : 10.1037/0033-2909.112.1.155 . ПМИД   19565683 . S2CID   14411587 .
• Кокс, Дэвид Р. (1958). Планирование экспериментов . Перепечатано как ISBN   978-0-471-57429-3
• Кокс, Дэвид Р. (2006). Принципы статистического вывода . Кембридж, Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-68567-2 .
• Фридман, Дэвид А. (2005). Статистические модели: теория и практика , Издательство Кембриджского университета. ISBN   978-0-521-67105-7
• Гельман, Эндрю (2005). «Дисперсионный анализ? Почему это важно как никогда». Анналы статистики . 33 : 1–53. arXiv : math/0504499 . дои : 10.1214/009053604000001048 . S2CID   13529149 .
• Гельман, Эндрю (2008). «Дисперсия, анализ». Новый экономический словарь Пэлгрейва (2-е изд.). Бейзингсток, Хэмпшир, Нью-Йорк: Пэлгрейв Макмиллан. ISBN  978-0-333-78676-5 .
• Хинкельманн, Клаус и Кемпторн, Оскар (2008). Планирование и анализ экспериментов . Том. I и II (Второе изд.). Уайли. ISBN  978-0-470-38551-7 .
• Хауэлл, Дэвид С. (2002). Статистические методы психологии (5-е изд.). Пасифик Гроув, Калифорния: Даксбери/Томсон Лиринг. ISBN  978-0-534-37770-0 .
• Кемпторн, Оскар (1979). Планирование и анализ экспериментов (исправленное переиздание (1952) под ред. Wiley). Роберт Э. Кригер. ISBN  978-0-88275-105-4 .
• Леманн, Э.Л. (1959) Проверка статистических гипотез. Джон Уайли и сыновья.
• Монтгомери, Дуглас К. (2001). Планирование и анализ экспериментов (5-е изд.). Нью-Йорк: Уайли. ISBN  978-0-471-31649-7 .
• Мур, Дэвид С. и Маккейб, Джордж П. (2003). Введение в практику статистики (4e). WH Фриман и Ко. ISBN   0-7167-9657-0
• Розенбаум, Пол Р. (2002). Наблюдательные исследования (2-е изд.). Нью-Йорк: Springer-Verlag. ISBN   978-0-387-98967-9
• Шеффе, Генри (1959). Дисперсионный анализ . Нью-Йорк: Уайли.
• Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Кембридж, Массачусетс: Belknap Press издательства Гарвардского университета. ISBN  978-0-674-40340-6 .
• Уилкинсон, Лиланд (1999). «Статистические методы в психологических журналах: рекомендации и пояснения». Американский психолог . 5 (8): 594–604. CiteSeerX   10.1.1.120.4818 . дои : 10.1037/0003-066X.54.8.594 . S2CID   428023 .

Дальнейшее чтение

• Фридман, Дэвид А .; Пизани, Роберт; Первс, Роджер (2007). Статистика (4-е изд.). WW Нортон и компания. ISBN  978-0-393-92972-0 .
• Табачник, Барбара Г.; Фиделл, Линда С. (2006). Использование многомерной статистики . Pearson International Edition (5-е изд.). Нидхэм, Массачусетс: Allyn & Bacon, Inc. ISBN  978-0-205-45938-4 .

• Вичура, Майкл Дж. (2006). Бескоординатный подход к линейным моделям . Кембриджская серия по статистической и вероятностной математике. Издательство Кембриджского университета. стр. xiv+199. ISBN  978-0-521-86842-6 . МР   2283455 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Кристенсен, Рональд (2002). Плоские ответы на сложные вопросы: теория линейных моделей (Третье изд.). Нью-Йорк: Спрингер. ISBN  978-0-387-95361-8 .
• Калинский, Тадеуш; Кагеяма, Санпей (2000). Блочные конструкции: подход рандомизации, Том I : Анализ . Конспект лекций по статистике. Том. 150. Нью-Йорк: Springer-Verlag. ISBN  978-0-387-98578-7 .
• Кокс, Дэвид Р .; Рид, Нэнси М. (2000). Теория планирования экспериментов . Чепмен и Холл/CRC. ISBN  978-1-58488-195-7 .
• Хеттманспергер, ТП; Маккин, JW (1998). Робастные непараметрические статистические методы . Статистическая библиотека Кендалла. Том. 5 (1-е изд.). Нью-Йорк: Публикация Ходдера Арнольда. стр. xiv+467. ISBN  978-0-340-54937-7 . МР   1604954 .
• Лентнер, Марвин; Бишоп, Томас (1993). Экспериментальный дизайн и анализ (2-е изд.). Блэксбург, Вирджиния: Книжная компания Valley. ISBN  978-0-9616255-2-8 .
• Пхадке, Мадхав С. (1989). Обеспечение качества с использованием надежной конструкции . Нью-Джерси: Прентис Холл PTR. ISBN  978-0-13-745167-8 .
• Коробка, ГЭП (1954). «Некоторые теоремы о квадратичных формах, применяемые при исследовании задач дисперсионного анализа, II. Эффекты неравенства дисперсии и корреляции между ошибками в двусторонней классификации» . Анналы математической статистики . 25 (3): 484. doi : 10.1214/aoms/1177728717 .
• Коробка, ГЭП (1954). «Некоторые теоремы о квадратичных формах, применяемые при исследовании задач дисперсионного анализа, I. Эффект неравенства дисперсии в односторонней классификации» . Анналы математической статистики . 25 (2): 290. дои : 10.1214/aoms/1177728786 .

• Коробка, ГЭП (1953). «Ненормальность и тесты на дисперсии». Биометрика . 40 (3/4): 318–335. дои : 10.1093/biomet/40.3-4.318 . JSTOR   2333350 .
• Фишер, Рональд (1918). «Исследования вариаций сельскохозяйственных культур. I. Исследование урожайности протравленного зерна из Бродбалка» (PDF) . Журнал сельскохозяйственных наук . 11 (2): 107–135. дои : 10.1017/S0021859600003750 . HDL : 2440/15170 . S2CID   86029217 . Архивировано (PDF) из оригинала 22 июня 2023 года . Проверено 5 февраля 2024 г.

Внешние ссылки

• SOCR : активность ANOVA
• Примеры всех моделей ANOVA и ANCOVA с тремя факторами обработки, включая рандомизированный блок, разделенный график, повторные измерения и латинские квадраты, а также их анализ в R (Университет Саутгемптона)
• Электронный справочник по статистическим методам NIST/SEMATECH, раздел 7.4.3: «Равны ли средние значения?»
• Дисперсионный анализ: Введение