Законы движения Ньютона

«Законы Ньютона» перенаправляется сюда. Чтобы узнать о других значениях, см. Закон Ньютона .

«F=ma» перенаправляется сюда. Информацию о соревнованиях по физике см. в Олимпиаде по физике США .

Законы движения Ньютона — это три физических закона , которые описывают связь между движением объекта и действующими на него силами . Эти законы, составляющие основу механики Ньютона , можно перефразировать следующим образом:

1. Тело остается в покое или движется с постоянной скоростью по прямой, за исключением случаев, когда на него действует сила.
2. В любой момент времени чистая сила, действующая на тело, равна ускорению тела, умноженному на его массу, или, что то же самое, скорости изменения импульса тела со временем.
3. Если два тела действуют друг на друга с силами, то эти силы имеют одинаковую величину, но противоположные направления.

Три закона движения были впервые сформулированы Исааком Ньютоном в его «Philosophiæ Naturalis Principia Mathematica» ( «Математические принципы естественной философии» ), первоначально опубликованном в 1687 году. Ньютон использовал их для исследования и объяснения движения многих физических объектов и систем. Со времени Ньютона новые идеи, особенно в отношении концепции энергии, построили на его фундаменте область классической механики . Также были обнаружены ограничения законов Ньютона; новые теории необходимы, когда объекты движутся с очень высокими скоростями ( специальная теория относительности ), очень массивны ( общая теория относительности ) или очень малы ( квантовая механика ).

Предварительные условия

Законы Ньютона часто формулируются в терминах масс точек или частиц , то есть тел, объем которых пренебрежимо мал. Это разумное приближение для реальных тел, когда движением внутренних частей можно пренебречь и когда расстояние между телами намного превышает размер каждого из них. Например, Землю и Солнце можно аппроксимировать как точечные, если рассматривать орбиту первого вокруг последнего, но Земля не является точечной, если рассматривать деятельность на ее поверхности.

Математическое описание движения, или кинематика , основано на идее указания положений с помощью числовых координат. Движение представлено этими числами, изменяющимися во времени: траектория тела представлена ​​функцией, которая присваивает каждому значению временной переменной значения всех координат положения. Самый простой случай — одномерный, то есть когда тело вынуждено двигаться только по прямой. Тогда его положение может быть задано одним числом, указывающим, где оно находится относительно некоторой выбранной контрольной точки. Например, тело может свободно скользить по дорожке, идущей слева направо, поэтому его местоположение можно указать по расстоянию от удобной нулевой точки или начала координат , при этом отрицательные числа обозначают положение слева, а положительные числа указывают позиции вправо. Если положение тела как функция времени $s(t)$, то его средняя скорость за интервал времени от $t_{0}$ к $t_{1}$ является $${\frac {\Delta s}{\Delta t}}={\frac {s(t_{1})-s(t_{0})}{t_{1}-t_{0}}}.$$Здесь греческая буква $\Delta$ ( дельта ) по традиции используется для обозначения «изменения». Положительная средняя скорость означает, что координата положения $s$ увеличивается в течение рассматриваемого интервала, отрицательная средняя скорость указывает на чистое уменьшение за этот интервал, а средняя скорость, равная нулю, означает, что тело заканчивает временной интервал в том же месте, где оно началось. Исчисление дает возможность определить мгновенную скорость, меру скорости и направления движения тела в один момент времени, а не за определенный интервал. Одним из обозначений мгновенной скорости является замена $\Delta$ с символом $d$, например, $$v={\frac {ds}{dt}}.$$Это означает, что мгновенная скорость является производной положения по времени. Грубо говоря, его можно рассматривать как соотношение бесконечно малого изменения положения $ds$ на бесконечно малый интервал времени $dt$ над которым это происходит. Более тщательно скорость и все другие производные можно определить, используя понятие предела . Функция $f(t)$ имеет предел в $L$ при заданном входном значении $t_{0}$ если разница между $f$ и $L$ можно сделать сколь угодно малым, выбрав вход достаточно близкий к $t_{0}$. Один пишет: $$\lim _{t\to t_{0}}f(t)=L.$$Мгновенную скорость можно определить как предел средней скорости, когда временной интервал сжимается до нуля: $${\frac {ds}{dt}}=\lim _{\Delta t\to 0}{\frac {s(t+\Delta t)-s(t)}{\Delta t}}.$$ Ускорение связано со скоростью, как скорость с положением: оно является производной скорости по времени. Ускорение также можно определить как предел: $$a={\frac {dv}{dt}}=\lim _{\Delta t\to 0}{\frac {v(t+\Delta t)-v(t)}{\Delta t}}.$$Следовательно, ускорение является второй производной положения, часто пишут ${\frac {d^{2}s}{dt^{2}}}$.

Положение, если рассматривать его как смещение от исходной точки, представляет собой вектор : величину, имеющую как величину, так и направление. Скорость и ускорение также являются векторными величинами. Математические инструменты векторной алгебры позволяют описывать движение в двух, трех и более измерениях. Векторы часто обозначаются стрелкой, например $\mathbf {s}$или жирным шрифтом, например ${\bf {s}}$. Часто векторы визуально представляются в виде стрелок, причем направление вектора соответствует направлению стрелки, а величина вектора обозначается длиной стрелки. В числовом виде вектор можно представить в виде списка; например, вектор скорости тела может быть $\mathbf {v} =(\mathrm {3~m/s} ,\mathrm {4~m/s} )$, что указывает на то, что он движется со скоростью 3 метра в секунду по горизонтальной оси и 4 метра в секунду по вертикальной оси. Одно и то же движение, описанное в другой системе координат, будет представлено разными числами, и для преобразования между этими альтернативами можно использовать векторную алгебру.

Изучение механики осложняется тем, что бытовые слова типа энергии употребляются с техническим смыслом. Более того, слова, являющиеся синонимами в повседневной речи, не являются синонимами в физике: сила — это не то же самое, что мощность или давление , например, а масса имеет иное значение, чем вес . Физическая концепция силы делает количественную повседневную идею толчка или притяжения. Силы в ньютоновской механике часто возникают из-за струн и веревок, трения, мышечных усилий, гравитации и т. д. Подобно перемещению, скорости и ускорению, сила является векторной величиной.

Законы

Первый закон

Искусственные спутники движутся по искривленным орбитам Земли , а не по прямым, из-за гравитации .

В переводе с латыни первый закон Ньютона гласит:

Каждый объект продолжает сохранять состояние покоя или равномерного прямолинейного движения, за исключением случаев, когда он вынужден изменить это состояние под действием приложенных к нему сил.

Первый закон Ньютона выражает принцип инерции : естественным поведением тела является движение по прямой с постоянной скоростью. Движение тела сохраняет статус-кво, но внешние силы могут его нарушить.

Современное понимание первого закона Ньютона состоит в том, что ни один инерциальный наблюдатель не имеет привилегий перед другими. Концепция инерционного наблюдателя делает количественным повседневную идею отсутствия ощущения воздействия движения. Например, человек, стоящий на земле и наблюдающий за проходящим мимо поездом, является инерционным наблюдателем. Если наблюдатель на земле видит, как поезд плавно движется по прямой с постоянной скоростью, то пассажир, сидящий в поезде, тоже будет инерционным наблюдателем: пассажир поезда не чувствует движения. Принцип, выраженный в первом законе Ньютона, заключается в том, что невозможно сказать, какой инерциальный наблюдатель «действительно» движется, а какой «действительно» стоит на месте. Состояние покоя одного наблюдателя — это состояние равномерного прямолинейного движения другого наблюдателя, и ни один эксперимент не может признать какую-либо точку зрения правильной или неправильной. Абсолютного стандарта отдыха не существует. Сам Ньютон считал, что абсолютные пространство и время существуют, но единственные меры пространства и времени, доступные эксперименту, относительны.

Второй закон

Изменение движения объекта пропорционально приложенной силе; и производится в направлении прямой линии, по которой действует сила.

Под «движением» Ньютон имел в виду величину, которую теперь называют импульсом , которая зависит от количества материи, содержащейся в теле, скорости, с которой движется это тело, и направления, в котором оно движется. В современных обозначениях импульс тела равен произведению его массы и скорости: $$\mathbf {p} =m\mathbf {v} \,,$$ где все три величины могут меняться с течением времени. Второй закон Ньютона в современной форме гласит, что производная импульса по времени — это сила: $$\mathbf {F} ={\frac {d\mathbf {p} }{dt}}\,.$$ Если масса $m$ не меняется со временем, то производная действует только на скорость, и поэтому сила равна произведению массы и производной скорости по времени, которая является ускорением: $$\mathbf {F} =m{\frac {d\mathbf {v} }{dt}}=m\mathbf {a} \,.$$ Поскольку ускорение является второй производной положения по времени, это также можно записать $$\mathbf {F} =m{\frac {d^{2}\mathbf {s} }{dt^{2}}}.$$

Диаграмма свободного тела для блока на наклонной плоскости, иллюстрирующая нормальную силу, перпендикулярную плоскости ( N ), нисходящую силу тяжести ( mg ) и силу f вдоль направления плоскости, которая может быть приложена, например , трением или веревкой

Силы, действующие на тело, складываются как векторы , и поэтому общая сила, действующая на тело, зависит как от величины, так и от направления отдельных сил. Когда результирующая сила, действующая на тело, равна нулю, то согласно второму закону Ньютона тело не ускоряется и считается, что оно находится в механическом равновесии . Состояние механического равновесия устойчиво , если при незначительном изменении положения тела тело остается вблизи этого равновесия. В противном случае равновесие неустойчиво.

Распространенным визуальным представлением сил, действующих согласованно, является диаграмма свободного тела , которая схематически изображает интересующее тело и силы, приложенные к нему внешними воздействиями. Например, диаграмма свободного тела блока, стоящего на наклонной плоскости, может иллюстрировать комбинацию силы гравитации, «нормальной» силы , трения и натяжения струны.

Второй закон Ньютона иногда представляют как определение силы, т. е. сила – это то, что существует, когда инерционный наблюдатель видит ускоряющееся тело. Чтобы это было больше, чем тавтология — ускорение подразумевает силу, сила подразумевает ускорение — необходимо также сделать какое-то другое утверждение о силе. Например, можно указать уравнение, подробно описывающее силу, как закон всемирного тяготения Ньютона . Подставив такое выражение для $\mathbf {F}$ во второй закон Ньютона можно записать уравнение с предсказательной силой. Второй закон Ньютона также рассматривается как определяющий исследовательскую программу физики, устанавливающий, что важными целями предмета являются выявление сил, присутствующих в природе, и каталогизация составляющих материи.

Третий закон

Каждому действию всегда противостоит равное противодействие; или взаимные действия двух тел друг на друга всегда равны и направлены в противоположные части.

Ракеты работают, создавая сильную силу реакции, направленную вниз, с помощью ракетных двигателей . Это толкает ракету вверх, независимо от земли или атмосферы .

Слишком краткие формулировки третьего закона, такие как «действие равно противодействию », могли вызвать путаницу среди поколений студентов: «действие» и «противодействие» применимы к разным телам. Например, рассмотрим книгу, лежащую на столе. Гравитация Земли давит на книгу. «Реакция» на это «действие» — это не сила поддержки стола, на котором держится книга, а гравитационное притяжение книги, действующее на Землю.

Третий закон Ньютона связан с более фундаментальным принципом сохранения импульса . Последнее остается верным даже в тех случаях, когда утверждение Ньютона не соответствует действительности, например, когда силовые поля , а также материальные тела переносят импульс, и когда импульс определен правильно, в том числе и в квантовой механике . В механике Ньютона, если два тела имеют импульсы $\mathbf {p} _{1}$ и $\mathbf {p} _{2}$ соответственно, то полный импульс пары равен $\mathbf {p} =\mathbf {p} _{1}+\mathbf {p} _{2}$, и скорость изменения $\mathbf {p}$ является $${\frac {d\mathbf {p} }{dt}}={\frac {d\mathbf {p} _{1}}{dt}}+{\frac {d\mathbf {p} _{2}}{dt}}.$$ Согласно второму закону Ньютона, первый член — это полная сила, действующая на первое тело, а второй член — это полная сила, действующая на второе тело. Если два тела изолированы от внешних влияний, единственная сила, действующая на первое тело, может быть со стороны второго, и наоборот. Согласно третьему закону Ньютона, эти силы имеют одинаковую величину, но противоположное направление, поэтому при сложении они взаимно сокращаются. $\mathbf {p}$ является постоянным. Альтернативно, если $\mathbf {p}$ как известно, постоянна, отсюда следует, что силы имеют одинаковую величину и противоположное направление.

Кандидаты в дополнительные законы

В различных источниках предлагалось возвысить до статуса законов Ньютона другие идеи, используемые в классической механике. Например, в механике Ньютона общая масса тела, образованного соединением двух меньших тел, равна сумме их индивидуальных масс. Фрэнк Вильчек предложил привлечь внимание к этому предположению, назвав его «нулевым законом Ньютона». Еще одним кандидатом на «нулевой закон» является тот факт, что в любой момент тело реагирует на силы, приложенные к нему в этот момент. Точно так же идея о том, что силы складываются одинаковыми векторами (или, другими словами, подчиняются принципу суперпозиции ), и идея о том, что силы изменяют энергию тела, были описаны как «четвертый закон».

Примеры

Изучение поведения массивных тел с помощью законов Ньютона известно как механика Ньютона. Некоторые примеры задач в механике Ньютона особенно примечательны по концептуальным или историческим причинам.

Равноускоренное движение

Основные статьи: Свободное падение и движение снаряда.

, Прыгающий мяч снятый со скоростью 25 кадров в секунду с использованием стробоскопической вспышки . В промежутках между отскоками высота мяча как функция времени близка к параболе , отклоняясь от параболической дуги из-за сопротивления воздуха, вращения и деформации в несферическую форму при ударе.

Если тело падает из состояния покоя вблизи поверхности Земли, то при отсутствии сопротивления воздуха оно будет ускоряться с постоянной скоростью. Это известно как свободное падение . Скорость, достигнутая во время свободного падения, пропорциональна затраченному времени, а пройденное расстояние пропорционально квадрату затраченного времени. Важно отметить, что ускорение одинаково для всех тел независимо от их массы. Это следует из объединения второго закона движения Ньютона с его законом всемирного тяготения . Последний утверждает, что величина силы гравитации Земли, действующей на тело, равна $$F={\frac {GMm}{r^{2}}},$$ где $m$ - масса падающего тела, $M$ это масса Земли, $G$ – постоянная Ньютона, а $r$ — это расстояние от центра Земли до местоположения тела, которое очень близко к радиусу Земли. Установка этого значения равным $ma$, масса тела $m$ сокращается с обеих сторон уравнения, оставляя ускорение, которое зависит от $G$, $M$, и $r$, и $r$ можно принять постоянным. Это конкретное значение ускорения обычно обозначается $g$: $$g={\frac {GM}{r^{2}}}\approx \mathrm {9.8~m/s^{2}} .$$

Если тело не выводится из состояния покоя, а вместо этого пускается вверх и/или горизонтально с ненулевой скоростью, то свободное падение становится движением снаряда . Когда сопротивлением воздуха можно пренебречь, снаряды следуют по траектории в форме параболы , поскольку сила тяжести влияет на вертикальное движение тела, а не на его горизонтальное. В пике траектории снаряда его вертикальная скорость равна нулю, но ускорение равно $g$ вниз, как всегда. Установка неправильного вектора, равного нулю, является распространенной путаницей среди студентов-физиков.

Равномерное круговое движение

Основная статья: Круговое движение

Два объекта находятся в равномерном круговом движении, вращаясь вокруг барицентра (центра масс обоих объектов).

Когда тело движется равномерно по кругу, сила, действующая на него, меняет направление его движения, но не скорость. Для тела, движущегося по окружности радиуса $r$ с постоянной скоростью $v$, его ускорение имеет величину $$a={\frac {v^{2}}{r}}$$и направлена ​​к центру круга. Поэтому сила, необходимая для поддержания этого ускорения, называемая центростремительной силой , также направлена ​​к центру круга и имеет величину $mv^{2}/r$. Многие орбиты , например орбиты Луны вокруг Земли, можно аппроксимировать равномерным круговым движением. В таких случаях центростремительная сила является гравитацией и по закону всемирного тяготения Ньютона имеет величину $GMm/r^{2}$, где $M$ - это масса большего тела, на орбите которого вращаются. Следовательно, массу тела можно рассчитать на основе наблюдений за другим телом, вращающимся вокруг него.

Пушечное ядро ​​Ньютона — это мысленный эксперимент , который интерполирует движение снаряда и равномерное круговое движение. Пушечное ядро, слабо брошенное с края высокой скалы, упадет на землю за то же время, как если бы оно было сброшено из состояния покоя, поскольку сила гравитации влияет только на импульс ядра в направлении вниз, и ее эффект не уменьшается при горизонтальном движении. Если ядро ​​запустить с большей начальной горизонтальной скоростью, то оно пролетит большее расстояние, прежде чем упадет на землю, но все равно упадет на землю за то же время. Однако если ядро ​​запустить с еще большей начальной скоростью, то кривизна Земли станет значительной: сама земля выгнется в сторону от падающего ядра. Очень быстрое пушечное ядро ​​упадет с инерционной прямой траектории с той же скоростью, с которой Земля изгибается под ним; другими словами, он будет находиться на орбите (представляя, что его не замедляет сопротивление воздуха или препятствия).

Гармоническое движение

Основная статья: Гармонический осциллятор

Недемпфированная система пружина-масса совершает простое гармоническое движение.

Рассмотрим тело массы $m$ способен передвигаться по $x$ оси и предположим, что точка равновесия существует в положении $x=0$. То есть на $x=0$, результирующая сила, действующая на тело, равна нулевому вектору, и согласно второму закону Ньютона тело не будет ускоряться. Если сила, действующая на тело, пропорциональна смещению от точки равновесия и направлена ​​к точке равновесия, то тело будет совершать простое гармоническое движение . Записав силу как $F=-kx$, второй закон Ньютона становится $$m{\frac {d^{2}x}{dt^{2}}}=-kx\,.$$ Это дифференциальное уравнение имеет решение $$x(t)=A\cos \omega t+B\sin \omega t\,$$ где частота $\omega$ равно ${\sqrt {k/m}}$и константы $A$ и $B$ можно вычислить, зная, например, положение и скорость тела в данный момент времени, например $t=0$.

Одна из причин, по которой гармонический осциллятор является концептуально важным примером, заключается в том, что он является хорошим приближением для многих систем, близких к устойчивому механическому равновесию. Например, маятник имеет устойчивое равновесие в вертикальном положении: если он там неподвижен, то он останется там, а если его слегка подтолкнуть, то он будет раскачиваться вперед и назад. Если пренебречь сопротивлением воздуха и трением в шарнире, то сила, действующая на маятник, равна силе тяжести, и второй закон Ньютона принимает вид $${\frac {d^{2}\theta }{dt^{2}}}=-{\frac {g}{L}}\sin \theta ,$$где $L$ длина маятника и $\theta$ это его угол от вертикали. Когда угол $\theta$ мал синус , $\theta$ почти равен $\theta$ (см. ряд Тейлора ), и поэтому это выражение упрощается до уравнения простого гармонического осциллятора с частотой $\omega ={\sqrt {g/L}}$.

Гармонический осциллятор может затухать, часто за счет трения или вязкого сопротивления, и в этом случае энергия истекает из осциллятора, и амплитуда колебаний со временем уменьшается. Кроме того, гармонический осциллятор может приводиться в движение приложенной силой, что может привести к явлению резонанса .

Объекты с переменной массой

Основная статья: Система переменной массы

Ракеты, такие как космический челнок «Атлантис» , толкают материю в одном направлении, а корабль толкают в другом. Это означает, что толкаемая масса ракеты и оставшийся в ней запас топлива постоянно меняются.

Ньютоновская физика рассматривает материю как нечто не созданное и не уничтоженное, хотя ее можно перестроить. Может случиться так, что интересующий объект приобретает или теряет массу из-за того, что к нему добавляется или удаляется материя. В такой ситуации законы Ньютона можно применить к отдельным частям материи, отслеживая, какие части принадлежат интересующему объекту с течением времени. Например, если ракета массой $M(t)$, движущийся со скоростью $\mathbf {v} (t)$, выбрасывает вещество со скоростью $\mathbf {u}$ относительно ракеты, то $$\mathbf {F} =M{\frac {d\mathbf {v} }{dt}}-\mathbf {u} {\frac {dM}{dt}}\,$$ где $\mathbf {F}$ — чистая внешняя сила (например, гравитационное притяжение планеты).

Работа и энергия

Физики разработали концепцию энергии после Ньютона, но она стала неотъемлемой частью того, что считается «ньютоновской» физикой. Энергию можно в общих чертах разделить на кинетическую , обусловленную движением тела, и потенциальную , обусловленную положением тела относительно других. Тепловая энергия , энергия, переносимая тепловым потоком, представляет собой тип кинетической энергии, связанный не с макроскопическим движением объектов, а с движением атомов и молекул, из которых они состоят. Согласно теореме о работе энергии , когда на тело действует сила, пока это тело движется вдоль линии силы, сила совершает работу над телом, и количество совершаемой работы равно изменению кинетической энергии тела. . Во многих представляющих интерес случаях чистая работа, совершаемая силой при движении тела по замкнутому контуру — начиная с точки, двигаясь по некоторой траектории и возвращаясь в исходную точку, — равна нулю. Если это так, то силу можно записать через градиент функции, называемой скалярным потенциалом : $$\mathbf {F} =-\mathbf {\nabla } U\,.$$ Это верно для многих сил, включая силу гравитации, но не для трения; действительно, почти любая задача в учебнике механики, не связанная с трением, может быть выражена таким образом. То, что силу можно записать таким образом, можно понять из закона сохранения энергии . Без трения, рассеивающего энергию тела в тепло, энергия тела будет обмениваться между потенциальной и (нетепловой) кинетической формой, в то время как общее количество остается постоянным. Любой прирост кинетической энергии, который происходит, когда результирующая сила, действующая на тело, ускоряет его до более высокой скорости, должна сопровождаться потерей потенциальной энергии. Таким образом, результирующая сила, действующая на тело, определяется тем, как уменьшается потенциальная энергия.

Движение и вращение твердого тела

Твердое тело — это объект, размер которого слишком велик, чтобы им можно было пренебречь, и который сохраняет одну и ту же форму с течением времени. В ньютоновской механике под движением твердого тела часто понимают разделение его на движение центра масс тела и движение вокруг центра масс.

Центр масс

Основная статья: Центр масс

Общий центр масс вилки , пробки и зубочистки находится на кончике ручки.

Важные аспекты движения протяженного тела можно понять, если представить массу этого тела сосредоточенной в одной точке, известной как центр масс. Местоположение центра масс тела зависит от того, как распределен материал этого тела. Для коллекции точечных объектов с массами $m_{1},\ldots ,m_{N}$ на позициях $\mathbf {r} _{1},\ldots ,\mathbf {r} _{N}$, центр масс находится в $$\mathbf {R} =\sum _{i=1}^{N}{\frac {m_{i}\mathbf {r} _{i}}{M}},$$ где $M$ — общая масса коллекции. В отсутствие внешней внешней силы центр масс движется с постоянной скоростью по прямой. Это относится, например, к столкновению двух тел. Если общая внешняя сила не равна нулю, то центр масс меняет скорость, как если бы он был точечным телом массы. $M$. Это следует из того факта, что внутренние силы внутри совокупности, силы, которые объекты оказывают друг на друга, возникают в сбалансированных парах согласно третьему закону Ньютона. В системе двух тел, одно из которых значительно массивнее другого, центр масс будет примерно совпадать с расположением более массивного тела.

Вращательные аналоги законов Ньютона.

Когда законы Ньютона применяются к вращающимся протяженным телам, они приводят к новым величинам, аналогичным тем, которые упоминались в первоначальных законах. Аналогом массы является момент инерции , аналогом импульса является угловой момент , а аналогом силы — крутящий момент .

Угловой момент рассчитывается относительно контрольной точки. Если вектор перемещения от опорной точки к телу равен $\mathbf {r}$ и тело имеет импульс $\mathbf {p}$, то угловой момент тела относительно этой точки, используя векторное векторное произведение , равен $$\mathbf {L} =\mathbf {r} \times \mathbf {p} .$$ Взяв производную по времени от углового момента, получим $${\frac {d\mathbf {L} }{dt}}=\left({\frac {d\mathbf {r} }{dt}}\right)\times \mathbf {p} +\mathbf {r} \times {\frac {d\mathbf {p} }{dt}}=\mathbf {v} \times m\mathbf {v} +\mathbf {r} \times \mathbf {F} .$$ Первый член исчезает, потому что $\mathbf {v}$ и $m\mathbf {v}$ указать в том же направлении. Оставшийся член представляет собой крутящий момент, $$\mathbf {\tau } =\mathbf {r} \times \mathbf {F} .$$ Когда крутящий момент равен нулю, угловой момент постоянен, точно так же, как когда сила равна нулю, импульс постоянен. Крутящий момент может обратиться в нуль даже при силе, отличной от нуля, если тело находится в опорной точке ( $\mathbf {r} =0$) или если сила $\mathbf {F}$ и вектор смещения $\mathbf {r}$ направлены вдоль одной линии.

Угловой момент совокупности точечных масс и, следовательно, протяженного тела, находится путем сложения вкладов каждой из точек. Это дает возможность охарактеризовать вращение тела вокруг оси путем сложения угловых моментов его отдельных частей. Результат зависит от выбранной оси, формы тела и скорости вращения.

Многочастичная гравитационная система

Основные статьи: Задача двух тел и Задача трех тел.

Анимация трех точек или тел, притягивающихся друг к другу

Закон всемирного тяготения Ньютона гласит, что любое тело притягивает любое другое тело вдоль соединяющей их прямой линии. Величина силы притяжения пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Поиск формы орбит, которую будет производить закон обратных квадратов силы, известен как проблема Кеплера . Проблему Кеплера можно решить несколькими способами, в том числе путем демонстрации вектора Лапласа – Рунге – Ленца : постоянства или применив преобразование двойственности к двумерному гармоническому осциллятору. Как бы она ни была решена, в результате орбиты будут иметь конические сечения , то есть эллипсы (включая круги), параболы или гиперболы . Эксцентриситет орбиты и, следовательно , тип конического сечения определяются энергией и угловым моментом вращающегося тела. Планеты не обладают достаточной энергией, чтобы покинуть Солнце, поэтому их орбиты в хорошем приближении представляют собой эллипсы; поскольку планеты притягиваются друг к другу, реальные орбиты не являются точно коническими сечениями.

Если добавить третью массу, то задача Кеплера становится задачей трёх тел, которая вообще не имеет точного решения в замкнутой форме . То есть невозможно начать с дифференциальных уравнений, подразумеваемых законами Ньютона, и после конечной последовательности стандартных математических операций получить уравнения, выражающие движение трех тел во времени. Численные методы можно применить для получения полезных, хотя и приблизительных результатов для задачи трех тел. Положения и скорости тел могут храниться в переменных в памяти компьютера; Законы Ньютона используются для расчета того, как скорости будут меняться за короткий промежуток времени, и, зная скорости, можно вычислить изменения положения за этот промежуток времени. Этот процесс зациклен для приблизительного расчета траекторий тел. Вообще говоря, чем короче временной интервал, тем точнее приближение.

Хаос и непредсказуемость

Нелинейная динамика

Основная статья: Теория хаоса

Три двойных маятника, инициализированные почти одинаковыми начальными условиями, со временем расходятся.

Законы движения Ньютона допускают возможность хаоса . То есть, качественно говоря, физические системы, подчиняющиеся законам Ньютона, могут проявлять чувствительную зависимость от своих начальных условий: небольшое изменение положения или скорости одной части системы может привести к тому, что вся система за короткое время поведет себя совершенно иным образом. . Примечательные примеры включают задачу трех тел, двойной маятник , динамический бильярд и задачу Ферми-Пасты-Улама-Цингу .

Законы Ньютона можно применить к жидкостям, если рассматривать жидкость как состоящую из бесконечно малых частей, каждая из которых оказывает воздействие на соседние части. Уравнение количества движения Эйлера является выражением второго закона Ньютона, адаптированного к гидродинамике. Жидкость описывается полем скоростей, т. е. функцией $\mathbf {v} (\mathbf {x} ,t)$ который присваивает вектор скорости каждой точке пространства и времени. Небольшой объект, увлекаемый потоком жидкости, может изменить скорость по двум причинам: во-первых, потому, что поле скорости в его положении меняется с течением времени, и, во-вторых, потому, что он перемещается в новое место, где поле скорости имеет другое значение. Следовательно, когда второй закон Ньютона применяется к бесконечно малой порции жидкости, ускорение $\mathbf {a}$ имеет два термина, комбинацию, известную как полная или материальная производная . Масса бесконечно малой части зависит от плотности жидкости , и на нее действует результирующая сила, если давление жидкости меняется от одной ее стороны к другой. Соответственно, $\mathbf {a} =\mathbf {F} /m$ становится $${\frac {\partial v}{\partial t}}+(\mathbf {\nabla } \cdot \mathbf {v} )\mathbf {v} =-{\frac {1}{\rho }}\mathbf {\nabla } P+\mathbf {f} ,$$ где $\rho$ плотность, $P$ это давление, и $\mathbf {f}$ означает внешнее воздействие, такое как гравитационное притяжение. Учет эффекта вязкости превращает уравнение Эйлера в уравнение Навье – Стокса : $${\frac {\partial v}{\partial t}}+(\mathbf {\nabla } \cdot \mathbf {v} )\mathbf {v} =-{\frac {1}{\rho }}\mathbf {\nabla } P+\nu \nabla ^{2}\mathbf {v} +\mathbf {f} ,$$ где $\nu$ – кинематическая вязкость .

Особенности

Математически возможно, что совокупность точечных масс, движущихся в соответствии с законами Ньютона, отбросит некоторые из них с такой силой, что они улетят в бесконечность за конечное время. Это нефизическое поведение, известное как «сингулярность отсутствия столкновений». зависит от того, что массы точечны и способны приближаться друг к другу сколь угодно близко, а также от отсутствия релятивистского ограничения скорости в ньютоновской физике.

Пока неизвестно, демонстрируют ли уравнения Эйлера и Навье – Стокса аналогичное поведение изначально гладких решений, «раздувающихся» за конечное время. Вопрос о существовании и гладкости решений Навье–Стокса является одной из задач Премии тысячелетия .

Связь с другими формулировками классической физики

Классическая механика может быть математически сформулирована множеством различных способов, кроме «ньютоновского» описания (которое само по себе, конечно, включает в себя вклад других авторов как до, так и после Ньютона). Физическое содержание этих различных формулировок такое же, как и у ньютоновских, но они дают разное понимание и облегчают различные типы вычислений. Например, механика Лагранжа помогает выявить связь между симметрией и законами сохранения, и она полезна при расчете движения связанных тел, таких как масса, ограниченная в движении по криволинейной траектории или по поверхности сферы. Гамильтонова механика удобна для статистической физики , приводит к дальнейшему пониманию симметрии, и могут быть развиты в сложные методы теории возмущений . Из-за широты этих тем обсуждение здесь будет ограничено кратким рассмотрением того, как они переформулируют законы движения Ньютона.

лагранжиан

Лагранжева механика отличается от ньютоновской формулировки тем, что рассматривает сразу все траектории, а не предсказывает движение тела в один момент. В лагранжевой механике традиционно положение обозначают через $q$ и скорость с ${\dot {q}}$. Простейшим примером является массивная точечная частица, лагранжиан которой можно записать как разность ее кинетической и потенциальной энергий: $$L(q,{\dot {q}})=T-V,$$ где кинетическая энергия $$T={\frac {1}{2}}m{\dot {q}}^{2}$$ а потенциальная энергия является некоторой функцией положения, $V(q)$. Физический путь, который пройдет частица между начальной точкой $q_{i}$ и финальная точка $q_{f}$ - это путь, для которого интеграл от лагранжиана является «стационарным». То есть физический путь обладает тем свойством, что небольшие его возмущения в первом приближении не изменят интеграл лагранжиана. Вариационное исчисление предоставляет математические инструменты для нахождения этого пути. Применение вариационного исчисления к задаче поиска пути дает уравнение Эйлера – Лагранжа для частицы: $${\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {q}}}}\right)={\frac {\partial L}{\partial q}}.$$ Оценка частных производных лагранжиана дает $${\frac {d}{dt}}(m{\dot {q}})=-{\frac {dV}{dq}},$$ что является повторением второго закона Ньютона. Левая часть — это производная импульса по времени, а правая часть — это сила, представленная через потенциальную энергию.

Ландау и Лифшиц утверждают, что лагранжева формулировка делает концептуальное содержание классической механики более ясным, чем начало с законов Ньютона. Лагранжева механика обеспечивает удобную основу для доказательства теоремы Нётер , связывающей симметрию и законы сохранения. Сохранение импульса можно получить, применив теорему Нётер к лагранжиану многочастичной системы, поэтому третий закон Ньютона — это скорее теорема, чем предположение.

гамильтониан

Эмми Нётер , чье доказательство знаменитой теоремы, связывающей симметрию и законы сохранения, в 1915 году стало ключевым достижением в современной физике и может быть удобно сформулировано на языке лагранжевой или гамильтоновой механики.

В гамильтоновой механике динамика системы представлена ​​функцией, называемой гамильтонианом, которая во многих интересующих случаях равна полной энергии системы. Гамильтониан является функцией положений и импульсов всех тел, составляющих систему, а также может явно зависеть от времени. Производные по времени переменных положения и импульса задаются частными производными гамильтониана через уравнения Гамильтона . Самый простой пример — точечная масса. $m$ вынужден двигаться прямолинейно под действием потенциала. Письмо $q$ для координаты положения и $p$ для импульса тела гамильтониан равен $${\mathcal {H}}(p,q)={\frac {p^{2}}{2m}}+V(q).$$ В этом примере уравнения Гамильтона имеют вид $${\frac {dq}{dt}}={\frac {\partial {\mathcal {H}}}{\partial p}}$$ и $${\frac {dp}{dt}}=-{\frac {\partial {\mathcal {H}}}{\partial q}}.$$ Оценивая эти частные производные, первое уравнение становится $${\frac {dq}{dt}}={\frac {p}{m}},$$ которое воспроизводит известное утверждение о том, что импульс тела является произведением его массы и скорости. Производная импульса по времени равна $${\frac {dp}{dt}}=-{\frac {dV}{dq}},$$ что, после отождествления отрицательной производной потенциала с силой, снова является вторым законом Ньютона.

Как и в лагранжевой формулировке, в гамильтоновой механике сохранение импульса можно вывести с помощью теоремы Нётер, что делает третий закон Ньютона идеей, которая скорее выводится, чем предполагается.

Среди предложений по реформированию стандартной вводной программы по физике есть одно, которое преподает концепцию энергии перед концепцией силы, по сути, «вводную гамильтонову механику».

Гамильтон – Якоби

Уравнение Гамильтона-Якоби дает еще одну формулировку классической механики, которая делает ее математически аналогичной волновой оптике . В этой формулировке также используются функции Гамильтона, но иначе, чем в формулировке, описанной выше. Пути, пройденные телами или совокупностями тел, выводятся из функции $S(\mathbf {q} _{1},\mathbf {q} _{2},\ldots ,t)$ позиций $\mathbf {q} _{i}$ и время $t$. Гамильтониан включен в уравнение Гамильтона – Якоби, дифференциальное уравнение для $S$. Тела движутся во времени так, что их траектории перпендикулярны поверхностям постоянных тел. $S$, аналогично тому, как луч света распространяется в направлении, перпендикулярном его волновому фронту. Проще всего это выразить для случая одной точечной массы, когда $S$ это функция $S(\mathbf {q} ,t)$, а точечная масса движется в направлении, вдоль которого $S$ меняется наиболее резко. Другими словами, импульс точечной массы — градиент это $S$: $$\mathbf {v} ={\frac {1}{m}}\mathbf {\nabla } S.$$ Уравнение Гамильтона – Якоби для точечной массы имеет вид $$-{\frac {\partial S}{\partial t}}=H\left(\mathbf {q} ,\mathbf {\nabla } S,t\right).$$ Связь с законами Ньютона можно увидеть, рассматривая точечную массу, движущуюся в независимом от времени потенциале. $V(\mathbf {q} )$, и в этом случае уравнение Гамильтона–Якоби принимает вид $$-{\frac {\partial S}{\partial t}}={\frac {1}{2m}}\left(\mathbf {\nabla } S\right)^{2}+V(\mathbf {q} ).$$ Учитывая градиент обеих сторон, это становится $$-\mathbf {\nabla } {\frac {\partial S}{\partial t}}={\frac {1}{2m}}\mathbf {\nabla } \left(\mathbf {\nabla } S\right)^{2}+\mathbf {\nabla } V.$$ Меняя порядок частных производных в левой части и используя правила степени и цепочки для первого члена в правой части, $$-{\frac {\partial }{\partial t}}\mathbf {\nabla } S={\frac {1}{m}}\left(\mathbf {\nabla } S\cdot \mathbf {\nabla } \right)\mathbf {\nabla } S+\mathbf {\nabla } V.$$ Собрав вместе члены, которые зависят от градиента $S$, $$\left[{\frac {\partial }{\partial t}}+{\frac {1}{m}}\left(\mathbf {\nabla } S\cdot \mathbf {\nabla } \right)\right]\mathbf {\nabla } S=-\mathbf {\nabla } V.$$ Это еще одно перевыражение второго закона Ньютона. Выражение в скобках представляет собой полную или материальную производную , как упоминалось выше, в котором первый член указывает, как дифференцируемая функция изменяется со временем в фиксированном месте, а второй член отражает то, как движущаяся частица будет видеть разные значения этой функции по мере своего перемещения из места в место: $$\left[{\frac {\partial }{\partial t}}+{\frac {1}{m}}\left(\mathbf {\nabla } S\cdot \mathbf {\nabla } \right)\right]=\left[{\frac {\partial }{\partial t}}+\mathbf {v} \cdot \mathbf {\nabla } \right]={\frac {d}{dt}}.$$

Связь с другими физическими теориями

Термодинамика и статистическая физика

Моделирование более крупной, но все же микроскопической частицы (желтого цвета), окруженной газом из более мелких частиц, иллюстрирующей броуновское движение.

В статистической физике кинетическая теория газов (обычно порядка числа Авогадро применяет законы движения Ньютона к большому числу частиц ). Кинетическая теория может объяснить, например, давление , которое газ оказывает на контейнер, удерживающий его, как совокупность множества ударов атомов, каждый из которых сообщает крошечный импульс.

Уравнение Ланжевена представляет собой частный случай второго закона Ньютона, адаптированный для случая описания небольшого объекта, стохастически бомбардируемого объектами еще меньшего размера. Это можно написать $$m\mathbf {a} =-\gamma \mathbf {v} +\mathbf {\xi } \,$$где $\gamma$ это коэффициент лобового сопротивления и $\mathbf {\xi }$ — это сила, которая случайным образом меняется от момента к моменту и представляет собой суммарный эффект столкновений с окружающими частицами. Это используется для моделирования броуновского движения .

Электромагнетизм

Три закона Ньютона можно применить к явлениям, связанным с электричеством и магнетизмом , хотя существуют тонкости и оговорки.

Закон Кулона для электрической силы между двумя неподвижными электрически заряженными телами имеет почти ту же математическую форму, что и закон всемирного тяготения Ньютона: сила пропорциональна произведению зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по прямой между ними. Кулоновская сила, благодаря которой заряд $q_{1}$ действует по обвинению $q_{2}$ равна по величине силе, которая $q_{2}$ оказывает на $q_{1}$, и он указывает в совершенно противоположном направлении. Таким образом, закон Кулона согласуется с третьим законом Ньютона.

Электромагнетизм рассматривает силы как создаваемые полями, действующими на заряды. Закон силы Лоренца дает выражение для силы, действующей на заряженное тело, которое можно включить во второй закон Ньютона, чтобы вычислить его ускорение. Согласно закону силы Лоренца, на заряженное тело, находящееся в электрическом поле, действует сила, пропорциональная его заряду. $q$ и напряженности электрического поля. Кроме того, на движущееся заряженное тело в магнитном поле действует сила, также пропорциональная его заряду, в направлении, перпендикулярном как полю, так и направлению движения тела. Используя векторное векторное произведение , $$\mathbf {F} =q\mathbf {E} +q\mathbf {v} \times \mathbf {B} .$$

Действует закон силы Лоренца: электроны изгибаются по круговой траектории под действием магнитного поля.

Если электрическое поле исчезает ( $\mathbf {E} =0$), то сила будет перпендикулярна движению заряда, как и в случае с равномерным круговым движением, изученным выше, и заряд будет вращаться (или, в более общем случае, двигаться по спирали ) вокруг силовых линий магнитного поля с циклотронной частотой $\omega =qB/m$. Масс-спектрометрия работает путем приложения электрических и/или магнитных полей к движущимся зарядам и измерения результирующего ускорения, которое по закону силы Лоренца дает отношение массы к заряду .

Совокупность заряженных тел не всегда подчиняется третьему закону Ньютона: может произойти изменение импульса одного тела без компенсаторного изменения импульса другого. Расхождение объясняется импульсом, переносимым самим электромагнитным полем. Импульс единицы объема электромагнитного поля пропорционален вектору Пойнтинга .

Существует тонкий концептуальный конфликт между электромагнетизмом и первым законом Ньютона: теория электромагнетизма Максвелла предсказывает, что электромагнитные волны будут распространяться через пустое пространство с постоянной, определенной скоростью. Таким образом, некоторые инерциальные наблюдатели, по-видимому, имеют привилегированный статус перед другими, а именно те, кто измеряет скорость света и находит ее значение, предсказанное уравнениями Максвелла. Другими словами, свет обеспечивает абсолютный стандарт скорости, однако принцип инерции утверждает, что такого стандарта не должно быть. Это противоречие разрешается в специальной теории относительности, которая пересматривает понятия пространства и времени таким образом, что все инерциальные наблюдатели соглашаются со скоростью света в вакууме.

Специальная теория относительности

Дополнительная информация: Релятивистская механика и ускорение (специальная теория относительности).

В специальной теории относительности нарушается правило, которое Вильчек назвал «нулевым законом Ньютона»: масса составного объекта — это не просто сумма масс отдельных частей. Первый закон Ньютона – движение по инерции – остается верным. Форма второго закона Ньютона, согласно которой сила — это скорость изменения импульса, также справедлива, как и закон сохранения импульса. Однако определение импульса изменено. Среди последствий этого — тот факт, что чем быстрее движется тело, тем труднее его ускорить, и поэтому, сколько бы сил ни прилагалось, тело не может быть ускорено до скорости света. В зависимости от решаемой задачи импульс в специальной теории относительности можно представить как трехмерный вектор: $\mathbf {p} =m\gamma \mathbf {v}$, где $m$ тела это масса покоя и $\gamma$ – фактор Лоренца , который зависит от скорости тела. Альтернативно, импульс и сила могут быть представлены в виде четырех векторов .

Третий закон Ньютона должен быть модифицирован в специальной теории относительности. Третий закон относится к силам, действующим между двумя телами в один и тот же момент времени, а ключевой особенностью специальной теории относительности является то, что одновременность относительна. События, происходящие в одно и то же время относительно одного наблюдателя, могут происходить в разное время относительно другого. Таким образом, в данной системе отсчета наблюдателя действие и противодействие не могут быть строго противоположными, и общий импульс взаимодействующих тел может не сохраняться. Сохранение импульса восстанавливается за счет включения импульса, запасенного в поле, описывающем взаимодействие тел.

Механика Ньютона является хорошим приближением к специальной теории относительности, когда задействованные скорости малы по сравнению со скоростью света.

Общая теория относительности

Общая теория относительности — это теория гравитации, превосходящая теорию Ньютона. В общей теории относительности гравитационная сила ньютоновской механики переосмысливается как искривление пространства-времени . Искривленная траектория, подобная орбите, приписываемая гравитационной силе в механике Ньютона, является не результатом силы, отклоняющей тело от идеальной прямой траектории, а, скорее, попыткой тела свободно падать через фон, который сам искривлен наличие других масс. Замечание Джона Арчибальда Уиллера, ставшее пословицей среди физиков, резюмирует теорию: «Пространство-время говорит материи, как двигаться; материя говорит пространству-времени, как искривляться». Сам Уиллер считал эту взаимосвязь современной обобщенной формой третьего закона Ньютона. Связь между распределением материи и кривизной пространства-времени задается уравнениями поля Эйнштейна которых требуется тензорное исчисление . , для выражения

Ньютоновская теория гравитации является хорошим приближением к предсказаниям общей теории относительности, когда гравитационные эффекты слабы и объекты движутся медленно по сравнению со скоростью света.

Квантовая механика

Квантовая механика — это теория физики, первоначально разработанная для понимания микроскопических явлений: поведения на уровне молекул, атомов или субатомных частиц. Грубо говоря, чем меньше система, тем больше адекватная математическая модель требует понимания квантовых эффектов. Концептуальная основа квантовой физики сильно отличается от классической физики . Вместо того, чтобы думать о таких величинах, как положение, импульс и энергия, как о свойствах объекта , нужно учитывать, какой результат может появиться при выполнении измерения выбранного типа. Квантовая механика позволяет физику рассчитать вероятность того, что выбранное измерение приведет к определенному результату. Ожидаемое значение измерения представляет собой среднее значение возможных результатов, которые оно может дать, взвешенное по вероятностям их появления.

Теорема Эренфеста обеспечивает связь между значениями квантового ожидания и вторым законом Ньютона, связь, которая обязательно является неточной, поскольку квантовая физика фундаментально отличается от классической. В квантовой физике положение и импульс представлены математическими объектами, известными как эрмитовы операторы , а правило Борна используется для расчета ожидаемых значений измерения положения или измерения импульса. Эти ожидаемые значения обычно меняются со временем; то есть в зависимости от времени, в которое (например) производится измерение положения, вероятности различных его возможных результатов будут различаться. Теорема Эренфеста, грубо говоря, гласит, что уравнения, описывающие, как эти математические ожидания изменяются с течением времени, имеют форму, напоминающую второй закон Ньютона. Однако чем более выражены квантовые эффекты в данной ситуации, тем труднее сделать из этого сходства осмысленные выводы.

История

• 
  Исаак Ньютон (1643–1727) на портрете Годфри Кнеллера 1689 года.
• 
  Собственный экземпляр Ньютона «Начал » с рукописными исправлениями для второго издания в Рена библиотеке Тринити-колледжа в Кембридже.
• 
  Первый и второй законы Ньютона на латыни из оригинального Principia Mathematica 1687 года.

Понятия, заложенные в законах движения Ньютона — масса, скорость, импульс, сила — имеют предшественников в более ранних работах, а содержание ньютоновской физики получило дальнейшее развитие после Ньютона. Ньютон объединил знания о небесных движениях с изучением событий на Земле и показал, что одна теория механики может охватывать и то, и другое.

Античность и средневековье

Аристотель и «насильственное» движение

Аристотель
(384–322 до н. э. )

Предмет физики часто восходит к Аристотелю , но история рассматриваемых концепций затенена множеством факторов. Точное соответствие между аристотелевскими и современными концепциями установить нелегко: Аристотель не различал четко того, что мы назвали бы скоростью и силой, использовал один и тот же термин для плотности и вязкости и понимал движение, как всегда, через среду, а не через пространство. . Кроме того, некоторые концепции, которые часто называют «аристотелевскими», лучше было бы приписать его последователям и комментаторам. Эти комментаторы обнаружили, что аристотелевская физика с трудом объясняет движение снаряда. Аристотель делил движение на два типа: «естественное» и «насильственное». «Естественным» движением земного твердого вещества было падение вниз, тогда как «насильственное» движение могло оттолкнуть тело в сторону. Более того, в физике Аристотеля «неистовое» движение требует непосредственной причины; отделенное от причины своего «неистового» движения, тело вернется к своему «естественному» поведению. Тем не менее, копье продолжает двигаться после того, как покинуло руку метателя. Аристотель пришел к выводу, что воздуху вокруг копья необходимо придать способность перемещать копье вперед.

Филопон и атака

Иоанн Филопон , византийский греческий мыслитель, действовавший в шестом веке, находил это абсурдным: одна и та же среда, воздух, каким-то образом отвечала как за поддержание движения, так и за его замедление. Если бы идея Аристотеля была верна, сказал Филопон, армии запускали бы оружие, дуя на них мехами. Филопон утверждал, что приведение тела в движение придает качество, импульс , который содержится внутри самого тела. Пока импульс сохранялся, тело продолжало двигаться. В последующие столетия версии теории импульса были выдвинуты такими людьми, как Нур ад-Дин аль-Битруджи , Авиценна , Абуль-Баракат аль-Багдади , Иоанн Буридан и Альберт Саксонский . Оглядываясь назад, идею импульса можно рассматривать как предшественника современной концепции импульса. Интуитивное представление о том, что объекты движутся согласно какому-то импульсу, сохраняется у многих студентов, изучающих вводную физику.

Инерция и первый закон

Смотрите также: Галилео Галилей § Инерция

Французский философ Рене Декарт ввел понятие инерции в своих «законах природы» в «Мире » ( Traité du monde et de la lumière ), написанном в 1629–1633 годах. Однако «Мир» претендовал на гелиоцентрическое мировоззрение, и в 1633 году эта точка зрения привела к большому конфликту между Галилео Галилеем и римско-католической инквизицией . Декарт знал об этом споре и не хотел вмешиваться. «Мир» не был опубликован до 1664 года, через десять лет после его смерти.

Галилео Галилей
(1564–1642)

Современная концепция инерции принадлежит Галилею. На основании своих экспериментов Галилей пришел к выводу, что «естественным» поведением движущегося тела является продолжение движения до тех пор, пока ему не помешает что-то другое. В «Двух новых науках» (1638 г.) Галилей писал:

Представьте себе любую частицу, спроецированную на горизонтальную плоскость без трения; тогда мы знаем, из того, что было более полно объяснено на предыдущих страницах, что эта частица будет двигаться вдоль той же самой плоскости с движением, которое является равномерным и вечным, при условии, что эта плоскость не имеет границ.

Рене Декарт
(1596–1650)

Галилей признал, что при движении снаряда гравитация Земли влияет на вертикальное, но не на горизонтальное движение. Однако идея инерции Галилея была не совсем той, которая была отражена в первом законе Ньютона. Галилей считал, что тело, движущееся по инерции на большое расстояние, будет повторять кривую Земли. Эту идею исправили Исаак Бекман , Декарт и Пьер Гассенди , которые признали, что движение по инерции должно быть движением по прямой линии. Декарт опубликовал свои законы природы (законы движения) с этой поправкой в ​​«Принципах философии» ( Principia Philosophiae ) в 1644 году, с приглушенной гелиоцентрической частью.

При круговом движении мяч перерезает веревку и отлетает по касательной.

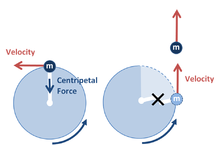
Первый закон природы: каждая вещь, предоставленная самой себе, продолжает оставаться в том же состоянии; поэтому любое движущееся тело продолжает двигаться, пока что-то не остановит его.

Второй закон природы: каждая движущаяся вещь, если ее предоставить самой себе, движется по прямой; поэтому любое тело, движущееся по кругу, всегда стремится отойти от центра круга.

По словам американского философа Ричарда Дж. Блэквелла , голландский учёный Христиан Гюйгенс разработал свою собственную, краткую версию закона в 1656 году. Оно не было опубликовано до 1703 года, через восемь лет после его смерти, в первом абзаце De Motu Corporum ex Percussione .

Гипотеза I: Любое тело, уже находящееся в движении, будет продолжать двигаться постоянно с той же скоростью и по прямой, если ему не помешать.

По мнению Гюйгенса, этот закон был известен, в частности, Галилею и Декарту.

Сила и второй закон

Кристиан Гюйгенс
(1629–1695)

Христиан Гюйгенс в своей книге «Horologium Oscillatorium» (1673) выдвинул гипотезу, что «под действием силы тяжести, каковы бы ни были ее источники, случается, что тела движутся посредством движения, состоящего как из равномерного движения в том или ином направлении, так и из движение вниз под действием силы тяжести». Второй закон Ньютона обобщил эту гипотезу гравитации на все силы.

Одной из важных характеристик ньютоновской физики является то, что силы могут действовать на расстоянии, не требуя физического контакта. Например, Солнце и Земля притягиваются друг к другу гравитацией, несмотря на то, что их разделяют миллионы километров. Это контрастирует с идеей, которую отстаивал среди других Декарт, о том, что гравитация Солнца удерживает планеты на орбитах, закручивая их в вихре прозрачной материи, эфира . Ньютон рассматривал эфирные объяснения силы, но в конечном итоге отверг их. Изучение магнетизма Уильямом Гилбертом и другими создало прецедент для размышлений о нематериальных силах. и не сумев найти количественно удовлетворительное объяснение своего закона гравитации в терминах эфирной модели, Ньютон в конце концов заявил: « Я не предполагаю никаких гипотез »: можно ли найти модель, подобную вихрям Декарта, лежащую в основе » теорий «Начал движения и гравитации, первым основанием для их оценки должны быть сделанные ими успешные предсказания. И действительно, со времен Ньютона все попытки создать такую ​​модель терпели неудачу .

Сохранение импульса и третий закон

Иоганнес Кеплер
(1571–1630)

Иоганн Кеплер предположил, что гравитационное притяжение взаимно — что, например, Луна притягивает Землю, а Земля — Луну, — но он не утверждал, что такие пары равны и противоположны. В своих «Принципах философии» (1644 г.) Декарт выдвинул идею о том, что при столкновении тел «количество движения» остается неизменным. Декарт определил эту величину несколько неточно, сложив произведения скорости и «размера» каждого тела, где «размер» для него включал как объем, так и площадь поверхности. Более того, Декарт думал о Вселенной как о пространстве , то есть наполненном материей, поэтому любое движение требовало, чтобы тело смещало среду при ее движении.

В 1650-х годах Гюйгенс изучал столкновения между твердыми сферами и вывел принцип, который сейчас называют сохранением импульса. Кристофер Рен позже вывел те же правила для упругих столкновений, что и Гюйгенс, а Джон Уоллис применил закон сохранения импульса для изучения неупругих столкновений . Ньютон цитировал работы Гюйгенса, Рена и Уоллиса в подтверждение справедливости своего третьего закона.

Ньютон постепенно пришел к своему набору трех законов. В рукописи 1684 года, написанной Гюйгенсу , он перечислил четыре закона: принцип инерции, изменение движения силой, утверждение об относительном движении, которое сегодня назвали бы инвариантностью Галилея , и правило, согласно которому взаимодействия между телами не меняют движение. их центра масс. В более поздней рукописи Ньютон добавил закон действия и противодействия, заявив при этом, что этот закон и закон о центре масс подразумевают друг друга. Ньютон, вероятно, остановился на изложении «Начал» с тремя основными законами, а затем и другими утверждениями, сведенными к следствиям, в 1685 году.

После « Начал»

Страница 157 из «Небесного механизма» (1831 г.), расширенная версия Мэри Сомервилль первых двух томов « Трактата о небесной механике» Лапласа. Здесь Сомервилль выводит закон обратных квадратов гравитации из законов движения планет Кеплера .

Ньютон сформулировал свой второй закон, сказав, что сила, действующая на тело, пропорциональна изменению его движения или импульса. К тому времени, когда он писал « Начала», он уже разработал исчисление (которое он называл « наукой о флюксиях »), но в « Началах» он не использовал его явно, возможно, потому, что считал геометрические аргументы в Евклида традиции более строгий. Следовательно, «Начала» не выражают ускорение как вторую производную от положения и поэтому не дают второго закона как $F=ma$. Эта форма второго закона была написана (для частного случая постоянной силы) по крайней мере еще в 1716 году Якобом Германом ; Леонард Эйлер использовал ее в качестве основной предпосылки в 1740-х годах. Эйлер стал пионером в изучении твердых тел. и основал основную теорию гидродинамики. Пьера-Симона Лапласа Пятитомный «Трактат о небесной механике» (1798–1825) отказался от геометрии и разработал механику исключительно посредством алгебраических выражений, одновременно решая вопросы, которые « Начала» оставили открытыми, как и полная теория приливов и отливов .

Концепция энергии стала ключевой частью ньютоновской механики в постньютоновский период. Решение Гюйгенса о столкновении твердых сфер показало, что в этом случае сохраняется не только импульс, но и кинетическая энергия (или, скорее, величина, которую, ретроспективно, мы можем определить как половину полной кинетической энергии). Вопрос о том, что сохраняется при всех других процессах, таких как неупругие столкновения и замедленное трением движение, не был решен до XIX века. Дебаты на эту тему перекликались с философскими спорами между метафизическими взглядами Ньютона и Лейбница, а варианты термина «сила» иногда использовались для обозначения того, что мы бы назвали типами энергии. Например, в 1742 году Эмили дю Шатле писала: «Мёртвая сила состоит из простой тенденции к движению: такова сила пружины, готовой расслабиться; живая сила — это то, чем обладает тело, когда оно находится в реальном движении». В современной терминологии «мертвая сила» и «живая сила» соответствуют потенциальной энергии и кинетической энергии соответственно. Сохранение энергии не было признано универсальным принципом до тех пор, пока не было понято, что энергия механической работы может рассеиваться в тепло. Получив прочное обоснование концепции энергии, законы Ньютона можно было бы вывести в формулировках классической механики, в которых энергия ставится на первое место, как в лагранжевых и гамильтоновых формулировках, описанных выше.

В современных представлениях законов Ньютона используется математика векторов - тема, которая не разрабатывалась до конца 19 - начала 20 веков. Векторная алгебра, впервые разработанная Джозией Уиллардом Гиббсом и Оливером Хевисайдом , возникла и в значительной степени вытеснила более раннюю систему кватернионов , изобретенную Уильямом Роуэном Гамильтоном .

См. также

• История классической механики
• Список одноименных законов
• Список уравнений классической механики
• Список научных законов, названных в честь людей
• Список учебников по классической механике и квантовой механике
• Купол Нортона

Дальнейшее чтение

• Законы динамики Ньютона - Фейнмановские лекции по физике
• Чакрабарти, Дипто; Дурмашкин, Петр; Томасик, Мишель; Фребель, Анна ; Вулетич, Владан (2016). «Классическая механика» . MIT OpenCourseWare . Проверено 17 января 2022 г.