Узоры в природе


Закономерности природы — это видимые закономерности форм, встречающиеся в мире природы . Эти закономерности повторяются в разных контекстах и иногда могут быть смоделированы математически . Естественные узоры включают симметрию , деревья , спирали , меандры , волны , пену , мозаику , трещины и полосы. [1] Ранние греческие философы изучали закономерности, а Платон , Пифагор и Эмпедокл пытались объяснить порядок в природе. Современное понимание видимых закономерностей развивалось постепенно с течением времени.
В 19 веке бельгийский физик Жозеф Плато исследовал мыльные пленки , что привело его к формулировке концепции минимальной поверхности . Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, чтобы подчеркнуть их симметрию . Шотландский биолог Д'Арси Томпсон стал пионером в изучении закономерностей роста растений и животных, показав, что простые уравнения могут объяснить спиральный рост. В 20 веке британский математик Алан Тьюринг предсказал механизмы морфогенеза , которые приводят к образованию пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа Мандельброт показали, как математика фракталов может создавать модели роста растений.
Математика , физика и химия могут объяснить закономерности в природе на разных уровнях и в разных масштабах. Закономерности в живых существах объясняются биологическими процессами естественного отбора и полового отбора . В исследованиях формирования паттернов используются компьютерные модели для моделирования широкого спектра паттернов.
История
[ редактировать ]Ранние греческие философы пытались объяснить порядок в природе , предвосхищая современные концепции. Пифагор (ок. 570–ок. 495 до н. э.) объяснял закономерности в природе, такие как гармонии музыки, возникающими из числа, которое он считал основной составляющей существования. [а] Эмпедокл (ок. 494–ок. 434 до н. э.) в некоторой степени предвосхитил дарвиновское эволюционное объяснение строения организмов. [б] Платон (ок. 427–ок. 347 до н. э.) доказывал существование естественных универсалий . Он считал, что они состоят из идеальных форм ( εἶδος eidos : «форма»), физические объекты которых всегда являются несовершенными копиями. Таким образом, цветок может иметь примерно круглую форму, но он никогда не бывает идеальным. [2] Теофраст (ок. 372–ок. 287 до н. э.) отмечал, что у растений, «имеющих плоские листья, они расположены в правильном ряду»; Плиний Старший (23–79 гг. н. э.) отметил их узорчатое круглое расположение. [3] Столетия спустя Леонардо да Винчи (1452–1519) заметил спиральное расположение узоров листьев, то, что стволы деревьев с возрастом приобретают последовательные кольца, и предложил правило, которому якобы удовлетворяют площади поперечного сечения ветвей деревьев. [4] [3]
В 1202 году Леонардо Фибоначчи представил последовательность Фибоначчи западному миру в своей книге Liber Abaci . [5] Фибоначчи представил мысленный эксперимент по росту идеализированной популяции кроликов . [6] Иоганн Кеплер (1571–1630) указал на наличие последовательности Фибоначчи в природе, используя ее для объяснения пятиугольной формы некоторых цветов. [3] В 1658 году английский врач и философ сэр Томас Браун обсуждал «как природа геометризирует» в «Саду Кира» , ссылаясь на пифагорейскую нумерологию, включающую число 5, и платоническую форму узора квинкунса . В центральной главе дискурса представлены примеры и наблюдения квинконса в ботанике. [7] В 1754 году Шарль Бонне заметил, что спиральный филлотаксис растений часто выражается в как по часовой стрелке , так и против часовой стрелки рядах золотого сечения . [3] Математические наблюдения за филлотаксисом последовали в работах Карла Фридриха Шимпера и его друга Александра Брауна 1830 и 1830 годов соответственно; Огюст Браве и его брат Луи связали отношения филлотаксиса с последовательностью Фибоначчи в 1837 году, также отметив ее появление в сосновых шишках и ананасах . [3] В своей книге 1854 года немецкий психолог Адольф Цейзинг исследовал золотое сечение, выраженное в расположении частей растений, скелетах животных и ветвях их вен и нервов, а также в кристаллах . [8] [9] [10]
В XIX веке бельгийский физик Жозеф Плато (1801–1883) сформулировал математическую задачу существования минимальной поверхности с заданной границей, названную теперь его именем. Он интенсивно изучал мыльные пленки, сформулировав законы Плато , которые описывают структуры, образуемые пленками в пене. [11] Лорд Кельвин определил проблему наиболее эффективного способа упаковки ячеек равного объема пене в 1887 году; в его решении используется только одно твердое тело - кубические соты с немного изогнутыми гранями, чтобы соответствовать законам Плато. Лучшего решения не было найдено до 1993 года, когда Денис Вейре и Роберт Фелан предложили структуру Вейра-Фелана ; Пекинский национальный центр водных видов спорта адаптировал конструкцию своей внешней стены во время летних Олимпийских игр 2008 года . [12] Эрнст Геккель (1834–1919) нарисовал прекрасные иллюстрации морских организмов, в частности радиолярий , подчеркивая их симметрию , чтобы поддержать свои псевдодарвиновские теории эволюции. [13] Американский фотограф Уилсон Бентли сделал первую микрофотографию снежинки в 1885 году. [14]
В 20 веке А.Х. Черч изучил закономерности филлотаксиса в своей книге 1904 года. [15] В 1917 году Д'Арси Вентворт Томпсон опубликовал «О росте и форме» ; его описание филлотаксиса и последовательности Фибоначчи, математических взаимосвязей в спиральном росте растений показало, что простые уравнения могут описывать спиральный рост рогов животных и раковин моллюсков . [16] В 1952 году учёный-компьютерщик Алан Тьюринг (1912–1954) написал «Химические основы морфогенеза» , анализ механизмов, которые будут необходимы для создания закономерностей в живых организмах в процессе, называемом морфогенезом . [17] Он предсказал осциллирующие химические реакции , в частности реакцию Белоусова-Жаботинского . Эти механизмы активатора-ингибитора, как предположил Тьюринг, могут генерировать узоры (получившие название « паттерны Тьюринга ») из полос и пятен у животных, а также способствовать образованию спиральных узоров, наблюдаемых в филлотаксисе растений. [18] В 1968 году венгерский биолог-теоретик Аристид Линденмайер (1925–1989) разработал L-систему — формальную грамматику , которую можно использовать для моделирования закономерностей роста растений в стиле фракталов . [19] L-системы имеют алфавит символов, которые можно комбинировать с помощью правил производства для создания более крупных строк символов, а также механизм перевода сгенерированных строк в геометрические структуры. В 1975 году, после столетий медленного развития математики закономерностей Готфридом Лейбницем , Георгом Кантором , Хельге фон Кохом , Вацлавом Серпинским и другими, Бенуа Мандельброт написал знаменитую статью « Какова длина побережья Британии?» Статистическая самоподобность и дробная размерность , кристаллизирующая математическую мысль в концепцию фрактала . [20]
-
Паттерны чисел Фибоначчи широко встречаются у таких растений, как королева саго, Cycas circinalis .
-
Пекинский национальный центр водных видов спорта к Олимпийским играм 2008 года имеет структуру Вейра-Фелана .
-
Д'Арси Томпсон стал пионером в изучении роста и формы в своей книге 1917 года.
Причины
[ редактировать ]
Живые существа, такие как орхидеи , колибри и хвост павлина , имеют абстрактные узоры с красотой форм, узоров и цветов, которым художники изо всех сил пытаются соответствовать. [21] Красота, которую люди воспринимают в природе, имеет причины на разных уровнях, особенно в математике, которая определяет, какие закономерности могут физически формироваться, а также среди живых существ в эффектах естественного отбора, которые управляют развитием закономерностей. [22]
Математика стремится открывать и объяснять абстрактные закономерности и закономерности всех видов. [23] [24] Визуальные закономерности в природе находят объяснения в теории хаоса , фракталах, логарифмических спиралях, топологии и других математических закономерностях. Например, L-системы образуют убедительные модели различных закономерностей роста деревьев. [19]
Законы физики применяют абстракции математики к реальному миру, часто так, как если бы он был совершенным . Например, кристалл идеален, когда он не имеет структурных дефектов, таких как дислокации, и полностью симметричен. Точное математическое совершенство может лишь приблизить реальные объекты. [25] Видимые закономерности в природе управляются физическими законами ; например, меандры можно объяснить с помощью гидродинамики .
В биологии может естественный отбор вызвать развитие закономерностей у живых существ по нескольким причинам, включая маскировку , [26] половой отбор , [26] и различные виды сигнализации, включая мимику [27] и симбиоз уборки . [28] У растений форма, цвет и узор , опыляемых насекомыми, цветков таких как лилия, эволюционировали, чтобы привлекать насекомых, например пчел . Радиальные узоры цветов и полос, некоторые из которых видны только в ультрафиолетовом свете, служат проводниками нектара , которые можно увидеть на расстоянии. [29]
Виды узора
[ редактировать ]Симметрия
[ редактировать ]Симметрия широко распространена в живых существах. Животные в основном обладают двусторонней или зеркальной симметрией , как и листья растений и некоторые цветы, например орхидеи . [30] Растения часто обладают радиальной или вращательной симметрией , как и многие цветы и некоторые группы животных, например морские анемоны . Пятикратная симметрия обнаружена у иглокожих — группы, в которую входят морские звезды , морские ежи и морские лилии . [31]
Среди неживых тел снежинки обладают поразительной шестикратной симметрией ; Структура каждой чешуйки отражает различные условия во время ее кристаллизации, с почти одинаковой схемой роста на каждом из шести плеч. [32] Кристаллы вообще имеют разнообразную симметрию и особенности кристаллов ; они могут быть кубическими или октаэдрическими, но настоящие кристаллы не могут иметь пятикратной симметрии (в отличие от квазикристаллов ). [33] Вращательная симметрия встречается в разных масштабах среди неживых существ, включая узор брызг в форме короны , образующийся при падении капли в пруд. [34] и сфероидальная форма, и кольца такой планеты , как Сатурн . [35]
Симметрия имеет множество причин. Радиальная симметрия подходит таким организмам, как морские анемоны, взрослые особи которых не двигаются: пища и угрозы могут прийти с любого направления. Но животные, движущиеся в одном направлении, обязательно имеют верхнюю и нижнюю стороны, головной и хвостовой концы, а значит, левую и правую сторону. Голова становится специализированной с ртом и органами чувств ( цефализация ), а тело становится двусторонне-симметричным (хотя внутренние органы не обязательно). [36] Еще более загадочной является причина пятилучевой (пятилучевой) симметрии иглокожих. Ранние иглокожие были двусторонне-симметричными, как и их личинки до сих пор. Самралл и Рэй утверждают, что утрата старой симметрии имела как эволюционные, так и экологические причины. [37] В случае с ледяными яйцами легкое взбалтывание воды, дуемое подходящим сильным бризом, приводит к образованию концентрических слоев льда на частице семени, которая затем превращается в плавающий шар, катящийся сквозь ледяные потоки. [38]
-
Животные часто демонстрируют зеркальную или двустороннюю симметрию , как этот тигр .
-
Пятикратную симметрию можно увидеть во многих цветах и некоторых фруктах, таких как мушмула .
-
Снежинки обладают шестикратной симметрией .
-
Флюорит с кубической кристаллической формой .
-
воды Всплеск приближается к радиальной симметрии .
-
Гранат с кристаллами ромбической додекаэдрической формы.
-
Морские анемоны обладают вращательной симметрией .
-
Вольвокс обладает сферической симметрией.
-
Ледяные яйца приобретают сферическую симметрию, катаясь под действием ветра и течений.
Деревья, фракталы
[ редактировать ]Схема ветвления деревьев была описана в эпоху итальянского Возрождения Леонардо да Винчи . В «Трактате о живописи» он заявил, что:
Все ветви дерева на каждой ступени его высоты, сложенные вместе, равны по толщине стволу [под ними]. [39]
Более общая версия гласит, что когда родительская ветвь разделяется на две или более дочерних ветвей, площадь поверхности дочерних ветвей суммируется с площадью поверхности родительской ветви. [40] Эквивалентная формулировка заключается в том, что если родительская ветвь разделяется на две дочерние ветви, то диаметры поперечного сечения родительской и двух дочерних ветвей образуют прямоугольный треугольник . Одно из объяснений заключается в том, что это позволяет деревьям лучше противостоять сильному ветру. [40] Моделирование биомеханических моделей согласуется с этим правилом. [41]
Фракталы — это бесконечно самоподобные повторяющиеся математические конструкции, имеющие фрактальную размерность . [20] [42] [43] Бесконечная итерация невозможна в природе, поэтому все «фрактальные» модели являются лишь приблизительными. Например, листья папоротников и зонтичных (Apiaceae) самоподобны (перистые) только на 2, 3 или 4 уровнях. Папоротниковые модели роста встречаются у растений и животных, включая мшанок , кораллов , гидрозоа, таких как воздушный папоротник , Sertularia argentea , а также у неживых существ, особенно электрических разрядов . Фракталы системы Линденмайера могут моделировать различные модели роста деревьев, изменяя небольшое количество параметров, включая угол ветвления, расстояние между узлами или точками ветвления ( длина междоузлия ) и количество ветвей на точку ветвления. [19]
Фрактальные модели широко встречаются в природе, в таких разнообразных явлениях, как облака, речные сети геологических , линии разломов , горы , береговые линии , [44] звериная окраска , хлопья снега , [45] кристаллы , [46] ветвление кровеносных сосудов , [47] клетки Пуркинье , [48] актиновые цитоскелеты , [49] и океанские волны . [50]
-
Модели роста некоторых деревьев напоминают фракталы системы Линденмайера .
-
Схема баобаба ветвления
-
Лист коровьей петрушки Anthriscus sylvestris 2- или 3- перистый , не бесконечный.
-
Деревья: дендритные кристаллы меди (под микроскопом).
Спирали
[ редактировать ]Спирали распространены у растений и некоторых животных, особенно у моллюсков . Например, у наутилуса , головоногих моллюсков, каждая камера его раковины представляет собой приблизительную копию следующей, масштабированную в постоянный коэффициент и расположенную по логарифмической спирали . [51] При современном понимании фракталов спираль роста можно рассматривать как частный случай самоподобия. [52]
Спирали растений можно увидеть в филлотаксисе , расположении листьев на стебле, а также в расположении ( парастихия). [53] ) других частей, например, в составных цветочных головках и семенных головках, таких как подсолнечник , или в фруктовых структурах, таких как ананас. [15] [54] : 337 и змеиный фрукт , а также в узоре из чешуек сосновых шишек , где множество спиралей проходят как по часовой стрелке, так и против часовой стрелки. Эти механизмы имеют объяснения на разных уровнях – математике, физике, химии, биологии – каждое из них верно по отдельности, но все они необходимы вместе. [55] Спирали филлотаксиса могут быть созданы из соотношений Фибоначчи : последовательность Фибоначчи состоит из 1, 1, 2, 3, 5, 8, 13... (каждое последующее число представляет собой сумму двух предыдущих). Например, когда листья чередуются вверх по стеблю, один оборот спирали касается двух листьев, поэтому узор или соотношение составляет 1/2. У лещины соотношение 1/3; у абрикоса — 2/5; в груше — 3/8; в миндале это 5/13. [56]
В дисковом филлотаксисе, как у подсолнечника и маргаритки , цветки расположены вдоль спирали Ферма , но это замаскировано, потому что последовательные цветки расположены далеко друг от друга, на золотой угол , 137,508 ° (делящий круг в золотом сечении ); когда цветочная головка созревает и все элементы имеют одинаковый размер, это расстояние создает число Фибоначчи, более очевидные спирали. [57]
С точки зрения физики спирали — это конфигурации с наименьшей энергией. [58] которые возникают спонтанно посредством процессов самоорганизации в динамических системах . [59] С точки зрения химии спираль может возникнуть в результате процесса реакции-диффузии, включающего как активацию, так и торможение. Филлотаксис контролируется белками, которые управляют концентрацией растительного гормона ауксина , который активирует рост меристемы , наряду с другими механизмами, контролирующими относительный угол почек вокруг стебля. [60] С биологической точки зрения естественный отбор благоприятствует расположению листьев как можно дальше друг от друга в любом пространстве, поскольку это максимизирует доступ к ресурсам, особенно солнечному свету, для фотосинтеза . [54]
-
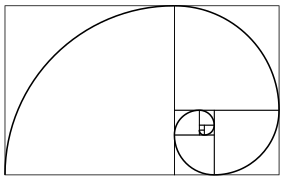
Фибоначчи Спираль
-
Снежный баран , Ovis canadensis
-
Спирали: филлотаксис спирального алоэ, Aloe polyphylla.
-
Наутилуса раковины Логарифмическая спираль роста
-
Спираль Ферма : семенная головка подсолнечника . Helianthus annuus
-
Множественные спирали Фибоначчи: краснокочанная капуста в поперечном сечении
-
Спиральная раковина Trochoidealiebetruti.
-
Капли воды слетают с мокрого вращающегося шара по равноугольным спиралям.
Хаос, поток, извилины
[ редактировать ]В математике динамическая система называется хаотичной, если она (высоко) чувствительна к начальным условиям (так называемый « эффект бабочки »). [61] ), что требует математических свойств топологического перемешивания и плотных периодических орбит . [62]
Наряду с фракталами теория хаоса считается по существу универсальным средством воздействия на закономерности в природе. Между хаосом и фракталами существует связь — странные аттракторы в хаотических системах имеют фрактальное измерение . [63] Некоторые клеточные автоматы , простые наборы математических правил, которые генерируют закономерности, ведут себя хаотично, например Стивена Вольфрама Правило 30 . [64]
Вихревые улицы зигзагообразные узоры из вихревых вихрей, создаваемых нестационарным разделением потока жидкости представляют собой , чаще всего воздуха или воды, над препятствующими объектами. [65] Гладкий ( ламинарный ) поток начинает разрушаться, когда размер препятствия или скорость потока становятся достаточно большими по сравнению с вязкостью жидкости.
Меандры — это извилистые изгибы рек или других каналов, которые образуются, когда жидкость, чаще всего вода, обтекает изгибы. Как только тропа слегка искривляется, размер и кривизна каждой петли увеличиваются, поскольку спиральный поток перетаскивает такие материалы, как песок и гравий, через реку внутрь изгиба. Внешняя часть петли остается чистой и незащищенной, поэтому эрозия ускоряется, еще больше увеличивая извилистость мощной петли положительной обратной связи . [66]
-
Хаос: раковина брюхоногого моллюска, ткань золотого конуса, ткань Конуса , напоминает Правила 30. клеточный автомат
-
Поток: вихревая улица облаков на островах Хуана Фернандеса
-
Меандры: извилистая тропа Рио-Кауто , Куба
-
Меандры: извилистое ползание змеи.
-
Меандры: симметричный мозговой коралл , Diploria strigosa.
Волны, дюны
[ редактировать ]Волны — это возмущения, которые переносят энергию при движении. Механические волны распространяются через среду – воздух или воду, заставляя ее колебаться при прохождении. [67] Ветровые волны моря — это волны на поверхности , которые создают характерный хаотичный рисунок любого большого водоема, хотя их статистическое поведение можно предсказать с помощью моделей ветровых волн. [68] Когда волны в воде или ветер проходят по песку, они создают узоры ряби. Когда ветры дуют над большими песчаными массами, они создают дюны , иногда на обширных дюнных полях, как в пустыне Такла-Макан . Дюны могут образовывать самые разные узоры, включая полумесяцы, очень длинные прямые линии, звезды, купола, параболы, а также продольные формы или формы («меч»). [69]
Барханы или серповидные дюны образуются под воздействием ветра на песок пустыни; два рога полумесяца и скользящая поверхность направлены по ветру. Песок обдувает наветренную поверхность, расположенную под углом около 15 градусов к горизонтали, и падает на поверхность скольжения, где он скапливается до угла естественного откоса песка, составляющего около 35 градусов. Когда поверхность скольжения превышает угол естественного откоса, песчаные лавины скатываются , что является нелинейным поведением: добавление большого количества небольшого количества песка не вызывает ничего особенного, но затем добавление еще небольшого количества внезапно приводит к сходу большого количества песка. . [70] Если не считать этой нелинейности, барханы ведут себя скорее как одиночные волны . [71]
-
Волны: прибойная волна в кильватере корабля
-
Дюны: песчаные дюны в пустыне Такла-Макан , из космоса.
-
Дюны: бархан -полумесяц. песчаная дюна
Пузырьки, пена
[ редактировать ]Мыльный пузырь образует сферу , поверхность с минимальной площадью ( minimum Surface ) — наименьшую возможную площадь поверхности для заключенного в ней объема. Два пузыря вместе образуют более сложную форму: внешние поверхности обоих пузырьков сферические; эти поверхности соединены третьей сферической поверхностью, поскольку меньший пузырек слегка выпячивается в больший. [11]
Пена ; представляет собой массу пузырьков В природе встречаются пены из разных материалов. Пены, состоящие из мыльных пленок , подчиняются законам Плато , которые требуют, чтобы три мыльные пленки встретились на каждом краю под углом 120 ° и четыре мыльных края встретились в каждой вершине под тетраэдрическим углом около 109,5 °. Законы Плато также требуют, чтобы пленки были гладкими и непрерывными, а также имели постоянную среднюю кривизну в каждой точке. Например, пленка в среднем может оставаться почти плоской, будучи изогнутой вверх в одном направлении (скажем, слева направо) и изогнутой вниз в другом направлении (скажем, спереди назад). [72] [73] В качестве палаток можно использовать конструкции с минимальными поверхностями.
В масштабе живых клеток часто встречаются структуры пены; радиолярии , губок спикулы , силикофлагеллят экзоскелеты и кальцитовый скелет ежа морского Cidaris Rugosa — все они напоминают минеральные слепки границ пены Плато. [74] [75] Скелет радиолярии Aulonia , выглядит так , hexagona , прекрасной морской формы, нарисованной Эрнстом Геккелем будто представляет собой сферу, состоящую целиком из шестиугольников, но это математически невозможно. гласит Характеристика Эйлера , что для любого выпуклого многогранника количество граней плюс количество вершин (углов) равно числу ребер плюс два. Результатом этой формулы является то, что любой замкнутый многогранник шестиугольников должен включать ровно 12 пятиугольников, как футбольный мяч , Бакминстера Фуллера геодезический купол или фуллерена молекула . Это можно представить, заметив, что сетка из шестиугольников плоская, как лист проволочной сетки, но каждый добавленный пятиугольник заставляет сетку изгибаться (углов меньше, поэтому сетка втягивается). [76]
-
Пена из мыльных пузырей : в каждой вершине сходятся четыре края под углами, близкими к 109,5°, как у двух связей CH в метане .
-
Радиолярии , нарисованные Геккелем в его «Художественных формах природы» (1904).
-
Геккеля Спумеллария ; скелеты этих радиолярий имеют пенообразную форму.
-
Брохосомы (секреторные микрочастицы , вырабатываемые цикадками ) часто приближаются по геометрии к фуллеренам .
-
Равные сферы (пузырьки газа) в поверхностной пене.
-
Цирковая палатка имеет минимальную поверхность.
Мозаика
[ редактировать ]Тесселяции — это узоры, образованные повторяющимися плитками по всей плоской поверхности. Существует 17 групп обоев плиток. [77] Хотя это обычное явление в искусстве и дизайне, точно повторяющиеся мозаики не так легко найти в живых существах. ячеек в бумажных гнездах социальных ос и восковых ячеек в сотах, Хорошо известны примеры построенных медоносными пчелами. Среди животных костистые рыбы, рептилии или ящеры , а также фрукты, такие как салак , защищены перекрывающимися чешуями или остеодермами , которые образуют более или менее точно повторяющиеся единицы, хотя часто чешуя на самом деле постоянно различается по размеру. Среди цветов рябчик змеиной головы, Fritillaria meleagris , имеет на лепестках мозаичный шахматный узор. Структуры минералов служат хорошим примером регулярно повторяющихся трехмерных массивов. Несмотря на сотни тысяч известных минералов, существует довольно мало возможных типов расположения атомов в кристалле , определяемых кристаллической структурой , кристаллической системой и точечной группой ; например, существует ровно 14 решеток Браве . для семи решетчатых систем в трехмерном пространстве [78]
-
Кристаллы: кубообразные кристаллы галита (каменной соли); кубическая кристаллическая система , изометрическая гексоктаэдрическая кристаллическая симметрия
-
Плитки: мозаичный цветок рябчика змеиной головы, Fritillaria meleagris.
-
Черепицы: перекрывающиеся чешуи плотвы Rutilus rutilus.
-
Черепица: перекрывающиеся чешуйки змеиного плода или салака , Salacca zalacca.
-
Мозаичный тротуар : редкое скальное образование на полуострове Тасман.
Трещины
[ редактировать ]Трещины — это линейные отверстия, которые образуются в материалах для снятия напряжения . Когда эластичный материал равномерно растягивается или сжимается, он в конечном итоге достигает предела прочности на разрыв, а затем внезапно разрушается во всех направлениях, образуя трещины со швами под углом 120 градусов, поэтому в узле встречаются три трещины. И наоборот, когда неэластичный материал разрушается, образуются прямые трещины для снятия напряжения. Дальнейшее напряжение в том же направлении просто открыло бы существующие трещины; напряжение под прямым углом может создать новые трещины под углом 90 градусов к старым. Таким образом, рисунок трещин показывает, эластичен материал или нет. [79] В жестком волокнистом материале, таком как кора дуба, обычно образуются трещины, чтобы снять напряжение, но они не растут долго, поскольку их рост прерывается пучками прочных эластичных волокон. Поскольку каждый вид дерева имеет свою собственную структуру на уровне клеток и молекул, у каждого своя закономерность расщепления коры. [80]
-
Поверхность старой керамики, белая глазурь с преимущественно трещинами под углом 90°.
-
Высыхающая неэластичная грязь в Ранн-оф-Катч с преимущественно трещинами под углом 90 °.
-
Высыхающая эластичная грязь на Сицилии с трещинами преимущественно под углом 120°.
-
Остывший базальт на Дороге Гигантов . Вертикальные трещины преимущественно под углом 120°, образующие шестиугольные колонны.
-
Ствол пальмы с ветвящимися вертикальными трещинами (и горизонтальными рубцами на листьях).
Пятна, полосы
[ редактировать ]Встречаются леопарды и божьи коровки; скалярии и зебры полосатые. [81] У этих моделей есть эволюционное объяснение: у них есть функции , которые увеличивают шансы на то, что потомство животного с таким рисунком выживет и сможет воспроизвести потомство. Одной из функций рисунков животных является маскировка ; [26] например, леопард , которого сложнее увидеть, ловит больше добычи. Еще одна функция – сигнализация. [27] - например, божья коровка с меньшей вероятностью подвергнется нападению хищных птиц, которые охотятся визуально, если она имеет смелую предупреждающую окраску, а также неприятно горька или ядовита или имитирует других неприятных насекомых. Молодая птица может увидеть насекомое с предупреждающим рисунком, такое как божья коровка, и попытаться съесть его, но сделает это только один раз; очень скоро оно выплюнет горькое насекомое; другие божьи коровки в этом районе останутся нетронутыми. Молодые леопарды и божьи коровки, унаследовав гены , которые каким-то образом создают пятнистость, выживают. Но хотя эти эволюционные и функциональные аргументы объясняют, почему этим животным нужны их закономерности, они не объясняют, как эти закономерности формируются. [81]
-
Бабочка-красавица Dirce, Colobura dirce
-
Grevy's zebra , Equus grevyi
-
Королевская рыба-ангел , Pygoplitesdiacanthus
-
Леопард , Panthera pardus pardus
-
Массив божьих коровок Г.Г. Джейкобсона
-
Схема размножения каракатицы Sepia officinalis.
Формирование узора
[ редактировать ]Алан Тьюринг, [17] а позже биолог-математик Джеймс Мюррей , [82] описал механизм, который спонтанно создает пятнистые или полосатые узоры: систему реакции-диффузии . [83] В клетках молодого организма есть гены, которые могут быть включены химическим сигналом, морфогеном , что приводит к росту структуры определенного типа, например, темного пигментированного участка кожи. Если морфоген присутствует повсюду, в результате получается равномерная пигментация, как у черного леопарда. Но если он распределен неравномерно, могут получиться пятна или полосы. может контролироваться по принципу обратной связи Тьюринг предположил, что производство самого морфогена . Это могло вызвать постоянные колебания количества морфогена, диффундирующего по телу. (что приводит к появлению пятен или полос) необходим второй механизм Для создания паттернов стоячих волн : химическое вещество-ингибитор, которое отключает выработку морфогена и которое само диффундирует по организму быстрее, чем морфоген, что приводит к схеме активатор-ингибитор. . Реакция Белоусова-Жаботинского представляет собой небиологический пример такого рода схемы химического генератора . [83]
Более поздние исследования позволили создать убедительные модели таких разнообразных узоров, как полосы зебры, пятна жирафа, пятна ягуара (средне-темные пятна, окруженные темными разорванными кольцами) и узоры на панцире божьих коровок (различное геометрическое расположение пятен и полос, см. иллюстрации). [84] Модели Ричарда Прума , разработанные на основе работ Тьюринга, используют шесть переменных для объяснения наблюдаемого диапазона девяти основных паттернов внутриперьевой пигментации, от простейшего, центрального пигментного пятна, до концентрических пятен, полосок, шевронов, глаз. пятно, пара центральных пятен, ряды парных пятен и массив точек. [85] [86] Более сложные модели имитируют сложные узоры перьев цесарки Numida meleagris , у которых отдельные перья имеют переходы от полос у основания к множеству точек на дальнем (дистальном) конце. Для этого требуются колебания, создаваемые двумя тормозящими сигналами, взаимодействующими как в пространстве, так и во времени. [86]
могут образовываться и по другим причинам. Узоры в растительном ландшафте тигрового кустарника [87] и еловые волны . [88] Полосы тигрового кустарника встречаются на засушливых склонах, где рост растений ограничен из-за осадков. Каждая примерно горизонтальная полоса растительности эффективно собирает дождевую воду из голой зоны непосредственно над ней. [87] Пихтовые волны возникают в лесах на склонах гор после ветрового возмущения, во время возобновления. Когда деревья падают, деревья, которые они укрывали, становятся обнаженными и, в свою очередь, с большей вероятностью будут повреждены, поэтому проломы имеют тенденцию расширяться с подветренной стороны. Тем временем с наветренной стороны растут молодые деревья, защищенные ветровой тенью остальных высоких деревьев. [88] Природные узоры иногда формируются животными, как, например, в курганах Мима на северо-западе США и в некоторых других районах, которые, по-видимому, создавались в течение многих лет в результате роющей деятельности карманных сусликов . [89] в то время как так называемые сказочные круги Намибии, по-видимому, созданы в результате взаимодействия конкурирующих групп песчаных термитов, а также конкуренции за воду среди пустынных растений. [90]
В вечномерзлых грунтах с активным верхним слоем, подверженным ежегодному замерзанию и оттаиванию, узорчатый грунт может образовываться , образующий круги, сети, многоугольники ледяных жил , ступеньки и полосы. Термическое сжатие приводит к образованию усадочных трещин; при оттепели вода заполняет трещины, расширяясь, образуя лед при следующем замерзании, и расширяя трещины в клинья. Эти трещины могут соединяться, образуя многоугольники и другие формы. [91]
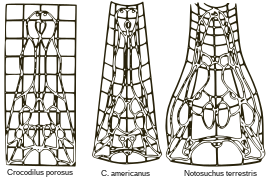
Паттерн трещин , который развивается в мозге позвоночных, вызван физическим процессом ограниченного расширения, зависящим от двух геометрических параметров: относительного тангенциального расширения коры и относительной толщины коры . Подобные паттерны извилин (пиков) и борозд (впадин) были продемонстрированы на моделях мозга, начиная с гладких, слоистых гелей, с паттернами, вызванными сжимающими механическими силами в результате расширения внешнего слоя (представляющего кору) после добавление растворителя. Численные модели компьютерного моделирования подтверждают естественные и экспериментальные наблюдения о том, что структура складок поверхности увеличивается в более крупном мозге. [92] [93]
-
Гигантская рыба-фугу , Tetraodon mbu
-
Деталь рисунка кожи гигантской рыбы-фугу
-
Снимок моделирования реакции Белоусова – Жаботинского
-
Шлемчатая цесарка, Numida meleagris , перья переходят от полосатых к пятнистым, как внутри перьев, так и поперек птицы.
-
Узорчатая земля : тающий пинго с окружающими его ледяных клиньев многоугольниками недалеко от Туктояктука , Канада.
-
Сказочные круги в районе Мариенфлюсстал в Намибии.
См. также
[ редактировать ]- Биология развития
- Появление
- Эволюционная история растений
- Математика и искусство
- Морфогенез
- Формирование узора
- Видманштеттенский узор
Ссылки
[ редактировать ]Сноски
- ^ Так называемые пифагорейцы , которые первыми занялись математикой, не только развили этот предмет, но и насытились им, они воображали, что принципы математики являются принципами всех вещей. Аристотель , Метафизика 1–5 , ок. 350 г. до н.э.
- ↑ Аристотель сообщает об Эмпедокле, утверждая, что «[где] тогда все обернулось бы так, как если бы это происходило с определенной целью, там существа выжили, случайно смешавшись подходящим образом; но там, где этого не произошло, существа погибли». The Physics , B8, 198b29 у Кирка и др., 304).
Цитаты
- ^ Стивенс 1974 , с. 3.
- ^ Балагер, Марк (7 апреля 2009 г.) [2004]. «Платонизм в метафизике» . Стэнфордская энциклопедия философии . Проверено 4 мая 2012 г.
- ^ Перейти обратно: а б с д и Ливио, Марио (2003) [2002]. Золотое сечение: история Фи, самого удивительного числа в мире (первое издание в мягкой обложке). Нью-Йорк: Бродвейские книги . п. 110. ИСБН 978-0-7679-0816-0 .
- ^ Да Винчи, Леонардо (1971). Тейлор, Памела (ред.). Записные книжки Леонардо да Винчи . Новая американская библиотека. п. 121.
- ^ Сингх, Пармананд (1986). «Ачарья Хемачандра и (так называемые) числа Фибоначчи». Математическое образование Сиван . 20 (1): 28–30. ISSN 0047-6269 .
- ^ Нотт, Рон. «Кролики Фибоначчи» . Университета Суррея Факультет инженерных и физических наук .
- ^ Браун, Томас (1658). «Глава III» . Сад Кира .
- ^ Падован, Ричард (1999). Пропорция: Наука, Философия, Архитектура . Тейлор и Фрэнсис. стр. 305–306. ISBN 978-0-419-22780-9 .
- ^ Падован, Ричард (2002). «Пропорция: Наука, Философия, Архитектура» . Сетевой журнал Nexus . 4 (1): 113–122. дои : 10.1007/s00004-001-0008-7 .
- ^ Цейзинг, Адольф (1854). Новое учение о пропорциях человеческого тела . предисловие.
- ^ Перейти обратно: а б Стюарт 2001 , стр. 108–109.
- ^ Болл 2009a , стр. 73–76.
- ^ Болл 2009a , с. 41.
- ^ Ханнави, Джон (2007). Энциклопедия фотографии девятнадцатого века . Том. 1. ЦРК Пресс. п. 149. ИСБН 978-0-415-97235-2 .
- ^ Перейти обратно: а б Ливио, Марио (2003) [2002]. Золотое сечение: история Фи, самого удивительного числа в мире . Нью-Йорк: Бродвейские книги . п. 111. ИСБН 978-0-7679-0816-0 .
- ^ О Д'Арси. Архивировано 1 июля 2017 г. в Wayback Machine . Д'Арси 150. Университет Данди и Университет Сент-Эндрюс . Проверено 16 октября 2012 г.
- ^ Перейти обратно: а б Тьюринг, AM (1952). «Химические основы морфогенеза». Философские труды Королевского общества Б. 237 (641): 37–72. Бибкод : 1952РСПТБ.237...37Т . дои : 10.1098/rstb.1952.0012 . S2CID 937133 .
- ^ Болл 2009a , стр. 163, 247–250.
- ^ Перейти обратно: а б с Розенберг, Гжегож ; Саломаа, Арто. Математическая теория L-систем . Академик Пресс , Нью-Йорк, 1980. ISBN 0-12-597140-0
- ^ Перейти обратно: а б Мандельброт, Бенуа Б. (1983). Фрактальная геометрия природы . Макмиллан.
- ^ Форбс, Питер. Вся эта бесполезная красота . Хранитель. Рецензия: Нон-фикшн. 11 февраля 2012 г.
- ^ Стивенс 1974 , с. 222.
- ^ Стин, Луизиана (1988). «Наука о закономерностях» . Наука . 240 (4852): 611–616. Бибкод : 1988Sci...240..611S . дои : 10.1126/science.240.4852.611 . ПМИД 17840903 . S2CID 4849363 . Архивировано из оригинала 28 октября 2010 г. Проверено 2 мая 2012 г.
- ^ Девлин, Кейт . Математика: наука о закономерностях: поиск порядка в жизни, разуме и Вселенной (Научно-американская библиотека в мягкой обложке), 1996 г.
- ^ Татаркевич, Владислав . «Совершенство в науках. II. Совершенство в физике и химии». Диалектика и гуманизм . 7 (2 (весна 1980 г.)): 139.
- ^ Перейти обратно: а б с Дарвин, Чарльз . О происхождении видов . 1859 г., глава 4.
- ^ Перейти обратно: а б Виклер, Вольфганг (1968). Мимикрия у растений и животных . Нью-Йорк: МакГроу-Хилл.
- ^ Пулен, Р.; Груттер, А.С. (1996). «Очистка симбиозов: приближенные и адаптивные объяснения» . Бионаука . 46 (7): 512–517. дои : 10.2307/1312929 . JSTOR 1312929 .
- ^ Конинг, Росс (1994). «Информационный веб-сайт по физиологии растений» . Адаптации к опылению . Проверено 2 мая 2012 г.
- ^ Стюарт 2001 , стр. 48–49.
- ^ Стюарт 2001 , стр. 64–65.
- ^ Стюарт 2001 , с. 52.
- ^ Стюарт 2001 , стр. 82–84.
- ^ Стюарт 2001 , с. 60.
- ^ Стюарт 2001 , с. 71.
- ^ Хикман, Кливленд П.; Робертс, Ларри С.; Ларсон, Аллан (2002). «Разнообразие животных» (PDF) . Глава 8: Ацеломатные двусторонние животные (Третье изд.). п. 139. Архивировано из оригинала (PDF) 17 мая 2016 года . Проверено 25 октября 2012 г.
- ^ Самралл, Колин Д.; Рэй, Грегори А. (январь 2007 г.). «Онтогенез в летописи окаменелостей: разнообразие строения тела и эволюция «аберрантной» симметрии у палеозойских иглокожих». Палеобиология . 33 (1): 149–163. Бибкод : 2007Pbio...33..149S . дои : 10.1666/06053.1 . JSTOR 4500143 . S2CID 84195721 .
- ^ «Образ недели – Боже милостивый, огромные ледяные шарики!» . Криосферные науки . Проверено 23 апреля 2022 г.
- ^ Рихтер, Жан Поль, изд. (1970) [1880]. Записные книжки Леонардо да Винчи Дувр. ISBN 978-0-486-22572-2 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Перейти обратно: а б Палка, Джо (26 декабря 2011 г.). «Мудрость деревьев (Леонардо да Винчи это знал)» . Утренний выпуск . ЭНЕРГЕТИЧЕСКИЙ ЯДЕРНЫЙ РЕАКТОР . Проверено 16 июля 2019 г.
- ^ Минамино, Рёко; Татено, Масаки (2014). «Ветвление дерева: правило Леонардо да Винчи против биомеханических моделей». ПЛОС Один . Том. 9, нет. 4. с. е93535. дои : 10.1371/journal.pone.0093535 .
- ^ Фальконер, Кеннет (2003). Фрактальная геометрия: математические основы и приложения . Джон Уайли.
- ^ Бриггс, Джон (1992). Фракталы: закономерности хаоса . Темза и Гудзон. п. 148.
- ^ Бэтти, Майкл (4 апреля 1985 г.). «Фракталы – геометрия между измерениями». Новый учёный . 105 (1450): 31.
- ^ Мейер, Ив; Рокес, Сильви (1993). Прогресс в вейвлет-анализе и приложениях: материалы Международной конференции «Вейвлеты и приложения», Тулуза, Франция – июнь 1992 г. Атлантика Сегье Фронтьер. п. 25. ISBN 9782863321300 .
- ^ Карбоне, Алессандра; Громов, Михаил; Прусинкевич, Пшемыслав (2000). Формирование закономерностей в биологии, зрении и динамике . Всемирная научная. п. 78. ИСБН 978-9810237929 .
- ^ Хан, Хорст К.; Георг, Манфред; Пейтген, Хайнц-Отто (2005). «Фрактальные аспекты трехмерной сосудистой конструктивной оптимизации». В Лосе, Габриэле А.; Нонненмахер, Тео Ф. (ред.). Фракталы в биологии и медицине . Спрингер. стр. 55–66.
- ^ Такеда, Т; Исикава, А; Отомо, К; Кобаяши, Ю; Мацуока, Т. (февраль 1992 г.). «Фрактальная размерность дендритного дерева клетки Пуркинье мозжечка в процессе онто- и филогенетического развития». Неврологические исследования . 13 (1): 19–31. дои : 10.1016/0168-0102(92)90031-7 . ПМИД 1314350 . S2CID 4158401 .
- ^ Садег, Саназ (2017). «Плазменная мембрана разделена самоподобной кортикальной актиновой сеткой» . Физический обзор X . 7 (1): 011031. arXiv : 1702.03997 . Бибкод : 2017PhRvX...7a1031S . дои : 10.1103/PhysRevX.7.011031 . ПМК 5500227 . ПМИД 28690919 .
- ^ Аддисон, Пол С. (1997). Фракталы и хаос: иллюстрированный курс . ЦРК Пресс. стр. 44–46.
- ^ Маор, Эли. е: История числа . Издательство Принстонского университета, 2009. Страница 135.
- ^ Болл 2009a , стр. 29–32.
- ^ «Спиральные решетки и парастихия» . Смит-колледж . Архивировано из оригинала 26 мая 2010 года . Проверено 24 сентября 2013 г.
- ^ Перейти обратно: а б Каппрафф, Джей (2004). «Рост растений: количественное исследование» (PDF) . Форма . 19 : 335–354. Архивировано из оригинала (PDF) 4 марта 2016 г. Проверено 2 мая 2012 г.
- ^ Болл 2009a , с. 13.
- ^ Коксетер, HSM (1961). Введение в геометрию . Уайли. п. 169.
- ^ Прусинкевич, Пшемыслав ; Линденмайер, Аристид (1990). Алгоритмическая красота растений . Спрингер-Верлаг. стр. 101–107 . ISBN 978-0-387-97297-8 .
- ^ Левитов Л.С. (15 марта 1991 г.). «Энергетический подход к филлотаксису». Письма по еврофизике . 14 (6): 533–539. Бибкод : 1991EL.....14..533L . дои : 10.1209/0295-5075/14/6/006 . S2CID 250864634 .
- ^ Дуади, С.; Кудер, Ю. (март 1992 г.). «Филлотаксис как процесс физического самоорганизованного роста». Письма о физических отзывах . 68 (13): 2098–2101. Бибкод : 1992PhRvL..68.2098D . doi : 10.1103/PhysRevLett.68.2098 . ПМИД 10045303 .
- ^ Болл 2009a , стр. 163, 249–250.
- ^ Лоренц, Эдвард Н. (март 1963 г.). «Детерминированный непериодический поток» . Журнал атмосферных наук . 20 (2): 130–141. Бибкод : 1963JAtS...20..130L . doi : 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 .
- ^ Элайди, Сабер Н. (1999). Дискретный хаос . Чепмен и Холл/CRC. п. 117.
- ^ Рюэль, Дэвид (1991). Случайность и Хаос . Издательство Принстонского университета.
- ^ Вольфрам, Стивен (2002). Новый вид науки . Вольфрам Медиа.
- ^ фон Карман, Теодор (1963). Аэродинамика . МакГроу-Хилл. ISBN 978-0070676022 . . Дувр (1994): ISBN 978-0486434858 .
- ^ Левалле, Жак (2006). «Разделение потоков и вторичный поток: раздел 9.1» (PDF) . Конспект лекций по динамике несжимаемой жидкости: феноменология, концепции и аналитические инструменты . Сиракьюс, Нью-Йорк: Сиракузский университет. Архивировано из оригинала (PDF) 29 сентября 2011 года .
- ^ Французский, AP (1971). Вибрации и волны . Нельсон Торнс.
- ^ Толман, Х.Л. (2008). «Практическое моделирование ветровых волн» (PDF) . В Махмуде, МФ (ред.). Материалы конференции CBMS «Волны на воде: теория и эксперимент» . Университет Говарда, США, 13–18 мая 2008 г. World Scientific Publications.
- ^ «Виды дюн» . Геологическая служба США . 29 октября 1997 года . Проверено 2 мая 2012 г.
- ^ Стралер, А.; Арчибольд, Огайо (2008). Физическая география: наука и системы окружающей среды (4-е изд.). Джон Уайли. п. 442.
- ^ Швэммле, В.; Херрман, HJ (11 декабря 2003 г.). «Уединенное волновое поведение песчаных дюн». Природа . 426 (6967): 619–620. Бибкод : 2003Natur.426..619S . дои : 10.1038/426619а . PMID 14668849 . S2CID 688445 .
- ^ Болл 2009a , с. 68.
- ^ Альмгрен, Фредерик Дж. Младший; Тейлор, Джин Э. (июль 1976 г.). «Геометрия мыльных пленок и мыльных пузырей». Научный американец . 235 (235): 82–93. Бибкод : 1976SciAm.235a..82A . doi : 10.1038/scientificamerican0776-82 .
- ^ Болл 2009a , стр. 96–101.
- ^ Броди, Кристина (февраль 2005 г.). «Геометрия и закономерности в природе 3: дыры в тестах радиолярий и диатомей» . Микроскопия-Великобритания . Проверено 28 мая 2012 г.
- ^ Болл 2009a , стр. 51–54.
- ^ Армстронг, Массачусетс (1988). Группы и симметрия . Нью-Йорк: Springer-Verlag.
- ^ Крюк, младший; Холл, HE Физика твердого тела (2-е издание). Серия по Манчестерской физике, John Wiley & Sons, 2010. ISBN 978-0-471-92804-1
- ^ Стивенс 1974 , с. 207.
- ^ Стивенс 1974 , с. 208.
- ^ Перейти обратно: а б Болл 2009a , стр. 156–158.
- ^ Мюррей, Джеймс Д. (9 марта 2013 г.). Математическая биология . Springer Science & Business Media. стр. 436–450. ISBN 978-3-662-08539-4 .
- ^ Перейти обратно: а б Болл 2009a , стр. 159–167.
- ^ Болл 2009a , стр. 168–180.
- ^ Ротенберг 2011 , стр. 93–95.
- ^ Перейти обратно: а б Прум, Ричард О .; Уильямсон, Скотт (2002). «Реакционно-диффузионные модели формирования рисунка пигментации внутри пера» (PDF) . Труды Лондонского королевского общества Б. 269 (1493): 781–792. дои : 10.1098/рспб.2001.1896 . ПМК 1690965 . ПМИД 11958709 .
- ^ Перейти обратно: а б Тонгуэй, диджей; Валентин, К.; Сегиери, Дж. (2001). Полосатая растительность в засушливых и полузасушливых условиях . Нью-Йорк: Springer-Verlag.
- ^ Перейти обратно: а б Д'Аванзо, К. (22 февраля 2004 г.). «Пихтовые волны: регенерация хвойных лесов Новой Англии» . ГАЛСТУК . Проверено 26 мая 2012 г.
- ^ Морель, Ребекка (9 декабря 2013 г.). « Цифровые суслики» разгадали тайну кургана Мима» . Новости Би-би-си . Проверено 9 декабря 2013 г.
- ^ Сэмпл, Ян (18 января 2017 г.). «Наконец-то тайна «волшебных кругов» Намибии может быть объяснена» . Хранитель . Проверено 18 января 2017 г.
- ^ «Вечная мерзлота: узорчатая земля» . Инженерный корпус армии США . Архивировано из оригинала 7 марта 2015 года . Проверено 17 февраля 2015 г.
- ^ Гоуз, Тиа. «Причудливая структура человеческого мозга, воссозданная в чане» . Научный американец . Проверено 5 апреля 2018 г.
- ^ Таллинен, Туома; Чунг, Джун Ён; Биггинс, Джон С.; Махадеван, Л. (2014). «Гирификация вследствие ограниченного расширения коры» . Труды Национальной академии наук Соединенных Штатов Америки . 111 (35): 12667–12672. arXiv : 1503.03853 . Бибкод : 2014PNAS..11112667T . дои : 10.1073/pnas.1406015111 . ПМК 4156754 . ПМИД 25136099 .
Библиография
[ редактировать ]Авторы-новаторы
- Фибоначчи, Леонардо . Либер Абачи , 1202 год.
- ———— перевод Сиглера, Liber Abaci Лоуренса Э. Фибоначчи . Спрингер, 2002.
- Геккель, Эрнст . Формы искусства в природе , 1899–1904.
- Томпсон, Д'Арси Вентворт . О росте и форме . Кембридж, 1917 год.
Общие книги
- Адам, Джон А. Математика в природе: моделирование закономерностей в мире природы . Издательство Принстонского университета , 2006.
- Болл, Филип (2009a). Узоры природы: гобелен в трёх частях. 1: Формы . Издательство Оксфордского университета.
- Болл, Филип (2009b). Узоры природы: гобелен в трёх частях. 2: Поток . Издательство Оксфордского университета.
- Болл, Филип (2009c). Узоры природы: гобелен в трёх частях. 3. Филиалы . Издательство Оксфордского университета.
- Болл, Филип. Узоры в природе . Чикаго, 2016.
- Мерфи, Пэт и Нил, Уильям. По дизайну природы . Книги хроник , 1993.
- Ротенберг, Дэвид (2011). Выживание прекрасного: искусство, наука и эволюция . Блумсбери Пресс .
- Стивенс, Питер С. (1974). Узоры в природе . Литтл, Браун и Ко .
- Стюарт, Ян (2001). Какой формы снежинка? Магические числа в природе . Вайденфельд и Николсон .
Узоры с натуры (как искусство)
- Эдмайер, Бернар. Узоры Земли . Файдон Пресс , 2007.
- Макнаб, Мэгги. Дизайн от природы: использование универсальных форм и принципов в дизайне . Новые гонщики, 2012.
- Накамура, Сигэки. Справочник по узорам: 250 узоров, вдохновленных природой. . Книги 1 и 2. Рокпорт, 2009.
- О'Нил, Полли. Поверхности и текстуры: Визуальный справочник . Черный, 2008.
- Портер, Элиот и Глейк, Джеймс . Природный хаос . Пингвин-викинг , 1990 год.