Гравитация

| Часть серии о |
| Классическая механика |
|---|
В физике гравитация (от лат. gravitas «вес»). [1] ) — это фундаментальное взаимодействие , которое вызывает взаимное притяжение между всеми вещами, имеющими массу . Гравитация, безусловно, самое слабое из четырех фундаментальных взаимодействий, примерно 10 38 раз слабее сильного взаимодействия , в 10 раз 36 раз слабее электромагнитной силы и в 10 раз 29 раз слабее слабого взаимодействия . В результате он не оказывает существенного влияния на уровне субатомных частиц . [2] Однако гравитация является наиболее значимым взаимодействием между объектами в макроскопическом масштабе и определяет движение планет , звезд , галактик и даже света .
На Земле гравитация придает вес , физическим объектам а гравитация Луны отвечает за сублунные приливы и отливы в океанах. Соответствующий антиподальный прилив вызван инерцией Земли и Луны, вращающихся вокруг друг друга. Гравитация также выполняет множество важных биологических функций, помогая направлять рост растений посредством процесса гравитропизма и влияя на циркуляцию жидкостей в многоклеточных организмах .
Гравитационное притяжение между исходным газообразным веществом во Вселенной привело к его слиянию и образованию звезд , которые в конечном итоге конденсировались в галактики, поэтому гравитация ответственна за многие крупномасштабные структуры во Вселенной. Гравитация имеет бесконечный радиус действия, хотя ее воздействие становится слабее по мере удаления объектов.
Гравитация наиболее точно описывается общей теорией относительности , предложенной Альбертом Эйнштейном в 1915 году, которая описывает гравитацию не как силу, а как искривление пространства -времени , вызванное неравномерным распределением массы и заставляющее массы двигаться вдоль геодезических линий. . Самый крайний пример искривления пространства-времени — это черная дыра , из которой ничто — даже свет — не может покинуть горизонт событий черной дыры . [3] Однако для большинства приложений гравитация хорошо аппроксимируется законом всемирного тяготения Ньютона , который описывает гравитацию как силу, заставляющую любые два тела притягиваться друг к другу, величина которой пропорциональна произведению их масс и обратно пропорциональна квадрату силы тяжести. расстояние между ними .
Современные модели физики элементарных частиц предполагают, что самый ранний экземпляр гравитации во Вселенной, возможно, в форме квантовой гравитации , супергравитации или гравитационной сингулярности , наряду с обычным пространством и временем , развился в эпоху Планка (до 10 лет). −43 секунд после рождения Вселенной), возможно, из первобытного состояния, такого как ложный вакуум , квантовый вакуум или виртуальная частица , неизвестным в настоящее время способом. [4] В настоящее время ученые работают над разработкой теории гравитации, согласующейся с квантовой механикой , теории квантовой гравитации. [5] что позволило бы объединить гравитацию в общей математической структуре ( теории всего ) с тремя другими фундаментальными взаимодействиями физики.
Определения
Гравитация , также известная как гравитационное притяжение, — это взаимное притяжение между всеми массами во Вселенной. Гравитация — это гравитационное притяжение на поверхности планеты или другого небесного тела; [6] гравитация может также включать, помимо гравитации, центробежную силу, возникающую в результате вращения планеты. . [7]
История
Древний мир
Природа и механизм гравитации исследовались широким кругом древних ученых. В Греции считал, что объекты падали на Землю , Аристотель потому что Земля была центром Вселенной и притягивала к себе всю массу Вселенной. Он также считал, что скорость падающего объекта должна увеличиваться вместе с его весом, но позже выяснилось, что этот вывод ошибочен. [8] Хотя точка зрения Аристотеля была широко принята во всей Древней Греции, были и другие мыслители, такие как Плутарх, которые правильно предсказали, что гравитационное притяжение не уникально для Земли. [9]
Древнегреческий философ Архимед, хотя и не понимал гравитацию как силу, открыл центр тяжести треугольника. [10] Он постулировал, что если бы две равные гири не имели один и тот же центр тяжести, центр тяжести двух гирь вместе находился бы в середине линии, соединяющей их центры тяжести. [11] Два столетия спустя римский инженер и архитектор Витрувий в своей книге «Об архитектуре» утверждал , что гравитация зависит не от веса вещества, а скорее от его «природы». [12] В VI веке нашей эры византийский александрийский ученый Иоанн Филопон предложил теорию импульса, которая модифицирует теорию Аристотеля о том, что «продолжение движения зависит от продолжающегося действия силы», включая причинную силу, которая со временем уменьшается. [13]
В седьмом веке нашей эры индийский математик и астроном Брахмагупта термин гурутвакаршан . выдвинул идею о том, что гравитация — это сила притяжения, притягивающая объекты к Земле, и использовал для ее описания [14] [15] [16]
На древнем Ближнем Востоке гравитация была темой ожесточенных споров. Персидский небесные интеллектуал Аль-Бируни считал, что сила гравитации свойственна не только Земле, и он правильно предположил, что другие тела также должны оказывать гравитационное притяжение. [17] Напротив, Аль-Хазини придерживался той же позиции, что и Аристотель, согласно которой вся материя во Вселенной притягивается к центру Земли. [18]

Научная революция
В середине 16 века различные европейские ученые экспериментально опровергли аристотелевское представление о том, что более тяжелые объекты падают с большей скоростью. [19] В частности, испанский священник-доминиканец Доминго де Сото писал в 1551 году, что тела в свободном падении ускоряются равномерно. [19] На Де Сото, возможно, повлияли более ранние эксперименты, проведенные другими доминиканскими священниками в Италии, в том числе Бенедетто Варки , Франческо Беато, Лукой Гини и Джованом Белласо , которые противоречили учению Аристотеля о падении тел. [19]
Итальянский физик середины XVI века Джамбаттиста Бенедетти опубликовал работы, в которых утверждалось, что из-за удельного веса предметы, сделанные из одного и того же материала, но с разной массой, будут падать с одинаковой скоростью. [20] Во время эксперимента с Делфтской башней в 1586 году фламандский заметил, что два пушечных ядра разного размера и веса падали с одинаковой скоростью, когда их физик Саймон Стевин бросали с башни. [21] В конце XVI века тщательные измерения Галилео Галилеем шаров, катящихся по склону , позволили ему твердо установить, что гравитационное ускорение одинаково для всех объектов. [22] Галилей постулировал, что сопротивление воздуха является причиной того, что объекты с низкой плотностью и большой площадью поверхности падают в атмосфере медленнее.
В 1604 году Галилей правильно предположил, что расстояние до падающего предмета пропорционально квадрату прошедшего времени. [23] Позже это подтвердили итальянские ученые- иезуиты Гримальди и Риччоли между 1640 и 1650 годами. Они также рассчитали величину гравитации Земли , измеряя колебания маятника. [24]
Теория гравитации Ньютона
В 1657 году Роберт Гук опубликовал свою «Микрографию» , в которой выдвинул гипотезу, что Луна должна иметь собственную гравитацию. [25] В 1666 году он добавил еще два принципа: все тела движутся по прямым линиям, пока не будут отклонены какой-либо силой, и что сила притяжения сильнее для более близких тел. В сообщении Королевскому обществу в 1666 году Гук писал: [26]
Я объясню систему мира, сильно отличающуюся от любой другой, полученной до сих пор. В его основе лежат следующие положения. 1. Что все небесные тела имеют не только тяготение своих частей к собственному центру, но и взаимно притягивают друг друга в своих сферах действия. 2. Что все тела, совершающие простое движение, будут продолжать двигаться по прямой, если только их постоянно не отклоняет от нее какая-то посторонняя сила, заставляющая их описывать круг, эллипс или какую-либо другую кривую. 3. Это притяжение тем сильнее, чем ближе тела. Что же касается пропорции, в которой эти силы уменьшаются с увеличением расстояния, то, признаюсь, я ее не обнаружил...
В лекции Гука в Грешаме 1674 года « Попытка доказать годовое движение Земли » объяснялось, что гравитация применима ко «всем небесным телам». [27]

рукопись В 1684 году Ньютон отправил Эдмону Галлею под названием De motu corporum in gyrum («О движении тел по орбите») , в которой дано физическое обоснование законов движения планет Кеплера . [28] Галлей был впечатлен рукописью и призвал Ньютона расширить ее, а несколько лет спустя Ньютон опубликовал новаторскую книгу под названием Philosophiæ Naturalis Principia Mathematica ( «Математические принципы натуральной философии »). В этой книге Ньютон описал гравитацию как универсальную силу и заявил, что «силы, удерживающие планеты на их орбитах, должны быть пропорциональны квадратам их расстояний от центров, вокруг которых они вращаются». Позже это утверждение было преобразовано в следующий закон обратных квадратов:
где F – сила, m 1 и m 2 – массы взаимодействующих объектов, r – расстояние между центрами масс и G – гравитационная постоянная 6,674 × 10. −11 м 3 ⋅kg −1 ⋅s −2 . [29]
Ньютона «Начала» были хорошо приняты научным сообществом, а его закон гравитации быстро распространился по европейскому миру. [30] Более столетия спустя, в 1821 году, его теория гравитации приобрела еще большую известность, когда она была использована для предсказания существования Нептуна . В том же году французский астроном Алексис Бувар использовал эту теорию для создания таблицы, моделирующей орбиту Урана , которая, как было показано, значительно отличалась от фактической траектории планеты. Чтобы объяснить это несоответствие, многие астрономы предположили, что за орбитой Урана может находиться крупный объект, нарушающий его орбиту. В 1846 году астрономы Джон Коуч Адамс и Урбен Леверье независимо друг от друга использовали закон Ньютона, чтобы предсказать местоположение Нептуна на ночном небе, и планета была там обнаружена в течение суток. [31]
Общая теория относительности
| Общая теория относительности |
|---|
 |
В конце концов астрономы заметили эксцентриситет орбиты планеты Меркурий , который не мог быть объяснен теорией Ньютона: перигелий орбиты увеличивался примерно на 42,98 угловых секунд за столетие. Самым очевидным объяснением этого несоответствия было еще не открытое небесное тело, например, планета, вращающаяся вокруг Солнца даже ближе, чем Меркурий, но все усилия найти такое тело оказались бесплодными. В 1915 году Альберт Эйнштейн разработал общую теорию относительности , которая смогла точно смоделировать орбиту Меркурия. [32]
В общей теории относительности эффекты гравитации приписываются кривизне пространства-времени, а не силе. Эйнштейн начал экспериментировать с этой идеей в форме принципа эквивалентности — открытия, которое он позже назвал «самой счастливой мыслью в своей жизни». [33] В этой теории свободное падение считается эквивалентным движению по инерции, а это означает, что свободно падающие инерционные объекты ускоряются относительно неинерциальных наблюдателей на земле. [34] [35] В отличие от физики Ньютона , Эйнштейн считал, что это ускорение может происходить без приложения к объекту какой-либо силы.
Эйнштейн предположил, что пространство-время искривлено материей и что свободно падающие объекты движутся по локально прямым траекториям в искривленном пространстве-времени. Эти прямые пути называются геодезическими . Как и в первом законе движения Ньютона, Эйнштейн считал, что сила, приложенная к объекту, заставит его отклониться от геодезической. Например, люди, стоящие на поверхности Земли, не могут следовать по геодезическому пути, поскольку механическое сопротивление Земли оказывает на них направленную вверх силу. Это объясняет, почему движение по геодезическим в пространстве-времени считается инерционным.
Описание гравитации Эйнштейном было быстро принято большинством физиков, поскольку оно смогло объяснить широкий спектр ранее сбивающих с толку экспериментальных результатов. [36] В последующие годы широкий спектр экспериментов предоставил дополнительную поддержку идеи общей теории относительности. [37] [38] [39] [40] Сегодня теория относительности Эйнштейна используется для всех гравитационных расчетов, где требуется абсолютная точность, хотя закон обратных квадратов Ньютона продолжает оставаться полезным и довольно точным приближением. [41]
Современные исследования
В современной физике общая теория относительности остается основой понимания гравитации. [42] Физики продолжают работать над поиском решений уравнений поля Эйнштейна , которые составляют основу общей теории относительности, в то время как некоторые ученые предполагают, что общая теория относительности может быть вообще неприменима в определенных сценариях. [41]
Уравнения поля Эйнштейна
Уравнения поля Эйнштейна представляют собой систему из 10 уравнений в частных производных , которые описывают, как материя влияет на кривизну пространства-времени. Система часто выражается в виде где G µν – тензор Эйнштейна , g µν – метрический тензор , T µν – тензор энергии-импульса , Λ – космологическая постоянная , – ньютоновская постоянная гравитации и это скорость света . [43] Константа называется гравитационной постоянной Эйнштейна. [44]

Основной областью исследований является обнаружение точных решений уравнений поля Эйнштейна. Решение этих уравнений сводится к вычислению точного значения метрического тензора (который определяет кривизну и геометрию пространства-времени) при определенных физических условиях. Не существует формального определения того, что представляет собой такие решения, но большинство ученых согласны с тем, что их следует выражать с помощью элементарных функций или линейных дифференциальных уравнений . [45] Некоторые из наиболее известных решений уравнений включают:
- Решение Шварцшильда , которое описывает пространство-время, окружающее сферически-симметричный невращающийся незаряженный массивный объект. Для достаточно компактных объектов это решение породило черную дыру с центральной особенностью . [46] В точках, удаленных от центральной массы, ускорения, предсказанные решением Шварцшильда, практически идентичны ускорениям, предсказанным теорией гравитации Ньютона. [47]
- Решение Рейсснера -Нордстрема , которое анализирует невращающийся сферически-симметричный объект с зарядом и было независимо открыто несколькими разными исследователями в период с 1916 по 1921 год. [48] В некоторых случаях это решение может предсказать существование черных дыр с двойным горизонтом событий . [49]
- Решение Керра , которое обобщает решение Шварцшильда для вращения массивных объектов. Из-за сложности учета эффектов вращения в уравнениях поля Эйнштейна это решение не было обнаружено до 1963 года. [50]
- Решение Керра -Ньюмана для заряженных вращающихся массивных объектов. Это решение было получено в 1964 году с использованием той же техники комплексного преобразования координат, которая использовалась для решения Керра. [51]
- Космологическое решение Фридмана-Леметра- Робертсона -Уокера , открытое в 1922 году Александром Фридманом и затем подтвержденное в 1927 году Жоржем Леметром . Это решение было революционным для предсказания расширения Вселенной , что было подтверждено семь лет спустя после серии измерений Эдвина Хаббла . [52] Оно даже показало, что общая теория относительности несовместима со статичной Вселенной , а Эйнштейн позже признал, что он ошибался, разрабатывая свои уравнения поля для объяснения нерасширяющейся Вселенной. [53]
Сегодня остается много важных ситуаций, в которых уравнения поля Эйнштейна не решены. Главной среди них является проблема двух тел , которая касается геометрии пространства-времени вокруг двух взаимно взаимодействующих массивных объектов, таких как Солнце и Земля, или двух звезд в двойной звездной системе . Ситуация становится еще более сложной при рассмотрении взаимодействий трех и более массивных тел (« проблема n тел»), и некоторые ученые подозревают, что уравнения поля Эйнштейна никогда не будут решены в этом контексте. [54] Однако построить приближенное решение уравнений поля в задаче n тел все же возможно, используя технику постньютоновского разложения . [55] В общем, крайняя нелинейность уравнений поля Эйнштейна затрудняет их решение во всех случаях, кроме самых конкретных. [56]
Гравитация и квантовая механика
Несмотря на успех в предсказании эффектов гравитации в больших масштабах, общая теория относительности в конечном итоге несовместима с квантовой механикой . Это связано с тем, что общая теория относительности описывает гравитацию как плавное, непрерывное искажение пространства-времени, в то время как квантовая механика утверждает, что все силы возникают в результате обмена дискретными частицами, известными как кванты . Это противоречие особенно неприятно для физиков, поскольку три другие фундаментальные силы (сильное взаимодействие, слабое взаимодействие и электромагнетизм) были согласованы с квантовой структурой несколько десятилетий назад. [57] В результате современные исследователи начали поиск теории, которая могла бы объединить гравитацию и квантовую механику в более общих рамках. [58]
Один путь – описать гравитацию в рамках квантовой теории поля , которая успешно описывает другие фундаментальные взаимодействия . Электромагнитная сила возникает в результате обмена виртуальными фотонами , где гравитация в КТФ-описании заключается в обмене виртуальными гравитонами . [59] [60] Это описание воспроизводит общую теорию относительности в классическом пределе . Однако этот подход не работает на малых расстояниях порядка длины планковской [61] более полная теория квантовой гравитации где требуется (или новый подход к квантовой механике).
Тесты общей теории относительности
Проверка предсказаний общей теории относительности исторически была трудной, поскольку они почти идентичны предсказаниям ньютоновской гравитации для малых энергий и масс. [62] Тем не менее, с момента ее разработки продолжающаяся серия экспериментальных результатов подтвердила теорию: [62]

- В 1919 году британский астрофизик Артур Эддингтон смог подтвердить предсказанное гравитационное линзирование света во время солнечного затмения того года . [63] [64] Эддингтон измерил отклонения звездного света в два раза больше, чем предсказывает корпускулярная теория Ньютона, в соответствии с предсказаниями общей теории относительности. Хотя анализ Эддингтона позже был оспорен, этот эксперимент почти в мгновение ока прославил Эйнштейна и привел к тому, что общая теория относительности получила широкое признание в научном сообществе. [65]
- В 1959 году американские физики Роберт Паунд и Глен Ребка провели эксперимент , в котором они использовали гамма-лучи для подтверждения предсказания гравитационного замедления времени . Направив лучи вниз по 74-футовой башне и измерив их частоту внизу, ученые подтвердили, что свет смещается в красную сторону по мере движения к источнику гравитации. Наблюдаемое красное смещение также подтверждает идею о том, что время течет медленнее в присутствии гравитационного поля. [66]
- Временная задержка прохождения света вблизи массивного объекта была впервые обнаружена Ирвином И. Шапиро в 1964 году в сигналах межпланетных космических кораблей. [67]
- В 1971 году учёные обнаружили первую в истории чёрную дыру в галактике Лебедь . Черная дыра была обнаружена потому, что она испускала всплески рентгеновского излучения , поглощая меньшую звезду, и стала известна как Лебедь X-1 . [68] Это открытие подтвердило еще одно предсказание общей теории относительности, поскольку уравнения Эйнштейна подразумевали, что свет не может вырваться из достаточно большого и компактного объекта. [69]
- Общая теория относительности утверждает, что гравитация действует на свет и материю одинаково, а это означает, что достаточно массивный объект может искажать свет вокруг себя и создавать гравитационную линзу . Впервые это явление было подтверждено наблюдением в 1979 году с помощью 2,1-метрового телескопа Национальной обсерватории Китт-Пик в Аризоне, который увидел два зеркальных изображения одного и того же квазара, свет которого огибал галактику YGKOW G1 . [70] [71]
- Перетаскивание кадра , идея о том, что вращающийся массивный объект должен закручивать вокруг себя пространство-время, была подтверждена результатами Gravity Probe B в 2011 году. [72] [73]
- В 2015 году обсерватория LIGO обнаружила слабые гравитационные волны , существование которых было предсказано общей теорией относительности. Ученые полагают, что волны возникли в результате слияния черных дыр , произошедшего на расстоянии 1,5 миллиардов световых лет от нас. [74]
Особенности
Гравитация Земли

Каждое планетарное тело (включая Землю) окружено собственным гравитационным полем, которое с точки зрения ньютоновской физики можно представить как оказывающее силу притяжения на все объекты. Если предположить, что планета сферически симметрична, то сила этого поля в любой данной точке над поверхностью пропорциональна массе планетарного тела и обратно пропорциональна квадрату расстояния от центра тела.

Сила гравитационного поля численно равна ускорению объектов, находящихся под его воздействием. [75] Скорость ускорения падающих объектов у поверхности Земли очень незначительно варьируется в зависимости от широты, особенностей поверхности, таких как горы и хребты, и, возможно, необычно высокой или низкой плотности подповерхностных слоев. [76] Для целей мер и весов стандартное значение силы тяжести определяется Международным бюро мер и весов в соответствии с Международной системой единиц (СИ).
Сила гравитации на Земле является равнодействующей (векторной суммой) двух сил: [7] (а) Гравитационное притяжение в соответствии с универсальным законом тяготения Ньютона и (б) центробежная сила, возникающая в результате выбора связанной с Землей вращающейся системы отсчета. Сила гравитации самая слабая на экваторе из-за центробежной силы , вызванной вращением Земли, а также потому, что точки на экваторе находятся дальше всего от центра Земли. Сила гравитации меняется в зависимости от широты и увеличивается примерно с 9,780 м/с. 2 на экваторе примерно до 9,832 м/с. 2 на полюсах. [77] [78]
Источник
Самая ранняя гравитация (возможно, в форме квантовой гравитации, супергравитации или гравитационной сингулярности ), наряду с обычным пространством и временем, развивалась в эпоху Планка (до 10 −43 секунд после рождения Вселенной), возможно, из первобытного состояния (например, ложного вакуума , квантового вакуума или виртуальной частицы ), неизвестным в настоящее время способом. [4]
Гравитационное излучение

Общая теория относительности предсказывает, что энергия может переноситься из системы посредством гравитационного излучения. Первым косвенным свидетельством гравитационного излучения были измерения двойной системы Халса-Тейлора в 1973 году. Эта система состоит из пульсара и нейтронной звезды, вращающихся вокруг друг друга. Период его обращения уменьшился с момента его первоначального открытия из-за потери энергии, что соответствует количеству потерь энергии из-за гравитационного излучения. Это исследование было удостоено Нобелевской премии по физике в 1993 году. [79]
Первые прямые доказательства гравитационного излучения были измерены 14 сентября 2015 года детекторами LIGO . Были измерены гравитационные волны, излучаемые при столкновении двух черных дыр на расстоянии 1,3 миллиарда световых лет от Земли. [80] [81] Это наблюдение подтверждает теоретические предсказания Эйнштейна и других о существовании таких волн. Это также открывает путь к практическому наблюдению и пониманию природы гравитации и событий во Вселенной, включая Большой взрыв. [82] Образование нейтронных звезд и черных дыр также создает заметное количество гравитационного излучения. [83] Это исследование было удостоено Нобелевской премии по физике в 2017 году. [84]
Скорость гравитации
В декабре 2012 года исследовательская группа в Китае объявила, что она провела измерения фазового отставания земных приливов во время полнолуния и новолуния, которые, по-видимому, доказывают, что скорость гравитации равна скорости света. [85] Это означает, что если бы Солнце внезапно исчезло, Земля продолжала бы вращаться вокруг свободной точки в течение 8 минут — именно столько времени требуется свету, чтобы пройти это расстояние. Выводы команды были опубликованы в Science Bulletin в феврале 2013 года. [86]
В октябре 2017 года детекторы LIGO и Virgo получили сигналы гравитационных волн в течение 2 секунд после того, как спутники гамма-излучения и оптические телескопы увидели сигналы в том же направлении. Это подтвердило, что скорость гравитационных волн равна скорости света. [87]
Аномалии и несоответствия
Есть некоторые наблюдения, которые не получили должного объяснения и которые могут указывать на необходимость создания более совершенных теорий гравитации или, возможно, объясняться другими способами.
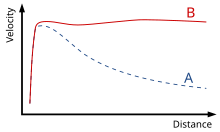
- Сверхбыстрые звезды : звезды в галактиках следуют такому распределению скоростей , при котором звезды на окраинах движутся быстрее, чем должны согласно наблюдаемому распределению нормальной материи. Галактики внутри скоплений галактик демонстрируют аналогичную картину. Темная материя , которая будет взаимодействовать посредством гравитации, а не электромагнитного взаимодействия, объясняет это несоответствие. различные модификации ньютоновской динамики . Также были предложены
- Аномалия пролета маневров испытывали большее ускорение, чем ожидалось : различные космические корабли во время гравитационных .
- Ускоренное расширение : расширение Вселенной, похоже, ускоряется. [88] темной энергией . Было предложено объяснить это [89]
- Аномальное увеличение астрономической единицы : недавние измерения показывают, что орбиты планет расширяются быстрее, чем если бы это происходило исключительно за счет потери массы Солнца за счет излучения энергии.
- Фотоны с дополнительной энергией : Фотоны, путешествующие через скопления галактик, должны набирать энергию, а затем снова терять ее на выходе. Ускоряющееся расширение Вселенной должно остановить фотоны, возвращающие всю энергию, но даже с учетом этого фотоны космического микроволнового фонового излучения получают вдвое больше энергии, чем ожидалось. Это может указывать на то, что гравитация падает быстрее, чем обратно квадратичная на определенных масштабах расстояний. [90]
- Сверхмассивные водородные облака . Спектральные линии леса Лайман-альфа предполагают, что водородные облака в определенных масштабах сгущены сильнее, чем ожидалось, и, подобно темному потоку , могут указывать на то, что гравитация спадает медленнее, чем в обратном квадрате, на определенных масштабах расстояний. [90]
Альтернативные теории
Исторические альтернативные теории
- Аристотелевская теория гравитации
- Теория гравитации Лесажа (1784 г.) также называлась гравитацией Лесажа, но первоначально была предложена Фатио и далее развита Жоржем-Луи Лесажем на основе объяснения, основанного на жидкости, где легкий газ заполняет всю Вселенную.
- Теория гравитации Ритца , Анн. хим. Физ. 13, 145, (1908), стр. 267–271, Электродинамика Вебера – Гаусса в применении к гравитации. Классическое развитие перигелий.
- Теория гравитации Нордстрема (1912, 1913), ранний конкурент общей теории относительности.
- Теория Калуцы – Клейна (1921)
- Теория гравитации Уайтхеда (1922 г.), еще один ранний конкурент общей теории относительности.
Современные альтернативные теории
- Бранса – Дике (1961) Теория гравитации [91]
- Индуцированная гравитация (1967), предложение Андрея Сахарова , согласно которому общая теория относительности может возникнуть из квантово-полевых теорий материи.
- Теория струн (конец 1960-х)
- ƒ(R) гравитация (1970)
- Теория Хорндески (1974) [92]
- Супергравитация (1976)
- В модифицированной ньютоновской динамике (МОНД) (1981) Мордехай Милгром предлагает модификацию Ньютона для малых ускорений. второго закона движения [93]
- Космологическая теория гравитации самосоздания (1982) Г. А. Барбера, в которой теория Бранса – Дике модифицирована, чтобы обеспечить создание массы.
- Петлевая квантовая гравитация (1988) Карло Ровелли , Ли Смолина и Абхая Аштекара
- Несимметричная теория гравитации (NGT) (1994) Джона Моффата
- Тензорно-векторно-скалярная гравитация (TeVeS) (2004), релятивистская модификация MOND Джейкоба Бекенштейна.
- Теория хамелеона (2004) Джастина Хури и Аманды Велтман .
- Теория давления (2013) Оливье Минаццоли и Орельена Хиса .
- Конформная гравитация [94]
- Гравитация как энтропийная сила , гравитация, возникающая как явление, возникающее из термодинамической концепции энтропии.
- В теории сверхтекучего вакуума гравитация и искривленное пространство-время возникают как коллективная мода возбуждения нерелятивистской фоновой сверхтекучей жидкости .
- Массивная гравитация — теория, согласно которой гравитоны и гравитационные волны имеют ненулевую массу.
См. также
- Антигравитация - идея создания места или объекта, свободного от силы гравитации.
- Искусственная гравитация – использование круговой вращательной силы для имитации гравитации.
- Уравнения падения тела - Математическое описание тела в свободном падении.
- Скорость убегания - понятие небесной механики.
- Выход из атмосферы - потеря планетарных атмосферных газов в космическое пространство.
- Закон гравитации Гаусса - повторение закона всемирного тяготения Ньютона.
- Гравитационный потенциал - Фундаментальное исследование теории потенциала
- Гравитационная биология - изучение воздействия гравитации на живые организмы.
- Законы движения Ньютона - Законы физики о силе и движении.
- Стандартный гравитационный параметр - Концепция небесной механики.
- Невесомость – нулевой кажущийся вес, микрогравитация.
Ссылки
- ^ "Словарь dict.cc :: graditas :: англо-латинский перевод" . Архивировано из оригинала 13 августа 2021 года . Проверено 11 сентября 2018 г.
- ^ Кребс, Роберт Э. (1999). Научное развитие и заблуждения на протяжении веков: Справочное руководство (иллюстрированное издание). Издательская группа Гринвуд. п. 133 . ISBN 978-0-313-30226-8 .
- ^ «ХабблСайт: Черные дыры: неумолимое притяжение гравитации» . сайт хабблсайт.org . Архивировано из оригинала 26 декабря 2018 года . Проверено 7 октября 2016 г.
- ^ Jump up to: а б Персонал. «Рождение Вселенной» . Университет Орегона . Архивировано из оригинала 28 ноября 2018 года . Проверено 24 сентября 2016 г. - обсуждает « Планковское время » и « Планковскую эру » в самом начале Вселенной.
- ^ До свидания, Деннис (10 октября 2022 г.). «Черные дыры могут скрывать невероятную тайну нашей Вселенной. Возьмите гравитацию, добавьте квантовую механику, перемешайте. Что вы получите? Возможно, голографический космос» . Нью-Йорк Таймс . Архивировано из оригинала 16 ноября 2022 года . Проверено 10 октября 2022 г.
- ^ Дикт Макгроу-Хилла (1989)
- ^ Jump up to: а б Хофманн-Велленхоф, Б.; Мориц, Х. (2006). Физическая геодезия (2-е изд.). Спрингер. ISBN 978-3-211-33544-4 .
§ 2.1: «Суммарная сила, действующая на тело, покоящееся на земной поверхности, есть равнодействующая силы гравитации и центробежной силы вращения Земли и называется гравитацией.
- ^ Каппи, Альберто. «Концепция гравитации до Ньютона» (PDF) . Культура и космос . Архивировано (PDF) из оригинала 9 октября 2022 года.
- ^ Баккер, Фредерик; Пальмерино, Карла Рита (1 июня 2020 г.). «Движение к центру или движение к целому? Взгляды Плутарха на гравитацию и их влияние на Галилея» . Исида . 111 (2): 217–238. дои : 10.1086/709138 . hdl : 2066/219256 . ISSN 0021-1753 . S2CID 219925047 . Архивировано из оригинала 2 мая 2022 года . Проверено 2 мая 2022 г.
- ^ Ревиль Нейтц; Уильям Ноэль (13 октября 2011 г.). Кодекс Архимеда: раскрываем тайны величайшего в мире палимпсеста . Хачетт Великобритания. п. 125. ИСБН 978-1-78022-198-4 . Архивировано из оригинала 7 января 2020 года . Проверено 10 апреля 2019 г.
- ^ Си Джей Таплин, Льюис Уолперт (2002). Наука и математика в древнегреческой культуре . Хачетт Великобритания. п. xi. ISBN 978-0-19-815248-4 . Архивировано из оригинала 17 января 2020 года . Проверено 10 апреля 2019 г.
- ^ Витрувий, Марк Поллион (1914). «7» . В Альфреде А. Ховарде (ред.). De Architectura libri decem [ Десять книг по архитектуре ]. Герберт Лэнгфорд Уоррен, Нельсон Робинсон (иллюстрация), Моррис Хики Морган. Гарвардский университет, Кембридж: Издательство Гарвардского университета. п. 215. Архивировано из оригинала 13 октября 2016 года . Проверено 10 апреля 2019 г.
- ^ Термин Филопона для обозначения импульса - «бестелесный мотив enérgeia »? см. CAG XVII, Иоаннис Филопони в Aristotelis Physicorum Libros Quinque Posteriores Commentaria. Архивировано 22 декабря 2023 г. в Wayback Machine , Уолтер де Грюйтер , 1888, стр. 642: «Я говорю, что импульс (бестелесная движущая энергия) передается от бросающего к брошенному».
- ^ Пиковер, Клиффорд (16 апреля 2008 г.). Архимед Хокингу: законы науки и великие умы, стоящие за ними . Издательство Оксфордского университета. ISBN 9780199792689 . Архивировано из оригинала 18 января 2017 года . Проверено 29 августа 2017 г.
- ^ Бозе, Майнак Кумар (1988). Поздняя классическая Индия . А. Мукерджи и компания. Архивировано из оригинала 13 августа 2021 года . Проверено 28 июля 2021 г.
- ^ * Сен, Амартия (2005). Спорный индеец . Аллен Лейн. п. 29. ISBN 978-0-7139-9687-6 .
- ^ Старр, С. Фредерик (2015). Утерянное Просвещение: Золотой век Центральной Азии от арабского завоевания до Тамерлана . Издательство Принстонского университета. п. 260. ИСБН 9780691165851 .
- ^ Рожанская, Мариам; Левинова, И.С. (1996). «Статика». В Рушди, Рашид (ред.). Энциклопедия истории арабской науки . Том. 2. Психология Пресс. стр. 614–642. ISBN 9780415124119 .
- ^ Jump up to: а б с Уоллес, Уильям А. (2018) [2004]. Доминго де Сото и ранний Галилей: Очерки интеллектуальной истории . Абингдон, Великобритания: Routledge . стр. 119, 121–22. ISBN 978-1-351-15959-3 . Архивировано из оригинала 16 июня 2021 года . Проверено 4 августа 2021 г.
- ^ Драбкин, И.Э. (1963). «Две версии демонстрации Бенедетти пропорций локальных движений». Исида 54 (2): 259–262. дои : 10.1086/349706 . ISSN 0021-1753 . JSTOR 228543 . S2CID 144883728 .
- ^ Шиллинг, Говерт (31 июля 2017 г.). Рябь в пространстве-времени: Эйнштейн, гравитационные волны и будущее астрономии . Издательство Гарвардского университета. п. 26. ISBN 9780674971660 . Архивировано из оригинала 16 декабря 2021 года . Проверено 16 декабря 2021 г.
- ^ Галилей (1638), Две новые науки , Первый день Сальвиати говорит: «Если бы это было то, что имел в виду Аристотель, вы бы обременяли его другой ошибкой, которая была бы равносильна лжи; потому что, поскольку на Земле нет такой чистой высоты, она ясно, что Аристотель не мог провести этот эксперимент, однако он хочет создать у нас впечатление, что он его осуществил, когда говорит о таком эффекте, который мы видим».
- ^ Гиллиспи, Чарльз Коулстон (1960). Грань объективности: Очерк истории научных идей . Издательство Принстонского университета. стр. 3–6. ISBN 0-691-02350-6 .
- ^ Дж. Л. Хейлброн, Электричество в 17 и 18 веках: исследование ранней современной физики (Беркли: University of California Press, 1979), 180.
- ^ Гриббин и Гриббин (2017) , с. 57.
- ^ Стюарт, Дугалд (1816). Элементы философии человеческого разума . Том. 2. Эдинбург; Лондон: Констебль и компания; Каделл и Дэвис. п. 434 .
- ^ Гук (1679) , Попытка доказать годовое движение Земли , стр. 2, 3 .
- ^ Саган, Карл и Друян, Энн (1997). Комета . Нью-Йорк: Рэндом Хаус. стр. 52–58. ISBN 978-0-3078-0105-0 . Архивировано из оригинала 15 июня 2021 года . Проверено 5 августа 2021 г.
- ^ «Значение CODATA 2022: гравитационная постоянная Ньютона» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
- ^ «Рецепция принципов Ньютона» (PDF) . Архивировано (PDF) из оригинала 9 октября 2022 года . Проверено 6 мая 2022 г.
- ^ «Этот месяц в истории физики» . www.aps.org . Архивировано из оригинала 6 мая 2022 года . Проверено 6 мая 2022 г.
- ^ Нобиль, Анна М. (март 1986 г.). «Реальная ценность продвижения перигелия Меркурия». Природа . 320 (6057): 39–41. Бибкод : 1986Natur.320...39N . дои : 10.1038/320039a0 . ISSN 0028-0836 . S2CID 4325839 .
- ^ Уэбб, Джо; Дуган, Даррен (23 ноября 2015 г.). «Без Эйнштейна потребовалось бы десятилетия, чтобы понять гравитацию» . Архивировано из оригинала 21 мая 2022 года . Проверено 21 мая 2022 г.
- ^ «Гравитация и искривленное пространство-время» . black-holes.org. Архивировано из оригинала 21 июня 2011 года . Проверено 16 октября 2010 г.
- ^ Дмитрий Погосян. «Лекция 20: Черные дыры – принцип эквивалентности Эйнштейна» . Университет Альберты. Архивировано из оригинала 8 сентября 2013 года . Проверено 14 октября 2011 г.
- ^ Браш, С.Г. (1 января 1999 г.). «Почему была принята теория относительности?» . Физика в перспективе . 1 (2): 184–214. Бибкод : 1999PhP.....1..184B . дои : 10.1007/s000160050015 . ISSN 1422-6944 . S2CID 51825180 . Архивировано из оригинала 8 апреля 2023 года . Проверено 22 мая 2022 г.
- ^ Линдли, Дэвид (12 июля 2005 г.). «Тяжесть света» . Физика . 16 . Архивировано из оригинала 25 мая 2022 года . Проверено 22 мая 2022 г.
- ^ «Эксперимент Хафеле-Китинга» . гиперфизика.phy-astr.gsu.edu . Архивировано из оригинала 18 апреля 2017 года . Проверено 22 мая 2022 г.
- ^ «Как солнечное затмение 1919 года сделало Эйнштейна самым известным ученым в мире» . Откройте для себя журнал . Архивировано из оригинала 22 мая 2022 года . Проверено 22 мая 2022 г.
- ^ «Наконец-то спутник Gravity Probe B доказывает правоту Эйнштейна» . www.science.org . Архивировано из оригинала 22 мая 2022 года . Проверено 22 мая 2022 г.
- ^ Jump up to: а б «Эйнштейн показал, что Ньютон ошибался насчет гравитации. Теперь ученые пришли за Эйнштейном» . Новости Эн-Би-Си . 3 августа 2019 года. Архивировано из оригинала 22 мая 2022 года . Проверено 22 мая 2022 г.
- ^ Стефани, Ганс (2003). Точные решения уравнений поля Эйнштейна . Издательство Кембриджского университета. п. 1. ISBN 978-0-521-46136-8 .
- ^ «Уравнения поля Эйнштейна (общая теория относительности)» . Университет Уорика . Архивировано из оригинала 25 мая 2022 года . Проверено 24 мая 2022 г.
- ^ «Как понять уравнение Эйнштейна общей теории относительности» . Большое Думай . 15 сентября 2021 года. Архивировано из оригинала 26 мая 2022 года . Проверено 24 мая 2022 г.
- ^ Исхак, Мустафа. «Точные решения уравнений Эйнштейна в астрофизике» (PDF) . Техасский университет в Далласе . Архивировано (PDF) из оригинала 9 октября 2022 года . Проверено 25 мая 2022 г.
- ^ «Метрика Шварцшильда и приложения» (PDF) . п. 36. Архивировано (PDF) из оригинала 9 октября 2022 года . Проверено 26 мая 2022 г.
- ^ Элерс, Юрген (1997). «Примеры ньютоновских пределов релятивистского пространства-времени» . Классическая квантовая гравитация . 14 (1А): 122–123. Бибкод : 1997CQGra..14A.119E . дои : 10.1088/0264-9381/14/1A/010 . hdl : 11858/00-001M-0000-0013-5AC5-F . S2CID 250804865 . Архивировано из оригинала 6 декабря 2022 года . Проверено 27 мая 2022 г.
- ^ «Сюрприз: Большой взрыв больше не является началом Вселенной» . Большое Думай . 13 октября 2021 года. Архивировано из оригинала 26 мая 2022 года . Проверено 26 мая 2022 г.
- ^ Норебо, Джонатан (16 марта 2016 г.). «Метрика Рейсснера-Нордстрема» (PDF) . Архивировано (PDF) из оригинала 9 октября 2022 года.
- ^ Теукольский, Саул (1 июня 2015 г.). «Метрика Керра» (PDF) . Классическая и квантовая гравитация . 32 (12): 124006. arXiv : 1410.2130 . Бибкод : 2015CQGra..32l4006T . дои : 10.1088/0264-9381/32/12/124006 . S2CID 119219499 . Архивировано (PDF) из оригинала 9 октября 2022 года.
- ^ Ньюман, ET; Коуч, Э.; Чиннапаред, К.; Экстон, А.; Пракаш, А.; Торренс, Р. (июнь 1965 г.). «Метрика вращающейся заряженной массы». Журнал математической физики . 6 (6): 918–919. Бибкод : 1965JMP.....6..918N . дои : 10.1063/1.1704351 . ISSN 0022-2488 . S2CID 122962090 .
- ^ Петтини, М. «РЕЛЯТИВИСТСКАЯ КОСМОЛОГИЯ» (PDF) . Архивировано (PDF) из оригинала 9 октября 2022 года . Проверено 27 мая 2022 г.
- ^ О'Рэйфертай, Кормак; О'Киф, Майкл (2017). «Статическая модель Вселенной Эйнштейна 1917 года: обзор столетия» . Европейский физический журнал H . 42 (3): 41. arXiv : 1701.07261 . Бибкод : 2017EPJH...42..431O . дои : 10.1140/epjh/e2017-80002-5 . S2CID 119461771 . Архивировано из оригинала 29 мая 2022 года . Проверено 29 мая 2022 г.
- ^ Сигел, Итан. «Вот почему ученые никогда точно не решат общую теорию относительности» . Форбс . Архивировано из оригинала 27 мая 2022 года . Проверено 27 мая 2022 г.
- ^ Спиру, Н. (1 мая 1975 г.). « Проблема N тел в общей теории относительности» . Астрофизический журнал . 197 : 725–743. Бибкод : 1975ApJ...197..725S . дои : 10.1086/153562 . ISSN 0004-637X .
- ^ Слитор, Дэниел (6 июня 1996 г.). «Герменевтика классической общей теории относительности» . Проверено 23 мая 2022 г.
- ^ «Гравитационный зонд B – Вопросы и ответы по специальной и общей теории относительности» . einstein.stanford.edu . Архивировано из оригинала 6 июня 2022 года . Проверено 1 августа 2022 г.
- ^ Хаггетт, Ник; Мацубара, Кейзо; Вютрих, Кристиан (2020). За пределами пространства-времени: основы квантовой гравитации . Издательство Кембриджского университета . п. 6. ISBN 9781108655705 .
- ^ Фейнман, Р.П.; Мориниго, ФБ; Вагнер, РГ; Хэтфилд, Б. (1995). Фейнман читает лекции по гравитации . Аддисон-Уэсли. ISBN 978-0-201-62734-3 .
- ^ Зи, А. (2003). Квантовая теория поля в двух словах . Издательство Принстонского университета. ISBN 978-0-691-01019-9 .
- ^ Рэндалл, Лиза (2005). Искаженные проходы: раскрытие скрытых измерений Вселенной . Экко. ISBN 978-0-06-053108-9 .
- ^ Jump up to: а б «Проверка общей теории относительности» . НАСА Блюшифт . Архивировано из оригинала 16 мая 2022 года . Проверено 29 мая 2022 г.
- ^ Дайсон, ФРВ ; Эддингтон, AS ; Дэвидсон, ЧР (1920). «Определение отклонения света гравитационным полем Солнца по наблюдениям, сделанным во время полного затмения 29 мая 1919 года» . Фил. Пер. Рой. Соц. А. 220 (571–581): 291–333. Бибкод : 1920RSPTA.220..291D . дои : 10.1098/rsta.1920.0009 . Архивировано из оригинала 15 мая 2020 года . Проверено 1 июля 2019 г. . Цитата, с. 332: «Таким образом, результаты экспедиций в Собрал и Принсипи не могут оставить мало сомнений в том, что отклонение света имеет место в окрестностях Солнца и что оно соответствует величине, требуемой обобщенной теорией относительности Эйнштейна, поскольку оно приписывается солнечному излучению». гравитационное поле».
- ^ Вайнберг, Стивен (1972). Гравитация и космология . Джон Уайли и сыновья. ISBN 9780471925675 . . Цитата, с. 192: «Всего было изучено около дюжины звезд, и были получены значения 1,98 ± 0,11 дюйма и 1,61 ± 0,31 дюйма, что в значительной степени соответствует предсказанию Эйнштейна θ ☉ = 1,75 дюйма».
- ^ Гилмор, Джерард; Тауш-Пебоди, Гудрун (20 марта 2022 г.). «Результаты затмения 1919 года, которые подтвердили общую теорию относительности и ее более поздних критиков: пересказанная история» . Примечания и записи: Журнал Королевского общества истории науки . 76 (1): 155–180. arXiv : 2010.13744 . дои : 10.1098/rsnr.2020.0040 . S2CID 225075861 .
- ^ «Приложение 10 к общей астрономии: Гравитационное красное смещение и замедление времени» . домашняя страница.физика.uiowa.edu . Архивировано из оригинала 14 мая 2022 года . Проверено 29 мая 2022 г.
- ^ Асада, Хидеки (20 марта 2008 г.). «Гравитационная задержка света для различных моделей модифицированной гравитации» . Буквы по физике Б. 661 (2–3): 78–81. arXiv : 0710.0477 . Бибкод : 2008PhLB..661...78A . дои : 10.1016/j.physletb.2008.02.006 . S2CID 118365884 . Архивировано из оригинала 29 мая 2022 года . Проверено 29 мая 2022 г.
- ^ «Судьба первой черной дыры» . www.science.org . Архивировано из оригинала 31 мая 2022 года . Проверено 30 мая 2022 г.
- ^ «Дирекция научной миссии по черным дырам» . webarchive.library.unt.edu . Архивировано из оригинала 8 апреля 2023 года . Проверено 30 мая 2022 г.
- ^ Субал Кар (2022). Физика и астрофизика: взгляд на прогресс (иллюстрированное издание). ЦРК Пресс. п. 106. ИСБН 978-1-000-55926-2 . Выдержка со страницы 106
- ^ «Хаббл, Хаббл, видя двойное!» . НАСА . 24 января 2014 г. Архивировано из оригинала 25 мая 2022 г. . Проверено 31 мая 2022 г.
- ^ «Гравитационный зонд НАСА B подтверждает две теории пространства-времени Эйнштейна» . НАСА.gov. Архивировано из оригинала 22 мая 2013 года . Проверено 23 июля 2013 г.
- ^ « «Перетаскивание кадров» в локальном пространстве-времени» (PDF) . Стэнфордский университет . Архивировано (PDF) из оригинала 9 октября 2022 года.
- ^ «Гравитационные волны обнаружены через 100 лет после предсказания Эйнштейна» . Лаборатория ЛИГО Калифорнийского технологического института . Архивировано из оригинала 27 мая 2019 года . Проверено 30 мая 2022 г.
- ^ Кантор, Г.Н.; Кристи, JRR; Ходж, MJS; Олби, RC (2006). Спутник истории современной науки . Рутледж. п. 448. ИСБН 978-1-134-97751-2 . Архивировано из оригинала 17 января 2020 года . Проверено 22 октября 2017 г.
- ^ Немиров Р.; Боннелл, Дж., ред. (15 декабря 2014 г.). «Потсдамская гравитационная картошка» . Астрономическая картина дня . НАСА .
- ^ Бойнтон, Ричард (2001). « Точное измерение массы » (PDF) . Бумага Саве № 3147 . Арлингтон, Техас: SAWE, Inc. Архивировано из оригинала (PDF) 27 февраля 2007 года . Проверено 22 декабря 2023 г.
- ^ «Интересно, что касается астрономии?» . Корнеллский университет . Архивировано из оригинала 28 июля 2013 года . Проверено 22 декабря 2023 г.
- ^ «Нобелевская премия по физике 1993 года» . Нобелевский фонд . 13 октября 1993 года. Архивировано из оригинала 10 августа 2018 года . Проверено 22 декабря 2023 г.
за открытие нового типа пульсара, открытие, открывшее новые возможности для изучения гравитации
- ^ Кларк, Стюарт (11 февраля 2016 г.). «Гравитационные волны: ученые заявляют: «Мы сделали это!» - жить" . Хранитель . Архивировано из оригинала 22 июня 2018 года . Проверено 11 февраля 2016 г. .
- ^ Кастельвекки, Давиде; Витце, Витце (11 февраля 2016 г.). «Наконец-то найдены гравитационные волны Эйнштейна» . Новости природы . дои : 10.1038/nature.2016.19361 . S2CID 182916902 . Архивировано из оригинала 12 февраля 2016 года . Проверено 11 февраля 2016 г. .
- ^ «ЧТО ТАКОЕ ГРАВИТАЦИОННЫЕ ВОЛНЫ И ПОЧЕМУ ОНИ ВАЖНЫ?» . popsci.com. 13 января 2016 г. Архивировано из оригинала 3 февраля 2016 г. . Проверено 12 февраля 2016 г.
- ^ Эбботт, BP; и др. ( Научное сотрудничество LIGO и сотрудничество Virgo ) (октябрь 2017 г.). «GW170817: Наблюдение гравитационных волн на спиральной двойной нейтронной звезде» (PDF) . Письма о физических отзывах . 119 (16): 161101. arXiv : 1710.05832 . Бибкод : 2017PhRvL.119p1101A . doi : 10.1103/PhysRevLett.119.161101 . ПМИД 29099225 . Архивировано (PDF) из оригинала 8 августа 2018 г. Проверено 28 сентября 2019 г.
- ^ Девлин, Ханна (3 октября 2017 г.). «Нобелевская премия по физике присуждена за открытие гравитационных волн» . Хранитель . Архивировано из оригинала 3 октября 2017 года . Проверено 3 октября 2017 г.
- ↑ Китайские учёные находят доказательства скорости гравитации. Архивировано 8 января 2013 года на Wayback Machine , astrowatch.com, 28 декабря 2012 года.
- ^ ТАН, Кэ Юн; ХУА Чанцай; ВЭНЬ Ву; ЧИ ШуньЛян; ВЫ ЦинЮй; Ю Дэн (февраль 2013 г.). «Наблюдательные данные о скорости гравитации, основанные на земном приливе» . Китайский научный бюллетень . 58 (4–5): 474–477. Бибкод : 2013ЧСБу..58..474Т . дои : 10.1007/s11434-012-5603-3 .
- ^ «GW170817 Пресс-релиз» . Лаборатория ЛИГО – Калифорнийский технологический институт . Архивировано из оригинала 17 октября 2017 года . Проверено 24 октября 2017 г.
- ^ «Нобелевская премия по физике 2011 года: факты об Адаме Г. Риссе» . NobelPrize.org . Архивировано из оригинала 28 мая 2020 года . Проверено 19 марта 2024 г.
- ^ «Что такое темная энергия? Внутри нашей ускоряющейся и расширяющейся Вселенной» . science.nasa.gov . Архивировано из оригинала 19 марта 2024 года . Проверено 19 марта 2024 г.
- ^ Jump up to: а б Чоун, Маркус (16 марта 2009 г.). «Гравитация может пойти туда, куда боится ступить материя» . Новый учёный . Архивировано из оригинала 18 декабря 2012 года . Проверено 4 августа 2013 г.
- ^ Филиалы, Швейцария (март 2014 г.). «Теория Джордана – Бранса – Дике» . Схоларпедия . 9 (4): 31358. arXiv : gr-qc/0207039 . Бибкод : 2014Schpj...931358B . doi : 10.4249/scholarpedia.31358 .
- ^ Хорндески, GW (сентябрь 1974 г.). «Уравнения скалярно-тензорного поля второго порядка в четырехмерном пространстве». Международный журнал теоретической физики . 88 (10): 363–384. Бибкод : 1974IJTP...10..363H . дои : 10.1007/BF01807638 . S2CID 122346086 .
- ^ Милгром, М. (июнь 2014 г.). «Парадигма модифицированной динамики MOND» . Схоларпедия . 9 (6): 31410. Бибкод : 2014SchpJ...931410M . doi : 10.4249/scholarpedia.31410 .
- ^ Хоган, Марк П; Лэммерзал, К. (2011). «Гравитация Эйнштейна из конформной гравитации». arXiv : 1105.5632 [ шестнадцатый ].
Источники
- Гриббин, Джон ; Гриббин, Мэри (2017). Из тени гиганта: Гук, Галлей и рождение британской науки . Лондон: Уильям Коллинз. ISBN 978-0-00-822059-4 . OCLC 966239842 .
- Словарь научных и технических терминов McGraw-Hill (4-е изд.), Нью-Йорк: McGraw-Hill , 1989, ISBN 0-07-045270-9
- Гук, Роберт (1679). Lectiones Cutlerianae, или Сборник лекций по физике, механике, географии и астрономии: неоднократно читался перед Королевским обществом в Грешам-колледже [т.е. колледже]: к которому добавлены различные различные беседы .
Дальнейшее чтение
- И. Бернард Коэн (1999) [1687]. «Путеводитель по Началам Ньютона». Начала: математические принципы натуральной философии . Ньютон, Исаак. Перевод И. Бернарда Коэна. Издательство Калифорнийского университета. ISBN 9780520088160 . OCLC 313895715 .
- Холлидей, Дэвид; Роберт Резник; Кеннет С. Крейн (2001). Физика т. 1 . Нью-Йорк: Джон Уайли и сыновья. ISBN 978-0-471-32057-9 .
- Сервей, Раймонд А.; Джуэтт, Джон В. (2004). Физика для ученых и инженеров (6-е изд.). Брукс/Коул. ISBN 978-0-534-40842-8 .
- Типлер, Пол (2004). Физика для ученых и инженеров: Механика, колебания и волны, Термодинамика (5-е изд.). У. Х. Фриман. ISBN 978-0-7167-0809-4 .
- Торн, Кип С .; Миснер, Чарльз В.; Уилер, Джон Арчибальд (1973). Гравитация . У. Х. Фриман. ISBN 978-0-7167-0344-0 .
- Панек, Ричард (2 августа 2019 г.). «Все, что вы знали о гравитации, неверно» . Вашингтон Пост .
Внешние ссылки
- Фейнмановские лекции по физике Vol. Я Ч. 7: Теория гравитации
- «Гравитация» , Математическая энциклопедия , EMS Press , 2001 [1994]
- «Гравитация, теория» , Энциклопедия Математики , EMS Press , 2001 [1994]






