Энтропия
| Энтропия | |
|---|---|
Общие символы | С |
| И объединились | джоули на кельвин (Дж⋅К −1 ) |
| В базовых единицах СИ | kg⋅m 2 ⋅s −2 ⋅K −1 |
| Термодинамика |
|---|
 |
| Entropy articles |
|---|
| Modern physics |
|---|
| |
| Complex systems |
|---|
| Topics |
Энтропия — это научная концепция, которая чаще всего ассоциируется с состоянием беспорядка, случайности или неопределенности. Этот термин и концепция используются в различных областях: от классической термодинамики , где он был впервые признан, до микроскопического описания природы в статистической физике и принципов теории информации . Он нашел широкое применение в химии и физике , в биологических системах и их связи с жизнью, в космологии , экономике , социологии , науке о погоде , изменении климата и информационных системах , включая передачу информации в телекоммуникациях . [1]
Энтропия занимает центральное место во втором законе термодинамики , который гласит, что энтропия изолированной системы, оставленной на самопроизвольную эволюцию, не может уменьшаться со временем. В результате изолированные системы стремятся к термодинамическому равновесию , где энтропия наибольшая. Следствием второго закона термодинамики является то, что некоторые процессы необратимы .
The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names thermodynamic function and heat-potential.[2] In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount of heat to the instantaneous temperature. He initially described it as transformation-content, in German Verwandlungsinhalt, and later coined the term entropy from a Greek word for transformation.[3]
Austrian physicist Ludwig Boltzmann explained entropy as the measure of the number of possible microscopic arrangements or states of individual atoms and molecules of a system that comply with the macroscopic condition of the system. He thereby introduced the concept of statistical disorder and probability distributions into a new field of thermodynamics, called statistical mechanics, and found the link between the microscopic interactions, which fluctuate about an average configuration, to the macroscopically observable behavior, in form of a simple logarithmic law, with a proportionality constant, the Boltzmann constant, that has become one of the defining universal constants for the modern International System of Units (SI).
History
[edit]
In his 1803 paper Fundamental Principles of Equilibrium and Movement, the French mathematician Lazare Carnot proposed that in any machine, the accelerations and shocks of the moving parts represent losses of moment of activity; in any natural process there exists an inherent tendency towards the dissipation of useful energy. In 1824, building on that work, Lazare's son, Sadi Carnot, published Reflections on the Motive Power of Fire, which posited that in all heat-engines, whenever "caloric" (what is now known as heat) falls through a temperature difference, work or motive power can be produced from the actions of its fall from a hot to cold body. He used an analogy with how water falls in a water wheel. That was an early insight into the second law of thermodynamics.[4] Carnot based his views of heat partially on the early 18th-century "Newtonian hypothesis" that both heat and light were types of indestructible forms of matter, which are attracted and repelled by other matter, and partially on the contemporary views of Count Rumford, who showed in 1789 that heat could be created by friction, as when cannon bores are machined.[5] Carnot reasoned that if the body of the working substance, such as a body of steam, is returned to its original state at the end of a complete engine cycle, "no change occurs in the condition of the working body".
The first law of thermodynamics, deduced from the heat-friction experiments of James Joule in 1843, expresses the concept of energy and its conservation in all processes; the first law, however, is unsuitable to separately quantify the effects of friction and dissipation.[citation needed]
In the 1850s and 1860s, German physicist Rudolf Clausius objected to the supposition that no change occurs in the working body, and gave that change a mathematical interpretation, by questioning the nature of the inherent loss of usable heat when work is done, e.g., heat produced by friction.[6] He described his observations as a dissipative use of energy, resulting in a transformation-content (Verwandlungsinhalt in German), of a thermodynamic system or working body of chemical species during a change of state.[6] That was in contrast to earlier views, based on the theories of Isaac Newton, that heat was an indestructible particle that had mass. Clausius discovered that the non-usable energy increases as steam proceeds from inlet to exhaust in a steam engine. From the prefix en-, as in 'energy', and from the Greek word τροπή [tropē], which is translated in an established lexicon as turning or change[7] and that he rendered in German as Verwandlung, a word often translated into English as transformation, in 1865 Clausius coined the name of that property as entropy.[8] The word was adopted into the English language in 1868.
Later, scientists such as Ludwig Boltzmann, Josiah Willard Gibbs, and James Clerk Maxwell gave entropy a statistical basis. In 1877, Boltzmann visualized a probabilistic way to measure the entropy of an ensemble of ideal gas particles, in which he defined entropy as proportional to the natural logarithm of the number of microstates such a gas could occupy. The proportionality constant in this definition, called the Boltzmann constant, has become one of the defining universal constants for the modern International System of Units (SI). Henceforth, the essential problem in statistical thermodynamics has been to determine the distribution of a given amount of energy E over N identical systems. Constantin Carathéodory, a Greek mathematician, linked entropy with a mathematical definition of irreversibility, in terms of trajectories and integrability.
Etymology
[edit]In 1865, Clausius named the concept of "the differential of a quantity which depends on the configuration of the system", entropy (Entropie) after the Greek word for 'transformation'.[9] He gave "transformational content" (Verwandlungsinhalt) as a synonym, paralleling his "thermal and ergonal content" (Wärme- und Werkinhalt) as the name of , but preferring the term entropy as a close parallel of the word energy, as he found the concepts nearly "analogous in their physical significance".[9] This term was formed by replacing the root of ἔργον ('ergon', 'work') by that of τροπή ('tropy', 'transformation').[8]
In more detail, Clausius explained his choice of "entropy" as a name as follows:[10]
I prefer going to the ancient languages for the names of important scientific quantities, so that they may mean the same thing in all living tongues. I propose, therefore, to call S the entropy of a body, after the Greek word "transformation". I have designedly coined the word entropy to be similar to energy, for these two quantities are so analogous in their physical significance, that an analogy of denominations seems to me helpful.
Leon Cooper added that in this way "he succeeded in coining a word that meant the same thing to everybody: nothing".[10]
Definitions and descriptions
[edit]Any method involving the notion of entropy, the very existence of which depends on the second law of thermodynamics, will doubtless seem to many far-fetched, and may repel beginners as obscure and difficult of comprehension.
Willard Gibbs, Graphical Methods in the Thermodynamics of Fluids[11]
The concept of entropy is described by two principal approaches, the macroscopic perspective of classical thermodynamics, and the microscopic description central to statistical mechanics. The classical approach defines entropy in terms of macroscopically measurable physical properties, such as bulk mass, volume, pressure, and temperature. The statistical definition of entropy defines it in terms of the statistics of the motions of the microscopic constituents of a system – modeled at first classically, e.g. Newtonian particles constituting a gas, and later quantum-mechanically (photons, phonons, spins, etc.). The two approaches form a consistent, unified view of the same phenomenon as expressed in the second law of thermodynamics, which has found universal applicability to physical processes.
State variables and functions of state
[edit]Many thermodynamic properties are defined by physical variables that define a state of thermodynamic equilibrium; these are state variables. State variables depend only on the equilibrium condition, not on the path evolution to that state. State variables can be functions of state, also called state functions, in a sense that one state variable is a mathematical function of other state variables. Often, if some properties of a system are determined, they are sufficient to determine the state of the system and thus other properties' values. For example, temperature and pressure of a given quantity of gas determine its state, and thus also its volume via the ideal gas law. A system composed of a pure substance of a single phase at a particular uniform temperature and pressure is determined, and is thus a particular state, and has not only a particular volume but also a specific entropy.[12] The fact that entropy is a function of state makes it useful. In the Carnot cycle, the working fluid returns to the same state that it had at the start of the cycle, hence the change or line integral of any state function, such as entropy, over this reversible cycle is zero.
Reversible process
[edit]Total entropy may be conserved during a reversible process. The entropy change of the system (not including the surroundings) is well-defined as heat transferred to the system divided by the system temperature , . A reversible process is a quasistatic one that deviates only infinitesimally from thermodynamic equilibrium and avoids friction or other dissipation. Any process that happens quickly enough to deviate from thermal equilibrium cannot be reversible, total entropy increases, and the potential for maximum work to be done in the process is also lost.[13] For example, in the Carnot cycle, while the heat flow from the hot reservoir to the cold reservoir represents an increase in entropy in the cold reservoir, the work output, if reversibly and perfectly stored in some energy storage mechanism, represents a decrease in entropy that could be used to operate the heat engine in reverse and return to the previous state; thus the total entropy change may still be zero at all times if the entire process is reversible. An irreversible process increases the total entropy of the system and surroundings.[14]
Carnot cycle
[edit]The concept of entropy arose from Rudolf Clausius's study of the Carnot cycle that is a thermodynamic cycle performed by a Carnot heat engine as a reversible heat engine.[15] In a Carnot cycle, heat QH is absorbed isothermally at temperature TH from a 'hot' reservoir (in the isothermal expansion stage) and given up isothermally as heat QC to a 'cold' reservoir at TC (in the isothermal compression stage). According to Carnot's principle or theorem, work from a heat engine with two thermal reservoirs can be produced only when there is a temperature difference between these reservoirs, and for reversible engines which are mostly and equally efficient among all heat engines for a given thermal reservoir pair, the work is a function of the reservoir temperatures and the heat absorbed to the engine QH (heat engine work output = heat engine efficiency × heat to the engine, where the efficiency is a function of the reservoir temperatures for reversible heat engines). Carnot did not distinguish between QH and QC, since he was using the incorrect hypothesis that caloric theory was valid, and hence heat was conserved (the incorrect assumption that QH and QC were equal in magnitude) when, in fact, the magnitude of QH is greater than the magnitude of QC.[16][17] Through the efforts of Clausius and Kelvin, it is now known that the work done by a reversible heat engine is the product of the Carnot efficiency (it is the efficiency of all reversible heat engines with the same thermal reservoir pairs according to the Carnot's theorem) and the heat absorbed from the hot reservoir:
| (1) |
Here is work done by the Carnot heat engine, is heat to the engine from the hot reservoir, and is heat to the cold reservoir from the engine. To derive the Carnot efficiency, which is 1 − TC/TH (a number less than one), Kelvin had to evaluate the ratio of the work output to the heat absorbed during the isothermal expansion with the help of the Carnot–Clapeyron equation, which contained an unknown function called the Carnot function. The possibility that the Carnot function could be the temperature as measured from a zero point of temperature was suggested by Joule in a letter to Kelvin. This allowed Kelvin to establish his absolute temperature scale.[18] It is also known that the net work W produced by the system in one cycle is the net heat absorbed, which is the sum (or difference of the magnitudes) of the heat QH > 0 absorbed from the hot reservoir and the waste heat QC < 0 given off to the cold reservoir:[19]
| (2) |
Since the latter is valid over the entire cycle, this gave Clausius the hint that at each stage of the cycle, work and heat would not be equal, but rather their difference would be the change of a state function that would vanish upon completion of the cycle. The state function was called the internal energy, that is central to the first law of thermodynamics.[20]
Now equating (1) and (2) gives, for the engine per Carnot cycle,[21][19]
| (3) |
This implies that there is a function of state whose change is Q/T and this state function is conserved over a complete Carnot cycle, like other state function such as the internal energy. Clausius called this state function entropy. One can see that entropy was discovered through mathematics rather than through laboratory experimental results.[citation needed] It is a mathematical construct and has no easy physical analogy.[citation needed] This makes the concept somewhat obscure or abstract, akin to how the concept of energy arose. This equation shows an entropy change per Carnot cycle is zero. In fact, an entropy change in the both thermal reservoirs per Carnot cycle is also zero since that change is simply expressed by reverting the sign of each term in the equation (3) according to the fact that, for example, for heat transfer from the hot reservoir to the engine, the engine receives the heat while the hot reservoir loses the same amount of the heat;
| (4) |
where we denote an entropy change for a thermal reservoir by ΔSr,i = – Qi/Ti, for i as either H (Hot reservoir) or C (Cold reservoir), by considering the above-mentioned signal convention of heat for the engine.
Clausius then asked what would happen if less work is produced by the system than that predicted by Carnot's principle for the same thermal reservoir pair and the same heat transfer from the hot reservoir to the engine QH. In this case, the right-hand side of the equation (1) would be the upper bound of the work output by the system, and the equation would now be converted into an inequalityWhen the equation (2) is used to express the work as a net or total heat exchanged in a cycle, we getorby considering the sign convention of heat where QH > 0 is heat that is from the hot reservoir and is absorbed by the engine and QC < 0 is the waste heat given off to the cold reservoir from the engine. So, more heat is given up to the cold reservoir than in the Carnot cycle. The above inequality can be written asIf we, again, denote an entropy change for a thermal reservoir by ΔSr,i = – Qi/Ti, for i as either H (Hot reservoir) or C (Cold reservoir), by considering the abovementioned signal convention of heat for the engine, thenor
| (5) |
telling that the magnitude of the entropy earned by the cold reservoir is greater than the entropy lost by the hot reservoir. The net entropy change in the engine per its thermodynamic cycle is zero, so the net entropy change in the engine and both the thermal reservoirs per cycle increases if work produced by the engine is less than the work achieved by a Carnot engine in the equation (1).
The Carnot cycle and Carnot efficiency as shown in the equation (1) are useful because they define the upper bound of the possible work output and the efficiency of any classical thermodynamic heat engine. Other cycles, such as the Otto cycle, Diesel cycle and Brayton cycle, can be analyzed from the standpoint of the Carnot cycle. Any machine or cyclic process that converts heat to work and is claimed to produce an efficiency greater than the Carnot efficiency is not viable because it violates the second law of thermodynamics.
For very small numbers of particles in the system, statistical thermodynamics must be used. The efficiency of devices such as photovoltaic cells requires an analysis from the standpoint of quantum mechanics.
Classical thermodynamics
[edit]| Conjugate variables of thermodynamics | ||||||||
|
The thermodynamic definition of entropy was developed in the early 1850s by Rudolf Clausius and essentially describes how to measure the entropy of an isolated system in thermodynamic equilibrium with its parts. Clausius created the term entropy as an extensive thermodynamic variable that was shown to be useful in characterizing the Carnot cycle. Heat transfer in the isotherm steps (isothermal expansion and isothermal compression) of the Carnot cycle was found to be proportional to the temperature of a system (known as its absolute temperature). This relationship was expressed in an increment of entropy that is equal to incremental heat transfer divided by temperature. Entropy was found to vary in the thermodynamic cycle but eventually returned to the same value at the end of every cycle. Thus it was found to be a function of state, specifically a thermodynamic state of the system.
While Clausius based his definition on a reversible process, there are also irreversible processes that change entropy. Following the second law of thermodynamics, entropy of an isolated system always increases for irreversible processes. The difference between an isolated system and closed system is that energy may not flow to and from an isolated system, but energy flow to and from a closed system is possible. Nevertheless, for both closed and isolated systems, and indeed, also in open systems, irreversible thermodynamics processes may occur.
According to the Clausius equality, for a reversible cyclic process: . This means the line integral is path-independent.
So we can define a state function S called entropy, which satisfies .
To find the entropy difference between any two states of a system, the integral must be evaluated for some reversible path between the initial and final states.[22] Since entropy is a state function, the entropy change of the system for an irreversible path is the same as for a reversible path between the same two states.[23] However, the heat transferred to or from, and the entropy change of, the surroundings is different.
We can only obtain the change of entropy by integrating the above formula. To obtain the absolute value of the entropy, we need the third law of thermodynamics, which states that S = 0 at absolute zero for perfect crystals.
From a macroscopic perspective, in classical thermodynamics the entropy is interpreted as a state function of a thermodynamic system: that is, a property depending only on the current state of the system, independent of how that state came to be achieved. In any process where the system gives up energy ΔE, and its entropy falls by ΔS, a quantity at least TR ΔS of that energy must be given up to the system's surroundings as heat (TR is the temperature of the system's external surroundings). Otherwise the process cannot go forward. In classical thermodynamics, the entropy of a system is defined only if it is in physical thermodynamic equilibrium. (But chemical equilibrium is not required: the entropy of a mixture of two moles of hydrogen and one mole of oxygen at 1 bar pressure and 298 K is well-defined.)
Statistical mechanics
[edit]The statistical definition was developed by Ludwig Boltzmann in the 1870s by analyzing the statistical behavior of the microscopic components of the system. Boltzmann showed that this definition of entropy was equivalent to the thermodynamic entropy to within a constant factor—known as the Boltzmann constant. In short, the thermodynamic definition of entropy provides the experimental verification of entropy, while the statistical definition of entropy extends the concept, providing an explanation and a deeper understanding of its nature.
The interpretation of entropy in statistical mechanics is the measure of uncertainty, disorder, or mixedupness in the phrase of Gibbs, which remains about a system after its observable macroscopic properties, such as temperature, pressure and volume, have been taken into account. For a given set of macroscopic variables, the entropy measures the degree to which the probability of the system is spread out over different possible microstates. In contrast to the macrostate, which characterizes plainly observable average quantities, a microstate specifies all molecular details about the system including the position and velocity of every molecule. The more such states are available to the system with appreciable probability, the greater the entropy. In statistical mechanics, entropy is a measure of the number of ways a system can be arranged, often taken to be a measure of "disorder" (the higher the entropy, the higher the disorder).[24][25][26] This definition describes the entropy as being proportional to the natural logarithm of the number of possible microscopic configurations of the individual atoms and molecules of the system (microstates) that could cause the observed macroscopic state (macrostate) of the system. The constant of proportionality is the Boltzmann constant.
The Boltzmann constant, and therefore entropy, have dimensions of energy divided by temperature, which has a unit of joules per kelvin (J⋅K−1) in the International System of Units (or kg⋅m2⋅s−2⋅K−1 in terms of base units). The entropy of a substance is usually given as an intensive property – either entropy per unit mass (SI unit: J⋅K−1⋅kg−1) or entropy per unit amount of substance (SI unit: J⋅K−1⋅mol−1).
Specifically, entropy is a logarithmic measure of the number of system states with significant probability of being occupied:
( is the probability that the system is in th state, usually given by the Boltzmann distribution; if states are defined in a continuous manner, the summation is replaced by an integral over all possible states) or, equivalently, the expected value of the logarithm of the probability that a microstate is occupied
where kB is the Boltzmann constant, equal to 1.38065×10−23 J/K.The summation is over all the possible microstates of the system, and pi is the probability that the system is in the i-th microstate.[27] This definition assumes that the basis set of states has been picked so that there is no information on their relative phases. In a different basis set, the more general expression is
where is the density matrix, is trace, and is the matrix logarithm. This density matrix formulation is not needed in cases of thermal equilibrium so long as the basis states are chosen to be energy eigenstates. For most practical purposes, this can be taken as the fundamental definition of entropy since all other formulas for S can be mathematically derived from it, but not vice versa.
In what has been called the fundamental assumption of statistical thermodynamics or the fundamental postulate in statistical mechanics, among system microstates of the same energy (degenerate microstates) each microstate is assumed to be populated with equal probability; this assumption is usually justified for an isolated system in equilibrium.[28] Then for an isolated system pi = 1/Ω, where Ω is the number of microstates whose energy equals the system's energy, and the previous equation reduces to
In thermodynamics, such a system is one in which the volume, number of molecules, and internal energy are fixed (the microcanonical ensemble).
The most general interpretation of entropy is as a measure of the extent of uncertainty about a system. The equilibrium state of a system maximizes the entropy because it does not reflect all information about the initial conditions, except for the conserved variables. This uncertainty is not of the everyday subjective kind, but rather the uncertainty inherent to the experimental method and interpretative model.[29]
The interpretative model has a central role in determining entropy. The qualifier "for a given set of macroscopic variables" above has deep implications: if two observers use different sets of macroscopic variables, they see different entropies. For example, if observer A uses the variables U, V and W, and observer B uses U, V, W, X, then, by changing X, observer B can cause an effect that looks like a violation of the second law of thermodynamics to observer A. In other words: the set of macroscopic variables one chooses must include everything that may change in the experiment, otherwise one might see decreasing entropy.[30]
Entropy can be defined for any Markov processes with reversible dynamics and the detailed balance property.
In Boltzmann's 1896 Lectures on Gas Theory, he showed that this expression gives a measure of entropy for systems of atoms and molecules in the gas phase, thus providing a measure for the entropy of classical thermodynamics.
Entropy of a system
[edit]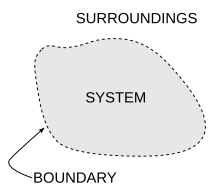

Entropy arises directly from the Carnot cycle. It can also be described as the reversible heat divided by temperature. Entropy is a fundamental function of state.
In a thermodynamic system, pressure and temperature tend to become uniform over time because the equilibrium state has higher probability (more possible combinations of microstates) than any other state.
As an example, for a glass of ice water in air at room temperature, the difference in temperature between the warm room (the surroundings) and the cold glass of ice and water (the system and not part of the room) decreases as portions of the thermal energy from the warm surroundings spread to the cooler system of ice and water. Over time the temperature of the glass and its contents and the temperature of the room become equal. In other words, the entropy of the room has decreased as some of its energy has been dispersed to the ice and water, of which the entropy has increased.
However, as calculated in the example, the entropy of the system of ice and water has increased more than the entropy of the surrounding room has decreased. In an isolated system such as the room and ice water taken together, the dispersal of energy from warmer to cooler always results in a net increase in entropy. Thus, when the "universe" of the room and ice water system has reached a temperature equilibrium, the entropy change from the initial state is at a maximum. The entropy of the thermodynamic system is a measure of how far the equalization has progressed.
Thermodynamic entropy is a non-conserved state function that is of great importance in the sciences of physics and chemistry.[24][31] Historically, the concept of entropy evolved to explain why some processes (permitted by conservation laws) occur spontaneously while their time reversals (also permitted by conservation laws) do not; systems tend to progress in the direction of increasing entropy.[32][33] For isolated systems, entropy never decreases.[31] This fact has several important consequences in science: first, it prohibits "perpetual motion" machines; and second, it implies the arrow of entropy has the same direction as the arrow of time. Increases in the total entropy of system and surroundings correspond to irreversible changes, because some energy is expended as waste heat, limiting the amount of work a system can do.[24][25][34][35]
Unlike many other functions of state, entropy cannot be directly observed but must be calculated. Absolute standard molar entropy of a substance can be calculated from the measured temperature dependence of its heat capacity. The molar entropy of ions is obtained as a difference in entropy from a reference state defined as zero entropy. The second law of thermodynamics states that the entropy of an isolated system must increase or remain constant. Therefore, entropy is not a conserved quantity: for example, in an isolated system with non-uniform temperature, heat might irreversibly flow and the temperature become more uniform such that entropy increases.[36] Chemical reactions cause changes in entropy and system entropy, in conjunction with enthalpy, plays an important role in determining in which direction a chemical reaction spontaneously proceeds.
One dictionary definition of entropy is that it is "a measure of thermal energy per unit temperature that is not available for useful work" in a cyclic process. For instance, a substance at uniform temperature is at maximum entropy and cannot drive a heat engine. A substance at non-uniform temperature is at a lower entropy (than if the heat distribution is allowed to even out) and some of the thermal energy can drive a heat engine.
A special case of entropy increase, the entropy of mixing, occurs when two or more different substances are mixed. If the substances are at the same temperature and pressure, there is no net exchange of heat or work – the entropy change is entirely due to the mixing of the different substances. At a statistical mechanical level, this results due to the change in available volume per particle with mixing.[37]
Equivalence of definitions
[edit]Proofs of equivalence between the definition of entropy in statistical mechanics (the Gibbs entropy formula ) and in classical thermodynamics ( together with the fundamental thermodynamic relation) are known for the microcanonical ensemble, the canonical ensemble, the grand canonical ensemble, and the isothermal–isobaric ensemble. These proofs are based on the probability density of microstates of the generalized Boltzmann distribution and the identification of the thermodynamic internal energy as the ensemble average .[38] Thermodynamic relations are then employed to derive the well-known Gibbs entropy formula. However, the equivalence between the Gibbs entropy formula and the thermodynamic definition of entropy is not a fundamental thermodynamic relation but rather a consequence of the form of the generalized Boltzmann distribution.[39]
Furthermore, it has been shown that the definitions of entropy in statistical mechanics is the only entropy that is equivalent to the classical thermodynamics entropy under the following postulates:[40]
- The probability density function is proportional to some function of the ensemble parameters and random variables.
- Thermodynamic state functions are described by ensemble averages of random variables.
- At infinite temperature, all the microstates have the same probability.
Second law of thermodynamics
[edit]The second law of thermodynamics requires that, in general, the total entropy of any system does not decrease other than by increasing the entropy of some other system. Hence, in a system isolated from its environment, the entropy of that system tends not to decrease. It follows that heat cannot flow from a colder body to a hotter body without the application of work to the colder body. Secondly, it is impossible for any device operating on a cycle to produce net work from a single temperature reservoir; the production of net work requires flow of heat from a hotter reservoir to a colder reservoir, or a single expanding reservoir undergoing adiabatic cooling, which performs adiabatic work. As a result, there is no possibility of a perpetual motion machine. It follows that a reduction in the increase of entropy in a specified process, such as a chemical reaction, means that it is energetically more efficient.
It follows from the second law of thermodynamics that the entropy of a system that is not isolated may decrease. An air conditioner, for example, may cool the air in a room, thus reducing the entropy of the air of that system. The heat expelled from the room (the system), which the air conditioner transports and discharges to the outside air, always makes a bigger contribution to the entropy of the environment than the decrease of the entropy of the air of that system. Thus, the total of entropy of the room plus the entropy of the environment increases, in agreement with the second law of thermodynamics.
In mechanics, the second law in conjunction with the fundamental thermodynamic relation places limits on a system's ability to do useful work.[41] The entropy change of a system at temperature absorbing an infinitesimal amount of heat in a reversible way, is given by . More explicitly, an energy is not available to do useful work, where is the temperature of the coldest accessible reservoir or heat sink external to the system. For further discussion, see Exergy.
Statistical mechanics demonstrates that entropy is governed by probability, thus allowing for a decrease in disorder even in an isolated system. Although this is possible, such an event has a small probability of occurring, making it unlikely.[42]
The applicability of a second law of thermodynamics is limited to systems in or sufficiently near equilibrium state, so that they have defined entropy.[43] Some inhomogeneous systems out of thermodynamic equilibrium still satisfy the hypothesis of local thermodynamic equilibrium, so that entropy density is locally defined as an intensive quantity. For such systems, there may apply a principle of maximum time rate of entropy production.[44][45] It states that such a system may evolve to a steady state that maximizes its time rate of entropy production. This does not mean that such a system is necessarily always in a condition of maximum time rate of entropy production; it means that it may evolve to such a steady state.[46][47]
Applications
[edit]The fundamental thermodynamic relation
[edit]The entropy of a system depends on its internal energy and its external parameters, such as its volume. In the thermodynamic limit, this fact leads to an equation relating the change in the internal energy to changes in the entropy and the external parameters. This relation is known as the fundamental thermodynamic relation. If external pressure bears on the volume as the only external parameter, this relation is:
Since both internal energy and entropy are monotonic functions of temperature , implying that the internal energy is fixed when one specifies the entropy and the volume, this relation is valid even if the change from one state of thermal equilibrium to another with infinitesimally larger entropy and volume happens in a non-quasistatic way (so during this change the system may be very far out of thermal equilibrium and then the whole-system entropy, pressure, and temperature may not exist).
The fundamental thermodynamic relation implies many thermodynamic identities that are valid in general, independent of the microscopic details of the system. Important examples are the Maxwell relations and the relations between heat capacities.
Entropy in chemical thermodynamics
[edit]Thermodynamic entropy is central in chemical thermodynamics, enabling changes to be quantified and the outcome of reactions predicted. The second law of thermodynamics states that entropy in an isolated system – the combination of a subsystem under study and its surroundings – increases during all spontaneous chemical and physical processes. The Clausius equation of introduces the measurement of entropy change, . Entropy change describes the direction and quantifies the magnitude of simple changes such as heat transfer between systems – always from hotter to cooler spontaneously.
The thermodynamic entropy therefore has the dimension of energy divided by temperature, and the unit joule per kelvin (J/K) in the International System of Units (SI).
Thermodynamic entropy is an extensive property, meaning that it scales with the size or extent of a system. In many processes it is useful to specify the entropy as an intensive property independent of the size, as a specific entropy characteristic of the type of system studied. Specific entropy may be expressed relative to a unit of mass, typically the kilogram (unit: J⋅kg−1⋅K−1). Alternatively, in chemistry, it is also referred to one mole of substance, in which case it is called the molar entropy with a unit of J⋅mol−1⋅K−1.
Thus, when one mole of substance at about 0 K is warmed by its surroundings to 298 K, the sum of the incremental values of constitute each element's or compound's standard molar entropy, an indicator of the amount of energy stored by a substance at 298 K.[48][49] Entropy change also measures the mixing of substances as a summation of their relative quantities in the final mixture.[50]
Энтропия одинаково важна для прогнозирования масштабов и направления сложных химических реакций. Для таких приложений должно быть включено в выражение, которое включает в себя как систему, так и ее окружение, . Через несколько шагов это выражение становится уравнением свободной энергии Гиббса для реагентов и продуктов в системе: [изменение свободной энергии Гиббса системы] [изменение энтальпии] [изменение энтропии]. [48]
Мировые технологические возможности для хранения и передачи энтропийной информации
[ редактировать ]Исследование, проведенное в журнале Science в 2011 году , оценило мировые технологические возможности для хранения и передачи оптимально сжатой информации, нормализованной с помощью наиболее эффективных алгоритмов сжатия, доступных в 2007 году, таким образом оценивая энтропию технологически доступных источников. [51] По оценкам автора, технологические возможности человечества по хранению информации выросли с 2,6 (энтропийно сжатых) в 1986 году до 295 (энтропийно сжатых) в 2007 году. эксабайт эксабайт сжатая) информация в 1986 году до 1,9 зеттабайта в 2007 году. Эффективная способность мира обмениваться информацией через двусторонние телекоммуникационные сети составляла от 281 петабайта (энтропийно сжатой) информации в 1986 году до 65 (энтропийно сжатой) эксабайт в 2007 году. [51]
Уравнение баланса энтропии для открытых систем
[ редактировать ]
В химической технологии принципы термодинамики обычно применяются к « открытым системам », то есть к тем, в которых тепло, работа и масса перетекают через границу системы. Потоки обоих тепла ( ) и работать, т.е. ( работа вала ) и (работа давление-объем), пересекающая границы системы, обычно вызывает изменения энтропии системы. Перенос в виде тепла влечет за собой перенос энтропии. , где – абсолютная термодинамическая температура системы в точке теплового потока. Если существуют массовые потоки через границы системы, они также влияют на общую энтропию системы. Этот учет в терминах теплоты и работы справедлив только для тех случаев, когда работа и теплопередача происходят по путям, физически отличным от путей входа и выхода вещества из системы. [52] [53]
Чтобы вывести обобщенное уравнение баланса энтропии, мы начинаем с общего уравнения баланса изменения любой экстенсивной величины. В термодинамической системе — величина, которая может сохраняться, например, энергия, или несохраняться, например, энтропия. Основное общее выражение баланса гласит, что , то есть скорость изменения в системе равна скорости, с которой поступает в систему на границах за вычетом скорости, с которой покидает систему за ее границы, плюс скорость, с которой генерируется внутри системы. Для открытой термодинамической системы, в которой тепло и работа передаются по путям, отличным от путей переноса вещества, используя это общее уравнение баланса, относительно скорости изменения со временем экстенсивной количественной энтропии , уравнение баланса энтропии имеет вид: [54] [55] [примечание 1]
где
- - чистая скорость потока энтропии из-за потоков массы в систему и из нее (где — энтропия на единицу массы).
- - скорость потока энтропии из-за потока тепла через границу системы.
- — это скорость производства энтропии внутри системы. Это производство энтропии возникает в результате процессов внутри системы, включая химические реакции, внутреннюю диффузию вещества, внутреннюю теплопередачу и эффекты трения, такие как вязкость, возникающие внутри системы в результате передачи механической работы в систему или из нее.
Если имеется несколько тепловых потоков, то термин заменяется на где это тепловой поток и это температура в порт теплового потока в систему.
Номенклатура «баланс энтропии» вводит в заблуждение и часто считается неуместной, поскольку энтропия не является сохраняющейся величиной. Другими словами, термин никогда не является известной величиной, а всегда является производной на основе приведенного выше выражения. Следовательно, версию второго закона для открытой системы более уместно описать как «уравнение генерации энтропии», поскольку оно определяет, что , с нулем для обратимых процессов или больше нуля для необратимых.
Формулы изменения энтропии для простых процессов
[ редактировать ]При некоторых простых преобразованиях в системах постоянного состава изменения энтропии задаются простыми формулами. [56]
Изотермическое расширение или сжатие идеального газа.
[ редактировать ]При расширении (или сжатии) идеального газа из начального объема и давление до окончательного тома и давление при любой постоянной температуре изменение энтропии определяется выражением:
Здесь количество газа (в молях ) и — постоянная идеального газа . Эти уравнения также применимы для расширения в конечный вакуум или процесса дросселирования , когда температура, внутренняя энергия и энтальпия идеального газа остаются постоянными.
Охлаждение и обогрев
[ редактировать ]Для чистого нагрева или охлаждения любой системы (газа, жидкости или твердого тела) при постоянном давлении от начальной температуры. до конечной температуры , изменение энтропии
при постоянном давлении при условии, что молярная теплоемкость (или удельная теплоемкость) C P постоянна и фазового перехода в этом температурном интервале не происходит .
Аналогично при постоянном объеме изменение энтропии равно
где молярная теплоемкость C v при постоянном объеме постоянна и фазовый переход отсутствует.
При низких температурах, близких к абсолютному нулю, теплоемкости твердых тел быстро падают почти до нуля , поэтому предположение о постоянной теплоемкости не применимо. [57]
Поскольку энтропия — это функция состояния , изменение энтропии любого процесса, в котором изменяются температура и объем, такое же, как и для пути, разделенного на два этапа — нагрев при постоянном объеме и расширение при постоянной температуре. Для идеального газа полное изменение энтропии равно [58]
Аналогично, если температура и давление идеального газа меняются,
Фазовые переходы
[ редактировать ]Обратимые фазовые переходы происходят при постоянных температуре и давлении. Обратимое тепло — это изменение энтальпии перехода, а изменение энтропии — это изменение энтальпии, деленное на термодинамическую температуру. [59] Для плавления ( плавления ) твердого тела в жидкость при температуре плавления T m энтропия плавления равна
Аналогично, для испарения жидкости в газ при температуре кипения T b энтропия испарения равна
Подходы к пониманию энтропии
[ редактировать ]В качестве фундаментального аспекта термодинамики и физики действительны несколько различных подходов к энтропии, помимо подходов Клаузиуса и Больцмана.
Стандартные определения учебника
[ редактировать ]Ниже приводится список дополнительных определений энтропии из сборника учебников:
- мера рассеяния энергии при определенной температуре.
- мера беспорядка во Вселенной или наличия в системе энергии для совершения работы. [60]
- системы мера тепловой энергии на единицу температуры, которая недоступна для совершения полезной работы . [61]
В анализе Больцмана с точки зрения составляющих частиц энтропия является мерой числа возможных микроскопических состояний (или микросостояний) системы, находящейся в термодинамическом равновесии.
Порядок и беспорядок
[ редактировать ]Энтропия часто слабо связана с уровнем порядка , беспорядка или хаоса в термодинамической системе . Традиционное качественное описание энтропии состоит в том, что она относится к изменениям состояния системы и является мерой «молекулярного беспорядка» и количества затраченной энергии при динамическом преобразовании энергии из одного состояния или формы в другое. В этом направлении несколько недавних авторов вывели точные формулы энтропии для объяснения и измерения беспорядка и порядка в атомных и молекулярных ансамблях. [62] [63] [64] Одна из простейших формул энтропийного порядка/беспорядка была выведена в 1984 году физиком-термодинамистом Питером Ландсбергом на основе сочетания аргументов термодинамики и теории информации . Он утверждает, что когда на систему действуют ограничения, препятствующие переходу в одно или несколько возможных или разрешенных состояний, в отличие от запрещенных состояний, мера общего количества «беспорядков» в системе определяется выражением : [63] [64]
Аналогично, общая сумма «заказа» в системе определяется как:
где CD — «беспорядочная» пропускная способность системы, которая представляет собой энтропию частей, содержащихся в разрешенном ансамбле, C I — «информационная» пропускная способность системы, выражение, аналогичное способности канала Шеннона , и CO пропускной — «порядковая» емкость системы. [62]
Рассредоточение энергии
[ редактировать ]Понятие энтропии можно качественно описать как меру рассеивания энергии при определенной температуре. [65] Подобные термины использовались с самого начала истории классической термодинамики , а с развитием статистической термодинамики и квантовой теории изменения энтропии описывались с точки зрения смешивания или «распространения» полной энергии каждого компонента системы. по его конкретным квантованным уровням энергии.
Неясности в терминах «беспорядок» и «хаос» , которые обычно имеют значения, прямо противоположные равновесию, способствуют широко распространенной путанице и затрудняют понимание энтропии для большинства студентов. [66] Как показывает второй закон термодинамики , в изолированной системе внутренние части с разными температурами имеют тенденцию приспосабливаться к одной однородной температуре и, таким образом, обеспечивать равновесие. Недавно разработанный образовательный подход избегает двусмысленных терминов и описывает такое распространение энергии как рассеяние, которое приводит к потере дифференциалов, необходимых для работы, даже если полная энергия остается постоянной в соответствии с первым законом термодинамики. [67] (сравните обсуждение в следующем разделе). Физический химик Питер Аткинс в своем учебнике «Физическая химия » вводит энтропию, утверждая, что «спонтанные изменения всегда сопровождаются рассеянием энергии или материи, а часто и того, и другого». [68]
Связь энтропии с полезностью энергии
[ редактировать ]Можно (в термическом контексте) рассматривать более низкую энтропию как меру эффективности или полезности определенного количества энергии. [69] Энергия, подаваемая при более высокой температуре (т.е. с низкой энтропией), имеет тенденцию быть более полезной, чем такое же количество энергии, доступное при более низкой температуре. Смешивание горячей порции жидкости с холодной дает порцию промежуточной температуры, в которой общее увеличение энтропии представляет собой «потерю», которую невозможно восполнить.
Поскольку энтропия Вселенной неуклонно возрастает, ее общая энергия становится менее полезной. Предполагается, что в конечном итоге это приведет к тепловой смерти Вселенной . [70]
Энтропия и адиабатическая доступность
[ редактировать ]Определение энтропии, полностью основанное на отношении адиабатической доступности между состояниями равновесия, было дано Э. Х. Либом и Дж. Ингвасоном в 1999 году. [71] У этого подхода есть несколько предшественников, в том числе новаторская работа Константина Каратеодори 1909 года. [72] и монография Р. Джайлза. [73] В подходе Либа и Ингвасона начинают с выбора для единицы количества рассматриваемого вещества двух эталонных состояний. и так что последнее адиабатически доступно из первого, но не наоборот. Определив энтропию эталонных состояний как 0 и 1 соответственно, энтропия состояния определяется как наибольшее число такой, что адиабатически доступен из сложного состояния, состоящего из количества в штате и дополнительную сумму, , в штате . Простой, но важный результат в этой ситуации состоит в том, что энтропия однозначно определяется, помимо выбора единицы измерения и аддитивной константы для каждого химического элемента, следующими свойствами: она монотонна по отношению к отношению адиабатической доступности, аддитивна по составному элементу. систем и обширное масштабирование.
Энтропия в квантовой механике
[ редактировать ]В квантовой статистической механике концепция энтропии была разработана Джоном фон Нейманом и обычно называется « энтропией фон Неймана ».
где ρ — матрица плотности , а Tr — оператор следа .
Это поддерживает принцип соответствия , поскольку в классическом пределе , когда фазы между базисными состояниями, используемыми для классических вероятностей, являются чисто случайными, это выражение эквивалентно знакомому классическому определению энтропии:
т.е. в таком базисе матрица плотности диагональна.
Фон Нейман создал строгую математическую основу для квантовой механики в своей работе Mathematische Grundlagen der Quantenmechanik . В этой работе он представил теорию измерения, в которой обычное представление о коллапсе волновой функции описывается как необратимый процесс (так называемое фон Неймана или проективное измерение ). Используя эту концепцию в сочетании с матрицей плотности, он расширил классическую концепцию энтропии на квантовую область.
Теория информации
[ редактировать ]Я думал назвать это «информацией», но это слово использовалось слишком часто, поэтому я решил назвать это «неопределенностью». [...] Фон Нейман сказал мне: «Вы должны назвать это энтропией по двум причинам. Во-первых, ваша функция неопределенности использовалась в статистической механике под этим именем, поэтому у нее уже есть имя. и что еще более важно, никто не знает, что такое энтропия на самом деле, поэтому в дебатах у вас всегда будет преимущество.
Разговор между Клодом Шенноном и Джоном фон Нейманом о том, как назвать затухание сигналов телефонной линии. [74]
Если рассматривать ее с точки зрения теории информации , функция состояния энтропии — это количество информации в системе, необходимое для полного определения микросостояния системы. Энтропия — это мера количества недостающей информации до ее получения. [75] Часто называемая энтропией Шеннона , она была первоначально разработана Клодом Шенноном в 1948 году для изучения размера информации передаваемого сообщения. Определение информационной энтропии выражается через дискретный набор вероятностей. так что
где основание логарифма определяет единицы измерения (например, двоичный логарифм соответствует битам ).
В случае передаваемых сообщений эти вероятности представляли собой вероятности того, что конкретное сообщение действительно было передано, а энтропия системы сообщений была мерой среднего размера информации сообщения. В случае равных вероятностей (т. е. каждое сообщение равновероятно) энтропия Шеннона (в битах) — это просто количество двоичных вопросов, необходимых для определения содержания сообщения. [27]
Большинство исследователей считают информационную энтропию и термодинамическую энтропию непосредственно связанными с одним и тем же понятием. [76] [77] [78] [79] [80] в то время как другие утверждают, что они различны. [81] Оба выражения математически схожи. Если - это количество микросостояний, которые могут создать данное макросостояние, и каждое микросостояние имеет одинаковую априорную вероятность, тогда эта вероятность равна . Энтропия Шеннона (в натс ) равна
и если энтропию измерять в единицах на нат, тогда энтропия определяется выражением
что представляет собой формулу энтропии Больцмана , где — константа Больцмана, которую можно интерпретировать как термодинамическую энтропию на физ. Некоторые авторы выступают за отказ от слова «энтропия» функцию теории информации и вместо этого использовать другой термин Шеннона - «неопределенность». [82]
Измерение
[ редактировать ]Энтропию вещества можно измерить, хотя и косвенным путем. Измерение, известное как энтропиметрия, [83] выполняется в закрытой системе (где число частиц N и объем V являются постоянными) и использует определение температуры [84] с точки зрения энтропии, ограничивая при этом обмен энергии на тепло ( ).
Полученное соотношение описывает, как изменяется энтропия когда небольшое количество энергии вводится в систему при определенной температуре .
Процесс измерения происходит следующим образом. Сначала образец вещества охлаждают максимально близко к абсолютному нулю. При таких температурах энтропия приближается к нулю – это связано с определением температуры. Затем в образец вводят небольшое количество тепла и регистрируют изменение температуры, пока температура не достигнет желаемого значения (обычно 25 °C). Полученные данные позволяют пользователю интегрировать приведенное выше уравнение, получая абсолютное значение энтропии вещества при конечной температуре. Эта величина энтропии называется калориметрической энтропией. [85]
Междисциплинарные приложения
[ редактировать ]Хотя концепция энтропии изначально была термодинамической концепцией, она была адаптирована в других областях исследований. [54] включая теорию информации , психодинамику , термоэкономику / экологическую экономику и эволюцию . [62] [86] [87] [88] [89]
Философия и теоретическая физика
[ редактировать ]Энтропия — единственная величина в физических науках, которая, по-видимому, предполагает определенное направление прогресса, иногда называемое стрелой времени . Второй закон термодинамики гласит, что с течением времени энтропия изолированной системы никогда не уменьшается в больших системах в течение значительных периодов времени. Следовательно, с этой точки зрения измерение энтропии в этих условиях рассматривается как часы. [90]
Биология
[ редактировать ]Кьяваццо и др. предположил, что то, где пещерные пауки откладывают яйца, можно объяснить минимизацией энтропии. [91]
Было доказано, что энтропия полезна при анализе последовательностей пар оснований в ДНК. Было показано, что многие меры, основанные на энтропии, позволяют различать различные структурные области генома, различать кодирующие и некодирующие области ДНК, а также могут применяться для воссоздания эволюционных деревьев путем определения эволюционной дистанции между различными видами. [92]
Космология
[ редактировать ]Предполагая, что конечная Вселенная является изолированной системой, второй закон термодинамики утверждает, что ее полная энтропия постоянно увеличивается. С 19 века высказывались предположения, что Вселенная обречена на тепловую смерть , при которой вся энергия превращается в однородное распределение тепловой энергии, так что больше невозможно извлечь работу из какого-либо источника.
Если считать, что во Вселенной в целом энтропия увеличивается, то, как Роджер Пенроуз отметил , гравитация играет важную роль в этом увеличении, поскольку гравитация заставляет рассеянную материю накапливаться в звезды, которые в конечном итоге коллапсируют в черные дыры . Энтропия черной дыры пропорциональна площади поверхности горизонта событий черной дыры . [93] [94] [95] Джейкоб Бекенштейн и Стивен Хокинг показали, что черные дыры обладают максимально возможной энтропией по сравнению с любым объектом равного размера. Это делает их вероятными конечными точками всех процессов, увеличивающих энтропию, если они являются полностью эффективными ловушками материи и энергии. [96] Однако выход энергии из черных дыр может быть возможен благодаря квантовой активности (см. Излучение Хокинга ).
Роль энтропии в космологии остается спорным вопросом со времен Людвига Больцмана . Недавние работы поставили под сомнение гипотезу тепловой смерти и применимость любой простой термодинамической модели ко Вселенной в целом. Хотя энтропия действительно увеличивается в модели расширяющейся Вселенной, максимально возможная энтропия растет гораздо быстрее, перемещая Вселенную со временем дальше от тепловой смерти, а не ближе. [97] [98] [99] Это приводит к «энтропийному разрыву», отталкивающему систему еще дальше от предполагаемого равновесия тепловой смерти. [100] Другие усложняющие факторы, такие как плотность энергии вакуума и макроскопические квантовые эффекты, трудно согласовать с термодинамическими моделями, что делает любые предсказания крупномасштабной термодинамики чрезвычайно трудными. [101]
Современные теории предполагают, что разрыв в энтропии изначально возник в результате раннего быстрого экспоненциального расширения Вселенной. [102]
Экономика
[ редактировать ]Американский экономист румынского происхождения Николас Джорджеску-Роген , прародитель экономики и основатель парадигмы экологической экономики , широко использовал концепцию энтропии в своем выдающемся труде «Закон энтропии и экономический процесс» . [77] Благодаря работам Джорджеску-Рогена законы термодинамики составляют неотъемлемую часть школы экологической экономики . [103] : 204f [104] : 29–35 Хотя его работа была несколько испорчена ошибками , целая глава по экономике Джорджеску-Рогена была одобрительно включена в один учебник элементарной физики, посвященный историческому развитию термодинамики. [105] : 95–112
В экономике работа Джорджеску-Рогена породила термин «энтропийный пессимизм» . [106] : 116 С 1990-х годов ведущий экономист-эколог и теоретик устойчивого состояния Герман Дейли – ученик Джорджеску-Рогена – был самым влиятельным сторонником позиции энтропийного пессимизма среди экономистов. [107] : 545f [108]
См. также
[ редактировать ]- Энтропия Больцмана
- Броуновский храповик
- Энтропия конфигурации
- Конформационная энтропия
- Энтропийный взрыв
- Энтропийная сила
- Энтропийное значение под угрозой
- Энтропия и жизнь
- Единица энтропии
- Свободная энтропия
- Гармоническая энтропия
- Инфо-метрика
- Негэнтропия (отрицательная энтропия)
- Фазовое пространство
- Принцип максимальной энтропии
- Остаточная энтропия
- Термодинамический потенциал
Примечания
[ редактировать ]- ^ Верхние точки представляют собой производные величин по времени.
Ссылки
[ редактировать ]- ^ Верль, Альфред (1 апреля 1978 г.). «Общие свойства энтропии» . Обзоры современной физики . 50 (2): 221–260. Бибкод : 1978РвМП...50..221Вт . дои : 10.1103/RevModPhys.50.221 .
- ^ Трусделл, К. (1980). Трагикомическая история термодинамики, 1822–1854 гг . Нью-Йорк: Springer-Verlag. п. 215. ИСБН 0387904034 – через Интернет-архив .
- ^ Кисть, С.Г. (1976). Вид движения, которое мы называем теплом: история кинетической теории газов в XIX веке, Книга 2, Статистическая физика и необратимые процессы , Elsevier, Амстердам, ISBN 0-444-87009-1 , стр. 576–577.
- ^ «Карно, Сади (1796–1832)» . Вольфрам Исследования. 2007 . Проверено 24 февраля 2010 г.
- ^ Маккалок, Ричард, С. (1876). «Трактат о механической теории тепла и ее приложениях к паровой машине» и т. д . Д. Ван Ностранд.
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Перейти обратно: а б Клаузиус, Рудольф (1850). «О движущей силе тепла и о законах, которые можно вывести из нее для теории самой теплоты». Анналы физики (на немецком языке). 155 (3): 368–397. Бибкод : 1850АнП...155..368С . дои : 10.1002/andp.18501550306 . hdl : 2027/uc1.$b242250 . [О движущей силе тепла и о законах, которые можно вывести из нее для теории тепла]: Анналы физики и химии Поггендорфа .
- ^ Лидделл, Х.Г., Скотт, Р. (1843/1978). Греко-английский лексикон, исправленное и дополненное издание, Oxford University Press, Oxford UK, ISBN 0198642148 , стр. 1826–1827.
- ^ Перейти обратно: а б Клаузиус, Рудольф (1865). «О различных формах основных уравнений механической теории теплоты, удобных для использования (Изложено в Обществе естественных исследований в Цюрихе 24 апреля 1865 г.)» . Анналы физики и химии (на немецком языке). 125 (7): 353–400. Бибкод : 1865АнП...201..353С . дои : 10.1002/andp.18652010702 . п. 390:
Если искать описательное имя для S , можно было бы сказать, подобно величине U , что это содержание тепла и работы тела, а о величине S можно было бы сказать , что это содержание трансформации тела. Но так как я считаю, что названия таких важных для науки величин лучше брать из старых языков, чтобы их можно было использовать в неизменном виде во всех новых языках, то предлагаю назвать величину S по греческому слову ἡ τροπή, которое Преобразование, энтропия тела. сделал слово «энтропия» Я намеренно как можно более похожим на слово «энергия» , потому что две величины, которые эти слова призваны назвать, настолько тесно связаны по своему физическому смыслу, что определенное сходство в наименовании кажется мне уместным.
- ^ Перейти обратно: а б Гиллиспи, Чарльз Коулстон (1960). Грань объективности: Очерк истории научных идей . Издательство Принстонского университета. п. 399 . ISBN 0-691-02350-6 .
Клаузиус ввел слово «энтропия» для обозначения : «Я предпочитаю обращаться к древним языкам за названиями важных научных величин, чтобы они могли означать одно и то же на всех живых языках. Предлагаю соответственно называть энтропия тела, от греческого слова «преобразование». Я намеренно придумал слово «энтропия», похожее на «энергию», поскольку эти две величины настолько аналогичны по своему физическому значению, что аналогия с номиналом показалась мне полезной».
- ^ Перейти обратно: а б Купер, Леон Н. (1968). Введение в смысл и структуру физики . Харпер. п. 331.
- ^ Научные труды Дж. Уилларда Гиббса в двух томах . Том. 1. Лонгманс, Грин и Ко, 1906. с. 11 . Проверено 26 февраля 2011 г.
- ^ Дж. А. Макговерн, «2,5 Энтропия» . Архивировано из оригинала 23 сентября 2012 года . Проверено 5 февраля 2013 г.
- ^ «6.5 Необратимость, изменения энтропии и потерянная работа » . web.mit.edu . Проверено 21 мая 2016 г.
- ^ Лоуэр, Стивен. «Что такое энтропия?» . chem1.com . Проверено 21 мая 2016 г.
- ^ Лавенда, Бернард Х. (2010). «2.3.4». Новый взгляд на термодинамику (онлайн-авторское изд.). Нью-Йорк: Спрингер. ISBN 978-1-4419-1430-9 .
- ^ Карно, Сади Карно (1986). Фокс, Роберт (ред.). Размышления о движущей силе огня . Нью-Йорк: Лилиан Барбер Пресс. стр. 26 . ISBN 978-0-936508-16-0 .
- ^ Трусделл, К. (1980). Трагикомическая история термодинамики 1822–1854 гг . Нью-Йорк: Спрингер. стр. 78–85 . ISBN 978-0-387-90403-0 .
- ^ Клерк Максвелл, Джеймс (2001). Пешич, Питер (ред.). Теория тепла . Минеола: Dover Publications. стр. 115–158. ISBN 978-0-486-41735-6 .
- ^ Перейти обратно: а б Планк, М. (1945). Трактат по термодинамике . Дуврские публикации. п. §90 и §137.
уравнения (39), (40) и (65)
. - ^ Рудольф Клаузиус (1867). Механическая теория тепла: с ее приложениями к паровой машине и физическим свойствам тел . Дж. Ван Ворст. п. 28. ISBN 978-1-4981-6733-8 .
- ^ Ферми, Э. (1956). Термодинамика . Dover Publications (все еще издается). п. 48.
уравнение (64)
. - ^ Аткинс, Питер; Хулио Де Паула (2006). Физическая химия, 8-е изд . Издательство Оксфордского университета. п. 79. ИСБН 978-0-19-870072-2 .
- ^ Энгель, Томас; Филип Рид (2006). Физическая химия . Пирсон Бенджамин Каммингс. п. 86. ИСБН 978-0-8053-3842-3 .
- ^ Перейти обратно: а б с Ликер, Марк Д. (2004). Краткая химическая энциклопедия МакГроу-Хилла . Нью-Йорк: McGraw-Hill Professional. ISBN 978-0-07-143953-4 .
- ^ Перейти обратно: а б Сетна, Джеймс П. (2006). Статистическая механика: энтропия, параметры порядка и сложность (изд. [Online-Ausg.]). Оксфорд: Издательство Оксфордского университета. п. 78 . ISBN 978-0-19-856677-9 .
- ^ Кларк, Джон О.Э. (2004). Основной научный словарь . Нью-Йорк: Barnes & Noble. ISBN 978-0-7607-4616-5 .
- ^ Перейти обратно: а б Фригг, Р. и Верндл, К. «Энтропия – руководство для недоумевающих». Архивировано 13 августа 2011 года в Wayback Machine . В вероятностях в физике ; Бейсбарт К. и Хартманн С. (ред.); Издательство Оксфордского университета, Оксфорд, 2010.
- ^ Шредер, Дэниел В. (2000). Введение в теплофизику . Сан-Франциско, Калифорния: Эддисон Уэсли. п. 57 . ISBN 978-0-201-38027-9 .
- ^ Джейнс, ET (1 мая 1965 г.). «Гиббс против энтропии Больцмана» . Американский журнал физики . 33 (5): 391–398. Бибкод : 1965AmJPh..33..391J . дои : 10.1119/1.1971557 . ISSN 0002-9505 .
- ^ Джейнс, ET (1992). «Парадокс Гиббса». В Смите, Чехия; Эриксон, Дж.Дж.; Нойдорфер, ПО (ред.). Максимальная энтропия и байесовские методы (PDF) . Клювер Академик: Дордрехт. стр. 1–22 . Проверено 17 августа 2012 г.
- ^ Перейти обратно: а б Сэндлер, Стэнли И. (2006). Химическая, биохимическая и инженерная термодинамика (4-е изд.). Нью-Йорк: Джон Уайли и сыновья. п. 91 . ISBN 978-0-471-66174-0 .
- ^ Саймон, Джон Д.; МакКуорри, Дональд А. (1997). Физическая химия: молекулярный подход (Переизданная ред.). Саусалито, Калифорния: Univ. Научные книги. п. 817. ИСБН 978-0-935702-99-6 .
- ^ Хейни, Дональд Т. (2001). Биологическая термодинамика . Издательство Кембриджского университета . ISBN 978-0-521-79165-6 .
- ^ Дэйнтит, Джон (2005). Научный словарь (5-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-280641-3 .
- ^ де Росне, Джоэл (1979). Макроскоп – новый взгляд на мир (написано биохимиком, прошедшим обучение в Массачусетском технологическом институте) . Харпер и Роу, Издательство. ISBN 978-0-06-011029-1 .
- ^ Макговерн, Дж. А. «Теплоемкость» . Архивировано из оригинала 19 августа 2012 года . Проверено 27 января 2013 г.
- ^ Бен-Наим, Арье (21 сентября 2007 г.). «О так называемом парадоксе Гиббса и о реальном парадоксе» (PDF) . Энтропия . 9 (3): 132–136. Бибкод : 2007Entrp...9..132B . дои : 10.3390/e9030133 .
- ^ Каллен, Герберт (2001). Термодинамика и введение в термостатику (2-е изд.) . Джон Уайли и сыновья. ISBN 978-0-471-86256-7 .
- ^ Гао, Сян; Галликкио, Эмилио; Ройтберг, Адриан (2019). «Обобщенное распределение Больцмана — единственное распределение, в котором энтропия Гиббса-Шеннона равна термодинамической энтропии». Журнал химической физики . 151 (3): 034113. arXiv : 1903.02121 . Бибкод : 2019JChPh.151c4113G . дои : 10.1063/1.5111333 . ПМИД 31325924 . S2CID 118981017 .
- ^ Гао, Сян (март 2022 г.). «Математика теории ансамбля» . Результаты по физике . 34 : 105230. arXiv : 2006.00485 . Бибкод : 2022ResPh..3405230G . дои : 10.1016/j.rinp.2022.105230 . S2CID 221978379 .
- ^ Дэйнтит, Джон (2005). Оксфордский физический словарь . Издательство Оксфордского университета. ISBN 978-0-19-280628-4 .
- ^ Саха, Арнаб; Лахири, Сураб; Джаяннавар, AM (2009). «Теоремы производства энтропии и некоторые следствия». Физический обзор E . 80 (1): 1–10. arXiv : 0903.4147 . Бибкод : 2009PhRvE..80a1117S . дои : 10.1103/PhysRevE.80.011117 . ПМИД 19658663 . S2CID 22204063 .
- ^ Мартюшев, Л.М.; Селезнев, В.Д. (2014). «Ограничения принципа производства максимальной энтропии». Физика А: Статистическая механика и ее приложения . 410 : 17–21. arXiv : 1311.2068 . Бибкод : 2014PhyA..410...17M . дои : 10.1016/j.physa.2014.05.014 . S2CID 119224112 .
- ^ Зиглер, Х. (1983). Введение в термомеханику . Северная Голландия, Амстердам.
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Онсагер, Ларс (1931). «Взаимные отношения в необратимых процессах» . Физ. Преподобный . 37 (4): 405. Бибкод : 1931ФРв...37..405О . дои : 10.1103/PhysRev.37.405 .
- ^ Клейдон, А.; и др., др. (2005). Неравновесная термодинамика и производство энтропии . Гейдельберг: Спрингер.
- ^ Белкин, Андрей; и др., др. (2015). «Самособирающиеся колеблющиеся наноструктуры и принцип производства максимальной энтропии» . Научные отчеты . 5 : 8323. Бибкод : 2015NatSR...5E8323B . дои : 10.1038/srep08323 . ПМК 4321171 . ПМИД 25662746 .
- ^ Перейти обратно: а б Мур, Дж.В.; К. Л. Станистский; ПК Юрс (2005). Химия, Молекулярная наука . Брукс Коул. ISBN 978-0-534-42201-1 .
- ^ Юнгерманн, АХ (2006). «Энтропия и модель полки: квантово-физический подход к физическому свойству». Журнал химического образования . 83 (11): 1686–1694. Бибкод : 2006JChEd..83.1686J . дои : 10.1021/ed083p1686 . S2CID 18081336 .
- ^ Левин, Индиана (2002). Физическая химия, 5-е изд . МакГроу-Хилл. ISBN 978-0-07-231808-1 .
- ^ Перейти обратно: а б Гильберт, Мартин; Лопес, Присцила (11 февраля 2011 г.). «Мировые технологические возможности для хранения, передачи и вычисления информации» . Наука . 332 (6025): 60–65. Бибкод : 2011Sci...332...60H . дои : 10.1126/science.1200970 . ISSN 0036-8075 . ПМИД 21310967 . S2CID 206531385 .
- ^ Покойный лауреат Нобелевской премии Макс Борн (8 августа 2015 г.). Естественная философия причины и случая . БиблиоЛайф. стр. 44, 146–147. ISBN 978-1-298-49740-6 .
- ^ Хаазе, Р. (1971). Термодинамика . Нью-Йорк: Академическая пресса. стр. 1–97. ISBN 978-0-12-245601-5 .
- ^ Перейти обратно: а б Покровский, Владимир (2020). Термодинамика сложных систем: принципы и приложения . Издательство IOP, Бристоль, Великобритания. Бибкод : 2020tcsp.book.....P .
- ^ Сэндлер, Стэнли, И. (1989). Химическая и техническая термодинамика . Джон Уайли и сыновья. ISBN 978-0-471-83050-4 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ «GRC.nasa.gov» . GRC.nasa.gov. 27 марта 2000 г. Архивировано из оригинала 21 августа 2011 г. Проверено 17 августа 2012 г.
- ^ Франзен, Стефан. «Третий закон» (PDF) . ncsu.edu. Архивировано из оригинала (PDF) 9 июля 2017 года.
- ^ «GRC.nasa.gov» . GRC.nasa.gov. 11 июля 2008 года . Проверено 17 августа 2012 г.
- ^ Старзак, Майкл Э. (2010). «Фазовые равновесия и коллигативные свойства» . Энергия и энтропия: равновесие в стационарных состояниях . Springer Science + Business Media. стр. 138–140. ISBN 978-1489983671 . Проверено 5 сентября 2019 г.
- ^ Гриббин, Джон (1999). Гриббин, Мэри (ред.). Q означает квант: энциклопедия физики элементарных частиц . Нью-Йорк: Свободная пресса. ISBN 978-0-684-85578-3 .
- ^ «Энтропия: определение и уравнение» . Британская энциклопедия . Проверено 22 мая 2016 г.
- ^ Перейти обратно: а б с Брукс, Дэниел Р.; Уайли, Э.О. (1988). Эволюция как энтропия: к единой теории биологии (2-е изд.). Чикаго [и др.]: Издательство Чикагского университета. ISBN 978-0-226-07574-7 .
- ^ Перейти обратно: а б Ландсберг, PT (1984). «Всегда ли равновесие является максимумом энтропии?». Дж. Стат. Физика . 35 (1–2): 159–169. Бибкод : 1984JSP....35..159L . дои : 10.1007/bf01017372 . S2CID 122424225 .
- ^ Перейти обратно: а б Ландсберг, PT (1984). «Могут ли энтропия и «порядок» увеличиваться вместе?». Письма по физике . 102А (4): 171–173. Бибкод : 1984PhLA..102..171L . дои : 10.1016/0375-9601(84)90934-4 .
- ^ Ламберт, Фрэнк Л. «Студенческий подход ко второму закону и энтропии» .
- ^ Уотсон-младший; Карсон, Э.М. (май 2002 г.). «Понимание студентами энтропии и свободной энергии Гиббса» (PDF) . Университетское химическое образование . 6 (1): 4. ISSN 1369-5614 .
- ^ Ламберт, Фрэнк Л. (февраль 2002 г.). «Беспорядок – сломанная опора для поддержки дискуссий об энтропии» . Журнал химического образования . 79 (2): 187. Бибкод : 2002JChEd..79..187L . дои : 10.1021/ed079p187 . S2CID 97102995 .
- ^ Питер Аткинс; Хулио де Паула; Джеймс Килер (2019). Физическая химия Аткинса 11e: Том 3: Молекулярная термодинамика и кинетика . Издательство Оксфордского университета. п. 89. ИСБН 978-0-19-882336-0 .
- ^ Сандра Саари (23 февраля 1993 г.). «Рецензия на книгу «Научный сборник» » . Халидж Таймс . ОАЭ: Галадари Пресс: xi.
- ^ Смит, Кросби; Уайз, М. Нортон (1989). Энергия и империя: биографическое исследование лорда Кельвина . Издательство Кембриджского университета. стр. 500–501. ISBN 978-0-521-26173-9 .
- ^ Либ, Эллиот Х.; Ингвасон, Якоб (март 1999 г.). «Физика и математика второго начала термодинамики». Отчеты по физике . 310 (1): 1–96. arXiv : cond-mat/9708200 . Бибкод : 1999PhR...310....1L . дои : 10.1016/S0370-1573(98)00082-9 . S2CID 119620408 .
- ^ Каратеодори, К. (сентябрь 1909 г.). «Исследования по основам термодинамики» . Математические анналы (на немецком языке). 67 (3): 355–386. дои : 10.1007/BF01450409 . S2CID 118230148 .
- ^ Р. Джайлз (2016). Математические основы термодинамики: Международная серия монографий по чистой и прикладной математике . Эльзевир Наука. ISBN 978-1-4831-8491-3 .
- ^ Трибус, М.; МакИрвин, ЕС (1971). «Энергия и информация» . Научный американец . 224 (3): 178–184. JSTOR 24923125 .
- ^ Балиан, Роджер (2004). «Энтропия, изменчивая концепция». В Далибаре, Жан (ред.). Семинар Пуанкаре 2003: Конденсация Бозе-Эйнштейна – энтропия . Базель: Биркхойзер. стр. 119–144. ISBN 978-3-7643-7116-6 .
- ^ Бриллюэн, Леон (1956). Наука и теория информации . Дуврские публикации. ISBN 978-0-486-43918-1 .
- ^ Перейти обратно: а б Джорджеску-Роген, Николас (1971). Закон энтропии и экономический процесс . Издательство Гарвардского университета. ISBN 978-0-674-25781-8 .
- ^ Чен, Цзин (2005). Физическая основа экономики – аналитическая термодинамическая теория . Всемирная научная. ISBN 978-981-256-323-1 .
- ^ Калинин, М.И.; Кононогов С.А. (2005). «Постоянная Больцмана». Методика измерения . 48 (7): 632–636. дои : 10.1007/s11018-005-0195-9 . S2CID 118726162 .
- ^ Бен-Наим, Арье (2008). Энтропия демистифицировала второй закон, сведя его к простому здравому смыслу (Расширенное издание). Сингапур: World Scientific. ISBN 9789812832269 .
- ^ Валлино, Джозеф Дж.; Алгар, Кристофер К.; Гонсалес, Нурия Фернандес; Хубер, Джули А. (2013). «Использование оптимального управления отступающим горизонтом для решения биогеохимических задач на основе MaxEP (максимальное производство энтропии)» . В Дьюаре, Родерик К.; Лайнвивер, Чарльз Х.; Нивен, Роберт К.; Регенауэр-Либ, Клаус (ред.). За пределами второго закона: производство энтропии и неравновесные системы . Живые системы как катализаторы. Спрингер. п. 340. ИСБН 978-3642401534 . Проверено 31 августа 2019 г.
Рукописная страница образует шаблон с информацией → энтропия страницы < страница различий со случайными буквами. Снижение энтропии тривиально по сравнению с энтропией чернильной бумаги. Если бумага сожжена, в термодинамическом контексте вряд ли имеет значение, содержит ли текст смысл жизни или просто тарабарщину [ sic ].
- ^ Шнайдер, Том, Система DELILA (язык библиотеки дезоксирибонуклеиновой кислоты), (Теория информации, анализ сайтов связывания), Лаборатория математической биологии, Национальный институт рака, Фредерик, доктор медицины.
- ^ Ким, Хе Джин; Пак, Ёнкю; Квон, Юнджин; Шин, Джэхо; Ким, Ён-Хан; Ан, Хён Сок; Язами, Рашид; Чхве, Чан Ук (2020). «Энтропиметрия для неразрушающего структурного анализа катодов LiCoO 2 » . Энергетика и экология . 13 (1): 286–296. дои : 10.1039/C9EE02964H . ISSN 1754-5692 . S2CID 212779004 .
- ^ Шредер, Дэниел В. (2000). Введение в теплофизику ([Начдр.] изд.). Сан-Франциско, Калифорния [ua]: Эддисон Уэсли. п. 88 . ISBN 978-0-201-38027-9 .
- ^ «Измерение энтропии» . chem.wisc.edu .
- ^ Эйвери, Джон (2003). Теория информации и эволюция . Всемирная научная. ISBN 978-981-238-399-0 .
- ^ Йоки, Хьюберт, П. (2005). Теория информации, эволюция и происхождение жизни . Издательство Кембриджского университета. ISBN 978-0-521-80293-2 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Кьяваццо, Элиодоро; Фазано, Маттео; Асинари, Пьетро (2013). «Вывод аналитических термодинамических моделей для биологических сетей» (PDF) . Физика А: Статистическая механика и ее приложения . 392 (5): 1122–1132. Бибкод : 2013PhyA..392.1122C . дои : 10.1016/j.physa.2012.11.030 . S2CID 12418973 .
- ^ Чен, Цзин (2015). Единство науки и экономики: новое основание экономической теории . Спрингер. дои : 10.1007/978-1-4939-3466-9 . ISBN 978-1-4939-3464-5 .
- ^ Крейн, Лия (май 2021 г.). «Цена хранения времени» . Новый учёный . 250 (3334): 15. Бибкод : 2021NewSc.250...15C . дои : 10.1016/S0262-4079(21)00816-2 .
- ^ Кьяваццо, Элиодоро; Исайя, Марко; Маммола, Стефано; Лепор, Эмилиано; Вентола, Луиджи; Асинари, Пьетро; Пуньо, Никола Мария (2015). «Пещерные пауки выбирают оптимальные факторы окружающей среды с точки зрения создаваемой энтропии при откладывании кокона» . Научные отчеты . 5 : 7611. Бибкод : 2015NatSR...5E7611C . дои : 10.1038/srep07611 . ПМК 5154591 . ПМИД 25556697 .
- ^ Танос, Димитриос; Ли, Вэньтянь; Провата, Астеро (1 марта 2018 г.). «Энтропийные флуктуации последовательностей ДНК». Физика А: Статистическая механика и ее приложения . 493 : 444–457. Бибкод : 2018PhyA..493..444T . дои : 10.1016/j.physa.2017.11.119 . ISSN 0378-4371 .
- ^ фон Байер, Кристиан, Х. (2003). Информация – новый язык науки . Издательство Гарвардского университета. ISBN 978-0-674-01387-2 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Средницкий М (август 1993 г.). «Энтропия и площадь». Физ. Преподобный Летт . 71 (5): 666–669. arXiv : hep-th/9303048 . Бибкод : 1993PhRvL..71..666S . дои : 10.1103/PhysRevLett.71.666 . ПМИД 10055336 . S2CID 9329564 .
- ^ Каллауэй DJE (апрель 1996 г.). «Поверхностное натяжение, гидрофобность и черные дыры: энтропийная связь». Физ. Преподобный Е. 53 (4): 3738–3744. arXiv : cond-mat/9601111 . Бибкод : 1996PhRvE..53.3738C . дои : 10.1103/PhysRevE.53.3738 . ПМИД 9964684 . S2CID 7115890 .
- ^ Саркар, ТК; Салазар-Пальма, М.; Моколе, Эрик Л. (2008). «Взгляд на концепцию пропускной способности канала с точки зрения Максвелла» . Физика многоантенных систем и широкополосной обработки . Уайли. п. 162. ИСБН 978-0470190401 . Проверено 31 августа 2019 г.
- ^ Лайзер, Дэвид (1990). Космогенез: рост порядка во Вселенной . Издательство Оксфордского университета.
- ^ Чессон, Эрик Дж. (2001). Космическая эволюция: рост сложности природы . Издательство Гарвардского университета. ISBN 978-0-674-00342-2 .
- ^ Лайнвивер, Чарльз Х.; Дэвис, Пол К.В.; Русе, Майкл, ред. (2013). Сложность и Стрела времени . Издательство Кембриджского университета. ISBN 978-1-107-02725-1 .
- ^ Стенгер, Виктор Дж. (2007). Бог: Неудачная гипотеза . Книги Прометея. ISBN 978-1-59102-481-1 .
- ^ Бенджамин Гал-Ор (1987). Космология, физика и философия . Спрингер Верлаг. ISBN 978-0-387-96526-0 .
- ^ Альбрехт, Андреас (2004). «Космическая инфляция и Стрела времени» (PDF) . В Барроу, Джон Д .; Дэвис, Пол CW ; Харпер, Чарльз Л. (ред.). Наука и высшая реальность: от квантов к космосу . Кембридж, Великобритания: Издательство Кембриджского университета. arXiv : astro-ph/0210527 . Бибкод : 2002astro.ph.10527A . Проверено 28 июня 2017 г. В честь 90-летия Джона Уиллера.
- ^ Кливленд, Катлер Дж .; Рут, Матиас (1997). «Когда, где и насколько биофизические ограничения ограничивают экономический процесс? Обзор вклада Николаса Джорджеску-Рогена в экологическую экономику» . Экологическая экономика . 22 (3). Амстердам: Эльзевир : 203–223. дои : 10.1016/s0921-8009(97)00079-7 .
- ^ Дейли, Герман Э .; Фарли, Джошуа (2011). Экологическая экономика. Принципы и приложения (PDF содержит полную книгу) (2-е изд.). Вашингтон: Island Press. ISBN 978-1-59726-681-9 .
- ^ Шмитц, Джон Э.Дж. (2007). Второй закон жизни: энергия, технологии и будущее Земли, какой мы ее знаем (ссылка на научный блог автора, основанный на его учебнике) . Норвич: Издательство Уильяма Эндрю. ISBN 978-0-8155-1537-1 .
- ^ Эйрс, Роберт У. (2007). «О практических пределах замены» (PDF) . Экологическая экономика . 61 . Амстердам: Эльзевир : 115–128. doi : 10.1016/j.ecolecon.2006.02.011 . S2CID 154728333 .
- ^ Кершнер, Кристиан (2010). «Экономический спад роста против устойчивой экономики» (PDF) . Журнал чистого производства . 18 (6). Амстердам: Эльзевир : 544–551. Бибкод : 2010JCPro..18..544K . дои : 10.1016/j.jclepro.2009.10.019 .
- ^ Дейли, Герман Э. (2015). «Экономика для полного мира» . Научный американец . 293 (3): 100–7. doi : 10.1038/scientificamerican0905-100 . ПМИД 16121860 . S2CID 13441670 . Проверено 23 ноября 2016 г.
- Дэвид, Ковер (14 августа 2018 г.). «Энтропия – физическая величина Вселенной и нашей жизни» . stejfree.sk Архивировано из оригинала 27 мая 2022 года . Проверено 13 апреля 2022 г.
Дальнейшее чтение
[ редактировать ]- Адам, Герхард; Отто Хитмайр (1992). Теория тепла . Видег, Брауншвейг. ISBN 978-3-528-33311-9 .
- Аткинс, Питер; Хулио Де Паула (2006). Физическая химия (8-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-870072-2 .
- Байерляйн, Ральф (2003). Теплофизика . Издательство Кембриджского университета. ISBN 978-0-521-65838-6 .
- Бен-Наим , Арье (2007). Энтропия демистифицирована . Всемирная научная. ISBN 978-981-270-055-1 .
- Каллен, Герберт, Б. (2001). Термодинамика и введение в термостатистику (2-е изд.). Джон Уайли и сыновья. ISBN 978-0-471-86256-7 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - Чанг, Раймонд (1998). Химия (6-е изд.). Нью-Йорк: МакГроу Хилл. ISBN 978-0-07-115221-1 .
- Катнелл, Джон, Д.; Джонсон, Кеннет, Дж. (1998). Физика (4-е изд.). Джон Уайли и сыновья, Inc. ISBN 978-0-471-19113-1 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - Дагдейл, Дж. С. (1996). Энтропия и ее физический смысл (2-е изд.). Тейлор и Фрэнсис (Великобритания); КПР (США). ISBN 978-0-7484-0569-5 .
- Ферми, Энрико (1937). Термодинамика . Прентис Холл. ISBN 978-0-486-60361-2 .
- Гольдштейн, Мартин; Инге, Ф (1993). Холодильник и Вселенная . Издательство Гарвардского университета. ISBN 978-0-674-75325-9 .
- Гифтопулос, ЕП; ГП Беретта (2010). Термодинамика. Основы и приложения . Дувр. ISBN 978-0-486-43932-7 .
- Хаддад, Васим М.; Челлабойна, Виджай Сехар; Нерсесов, Сергей Георгиевич (2005). Термодинамика – подход динамических систем . Издательство Принстонского университета . ISBN 978-0-691-12327-1 .
- Джонсон, Эрик (2018). Тревога и уравнение: понимание энтропии Больцмана . Массачусетский технологический институт Пресс. ISBN 978-0-262-03861-4 .
- Кремер, Герберт; Чарльз Киттель (1980). Теплофизика (2-е изд.). Компания WH Freeman. ISBN 978-0-7167-1088-2 .
- Ламберт, Фрэнк Л.; [1]
- Мюллер-Кирстен, Харальд Дж.В. (2013). Основы статистической физики (2-е изд.). Сингапур: World Scientific. ISBN 978-981-4449-53-3 .
- Пенроуз, Роджер (2005). Дорога к реальности: Полное руководство по законам Вселенной . Нью-Йорк: А.А. Кнопф. ISBN 978-0-679-45443-4 .
- Рейф, Ф. (1965). Основы статистической и теплофизики . МакГроу-Хилл. ISBN 978-0-07-051800-1 .
- Шредер, Дэниел В. (2000). Введение в теплофизику . Нью-Йорк: Эддисон Уэсли Лонгман. ISBN 978-0-201-38027-9 .
- Сервей, Раймонд, А. (1992). Физика для ученых и инженеров . Серия Сондерса «Золотой субвзрыв». ISBN 978-0-03-096026-0 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - Шарп, Ким (2019). Энтропия и Дао счета: краткое введение в статистическую механику и второй закон термодинамики (SpringerBriefs in Physics). Спрингер Природа. ISBN 978-3030354596 .
- Spirax-Sarco Limited, Энтропия – базовое понимание. Учебник по таблицам энтропии для паровой техники.
- фон Байер; Ганс Кристиан (1998). Демон Максвелла: Почему тепло рассеивается, а время проходит . Случайный дом. ISBN 978-0-679-43342-2 .
Внешние ссылки
[ редактировать ]- «Энтропия» в Scholarpedia
- Энтропия и неравенство Клаузиуса , лекция MIT OCW, часть 5.60 «Термодинамика и кинетика», весна 2008 г.
- Энтропия и второй закон термодинамики - лекция по физике уровня A с «выводом» энтропии на основе цикла Карно.
- Академия Хана: лекции по энтропии, часть плейлиста по химии
- Мориарти, Филип; Меррифилд, Майкл (2009). «С-энтропия» . Шестьдесят символов . Брэди Харан из Ноттингемского университета .
- Открытие энтропии Адама Шульмана. Часовое видео, январь 2013 г.
- Второй закон термодинамики и энтропии - лекция Йельского университета OYC, часть Основы физики I (PHYS 200)















































































































