Lagrangian mechanics

Joseph-Louis Lagrange (1736–1813)

In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least action). It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, Mécanique analytique.

Lagrangian mechanics describes a mechanical system as a pair (M, L) consisting of a configuration space M and a smooth function ${\textstyle L}$ within that space called a Lagrangian. For many systems, L = T − V, where T and V are the kinetic and potential energy of the system, respectively.

The stationary action principle requires that the action functional of the system derived from L must remain at a stationary point (a maximum, minimum, or saddle) throughout the time evolution of the system. This constraint allows the calculation of the equations of motion of the system using Lagrange's equations.

Introduction

Bead constrained to move on a frictionless wire. The wire exerts a reaction force C on the bead to keep it on the wire. The non-constraint force N in this case is gravity. Notice the initial position of the bead on the wire can lead to different motions.

Simple pendulum. Since the rod is rigid, the position of the bob is constrained according to the equation f(x, y) = 0, the constraint force C is the tension in the rod. Again the non-constraint force N in this case is gravity.

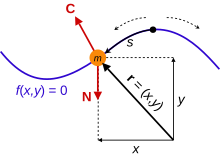
Suppose there exists a bead sliding around on a wire, or a swinging simple pendulum. If one tracks each of the massive objects (bead, pendulum bob) as a particle, calculation of the motion of the particle using Newtonian mechanics would require solving for the time-varying constraint force required to keep the particle in the constrained motion (reaction force exerted by the wire on the bead, or tension in the pendulum rod). For the same problem using Lagrangian mechanics, one looks at the path the particle can take and chooses a convenient set of independent generalized coordinates that completely characterize the possible motion of the particle. This choice eliminates the need for the constraint force to enter into the resultant system of equations. There are fewer equations since one is not directly calculating the influence of the constraint on the particle at a given moment.

For a wide variety of physical systems, if the size and shape of a massive object are negligible, it is a useful simplification to treat it as a point particle. For a system of N point particles with masses m₁, m₂, ..., m_N, each particle has a position vector, denoted r₁, r₂, ..., r_N. Cartesian coordinates are often sufficient, so r₁ = (x₁, y₁, z₁), r₂ = (x₂, y₂, z₂) and so on. In three-dimensional space, each position vector requires three coordinates to uniquely define the location of a point, so there are 3N coordinates to uniquely define the configuration of the system. These are all specific points in space to locate the particles; a general point in space is written r = (x, y, z). The velocity of each particle is how fast the particle moves along its path of motion, and is the time derivative of its position, thus$$\mathbf {v} _{1}={\frac {d\mathbf {r} _{1}}{dt}},\mathbf {v} _{2}={\frac {d\mathbf {r} _{2}}{dt}},\ldots ,\mathbf {v} _{N}={\frac {d\mathbf {r} _{N}}{dt}}.$$In Newtonian mechanics, the equations of motion are given by Newton's laws. The second law "net force equals mass times acceleration",$$\sum \mathbf {F} =m{\frac {d^{2}\mathbf {r} }{dt^{2}}},$$applies to each particle. For an N-particle system in 3 dimensions, there are 3N second-order ordinary differential equations in the positions of the particles to solve for.

Lagrangian

Instead of forces, Lagrangian mechanics uses the energies in the system. The central quantity of Lagrangian mechanics is the Lagrangian, a function which summarizes the dynamics of the entire system. Overall, the Lagrangian has units of energy, but no single expression for all physical systems. Any function which generates the correct equations of motion, in agreement with physical laws, can be taken as a Lagrangian. It is nevertheless possible to construct general expressions for large classes of applications. The non-relativistic Lagrangian for a system of particles in the absence of an electromagnetic field is given by$$L=T-V,$$where$$T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}v_{k}^{2}$$is the total kinetic energy of the system, equaling the sum Σ of the kinetic energies of the $N$ particles. Each particle labeled $k$ has mass $m_{k},$ and v_k² = v_k · v_k is the magnitude squared of its velocity, equivalent to the dot product of the velocity with itself.

Kinetic energy T = T(v₁, v₂, ...) is the energy of the system's motion and is a function only of the velocities v_k, not the positions r_k, nor time t, so T = T(v₁, v₂, ...).

V, the potential energy of the system, reflects the energy of interaction between the particles, i.e. how much energy any one particle has due to all the others, together with any external influences. For conservative forces (e.g. Newtonian gravity), it is a function of the position vectors of the particles only, so V = V(r₁, r₂, ...). For those non-conservative forces which can be derived from an appropriate potential (e.g. electromagnetic potential), the velocities will appear also, V = V(r₁, r₂, ..., v₁, v₂, ...). If there is some external field or external driving force changing with time, the potential changes with time, so most generally V = V(r₁, r₂, ..., v₁, v₂, ..., t).

As already noted, this form of L is applicable to many important classes of system, but not everywhere. For relativistic Lagrangian mechanics it must be replaced as a whole by a function consistent with special or general relativity. Where a magnetic field is present, the expression for the potential energy needs restating. And for dissipative forces (e.g., friction), another function must be introduced alongside L.

One or more of the particles may each be subject to one or more holonomic constraints; such a constraint is described by an equation of the form f(r, t) = 0. If the number of constraints in the system is C, then each constraint has an equation f₁(r, t) = 0, f₂(r, t) = 0, ..., f_C(r, t) = 0, each of which could apply to any of the particles. If particle k is subject to constraint i, then f_i(r_k, t) = 0. At any instant of time, the coordinates of a constrained particle are linked together and not independent. The constraint equations determine the allowed paths the particles can move along, but not where they are or how fast they go at every instant of time. Nonholonomic constraints depend on the particle velocities, accelerations, or higher derivatives of position. Lagrangian mechanics can only be applied to systems whose constraints, if any, are all holonomic. Three examples of nonholonomic constraints are: when the constraint equations are nonintegrable, when the constraints have inequalities, or with complicated non-conservative forces like friction. Nonholonomic constraints require special treatment, and one may have to revert to Newtonian mechanics or use other methods.

If T or V or both depend explicitly on time due to time-varying constraints or external influences, the Lagrangian L(r₁, r₂, ... v₁, v₂, ... t) is explicitly time-dependent. If neither the potential nor the kinetic energy depend on time, then the Lagrangian L(r₁, r₂, ... v₁, v₂, ...) is explicitly independent of time. In either case, the Lagrangian always has implicit time dependence through the generalized coordinates.

With these definitions, Lagrange's equations of the first kind are

Lagrange's equations (first kind)

${\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,$

where k = 1, 2, ..., N labels the particles, there is a Lagrange multiplier λ_i for each constraint equation f_i, and$${\frac {\partial }{\partial \mathbf {r} _{k}}}\equiv \left({\frac {\partial }{\partial x_{k}}},{\frac {\partial }{\partial y_{k}}},{\frac {\partial }{\partial z_{k}}}\right),\quad {\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}\equiv \left({\frac {\partial }{\partial {\dot {x}}_{k}}},{\frac {\partial }{\partial {\dot {y}}_{k}}},{\frac {\partial }{\partial {\dot {z}}_{k}}}\right)$$are each shorthands for a vector of partial derivatives ∂/∂ with respect to the indicated variables (not a derivative with respect to the entire vector). Each overdot is a shorthand for a time derivative. This procedure does increase the number of equations to solve compared to Newton's laws, from 3N to 3N + C, because there are 3N coupled second-order differential equations in the position coordinates and multipliers, plus C constraint equations. However, when solved alongside the position coordinates of the particles, the multipliers can yield information about the constraint forces. The coordinates do not need to be eliminated by solving the constraint equations.

In the Lagrangian, the position coordinates and velocity components are all independent variables, and derivatives of the Lagrangian are taken with respect to these separately according to the usual differentiation rules (e.g. the partial derivative of L with respect to the z velocity component of particle 2, defined by v_z,2 = dz₂/dt, is just ∂L/∂v_z,2; no awkward chain rules or total derivatives need to be used to relate the velocity component to the corresponding coordinate z₂).

In each constraint equation, one coordinate is redundant because it is determined from the other coordinates. The number of independent coordinates is therefore n = 3N − C. We can transform each position vector to a common set of n generalized coordinates, conveniently written as an n-tuple q = (q₁, q₂, ... q_n), by expressing each position vector, and hence the position coordinates, as functions of the generalized coordinates and time:$$\mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} ,t)={\big (}x_{k}(\mathbf {q} ,t),y_{k}(\mathbf {q} ,t),z_{k}(\mathbf {q} ,t),t{\big )}.$$

The vector q is a point in the configuration space of the system. The time derivatives of the generalized coordinates are called the generalized velocities, and for each particle the transformation of its velocity vector, the total derivative of its position with respect to time, is$${\dot {q}}_{j}={\frac {\mathrm {d} q_{j}}{\mathrm {d} t}},\quad \mathbf {v} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}+{\frac {\partial \mathbf {r} _{k}}{\partial t}}.$$

Given this v_k, the kinetic energy in generalized coordinates depends on the generalized velocities, generalized coordinates, and time if the position vectors depend explicitly on time due to time-varying constraints, so $T=T(\mathbf {q} ,{\dot {\mathbf {q} }},t).$

With these definitions, the Euler–Lagrange equations, or Lagrange's equations of the second kind

Lagrange's equations (second kind)

${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)={\frac {\partial L}{\partial q_{j}}}$

are mathematical results from the calculus of variations, which can also be used in mechanics. Substituting in the Lagrangian L(q, dq/dt, t) gives the equations of motion of the system. The number of equations has decreased compared to Newtonian mechanics, from 3N to n = 3N − C coupled second-order differential equations in the generalized coordinates. These equations do not include constraint forces at all, only non-constraint forces need to be accounted for.

Although the equations of motion include partial derivatives, the results of the partial derivatives are still ordinary differential equations in the position coordinates of the particles. The total time derivative denoted d/dt often involves implicit differentiation. Both equations are linear in the Lagrangian, but generally are nonlinear coupled equations in the coordinates.

From Newtonian to Lagrangian mechanics

Newton's laws

Isaac Newton (1642–1727)

For simplicity, Newton's laws can be illustrated for one particle without much loss of generality (for a system of N particles, all of these equations apply to each particle in the system). The equation of motion for a particle of constant mass m is Newton's second law of 1687, in modern vector notation$$\mathbf {F} =m\mathbf {a} ,$$where a is its acceleration and F the resultant force acting on it. Where the mass is varying, the equation needs to be generalised to take the time derivative of the momentum. In three spatial dimensions, this is a system of three coupled second-order ordinary differential equations to solve, since there are three components in this vector equation. The solution is the position vector r of the particle at time t, subject to the initial conditions of r and v when t = 0.

Newton's laws are easy to use in Cartesian coordinates, but Cartesian coordinates are not always convenient, and for other coordinate systems the equations of motion can become complicated. In a set of curvilinear coordinates ξ = (ξ¹, ξ², ξ³), the law in tensor index notation is the "Lagrangian form"$$F^{a}=m\left({\frac {\mathrm {d} ^{2}\xi ^{a}}{\mathrm {d} t^{2}}}+\Gamma ^{a}{}_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}\right)=g^{ak}\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\xi }}^{k}}}-{\frac {\partial T}{\partial \xi ^{k}}}\right),\quad {\dot {\xi }}^{a}\equiv {\frac {\mathrm {d} \xi ^{a}}{\mathrm {d} t}},$$where F^a is the a-th contravariant component of the resultant force acting on the particle, Γ^a_bc are the Christoffel symbols of the second kind,$$T={\frac {1}{2}}mg_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}$$is the kinetic energy of the particle, and g_bc the covariant components of the metric tensor of the curvilinear coordinate system. All the indices a, b, c, each take the values 1, 2, 3. Curvilinear coordinates are not the same as generalized coordinates.

It may seem like an overcomplication to cast Newton's law in this form, but there are advantages. The acceleration components in terms of the Christoffel symbols can be avoided by evaluating derivatives of the kinetic energy instead. If there is no resultant force acting on the particle, F = 0, it does not accelerate, but moves with constant velocity in a straight line. Mathematically, the solutions of the differential equation are geodesics, the curves of extremal length between two points in space (these may end up being minimal, that is the shortest paths, but not necessarily). In flat 3D real space the geodesics are simply straight lines. So for a free particle, Newton's second law coincides with the geodesic equation and states that free particles follow geodesics, the extremal trajectories it can move along. If the particle is subject to forces F ≠ 0, the particle accelerates due to forces acting on it and deviates away from the geodesics it would follow if free. With appropriate extensions of the quantities given here in flat 3D space to 4D curved spacetime, the above form of Newton's law also carries over to Einstein's general relativity, in which case free particles follow geodesics in curved spacetime that are no longer "straight lines" in the ordinary sense.

However, we still need to know the total resultant force F acting on the particle, which in turn requires the resultant non-constraint force N plus the resultant constraint force C,$$\mathbf {F} =\mathbf {C} +\mathbf {N} .$$

The constraint forces can be complicated, since they generally depend on time. Also, if there are constraints, the curvilinear coordinates are not independent but related by one or more constraint equations.

The constraint forces can either be eliminated from the equations of motion, so only the non-constraint forces remain, or included by including the constraint equations in the equations of motion.

D'Alembert's principle

Jean d'Alembert (1717—1783)

One degree of freedom.

Two degrees of freedom.

Constraint force C and virtual displacement δr for a particle of mass m confined to a curve. The resultant non-constraint force is N.

A fundamental result in analytical mechanics is D'Alembert's principle, introduced in 1708 by Jacques Bernoulli to understand static equilibrium, and developed by D'Alembert in 1743 to solve dynamical problems. The principle asserts for N particles the virtual work, i.e. the work along a virtual displacement, δr_k, is zero:$$\sum _{k=1}^{N}(\mathbf {N} _{k}+\mathbf {C} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0.$$

The virtual displacements, δr_k, are by definition infinitesimal changes in the configuration of the system consistent with the constraint forces acting on the system at an instant of time, i.e. in such a way that the constraint forces maintain the constrained motion. They are not the same as the actual displacements in the system, which are caused by the resultant constraint and non-constraint forces acting on the particle to accelerate and move it. Virtual work is the work done along a virtual displacement for any force (constraint or non-constraint).

Since the constraint forces act perpendicular to the motion of each particle in the system to maintain the constraints, the total virtual work by the constraint forces acting on the system is zero:$$\sum _{k=1}^{N}\mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0,$$so that$$\sum _{k=1}^{N}(\mathbf {N} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0.$$

Thus D'Alembert's principle allows us to concentrate on only the applied non-constraint forces, and exclude the constraint forces in the equations of motion. The form shown is also independent of the choice of coordinates. However, it cannot be readily used to set up the equations of motion in an arbitrary coordinate system since the displacements δr_k might be connected by a constraint equation, which prevents us from setting the N individual summands to 0. We will therefore seek a system of mutually independent coordinates for which the total sum will be 0 if and only if the individual summands are 0. Setting each of the summands to 0 will eventually give us our separated equations of motion.

Equations of motion from D'Alembert's principle

If there are constraints on particle k, then since the coordinates of the position r_k = (x_k, y_k, z_k) are linked together by a constraint equation, so are those of the virtual displacements δr_k = (δx_k, δy_k, δz_k). Since the generalized coordinates are independent, we can avoid the complications with the δr_k by converting to virtual displacements in the generalized coordinates. These are related in the same form as a total differential,$$\delta \mathbf {r} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}.$$

There is no partial time derivative with respect to time multiplied by a time increment, since this is a virtual displacement, one along the constraints in an instant of time.

The first term in D'Alembert's principle above is the virtual work done by the non-constraint forces N_k along the virtual displacements δr_k, and can without loss of generality be converted into the generalized analogues by the definition of generalized forces$$Q_{j}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}},$$so that$$\sum _{k=1}^{N}\mathbf {N} _{k}\cdot \delta \mathbf {r} _{k}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot \sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}=\sum _{j=1}^{n}Q_{j}\delta q_{j}.$$

This is half of the conversion to generalized coordinates. It remains to convert the acceleration term into generalized coordinates, which is not immediately obvious. Recalling the Lagrange form of Newton's second law, the partial derivatives of the kinetic energy with respect to the generalized coordinates and velocities can be found to give the desired result:$$\sum _{k=1}^{N}m_{k}\mathbf {a} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}.$$

Now D'Alembert's principle is in the generalized coordinates as required,$$\sum _{j=1}^{n}\left[Q_{j}-\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}=0,$$and since these virtual displacements δq_j are independent and nonzero, the coefficients can be equated to zero, resulting in Lagrange's equations or the generalized equations of motion,$$Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}$$

These equations are equivalent to Newton's laws for the non-constraint forces. The generalized forces in this equation are derived from the non-constraint forces only – the constraint forces have been excluded from D'Alembert's principle and do not need to be found. The generalized forces may be non-conservative, provided they satisfy D'Alembert's principle.

Euler–Lagrange equations and Hamilton's principle

As the system evolves, q traces a path through configuration space (only some are shown). The path taken by the system (red) has a stationary action (δS = 0) under small changes in the configuration of the system (δq).

For a non-conservative force which depends on velocity, it may be possible to find a potential energy function V that depends on positions and velocities. If the generalized forces Q_i can be derived from a potential V such that$$Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}},$$equating to Lagrange's equations and defining the Lagrangian as L = T − V obtains Lagrange's equations of the second kind or the Euler–Lagrange equations of motion$${\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}=0.$$

However, the Euler–Lagrange equations can only account for non-conservative forces if a potential can be found as shown. This may not always be possible for non-conservative forces, and Lagrange's equations do not involve any potential, only generalized forces; therefore they are more general than the Euler–Lagrange equations.

The Euler–Lagrange equations also follow from the calculus of variations. The variation of the Lagrangian is$$\delta L=\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta {\dot {q}}_{j}\right),\quad \delta {\dot {q}}_{j}\equiv \delta {\frac {\mathrm {d} q_{j}}{\mathrm {d} t}}\equiv {\frac {\mathrm {d} (\delta q_{j})}{\mathrm {d} t}},$$which has a form similar to the total differential of L, but the virtual displacements and their time derivatives replace differentials, and there is no time increment in accordance with the definition of the virtual displacements. An integration by parts with respect to time can transfer the time derivative of δq_j to the ∂L/∂(dq_j/dt), in the process exchanging d(δq_j)/dt for δq_j, allowing the independent virtual displacements to be factorized from the derivatives of the Lagrangian,$${\begin{aligned}\int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t&=\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)\,\mathrm {d} t\\&=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,\mathrm {d} t.\end{aligned}}$$

Now, if the condition δq_j(t₁) = δq_j(t₂) = 0 holds for all j, the terms not integrated are zero. If in addition the entire time integral of δL is zero, then because the δq_j are independent, and the only way for a definite integral to be zero is if the integrand equals zero, each of the coefficients of δq_j must also be zero. Then we obtain the equations of motion. This can be summarized by Hamilton's principle:$$\int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=0.$$

The time integral of the Lagrangian is another quantity called the action, defined as$$S=\int _{t_{1}}^{t_{2}}L\,\mathrm {d} t,$$which is a functional; it takes in the Lagrangian function for all times between t₁ and t₂ and returns a scalar value. Its dimensions are the same as [angular momentum], [energy]·[time], or [length]·[momentum]. With this definition Hamilton's principle is$$\delta S=0.$$

Instead of thinking about particles accelerating in response to applied forces, one might think of them picking out the path with a stationary action, with the end points of the path in configuration space held fixed at the initial and final times. Hamilton's principle is one of several action principles.

Historically, the idea of finding the shortest path a particle can follow subject to a force motivated the first applications of the calculus of variations to mechanical problems, such as the Brachistochrone problem solved by Jean Bernoulli in 1696, as well as Leibniz, Daniel Bernoulli, L'Hôpital around the same time, and Newton the following year. Newton himself was thinking along the lines of the variational calculus, but did not publish. These ideas in turn lead to the variational principles of mechanics, of Fermat, Maupertuis, Euler, Hamilton, and others.

Hamilton's principle can be applied to nonholonomic constraints if the constraint equations can be put into a certain form, a linear combination of first order differentials in the coordinates. The resulting constraint equation can be rearranged into first order differential equation. This will not be given here.

Lagrange multipliers and constraints

The Lagrangian L can be varied in the Cartesian r_k coordinates, for N particles,$$\int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0.$$

Hamilton's principle is still valid even if the coordinates L is expressed in are not independent, here r_k, but the constraints are still assumed to be holonomic. As always the end points are fixed δr_k(t₁) = δr_k(t₂) = 0 for all k. What cannot be done is to simply equate the coefficients of δr_k to zero because the δr_k are not independent. Instead, the method of Lagrange multipliers can be used to include the constraints. Multiplying each constraint equation f_i(r_k, t) = 0 by a Lagrange multiplier λ_i for i = 1, 2, ..., C, and adding the results to the original Lagrangian, gives the new Lagrangian$$L'=L(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,{\dot {\mathbf {r} }}_{1},{\dot {\mathbf {r} }}_{2},\ldots ,t)+\sum _{i=1}^{C}\lambda _{i}(t)f_{i}(\mathbf {r} _{k},t).$$

The Lagrange multipliers are arbitrary functions of time t, but not functions of the coordinates r_k, so the multipliers are on equal footing with the position coordinates. Varying this new Lagrangian and integrating with respect to time gives$$\int _{t_{1}}^{t_{2}}\delta L'\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0.$$

The introduced multipliers can be found so that the coefficients of δr_k are zero, even though the r_k are not independent. The equations of motion follow. From the preceding analysis, obtaining the solution to this integral is equivalent to the statement$${\frac {\partial L'}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\mathbf {r} }}_{k}}}=0\quad \Rightarrow \quad {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,$$which are Lagrange's equations of the first kind. Also, the λ_i Euler-Lagrange equations for the new Lagrangian return the constraint equations$${\frac {\partial L'}{\partial \lambda _{i}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\lambda }}_{i}}}=0\quad \Rightarrow \quad f_{i}(\mathbf {r} _{k},t)=0.$$

For the case of a conservative force given by the gradient of some potential energy V, a function of the r_k coordinates only, substituting the Lagrangian L = T − V gives$$\underbrace {{\frac {\partial T}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\mathbf {r} }}_{k}}}} _{-\mathbf {F} _{k}}+\underbrace {-{\frac {\partial V}{\partial \mathbf {r} _{k}}}} _{\mathbf {N} _{k}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,$$and identifying the derivatives of kinetic energy as the (negative of the) resultant force, and the derivatives of the potential equaling the non-constraint force, it follows the constraint forces are$$\mathbf {C} _{k}=\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}},$$thus giving the constraint forces explicitly in terms of the constraint equations and the Lagrange multipliers.

Properties of the Lagrangian

Non-uniqueness

The Lagrangian of a given system is not unique. A Lagrangian L can be multiplied by a nonzero constant a and shifted by an arbitrary constant b, and the new Lagrangian L′ = aL + b will describe the same motion as L. If one restricts as above to trajectories q over a given time interval [t_st, t_fin]} and fixed end points P_st = q(t_st) and P_fin = q(t_fin), then two Lagrangians describing the same system can differ by the "total time derivative" of a function f(q, t):$$L'(\mathbf {q} ,{\dot {\mathbf {q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t)+{\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}},$$where ${\textstyle {\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}}}$ means ${\textstyle {\frac {\partial f(\mathbf {q} ,t)}{\partial t}}+\sum _{i}{\frac {\partial f(\mathbf {q} ,t)}{\partial q_{i}}}{\dot {q}}_{i}.}$

Both Lagrangians L and L′ produce the same equations of motion since the corresponding actions S and S′ are related via$${\begin{aligned}S'[\mathbf {q} ]&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L'(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt\\&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt+\int _{t_{\text{st}}}^{t_{\text{fin}}}{\frac {\mathrm {d} f(\mathbf {q} (t),t)}{\mathrm {d} t}}\,dt\\&=S[\mathbf {q} ]+f(P_{\text{fin}},t_{\text{fin}})-f(P_{\text{st}},t_{\text{st}}),\end{aligned}}$$with the last two components f(P_fin, t_fin) and f(P_st, t_st) independent of q.

Invariance under point transformations

Given a set of generalized coordinates q, if we change these variables to a new set of generalized coordinates Q according to a point transformation Q = Q(q, t) which is invertible as q = q(Q, t), the new Lagrangian L′ is a function of the new coordinates$$L'(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} (\mathbf {Q} ,t),{\dot {\mathbf {q} }}(\mathbf {Q} ,{\dot {\mathbf {Q} }},t),t),$$and by the chain rule for partial differentiation, Lagrange's equations are invariant under this transformation;$${\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {Q}}_{i}}}={\frac {\partial L'}{\partial Q_{i}}}.$$

This may simplify the equations of motion.

Proof

For a coordinate transformation $Q_{i}=Q_{i}(\mathbf {q} ,t)$, we have$$d{Q_{i}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}d{q_{k}}+{\frac {\partial Q_{k}}{\partial t}}dt,$$which implies that ${\dot {Q_{i}}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial Q_{k}}{\partial t}}(\mathbf {q} ,t)$ which implies that ${\frac {\partial {\dot {Q_{i}}}}{\partial {\dot {q}}_{k}}}={\frac {\partial Q_{i}}{\partial q_{k}}}$.

It also follows that:$${\frac {\partial {\dot {Q_{i}}}}{\partial q_{j}}}=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{j}\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial q_{j}\partial t}}(\mathbf {q} ,t)$$and similarly:$${\frac {d}{dt}}\left({\frac {\partial {Q_{i}}}{\partial q_{j}}}\right)=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{k}\partial q_{j}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial t\partial q_{j}}}(\mathbf {q} ,t)$$which imply that ${\frac {d}{dt}}\left({\frac {\partial Q_{i}}{\partial q_{k}}}\right)={\frac {\partial {\dot {Q}}_{i}}{\partial q_{k}}}$. The two derived relations can be employed in the proof.

Starting from Euler Lagrange equations in initial set of generalized coordinates, we have:$${\begin{aligned}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial q_{i}}}=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial Q_{k}}{\partial {q}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {q}_{i}}}\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}+{\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial Q_{k}}{\partial q_{i}}}\right)\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right)-{\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial Q_{k}}{\partial q_{i}}}=0\\\end{aligned}}$$

Since the transformation from $q\rightarrow Q$ is invertible, it follows that the form of the Euler-Lagrange equation is invariant i.e.,$${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {Q}}_{i}}}-{\frac {{\partial }L}{\partial Q_{i}}}=0.$$

Cyclic coordinates and conserved momenta

An important property of the Lagrangian is that conserved quantities can easily be read off from it. The generalized momentum "canonically conjugate to" the coordinate q_i is defined by$$p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.$$

If the Lagrangian L does not depend on some coordinate q_i, it follows immediately from the Euler–Lagrange equations that$${\dot {p}}_{i}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\frac {\partial L}{\partial q_{i}}}=0$$and integrating shows the corresponding generalized momentum equals a constant, a conserved quantity. This is a special case of Noether's theorem. Such coordinates are called "cyclic" or "ignorable".

For example, a system may have a Lagrangian$$L(r,\theta ,{\dot {s}},{\dot {z}},{\dot {r}},{\dot {\theta }},{\dot {\phi }},t),$$where r and z are lengths along straight lines, s is an arc length along some curve, and θ and φ are angles. Notice z, s, and φ are all absent in the Lagrangian even though their velocities are not. Then the momenta$$p_{z}={\frac {\partial L}{\partial {\dot {z}}}},\quad p_{s}={\frac {\partial L}{\partial {\dot {s}}}},\quad p_{\phi }={\frac {\partial L}{\partial {\dot {\phi }}}},$$are all conserved quantities. The units and nature of each generalized momentum will depend on the corresponding coordinate; in this case p_z is a translational momentum in the z direction, p_s is also a translational momentum along the curve s is measured, and p_φ is an angular momentum in the plane the angle φ is measured in. However complicated the motion of the system is, all the coordinates and velocities will vary in such a way that these momenta are conserved.

Energy

Given a Lagrangian $L,$ the Hamiltonian of the corresponding mechanical system is, by definition,$$H={\biggl (}\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}{\biggr )}-L.$$This quantity will be equivalent to energy if the generalized coordinates are natural coordinates, i.e., they have no explicit time dependence when expressing position vector: $\mathbf {r} =\mathbf {r} (q_{1},\cdots ,q_{n})$. From:$$T={\frac {m}{2}}v^{2}={\frac {m}{2}}\sum _{i,j}\left({\frac {\partial {\vec {r}}}{\partial q_{i}}}{\dot {q}}_{i}\right)\cdot \left({\frac {\partial {\vec {r}}}{\partial q_{j}}}{\dot {q}}_{j}\right)={\frac {m}{2}}\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}$$$$\sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial L}{\partial {\dot {q}}_{k}}}=\sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial T}{\partial {\dot {q}}_{k}}}={\frac {m}{2}}\left(2\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}\right)=2T$$$$H=\left(\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)-L=2T-(T-V)=T+V=E$$where $a_{ij}={\frac {\partial \mathbf {r} }{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} }{\partial q_{j}}}$ is a symmetric matrix that is defined for the derivation.

Invariance under coordinate transformations

At every time instant t, the energy is invariant under configuration space coordinate changes q → Q, i.e. (using natural coordinates)$$E(\mathbf {q} ,{\dot {\mathbf {q} }},t)=E(\mathbf {Q} ,{\dot {\mathbf {Q} }},t).$$Besides this result, the proof below shows that, under such change of coordinates, the derivatives $\partial L/\partial {\dot {q}}_{i}$ change as coefficients of a linear form.

Proof

For a coordinate transformation Q = F(q), we have$$d\mathbf {Q} =F_{*}(\mathbf {q} )d\mathbf {q} ,$$where $F_{*}(\mathbf {q} )$ is the tangent map of the vector space$$\left\{\sum _{i=1}^{n}{\dot {q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial q_{i}}}\right|_{\mathbf {q} }\right)\ {\biggl |}\ {\dot {q}}_{i}\in \mathbb {R} \right\}$$to the vector space$$\left\{\sum _{i=1}^{n}{\dot {Q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial Q_{i}}}\right|_{F(\mathbf {q} )}\right)\ {\biggl |}\ {\dot {Q}}_{i}\in \mathbb {R} \right\},$$and$$\textstyle F_{*}(\mathbf {q} )=\left(\left.{\frac {\partial F_{i}}{\partial q_{j}}}\right|_{\mathbf {q} }\right)_{i,j=1}^{n}$$is the Jacobian. In the coordinates ${\dot {q}}_{i}$ and ${\dot {Q}}_{i},$ the previous formula for $d\mathbf {Q}$ has the form ${\dot {\mathbf {Q} }}=F_{*}(\mathbf {q} ){\dot {\mathbf {q} }}.$ After differentiation involving the product rule,$$d{\dot {\mathbf {Q} }}=G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} +F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }},$$where$${\begin{aligned}G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} &\,{\stackrel {\text{def}}{=}}\,d(F_{*}(\mathbf {q} )){\dot {\mathbf {q} }}=\left(\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i,j=1}^{n}{\dot {\mathbf {q} }}=\left(\sum _{j=1}^{n}{\dot {q}}_{j}\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i=1,\ldots ,n}^{T}\\&=\left(\sum _{k=1}^{n}dq_{k}\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i=1,\ldots ,n}^{T}=\left(\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i,k=1}^{n}d\mathbf {q} .\end{aligned}}$$

In vector notation,$${\begin{aligned}dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)&={\frac {\partial L}{\partial \mathbf {Q} }}d\mathbf {Q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}d{\dot {\mathbf {Q} }}+{\frac {\partial L}{\partial t}}dt\\&=\left({\frac {\partial L}{\partial \mathbf {Q} }}F_{*}(\mathbf {q} )+{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}G(\mathbf {q} ,{\dot {\mathbf {q} }})\right)d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}.\end{aligned}}$$

On the other hand,$$dL(\mathbf {q} ,{\dot {\mathbf {q} }},t)={\frac {\partial L}{\partial \mathbf {q} }}d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}dt.$$

It was mentioned earlier that Lagrangians do not depend on the choice of configuration space coordinates, i.e. $L(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t).$ One implication of this is that $dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=dL(\mathbf {q} ,{\dot {\mathbf {q} }},t),$ and$${\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )={\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.$$This demonstrates that, for each $\mathbf {q} ,$ ${\dot {\mathbf {q} }},$ and $t,$ $\textstyle \sum \limits _{i=1}^{n}{\frac {\partial L}{\partial {\dot {q}}_{i}}}d{\dot {q}}_{i}$ is a well-defined linear form whose coefficients $\textstyle {\frac {\partial L}{\partial {\dot {q}}_{i}}}$ are contravariant 1-tensors. Applying both sides of the equation to ${\dot {\mathbf {q} }}$ and using the above formula for ${\dot {\mathbf {Q} }}$ yields$${\dot {\mathbf {Q} }}{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}={\dot {\mathbf {q} }}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.$$The invariance of the energy $E$ follows.

Conservation

In Lagrangian mechanics, the system is closed if and only if its Lagrangian $L$ does not explicitly depend on time. The energy conservation law states that the energy $E$ of a closed system is an integral of motion.

More precisely, let q = q(t) be an extremal. (In other words, q satisfies the Euler–Lagrange equations). Taking the total time-derivative of L along this extremal and using the EL equations leads to$${\begin{aligned}{\frac {dL}{dt}}&={\dot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}+{\frac {\partial L}{\partial t}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\right){\dot {\mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}-{\dot {L}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\mathbf {\dot {q}} -L\right)={\frac {dH}{dt}}\end{aligned}}$$

If the Lagrangian L does not explicitly depend on time, then ∂L/∂t = 0, then H does not vary with time evolution of particle, indeed, an integral of motion, meaning that$$H(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)={\text{constant of time}}.$$Hence, if the chosen coordinates were natural coordinates, the energy is conserved.

Kinetic and potential energies

Under all these circumstances, the constant$$E=T+V$$is the total energy of the system. The kinetic and potential energies still change as the system evolves, but the motion of the system will be such that their sum, the total energy, is constant. This is a valuable simplification, since the energy E is a constant of integration that counts as an arbitrary constant for the problem, and it may be possible to integrate the velocities from this energy relation to solve for the coordinates.

Mechanical similarity

Main article: Mechanical similarity

If the potential energy is a homogeneous function of the coordinates and independent of time, and all position vectors are scaled by the same nonzero constant α, r_k′ = αr_k, so that$$V(\alpha \mathbf {r} _{1},\alpha \mathbf {r} _{2},\ldots ,\alpha \mathbf {r} _{N})=\alpha ^{N}V(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})$$and time is scaled by a factor β, t′ = βt, then the velocities v_k are scaled by a factor of α/β and the kinetic energy T by (α/β)². The entire Lagrangian has been scaled by the same factor if$${\frac {\alpha ^{2}}{\beta ^{2}}}=\alpha ^{N}\quad \Rightarrow \quad \beta =\alpha ^{1-{\frac {N}{2}}}.$$

Поскольку длины и времена масштабированы, траектории частиц в системе следуют геометрически схожим путям, различающимся по размеру. Длина l, пройденная за время t по исходной траектории, соответствует новой длине l ′, пройденной за время t ′ по новой траектории, определяемой соотношениями $${\frac {t'}{t}}=\left({\frac {l'}{l}}\right)^{1-{\frac {N}{2}}}.$$

Взаимодействующие частицы

Для данной системы, если две подсистемы A и B не взаимодействуют, лагранжиан L всей системы представляет собой сумму лагранжианов L _A и L _B для подсистем: $$L=L_{A}+L_{B}.$$

Если они взаимодействуют, это невозможно. В некоторых ситуациях можно разделить лагранжиан системы L на сумму невзаимодействующих лагранжианов плюс еще один лагранжиан L _AB, содержащий информацию о взаимодействии: $$L=L_{A}+L_{B}+L_{AB}.$$

Это может быть физически мотивировано тем, что невзаимодействующие лагранжианы представляют собой только кинетические энергии, тогда как лагранжиан взаимодействия представляет собой полную потенциальную энергию системы. Кроме того, в предельном случае незначительного взаимодействия L _AB стремится к нулю, что приводит к описанному выше случаю невзаимодействия.

Распространение на более чем две невзаимодействующие подсистемы является простым: общий лагранжиан представляет собой сумму отдельных лагранжианов для каждой подсистемы. Если есть взаимодействия, то можно добавить лагранжианы взаимодействия.

Следствия сингулярных лагранжианов

Из уравнений Эйлера-Лагранжа следует, что: $${\begin{aligned}&{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0\\&{\frac {\partial ^{2}L}{\partial q_{j}\partial {\dot {q}}_{i}}}{\frac {dq_{j}}{dt}}+{\frac {\partial ^{2}L}{\partial {\dot {q}}_{j}\partial {\dot {q}}_{i}}}{\frac {d{\dot {q}}_{j}}{dt}}+{\frac {\partial L}{\partial t}}-{\frac {\partial L}{\partial q_{i}}}=0\\&\sum _{j}W_{ij}(q,{\dot {q}},t){\ddot {q}}_{j}={\frac {\partial L}{\partial q_{i}}}-{\frac {\partial L}{\partial t}}-\sum _{j}{\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial q_{j}}}{\dot {q}}_{j},\\\end{aligned}}$$

где матрица определяется как $W_{ij}={\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}$. Если матрица $W$ не является сингулярным, приведенные выше уравнения можно решить, чтобы представить ${\ddot {q}}$ как функция $({\dot {q}},q,t)$. Если матрица необратима, невозможно представить все ${\ddot {q}}$как функция $({\dot {q}},q,t)$ но также гамильтоновы уравнения движения не примут стандартную форму.

Примеры

Следующие примеры применяют уравнения Лагранжа второго рода к механическим задачам.

Консервативная сила

Частица массы m движется под действием консервативной силы, возникающей из градиента ∇ скалярного потенциала , $$\mathbf {F} =-{\boldsymbol {\nabla }}V(\mathbf {r} ).$$

Если частиц больше, то в соответствии с приведенными выше результатами полная кинетическая энергия представляет собой сумму по всем кинетическим энергиям частиц, а потенциал является функцией всех координат.

Декартовы координаты

Лагранжиан частицы можно записать $$L(x,y,z,{\dot {x}},{\dot {y}},{\dot {z}})={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})-V(x,y,z).$$

Уравнения движения частицы находятся применением уравнения Эйлера–Лагранжа для x координаты $${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)={\frac {\partial L}{\partial x}},$$с деривативами $${\frac {\partial L}{\partial x}}=-{\frac {\partial V}{\partial x}},\quad {\frac {\partial L}{\partial {\dot {x}}}}=m{\dot {x}},\quad {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=m{\ddot {x}},$$следовательно $$m{\ddot {x}}=-{\frac {\partial V}{\partial x}},$$и аналогично для координат y и z . Собирая уравнения в векторную форму, находим $$m{\ddot {\mathbf {r} }}=-{\boldsymbol {\nabla }}V$$что является вторым законом движения Ньютона для частицы, на которую действует консервативная сила.

Полярные координаты в 2D и 3D

Используя сферические координаты ( r , θ , φ ) , обычно используемые в физике (конвенция ISO 80000-2: 2019), где r — радиальное расстояние до начала координат, θ — полярный угол (также известный как широта, зенитный угол, нормальный угол). , или угол наклона), а φ — азимутальный угол, лагранжиан для центрального потенциала равен $$L={\frac {m}{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2})-V(r).$$Итак, в сферических координатах уравнения Эйлера–Лагранжа имеют вид $$m{\ddot {r}}-mr({\dot {\theta }}^{2}+\sin ^{2}\theta \,{\dot {\varphi }}^{2})+{\frac {\partial V}{\partial r}}=0,$$$${\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}{\dot {\theta }})-mr^{2}\sin \theta \cos \theta \,{\dot {\varphi }}^{2}=0,$$$${\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}\sin ^{2}\theta \,{\dot {\varphi }})=0.$$Координата φ является циклической, поскольку она не входит в лагранжиан, поэтому сохраняющимся импульсом в системе является угловой момент. $$p_{\varphi }={\frac {\partial L}{\partial {\dot {\varphi }}}}=mr^{2}\sin ^{2}\theta {\dot {\varphi }},$$в котором r , θ и dφ / dt могут меняться со временем, но только таким образом, чтобы p _φ было постоянным.

Лагранжиан в двумерных полярных координатах восстанавливается путем привязки θ к постоянному значению π /2.

Маятник на подвижной опоре

Эскиз ситуации с определением координат (кликните для увеличения)

Рассмотрим маятник массы m и длины ℓ , прикрепленный к опоре массы M , которая может двигаться вдоль прямой в $x$-направление. Позволять $x$ – координата вдоль линии опоры, а положение маятника обозначим углом $\theta$ от вертикали. Координаты и компоненты скорости качания маятника равны $${\begin{array}{rll}&x_{\mathrm {pend} }=x+\ell \sin \theta &\quad \Rightarrow \quad {\dot {x}}_{\mathrm {pend} }={\dot {x}}+\ell {\dot {\theta }}\cos \theta \\&y_{\mathrm {pend} }=-\ell \cos \theta &\quad \Rightarrow \quad {\dot {y}}_{\mathrm {pend} }=\ell {\dot {\theta }}\sin \theta .\end{array}}$$

Обобщёнными координатами можно считать $x$ и $\theta$. Тогда кинетическая энергия системы равна $$T={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)$$а потенциальная энергия $$V=mgy_{\mathrm {pend} }$$давая лагранжиан $${\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}+mg\ell \cos \theta .\end{array}}$$

Поскольку x отсутствует в лагранжиане, это циклическая координата. Сохраняющийся импульс равен $$p_{x}={\frac {\partial L}{\partial {\dot {x}}}}=(M+m){\dot {x}}+m\ell {\dot {\theta }}\cos \theta ,$$и уравнение Лагранжа для опорной координаты $x$ является $$(M+m){\ddot {x}}+m\ell {\ddot {\theta }}\cos \theta -m\ell {\dot {\theta }}^{2}\sin \theta =0.$$

Уравнение Лагранжа для угла θ имеет вид $${\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}\ell \cos \theta +\ell ^{2}{\dot {\theta }})\right]+m\ell ({\dot {x}}{\dot {\theta }}+g)\sin \theta =0;$$и упрощение $${\ddot {\theta }}+{\frac {\ddot {x}}{\ell }}\cos \theta +{\frac {g}{\ell }}\sin \theta =0.$$

Эти уравнения могут показаться довольно сложными, но их нахождение с помощью законов Ньютона потребовало бы тщательного определения всех сил, что было бы гораздо более трудоемким и подверженным ошибкам. Рассмотрев предельные случаи, можно проверить правильность этой системы: например, ${\ddot {x}}\to 0$ должно дать уравнения движения простого маятника , покоящегося в некоторой инерциальной системе отсчета , а ${\ddot {\theta }}\to 0$ должно дать уравнения маятника в постоянно ускоряющейся системе и т. д. Более того, при подходящих начальных условиях и выбранном шаге по времени тривиально получить результаты численно, проходя результаты итеративно .

Задача двух тел о центральной силе

Основные статьи: Задача двух тел и Центральная сила

Два тела массами m ₁ и m ₂ с векторами положения r ₁ и r ₂ находятся на орбите друг друга благодаря притяжению центрального потенциала V . Мы можем записать лагранжиан в терминах координат положения, как они есть, но общепринятой процедурой является преобразование задачи двух тел в задачу одного тела следующим образом. Введем координаты Якоби ; разделение тел р знак равно р ₂ - р ₁ и расположение центра масс R знак равно ( м ₁ р ₁ + м ₂ р ₂ )/( м ₁ + м ₂ ) . Лагранжиан тогда $$L=\underbrace {{\frac {1}{2}}M{\dot {\mathbf {R} }}^{2}} _{L_{\text{cm}}}+\underbrace {{\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}-V(|\mathbf {r} |)} _{L_{\text{rel}}}$$где М = м ₁ + м ₂ - полная масса, ц ​​= м ₁ м ₂ /( м ₁ + м ₂ ) - приведенная масса , а V - потенциал радиальной силы, который зависит только от величины отрыва | р | = | р ₂ - р ₁ | . Лагранжиан распадается на центра масс член L _cm и относительного движения член L _rel .

Уравнение Эйлера–Лагранжа для R просто $$M{\ddot {\mathbf {R} }}=0,$$который утверждает, что центр масс движется по прямой с постоянной скоростью.

Поскольку относительное движение зависит только от величины разделения, идеально использовать полярные координаты ( r , θ ) и взять r = | р | , $$L_{\text{rel}}={\frac {1}{2}}\mu \left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)-V(r),$$поэтому θ - циклическая координата с соответствующим сохраняющимся (угловым) моментом. $$p_{\theta }={\frac {\partial L_{\text{rel}}}{\partial {\dot {\theta }}}}=\mu r^{2}{\dot {\theta }}=\ell .$$

Радиальная координата r и угловая скорость d θ /d t могут меняться со временем, но только таким образом, чтобы ℓ была постоянной. Уравнение Лагранжа для r имеет вид $$\mu r{\dot {\theta }}^{2}-{\frac {dV}{dr}}=\mu {\ddot {r}}.$$

Это уравнение идентично радиальному уравнению, полученному с использованием законов Ньютона во вращающейся системе отсчета, то есть системе, вращающейся с уменьшенной массой, поэтому она кажется неподвижной. Исключив угловую скорость d θ /d t из этого радиального уравнения, $$\mu {\ddot {r}}=-{\frac {\mathrm {d} V}{\mathrm {d} r}}+{\frac {\ell ^{2}}{\mu r^{3}}}.$$которое представляет собой уравнение движения для одномерной задачи, в которой частица массы μ подвергается действию внутренней центральной силы −d V /d r и второй внешней силы, называемой в этом контексте (лагранжевой) центробежной силой (см. центробежная сила#Другие варианты использования термина ): $$F_{\mathrm {cf} }=\mu r{\dot {\theta }}^{2}={\frac {\ell ^{2}}{\mu r^{3}}}.$$

Конечно, если полностью оставаться в рамках одномерной формулировки, ℓ входит только как некий навязанный параметр внешней внешней силы, а его интерпретация как углового момента зависит от более общей двумерной задачи, из которой возникла одномерная проблема. .

Если прийти к этому уравнению, используя механику Ньютона в системе отсчета, вращающейся вместе, интерпретация очевидна как центробежная сила в этой системе отсчета, возникающая из-за вращения самой системы отсчета. Если кто-то приходит к этому уравнению напрямую, используя обобщенные координаты ( r , θ ) и просто следуя лагранжевой формулировке, вообще не задумываясь о системе отсчета, интерпретация такова, что центробежная сила является результатом использования полярных координат . Как говорит Хильдебранд:

«Поскольку такие величины не являются истинными физическими силами, их часто называют силами инерции . Их наличие или отсутствие зависит не от конкретной рассматриваемой проблемы, а от выбранной системы координат ». В частности, если выбраны декартовы координаты, центробежная сила исчезает, и в формулировке участвует только сама центральная сила, которая обеспечивает центростремительную силу для криволинейного движения.

Точку зрения, что фиктивные силы возникают при выборе координат, часто высказывают пользователи метода Лагранжа. Эта точка зрения естественным образом возникает в лагранжевом подходе, поскольку система отсчета (возможно, бессознательно) выбирается путем выбора координат. Например, см. для сравнения лагранжианов в инерциальной и неинерциальной системе отсчета. См. также обсуждение «полных» и «обновленных» лагранжевых формулировок в . К сожалению, такое использование «силы инерции» противоречит ньютоновской идее силы инерции. С точки зрения Ньютона, сила инерции возникает в ускорении системы наблюдения (тот факт, что это не инерциальная система отсчета ), а не в выборе системы координат. Чтобы внести ясность, безопаснее всего называть лагранжевы силы инерции обобщенными силами инерции, чтобы отличать их от ньютоновских векторных сил инерции. То есть не следует следовать Хильдебранду, когда он говорит (стр. 155): «Мы всегда имеем дело с обобщенными силами, скоростями, ускорениями и импульсами. Для краткости прилагательное «обобщенный» будет часто опускаться».

Известно, что лагранжиан системы не единственен. В рамках лагранжева формализма фиктивные силы Ньютона можно идентифицировать по существованию альтернативных лагранжианов, в которых фиктивные силы исчезают, иногда обнаруживаемые путем использования симметрии системы.

Расширение за счет включения неконсервативных сил

Диссипативные силы

Диссипацию (т.е. неконсервативные системы) также можно рассматривать с помощью эффективного лагранжиана, сформулированного путем определенного удвоения степеней свободы.

В более общей формулировке силы могут быть как консервативными, так и вязкими . подходящее преобразование можно найти из F _i , Рэлей предлагает использовать функцию диссипации D Если следующей формы: $$D={\frac {1}{2}}\sum _{j=1}^{m}\sum _{k=1}^{m}C_{jk}{\dot {q}}_{j}{\dot {q}}_{k},$$где C _jk — константы, связанные с коэффициентами затухания в физической системе, но не обязательно равные им. Если D определено таким образом, то $$Q_{j}=-{\frac {\partial V}{\partial q_{j}}}-{\frac {\partial D}{\partial {\dot {q}}_{j}}}$$и $${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial D}{\partial {\dot {q}}_{j}}}=0.$$

Электромагнетизм

Пробная частица — это частица, масса и заряд которой предполагаются настолько малыми, что ее влияние на внешнюю систему незначительно. Часто это гипотетическая упрощенная точечная частица, не имеющая никаких свойств, кроме массы и заряда. Реальные частицы, такие как электроны и ап-кварки, более сложны и имеют дополнительные члены в своих лагранжианах. Поля могут не только образовывать неконсервативные потенциалы, но и эти потенциалы могут зависеть от скорости.

Лагранжиан для заряженной частицы с электрическим зарядом q , взаимодействующей с электромагнитным полем , является типичным примером потенциала, зависящего от скорости. Электрический скалярный потенциал φ = φ ( r , t ) и магнитный векторный потенциал A = A ( r , t ) определяются из электрического поля E = E ( r , t ) и магнитного поля B = B ( r , t ) как следует: $$\mathbf {E} =-{\boldsymbol {\nabla }}\phi -{\frac {\partial \mathbf {A} }{\partial t}},\quad \mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A} .$$

Лагранжиан массивной заряженной пробной частицы в электромагнитном поле $$L={\tfrac {1}{2}}m{\dot {\mathbf {r} }}^{2}+q\,{\dot {\mathbf {r} }}\cdot \mathbf {A} -q\phi ,$$называется минимальной связью . Это хороший пример того, когда общее эмпирическое правило , согласно которому лагранжиан равен кинетической энергии минус потенциальная энергия, неверно. В сочетании с уравнением Эйлера-Лагранжа это дает силы Лоренца закон . $$m{\ddot {\mathbf {r} }}=q\mathbf {E} +q{\dot {\mathbf {r} }}\times \mathbf {B}$$

При калибровочном преобразовании : $$\mathbf {A} \rightarrow \mathbf {A} +{\boldsymbol {\nabla }}f,\quad \phi \rightarrow \phi -{\dot {f}},$$где f ( r , t ) — любая скалярная функция пространства и времени, вышеупомянутый лагранжиан преобразуется следующим образом: $$L\rightarrow L+q\left({\dot {\mathbf {r} }}\cdot {\boldsymbol {\nabla }}+{\frac {\partial }{\partial t}}\right)f=L+q{\frac {df}{dt}},$$который по-прежнему приводит к тому же закону силы Лоренца.

Обратите внимание, что канонический импульс (сопряженный с положением r ) представляет собой кинетический импульс плюс вклад поля A (известный как потенциальный импульс): $$\mathbf {p} ={\frac {\partial L}{\partial {\dot {\mathbf {r} }}}}=m{\dot {\mathbf {r} }}+q\mathbf {A} .$$

Это соотношение также используется в рецепте минимальной связи в квантовой механике и квантовой теории поля . Из этого выражения мы видим, что канонический импульс p не является калибровочно-инвариантным и, следовательно, не является измеримой физической величиной; Однако если r является циклическим (т. е. лагранжиан не зависит от положения r ), что происходит, если поля φ и A однородны, то данный здесь канонический импульс p является сохраняющимся импульсом, а измеримый физический кинетический импульс m v — нет.

Другие контексты и формулировки

Идеи лагранжевой механики имеют многочисленные применения в других областях физики и могут использовать обобщенные результаты вариационного исчисления.

Альтернативные формулировки классической механики

Близкой формулировкой классической механики является гамильтонова механика . Гамильтониан определяется формулой $$H=\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-L$$и может быть получен путем выполнения преобразования Лежандра к лагранжиану, которое вводит новые переменные, канонически сопряженные с исходными переменными. Например, для данного набора обобщенных координат канонически сопряженные переменные представляют собой обобщенные импульсы. Это удваивает количество переменных, но делает дифференциальные уравнения первого порядка. Гамильтониан — особенно распространенная величина в квантовой механике (см. Гамильтониан (квантовая механика) ).

Механика Рутиана представляет собой гибридную формулировку механики Лагранжа и Гамильтона, которая не часто используется на практике, но является эффективной формулировкой для циклических координат.

Формулировка пространства импульса

Основная статья: Пространство положения и импульса § Лагранжева механика

Уравнения Эйлера – Лагранжа также можно сформулировать в терминах обобщенных импульсов, а не обобщенных координат. Выполнение преобразования Лежандра над обобщенным координатным лагранжианом L ( q , d q /d t , t ) дает обобщенный лагранжиан импульсов L ′( p , d p /d t , t ) в терминах исходного лагранжиана, а также EL уравнения в терминах обобщенных импульсов. Оба лагранжиана содержат одну и ту же информацию, и любой из них можно использовать для определения движения системы. На практике обобщенные координаты удобнее использовать и интерпретировать, чем обобщенные импульсы.

Высшие производные обобщенных координат

Нет никаких математических оснований ограничивать производные обобщенных координат только первым порядком. Можно вывести модифицированные уравнения EL для лагранжиана, содержащего производные более высокого порядка, см. в уравнении Эйлера – Лагранжа подробности . Однако с физической точки зрения существует препятствие для включения производных по времени выше первого порядка, что следует из построения Остроградским канонического формализма для невырожденных лагранжианов с высшими производными, см. Неустойчивость Остроградского.

Оптика

Основная статья: гамильтонова оптика

Лагранжева механика может быть применена к геометрической оптике , применяя вариационные принципы к лучам света в среде, а решение уравнений ЭЛ дает уравнения путей, по которым следуют световые лучи.

Релятивистская формулировка

Основная статья: Релятивистская лагранжева механика

Лагранжева механика может быть сформулирована в специальной теории относительности и общей теории относительности . Некоторые черты лагранжевой механики сохраняются в релятивистских теориях, но быстро возникают трудности в других отношениях. В частности, уравнения ЭЛ принимают ту же форму, и связь между циклическими координатами и сохраняющимися импульсами по-прежнему сохраняется, однако лагранжиан должен быть изменен и не является просто кинетической минус потенциальная энергия частицы. Кроме того, непросто обращаться с многочастичными системами явно ковариантным образом; это может быть возможно, если выделить конкретную систему отсчета.

Квантовая механика

В квантовой механике действие и квантово-механическая фаза связаны через постоянную Планка , а принцип стационарного действия можно понять с точки зрения конструктивной интерференции волновых функций .

В 1948 году Фейнман открыл формулировку интеграла по траекториям, распространяющую принцип наименьшего действия на квантовую механику для электронов и фотонов . В этой формулировке частицы проходят все возможные пути между начальным и конечным состояниями; вероятность конкретного конечного состояния получается суммированием по всем возможным траекториям, ведущим к нему. В классическом режиме формулировка интеграла по траекториям четко воспроизводит принцип Гамильтона и принцип Ферма в оптике .

Классическая теория поля

В лагранжевой механике обобщенные координаты образуют дискретный набор переменных, определяющих конфигурацию системы. В классической теории поля физическая система представляет собой не набор дискретных частиц, а скорее непрерывное поле φ ( r , t ), определенное в области трехмерного пространства. С полем связана лагранжева плотность $${\mathcal {L}}(\phi ,\nabla \phi ,{\dot {\phi }},\mathbf {r} ,t)$$определяется через поле и его производные по пространству и времени в точке r и времени t . Аналогично случаю с частицами, для нерелятивистских приложений плотность лагранжа также является плотностью кинетической энергии поля за вычетом плотности его потенциальной энергии (в целом это неверно, и плотность лагранжа должна быть «обратно спроектирована»). Тогда лагранжиан представляет собой объемный интеграл от плотности лагранжа в трехмерном пространстве. $$L(t)=\int {\mathcal {L}}\,\mathrm {d} ^{3}\mathbf {r}$$где d ³ r — элемент трехмерного дифференциального объема . Лагранжиан является функцией времени, поскольку плотность лагранжиана имеет неявную пространственную зависимость через поля и может иметь явную пространственную зависимость, но они удаляются в интеграле, оставляя только время в качестве переменной для лагранжиана.

Теорема Нётер

Принцип действия и лагранжев формализм тесно связаны с теоремой Нётер , которая связывает физические сохраняющиеся величины с непрерывными симметриями физической системы.

Если лагранжиан инвариантен относительно симметрии, то полученные уравнения движения также инвариантны относительно этой симметрии. Эта характеристика очень полезна для демонстрации того, что теории согласуются либо со специальной теорией относительности , либо с общей теорией относительности .

См. также

• Канонические координаты
• Основная лемма вариационного исчисления
• Функциональная производная
• Обобщенные координаты
• гамильтонова механика
• Гамильтонова оптика
• Обратная задача лагранжевой механики — общая тема поиска лагранжиана для системы с учетом уравнений движения.
• Лагранжева и эйлерова спецификация поля течения
• точка Лагранжа
• Лагранжева система
• Неавтономная механика
• Проблема Плато
• Ограниченная задача трех тел.

Ссылки

• Лагранж, JL (1811). Аналитическая механика . Полет. 1.
• Лагранж, Дж. Л. (1815). Аналитическая механика . Полет. 2.
• Пенроуз, Роджер (2007). Дорога к реальности . Винтажные книги. ISBN  978-0-679-77631-4 .
• Ландау, LD ; Лифшиц, Э.М. (15 января 1976 г.). Механика (3-е изд.). Баттерворт Хайнеманн. п. 134. ИСБН  9780750628969 .
• Ландау, Лев ; Лифшиц, Евгений (1975). Классическая теория полей . ООО "Эльзевир" ISBN  978-0-7506-2768-9 .
• Рука, Л.Н.; Финч, доктор юридических наук (1998). Аналитическая механика (2-е изд.). Издательство Кембриджского университета. ISBN  9780521575720 .
• Салетан, Э.Дж.; Хосе, СП (1998). Классическая динамика: современный подход . Издательство Кембриджского университета. ISBN  9780521636360 .
• Киббл, TWB; Беркшир, FH (2004). Классическая механика (5-е изд.). Издательство Имперского колледжа. п. 236. ИСБН  9781860944352 .
• Гольдштейн, Герберт (1980). Классическая механика (2-е изд.). Сан-Франциско, Калифорния: Эддисон Уэсли. ISBN  0201029189 .
• Гольдштейн, Герберт ; Пул, Чарльз П. младший ; Сафко, Джон Л. (2002). Классическая механика (3-е изд.). Сан-Франциско, Калифорния: Эддисон Уэсли. ISBN  0-201-65702-3 .
• Ланцос, Корнелиус (1986). «II §5 Вспомогательные условия: лагранжев λ-метод» . Вариационные принципы механики (Переиздание Университета Торонто, 1970 г., 4-е изд.). Курьер Дувр. п. 43. ИСБН  0-486-65067-7 .
• Феттер, Алабама; Валецка, JD (1980). Теоретическая механика частиц и сплошных сред . Дувр. стр. 53–57. ISBN  978-0-486-43261-8 .
• Принцип наименьшего действия , Р. Фейнман.
• Дворжак Р.; Фрайстеттер, Флориан (2005). «§ 3.2 Уравнения Лагранжа первого рода» . Хаос и стабильность в планетных системах . Биркхойзер. п. 24. ISBN  3-540-28208-4 .
• Хакен, Х (2006). Информация и самоорганизация (3-е изд.). Спрингер. п. 61. ИСБН  3-540-33021-6 .
• Генри Зацкис (1960). «§1.4 Уравнения Лагранжа второго рода» . В Д. Х. Мензеле (ред.). Основные формулы физики . Том. 1 (2-е изд.). Курьер Дувр. п. 160. ИСБН  0-486-60595-7 .
• Хильдебранд, Фрэнсис Бегно (1992). Методы прикладной математики (Перепечатка Прентис-Холла, 1965, 2-е изд.). Курьер Дувр. п. 156. ИСБН  0-486-67002-3 .
• Зак, Михаил; Збилут, Джозеф П.; Мейерс, Рональд Э. (1997). От нестабильности к интеллекту . Спрингер. п. 202. ИСБН  3-540-63055-4 .
• Шабана, Ахмед А. (2008). Вычислительная механика сплошной среды . Издательство Кембриджского университета. стр. 118–119. ISBN  978-0-521-88569-0 .
• Тейлор, Джон Роберт (2005). Классическая механика . Университетские научные книги. п. 297. ИСБН  1-891389-22-Х .
• Падманабхан, Тану (2000). «§2.3.2 Движение во вращающейся системе отсчета» . Теоретическая астрофизика: Астрофизические процессы (3-е изд.). Издательство Кембриджского университета. п. 48. ИСБН  0-521-56632-0 .
• Даути, Ноэль А. (1990). Лагранжево взаимодействие . Addison-Wesley Publishers Ltd. ISBN  0-201-41625-5 .
• Косяков, Б.П. (2007). Введение в классическую теорию частиц и полей . Берлин, Германия: Шпрингер. дои : 10.1007/978-3-540-40934-2 . ISBN  978-3-540-40933-5 .
• Галли, Чад Р. (2013). «Классическая механика неконсервативных систем». Письма о физических отзывах . 110 (17): 174301. arXiv : 1210.2745 . Бибкод : 2013PhRvL.110q4301G . doi : 10.1103/PhysRevLett.110.174301 . ПМИД   23679733 . S2CID   14591873 .
• Бирнхольц, Офек; Хадар, Шахар; Кол, Барак (2014). «Радиационная реакция на уровне действия». Международный журнал современной физики А. 29 (24): 1450132–1450190. arXiv : 1402.2610 . Бибкод : 2014IJMPA..2950132B . дои : 10.1142/S0217751X14501322 . S2CID   118541484 .
• Бирнхольц, Офек; Хадар, Шахар; Кол, Барак (2013). «Теория постньютоновского излучения и реакции». Физический обзор D . 88 (10): 104037. arXiv : 1305.6930 . Бибкод : 2013PhRvD..88j4037B . дои : 10.1103/PhysRevD.88.104037 . S2CID   119170985 .
• Роджер Ф. Ганс (2013). Инженерная динамика: от лагранжиана к моделированию . Нью-Йорк: Спрингер. ISBN  978-1-4614-3929-5 .
• Ганнон, Терри (2006). Самогон за пределами монстра: мост, соединяющий алгебру, модульные формы и физику . Издательство Кембриджского университета. п. 267. ИСБН  0-521-83531-3 .
• Торби, Брюс (1984). «Энергетические методы». Advanced Dynamics для инженеров . Серия HRW в области машиностроения. Соединенные Штаты Америки: Издательство CBS College Publishing. ISBN  0-03-063366-4 .
• Фостер, Дж; Найтингейл, Джей Ди (1995). Краткий курс общей теории относительности (2-е изд.). Спрингер. ISBN  0-03-063366-4 .
• член парламента Хобсон; ГП Эфстатиу; А. Н. Ласенби (2006). Общая теория относительности: введение для физиков . Издательство Кембриджского университета. стр. 79–80. ISBN  9780521829519 .
• Синг, Дж.Л.; Шильд, А. (1949). Тензорное исчисление . первое издание Dover Publications 1978 года. ISBN  978-0-486-63612-2 .
• Кей, Дэвид (апрель 1988 г.). Схема тензорного исчисления Шаума . МакГроу Хилл Профессионал. ISBN  978-0-07-033484-7 .

Дальнейшее чтение

• Гупта, Киран Чандра, Классическая механика частиц и твердых тел (Wiley, 1988).
• Кассель, Кевин (2013). Вариационные методы с применением в науке и технике . Кембридж: Издательство Кембриджского университета. ISBN  978-1-107-02258-4 .
• Гольдштейн , Герберт и др. Классическая механика . 3-е изд., Пирсон, 2002.

Внешние ссылки

• Дэвид Тонг. «Конспекты Кембриджских лекций по классической динамике» . ДАМТП . Проверено 8 июня 2017 г.
• Принцип наименьшего интерактивного действия Отличное интерактивное объяснение/веб-страница
• Жозеф Луи де Лагранж - Полное собрание сочинений (Gallica-Math)
• Вынужденное движение и обобщенные координаты , стр. 4