Квадратура круга

Чтобы узнать о других значениях, см. Квадратирование круга (значения) , Квадратирование круга (значения) и Квадратирование круга (значения) .

Не путать с квадратным колышком в круглом отверстии .

Квадратура круга: площади этого квадрата и этого круга равны π . В 1882 году было доказано, что эту фигуру невозможно построить за конечное число шагов с помощью идеализированного циркуля и линейки .

Квадратура круга задача — геометрическая , впервые предложенная в греческой математике . Это задача построить квадрат с площадью заданного круга , используя только конечное число шагов с помощью циркуля и линейки . Сложность проблемы поставила вопрос о том, предполагают ли указанные аксиомы евклидовой геометрии, касающиеся существования прямых и кругов, существование такого квадрата.

В 1882 году задача оказалась невыполнимой, как следствие теоремы Линдемана-Вейерштрасса , доказывающей, что pi ( $\pi$) — трансцендентное число .То есть, $\pi$ не является корнем любого многочлена с рациональными коэффициентами. Уже несколько десятилетий было известно, что строительство будет невозможным, если $\pi$ были трансцендентными, но этот факт не был доказан до 1882 года. Приближенные конструкции с любой заданной несовершенной точностью существуют, и таких конструкций было найдено множество.

Несмотря на доказательство того, что это невозможно, попытки квадратуры круга были обычным явлением в псевдоматематике (т. е. в работе математических чудаков). Выражение «квадратура круга» иногда используется как метафора попытки сделать невозможное.

Термин квадратура круга иногда используется как синоним квадратуры круга. Это также может относиться к приближенным или численным методам определения площади круга . В общем, квадратуру или возведение в квадрат можно применять и к другим плоским фигурам.

История

Методы расчета приблизительной площади данного круга, которые можно рассматривать как предысторию задачи квадратуры круга, были известны уже во многих древних культурах. Эти методы можно резюмировать, указав приближение к π , которое они производят. Примерно в 2000 году до нашей эры вавилонские математики использовали приближение $\pi \approx {\tfrac {25}{8}}=3.125$, и примерно в то же время древнеегипетские математики использовали $\pi \approx {\tfrac {256}{81}}\approx 3.16$. Более 1000 лет спустя Ветхого Завета в «Книгах Царств» использовалось более простое приближение. $\pi \approx 3$. Древняя индийская математика , записанная в « Шатапатха Брахмане» и «Шулба Сутрах» , использовала несколько различных приближений к $\pi$. Архимед доказал формулу площади круга, согласно которой $3\,{\tfrac {10}{71}}\approx 3.141<\pi <3\,{\tfrac {1}{7}}\approx 3.143$. В китайской математике в третьем веке нашей эры Лю Хуэй нашел еще более точные приближения, используя метод, аналогичный методу Архимеда, а в пятом веке Цзу Чунчжи нашел $\pi \approx 355/113\approx 3.141593$, приближение, известное как Милю .

Проблема построения квадрата, площадь которого равна площади круга, а не его приближения, пришла из греческой математики . Греческие математики нашли конструкции циркуля и линейки, позволяющие превратить любой многоугольник в квадрат эквивалентной площади. Они использовали эту конструкцию для геометрического сравнения площадей многоугольников, а не для численного вычисления площади, что было бы более типично в современной математике. Как писал Прокл много столетий спустя, это побудило поиск методов, позволяющих проводить сравнения с неполигональными формами:

Взяв за основу эту проблему, я полагаю, древние также искали квадратуру круга. Ибо если параллелограмм оказывается равным какой-либо прямолинейной фигуре, то стоит исследовать, можно ли доказать, что прямолинейные фигуры равны фигурам, связанным дугами окружностей.

Некоторые очевидные частичные решения долгое время давали ложную надежду. На этом рисунке заштрихованная фигура — луна Гиппократа . Его площадь равна площади треугольника ABC (найденного Гиппократом Хиосским ).

Первым известным греком, изучавшим эту проблему, был Анаксагор , который работал над ней, находясь в тюрьме. Гиппократ Хиосский решил эту проблему, найдя форму, ограниченную круговыми дугами, луну Гиппократа , которую можно было возвести в квадрат. Антифон Софист считал, что вписание правильных многоугольников в круг и удвоение числа сторон со временем заполнит площадь круга (это метод истощения ). Поскольку любой многоугольник можно возвести в квадрат, он утверждал, что круг можно возвести в квадрат. Напротив, Евдем утверждал, что величины можно делить без ограничений, поэтому площадь круга никогда не будет использована. Одновременно с Антифоном Брайсон из Гераклеи утверждал, что, поскольку существуют как большие, так и меньшие круги, должен быть круг равной площади; этот принцип можно рассматривать как форму современной теоремы о промежуточной стоимости . Более общую цель выполнения всех геометрических построений с использованием только циркуля и линейки часто приписывали Энопиду , но доказательства этого косвенные.

Проблема нахождения площади под произвольной кривой, ныне известная как интегрирование в исчислении или квадратура в численном анализе была известна как возведение в квадрат . , до изобретения исчисления Поскольку методы исчисления были неизвестны, обычно предполагалось, что возведение в квадрат должно производиться с помощью геометрических построений, то есть с помощью циркуля и линейки. Например, Ньютон писал Ольденбургу в 1676 году: «Я думаю, что М. Лейбницу не понравится теорема в начале моего письма, стр. 4, о геометрическом возведении кривых в квадрат». В современной математике эти термины разошлись по значению: квадратура обычно используется, когда разрешены методы исчисления, тогда как возведение в квадрат кривой сохраняет идею использования только ограниченных геометрических методов.

Джеймс Грегори попытался доказать невозможность квадратуры круга в книге Vera Circuli et Hyperbolae Quadratura (Истинное квадратура круга и гиперболы) в 1667 году. Хотя его доказательство было ошибочным, это была первая статья, в которой была предпринята попытка решить проблему. используя алгебраические свойства $\pi$. Иоганн Генрих Ламберт доказал в 1761 году, что $\pi$ это иррациональное число . Лишь в 1882 году Фердинанду фон Линдеманну удалось более убедительно доказать, что π — трансцендентное число , и тем самым также доказать невозможность квадратуры круга с помощью циркуля и линейки.

После доказательства невозможности Линдеманна проблема считалась решенной профессиональными математиками, и в ее последующей математической истории доминировали псевдоматематические попытки построения конструкций квадрата круга, в основном сделанные любителями, и разоблачение этих усилий. Кроме того, несколько более поздних математиков, в том числе Шриниваса Рамануджан, разработали конструкции циркуля и линейки, которые точно аппроксимируют задачу за несколько шагов.

Двумя другими классическими задачами античности, известными своей невозможностью, были удвоение куба и трисекция угла . Подобно квадратуре круга, эти задачи невозможно решить с помощью циркуля и линейки. Однако они имеют иной характер, чем квадратура круга, поскольку их решение включает корень кубического уравнения , а не трансцендентное. Следовательно, для построения решений этих проблем можно использовать более мощные методы, чем конструкции циркуля и линейки, такие как построение neusis или математическое складывание бумаги .

Невозможность

Решение задачи о квадратуре круга с помощью циркуля и линейки требует построения числа ${\sqrt {\pi }}$, длина стороны квадрата, площадь которого равна площади единичного круга. Если ${\sqrt {\pi }}$ были конструктивным числом следовало бы , что циркуля и линейки , то из стандартных конструкций $\pi$ также будет конструктивным. В 1837 году Пьер Ванцель показал, что длины, которые можно построить с помощью циркуля и линейки, должны быть решениями некоторых полиномиальных уравнений с рациональными коэффициентами. Таким образом, конструктивные длины должны быть алгебраическими числами . Если бы круг можно было возвести в квадрат, используя только циркуль и линейку, то $\pi$ должно быть алгебраическим числом. Лишь в 1882 году Фердинанд фон Линдеманн доказал трансцендентность $\pi$ и так показала невозможность этой конструкции. Идея Линдеманна заключалась в том, чтобы объединить доказательство трансцендентности числа Эйлера $e$, показанный Чарльзом Эрмитом в 1873 году, с личностью Эйлера.

$$e^{i\pi }=-1.$$

Это тождество сразу показывает, что $\pi$ является иррациональным числом , поскольку рациональная степень трансцендентного числа остается трансцендентной. Линдеманну удалось расширить этот аргумент с помощью теоремы Линдеманна – Вейерштрасса о линейной независимости алгебраических степеней. $e$, чтобы показать это $\pi$ трансцендентно, и поэтому квадратура круга невозможна.

Нарушение правил за счет введения дополнительного инструмента, допускающего бесконечное количество операций с циркулем и линейкой или выполнения операций в определенных неевклидовых геометриях, делает в некотором смысле возможным квадратуру круга. Например, теорема Динострата использует квадратрису Гиппия для квадратуры круга, а это означает, что если эта кривая каким-то образом уже задана, то из нее можно построить квадрат и круг равных площадей. Спираль Архимеда можно использовать для другой подобной конструкции. Хотя круг не может быть квадратурован в евклидовом пространстве , иногда это может быть в гиперболической геометрии при подходящей интерпретации терминов. Гиперболическая плоскость не содержит квадратов (четырехугольников с четырьмя прямыми углами и четырьмя равными сторонами), но вместо этого содержит правильные четырехугольники , фигуры с четырьмя равными сторонами и четырьмя равными углами, более острыми, чем прямые углы. В гиперболической плоскости существует ( счетное ) бесконечное число пар конструктивных окружностей и конструктивных правильных четырехугольников равной площади, которые, однако, строятся одновременно. Не существует способа начать с произвольного правильного четырехугольника и построить круг равной площади. Симметрично, не существует способа начать с произвольного круга и построить правильный четырехугольник равной площади, а для достаточно больших кругов такого четырехугольника не существует.

Примерные конструкции

Хотя точное квадратурирование круга с помощью циркуля и линейки невозможно, приближения к квадратуре круга можно получить, построив длины, близкие к $\pi$.Требуется только элементарная геометрия, чтобы преобразовать любое данное рациональное приближение $\pi$ в соответствующую конструкцию циркуля и линейки , но такие конструкции имеют тенденцию быть очень многословными по сравнению с точностью, которую они достигают. После того, как точная задача оказалась неразрешимой, некоторые математики применили свою изобретательность, чтобы найти приближения к квадратуре круга, которые являются особенно простыми среди других мыслимых конструкций, дающих аналогичную точность.

Строительство Кочанского

Кочанского Примерная конструкция

Продолжение с равновеликим кругом и квадратом; $r$ обозначает начальный радиус

Одна из многих ранних исторических приблизительных конструкций циркуля и линейки взята из статьи 1685 года польского иезуита Адама Адаманди Кочанского , в которой дано приближение, отклоняющееся от $\pi$ в 5-м десятичном знаке. Хотя гораздо более точные численные аппроксимации $\pi$ были уже известны, конструкция Кочанского имеет то преимущество, что она довольно проста. На левой схеме

$$|P_{3}P_{9}|=|P_{1}P_{2}|{\sqrt {{\frac {40}{3}}-2{\sqrt {3}}}}\approx 3.141\,5{\color {red}33\,338}\cdot |P_{1}P_{2}|\approx \pi r.$$

В той же работе Кочанский также вывел последовательность все более точных рациональных приближений для $\pi$.

Конструкции с использованием 355/113

Конструкция 355/113 Якоба де Гелдера

Строительство Рамануджана 355/113

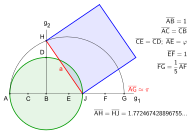
Якоб де Гельдер опубликовал в 1849 г. конструкцию, основанную на приближении

$$\pi \approx {\frac {355}{113}}=3.141\;592{\color {red}\;920\;\ldots }$$

Это значение имеет точность до шести десятичных знаков и известно в Китае с V века как Милю , а в Европе — с 17 века.

Гелдер не строил сторону квадрата; ему было достаточно найти значение

$${\overline {AH}}={\frac {4^{2}}{7^{2}+8^{2}}}.$$

На иллюстрации показана конструкция де Гельдера.

В 1914 году индийский математик Шриниваса Рамануджан предложил другую геометрическую конструкцию для того же приближения.

Конструкции с использованием золотого сечения

Конструкция золотого сечения Хобсона

Конструкция золотого сечения Диксона

13-ступенчатая конструкция Беатрикс

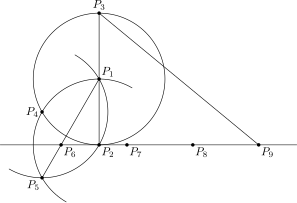
Примерная конструкция Э. В. Хобсона в 1913 году. имеет точность до трех десятичных знаков. Конструкция Гобсона соответствует приблизительному значению

$${\frac {6}{5}}\cdot \left(1+\varphi \right)=3.141\;{\color {red}640\;\ldots },$$

где $\varphi$ это золотое сечение , $\varphi =(1+{\sqrt {5}})/2$.

Такая же приблизительная стоимость указана в конструкции Роберта Диксона 1991 года . В 2022 году Фредерик Беатрикс представил геометрическую конструкцию, состоящую из 13 шагов.

Рамануджана

Квадратура круга, примерное построение по Рамануджану 1914 года, с продолжением построения (пунктирные линии, средняя пропорциональная красная линия), см. анимацию .

Эскиз «Рукописной книги 1 Шриниваса Рамануджана» с. 54, постройка Рамануджана 355/113

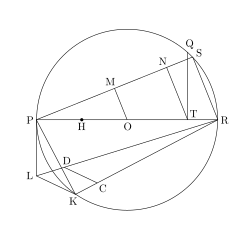
В 1914 году Рамануджан дал конструкцию, которая была эквивалентна принятию приблизительного значения для $\pi$ быть

$$\left(9^{2}+{\frac {19^{2}}{22}}\right)^{\frac {1}{4}}={\sqrt[{4}]{\frac {2143}{22}}}=3.141\;592\;65{\color {red}2\;582\;\ldots }$$

давая восемь десятичных знаков $\pi$. Он описывает построение ОС сегмента линии следующим образом.

Пусть AB (рис.2) — диаметр круга, центр которого равен O. Разделите дугу ACB пополам в точке C и разделите AO пополам в точке T. Соедините BC и отрежьте от нее CM и MN, равные AT. Соединить АМ и АН и отрезать от последнего АП, равный АМ. Через P проведите PQ параллельно MN и встретимся с AM в точке Q. Соедините OQ и через T проведите TR, параллельно OQ и встретившись с AQ в точке R. Нарисуйте AS, перпендикулярную AO и равную AR, и соедините OS. Тогда среднее пропорциональное между OS и OB будет почти равно одной шестой окружности, а ошибка составит менее двенадцатой дюйма, когда диаметр составляет 8000 миль.

Неправильные конструкции

В преклонном возрасте английский философ Томас Гоббс убедил себя, что ему удалось квадратура круга, утверждение, опровергнутое Джоном Уоллисом в рамках спора Гоббса-Уоллиса . В XVIII и XIX веках среди потенциальных квадратурщиков круга стали преобладать ложные представления о том, что проблема квадратуры круга каким-то образом связана с проблемой долготы и что за решение будет дана большая награда. В 1851 году Джон Паркер опубликовал книгу «Квадратура круга» , в которой утверждал, что квадратировал круг. Его метод фактически позволил приблизить $\pi$ с точностью до шести цифр.

Математик викторианской , логик и писатель эпохи Чарльз Лютвидж Доджсон, более известный под псевдонимом Льюис Кэрролл , также проявил интерес к разоблачению нелогичных теорий квадратуры круга. В одной из своих дневниковых записей за 1855 год Доджсон перечислил книги, которые он надеялся написать, в том числе книгу под названием «Простые факты для тех, кто квадратирует круг». Во введении к «Новой теории параллелей» Доджсон рассказал о попытке продемонстрировать логические ошибки паре исследователей квадратов круга, заявив:

Первый из этих двух заблудших провидцев наполнил меня великим стремлением совершить подвиг, о котором я никогда не слышал, как совершенный человеком, а именно убедить квадратного круга в его ошибке! Значение, которое мой друг выбрал для числа Пи, было 3,2: огромная ошибка соблазнила меня мыслью, что можно легко продемонстрировать, что она БЫЛА ошибкой. Было обменяно более двадцати писем, прежде чем я с грустью убедился, что у меня нет шансов.

Высмеивание квадратуры круга появляется в Огастеса Де Моргана книге «Бюджет парадоксов» , опубликованной посмертно его вдовой в 1872 году. Первоначально опубликовав эту работу в виде серии статей в «Атенеуме» , он редактировал ее для публикации во время его смерть. Популярность квадратуры круга снизилась после девятнадцатого века, и считается, что этому способствовала работа Де Моргана.

Книга Хейзеля 1934 года

Даже после того, как это было доказано невозможно, в 1894 году математик-любитель Эдвин Дж. Гудвин заявил, что разработал метод квадратуры круга. Разработанная им техника неточно выровняла круг и предоставила неверную площадь круга, что, по сути, переопределило его. $\pi$ равным 3,2. Затем Гудвин предложил в законодательном собрании штата Индиана законопроект о числе Пи, позволяющий штату использовать его метод в образовании без выплаты ему гонораров. Законопроект был принят без возражений в палате штата, но он был внесен на рассмотрение и так и не проголосован в Сенате на фоне растущих насмешек со стороны прессы.

Математический чудак Карл Теодор Хейзель также утверждал, что квадратировал круг в своей книге 1934 года «Вот!: великая проблема больше не является нерешенной: квадрат круга не подлежит опровержению». Пол Халмос назвал эту книгу «классической чудаковатой книгой».

В литературе

Проблема квадратуры круга упоминалась в самых разных литературных эпохах и имела множество метафорических значений. ​​пьеса «Птицы Аристофана » Его литературное использование восходит как минимум к 414 году до нашей эры, когда впервые была поставлена . В нем персонаж Метон из Афин упоминает квадратуру круга, возможно, чтобы указать на парадоксальную природу своего утопического города.

Витрувианский человек

Данте» «Рай , песнь XXXIII, строки 133–135, содержат стих:

Как геометр, его ум применяется
Чтобы квадратировать круг, ни при всем своем остроумии
Находит правильную формулу, как бы он ни старался

Какой геодезист, который все чинит
измерить круг и не может его найти,
мышление, тот принцип, который ему нужен,

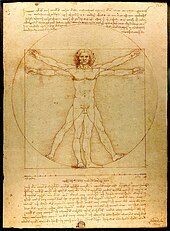
Для Данте квадратура круга представляет собой задачу, превосходящую человеческое понимание, которую он сравнивает со своей собственной неспособностью постичь Рай. Образ Данте также напоминает отрывок из Витрувия , знаменито проиллюстрированный позже в Леонардо да Винчи » «Витрувианском человеке , о человеке, одновременно вписанном в круг и квадрат. Данте использует круг как символ Бога и, возможно, упомянул это сочетание форм в отношении одновременной божественной и человеческой природы Иисуса. Ранее, в песне XIII, Данте называет греческого квадратора Брайсона, который искал знания, а не мудрости.

В нескольких работах поэтессы 17-го века Маргарет Кавендиш подробно рассматриваются проблема квадратуры круга и ее метафорические значения, включая контраст между единством истины и фракционностью, а также невозможность рационализации «фантазийной и женской природы». К 1742 году, когда Александр Поуп опубликовал четвертую книгу своей «Дунсиады» , попытки квадратуры круга стали рассматриваться как «дикие и бесплодные»:

Один только Безумный Матезис был неограничен,
Слишком безумен, чтобы связать его простыми материальными цепями,
Теперь к чистому пространству возводит ее восторженный взор,
Теперь, бегая по кругу, он находит его квадратным.

Точно так же в Гилберта и Салливана комической опере «Принцесса Ида» есть песня, в которой сатирически перечисляются невозможные цели женского университета, которым руководит главный герой, такие как поиск вечного двигателя . Одна из таких целей: «И круг – квадратуру / В какой-нибудь прекрасный день».

шести . повторяющихся слов Говорят, что сестина, поэтическая форма, впервые использованная в XII веке Арнаутом Даниэлем, метафорически квадратизирует круг, используя квадратное количество строк (шесть строф по шесть строк в каждой) с круговой схемой из Спанос (1978) пишет, что эта форма имеет символическое значение, в котором круг обозначает небо, а квадрат — землю. Похожая метафора была использована в рассказе О. Генри «Квадратура круга» 1908 года о давней семейной вражде. В названии этой истории круг представляет мир природы, а квадрат — город, мир человека.

В более поздних работах такие люди, занимающиеся квадратурой круга, как Леопольд Блум в Джеймса Джойса романе «Улисс» и адвокат Паравант в Томаса Манна » «Волшебной горе , рассматриваются как печально заблуждающиеся или потусторонние мечтатели, не осознающие математической невозможности этого круга и строящие грандиозные планы для результата они никогда не достигнут.

См. также

• Задача миссис Минивер - Задача о площадях пересекающихся кругов.
• Круглая квадратная копула - Философская трактовка оксюморонов. Страницы с краткими описаниями целей перенаправления.
• Сквиркл – форма между квадратом и кругом.
• Задача Тарского о квадратуре круга - Задача разрезания и сборки диска в квадрат.

Дальнейшее чтение и внешние ссылки

• Богомольный, Александр. «Квадратура круга» . разрезать узел .
• Грайм, Джеймс. «Квадратура круга» . Числофил . Брэди Харан – через YouTube.
• Харпер, Сюзанна; Дрискелл, Шеннон (август 2010 г.). «Исследование исторических геометрических построений» . Конвергенция . Математическая ассоциация Америки.
• О'Коннор, Джей-Джей; Робертсон, EF (апрель 1999 г.). «Квадратура круга» . MacTutor Архив истории математики .
• Отеро, Дэниел Э. (июль 2010 г.). «Квадратура круга и луны Гиппократа» . Конвергенция . Математическая ассоциация Америки.
• Польстер, Буркард . «2000 лет неразгаданы: почему невозможно удвоить кубы и возвести в квадрат круг?» . Матолог – через YouTube.