Нормальное распределение
Функция плотности вероятности 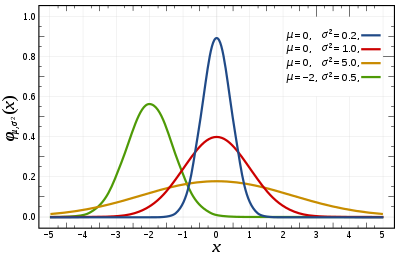 Красная кривая — стандартное нормальное распределение . | |||
Кумулятивная функция распределения 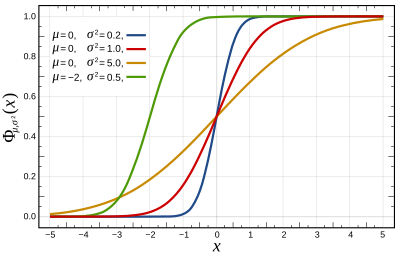 | |||
| Notation | |||
|---|---|---|---|
| Parameters | = mean (location) = variance (squared scale) | ||
| Support | |||
| CDF | |||
| Quantile | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| MAD | |||
| Skewness | |||
| Excess kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | |||
| Fisher information | |||
| Kullback–Leibler divergence | |||
| Expected shortfall | [1] | ||
| Part of a series on statistics |
| Probability theory |
|---|
 |
В теории вероятностей и статистике нормальное распределение или распределение Гаусса — это тип непрерывного распределения вероятностей для вещественной случайной величины . Общий вид его функции плотности вероятности : Параметр — среднее или математическое ожидание распределения (а также его медиана и мода ), а параметр это дисперсия . Стандартное отклонение распределения равно . Случайная величина с распределением Гаусса называется нормально распределенной и называется нормальным отклонением .
Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known.[2][3] Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal distribution as the number of samples increases. Therefore, physical quantities that are expected to be the sum of many independent processes, such as measurement errors, often have distributions that are nearly normal.[4]
Moreover, Gaussian distributions have some unique properties that are valuable in analytic studies. For instance, any linear combination of a fixed collection of independent normal deviates is a normal deviate. Many results and methods, such as propagation of uncertainty and least squares[5] parameter fitting, can be derived analytically in explicit form when the relevant variables are normally distributed.
A normal distribution is sometimes informally called a bell curve.[6] However, many other distributions are bell-shaped (such as the Cauchy, Student's t, and logistic distributions). For other names, see Naming.
The univariate probability distribution is generalized for vectors in the multivariate normal distribution and for matrices in the matrix normal distribution.
Definitions
[edit]Standard normal distribution
[edit]The simplest case of a normal distribution is known as the standard normal distribution or unit normal distribution. This is a special case when and , and it is described by this probability density function (or density):The variable has a mean of 0 and a variance and standard deviation of 1. The density has its peak at and inflection points at and .
Although the density above is most commonly known as the standard normal, a few authors have used that term to describe other versions of the normal distribution. Carl Friedrich Gauss, for example, once defined the standard normal aswhich has a variance of 1/2, and Stephen Stigler[7] once defined the standard normal aswhich has a simple functional form and a variance of
General normal distribution
[edit]Every normal distribution is a version of the standard normal distribution, whose domain has been stretched by a factor (the standard deviation) and then translated by (the mean value):
The probability density must be scaled by so that the integral is still 1.
If is a standard normal deviate, then will have a normal distribution with expected value and standard deviation . This is equivalent to saying that the standard normal distribution can be scaled/stretched by a factor of and shifted by to yield a different normal distribution, called . Conversely, if is a normal deviate with parameters and , then this distribution can be re-scaled and shifted via the formula to convert it to the standard normal distribution. This variate is also called the standardized form of .
Notation
[edit]The probability density of the standard Gaussian distribution (standard normal distribution, with zero mean and unit variance) is often denoted with the Greek letter (phi).[8] The alternative form of the Greek letter phi, , is also used quite often.
The normal distribution is often referred to as or .[9] Thus when a random variable is normally distributed with mean and standard deviation , one may write
Alternative parameterizations
[edit]Some authors advocate using the precision as the parameter defining the width of the distribution, instead of the standard deviation or the variance . The precision is normally defined as the reciprocal of the variance, .[10] The formula for the distribution then becomes
This choice is claimed to have advantages in numerical computations when is very close to zero, and simplifies formulas in some contexts, such as in the Bayesian inference of variables with multivariate normal distribution.
Alternatively, the reciprocal of the standard deviation might be defined as the precision, in which case the expression of the normal distribution becomes
According to Stigler, this formulation is advantageous because of a much simpler and easier-to-remember formula, and simple approximate formulas for the quantiles of the distribution.
Normal distributions form an exponential family with natural parameters and , and natural statistics x and x2. The dual expectation parameters for normal distribution are η1 = μ and η2 = μ2 + σ2.
Cumulative distribution function
[edit]The cumulative distribution function (CDF) of the standard normal distribution, usually denoted with the capital Greek letter (phi), is the integral
Error Function
[edit]The related error function gives the probability of a random variable, with normal distribution of mean 0 and variance 1/2 falling in the range . That is:
These integrals cannot be expressed in terms of elementary functions, and are often said to be special functions. However, many numerical approximations are known; see below for more.
The two functions are closely related, namely
For a generic normal distribution with density , mean and variance , the cumulative distribution function is
The complement of the standard normal cumulative distribution function, , is often called the Q-function, especially in engineering texts.[11][12] It gives the probability that the value of a standard normal random variable will exceed : . Other definitions of the -function, all of which are simple transformations of , are also used occasionally.[13]
The graph of the standard normal cumulative distribution function has 2-fold rotational symmetry around the point (0,1/2); that is, . Its antiderivative (indefinite integral) can be expressed as follows:
The cumulative distribution function of the standard normal distribution can be expanded by Integration by parts into a series:
where denotes the double factorial.
An asymptotic expansion of the cumulative distribution function for large x can also be derived using integration by parts. For more, see Error function#Asymptotic expansion.[14]
A quick approximation to the standard normal distribution's cumulative distribution function can be found by using a Taylor series approximation:
Recursive computation with Taylor series expansion
[edit]The recursive nature of the family of derivatives may be used to easily construct a rapidly converging Taylor series expansion using recursive entries about any point of known value of the distribution,:
where:
Using the Taylor series and Newton's method for the inverse function
[edit]An application for the above Taylor series expansion is to use Newton's method to reverse the computation. That is, if we have a value for the cumulative distribution function, , but do not know the x needed to obtain the , we can use Newton's method to find x, and use the Taylor series expansion above to minimize the number of computations. Newton's method is ideal to solve this problem because the first derivative of , which is an integral of the normal standard distribution, is the normal standard distribution, and is readily available to use in the Newton's method solution.
To solve, select a known approximate solution, , to the desired . may be a value from a distribution table, or an intelligent estimate followed by a computation of using any desired means to compute. Use this value of and the Taylor series expansion above to minimize computations.
Repeat the following process until the difference between the computed and the desired , which we will call , is below a chosen acceptably small error, such as 10−5, 10−15, etc.:
where
- is the from a Taylor series solution using and
When the repeated computations converge to an error below the chosen acceptably small value, x will be the value needed to obtain a of the desired value, .
Standard deviation and coverage
[edit]
About 68% of values drawn from a normal distribution are within one standard deviation σ from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations.[6] This fact is known as the 68–95–99.7 (empirical) rule, or the 3-sigma rule.
More precisely, the probability that a normal deviate lies in the range between and is given byTo 12 significant digits, the values for are:[citation needed]
| OEIS | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.682689492137 | 0.317310507863 |
| OEIS: A178647 | ||
| 2 | 0.954499736104 | 0.045500263896 |
| OEIS: A110894 | ||
| 3 | 0.997300203937 | 0.002699796063 |
| OEIS: A270712 | ||
| 4 | 0.999936657516 | 0.000063342484 |
| |||
| 5 | 0.999999426697 | 0.000000573303 |
| |||
| 6 | 0.999999998027 | 0.000000001973 |
|
For large , one can use the approximation .
Quantile function
[edit]The quantile function of a distribution is the inverse of the cumulative distribution function. The quantile function of the standard normal distribution is called the probit function, and can be expressed in terms of the inverse error function:For a normal random variable with mean and variance , the quantile function isThe quantile of the standard normal distribution is commonly denoted as . These values are used in hypothesis testing, construction of confidence intervals and Q–Q plots. A normal random variable will exceed with probability , and will lie outside the interval with probability . In particular, the quantile is 1.96; therefore a normal random variable will lie outside the interval in only 5% of cases.
The following table gives the quantile such that will lie in the range with a specified probability . These values are useful to determine tolerance interval for sample averages and other statistical estimators with normal (or asymptotically normal) distributions.[15] The following table shows , not as defined above.
| 0.80 | 1.281551565545 | 0.999 | 3.290526731492 | |
| 0.90 | 1.644853626951 | 0.9999 | 3.890591886413 | |
| 0.95 | 1.959963984540 | 0.99999 | 4.417173413469 | |
| 0.98 | 2.326347874041 | 0.999999 | 4.891638475699 | |
| 0.99 | 2.575829303549 | 0.9999999 | 5.326723886384 | |
| 0.995 | 2.807033768344 | 0.99999999 | 5.730728868236 | |
| 0.998 | 3.090232306168 | 0.999999999 | 6.109410204869 |
For small , the quantile function has the useful asymptotic expansion[citation needed]
Properties
[edit]The normal distribution is the only distribution whose cumulants beyond the first two (i.e., other than the mean and variance) are zero. It is also the continuous distribution with the maximum entropy for a specified mean and variance.[16][17] Geary has shown, assuming that the mean and variance are finite, that the normal distribution is the only distribution where the mean and variance calculated from a set of independent draws are independent of each other.[18][19]
The normal distribution is a subclass of the elliptical distributions. The normal distribution is symmetric about its mean, and is non-zero over the entire real line. As such it may not be a suitable model for variables that are inherently positive or strongly skewed, such as the weight of a person or the price of a share. Such variables may be better described by other distributions, such as the log-normal distribution or the Pareto distribution.
The value of the normal distribution is practically zero when the value lies more than a few standard deviations away from the mean (e.g., a spread of three standard deviations covers all but 0.27% of the total distribution). Therefore, it may not be an appropriate model when one expects a significant fraction of outliers—values that lie many standard deviations away from the mean—and least squares and other statistical inference methods that are optimal for normally distributed variables often become highly unreliable when applied to such data. In those cases, a more heavy-tailed distribution should be assumed and the appropriate robust statistical inference methods applied.
The Gaussian distribution belongs to the family of stable distributions which are the attractors of sums of independent, identically distributed distributions whether or not the mean or variance is finite. Except for the Gaussian which is a limiting case, all stable distributions have heavy tails and infinite variance. It is one of the few distributions that are stable and that have probability density functions that can be expressed analytically, the others being the Cauchy distribution and the Lévy distribution.
Symmetries and derivatives
[edit]The normal distribution with density (mean and variance ) has the following properties:
- It is symmetric around the point which is at the same time the mode, the median and the mean of the distribution.[20]
- It is unimodal: its first derivative is positive for negative for and zero only at
- The area bounded by the curve and the -axis is unity (i.e. equal to one).
- Its first derivative is
- Its second derivative is
- Its density has two inflection points (where the second derivative of is zero and changes sign), located one standard deviation away from the mean, namely at and [20]
- Its density is log-concave.[20]
- Its density is infinitely differentiable, indeed supersmooth of order 2.[21]
Furthermore, the density of the standard normal distribution (i.e. and ) also has the following properties:
- Its first derivative is
- Its second derivative is
- More generally, its nth derivative is where is the nth (probabilist) Hermite polynomial.[22]
- The probability that a normally distributed variable with known and is in a particular set, can be calculated by using the fact that the fraction has a standard normal distribution.
Moments
[edit]The plain and absolute moments of a variable are the expected values of and , respectively. If the expected value of is zero, these parameters are called central moments; otherwise, these parameters are called non-central moments. Usually we are interested only in moments with integer order .
If has a normal distribution, the non-central moments exist and are finite for any whose real part is greater than −1. For any non-negative integer , the plain central moments are:[23]Here denotes the double factorial, that is, the product of all numbers from to 1 that have the same parity as
The central absolute moments coincide with plain moments for all even orders, but are nonzero for odd orders. For any non-negative integer
The last formula is valid also for any non-integer When the mean the plain and absolute moments can be expressed in terms of confluent hypergeometric functions and [24]
These expressions remain valid even if is not an integer. See also generalized Hermite polynomials.
| Order | Non-central moment | Central moment |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
The expectation of conditioned on the event that lies in an interval is given bywhere and respectively are the density and the cumulative distribution function of . For this is known as the inverse Mills ratio. Note that above, density of is used instead of standard normal density as in inverse Mills ratio, so here we have instead of .
Fourier transform and characteristic function
[edit]The Fourier transform of a normal density with mean and variance is[25]
where is the imaginary unit. If the mean , the first factor is 1, and the Fourier transform is, apart from a constant factor, a normal density on the frequency domain, with mean 0 and variance . In particular, the standard normal distribution is an eigenfunction of the Fourier transform.
In probability theory, the Fourier transform of the probability distribution of a real-valued random variable is closely connected to the characteristic function of that variable, which is defined as the expected value of , as a function of the real variable (the frequency parameter of the Fourier transform). This definition can be analytically extended to a complex-value variable .[26] The relation between both is:
Moment- and cumulant-generating functions
[edit]The moment generating function of a real random variable is the expected value of , as a function of the real parameter . For a normal distribution with density , mean and variance , the moment generating function exists and is equal to
The cumulant generating function is the logarithm of the moment generating function, namely
Since this is a quadratic polynomial in , only the first two cumulants are nonzero, namely the mean and the variance .
Some authors prefer to instead work with E[eitX] = eiμt − σ2t2/2 and ln E[eitX] = iμt − 1/2σ2t2.
Stein operator and class
[edit]Within Stein's method the Stein operator and class of a random variable are and the class of all absolutely continuous functions .
Zero-variance limit
[edit]In the limit when tends to zero, the probability density eventually tends to zero at any , but grows without limit if , while its integral remains equal to 1. Therefore, the normal distribution cannot be defined as an ordinary function when .
However, one can define the normal distribution with zero variance as a generalized function; specifically, as a Dirac delta function translated by the mean , that is Its cumulative distribution function is then the Heaviside step function translated by the mean , namely
Maximum entropy
[edit]Of all probability distributions over the reals with a specified finite mean and finite variance , the normal distribution is the one with maximum entropy.[27] To see this, let be a continuous random variable with probability density . The entropy of is defined as[28][29][30]
where is understood to be zero whenever . This functional can be maximized, subject to the constraints that the distribution is properly normalized and has a specified mean and variance, by using variational calculus. A function with three Lagrange multipliers is defined:
At maximum entropy, a small variation about will produce a variation about which is equal to 0:
Since this must hold for any small , the factor multiplying must be zero, and solving for yields:
The Lagrange constraints that is properly normalized and has the specified mean and variance are satisfied if and only if , , and are chosen so thatThe entropy of a normal distribution is equal towhich is independent of the mean .
Other properties
[edit]- If the characteristic function of some random variable is of the form in a neighborhood of zero, where is a polynomial, then the Marcinkiewicz theorem (named after Józef Marcinkiewicz) asserts that can be at most a quadratic polynomial, and therefore is a normal random variable.[31] The consequence of this result is that the normal distribution is the only distribution with a finite number (two) of non-zero cumulants.
- If and are jointly normal and uncorrelated, then they are independent. The requirement that and should be jointly normal is essential; without it the property does not hold.[32][33][proof] For non-normal random variables uncorrelatedness does not imply independence.
- The Kullback–Leibler divergence of one normal distribution from another is given by:[34] The Hellinger distance between the same distributions is equal to
- The Fisher information matrix for a normal distribution w.r.t. and is diagonal and takes the form
- The conjugate prior of the mean of a normal distribution is another normal distribution.[35] Specifically, if are iid and the prior is , then the posterior distribution for the estimator of will be
- The family of normal distributions not only forms an exponential family (EF), but in fact forms a natural exponential family (NEF) with quadratic variance function (NEF-QVF). Many properties of normal distributions generalize to properties of NEF-QVF distributions, NEF distributions, or EF distributions generally. NEF-QVF distributions comprises 6 families, including Poisson, Gamma, binomial, and negative binomial distributions, while many of the common families studied in probability and statistics are NEF or EF.
- In information geometry, the family of normal distributions forms a statistical manifold with constant curvature . The same family is flat with respect to the (±1)-connections and .[36]
- If are distributed according to , then . Note that there is no assumption of independence.[37]
Related distributions
[edit]Central limit theorem
[edit]

The central limit theorem states that under certain (fairly common) conditions, the sum of many random variables will have an approximately normal distribution. More specifically, where are independent and identically distributed random variables with the same arbitrary distribution, zero mean, and variance and is theirmean scaled by Then, as increases, the probability distribution of will tend to the normal distribution with zero mean and variance .
The theorem can be extended to variables that are not independent and/or not identically distributed if certain constraints are placed on the degree of dependence and the moments of the distributions.
Many test statistics, scores, and estimators encountered in practice contain sums of certain random variables in them, and even more estimators can be represented as sums of random variables through the use of influence functions. The central limit theorem implies that those statistical parameters will have asymptotically normal distributions.
The central limit theorem also implies that certain distributions can be approximated by the normal distribution, for example:
- The binomial distribution is approximately normal with mean and variance for large and for not too close to 0 or 1.
- The Poisson distribution with parameter is approximately normal with mean and variance , for large values of .[38]
- The chi-squared distribution is approximately normal with mean and variance , for large .
- The Student's t-distribution is approximately normal with mean 0 and variance 1 when is large.
Whether these approximations are sufficiently accurate depends on the purpose for which they are needed, and the rate of convergence to the normal distribution. It is typically the case that such approximations are less accurate in the tails of the distribution.
A general upper bound for the approximation error in the central limit theorem is given by the Berry–Esseen theorem, improvements of the approximation are given by the Edgeworth expansions.
This theorem can also be used to justify modeling the sum of many uniform noise sources as Gaussian noise. See AWGN.
Operations and functions of normal variables
[edit]
The probability density, cumulative distribution, and inverse cumulative distribution of any function of one or more independent or correlated normal variables can be computed with the numerical method of ray-tracing[39] (Matlab code). In the following sections we look at some special cases.
Operations on a single normal variable
[edit]If is distributed normally with mean and variance , then
- , for any real numbers and , is also normally distributed, with mean and variance . That is, the family of normal distributions is closed under linear transformations.
- The exponential of is distributed log-normally: .
- The standard sigmoid of is logit-normally distributed: .
- The absolute value of has folded normal distribution: . If this is known as the half-normal distribution.
- The absolute value of normalized residuals, , has chi distribution with one degree of freedom: .
- The square of has the noncentral chi-squared distribution with one degree of freedom: . If , the distribution is called simply chi-squared.
- The log-likelihood of a normal variable is simply the log of its probability density function: Since this is a scaled and shifted square of a standard normal variable, it is distributed as a scaled and shifted chi-squared variable.
- The distribution of the variable restricted to an interval is called the truncated normal distribution.
- has a Lévy distribution with location 0 and scale .
Operations on two independent normal variables
[edit]- If and are two independent normal random variables, with means , and variances , , then their sum will also be normally distributed,[proof] with mean and variance .
- In particular, if and are independent normal deviates with zero mean and variance , then and are also independent and normally distributed, with zero mean and variance . This is a special case of the polarization identity.[40]
- If , are two independent normal deviates with mean and variance , and , are arbitrary real numbers, then the variable is also normally distributed with mean and variance . It follows that the normal distribution is stable (with exponent ).
- If , are normal distributions, then their normalized geometric mean is a normal distribution with and (see here for a visualization).
Operations on two independent standard normal variables
[edit]If and are two independent standard normal random variables with mean 0 and variance 1, then
- Their sum and difference is distributed normally with mean zero and variance two: .
- Their product follows the product distribution[41] with density function where is the modified Bessel function of the second kind. This distribution is symmetric around zero, unbounded at , and has the characteristic function .
- Their ratio follows the standard Cauchy distribution: .
- Their Euclidean norm has the Rayleigh distribution.
Operations on multiple independent normal variables
[edit]- Any linear combination of independent normal deviates is a normal deviate.
- If are independent standard normal random variables, then the sum of their squares has the chi-squared distribution with degrees of freedom
- If are independent normally distributed random variables with means and variances , then their sample mean is independent from the sample standard deviation,[42] which can be demonstrated using Basu's theorem or Cochran's theorem.[43] The ratio of these two quantities will have the Student's t-distribution with degrees of freedom:
- If , are independent standard normal random variables, then the ratio of their normalized sums of squares will have the F-distribution with (n, m) degrees of freedom:[44]
Operations on multiple correlated normal variables
[edit]- A quadratic form of a normal vector, i.e. a quadratic function of multiple independent or correlated normal variables, is a generalized chi-square variable.
Operations on the density function
[edit]The split normal distribution is most directly defined in terms of joining scaled sections of the density functions of different normal distributions and rescaling the density to integrate to one. The truncated normal distribution results from rescaling a section of a single density function.
Infinite divisibility and Cramér's theorem
[edit]For any positive integer , any normal distribution with mean and variance is the distribution of the sum of independent normal deviates, each with mean and variance . This property is called infinite divisibility.[45]
Conversely, if and are independent random variables and their sum has a normal distribution, then both and must be normal deviates.[46]
This result is known as Cramér's decomposition theorem, and is equivalent to saying that the convolution of two distributions is normal if and only if both are normal. Cramér's theorem implies that a linear combination of independent non-Gaussian variables will never have an exactly normal distribution, although it may approach it arbitrarily closely.[31]
Bernstein's theorem
[edit]Bernstein's theorem states that if and are independent and and are also independent, then both X and Y must necessarily have normal distributions.[47][48]
More generally, if are independent random variables, then two distinct linear combinations and will be independent if and only if all are normal and , where denotes the variance of .[47]
Extensions
[edit]The notion of normal distribution, being one of the most important distributions in probability theory, has been extended far beyond the standard framework of the univariate (that is one-dimensional) case (Case 1). All these extensions are also called normal or Gaussian laws, so a certain ambiguity in names exists.
- The multivariate normal distribution describes the Gaussian law in the k-dimensional Euclidean space. A vector X ∈ Rk is multivariate-normally distributed if any linear combination of its components Σk
j=1aj Xj has a (univariate) normal distribution. The variance of X is a k×k symmetric positive-definite matrix V. The multivariate normal distribution is a special case of the elliptical distributions. As such, its iso-density loci in the k = 2 case are ellipses and in the case of arbitrary k are ellipsoids. - Rectified Gaussian distribution a rectified version of normal distribution with all the negative elements reset to 0
- Complex normal distribution deals with the complex normal vectors. A complex vector X ∈ Ck is said to be normal if both its real and imaginary components jointly possess a 2k-dimensional multivariate normal distribution. The variance-covariance structure of X is described by two matrices: the variance matrix Γ, and the relation matrix C.
- Matrix normal distribution describes the case of normally distributed matrices.
- Gaussian processes are the normally distributed stochastic processes. These can be viewed as elements of some infinite-dimensional Hilbert space H, and thus are the analogues of multivariate normal vectors for the case k = ∞. A random element h ∈ H is said to be normal if for any constant a ∈ H the scalar product (a, h) has a (univariate) normal distribution. The variance structure of such Gaussian random element can be described in terms of the linear covariance operator K: H → H. Several Gaussian processes became popular enough to have their own names:
- Gaussian q-distribution is an abstract mathematical construction that represents a q-analogue of the normal distribution.
- the q-Gaussian is an analogue of the Gaussian distribution, in the sense that it maximises the Tsallis entropy, and is one type of Tsallis distribution. This distribution is different from the Gaussian q-distribution above.
- The Kaniadakis κ-Gaussian distribution is a generalization of the Gaussian distribution which arises from the Kaniadakis statistics, being one of the Kaniadakis distributions.
A random variable X has a two-piece normal distribution if it has a distribution
where μ is the mean and σ12 and σ22 are the variances of the distribution to the left and right of the mean respectively.
The mean, variance and third central moment of this distribution have been determined[49]
where E(X), V(X) and T(X) are the mean, variance, and third central moment respectively.
One of the main practical uses of the Gaussian law is to model the empirical distributions of many different random variables encountered in practice. In such case a possible extension would be a richer family of distributions, having more than two parameters and therefore being able to fit the empirical distribution more accurately. The examples of such extensions are:
- Pearson distribution — a four-parameter family of probability distributions that extend the normal law to include different skewness and kurtosis values.
- The generalized normal distribution, also known as the exponential power distribution, allows for distribution tails with thicker or thinner asymptotic behaviors.
Statistical inference
[edit]Estimation of parameters
[edit]It is often the case that we do not know the parameters of the normal distribution, but instead want to estimate them. That is, having a sample from a normal population we would like to learn the approximate values of parameters and . The standard approach to this problem is the maximum likelihood method, which requires maximization of the log-likelihood function:Taking derivatives with respect to and and solving the resulting system of first order conditions yields the maximum likelihood estimates:
Then is as follows:
Sample mean
[edit]Estimator is called the sample mean, since it is the arithmetic mean of all observations. The statistic is complete and sufficient for , and therefore by the Lehmann–Scheffé theorem, is the uniformly minimum variance unbiased (UMVU) estimator.[50] In finite samples it is distributed normally:The variance of this estimator is equal to the μμ-element of the inverse Fisher information matrix . This implies that the estimator is finite-sample efficient. Of practical importance is the fact that the standard error of is proportional to , that is, if one wishes to decrease the standard error by a factor of 10, one must increase the number of points in the sample by a factor of 100. This fact is widely used in determining sample sizes for opinion polls and the number of trials in Monte Carlo simulations.
From the standpoint of the asymptotic theory, is consistent, that is, it converges in probability to as . The estimator is also asymptotically normal, which is a simple corollary of the fact that it is normal in finite samples:
Sample variance
[edit]The estimator is called the sample variance, since it is the variance of the sample (). In practice, another estimator is often used instead of the . This other estimator is denoted , and is also called the sample variance, which represents a certain ambiguity in terminology; its square root is called the sample standard deviation. The estimator differs from by having (n − 1) instead of n in the denominator (the so-called Bessel's correction):The difference between and becomes negligibly small for large n's. In finite samples however, the motivation behind the use of is that it is an unbiased estimator of the underlying parameter , whereas is biased. Also, by the Lehmann–Scheffé theorem the estimator is uniformly minimum variance unbiased (UMVU),[50] which makes it the "best" estimator among all unbiased ones. However it can be shown that the biased estimator is better than the in terms of the mean squared error (MSE) criterion. In finite samples both and have scaled chi-squared distribution with (n − 1) degrees of freedom:The first of these expressions shows that the variance of is equal to , which is slightly greater than the σσ-element of the inverse Fisher information matrix . Thus, is not an efficient estimator for , and moreover, since is UMVU, we can conclude that the finite-sample efficient estimator for does not exist.
Applying the asymptotic theory, both estimators and are consistent, that is they converge in probability to as the sample size . The two estimators are also both asymptotically normal:In particular, both estimators are asymptotically efficient for .
Confidence intervals
[edit]By Cochran's theorem, for normal distributions the sample mean and the sample variance s2 are independent, which means there can be no gain in considering their joint distribution. There is also a converse theorem: if in a sample the sample mean and sample variance are independent, then the sample must have come from the normal distribution. The independence between and s can be employed to construct the so-called t-statistic:This quantity t has the Student's t-distribution with (n − 1) degrees of freedom, and it is an ancillary statistic (independent of the value of the parameters). Inverting the distribution of this t-statistics will allow us to construct the confidence interval for μ;[51] similarly, inverting the χ2 distribution of the statistic s2 will give us the confidence interval for σ2:[52]where tk,p and χ 2
k,p are the pth quantiles of the t- and χ2-distributions respectively. These confidence intervals are of the confidence level 1 − α, meaning that the true values μ and σ2 fall outside of these intervals with probability (or significance level) α. In practice people usually take α = 5%, resulting in the 95% confidence intervals.
Approximate formulas can be derived from the asymptotic distributions of and s2:The approximate formulas become valid for large values of n, and are more convenient for the manual calculation since the standard normal quantiles zα/2 do not depend on n. In particular, the most popular value of α = 5%, results in |z0.025| = 1.96.
Normality tests
[edit]Normality tests assess the likelihood that the given data set {x1, ..., xn} comes from a normal distribution. Typically the null hypothesis H0 is that the observations are distributed normally with unspecified mean μ and variance σ2, versus the alternative Ha that the distribution is arbitrary. Many tests (over 40) have been devised for this problem. The more prominent of them are outlined below:
Diagnostic plots are more intuitively appealing but subjective at the same time, as they rely on informal human judgement to accept or reject the null hypothesis.
- Q–Q plot, also known as normal probability plot or rankit plot—is a plot of the sorted values from the data set against the expected values of the corresponding quantiles from the standard normal distribution. That is, it is a plot of point of the form (Φ−1(pk), x(k)), where plotting points pk are equal to pk = (k − α)/(n + 1 − 2α) and α is an adjustment constant, which can be anything between 0 and 1. If the null hypothesis is true, the plotted points should approximately lie on a straight line.
- P–P plot – similar to the Q–Q plot, but used much less frequently. This method consists of plotting the points (Φ(z(k)), pk), where . For normally distributed data this plot should lie on a 45° line between (0, 0) and (1, 1).
Goodness-of-fit tests:
Moment-based tests:
- D'Agostino's K-squared test
- Jarque–Bera test
- Shapiro–Wilk test: This is based on the fact that the line in the Q–Q plot has the slope of σ. The test compares the least squares estimate of that slope with the value of the sample variance, and rejects the null hypothesis if these two quantities differ significantly.
Tests based on the empirical distribution function:
- Anderson–Darling test
- Lilliefors test (an adaptation of the Kolmogorov–Smirnov test)
Bayesian analysis of the normal distribution
[edit]Bayesian analysis of normally distributed data is complicated by the many different possibilities that may be considered:
- Either the mean, or the variance, or neither, may be considered a fixed quantity.
- When the variance is unknown, analysis may be done directly in terms of the variance, or in terms of the precision, the reciprocal of the variance. The reason for expressing the formulas in terms of precision is that the analysis of most cases is simplified.
- Both univariate and multivariate cases need to be considered.
- Either conjugate or improper prior distributions may be placed on the unknown variables.
- An additional set of cases occurs in Bayesian linear regression, where in the basic model the data is assumed to be normally distributed, and normal priors are placed on the regression coefficients. The resulting analysis is similar to the basic cases of independent identically distributed data.
The formulas for the non-linear-regression cases are summarized in the conjugate prior article.
Sum of two quadratics
[edit]Scalar form
[edit]The following auxiliary formula is useful for simplifying the posterior update equations, which otherwise become fairly tedious.
This equation rewrites the sum of two quadratics in x by expanding the squares, grouping the terms in x, and completing the square. Note the following about the complex constant factors attached to some of the terms:
- The factor has the form of a weighted average of y and z.
- This shows that this factor can be thought of as resulting from a situation where the reciprocals of quantities a and b add directly, so to combine a and b themselves, it is necessary to reciprocate, add, and reciprocate the result again to get back into the original units. This is exactly the sort of operation performed by the harmonic mean, so it is not surprising that is one-half the harmonic mean of a and b.
Vector form
[edit]A similar formula can be written for the sum of two vector quadratics: If x, y, z are vectors of length k, and A and B are symmetric, invertible matrices of size , then
where
The form x′ A x is called a quadratic form and is a scalar:In other words, it sums up all possible combinations of products of pairs of elements from x, with a separate coefficient for each. In addition, since , only the sum matters for any off-diagonal elements of A, and there is no loss of generality in assuming that A is symmetric. Furthermore, if A is symmetric, then the form
Sum of differences from the mean
[edit]Another useful formula is as follows:where
With known variance
[edit]For a set of i.i.d. normally distributed data points X of size n where each individual point x follows with known variance σ2, the conjugate prior distribution is also normally distributed.
This can be shown more easily by rewriting the variance as the precision, i.e. using τ = 1/σ2. Then if and we proceed as follows.
First, the likelihood function is (using the formula above for the sum of differences from the mean):
Then, we proceed as follows:
In the above derivation, we used the formula above for the sum of two quadratics and eliminated all constant factors not involving μ. The result is the kernel of a normal distribution, with mean and precision , i.e.
This can be written as a set of Bayesian update equations for the posterior parameters in terms of the prior parameters:
That is, to combine n data points with total precision of nτ (or equivalently, total variance of n/σ2) and mean of values , derive a new total precision simply by adding the total precision of the data to the prior total precision, and form a new mean through a precision-weighted average, i.e. a weighted average of the data mean and the prior mean, each weighted by the associated total precision. This makes logical sense if the precision is thought of as indicating the certainty of the observations: In the distribution of the posterior mean, each of the input components is weighted by its certainty, and the certainty of this distribution is the sum of the individual certainties. (For the intuition of this, compare the expression "the whole is (or is not) greater than the sum of its parts". In addition, consider that the knowledge of the posterior comes from a combination of the knowledge of the prior and likelihood, so it makes sense that we are more certain of it than of either of its components.)
The above formula reveals why it is more convenient to do Bayesian analysis of conjugate priors for the normal distribution in terms of the precision. The posterior precision is simply the sum of the prior and likelihood precisions, and the posterior mean is computed through a precision-weighted average, as described above. The same formulas can be written in terms of variance by reciprocating all the precisions, yielding the more ugly formulas
With known mean
[edit]For a set of i.i.d. normally distributed data points X of size n where each individual point x follows with known mean μ, the conjugate prior of the variance has an inverse gamma distribution or a scaled inverse chi-squared distribution. The two are equivalent except for having different parameterizations. Although the inverse gamma is more commonly used, we use the scaled inverse chi-squared for the sake of convenience. The prior for σ2 is as follows:
The likelihood function from above, written in terms of the variance, is:
where
Then:
The above is also a scaled inverse chi-squared distribution where
or equivalently
Reparameterizing in terms of an inverse gamma distribution, the result is:
With unknown mean and unknown variance
[edit]For a set of i.i.d. normally distributed data points X of size n where each individual point x follows with unknown mean μ and unknown variance σ2, a combined (multivariate) conjugate prior is placed over the mean and variance, consisting of a normal-inverse-gamma distribution.Logically, this originates as follows:
- From the analysis of the case with unknown mean but known variance, we see that the update equations involve sufficient statistics computed from the data consisting of the mean of the data points and the total variance of the data points, computed in turn from the known variance divided by the number of data points.
- From the analysis of the case with unknown variance but known mean, we see that the update equations involve sufficient statistics over the data consisting of the number of data points and sum of squared deviations.
- Keep in mind that the posterior update values serve as the prior distribution when further data is handled. Thus, we should logically think of our priors in terms of the sufficient statistics just described, with the same semantics kept in mind as much as possible.
- To handle the case where both mean and variance are unknown, we could place independent priors over the mean and variance, with fixed estimates of the average mean, total variance, number of data points used to compute the variance prior, and sum of squared deviations. Note however that in reality, the total variance of the mean depends on the unknown variance, and the sum of squared deviations that goes into the variance prior (appears to) depend on the unknown mean. In practice, the latter dependence is relatively unimportant: Shifting the actual mean shifts the generated points by an equal amount, and on average the squared deviations will remain the same. This is not the case, however, with the total variance of the mean: As the unknown variance increases, the total variance of the mean will increase proportionately, and we would like to capture this dependence.
- This suggests that we create a conditional prior of the mean on the unknown variance, with a hyperparameter specifying the mean of the pseudo-observations associated with the prior, and another parameter specifying the number of pseudo-observations. This number serves as a scaling parameter on the variance, making it possible to control the overall variance of the mean relative to the actual variance parameter. The prior for the variance also has two hyperparameters, one specifying the sum of squared deviations of the pseudo-observations associated with the prior, and another specifying once again the number of pseudo-observations. Each of the priors has a hyperparameter specifying the number of pseudo-observations, and in each case this controls the relative variance of that prior. These are given as two separate hyperparameters so that the variance (aka the confidence) of the two priors can be controlled separately.
- This leads immediately to the normal-inverse-gamma distribution, which is the product of the two distributions just defined, with conjugate priors used (an inverse gamma distribution over the variance, and a normal distribution over the mean, conditional on the variance) and with the same four parameters just defined.
The priors are normally defined as follows:
The update equations can be derived, and look as follows:
The respective numbers of pseudo-observations add the number of actual observations to them. The new mean hyperparameter is once again a weighted average, this time weighted by the relative numbers of observations. Finally, the update for is similar to the case with known mean, but in this case the sum of squared deviations is taken with respect to the observed data mean rather than the true mean, and as a result a new interaction term needs to be added to take care of the additional error source stemming from the deviation between prior and data mean.
The prior distributions are
Therefore, the joint prior is
The likelihood function from the section above with known variance is:
Writing it in terms of variance rather than precision, we get:where
Therefore, the posterior is (dropping the hyperparameters as conditioning factors):
In other words, the posterior distribution has the form of a product of a normal distribution over times an inverse gamma distribution over , with parameters that are the same as the update equations above.
Occurrence and applications
[edit]Возникновение нормального распределения в практических задачах можно условно разделить на четыре категории:
- Точно нормальные распределения;
- Приблизительно нормальные законы, например, когда такое приближение оправдано центральной предельной теоремой ; и
- Распределения моделируются как нормальные: нормальное распределение представляет собой распределение с максимальной энтропией для заданного среднего значения и дисперсии.
- Проблемы регрессии – нормальное распределение обнаруживается после того, как систематические эффекты были достаточно хорошо смоделированы.
Точная нормальность
[ редактировать ]
Некоторые величины в физике распределяются нормально, как это впервые продемонстрировал Джеймс Клерк Максвелл . Примеры таких величин:
- Функция плотности вероятности основного состояния квантового гармонического осциллятора .
- Положение частицы, испытывающей диффузию . Если изначально частица находится в конкретной точке (то есть ее распределение вероятностей — дельта-функция Дирака ), то по истечении времени t ее местоположение описывается нормальным распределением с дисперсией t , которое удовлетворяет уравнению диффузии . Если начальное местоположение задано некоторой функцией плотности то плотность в момент времени t представляет собой свертку g , и нормальной функции плотности вероятности.
Приблизительная нормальность
[ редактировать ]Приблизительно нормальное распределение встречается во многих ситуациях, как это объясняется центральной предельной теоремой . Когда результат создается множеством небольших эффектов, действующих аддитивно и независимо , его распределение будет близко к нормальному. Нормальное приближение не будет действительным, если эффекты действуют мультипликативно (а не аддитивно) или если существует одно внешнее влияние, которое имеет значительно большую величину, чем остальные эффекты.
- В задачах счета, где центральная предельная теорема включает приближение от дискретного к континуальному и где бесконечно делимые и разложимые задействованы распределения, такие как
- Биномиальные случайные величины , связанные с бинарными переменными отклика;
- Случайные величины Пуассона , связанные с редкими событиями;
- Тепловое излучение имеет распределение Бозе-Эйнштейна на очень коротких временных масштабах и нормальное распределение на более длительных временных масштабах из-за центральной предельной теоремы.
Предполагаемая нормальность
[ редактировать ]
Я могу лишь признать появление нормальной кривой – лапласовой кривой ошибок – весьма ненормальным явлением. В некоторых дистрибутивах он примерно приближается к ; по этой причине, а также ввиду его прекрасной простоты, мы, возможно, можем использовать его в качестве первого приближения, особенно в теоретических исследованиях.
Существуют статистические методы эмпирической проверки этого предположения; см. выше раздел «Тестирование нормальности» .
- В биологии логарифмы (после разделения на мужские различных переменных имеют тенденцию иметь нормальное распределение, то есть они имеют тенденцию иметь логарифмически нормальное распределение и женские субпопуляции), в том числе примеры:
- Меры размера живой ткани (длина, высота, площадь кожи, вес); [53]
- Длина в придатков инертных (волос, когтей, ногтей, зубов) биологических особей направлении роста ; предположительно, под эту категорию подпадает и толщина древесной коры;
- Определенные физиологические измерения, такие как артериальное давление взрослых людей.
- В финансах, в частности в модели Блэка-Шоулза , изменения логарифма обменных курсов, индексов цен и индексов фондового рынка считаются нормальными (эти переменные ведут себя как сложные проценты , а не как простые проценты, и поэтому являются мультипликативными). Некоторые математики, такие как Бенуа Мандельброт, утверждали, что лог-распределения Леви с тяжелыми хвостами были бы более подходящей моделью, в частности, для анализа обвалов фондового рынка . Использование предположения о нормальном распределении в финансовых моделях также подвергалось критике со стороны Нассима Николаса Талеба в его работах.
- Ошибки измерений в физических экспериментах часто моделируются нормальным распределением. Такое использование нормального распределения не означает, что предполагается, что ошибки измерения имеют нормальное распределение; скорее, использование нормального распределения дает наиболее консервативные прогнозы, возможные при условии знания только среднего значения и дисперсии ошибок. [54]
- При стандартизированном тестировании результаты могут иметь нормальное распределение, выбирая количество и сложность вопросов (как в тесте IQ ) или преобразуя необработанные результаты теста в выходные баллы, подгоняя их к нормальному распределению. Например, традиционный диапазон SAT 200–800 основан на нормальном распределении со средним значением 500 и стандартным отклонением 100.

- Многие оценки получены на основе нормального распределения, включая процентильные ранги (процентили или квантили), эквиваленты нормальной кривой , станины , z-показатели и T-показатели. Кроме того, некоторые поведенческие статистические процедуры предполагают, что баллы распределяются нормально; например, t-тесты и ANOVA . Оценивание по кривой колокола присваивает относительные оценки на основе нормального распределения баллов.
- В гидрологии распределение долговременного речного стока или осадков, например, месячных и годовых сумм, часто считается практически нормальным в соответствии с центральной предельной теоремой . [55] Синее изображение, сделанное с помощью CumFreq , иллюстрирует пример подбора нормального распределения к ранжированным октябрьским осадкам, показывающим 90% доверительный интервал на основе биномиального распределения . Данные об осадках представлены в виде координат на графике в рамках кумулятивного частотного анализа .
Методологические проблемы и экспертная оценка
[ редактировать ]Джон Иоаннидис утверждал , что использование нормально распределенных стандартных отклонений в качестве стандартов для проверки результатов исследований оставляет непроверенными фальсифицируемые предсказания о явлениях, которые обычно не распределяются. Сюда относятся, например, явления, которые возникают только при наличии всех необходимых условий и одно не может быть заменено другим путем сложения, и явления, которые не распределены случайным образом. Иоаннидис утверждает, что проверка, ориентированная на стандартное отклонение, создает ложную видимость достоверности гипотез и теорий, в которых некоторые, но не все фальсифицируемые прогнозы нормально распределены, поскольку часть фальсифицируемых прогнозов, против которых имеются доказательства, может, а в некоторых случаях, находится в ненормально распределенные части диапазона фальсифицируемых предсказаний, а также безосновательное отвержение гипотез, для которых ни одно из фальсифицируемых предсказаний обычно не распределяется так, как если бы они были нефальсифицируемы, тогда как на самом деле они делают фальсифицируемые предсказания. Иоаннидис утверждает, что многие случаи принятия взаимоисключающих теорий как подтвержденные исследовательскими журналами вызваны неспособностью журналов принять эмпирические фальсификации предсказаний с ненормально распределенным распределением, а не потому, что взаимоисключающие теории верны, чего они не могут сделать. быть, хотя две взаимоисключающие теории могут быть как неправильными, так и третья правильной. [56]
Вычислительные методы
[ редактировать ]Генерация значений из нормального распределения
[ редактировать ]
В компьютерном моделировании, особенно в приложениях метода Монте-Карло , часто желательно генерировать значения, которые имеют нормальное распределение. Все перечисленные ниже алгоритмы генерируют стандартные нормальные отклонения, поскольку N ( µ , σ 2 ) может быть сгенерирован как X = µ + σZ , где Z — стандартная нормаль. Все эти алгоритмы полагаются на наличие генератора случайных чисел U, способного генерировать однородные случайные величины.
- Самый простой метод основан на свойстве преобразования интеграла вероятности : если U распределено равномерно на (0,1), то Φ −1 ( U ) будет иметь стандартное нормальное распределение. Недостатком этого метода является то, что он основан на вычислении пробит-функции Φ −1 , что невозможно сделать аналитически. Некоторые приближенные методы описаны у Харта (1968) и в статье erf . Вичура предлагает быстрый алгоритм вычисления этой функции с точностью до 16 знаков после запятой. [57] который используется R для вычисления случайных величин нормального распределения.
- Простой в программировании приближенный подход , основанный на центральной предельной теореме, заключается в следующем: сгенерируйте 12 равномерных отклонений U (0,1), сложите их все и вычтите 6 – полученная случайная величина будет иметь примерно стандартное нормальное распределение. По правде говоря, распределение будет Ирвина-Холла , которое представляет собой аппроксимацию нормального распределения полиномом одиннадцатого порядка из 12 секций. Это случайное отклонение будет иметь ограниченный диапазон (-6, 6). [58] Обратите внимание, что при истинно нормальном распределении только 0,00034% всех выборок выходят за пределы ±6σ.
- Метод Бокса – Мюллера использует два независимых случайных числа U и V распределенных , равномерно по (0,1). Тогда две случайные величины X и Y оба будут иметь стандартное нормальное распределение и будут независимыми . Эта формулировка возникает потому, что для двумерного нормального случайного вектора ( X , Y ) квадрат нормы X 2 + И 2 будет иметь распределение хи-квадрат с двумя степенями свободы, которое представляет собой легко генерируемую экспоненциальную случайную величину, соответствующую величине −2 ln( U ) в этих уравнениях; и угол равномерно распределен по кругу, выбранному случайной величиной V .
- представляет Полярный метод Марсальи собой модификацию метода Бокса – Мюллера, которая не требует вычисления функций синуса и косинуса. В этом методе U и V извлекаются из равномерного (−1,1) распределения, а затем S = U 2 + V 2 вычисляется. Если S больше или равно 1, метод начинается заново, в противном случае две величины возвращаются. Опять же, X и Y — независимые стандартные нормальные случайные величины.
- Метод отношений [59] это метод отказа. Алгоритм действует следующим образом:
- Сгенерируйте два независимых равномерных отклонения U и V ;
- Вычислить X = √ 8/ e ( V - 0,5)/ U ;
- Необязательно: если X 2 ≤ 5 − 4 е 1/4 Затем вы принимаете X и завершаете алгоритм;
- Необязательно: если X 2 ≥ 4 е −1.35 / U + 1,4, затем отклоните X и начните заново с шага 1;
- Если Х 2 ≤ −4 ln U, тогда примите X , иначе начните алгоритм заново.
- Два дополнительных шага позволяют в большинстве случаев избежать вычисления логарифма на последнем шаге. Эти шаги можно значительно улучшить [60] так что логарифм вычисляется редко.
- Алгоритм зиккурата [61] быстрее, чем преобразование Бокса-Мюллера, но при этом является точным. Примерно в 97% всех случаев он использует только два случайных числа: одно случайное целое и одно случайное равномерное, одно умножение и проверку if. Только в 3% случаев, когда комбинация этих двух факторов выходит за пределы «ядра зиккурата» (своего рода отбраковочная выборка с использованием логарифмов), приходится использовать экспоненту и более однородные случайные числа.
- Целочисленную арифметику можно использовать для выборки из стандартного нормального распределения. [62] Этот метод точен в том смысле, что он удовлетворяет условиям идеального приближения ; [63] т. е. это эквивалентно выборке действительного числа из стандартного нормального распределения и округлению его до ближайшего представимого числа с плавающей запятой.
- Также есть расследование [64] в связь между быстрым преобразованием Адамара и нормальным распределением, поскольку преобразование использует только сложение и вычитание, и согласно центральной предельной теореме случайные числа практически из любого распределения будут преобразованы в нормальное распределение. В этом отношении серию преобразований Адамара можно комбинировать со случайными перестановками, чтобы превратить произвольные наборы данных в нормально распределенные данные.
Численные аппроксимации нормальной кумулятивной функции распределения и нормальной функции квантиля
[ редактировать ]Стандартная функция нормального кумулятивного распределения широко используется в научных и статистических вычислениях.
Значения Φ( x ) могут быть очень точно аппроксимированы различными методами, такими как численное интегрирование , ряд Тейлора , асимптотический ряд и цепные дроби . В зависимости от желаемого уровня точности используются различные приближения.
- Зелен и Северо (1964) дают аппроксимацию Φ( x ) для x > 0 с абсолютной ошибкой | ε ( Икс ) | < 7,5·10 −8 (алгоритм 26.2.17 ): где φ ( x ) — стандартная нормальная функция плотности вероятности, а b 0 = 0,2316419, b 1 = 0,319381530, b 2 = -0,356563782, b 3 = 1,781477937, b 4 = -1,821255978, b 5 = 1,330274429.
- Харт (1968) перечисляет несколько десятков аппроксимаций – с помощью рациональных функций, с экспонентами или без них – для функция erfc() . Его алгоритмы различаются по степени сложности и получаемой точности: максимальная абсолютная точность составляет 24 цифры. Алгоритм Уэста (2009) сочетает в себе алгоритм Харта 5666 с аппроксимацией непрерывной дроби в хвосте, чтобы обеспечить быстрый алгоритм вычислений с точностью до 16 цифр.
- Коди (1969), вспомнив, что решение Hart68 не подходит для erf, дает решение как для erf, так и для erfc с максимальной границей относительной ошибки с помощью рационального приближения Чебышева .
- Марсалья (2004) предложил простой алгоритм. [примечание 1] на основе разложения в ряд Тейлора для вычисления Φ( x ) с произвольной точностью. Недостатком этого алгоритма является сравнительно медленное время расчета (например, для вычисления функции с точностью до 16 знаков при x = 10 требуется более 300 итераций ).
- Научная библиотека GNU вычисляет значения стандартной нормальной кумулятивной функции распределения, используя алгоритмы Харта и аппроксимации с помощью полиномов Чебышева .
- Диа (2023) предлагает следующее приближение с максимальной относительной погрешностью менее по абсолютной величине: за и для ,
Шор (1982) представил простые аппроксимации, которые могут быть включены в модели стохастической оптимизации инженерных и эксплуатационных исследований, такие как проектирование надежности и анализ запасов. Обозначая p = Φ( z ) , простейшим приближением для функции квантиля является:
Это приближение дает для z максимальную абсолютную ошибку 0,026 (для 0,5 ≤ p ≤ 0,9999 , что соответствует 0 ≤ z ≤ 3,719 ). Для p < 1/2 замените p на 1 − p и поменяйте знак. Другое приближение, несколько менее точное, — это однопараметрическое приближение:
Последнее послужило для получения простой аппроксимации интеграла потерь нормального распределения, определяемого формулой
Это приближение особенно точно для правого дальнего хвоста (максимальная ошибка 10 −3 для z≥1,4). Высокоточные аппроксимации кумулятивной функции распределения, основанные на методологии моделирования отклика (RMM, Shore, 2011, 2012), показаны в Shore (2005).
Еще несколько приближений можно найти по адресу: Функция ошибки#Приближение элементарными функциями . В частности, небольшая относительная ошибка во всей области для кумулятивной функции распределения и функция квантиля также достигается с помощью явно обратимой формулы Сергея Виницкого в 2008 году.
История
[ редактировать ]Разработка
[ редактировать ]Некоторые авторы [65] [66] приписывают заслугу открытия нормального распределения де Муавра , который в 1738 г. [примечание 2] опубликовал во втором издании своей «Доктрины шансов» исследование коэффициентов разложения биномиального ( a + b ) н . Де Муавр доказал, что средний член этого расширения имеет приблизительную величину , и что «Если m или 1 / 2 n — бесконечно большая Величина, то логарифм отношения, которое Член, отстоящий от середины на Интервал ℓ , имеет к среднему Члену, равен ." [67] Хотя эту теорему можно интерпретировать как первое неясное выражение нормального закона вероятности, Стиглер указывает, что сам де Муавр не интерпретировал свои результаты как нечто большее, чем приближенное правило для биномиальных коэффициентов, и, в частности, у де Муавра не было концепции функция плотности вероятности. [68]

В 1823 году Гаусс опубликовал свою монографию « Theoria Combinis Observeum erroribus minimis obnoxiae », где, среди прочего, он вводит несколько важных статистических понятий, таких как метод наименьших квадратов , метод максимального правдоподобия и нормальное распределение . Гаусс использовал M , M ′ , M ", ... для обозначения измерений некоторой неизвестной величины V и искал наиболее вероятную оценку этой величины: ту, которая максимизирует вероятность φ ( M − V ) · φ ( M ′ − V ) · φ ( M » − V ) · ... получения наблюдаемых экспериментальных результатов. В его обозначениях φΔ — функция плотности вероятности ошибок измерения величины Δ. Не зная, что такое функция φ , Гаусс требует, чтобы его метод сводился к известному ответу: среднему арифметическому измеренных величин. [примечание 3] Исходя из этих принципов, Гаусс показывает, что единственным законом, который рационализирует выбор среднего арифметического в качестве оценки параметра местоположения, является нормальный закон ошибок: [69] где h - «мера точности наблюдений». Используя этот нормальный закон в качестве общей модели ошибок в экспериментах, Гаусс формулирует то, что сейчас известно как нелинейный взвешенный метод наименьших квадратов . [70]

Хотя Гаусс был первым, кто предложил закон нормального распределения, Лаплас внес значительный вклад. [примечание 4] Именно Лаплас впервые поставил задачу объединения нескольких наблюдений в 1774 году. [71] хотя его собственное решение привело к распределению Лапласа . Именно Лаплас первым вычислил значение интеграла ∫ e − т 2 dt = √ π в 1782 году, что обеспечивает константу нормализации нормального распределения. [72] Наконец, именно Лаплас в 1810 году доказал и представил академии фундаментальную центральную предельную теорему , подчеркивавшую теоретическую важность нормального распределения. [73]
Интересно отметить, что в 1809 году американский математик ирландского происхождения Роберт Адрейн опубликовал два проницательных, но ошибочных вывода нормального закона вероятности, одновременно и независимо от Гаусса. [74] Его работы оставались по большей части незамеченными научным сообществом, пока в 1871 году их не эксгумировал Аббе . [75]
В середине XIX века Максвелл продемонстрировал, что нормальное распределение является не только удобным математическим инструментом, но может встречаться и в природных явлениях: [76] Число частиц, скорость которых, разрешенная в определенном направлении, лежит между x и x + dx, равна
Мы
[ редактировать ]Сегодня эта концепция обычно известна на английском языке как нормальное распределение или распределение Гаусса . Другие менее распространенные названия включают распределение Гаусса, распределение Лапласа-Гаусса, закон ошибок, закон возможности ошибок, второй закон Лапласа и закон Гаусса.
Сам Гаусс, по-видимому, придумал этот термин в отношении «нормальных уравнений», используемых в его приложениях, причем «нормальный» имеет техническое значение «ортогональный», а не «обычный». [77] Однако к концу XIX века некоторые авторы [примечание 5] начал использовать название «нормальное распределение », где слово «нормальный» использовалось как прилагательное – этот термин теперь рассматривается как отражение того факта, что это распределение считалось типичным, распространенным – и, следовательно, нормальным. Пирс (один из этих авторов) однажды определил понятие «нормальности» следующим образом: «...«норма» — это не среднее (или какое-либо другое среднее значение) того, что происходит на самом деле, а то, что произойдет в долгосрочной перспективе. при определенных обстоятельствах». [78] Примерно на рубеже 20-го века Пирсон популяризировал термин «норма» как обозначение этого распределения. [79]
Много лет назад я назвал кривую Лапласа-Гаусса нормальной кривой, это название, хотя оно и избегает международного вопроса о приоритете, имеет тот недостаток, что заставляет людей поверить, что все другие распределения частот в том или ином смысле являются «ненормальными».
Кроме того, именно Пирсон первым записал распределение в терминах стандартного отклонения σ в современных обозначениях. Вскоре после этого, в 1915 году, Фишер добавил в формулу нормального распределения параметр местоположения, выразив его так, как он пишется сейчас:
Термин «стандартное нормальное», обозначающий нормальное распределение с нулевым средним значением и единичной дисперсией, стал широко использоваться примерно в 1950-х годах, появившись в популярных учебниках П. Г. Хоэля (1947) « Введение в математическую статистику» и А. М. Муда (1950) « Введение в математическую статистику ». Теория статистики . [80]
См. также
[ редактировать ]- Распределение Бейтса - аналогично распределению Ирвина – Холла, но масштабировано обратно в диапазон от 0 до 1.
- Проблема Беренса-Фишера - давняя проблема проверки того, имеют ли две нормальные выборки с разными дисперсиями одинаковые средние значения;
- Расстояние Бхаттачарьи - метод, используемый для разделения смесей нормальных распределений.
- Теорема Эрдеша – Каца - о возникновении нормального распределения в теории чисел.
- Полная ширина на половине максимума
- Размытие по Гауссу — свертка , использующая в качестве ядра нормальное распределение.
- Модифицированное полунормальное распределение [81] с PDF-файлом на дается как , где обозначает Пси-функцию Фокса–Райта .
- Нормально распределенные и некоррелированные не означают независимости.
- Отношение нормального распределения
- Взаимное нормальное распределение
- Стандартный обычный стол
- Лемма Штейна
- Субгауссово распределение
- Сумма нормально распределенных случайных величин
- Распределение Твиди . Нормальное распределение является членом семейства моделей экспоненциальной дисперсии Твиди .
- Обернутое нормальное распределение - нормальное распределение, примененное к круговой области.
- Z-тест – использование нормального распределения
Примечания
[ редактировать ]- ^ Например, этот алгоритм приведен в статье Язык программирования Bc .
- ^ Де Муавр впервые опубликовал эти результаты в 1733 году в брошюре «Приближение суммы биномиальных членов ( a + b )». n в Seriem Expansi , предназначенный только для частного обращения. Но только в 1738 году он обнародовал свои результаты. Оригинальная брошюра переиздавалась несколько раз, см., например, Walker (1985) .
- ^ «Было принято считать аксиомой гипотезу о том, что если какая-либо величина была определена путем нескольких прямых наблюдений, выполненных при одинаковых обстоятельствах и с одинаковой тщательностью, то среднее арифметическое наблюдаемых значений дает наиболее вероятное значение, если не строго, но, по крайней мере, почти так, чтобы всегда было безопаснее придерживаться его». — Гаусс (1809 , раздел 177)
- ^ «Мой обычай называть кривую кривой Гаусса-Лапласа или нормальной кривой спасает нас от пропорционального распределения заслуг открытия между двумя великими астрономами-математиками». цитата Пирсона (1905 , стр. 189)
- ^ Помимо тех, которые специально упомянуты здесь, такое использование встречается в работах Пирса , Гальтона ( Galton (1889 , глава V)) и Lexis ( Lexis (1878) , Rohrbasser & Véron (2003) ) c. 1875. [ нужна ссылка ]
Ссылки
[ редактировать ]Цитаты
[ редактировать ]- ^ Нортон, Мэтью; Хохлов, Валентин; Урясев, Стэн (2019). «Расчет CVaR и bPOE для распространенных распределений вероятностей с применением для оптимизации портфеля и оценки плотности» (PDF) . Анналы исследования операций . 299 (1–2). Спрингер: 1281–1315. arXiv : 1811.11301 . дои : 10.1007/s10479-019-03373-1 . S2CID 254231768 . Проверено 27 февраля 2023 г.
- ^ Нормальное распределение , Энциклопедия психологии Гейла
- ^ Казелла и Бергер (2001 , стр. 102)
- ^ Лион, А. (2014). Почему нормальные распределения нормальны? , Британский журнал философии науки.
- ^ Хорхе, Носедаль; Стефан, Дж. Райт (2006). Численная оптимизация (2-е изд.). Спрингер. п. 249. ИСБН 978-0387-30303-1 .
- ^ Перейти обратно: а б «Нормальное распределение» . www.mathsisfun.com . Проверено 15 августа 2020 г.
- ^ Стиглер (1982)
- ^ Гальперин, Хартли и Хоэл (1965 , пункт 7)
- ^ Макферсон (1990 , стр. 110)
- ^ Бернардо и Смит (2000 , стр. 121)
- ^ Скотт, Клейтон; Новак, Роберт (7 августа 2003 г.). «Q-функция» . Связи .
- ^ Барак, Охад (6 апреля 2006 г.). «Функция Q и функция ошибки» (PDF) . Тель-Авивский университет. Архивировано из оригинала (PDF) 25 марта 2009 г.
- ^ Вайсштейн, Эрик В. «Функция нормального распределения» . Математический мир .
- ^ Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 26, уравнение 26.2.12» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. п. 932. ИСБН 978-0-486-61272-0 . LCCN 64-60036 . МР 0167642 . LCCN 65-12253 .
- ^ Ваарт, А.В. ван дер (13 октября 1998 г.). Асимптотическая статистика . Издательство Кембриджского университета. дои : 10.1017/cbo9780511802256 . ISBN 978-0-511-80225-6 .
- ^ Обложка, Томас М.; Томас, Джой А. (2006). Элементы теории информации . Джон Уайли и сыновья. п. 254 . ISBN 9780471748816 .
- ^ Пак, Сон Ю.; Бера, Анил К. (2009). «Модель условной гетероскедастичности с максимальной энтропией авторегрессии» (PDF) . Журнал эконометрики . 150 (2): 219–230. CiteSeerX 10.1.1.511.9750 . doi : 10.1016/j.jeconom.2008.12.014 . Архивировано из оригинала (PDF) 7 марта 2016 года . Проверено 2 июня 2011 г.
- ^ Гири RC (1936) Распределение «коэффициента Стьюдента для ненормальных выборок». Приложение к журналу Королевского статистического общества 3 (2): 178–184.
- ^ Лукач, Евгений (март 1942 г.). «Характеристика нормального распределения». Анналы математической статистики . 13 (1): 91–93. дои : 10.1214/AOMS/1177731647 . ISSN 0003-4851 . JSTOR 2236166 . МР 0006626 . Збл 0060.28509 . Викиданные Q55897617 .
- ^ Перейти обратно: а б с Патель и Рид (1996 , [2.1.4])
- ^ Из (1991 , стр. 1258)
- ^ Патель и Рид (1996 , [2.1.8])
- ^ Папулис, Афанасий. Вероятность, случайные величины и случайные процессы (4-е изд.). п. 148.
- ^ Винкельбауэр, Андреас (2012). «Моменты и абсолютные моменты нормального распределения». arXiv : 1209.4340 [ math.ST ].
- ^ Брик (1995 , стр. 23)
- ^ Брик (1995 , стр. 24)
- ^ Обложка и Томас (2006 , стр. 254)
- ^ Уильямс, Дэвид (2001). Взвешивание шансов: курс вероятности и статистики (перепечатано под ред.). Кембридж [ua]: Cambridge Univ. Нажимать. стр. 197–199 . ISBN 978-0-521-00618-7 .
- ^ Смит, Хосе М. Бернардо; Адриан Ф.М. (2000). Байесовская теория (Переиздание). Чичестер [ua]: Уайли. стр. 209 , 366. ISBN. 978-0-471-49464-5 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ О'Хаган, А. (1994) Продвинутая теория статистики Кендалла, Том 2B, Байесовский вывод , Эдвард Арнольд. ISBN 0-340-52922-9 (раздел 5.40)
- ^ Перейти обратно: а б Брык (1995 , стр. 35)
- ^ UIUC, Лекция 21. Многомерное нормальное распределение , 21.6: «Индивидуально гауссово против совместно гауссово».
- ^ Эдвард Л. Мельник и Аарон Тененбейн, «Неверные спецификации нормального распределения», The American Statistician , том 36, номер 4, ноябрь 1982 г., страницы 372–373
- ^ «Кульбак Лейблер (KL) Расстояние двух нормальных (гауссовских) распределений вероятностей» . Allisons.org . 5 декабря 2007 года . Проверено 3 марта 2017 г.
- ^ Джордан, Майкл И. (8 февраля 2010 г.). «Stat260: Байесовское моделирование и вывод: сопряженный априор для нормального распределения» (PDF) .
- ^ Амари и Нагаока (2000)
- ^ «Ожидание максимума гауссовских случайных величин» . Математический обмен стеками . Проверено 7 апреля 2024 г.
- ^ «Нормальное приближение к распределению Пуассона» . Stat.ucla.edu . Проверено 3 марта 2017 г.
- ^ Перейти обратно: а б Дас, Абхранил (2021). «Метод интеграции и классификации нормальных распределений» . Журнал видения . 21 (10): 1. arXiv : 2012.14331 . дои : 10.1167/jov.21.10.1 . ПМЦ 8419883 . ПМИД 34468706 .
- ^ Брик (1995 , стр. 27)
- ^ Вайсштейн, Эрик В. «Нормальное распределение продукции» . Математический мир . wolfram.com.
- ^ Лукач, Евгений (1942). «Характеристика нормального распределения» . Анналы математической статистики . 13 (1): 91–3. дои : 10.1214/aoms/1177731647 . ISSN 0003-4851 . JSTOR 2236166 .
- ^ Басу, Д.; Лаха, Р.Г. (1954). «О некоторых характеристиках нормального распределения». Санкхья . 13 (4): 359–62. ISSN 0036-4452 . JSTOR 25048183 .
- ^ Леманн, Э.Л. (1997). Проверка статистических гипотез (2-е изд.). Спрингер. п. 199. ИСБН 978-0-387-94919-2 .
- ^ Патель и Рид (1996 , [2.3.6])
- ^ Галамбос и Симонелли (2004 , Теорема 3.5)
- ^ Перейти обратно: а б Лукач и Кинг (1954)
- ^ Куайн, член парламента (1993). «О трёх характеристиках нормального распределения» . Вероятность и математическая статистика . 14 (2): 257–263.
- ^ Джон, С. (1982). «Трехпараметрическое двухчастное нормальное семейство распределений и его аппроксимация». Коммуникации в статистике – теория и методы . 11 (8): 879–885. дои : 10.1080/03610928208828279 .
- ^ Перейти обратно: а б Кришнамурти (2006 , стр. 127)
- ^ Кришнамурти (2006 , стр. 130)
- ^ Кришнамурти (2006 , стр. 133)
- ^ Хаксли (1932)
- ^ Джейнс, Эдвин Т. (2003). Теория вероятностей: логика науки . Издательство Кембриджского университета. стр. 592–593. ISBN 9780521592710 .
- ^ Остербан, Роланд Дж. (1994). «Глава 6: Частотный и регрессионный анализ гидрологических данных» (PDF) . В Ритземе, Хенк П. (ред.). Принципы и применение дренажа, Публикация 16 (второе исправленное издание). Вагенинген, Нидерланды: Международный институт мелиорации и улучшения земель (ILRI). стр. 175–224. ISBN 978-90-70754-33-4 .
- ^ Почему большинство опубликованных результатов исследований ложны, Джон П.А. Иоаннидис, 2005 г.
- ^ Вичура, Майкл Дж. (1988). «Алгоритм AS241: Процентные точки нормального распределения». Прикладная статистика . 37 (3): 477–84. дои : 10.2307/2347330 . JSTOR 2347330 .
- ^ Джонсон, Коц и Балакришнан (1995 , уравнение (26.48))
- ^ Киндерман и Монахан (1977)
- ^ Лева (1992)
- ^ Марсалья и Цанг (2000)
- ^ Карни (2016)
- ^ Монахан (1985 , раздел 2)
- ^ Уоллес (1996)
- ^ Джонсон, Коц и Балакришнан (1994 , стр. 85)
- ^ Ле Кам и Ло Ян (2000 , стр. 74)
- ^ Де Муавр, Авраам (1733), Следствие I - см. Уокер (1985 , стр. 77).
- ^ Стиглер (1986 , стр. 76)
- ^ Гаусс (1809 , раздел 177)
- ^ Гаусс (1809 , раздел 179)
- ^ Лаплас (1774 , Задача III)
- ^ Пирсон (1905 , стр. 189)
- ^ Стиглер (1986 , стр. 144)
- ^ Стиглер (1978 , стр. 243)
- ^ Стиглер (1978 , стр. 244)
- ^ Максвелл (1860 , стр. 23)
- ^ Джейнс, Эдвин Дж.; Теория вероятностей: Логика науки , Гл. 7 .
- ^ Пирс, Чарльз С. (ок. 1909 г.), Сборник статей, т. 6, параграф 327.
- ^ Краскал и Стиглер (1997) .
- ^ «Самое раннее использование... (Входная стандартная нормальная кривая)» .
- ^ Сунь, Цзинчао; Конг, Майинг; Пал, Субхадип (22 июня 2021 г.). «Модифицированное полунормальное распределение: свойства и эффективная схема выборки» . Коммуникации в статистике – теория и методы . 52 (5): 1591–1613. дои : 10.1080/03610926.2021.1934700 . ISSN 0361-0926 . S2CID 237919587 .
Источники
[ редактировать ]- Олдрич, Джон; Миллер, Джефф. «Самое раннее использование символов в теории вероятности и статистике» .
- Олдрич, Джон; Миллер, Джефф. «Самые ранние известные варианты использования некоторых математических слов» . В частности, записи «Колоколообразная и колоколообразная кривая» , «Нормальное (распределение)» , «Гауссово» и «Ошибка, закон ошибок, теория ошибок и т. д.» .
- Амари, Сюн-ичи; Нагаока, Хироши (2000). Методы информационной геометрии . Издательство Оксфордского университета. ISBN 978-0-8218-0531-2 .
- Бернардо, Хосе М.; Смит, Адриан FM (2000). Байесовская теория . Уайли. ISBN 978-0-471-49464-5 .
- Брик, Влодзимеж (1995). Нормальное распределение: характеристики с приложениями . Спрингер-Верлаг. ISBN 978-0-387-97990-8 .
- Казелла, Джордж; Бергер, Роджер Л. (2001). Статистический вывод (2-е изд.). Даксбери. ISBN 978-0-534-24312-8 .
- Коди, Уильям Дж. (1969). «Рациональные чебышевские аппроксимации функции ошибки» . Математика вычислений . 23 (107): 631–638. дои : 10.1090/S0025-5718-1969-0247736-4 .
- Обложка, Томас М.; Томас, Джой А. (2006). Элементы теории информации . Джон Уайли и сыновья.
- Диа, Яя Д. (2023). «Приближенные неполные интегралы, приложение к дополнительной функции ошибки» . ССРН . дои : 10.2139/ssrn.4487559 . S2CID 259689086 .
- де Муавр, Авраам (1738). Доктрина шансов . Американское математическое общество. ISBN 978-0-8218-2103-9 .
- Фань, Цзяньцин (1991). «Об оптимальных скоростях сходимости для непараметрических задач деконволюции» . Анналы статистики . 19 (3): 1257–1272. дои : 10.1214/aos/1176348248 . JSTOR 2241949 .
- Гальтон, Фрэнсис (1889). Естественное наследование (PDF) . Лондон, Великобритания: Ричард Клей и сыновья.
- Галамбос, Янош; Симонелли, Итало (2004). Произведения случайных величин: приложения к задачам физики и арифметическим функциям . Марсель Деккер, Inc. ISBN 978-0-8247-5402-0 .
- Гаусс, Кароло Фридерико (1809). Theoria motvs corporvm coelestivm insectionibvs conicis Solemambiivm [ Теория движения небесных тел, движущихся вокруг Солнца в конических сечениях ] (на латыни). Хамбврги, Свмтибс Ф. Пертес и И.Х. Бессер. Английский перевод .
- Гулд, Стивен Джей (1981). Неизмерение человека (первое изд.). WW Нортон. ISBN 978-0-393-01489-1 .
- Гальперин, Макс; Хартли, Герман О.; Хоэл, Пол Г. (1965). «Рекомендуемые стандарты статистических символов и обозначений. Комитет COPSS по символам и обозначениям». Американский статистик . 19 (3): 12–14. дои : 10.2307/2681417 . JSTOR 2681417 .
- Харт, Джон Ф.; и др. (1968). Компьютерные приближения . Нью-Йорк, штат Нью-Йорк: ISBN John Wiley & Sons, Inc. 978-0-88275-642-4 .
- «Нормальное распределение» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Хернштейн, Ричард Дж.; Мюррей, Чарльз (1994). Колоколовая кривая: интеллект и классовая структура в американской жизни . Свободная пресса . ISBN 978-0-02-914673-6 .
- Хаксли, Джулиан С. (1932). Проблемы относительного роста . Лондон. ISBN 978-0-486-61114-3 . OCLC 476909537 .
- Джонсон, Норман Л.; Коц, Сэмюэл; Балакришнан, Нараянасвами (1994). Непрерывные одномерные распределения, Том 1 . Уайли. ISBN 978-0-471-58495-7 .
- Джонсон, Норман Л.; Коц, Сэмюэл; Балакришнан, Нараянасвами (1995). Непрерывные одномерные распределения, Том 2 . Уайли. ISBN 978-0-471-58494-0 .
- Карни, CFF (2016). «Выборка точно из нормального распределения». Транзакции ACM в математическом программном обеспечении . 42 (1): 3:1–14. arXiv : 1303.6257 . дои : 10.1145/2710016 . S2CID 14252035 .
- Киндерман, Альберт Дж.; Монахан, Джон Ф. (1977). «Компьютерная генерация случайных величин с использованием соотношения равномерных отклонений» . Транзакции ACM в математическом программном обеспечении . 3 (3): 257–260. дои : 10.1145/355744.355750 . S2CID 12884505 .
- Кришнамурти, Калимуту (2006). Справочник по статистическим распределениям с приложениями . Чепмен и Холл/CRC. ISBN 978-1-58488-635-8 .
- Краскал, Уильям Х.; Стиглер, Стивен М. (1997). Спенсер, Брюс Д. (ред.). Нормативная терминология: «нормальный» в статистике и других источниках . Статистика и государственная политика. Издательство Оксфордского университета. ISBN 978-0-19-852341-3 .
- Лаплас, Пьер-Симон де (1774). «Память о вероятности причин по событиям» . Мемуары Парижской королевской академии наук (иностранные ученые), том 6 : 621–656. Перевод Стивена М. Стиглера в журнале Statistical Science 1 (3), 1986: JSTOR 2245476 .
- Лаплас, Пьер-Симон (1812). вероятностей Аналитическая теория . Париж, пятница. Курьер.
- Ле Кам, Люсьен; Ло Ян, Грейс (2000). Асимптотика в статистике: некоторые основные понятия (второе изд.). Спрингер. ISBN 978-0-387-95036-5 .
- Лева, Джозеф Л. (1992). «Быстрый нормальный генератор случайных чисел» (PDF) . Транзакции ACM в математическом программном обеспечении . 18 (4): 449–453. CiteSeerX 10.1.1.544.5806 . дои : 10.1145/138351.138364 . S2CID 15802663 . Архивировано из оригинала (PDF) 16 июля 2010 г.
- Лексис, Вильгельм (1878). «О нормальной продолжительности жизни человека и о теории устойчивости статистических связей». Анналы международной демографии . II . Париж: 447–462.
- Лукач, Евгений; Кинг, Эдгар П. (1954). «Свойство нормального распределения» . Анналы математической статистики . 25 (2): 389–394. дои : 10.1214/aoms/1177728796 . JSTOR 2236741 .
- Макферсон, Глен (1990). Статистика в научных исследованиях: ее основы, применение и интерпретация . Спрингер-Верлаг. ISBN 978-0-387-97137-7 .
- Марсалья, Джордж ; Цанг, Вай Ван (2000). «Метод Зиккурата для генерации случайных величин» . Журнал статистического программного обеспечения . 5 (8). дои : 10.18637/jss.v005.i08 .
- Марсалья, Джордж (2004). «Оценка нормального распределения» . Журнал статистического программного обеспечения . 11 (4). дои : 10.18637/jss.v011.i04 .
- Максвелл, Джеймс Клерк (1860). «V. Иллюстрации динамической теории газов. — Часть I: О движении и столкновениях идеально упругих сфер». Философский журнал . Ряд 4. 19 (124): 19–32. дои : 10.1080/14786446008642818 .
- Монахан, Дж. Ф. (1985). «Точность генерации случайных чисел» . Математика вычислений . 45 (172): 559–568. doi : 10.1090/S0025-5718-1985-0804945-X .
- Патель, Джагдиш К.; Прочтите, Кэмпбелл Б. (1996). Справочник по нормальному распределению (2-е изд.). ЦРК Пресс. ISBN 978-0-8247-9342-5 .
- Пирсон, Карл (1901). «О линиях и плоскостях, наиболее близких к системам точек в пространстве» (PDF) . Философский журнал . 6. 2 (11): 559–572. дои : 10.1080/14786440109462720 . S2CID 125037489 .
- Пирсон, Карл (1905). « Закон ошибок и его обобщения Фехнера и Пирсона». Возражение» . Биометрия . 4 (1): 169–212. дои : 10.2307/2331536 . JSTOR 2331536 .
- Пирсон, Карл (1920). «Заметки по истории корреляции» . Биометрика . 13 (1): 25–45. дои : 10.1093/biomet/13.1.25 . JSTOR 2331722 .
- Рорбассер, Жан-Марк; Верон, Жак (2003). «Лексика Вильгельма: Нормальная продолжительность жизни как выражение «природы вещей» » . Население . 58 (3): 303–322. дои : 10.3917/папа.303.0303 .
- Шор, Х. (1982). «Простые приближения для обратной кумулятивной функции, функции плотности и интеграла потерь нормального распределения». Журнал Королевского статистического общества. Серия C (Прикладная статистика) . 31 (2): 108–114. дои : 10.2307/2347972 . JSTOR 2347972 .
- Шор, Х. (2005). «Точные аппроксимации на основе RMM для CDF нормального распределения». Коммуникации в статистике – теория и методы . 34 (3): 507–513. дои : 10.1081/sta-200052102 . S2CID 122148043 .
- Шор, Х (2011). «Методология моделирования реагирования». ПРОВОДА Вычисление Стат . 3 (4): 357–372. дои : 10.1002/wics.151 . S2CID 62021374 .
- Шор, Х (2012). «Модели методологии моделирования реакции». ПРОВОДА Вычисление Стат . 4 (3): 323–333. дои : 10.1002/wics.1199 . S2CID 122366147 .
- Стиглер, Стивен М. (1978). «Математическая статистика в ранних государствах» . Анналы статистики . 6 (2): 239–265. дои : 10.1214/aos/1176344123 . JSTOR 2958876 .
- Стиглер, Стивен М. (1982). «Скромное предложение: новый стандарт нормальности». Американский статистик . 36 (2): 137–138. дои : 10.2307/2684031 . JSTOR 2684031 .
- Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Издательство Гарвардского университета. ISBN 978-0-674-40340-6 .
- Стиглер, Стивен М. (1999). Статистика в таблице . Издательство Гарвардского университета. ISBN 978-0-674-83601-3 .
- Уокер, Хелен М. (1985). «Де Муавр о законе нормальной вероятности» (PDF) . В Смите, Дэвид Юджин (ред.). Справочник по математике . Дувр. ISBN 978-0-486-64690-9 .
- Уоллес, CS (1996). «Быстрые псевдослучайные генераторы для нормальных и экспоненциальных переменных» . Транзакции ACM в математическом программном обеспечении . 22 (1): 119–127. дои : 10.1145/225545.225554 . S2CID 18514848 .
- Вайсштейн, Эрик В. «Нормальное распределение» . Математический мир .
- Уэст, Грэм (2009). «Лучшие приближения кумулятивных нормальных функций» (PDF) . Журнал Уилмотт : 70–76. Архивировано из оригинала (PDF) 29 февраля 2012 г.
- Зелен, Марвин; Северо, Норман К. (1964). Функции вероятности (глава 26) . Справочник по математическим функциям с формулами, графиками и математическими таблицами Абрамовица М .; и Стегун, Айова : Национальное бюро стандартов. Нью-Йорк, штат Нью-Йорк: Дувр. ISBN 978-0-486-61272-0 .





![{\displaystyle \Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0fed43e25966344745178c406f04b15d0fa3783)

















































![{\textstyle [-x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4939f2eb7c55ff4e7d13331fc0599a5f2452b479)

![{\displaystyle \Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7831a9a5f630df7170fa805c186f4c53219ca36)

![{\displaystyle F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75deccfbc473d782dacb783f1524abb09b8135c0)






![{\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54d12af9a3b12a7f859e4e7be105d172b53bcfb8)




















































![{\displaystyle \operatorname {E} \left[(X-\mu )^{p}\right]={\begin{cases}0&{\text{if }}p{\text{ is odd,}}\\\sigma ^{p}(p-1)!!&{\text{if }}p{\text{ is even.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1d2c92b62ac2bbe07a8e475faac29c8cc5f7755)



![{\displaystyle {\begin{aligned}\operatorname {E} \left[|X-\mu |^{p}\right]&=\sigma ^{p}(p-1)!!\cdot {\begin{cases}{\sqrt {\frac {2}{\pi }}}&{\text{if }}p{\text{ is odd}}\\1&{\text{if }}p{\text{ is even}}\end{cases}}\\&=\sigma ^{p}\cdot {\frac {2^{p/2}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b196371c491676efa7ea7770ef56773db7652cd)




![{\displaystyle {\begin{aligned}\operatorname {E} \left[X^{p}\right]&=\sigma ^{p}\cdot (-i{\sqrt {2}})^{p}U\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right),\\\operatorname {E} \left[|X|^{p}\right]&=\sigma ^{p}\cdot 2^{p/2}{\frac {\Gamma \left({\frac {1+p}{2}}\right)}{\sqrt {\pi }}}{}_{1}F_{1}\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c17bf881593b86e728bf5dfbdb41a4b86da3875)











![{\textstyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c780cbaafb5b1d4a6912aa65d2b0b1982097108)
![{\displaystyle \operatorname {E} \left[X\mid a<X<b\right]=\mu -\sigma ^{2}{\frac {f(b)-f(a)}{F(b)-F(a)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d82ec10bf31f0b63137699ae6e2b5a346770b097)









![{\displaystyle M(t)=\operatorname {E} \left[e^{tX}\right]={\hat {f}}(it)=e^{\mu t}e^{\sigma ^{2}t^{2}/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/935bdfb329038ee45bf7cc94d83f68b66a5c74c5)




![{\textstyle f:\mathbb {R} \to \mathbb {R} {\mbox{ such that }}\mathbb {E} [|f'(X)|]<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/533b737bedccd7496f904d18a4fd39fade40b282)







































![{\textstyle E[\max _{i}X_{i}]\leq \sigma {\sqrt {2\ln n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dfb87c9b047ccf23ace2139d97810dff1ed6670)












































































![{\displaystyle t={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}={\frac {{\frac {1}{n}}(X_{1}+\cdots +X_{n})-\mu }{\sqrt {{\frac {1}{n(n-1)}}\left[(X_{1}-{\overline {X}})^{2}+\cdots +(X_{n}-{\overline {X}})^{2}\right]}}}\sim t_{n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36ff0d3c79a0504e8f259ef99192b825357914d7)















![{\displaystyle \operatorname {T} (X)={\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})\left[\left({\frac {4}{\pi }}-1\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9959f2c5186e2ed76884054edaf837a602ac6fac)




![{\displaystyle \ln {\mathcal {L}}({\hat {\mu }},{\hat {\sigma }}^{2})=(-n/2)[\ln(2\pi {\hat {\sigma }}^{2})+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561353e6bc80d226fddd9510be61d21bc67b3aee)















![{\displaystyle \mu \in \left[{\hat {\mu }}-t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e3068587bfbaf61a549a39b518757119bfb846)
![{\displaystyle \sigma ^{2}\in \left[{\frac {(n-1)s^{2}}{\chi _{n-1,1-\alpha /2}^{2}}},{\frac {(n-1)s^{2}}{\chi _{n-1,\alpha /2}^{2}}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3549a31cb861d9e479c232271cb88b019cfa9fd5)
![{\displaystyle \mu \in \left[{\hat {\mu }}-|z_{\alpha /2}|{\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+|z_{\alpha /2}|{\frac {1}{\sqrt {n}}}s\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e13883f93c0a1405e71bd105685ecac6b4c84089)
![{\displaystyle \sigma ^{2}\in \left[s^{2}-|z_{\alpha /2}|{\frac {\sqrt {2}}{\sqrt {n}}}s^{2},s^{2}+|z_{\alpha /2}|{\frac {\sqrt {2}}{\sqrt {n}}}s^{2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3e7c940eb3f6f50af62200ae75e10435ef8dfe6)

















![{\displaystyle {\begin{aligned}p(\mathbf {X} \mid \mu ,\tau )&=\prod _{i=1}^{n}{\sqrt {\frac {\tau }{2\pi }}}\exp \left(-{\frac {1}{2}}\tau (x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left(-{\frac {1}{2}}\tau \sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2bcd1c34520a24e29b758a0f7427e79e9d8a414)
![{\displaystyle {\begin{aligned}p(\mu \mid \mathbf {X} )&\propto p(\mathbf {X} \mid \mu )p(\mu )\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]{\sqrt {\frac {\tau _{0}}{2\pi }}}\exp \left(-{\frac {1}{2}}\tau _{0}(\mu -\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(n\tau ({\bar {x}}-\mu )^{2}+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&=\exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}+{\frac {n\tau \tau _{0}}{n\tau +\tau _{0}}}({\bar {x}}-\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96e309ead00fbc8603eced5342aa5df534522d6a)



![{\displaystyle {\begin{aligned}\tau _{0}'&=\tau _{0}+n\tau \\[5pt]\mu _{0}'&={\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\\[5pt]{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6cfbdf504b1a9ce4cbe79561b4ae983fdf7271d)

![{\displaystyle {\begin{aligned}{\sigma _{0}^{2}}'&={\frac {1}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\[5pt]\mu _{0}'&={\frac {{\frac {n{\bar {x}}}{\sigma ^{2}}}+{\frac {\mu _{0}}{\sigma _{0}^{2}}}}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\[5pt]{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea454c8840683777ce8192d9ae63068c63962858)
![{\displaystyle p(\sigma ^{2}\mid \nu _{0},\sigma _{0}^{2})={\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\nu _{0}/2}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\propto {\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef2528fe4774a93087d4adae570ef9ab84707f52)
![{\displaystyle {\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right]\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc06aa31588bba03e4748f8f345f0638a75dc156)

![{\displaystyle {\begin{aligned}p(\sigma ^{2}\mid \mathbf {X} )&\propto p(\mathbf {X} \mid \sigma ^{2})p(\sigma ^{2})\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]{\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\frac {\nu _{0}}{2}}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\\&\propto \left({\frac {1}{\sigma ^{2}}}\right)^{n/2}{\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\exp \left[-{\frac {S}{2\sigma ^{2}}}+{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]\\&={\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}+n}{2}}}}}\exp \left[-{\frac {\nu _{0}\sigma _{0}^{2}+S}{2\sigma ^{2}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/381c1b93f6dc76e2cdca9f3f1f77132dd51dc55f)






![{\displaystyle {\begin{aligned}p(\mu \mid \sigma ^{2};\mu _{0},n_{0})&\sim {\mathcal {N}}(\mu _{0},\sigma ^{2}/n_{0})={\frac {1}{\sqrt {2\pi {\frac {\sigma ^{2}}{n_{0}}}}}}\exp \left(-{\frac {n_{0}}{2\sigma ^{2}}}(\mu -\mu _{0})^{2}\right)\\&\propto (\sigma ^{2})^{-1/2}\exp \left(-{\frac {n_{0}}{2\sigma ^{2}}}(\mu -\mu _{0})^{2}\right)\\p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})&\sim I\chi ^{2}(\nu _{0},\sigma _{0}^{2})=IG(\nu _{0}/2,\nu _{0}\sigma _{0}^{2}/2)\\&={\frac {(\sigma _{0}^{2}\nu _{0}/2)^{\nu _{0}/2}}{\Gamma (\nu _{0}/2)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+\nu _{0}/2}}}\\&\propto {(\sigma ^{2})^{-(1+\nu _{0}/2)}}\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf7afb8e3b63fb1526171840344b32458e55cf8b)
![{\displaystyle {\begin{aligned}p(\mu ,\sigma ^{2};\mu _{0},n_{0},\nu _{0},\sigma _{0}^{2})&=p(\mu \mid \sigma ^{2};\mu _{0},n_{0})\,p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})\\&\propto (\sigma ^{2})^{-(\nu _{0}+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+n_{0}(\mu -\mu _{0})^{2}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6f808161077baef3854dbfd90b870698d721090)
![{\displaystyle {\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3d77342aadcb34c5d84418cecaefdb52842b6b7)
![{\displaystyle {\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]\\&\propto {\sigma ^{2}}^{-n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(S+n({\bar {x}}-\mu )^{2}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29b915f070b522a1e9f419be05624c86c854ca14)

![{\displaystyle {\begin{aligned}p(\mu ,\sigma ^{2}\mid \mathbf {X} )&\propto p(\mu ,\sigma ^{2})\,p(\mathbf {X} \mid \mu ,\sigma ^{2})\\&\propto (\sigma ^{2})^{-(\nu _{0}+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+n_{0}(\mu -\mu _{0})^{2}\right)\right]{\sigma ^{2}}^{-n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(S+n({\bar {x}}-\mu )^{2}\right)\right]\\&=(\sigma ^{2})^{-(\nu _{0}+n+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+n_{0}(\mu -\mu _{0})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]\\&=(\sigma ^{2})^{-(\nu _{0}+n+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}+(n_{0}+n)\left(\mu -{\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\right)^{2}\right)\right]\\&\propto (\sigma ^{2})^{-1/2}\exp \left[-{\frac {n_{0}+n}{2\sigma ^{2}}}\left(\mu -{\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\right)^{2}\right]\\&\quad \times (\sigma ^{2})^{-(\nu _{0}/2+n/2+1)}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\right)\right]\\&={\mathcal {N}}_{\mu \mid \sigma ^{2}}\left({\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}},{\frac {\sigma ^{2}}{n_{0}+n}}\right)\cdot {\rm {IG}}_{\sigma ^{2}}\left({\frac {1}{2}}(\nu _{0}+n),{\frac {1}{2}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cad9489034d77d53c12c7ee6044f712cfdb77831)















![{\displaystyle z=\Phi ^{-1}(p)=5,5556\left[1-\left({\frac {1-p}{p}}\right)^{0,1186}\right],\qquad p\geq 1/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f2df7f1427d0c90d075faef38f4f5ab7acce5c9)
![{\displaystyle z=-0,4115\left\{{\frac {1-p}{p}}+\log \left[{\frac {1-p}{p}}\right]-1\right\} ,\qquad p\geq 1/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1edea9f990058f741db6735799c8b40999b833b)
![{\displaystyle {\begin{aligned}L(z)&=\int _{z}^{\infty }(uz)\varphi (u)\,du=\int _{z}^{\infty }[ 1-\Phi (u)]\,du\\[5pt]L(z)&\approx {\begin{cases}0.4115\left({\dfrac {p}{1-p}}\right)-z ,&p<1/2,\\\\0.4115\left({\dfrac {1-p}{p}}\right),&p\geq 1/2.\end{cases}}\\[5pt]{ \text{или, что то же самое,}}\\L(z)&\approx {\begin{cases}0.4115\left\{1-\log \left[{\frac {p}{1-p}}\right ]\right\},&p<1/2,\\\\0.4115{\dfrac {1-p}{p}},&p\geq 1/2.\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4b69fa586cffdfbbd40a94c65629726e4ae78bf)








