t-распределение Стьюдента

-распределения Стьюдента Эта статья о математике t . Информацию о его использовании в статистике см. в разделе «Т-критерий Стьюдента» .

Студенческая т

Функция плотности вероятности
Кумулятивная функция распределения
Параметры	$\ \nu >0\$ степени свободы ( действительные , почти всегда положительное целое число )
Поддерживать	$\ x\in (-\infty ,\infty )$
PDF	$\textstyle \ {\frac {\Gamma \left({\frac {\ \nu +1\ }{2}}\right)}{{\sqrt {\pi \ \nu \ }}\ \Gamma \left({\frac {\nu }{\ 2\ }}\right)}}\ \left(\ 1+{\frac {~x^{2}\ }{\nu }}\ \right)^{-{\frac {\ \nu +1\ }{2}}}\$
CDF	$${\begin{matrix}\ {\frac {\ 1\ }{2}}+x\ \Gamma \left({\frac {\ \nu +1\ }{2}}\right)\times \\[0.5em]{\frac {\ {{}_{2}F_{1}}\!\left(\ {\frac {\ 1\ }{2}},\ {\frac {\ \nu +1\ }{2}};\ {\frac {3}{\ 2\ }};\ -{\frac {~x^{2}\ }{\nu }}\ \right)\ }{\ {\sqrt {\pi \nu }}\ \Gamma \left({\frac {\ \nu \ }{2}}\right)\ }}\ ,\end{matrix}}$$ где $\ {}_{2}F_{1}\!(\ ,\ ;\ ;\ )\$ это гипергеометрическая функция
Иметь в виду	$\ 0\$ для $\ \nu >1\ ,$ в противном случае не определено
медиана	$\ 0\$
Режим	$\ 0\$
Дисперсия	$\textstyle \ {\frac {\nu }{\ \nu -2\ }}\$ для $\ \nu >2\ ,$ ∞ для $\ 1<\nu \leq 2\ ,$ в противном случае не определено
асимметрия	$\ 0\$ для $\ \nu >3\ ,$ в противном случае не определено
Избыточный эксцесс	$\textstyle \ {\frac {6}{\ \nu -4\ }}$ для $\ \nu >4\ ,$ ∞ для $\ 2<\nu \leq 4\ ,$ в противном случае не определено
Энтропия	$\ {\begin{matrix}{\frac {\ \nu +1\ }{2}}\left[\ \psi \left({\frac {\ \nu +1\ }{2}}\right)-\psi \left({\frac {\ \nu \ }{2}}\right)\ \right]\\[0.5em]+\ln \left[{\sqrt {\nu \ }}\ {\mathrm {B} }\left(\ {\frac {\ \nu \ }{2}},\ {\frac {\ 1\ }{2}}\ \right)\right]\ {\scriptstyle {\text{(nats)}}}\ \end{matrix}}$ где $\psi ()\$ это дигамма-функция , $\ {\mathrm {B} }(\ ,\ )\$ это бета-функция .
МГФ	неопределенный
CF	$\textstyle {\frac {\ \left(\ {\sqrt {\nu \ }}\ |t|\ \right)^{\nu /2}\ K_{\nu /2}\left(\ {\sqrt {\nu \ }}\ |t|\ \right)\ }{\ \Gamma (\nu /2)\ 2^{\nu /2-1}\ }}\$ для $\ \nu >0\$ $\ K_{\nu }(x)\$ — модифицированная функция Бесселя второго рода
Ожидаемый дефицит	$\ \mu +s\ \left(\ {\frac {\ \nu +T^{-1}(1-p)^{2}\ \times \ \tau \left(T^{-1}(1-p)^{2}\right)\ }{\ (\nu -1)(1-p)\ }}\ \right)\$ Где $\ T^{-1}(\ )\$ является обратным стандартизированным Стьюдентом t CDF и $\ \tau (\ )\$ представляет собой стандартизированный студенческий PDF-файл .

В вероятности и статистике распределение ( t- Стьюдента или просто t- распределение ) $\ t_{\nu }\$ является непрерывное распределение вероятностей , которое обобщает стандартное нормальное распределение . Как и последний, он симметричен вокруг нуля и имеет колоколообразную форму.

Однако, $\ t_{\nu }\$ имеет более тяжелые хвосты , а количество вероятностной массы в хвостах контролируется параметром $\ \nu ~~.$ Для $\ \nu =1\$ Стьюдента ​ распределение $t_{\nu }$ становится стандартным распределением Коши , имеющим очень «толстые» хвосты ; тогда как для $\ \nu \rightarrow \infty \$ оно становится стандартным нормальным распределением $\ {\mathcal {N}}(0,1)\,$ у которого очень «тонкие» хвосты.

Стьюдента Распределение играет роль в ряде широко используемых статистических анализов, включая Стьюдента критерий регрессии для оценки статистической значимости разницы между двумя выборочными средними, построения доверительных интервалов для разницы между двумя генеральными средними и в линейной . анализ .

В виде в масштабе местоположения t распределения $lst(\mu ,\tau ^{2},\nu )$ оно обобщает нормальное распределение , а также возникает при байесовском анализе данных нормального семейства как составного распределения при маргинализации по параметру дисперсии.

История и этимология

Статистик Уильям Сили Госсет, известный как «Студент»

В статистике t- распределение было впервые получено как апостериорное распределение в 1876 году Гельмертом. и Люрот . Таким образом, t-распределение Стьюдента является примером закона эпонимии Стиглера . Распределение t также появилось в более общей форме как распределение Пирсона типа IV в статье Карла Пирсона 1895 года.

В англоязычной литературе распространение получило свое название от статьи Уильяма Сили Госсета 1908 года в журнале «Биометрика» под псевдонимом «Студент». Одна из версий происхождения псевдонима заключается в том, что работодатель Госсета предпочитал, чтобы сотрудники при публикации научных статей использовали псевдонимы вместо своего настоящего имени, поэтому он использовал имя «Студент», чтобы скрыть свою личность. Другая версия заключается в том, что компания Guinness не хотела, чтобы конкуренты знали, что они используют t- тест для определения качества сырья.

Госсет работал на пивоварне Guinness Brewery в Дублине, Ирландия , и интересовался проблемами небольших образцов – например, химическими свойствами ячменя, где размеры выборок могли составлять всего 3. В статье Госсета это распределение называется «частотным распределением». стандартных отклонений выборок, взятых из нормальной популяции». Оно стало широко известно благодаря работе Рональда Фишера , который назвал распределение «распределением Стьюдента» и обозначил проверочное значение буквой t .

Определение

Функция плотности вероятности

Стьюдента Распределение (PDF) , имеет функцию плотности вероятности определяемую выражением

$f(t)\ =\ {\frac {\ \Gamma \!\left({\frac {\ \nu +1\ }{2}}\right)\ }{\ {\sqrt {\pi \ \nu \ }}\;\Gamma \!\left({\frac {\nu }{2}}\right)}}\;\left(\ 1+{\frac {~t^{2}\ }{\nu }}\ \right)^{-(\nu +1)/2}\ ,$

где $\ \nu \$ число степеней свободы и $\ \Gamma \$ это гамма-функция . Это также можно записать как

$f(t)\ =\ {\frac {1}{\ {\sqrt {\nu \ }}\ {\mathrm {B} }\!\left({\frac {\ 1\ }{2}},\ {\frac {\ \nu \ }{2}}\right)\ }}\;\left(\ 1+{\frac {\ t^{2}\ }{\nu }}\ \right)^{-(\nu +1)/2}\ ,$

где $\ {\mathrm {B} }\$это бета-функция . В частности, для целочисленных степеней свободы. $\ \nu \$ у нас есть:

Для $\ \nu >1\$ и даже,

$\ {\frac {\ \Gamma \!\left({\frac {\ \nu +1\ }{2}}\right)\ }{\ {\sqrt {\pi \ \nu \ }}\;\Gamma \!\left({\frac {\ \nu \ }{2}}\right)\ }}\ =\ {\frac {1}{\ 2{\sqrt {\nu \ }}\ }}\ \cdot \ {\frac {\ (\nu -1)\cdot (\nu -3)\cdots 5\cdot 3\ }{\ (\nu -2)\cdot (\nu -4)\cdots 4\cdot 2\ }}~.$

Для $\ \nu >1\$ и странно,

$\ {\frac {\ \Gamma \!\left({\frac {\ \nu +1\ }{2}}\right)\ }{\ {\sqrt {\pi \ \nu \ }}\ \Gamma \!\left({\frac {\ \nu \ }{2}}\right)}}\ =\ {\frac {1}{\ \pi {\sqrt {\nu \ }}\ }}\ \cdot \ {\frac {(\nu -1)\cdot (\nu -3)\cdots 4\cdot 2\ }{\ (\nu -2)\cdot (\nu -4)\cdots 5\cdot 3\ }}~.$

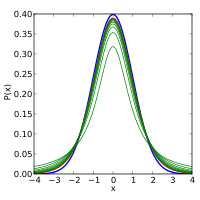
Функция плотности вероятности симметрична , и ее общая форма напоминает колоколообразную форму нормально распределенной переменной со средним значением 0 и дисперсией 1, за исключением того, что она немного ниже и шире. По мере роста числа степеней свободы распределение t приближается к нормальному распределению со средним значением 0 и дисперсией 1. По этой причине ${\ \nu \ }$ также известен как параметр нормальности.

На следующих изображениях показана плотность распределения t для возрастающих значений $\ \nu ~.$ Нормальное распределение показано для сравнения синей линией. Обратите внимание, что распределение t (красная линия) становится ближе к нормальному распределению по мере того, как $\ \nu \$ увеличивается.

Плотность t - распределения (красный) для 1, 2, 3, 5, 10 и 30 степеней свободы по сравнению со стандартным нормальным распределением (синий).
Предыдущие графики показаны зеленым цветом.

1 степень свободы

2 степени свободы

3 степени свободы

5 степеней свободы

10 степеней свободы

30 степеней свободы

Кумулятивная функция распределения

Кумулятивную функцию распределения (CDF) можно записать через I , регуляризованную неполная бета-функция . Для t > 0 ,

$F(t)=\int _{-\infty }^{t}\ f(u)\ \operatorname {d} u~=~1-{\frac {1}{2}}I_{x(t)}\!\left({\frac {\ \nu \ }{2}},\ {\frac {\ 1\ }{2}}\right)\ ,$

где

$x(t)={\frac {\nu }{\ t^{2}+\nu \ }}~.$

Другие значения будут получены путем симметрии. Альтернативная формула, справедливая для $\ t^{2}<\nu \ ,$ является

$\int _{-\infty }^{t}f(u)\ \operatorname {d} u~=~{\frac {1}{2}}+t\ {\frac {\ \Gamma \!\left({\frac {\ \nu +1\ }{2}}\right)\ }{\ {\sqrt {\pi \ \nu \ }}\ \Gamma \!\left({\frac {\nu }{\ 2\ }}\right)\ }}\ {}_{2}F_{1}\!\left(\ {\frac {1}{2}},{\frac {\ \nu +1\ }{2}}\ ;{\frac {3}{\ 2\ }}\ ;\ -{\frac {~t^{2}\ }{\nu }}\ \right)\ ,$

где $\ {}_{2}F_{1}(\ ,\ ;\ ;\ )\$ является частным примером гипергеометрической функции .

Информацию об обратной кумулятивной функции распределения см. в разделе « Функция квантиля § t-распределение Стьюдента» .

Особые случаи

Определенные значения $\ \nu \$ приведите простую форму t-распределения Стьюдента.

$\ \nu \$	PDF	CDF	примечания
1	$\ {\frac {\ 1\ }{\ \pi \ (1+t^{2})\ }}\$	$\ {\frac {\ 1\ }{2}}+{\frac {\ 1\ }{\pi }}\ \arctan(\ t\ )\$	См. Распределение Коши.
2	$\ {\frac {1}{\ 2\ {\sqrt {2\ }}\ \left(1+{\frac {t^{2}}{2}}\right)^{3/2}}}\$	$\ {\frac {1}{\ 2\ }}+{\frac {t}{\ 2{\sqrt {2\ }}\ {\sqrt {1+{\frac {~t^{2}\ }{2}}\ }}\ }}\$
3	$\ {\frac {2}{\ \pi \ {\sqrt {3\ }}\ \left(\ 1+{\frac {~t^{2}\ }{3}}\ \right)^{2}\ }}\$	$\ {\frac {\ 1\ }{2}}+{\frac {\ 1\ }{\pi }}\ \left[{\frac {\left(\ {\frac {t}{\ {\sqrt {3\ }}\ }}\ \right)}{\left(\ 1+{\frac {~t^{2}\ }{3}}\ \right)}}+\arctan \left(\ {\frac {t}{\ {\sqrt {3\ }}\ }}\ \right)\ \right]\$
4	$\ {\frac {\ 3\ }{\ 8\ \left(\ 1+{\frac {~t^{2}\ }{4}}\ \right)^{5/2}}}\$	$\ {\frac {\ 1\ }{2}}+{\frac {\ 3\ }{8}}\left[\ {\frac {t}{\ {\sqrt {1+{\frac {~t^{2}\ }{4}}~}}\ }}\right]\left[\ 1-{\frac {~t^{2}\ }{\ 12\ \left(\ 1+{\frac {~t^{2}\ }{4}}\ \right)\ }}\ \right]\$
5	$\ {\frac {8}{\ 3\pi {\sqrt {5\ }}\left(1+{\frac {\ t^{2}\ }{5}}\right)^{3}\ }}\$	$\ {\frac {\ 1\ }{2}}+{\frac {\ 1\ }{\pi }}{\left[{\frac {t}{\ {\sqrt {5\ }}\left(1+{\frac {\ t^{2}\ }{5}}\right)\ }}\left(1+{\frac {2}{\ 3\left(1+{\frac {\ t^{2}\ }{5}}\right)\ }}\right)+\arctan \left({\frac {t}{\ {\sqrt {\ 5\ }}\ }}\right)\right]}\$
$\ \infty \$	$\ {\frac {1}{\ {\sqrt {2\pi \ }}\ }}\ e^{-t^{2}/2}$	$\ {\frac {\ 1\ }{2}}\ {\left[1+\operatorname {erf} \left({\frac {t}{\ {\sqrt {2\ }}\ }}\right)\right]}\$	См. Нормальное распределение , Функция ошибки.

Моменты

Для $\nu >1\ ,$ необработанные моменты распределения t равны

$\operatorname {\mathbb {E} } \left\{\ T^{k}\ \right\}={\begin{cases}\quad 0&k{\text{ odd }},\quad 0<k<\nu \ ,\\{}\\{\frac {1}{\ {\sqrt {\pi \ }}\ \Gamma \left({\frac {\ \nu \ }{2}}\right)}}\ \left[\ \Gamma \!\left({\frac {\ k+1\ }{2}}\right)\ \Gamma \!\left({\frac {\ \nu -k\ }{2}}\right)\ \nu ^{\frac {\ k\ }{2}}\ \right]&k{\text{ even }},\quad 0<k<\nu ~.\\\end{cases}}$

Моменты заказа $\ \nu \$ и выше не существует.

Срок для $\ 0<k<\nu \ ,$ даже k , можно упростить, используя свойства гамма-функции :

$\operatorname {\mathbb {E} } \left\{\ T^{k}\ \right\}=\nu ^{\frac {\ k\ }{2}}\ \prod _{j=1}^{k/2}\ {\frac {~2j-1~}{\nu -2j}}\qquad k{\text{ even}},\quad 0<k<\nu ~.$

Для распределения t с $\ \nu \$ степеней свободы, ожидаемое значение равно $\ 0\$ если $\ \nu >1\ ,$ его дисперсия и $\ {\frac {\nu }{\ \nu -2\ }}\$ если $\ \nu >2~.$ Асимметрия равна 0 , если $\ \nu >3\$ и эксцесс избыточный $\ {\frac {6}{\ \nu -4\ }}\$ если $\ \nu >4~.$

в масштабе местоположения t Распределение

Преобразование в масштабе местоположения

Распределение Стьюдента t обобщает трехпараметрическое в масштабе местоположения . распределение $\ {\mathcal {lst}}(\mu ,\ \tau ^{2},\ \nu )\$ путем введения параметра местоположения $\ \mu \$ и параметр масштаба $\ \tau ~.$ С

$\ T\sim t_{\nu }\$

и семьи в масштабе локации трансформация

$\ X=\mu +\tau \ T\$

мы получаем

$\ X\sim {\mathcal {lst}}(\mu ,\ \tau ^{2},\ \nu )~.$

Полученное распределение также называют нестандартизованным t- распределением Стьюдента .

Плотность и первые два момента

в масштабе местоположения Распределение t имеет плотность, определяемую следующим образом:

$p(x\mid \nu ,\mu ,\tau )={\frac {\ \Gamma \left({\frac {\ \nu +1\ }{2}}\right)\ }{\ \Gamma \left({\frac {\ \nu \ }{2}}\right)\ {\sqrt {\pi \ \nu \ }}\ \tau \ }}\ \left(1+{\frac {\ 1\ }{\nu }}\ \left(\ {\frac {\ x-\mu \ }{\tau }}\ \right)^{2}\ \right)^{-(\nu +1)/2}\$

Эквивалентно плотность можно записать через $\tau ^{2}$:

$\ p(x\ \mid \ \nu ,\ \mu ,\ \tau ^{2})={\frac {\ \Gamma ({\frac {\nu +1}{2}})\ }{\ \Gamma \left({\frac {\ \nu \ }{2}}\right)\ {\sqrt {\pi \ \nu \ \tau ^{2}}}\ }}\ \left(\ 1+{\frac {\ 1\ }{\nu }}\ {\frac {\ (x-\mu )^{2}\ }{\ \tau ^{2}\ }}\ \right)^{-(\nu +1)/2}\$

Другие свойства этой версии дистрибутива:

${\begin{aligned}\operatorname {\mathbb {E} } \{\ X\ \}&=\mu &{\text{ for }}\nu >1\ ,\\\operatorname {var} \{\ X\ \}&=\tau ^{2}{\frac {\nu }{\nu -2}}&{\text{ for }}\nu >2\ ,\\\operatorname {mode} \{\ X\ \}&=\mu ~.\end{aligned}}$

Особые случаи

• Если $\ X\$ в масштабе местоположения следует t - распределению $\ X\sim {\mathcal {lst}}\left(\mu ,\ \tau ^{2},\ \nu \right)\$ тогда для $\ \nu \rightarrow \infty \$ $\ X\$ нормально распределяется $X\sim \mathrm {N} \left(\mu ,\tau ^{2}\right)$ со средним $\mu$ и дисперсия $\ \tau ^{2}~.$
• в масштабе местоположения t Распределение $\ {\mathcal {lst}}\left(\mu ,\ \tau ^{2},\ \nu =1\right)\$ со степенью свободы $\nu =1$ эквивалентно распределению Коши $\mathrm {Cau} \left(\mu ,\tau \right)~.$
• в масштабе местоположения t Распределение $\ {\mathcal {lst}}\left(\mu =0,\ \tau ^{2}=1,\ \nu \right)\$ с $\mu =0$ и $\ \tau ^{2}=1\$ Стьюдента сводится к t- распределению $\ t_{\nu }~.$

Как возникает распределение t (характеристика)

Как распределение тестовой статистики

-распределение Стьюдента t с $\nu$ степени свободы можно определить как распределение случайной величины T с

$T={\frac {Z}{\sqrt {V/\nu }}}=Z{\sqrt {\frac {\nu }{V}}},$

где

• Z — стандартная норма с ожидаемым значением 0 и дисперсией 1;
• V имеет распределение хи-квадрат ( χ ² -распределение ) с $\nu$ степени свободы ;
• Z и V независимы ​ ;

Другое распределение определяется как распределение случайной величины, определяемой для данной константы µ формулой

$(Z+\mu ){\sqrt {\frac {\nu }{V}}}.$

Эта случайная величина имеет нецентральное t -распределение с параметром нецентральности μ . Это распределение важно при изучении силы t критерия Стьюдента - .

Вывод

Предположим, что X ₁ , ..., X _n являются независимыми реализациями нормально распределенной случайной величины X , которая имеет ожидаемое значение µ и дисперсию σ. ² . Позволять

${\overline {X}}_{n}={\frac {1}{n}}(X_{1}+\cdots +X_{n})$

быть выборочным средним, и

$S_{n}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}\left(X_{i}-{\overline {X}}_{n}\right)^{2}$

быть несмещенной оценкой отклонения от выборки. Можно показать, что случайная величина

$V=(n-1){\frac {S_{n}^{2}}{\sigma ^{2}}}$

имеет распределение хи-квадрат с $\nu =n-1$ степени свободы (по теореме Кокрена ). Легко показать, что величина

$Z=\left({\overline {X}}_{n}-\mu \right){\frac {\sqrt {n}}{\sigma }}$

обычно распределяется со средним значением 0 и дисперсией 1, поскольку выборочное среднее ${\overline {X}}_{n}$ нормально распределяется со средним значением µ и дисперсией σ ² / н . Более того, можно показать, что эти две случайные величины (нормально распределенная Z и распределенная по хи-квадрату V ) независимы. Следовательно ключевое количество

${\textstyle T\equiv {\frac {Z}{\sqrt {V/\nu }}}=\left({\overline {X}}_{n}-\mu \right){\frac {\sqrt {n}}{S_{n}}},}$

которое отличается от Z тем, что точное стандартное отклонение σ заменяется случайной величиной S _n -распределение Стьюдента , имеет t , определенное выше. Обратите внимание, что неизвестная дисперсия совокупности σ ² не появляется в T , поскольку он был и в числителе, и в знаменателе, поэтому он отменяется. Госсет интуитивно получил указанную выше функцию плотности вероятности: $\nu$ равен n − 1, и Фишер доказал это в 1925 году.

Распределение тестовой статистики T зависит от $\nu$, но не µ или σ ; Отсутствие зависимости от µ и σ делает t -распределение важным как в теории, так и на практике.

Выборочное распределение t-статистики

Распределение t возникает как выборочное распределение статистики t- . статистика для одной выборки t- Ниже обсуждается , соответствующую t- статистику для двух выборок см. в t-критерии Стьюдента .

Несмещенная оценка дисперсии

Позволять $\ x_{1},\ldots ,x_{n}\sim {\mathcal {N}}(\mu ,\sigma ^{2})\$ быть независимыми и одинаково распределенными выборками из нормального распределения со средним значением $\mu$ и дисперсия $\ \sigma ^{2}~.$ Выборочное среднее и несмещенная выборочная дисперсия определяются по формуле:

${\begin{aligned}{\bar {x}}&={\frac {\ x_{1}+\cdots +x_{n}\ }{n}}\ ,\\[5pt]s^{2}&={\frac {1}{\ n-1\ }}\ \sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}~.\end{aligned}}$

Результирующая (одна выборка) t- статистика определяется выражением

$t={\frac {{\bar {x}}-\mu }{\ {\sqrt {s^{2}/n\ }}\ }}\sim t_{n-1}~.$

распределению Стьюдента и распределяется согласно t- с $\ n-1\$ степени свободы.

Таким образом, для целей вывода t- статистика является полезной « ключевой величиной » в случае, когда среднее значение и дисперсия $(\mu ,\sigma ^{2})$ являются неизвестными параметрами совокупности в том смысле, что t- статистика имеет распределение вероятностей, которое не зависит ни от $\mu$ ни $\ \sigma ^{2}~.$

Оценка отклонения ML

Вместо несмещенной оценки $\ s^{2}\$ мы также можем использовать оценку максимального правдоподобия

$\ s_{\mathsf {ML}}^{2}={\frac {\ 1\ }{n}}\ \sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}\$

получение статистики

$\ t_{\mathsf {ML}}={\frac {{\bar {x}}-\mu }{\sqrt {s_{\mathsf {ML}}^{2}/n\ }}}={\sqrt {{\frac {n}{n-1}}\ }}\ t~.$

Оно распределяется в соответствии с распределением t в масштабе местоположения :

$t_{\mathsf {ML}}\sim {\mathcal {lst}}(0,\ \tau ^{2}=n/(n-1),\ n-1)~.$

Сложное распределение нормального с обратным гамма-распределением

в масштабе местоположения Распределение t получается в результате объединения ( распределения Гаусса нормального распределения) со средним значением . $\ \mu \$ и неизвестная дисперсия с обратным гамма-распределением, помещенным поверх дисперсии с параметрами $\ a={\frac {\ \nu \ }{2}}\$ и $b={\frac {\ \nu \ \tau ^{2}\ }{2}}~.$ Другими словами, случайная величина X предполагается, что имеет гауссово распределение с неизвестной дисперсией, распределенной как обратная гамма, а затем дисперсия исключается (интегрируется).

Эквивалентно, это распределение является результатом объединения распределения Гаусса с масштабированным распределением обратного хи-квадрата с параметрами $\nu$ и $\ \tau ^{2}~.$ Масштабированное обратное распределение хи-квадрат представляет собой точно такое же распределение, как и обратное гамма-распределение, но с другой параметризацией, т.е. $\ \nu =2\ a,\;{\tau }^{2}={\frac {\ b\ }{a}}~.$

Причина полезности этой характеристики заключается в том, что в байесовской статистике обратное гамма-распределение представляет собой сопряженное априорное распределение дисперсии гауссовского распределения. В результате распределение t в масштабе местоположения естественным образом возникает во многих задачах байесовского вывода.

Максимальное распределение энтропии

Стьюдента Распределение — это распределение вероятностей максимальной энтропии для случайной величины X , для которого $\ \operatorname {\mathbb {E} } \left\{\ \ln(\nu +X^{2})\ \right\}\$ фиксировано.

Дополнительные свойства

Выборка Монте-Карло

распределения Стьюдента Существуют различные подходы к построению случайных выборок на основе t- . Вопрос зависит от того, требуются ли выборки на отдельной основе или они должны быть построены путем применения функции квантиля к однородным выборкам; например, в многомерных приложениях, основанных на зависимости от копулы . В случае автономной выборки расширение метода Бокса-Мюллера и его полярную форму . легко применить Его достоинство заключается в том, что он одинаково хорошо применим ко всем реальным положительным степеням свободы ν ν , в то время как многие другие методы-кандидаты терпят неудачу, если близка к нулю.

Интеграл от функции плотности вероятности Стьюдента и p значения

Функция A ( t | ν ) является интегралом функции плотности вероятности Стьюдента f ( t ) между -t и t , для t ≥ 0 . Таким образом, это дает вероятность того, что значение t меньше, чем рассчитанное на основе наблюдаемых данных, возникнет случайно. Следовательно, функцию A ( t | ν ) можно использовать при проверке того, является ли разница между средними значениями двух наборов данных статистически значимой, путем расчета соответствующего значения t и вероятности его возникновения, если два набора данных были взятые из того же населения. Это используется в различных ситуациях, особенно в t- тестах . Для статистики t с ν степенями свободы A ( t | ν ) — это вероятность того, что t будет меньше наблюдаемого значения, если бы два средних были одинаковыми (при условии, что меньшее среднее вычитается из большего, так что т ≥ 0 ). Его можно легко вычислить из кумулятивной функции распределения F _ν ( t ) -распределения t :

$A(t\mid \nu )=F_{\nu }(t)-F_{\nu }(-t)=1-I_{\frac {\nu }{\nu +t^{2}}}\!\left({\frac {\nu }{2}},{\frac {1}{2}}\right),$

где Ix _{функция} ( a , b ) — регуляризованная неполная бета- .

Для проверки статистических гипотез эта функция используется для построения p значения .

Связанные дистрибутивы

• Нецентральное , t распределение обобщает распределение t включив в него параметр нецентральности. В отличие от нестандартизованных t- распределений, нецентральные распределения не симметричны (медиана не совпадает с модой).
• Дискретное Стьюдента t- распределение определяется его функцией массы вероятности при r, пропорциональной: $$\prod _{j=1}^{k}{\frac {1}{(r+j+a)^{2}+b^{2}}}\quad \quad r=\ldots ,-1,0,1,\ldots ~.$$ Здесь a , b и k — параметры. Это распределение возникает в результате построения системы дискретных распределений, аналогичной системе распределений Пирсона для непрерывных распределений.
• Можно сгенерировать выборки Стьюдента A ( t | ν ), взяв соотношение переменных из нормального распределения и квадратный корень χ² распределения из . Если мы используем вместо нормального распределения, например, распределение Ирвина-Холла , мы получаем в целом симметричное распределение с четырьмя параметрами, которое включает нормальное, равномерное , треугольное Стьюдента и Коши , распределение . Это также более гибко, чем некоторые другие симметричные обобщения нормального распределения.
• Распределение t является примером распределения соотношений .

Использование

В частотном статистическом выводе

Распределение Стьюдента аддитивными возникает в различных задачах статистического оценивания, цель которых состоит в том, чтобы оценить неизвестный параметр, например среднее значение, в условиях, когда данные наблюдаются с ошибками . Если (как почти во всех практических статистических работах) стандартное отклонение генеральной совокупности этих ошибок неизвестно и должно быть оценено на основе данных, t- распределение часто используется для учета дополнительной неопределенности, возникающей в результате этой оценки. В большинстве таких задач, если бы было известно стандартное отклонение ошибок, вместо t- распределения использовалось бы нормальное распределение.

Доверительные интервалы и проверка гипотез — это две статистические процедуры, в которых квантили выборочного распределения конкретной статистики (например, стандартного балла требуются ). В любой ситуации, когда эта статистика является линейной функцией данных t , разделенной на обычную оценку стандартного отклонения, полученную величину можно масштабировать и центрировать, чтобы она соответствовала - распределению Стьюдента. Статистический анализ, включающий средние, взвешенные средние и коэффициенты регрессии, приводит к тому, что статистика имеет такую ​​форму.

распределения Стьюдента Довольно часто в задачах учебников стандартное отклонение генеральной совокупности рассматривается так, как если бы оно было известно, и тем самым устраняется необходимость использования t- . Эти проблемы обычно бывают двух видов: (1) те, в которых размер выборки настолько велик, что можно рассматривать основанную на данных оценку дисперсии, как если бы она была достоверной, и (2) те, которые иллюстрируют математические рассуждения, в которых проблема оценки стандартного отклонения временно игнорируется, потому что это не тот момент, который затем объясняет автор или преподаватель.

Проверка гипотез

Можно показать, что ряд статистических данных имеют распределения t для выборок среднего размера при нулевых гипотезах , которые представляют интерес, так что распределение t формирует основу для тестов значимости. Например, распределение коэффициента ранговой корреляции Спирмена ρ в нулевом случае (нулевая корреляция) хорошо аппроксимируется распределением t для размеров выборки выше примерно 20.

Доверительные интервалы

Предположим, что число A выбрано так, что

$\ \operatorname {\mathbb {P} } \left\{\ -A<T<A\ \right\}=0.9\ ,$

когда T имеет распределение t с n - 1   степенями свободы. По симметрии это то же самое, что сказать, что A удовлетворяет

$\ \operatorname {\mathbb {P} } \left\{\ T<A\ \right\}=0.95\ ,$

поэтому A — это «95-й процентиль» этого распределения вероятностей, или $\ A=t_{(0.05,n-1)}~.$ Затем

$\ \operatorname {\mathbb {P} } \left\{\ -A<{\frac {\ {\overline {X}}_{n}-\mu \ }{S_{n}/{\sqrt {n\ }}}}<A\ \right\}=0.9\ ,$

и это эквивалентно

$\ \operatorname {\mathbb {P} } \left\{\ {\overline {X}}_{n}-A{\frac {S_{n}}{\ {\sqrt {n\ }}\ }}<\mu <{\overline {X}}_{n}+A\ {\frac {S_{n}}{\ {\sqrt {n\ }}\ }}\ \right\}=0.9.$

Следовательно, интервал, конечные точки которого

$\ {\overline {X}}_{n}\ \pm A\ {\frac {S_{n}}{\ {\sqrt {n\ }}\ }}\$

представляет собой 90% доверительный интервал для μ. Следовательно, если мы найдем среднее значение набора наблюдений, которые, как мы можем разумно ожидать, будут иметь нормальное распределение, мы можем использовать t- распределение, чтобы проверить, включают ли доверительные пределы этого среднего значения какое-либо теоретически предсказанное значение - например, значение, предсказанное на гипотеза нулевая .

Именно этот результат используется в Стьюдента t- тестах : поскольку разница между средними значениями выборок из двух нормальных распределений сама по себе распределяется нормально, t- распределение можно использовать для проверки того, можно ли разумно предположить, что эта разница равна нулю.

Если данные нормально распределены, односторонний (1 − α ) верхний доверительный предел (UCL) среднего значения можно рассчитать с помощью следующего уравнения:

${\mathsf {UCL}}_{1-\alpha }={\overline {X}}_{n}+t_{\alpha ,n-1}\ {\frac {S_{n}}{\ {\sqrt {n\ }}\ }}~.$

Результирующий UCL будет наибольшим средним значением, которое может возникнуть для данного доверительного интервала и размера популяции. Другими словами, ${\overline {X}}_{n}$ будучи средним значением набора наблюдений, вероятность того, что среднее значение распределения ниже UCL _{1 − α,} равна уровню достоверности 1 − α .

Интервалы прогнозирования

Распределение t можно использовать для построения интервала прогнозирования для ненаблюдаемой выборки на основе нормального распределения с неизвестным средним значением и дисперсией.

В байесовской статистике

Стьюдента Распределение , особенно в его трехпараметрической (шкале местоположения) версии, часто возникает в байесовской статистике в результате его связи с нормальным распределением. Всякий раз, когда дисперсия нормально распределенной случайной величины неизвестна и над ней помещается сопряженная априорная величина , следующая обратному гамма-распределению , результирующее предельное распределение переменной будет следовать t -распределению Стьюдента. Эквивалентные конструкции с одинаковыми результатами включают сопряженное масштабированное распределение обратного хи-квадрата по дисперсии или сопряженное гамма-распределение по точности . Если неправильный априор пропорционален ⁠ 1 /   σ ² ⁠ помещается над дисперсией, также возникает t- распределение. Это имеет место независимо от того, известно ли среднее значение нормально распределенной переменной, неизвестно, распределено ли в соответствии с сопряженной, нормально распределенной априорной величиной, или неизвестно, распределенной в соответствии с неправильной априорной константой.

Связанные ситуации, которые также приводят к t- распределению:

• Маргинальное неизвестного среднего значения нормально апостериорное распределение распределенной переменной с неизвестным априорным средним значением и дисперсией в соответствии с вышеуказанной моделью.
• Априорное прогнозируемое распределение и апостериорное прогнозируемое распределение серия независимых одинаково распределенных нормально распределенных точек данных с априорным средним значением и дисперсией, как в приведенной выше модели. новой точки данных с нормальным распределением, когда наблюдалась

Надежное параметрическое моделирование

Распределение t часто используется в качестве альтернативы нормальному распределению в качестве модели данных, которые часто имеют более тяжелые хвосты, чем допускает нормальное распределение; см., например, Lange et al. Классический подход заключался в выявлении выбросов (например, с помощью критерия Граббса ) и их исключении или понижении их веса каким-либо образом. Однако не всегда легко выявить выбросы (особенно в больших размерностях ), а распределение t является естественным выбором модели для таких данных и обеспечивает параметрический подход к надежной статистике .

Байесовский подход можно найти у Gelman et al. Параметр степеней свободы контролирует эксцесс распределения и коррелирует с параметром масштаба. Вероятность может иметь несколько локальных максимумов, и поэтому часто необходимо зафиксировать достаточно низкое значение степеней свободы и оценить другие параметры, принимая это как заданное. Некоторые авторы сообщают, что значения от 3 до 9 часто являются хорошим выбором. Венейблс и Рипли предполагают, что значение 5 часто является хорошим выбором.

Студенческий процесс ​

Для практических нужд регрессии и прогнозирования процессы Стьюдента были введены t- , которые являются обобщением t- распределений Стьюдента для функций. процесс Стьюдента t- строится на основе t- распределений Стьюдента, так же как гауссов процесс строится на основе гауссовских распределений . Для гауссовского процесса все наборы значений имеют многомерное гауссово распределение. Аналогично, $X(t)$ является процессом Стьюдента на интервале $I=[a,b]$ если соответствующие значения процесса $\ X(t_{1}),\ \ldots \ ,X(t_{n})\$ ( $t_{i}\in I$) имеют совместное многомерное Стьюдента распределение . Эти процессы используются для регрессии, прогнозирования, байесовской оптимизации и связанных с ними задач. многомерные t- процессы Стьюдента. Для многомерной регрессии и прогнозирования с несколькими выходами вводятся и используются

Таблица выбранных значений

В следующей таблице перечислены значения t- распределений со степенями свободы ν для диапазона односторонних или двусторонних критических областей. Первый столбец — ν , проценты вверху — уровни уверенности. $\ \alpha \ ,$ а цифры в основной части таблицы — это $t_{\alpha ,n-1}$ факторы, описанные в разделе доверительных интервалов .

Последняя строка с бесконечным ν дает критические точки для нормального распределения, поскольку распределение t с бесконечным числом степеней свободы является нормальным распределением. (См. Связанные дистрибутивы выше).

Односторонний	75%	80%	85%	90%	95%	97.5%	99%	99.5%	99.75%	99.9%	99.95%
Двусторонний	50%	60%	70%	80%	90%	95%	98%	99%	99.5%	99.8%	99.9%
1	1.000	1.376	1.963	3.078	6.314	12.706	31.821	63.657	127.321	318.309	636.619
2	0.816	1.061	1.386	1.886	2.920	4.303	6.965	9.925	14.089	22.327	31.599
3	0.765	0.978	1.250	1.638	2.353	3.182	4.541	5.841	7.453	10.215	12.924
4	0.741	0.941	1.190	1.533	2.132	2.776	3.747	4.604	5.598	7.173	8.610
5	0.727	0.920	1.156	1.476	2.015	2.571	3.365	4.032	4.773	5.893	6.869
6	0.718	0.906	1.134	1.440	1.943	2.447	3.143	3.707	4.317	5.208	5.959
7	0.711	0.896	1.119	1.415	1.895	2.365	2.998	3.499	4.029	4.785	5.408
8	0.706	0.889	1.108	1.397	1.860	2.306	2.896	3.355	3.833	4.501	5.041
9	0.703	0.883	1.100	1.383	1.833	2.262	2.821	3.250	3.690	4.297	4.781
10	0.700	0.879	1.093	1.372	1.812	2.228	2.764	3.169	3.581	4.144	4.587
11	0.697	0.876	1.088	1.363	1.796	2.201	2.718	3.106	3.497	4.025	4.437
12	0.695	0.873	1.083	1.356	1.782	2.179	2.681	3.055	3.428	3.930	4.318
13	0.694	0.870	1.079	1.350	1.771	2.160	2.650	3.012	3.372	3.852	4.221
14	0.692	0.868	1.076	1.345	1.761	2.145	2.624	2.977	3.326	3.787	4.140
15	0.691	0.866	1.074	1.341	1.753	2.131	2.602	2.947	3.286	3.733	4.073
16	0.690	0.865	1.071	1.337	1.746	2.120	2.583	2.921	3.252	3.686	4.015
17	0.689	0.863	1.069	1.333	1.740	2.110	2.567	2.898	3.222	3.646	3.965
18	0.688	0.862	1.067	1.330	1.734	2.101	2.552	2.878	3.197	3.610	3.922
19	0.688	0.861	1.066	1.328	1.729	2.093	2.539	2.861	3.174	3.579	3.883
20	0.687	0.860	1.064	1.325	1.725	2.086	2.528	2.845	3.153	3.552	3.850
21	0.686	0.859	1.063	1.323	1.721	2.080	2.518	2.831	3.135	3.527	3.819
22	0.686	0.858	1.061	1.321	1.717	2.074	2.508	2.819	3.119	3.505	3.792
23	0.685	0.858	1.060	1.319	1.714	2.069	2.500	2.807	3.104	3.485	3.767
24	0.685	0.857	1.059	1.318	1.711	2.064	2.492	2.797	3.091	3.467	3.745
25	0.684	0.856	1.058	1.316	1.708	2.060	2.485	2.787	3.078	3.450	3.725
26	0.684	0.856	1.058	1.315	1.706	2.056	2.479	2.779	3.067	3.435	3.707
27	0.684	0.855	1.057	1.314	1.703	2.052	2.473	2.771	3.057	3.421	3.690
28	0.683	0.855	1.056	1.313	1.701	2.048	2.467	2.763	3.047	3.408	3.674
29	0.683	0.854	1.055	1.311	1.699	2.045	2.462	2.756	3.038	3.396	3.659
30	0.683	0.854	1.055	1.310	1.697	2.042	2.457	2.750	3.030	3.385	3.646
40	0.681	0.851	1.050	1.303	1.684	2.021	2.423	2.704	2.971	3.307	3.551
50	0.679	0.849	1.047	1.299	1.676	2.009	2.403	2.678	2.937	3.261	3.496
60	0.679	0.848	1.045	1.296	1.671	2.000	2.390	2.660	2.915	3.232	3.460
80	0.678	0.846	1.043	1.292	1.664	1.990	2.374	2.639	2.887	3.195	3.416
100	0.677	0.845	1.042	1.290	1.660	1.984	2.364	2.626	2.871	3.174	3.390
120	0.677	0.845	1.041	1.289	1.658	1.980	2.358	2.617	2.860	3.160	3.373
∞	0.674	0.842	1.036	1.282	1.645	1.960	2.326	2.576	2.807	3.090	3.291
Односторонний	75%	80%	85%	90%	95%	97.5%	99%	99.5%	99.75%	99.9%	99.95%
Двусторонний	50%	60%	70%	80%	90%	95%	98%	99%	99.5%	99.8%	99.9%

Расчет доверительного интервала

Допустим, у нас есть выборка размером 11, средним значением выборки 10 и дисперсией выборки 2. Для 90% уверенности с 10 степенями свободы одностороннее значение t из таблицы равно 1,372. Затем с доверительным интервалом, рассчитанным по формуле

$\ {\overline {X}}_{n}\pm t_{\alpha ,\nu }\ {\frac {S_{n}}{\ {\sqrt {n\ }}\ }}\ ,$

мы определяем, что с 90% уверенностью имеем истинное среднее значение, лежащее ниже

$\ 10+1.372\ {\frac {\sqrt {2\ }}{\ {\sqrt {11\ }}\ }}=10.585~.$

Другими словами, в 90% случаев, когда верхний порог рассчитывается этим методом на основе конкретных образцов, этот верхний порог превышает истинное среднее значение.

И с уверенностью 90% мы имеем истинное среднее значение, лежащее выше

$\ 10-1.372\ {\frac {\sqrt {2\ }}{\ {\sqrt {11\ }}\ }}=9.414~.$

Другими словами, в 90% случаев, когда нижний порог рассчитывается этим методом на основе конкретных образцов, этот нижний порог лежит ниже истинного среднего значения.

Таким образом, при доверительной вероятности 80 % (рассчитанной по формуле 100 % – 2 × (1 – 90 %) = 80 %) мы имеем истинное среднее значение, лежащее в пределах интервала

$\left(\ 10-1.372\ {\frac {\sqrt {2\ }}{\ {\sqrt {11\ }}\ }},\ 10+1.372\ {\frac {\sqrt {2\ }}{\ {\sqrt {11\ }}\ }}\ \right)=(\ 9.414,\ 10.585\ )~.$

Сказать, что в 80% случаев, когда верхний и нижний пороговые значения рассчитываются с помощью этого метода на основе данной выборки, истинное среднее значение находится как ниже верхнего порога, так и выше нижнего порога, это не то же самое, что сказать, что существует 80% вероятность того, что истинное среднее находится между определенной парой верхних и нижних порогов, рассчитанных с помощью этого метода; см. доверительный интервал и ошибку прокурора .

В настоящее время статистическое программное обеспечение, такое как язык программирования R , и функции, доступные во многих программах для работы с электронными таблицами, вычисляют значения распределения t и обратного ему без таблиц.

См. также

• F -распределение
• сложенных t и половинных t Распределения
• Хотеллинга T² Распределение
• Многомерное распределение студентов
• Стандартная нормальная таблица ( Z -распределения) таблица
• статистика ​
• Распределение Тау для внутренне стьюдентизированных остатков
• Лямбда-распределение Уилкса
• Распределение желаний
• Модифицированное полунормальное распределение с PDF-файлом на $(0,\infty )$ дается как $f(x)={\frac {2\beta ^{\frac {\alpha }{2}}x^{\alpha -1}\exp(-\beta x^{2}+\gamma x)}{\Psi {\left({\frac {\alpha }{2}},{\frac {\gamma }{\sqrt {\beta }}}\right)}}}\ ,$ где $\Psi (\alpha ,z)={}_{1}\Psi _{1}\left({\begin{matrix}\left(\alpha ,{\frac {1}{2}}\right)\\(1,0)\end{matrix}};z\right)$ обозначает Пси-функцию Фокса–Райта .

Ссылки

• Сенн, С.; Ричардсон, В. (1994). «Первый т- тест». Статистика в медицине . 13 (8): 785–803. дои : 10.1002/сим.4780130802 . ПМИД   8047737 .
• Хогг Р.В. , Крейг А.Т. (1978). Введение в математическую статистику (4-е изд.). Нью-Йорк: Макмиллан. ASIN   B010WFO0SA .
• Венейблс, Западная Нью-Йорк; Рипли, Б.Д. (2002). Современная прикладная статистика с S (Четвертое изд.). Спрингер.
• Гельман, Эндрю; Джон Б. Карлин; Хэл С. Стерн; Дональд Б. Рубин (2003). Байесовский анализ данных (второе изд.). CRC/Чепмен и Холл. ISBN  1-58488-388-Х .

Внешние ссылки

• «Распределение студентов» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Самые ранние известные варианты использования некоторых математических слов (S) (Замечания об истории термина «Распределение Стьюдента»)
• Руо, М. (2013), Вероятность, статистика и оценка (PDF) (краткая редакция), Первые студенты, стр. 112.
• t-распределение студента , архивировано 10 апреля 2021 г. в Wayback Machine.