Омар Хайям

Судить
Омар Хайям
Судить Омар Хайям
Омар Хайям
	Статуя Хайяма работы Абольхасана Садиги
Рожденный	18 мая 1048 г. ; Нишапур , Хорасан , Персия
Умер	4 декабря 1131 г. (83 года) ; Нишапур, Хорасан, Персия
Академическое образование
Влияния	Авиценна ; аль-Хорезми ; Евклид ; Аполлоний Пергский ;
Академическая работа
Основные интересы	Математика ; Астрономия ; Персидская философия ; Персидская поэзия ;
Под влиянием	Книга ; Аль-Хазини ; Низами Арузи из Самарканда ; Хафез ; Садег Хедаят ; Андре Жид ; Джон Уоллис ; Саккери ; Эдвард Фитцджеральд ; Морис Бушор ; Анри Казалис ; Жан Капеллан ; Амин Маалуф ;

Гияс ад-Дин Абу аль-Фатх Умар ибн Ибрагим Нисабури ^{[ 1 ]}^{[ 3 ]} (18 мая 1048 г. - 4 декабря 1131 г.), широко известный как Омар Хайям ( персидский : عمر خیّام ), ^{[ а ]} был персидским эрудитом , известным своим вкладом в математику , астрономию , философию и поэзию . ^{[ 4 ]}^: 94 Он родился в Нишапуре , первоначальной столице Сельджукской империи , и жил в период правления династии Сельджуков , примерно во времена Первого крестового похода .

Как математик, он наиболее известен своей работой по классификации и решению кубических уравнений , где он предоставил геометрическую формулировку, основанную на пересечении коник . ^{[ 5 ]} Он также способствовал более глубокому пониманию аксиомы Евклида о параллельности . ^{[ 6 ]}^: 284 Как астроном, он рассчитал продолжительность солнечного года с поразительной точностью и точностью и разработал календарь Джалали , солнечный календарь с очень точным 33-летним вставочным циклом. ^{[ 7 ]}^: 659 ^{[ б ]} который послужил основой для персидского календаря , который до сих пор используется спустя почти тысячелетие.

Существует традиция приписывать Омару Хайяму стихи , написанные в форме четверостиший ( рубаият رباعیات ). Эта поэзия стала широко известна англочитающему миру в переводе Эдварда Фитцджеральда ( «Рубайят Омара Хайяма» , 1859), который пользовался большим успехом в ориентализме конца века .

Жизнь

Омар Хайям родился в Нишапуре — мегаполисе в Хорасан провинции , персидского происхождения, в 1048 году. ^{[ 8 ]}^{[ 9 ]}^{[ 10 ]}^{[ 11 ]}^{[ 12 ]} В средневековых персидских текстах его обычно называют просто Омар Хайям . ^{[ 7 ]}^: 658^{[ с ]} Хотя это и вызывает сомнения, часто предполагалось, что его предки занимались изготовлением палаток, поскольку Хайям по-арабски означает «изготовитель палаток». ^{[ 15 ]}^: 30 Историк Байхаки , лично знакомый с Хайямом, приводит полную информацию о его гороскопе: «он был Близнецами, Солнце и Меркурий находились в асценденте [...]». ^{[ 16 ]}^: 471^{[ 17 ]}^{: 172–175, вып. 66} Это было использовано современными учеными, чтобы установить дату его рождения 18 мая 1048 года. ^{[ 7 ]}^: 658

Детство Хайяма прошло в Нишапуре. ^{[ 7 ]}^: 659 ведущий мегаполис империи Великих Сельджуков , ^{[ 18 ]}^: 15^{[ 19 ]} который ранее был крупным центром зороастрийской религии . ^{[ 8 ]}^: 68 Его полное имя, как следует из арабских источников, было Абуль Фатх Омар ибн Ибрагим аль-Хайям . ^{[ д ]} Его дарования были признаны его первыми наставниками, которые отправили его учиться к имаму Муваффаку Нишабури, величайшему учителю региона Хорасан, который обучал детей высшей знати, и на протяжении многих лет у Хайяма с ним сложилась крепкая дружба. ^{[ 8 ]}^: 20 Хайям, возможно, встречался и учился у Бахманьяра , ученика Авиценны . ^{[ 8 ]}^: 20–21 провинцию После изучения естественных наук, философии, математики и астрономии в Нишапуре около 1068 года он отправился в Бухарскую , где часто посещал знаменитую библиотеку Ковчега . Примерно в 1070 году он переехал в Самарканд , где приступил к написанию своего знаменитого «Трактата по алгебре» под патронажем Абу Тахира Абд ар-Рахмана ибн Алака, губернатора и главного судьи города. ^{[ 20 ]}^{: 4330b} Хайям был любезно принят караханидским правителем Шамсом аль-Мульком Насром , который, по словам Байхаки, «окажет ему величайшую честь, настолько, что он посадит [Хайяма] рядом с ним на свой трон ». ^{[ 15 ]}^: 34^{[ 8 ]}^: 47

В 1073–1074 гг. был заключен мир с султаном Малик-шахом I, совершавшим вторжения во владения Караханидов. Хайям поступил на службу к Малик-шаху в 1074 году, когда он был приглашен великим визирем Низамом аль-Мульком для встречи с Малик-шахом в городе Марв . Впоследствии Хайяму было поручено создать обсерваторию в Исфахане и возглавить группу ученых для проведения точных астрономических наблюдений с целью пересмотра персидского календаря. Предприятие, вероятно, началось с открытия обсерватории в 1074 году и закончилось в 1079 году. ^{[ 8 ]}^: 28–29 когда Омар Хайям и его коллеги завершили свои измерения продолжительности года, сообщив, что он составляет 365,24219858156 дней. ^{[ 5 ]} Учитывая, что продолжительность года меняется в шестом десятичном знаке в течение жизни человека, это исключительно точно. Для сравнения, продолжительность года в конце XIX века составляла 365,242196 дней, а сегодня – 365,242190 дней.

После смерти Малик-шаха и его визиря (убитых, как полагают, исмаилитским орденом ассасинов ) Хайям впал в немилость при дворе, и в результате вскоре отправился в паломничество в Мекку . Возможным скрытым мотивом его паломничества, о котором сообщил Аль-Кифти , была публичная демонстрация своей веры с целью развеять подозрения в скептицизме и опровергнуть обвинения в неортодоксальности (включая возможную симпатию или приверженность зороастризму), выдвинутые против него враждебным духовенством. . ^{[ 8 ]}^: 29^{[ 8 ]}^: 29^{[ 21 ]} пригласил его Затем новый султан Санжар в Марв, возможно, для работы придворным астрологом . ^{[ 1 ]} Позже ему разрешили вернуться в Нишапур из-за ухудшения его здоровья. По возвращении он, похоже, вел жизнь отшельника. ^{[ 22 ]}^: 99

Омар Хайям умер в возрасте 83 лет в своем родном городе Нишапуре 4 декабря 1131 года и похоронен в том месте, где сейчас находится мавзолей Омара Хайяма . Один из его учеников Низами Арузи рассказывает историю, что где-то в 1112–1112 годах Хайям был в Балхе в компании Исфизари (одного из ученых, сотрудничавших с ним в составлении календаря Джалали), когда он сделал пророчество о том, что «моя могила будет в таком месте, где северный ветер может разбросать по нему розы». ^{[ 15 ]}^: 36^{[ 19 ]} Через четыре года после своей смерти Арузи обнаружил его могилу на кладбище в тогдашнем большом и известном квартале Нишапура по дороге в Марв. Как и предвидел Хайям, Арузи нашел могилу, расположенную у подножия садовой стены, над которой склонились головы грушевые и персиковые деревья и уронили свои цветы, так что его надгробие скрылось под ними. ^{[ 15 ]}^: 37

Математика

Хайям при жизни прославился как математик . Среди его сохранившихся математических работ: (i) «Комментарий к трудностям, касающимся постулатов об элементах Евклида» ( Risāla fī Sharḥ mā Ashkal min Muṣādarāt Kitāb Uqlīdis ), завершенный в декабре 1077 года; ^{[ 11 ]}^{: 832а}^{[ 23 ]}^{[ 24 ]}^{: § 1}^{[ 25 ]}^{: 324б} (ii) «Трактат о разделении квадранта круга» ( Risālah fī Qismah Rub' al-Dā'irah ), без даты, но завершенный до «Трактата по алгебре» , ^{[ 11 ]}^{: 831б}^{[ 24 ]}^{: § 2} и (iii) Трактат по алгебре ( Рисалах фи аль-Джабр ва'ль-Мукабала ), ^{[ 11 ]}^{: 831б–832а}^{[ 24 ]}^{: § 3} скорее всего, завершено в 1079 году. ^{[ 6 ]}^: 281 Кроме того, он написал трактат о биномиальной теореме и извлечении n ^й корень натуральных чисел, который утерян. ^{[ 8 ]}^: 197^{[ 11 ]}^{: 832а}^{[ 24 ]}^{: § 4}^{[ 25 ]}^{: 325б–326б}

Теория параллелей

Часть «Комментариев Хайяма к трудностям, касающимся постулатов «Элементов» Евклида», посвящена аксиоме параллельности . ^{[ 6 ]}^: 282 Трактат Хайяма можно считать первой трактовкой аксиомы, основанной не на petitio principii , а на более интуитивном постулате. Хайям опровергает предыдущие попытки других математиков доказать это положение, главным образом на том основании, что каждый из них постулировал нечто, что ни в коем случае не легче было признать, чем сам Пятый Постулат. ^{[ 24 ]}^{: § 1}^{[ 25 ]}^{: 326б–327б}^{[ 26 ]}^: 75 Опираясь на взгляды Аристотеля , он отвергает использование движения в геометрии и поэтому отвергает другую попытку Ибн аль-Хайсама . ^{[ 27 ]}^: 64–65^{[ 28 ]}^: 270^{[ и ]} Неудовлетворенный тем, что математикам не удалось доказать утверждение Евклида с помощью других его постулатов, Хайям попытался связать аксиому с Четвертым постулатом, утверждающим, что все прямые углы равны между собой. ^{[ 6 ]}^: 282

Хайям был первым, кто рассмотрел три различных случая острого, тупого и прямого угла для вершинных углов четырехугольника Хайяма-Саккери . ^{[ 6 ]}^: 283 Доказав ряд теорем о них, он показал, что Постулат V следует из гипотезы прямого угла, и опроверг тупые и острые случаи как противоречивые. ^{[ 28 ]}^: 270^{[ 29 ]}^: 133 Его тщательно продуманная попытка доказать постулат о параллельности имела важное значение для дальнейшего развития геометрии, поскольку ясно показывает возможность неевклидовой геометрии. Теперь известно, что гипотезы острого, тупого и прямого углов приводят соответственно к неевклидовой гиперболической геометрии Гаусса-Бойяи-Лобачевского, к римановой геометрии и к евклидовой геометрии . ^{[ 30 ]}

«Кубическое уравнение и пересечение конических сечений» — первая страница двухглавой рукописи, хранящейся в Тегеранском университете.

Комментарии Туси по поводу подхода Хайяма к параллелям дошли до Европы. Джон Уоллис , профессор геометрии в Оксфорде , перевел комментарий Туси на латынь. Геометр-иезуит Джироламо Саккери , работа которого ( Euclides ab omni naevo vindicatus , 1733) обычно считается первым шагом в конечном развитии неевклидовой геометрии , был знаком с работами Уоллиса. Американский историк математики Дэвид Юджин Смит упоминает, что Саккери «использовал ту же лемму, что и лемма Туси, даже написав цифру точно так же и используя лемму с той же целью». Далее он говорит, что «Туси ясно заявляет, что это заслуга Омара Хайяма, и из текста кажется очевидным, что последний был его вдохновителем». ^{[ 8 ]}^: 195^{[ 22 ]}^: 104^{[ 31 ]}

Концепция реального числа

Этот трактат о Евклиде содержит еще один вклад, посвященный теории пропорций и составлению пропорций. Хайям обсуждает взаимосвязь между концепцией отношения и концепцией числа и явно поднимает различные теоретические трудности. В частности, он способствует теоретическому изучению понятия иррационального числа . ^{[ 32 ]} Недовольный определением равных отношений Евклидом, он переопределил понятие числа, используя непрерывную дробь как средство выражения отношения. Юшкевич и Розенфельд утверждают, что «поместив иррациональные количества и числа в один и тот же оперативный масштаб, [Хайям] начал настоящую революцию в доктрине чисел». ^{[ 25 ]}^{: 327б} отметил, Аналогичным образом, DJ Струик что Омар «был на пути к тому расширению концепции числа, которое ведет к понятию действительного числа ». ^{[ 6 ]}^: 284

Геометрическая алгебра

Рашед и Вахабзаде (2000) утверждали, что благодаря его основательному геометрическому подходу к алгебраическим уравнениям Хайяма можно считать предшественником Декарта в изобретении аналитической геометрии . ^{[ 33 ]}^: 248 В «Трактате о разделении квадранта круга» Хайям применил алгебру к геометрии. В этой работе он посвятил себя главным образом исследованию, можно ли разделить круговой квадрант на две части так, чтобы отрезки, проецируемые из точки разделения на перпендикулярные диаметры круга, образовывали определенное соотношение. В его решении, в свою очередь, использовалось несколько конструкций кривых, которые привели к уравнениям, содержащим кубические и квадратичные члены. ^{[ 33 ]}^: 248

Решение кубических уравнений

Хайям, по-видимому, был первым, кто разработал общую теорию кубических уравнений. ^{[ 5 ]}^{[ ж ]} и первым, кто геометрически решил все типы кубических уравнений, если речь идет о положительных корнях. ^{[ 34 ]} В « Трактате по алгебре» содержатся его работы по кубическим уравнениям . ^{[ 35 ]}^: 9 Оно разделено на три части: (i) уравнения, которые можно решить с помощью циркуля и линейки , (ii) уравнения, которые можно решить с помощью конических сечений , и (iii) уравнения, включающие обратное неизвестное. ^{[ 24 ]}^{: § 3}

Хайям составил исчерпывающий список всех возможных уравнений, включающих прямые, квадраты и кубы. ^{[ 36 ]}^: 43 Он рассмотрел три биномиальных уравнения, девять триномиальных уравнений и семь тетраномиальных уравнений. ^{[ 6 ]}^: 281 Для полиномов первой и второй степени он дал численные решения с помощью геометрического построения. Он пришел к выводу, что существует четырнадцать различных типов кубик, которые нельзя свести к уравнению меньшей степени. ^{[ 11 ]}^{: 831б}^{[ 25 ]}^{: 328а}^{[ 37 ]}^: 49 Для этого он не смог выполнить построение своего неизвестного отрезка с помощью циркуля и линейки. Он приступил к представлению геометрических решений всех типов кубических уравнений, используя свойства конических сечений. ^{[ 6 ]}^: 281^{[ 38 ]}^: 157 Необходимые леммы для геометрического доказательства Хайяма включают Евклида VI , предложение 13, и Аполлония II , предложение 12. ^{[ 38 ]}^: 155 Положительный корень кубического уравнения определялся как абсцисса точки пересечения двух коник, например пересечения двух парабол или пересечения параболы и окружности и т. д. ^{[ 39 ]}^: 141 Однако он признал, что арифметическая задача этих кубов до сих пор не решена, добавив, что «возможно, после нас ее узнает кто-то другой». ^{[ 38 ]}^: 158 Эта задача оставалась открытой до XVI века, когда алгебраическое решение кубического уравнения было найдено в его общности Кардано , Дель Ферро и Тартальей в Италии эпохи Возрождения . ^{[ 6 ]}^: 282

Тот, кто думает, что алгебра — это трюк с получением неизвестных, думает это напрасно. Не следует обращать внимания на то, что алгебра и геометрия внешне различны. Алгебры — это геометрические факты, которые доказываются предложениями пятым и шестым второй книги « Начал» .

—Омар Хайям ^{[ 40 ]}

По сути, работа Хайяма представляет собой попытку объединить алгебру и геометрию. ^{[ 41 ]}^: 241 Это конкретное геометрическое решение кубических уравнений было дополнительно исследовано М. Хачтруди и распространено на решение уравнений четвертой степени. ^{[ 42 ]} Хотя подобные методы время от времени появлялись со времен Менехма и были развиты математиком 10-го века Абу аль-Джудом , ^{[ 43 ]}^: 29^{[ 44 ]}^: 110 Работу Хайяма можно считать первым систематическим исследованием и первым точным методом решения кубических уравнений. ^{[ 45 ]}^: 92 Математик Вепке (1851), предложивший перевод алгебры Хайяма на французский язык, похвалил его за «силу обобщения и строго систематическую процедуру». ^{[ 46 ]}^: 10

Биномиальная теорема и извлечение корней

У индусов известны методы получения квадратных и кубических корней , методы, основанные на знании отдельных случаев, а именно знание квадратов девяти цифр 1. ², 2 ², 3 ² (и т. д.) и их соответствующие произведения, т. е. 2 × 3 и т. д. Мы написали трактат о доказательстве справедливости этих методов и того, что они удовлетворяют условиям. Кроме того, мы увеличили их типы, а именно в виде определения корней четвертой, пятой, шестой степени до любой желаемой степени. Никто не предшествовал нам в этом, и эти доказательства являются чисто арифметическими, основанными на арифметике « Начал» .

— Омар Хайям, Трактат по алгебре ^{[ 47 ]}

В своем алгебраическом трактате Хайям ссылается на написанную им книгу по извлечению $n$ из натуральных чисел, используя открытый им закон, не зависящий от геометрических фигур. ^{[ 39 ]} Эта книга, скорее всего, называлась « Трудности арифметики» ( Мушкилат аль-Хисаб ). ^{[ 11 ]}^{: 832а}^{[ 24 ]}^{: § 4} и не сохранилось. ^{[ 25 ]}^{: 325б} Основываясь на контексте, некоторые историки математики, такие как Дж. Струик, полагают, что Омар, должно быть, знал формулу разложения бинома. $(a+b)^{n}$ , где $n$ — положительное целое число. ^{[ 6 ]}^: 282 Случай степени 2 явно указан в элементах Евклида, а случай не более степени 3 был установлен индийскими математиками. Хайям был математиком , который заметил важность общей биномиальной теоремы. Аргумент, подтверждающий утверждение о том, что Хайям имел общую биномиальную теорему, основан на его способности извлекать корни. ^{[ 48 ]} Один из предшественников Хайяма, аль-Караджи , уже открыл треугольное расположение коэффициентов биномиальных разложений, которое позже стало известно европейцам как треугольник Паскаля ; ^{[ 49 ]}^: 60 Хайям популяризировал этот треугольный массив в Иране, так что теперь он известен как треугольник Омара Хайяма. ^{[ 39 ]}

Астрономия

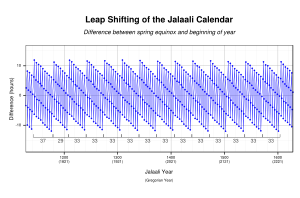
В 1074–1075 годах султан Малик-Шах поручил Омару Хайяму построить обсерваторию в Исфахане и реформировать персидский календарь . Под руководством Хайяма работала группа из восьми ученых, которая проводила крупномасштабные астрономические наблюдения и пересматривала астрономические таблицы. ^{[ 39 ]}^: 141 Перекалибровка календаря зафиксировала первый день года в точный момент прохождения центра Солнца через точку весеннего равноденствия . Это знаменует начало весны или Навруз , день, когда Солнце входит в первый градус Овна . перед полуднем ^{[ 50 ]}^: 10–11^{[ 51 ]} Полученный календарь был назван в честь Малик-Шаха календарем Джалали и был открыт 15 марта 1079 года. ^{[ 52 ]}^: 269 Сама обсерватория была заброшена после смерти Малик-шаха в 1092 году. ^{[ 7 ]}^: 659

Календарь Джалали был настоящим солнечным календарем , в котором продолжительность каждого месяца равна времени прохождения Солнца через соответствующий знак Зодиака . Календарная реформа ввела уникальный 33-летний интеркаляционный цикл. Как указывают работы Хазини , группа Хайяма реализовала систему вставок, основанную на четырехлетних и пятилетних високосных годах . Таким образом, календарь состоял из 25 обычных лет, включавших 365 дней, и 8 високосных лет, включавших 366 дней. ^{[ 53 ]}^: 13 Календарь использовался в Большом Иране с 11 по 20 века. В 1911 году календарь Джалали стал официальным национальным календарем Каджара Ирана . В 1925 году этот календарь был упрощен, а названия месяцев модернизированы, в результате чего появился современный иранский календарь . Календарь Джалали более точен, чем григорианский календарь 1582 года. ^{[ 7 ]}^: 659 с ошибкой в один день, накопленной за 5000 лет, по сравнению с одним днем каждые 3330 лет в григорианском календаре. ^{[ 8 ]}^: 200 Мориц Кантор считал его самым совершенным календарем, когда-либо созданным. ^{[ 22 ]}^: 101

Один из его учеников Низами Арузи из Самарканда рассказывает, что Хайям, по-видимому, не верил в астрологию и гадание: «Я не заметил, чтобы он ( ученый Омар Хайям) сильно верил в астрологические предсказания, и я не видел и не слышал о любой из великих [ученых], который верил в это». ^{[ 46 ]}^: 11 Когда он работал астрологом у Султана Санджара, его попросили предсказать погоду – работа, с которой он, очевидно, не очень хорошо справился. ^{[ 8 ]}^: 30 Джордж Салиба объясняет, что термин «илм ан-нуджум» , используемый в различных источниках, в которых можно найти ссылки на жизнь и творчество Хайяма, иногда неправильно переводился как означающий астрологию. Он добавляет: «по крайней мере, с середины десятого века, согласно « Фараби » Перечню наук , эта наука, илм ан-нуджум , уже была разделена на две части: одна занималась астрологией, а другая — теоретическими исследованиями. математическая астрономия». ^{[ 54 ]}^: 224

Другие работы

У Хайяма есть небольшой трактат, посвященный принципу Архимеда (полное название — « Об обмане знания двух количеств золота и серебра в соединении, состоящем из двух »). Для соединения золота, смешанного с серебром, он описывает метод более точного измерения веса на единицу емкости каждого элемента. Он предполагает взвешивание соединения как на воздухе, так и в воде, поскольку вес легче измерить точно, чем объем. Повторив то же самое с золотом и серебром, можно точно определить, насколько тяжелее воды было золото, серебро и его соединения. Этот трактат был тщательно изучен Эйльхардом Видеманом, который считал, что решение Хайяма было более точным и сложным, чем решение Хазини и ан-Найризи, которые также занимались этой темой в других местах. ^{[ 8 ]}^: 198

Другой короткий трактат посвящен теории музыки , в котором он обсуждает связь между музыкой и арифметикой. Вклад Хайяма заключался в систематической классификации музыкальных гамм и обсуждении математических отношений между нотами, минорными, мажорными и тетрахордами . ^{[ 8 ]}^: 198

Поэзия

Самый ранний намек на поэзию Омара Хайяма принадлежит историку Имаду ад-Дину аль-Исфахани , младшему современнику Хайяма, который прямо идентифицирует его как поэта и ученого ( Харидат аль-Каср , 1174). ^{[ 8 ]}^: 49^{[ 55 ]}^: 35 Один из самых ранних образцов Рубията Омара Хайяма находится в Фахр ад-Дине Рази . В своей работе «ат-Танбих ала баад асрар аль-маудат фил-Коран» ( ок. 1160 г. ) он цитирует одно из своих стихотворений (соответствующее катрену LXII первого издания Фитцджеральда). Дайя в своих сочинениях ( Миршад аль-Ибад , ок. 1230) цитирует два четверостишия, одно из которых совпадает с уже сообщенным Рази. Дополнительное четверостишие цитируется историком Джувейни ( Тарих-и Джахангушай , ок. 1226–1283). ^{[ 55 ]}^: 36–37^{[ 8 ]}^: 92 В 1340 году Джаджарми включает тринадцать четверостиший Хайяма в свой труд, содержащий антологию произведений известных персидских поэтов ( Мунис аль-ахрар ), два из которых до сих пор известны из более древних источников. ^{[ 56 ]}^: 434 Сравнительно поздняя рукопись — это Бодлианская рукопись. Узли 140, написанный в Ширазе в 1460 году, содержит 158 четверостиший на 47 листах. Рукопись принадлежала Уильяму Оузли (1767–1842) и была куплена Бодлианской библиотекой в 1844 году.

В текстах, приписываемых авторам XIII и XIV веков, встречаются отдельные цитаты стихов, приписываемых Хайяму, но их подлинность сомнительна, так что скептически настроенные ученые отмечают, что вся традиция может быть псевдоэпиграфической . ^{[ 55 ]}^: 11 Ганс Генрих Шедер в 1934 году заметил, что имя Омара Хайяма «следует вычеркнуть из истории персидской литературы» из-за отсутствия какого-либо материала, который можно было бы с уверенностью приписать ему. Де Блуа представляет библиографию рукописной традиции, пессимистично заключая, что ситуация существенно не изменилась со времен Шедера. ^{[ 57 ]}^:307

Пять катренов, позже приписываемых Омару Хайяму, найдены уже через 30 лет после его смерти, цитируются в «Синдбад-Наме» . Хотя это и устанавливает, что эти конкретные стихи были в обращении во времена Омара или вскоре после него, это не означает, что эти стихи должны принадлежать ему. Де Блуа заключает, что, по крайней мере, процесс приписывания поэзии Омару Хайяму, по-видимому, начался уже в 13 веке. ^{[ 57 ]}^:305 Эдвард Грэнвилл Браун (1906) отмечает сложность отделения подлинных четверостиший от поддельных: «Хотя и несомненно, что Хайям написал множество четверостиший, вряд ли возможно, за исключением нескольких исключительных случаев, утверждать положительно, что он написал какое-либо из тех, которые приписывают ему". ^{[ 7 ]}^: 663

Помимо персидских четверостиший, существует двадцать пять арабских стихотворений, приписываемых Хайяму, что засвидетельствовано такими историками, как аль-Исфахани, Шахразури ( Нужат аль-Арва , ок. 1201–1211), Кифти ( Тарих аль-хукама ,) и Хамдаллах Муставфи ( Тарих-и-Зизида , 1339 г.). ^{[ 8 ]}^: 39

Бойль подчеркнул, что существует ряд других персидских ученых , которые время от времени писали четверостишия, в том числе Авиценна , Газали и Туси . Они заключают, что также возможно, что для Хайяма поэзия была развлечением в часы досуга: «Эти краткие стихотворения, кажется, часто были работой ученых и ученых, которые сочиняли их, возможно, в минуты отдыха, чтобы назидать или развлечь внутреннего круг своих учеников». ^{[ 7 ]}^: 662

Поэзия, приписываемая Омару Хайяму, во многом способствовала его популярной известности в современный период, что является прямым результатом чрезвычайной популярности перевода таких стихов на английский язык Эдвардом Фитцджеральдом (1859 г.). Фитцджеральда «Рубайят Омара Хайяма» содержит вольные переводы четверостиший из бодлианской рукописи. оно пользовалось таким успехом В период конца века , что в библиографии, составленной в 1929 году, насчитывалось более 300 отдельных изданий. ^{[ 58 ]} и многие другие были опубликованы с тех пор. ^{[ 57 ]}^:312

Философия

Хайям считал себя интеллектуально учеником Авиценны . ^{[ 2 ]}^: 474 Авиценны . он читал метафизику «Книги исцеления» По словам Аль-Байхаки, перед смертью ^{[ 7 ]}^: 661 Считается, что Хайям написал шесть философских статей. Один из них, «О существовании» ( Фил-вуджуд ), первоначально был написан на персидском языке и посвящен теме существования и его связи с универсалиями. Другая статья, озаглавленная «Необходимость противоречия в мире, детерминизм и существование» ( Дарурат ат-тадад фил-'алам ва'ль-джабр ва'л-бака' ), написана на арабском языке и посвящена свободе воли и детерминизму. . ^{[ 2 ]}^: 475 Названия других его работ: « О бытии и необходимости» ( Рисала фил-каун ва'л-таклиф ), «Трактат о трансцендентном существовании» ( ар-Рисала аль-ула фил-вуджуд ), «О познании универсальные принципы существования ( Рисалах дар 'илм куллият-и вуджуд ) и Сокращение природных явлений ( Мухтасар фил-Табиийят ).

Сам Хайям однажды сказал: ^{[ 59 ]}^: 431

Мы являемся жертвами эпохи, когда люди науки дискредитированы и остаются лишь немногие, способные заниматься научными исследованиями. Наши философы все время смешивают истину с ложью и не интересуются ничем, кроме внешней показухи; несмотря на то, что у них мало знаний, они преследуют материальные цели. Когда они видят человека искреннего и неустанного в поисках истины, человека, который не желает иметь ничего общего с ложью и притворством, они насмехаются и презирают его.

Религиозные взгляды

Буквальное прочтение катренов Хайяма приводит к интерпретации его философского отношения к жизни как сочетания пессимизма , нигилизма , эпикурейства , фатализма и агностицизма . ^{[ 8 ]}^: 6^{[ 60 ]} Этой точки зрения придерживаются такие иранологи , как Артур Кристенсен , Ганс Генрих Шедер , Джон Эндрю Бойл , Эдвард Денисон Росс , ^{[ 61 ]}^: 365 Эдвард Генри Уинфилд ^{[ 46 ]}^: 40 и Джордж Сартон . ^{[ 18 ]}^: 18 И наоборот, четверостишия Хайяма также называют мистической суфийской поэзией. ^{[ 62 ]} В дополнение к своим персидским четверостишиям Дж. К. Э. Боуэн упоминает, что арабские стихи Хайяма также «выражают пессимистическую точку зрения, которая полностью созвучна мировоззрению глубоко вдумчивого философа-рационалиста, которым исторически известен Хайям». ^{[ 63 ]}^: 69 Эдвард Фитцджеральд подчеркнул религиозный скептицизм, который он обнаружил у Хайяма. ^{[ 64 ]} В своем предисловии к « Рубайату» он утверждал, что суфии «ненавидели и боялись его». ^{[ 65 ]} и отрицал любые претензии на божественную аллегорию: «его вино — это настоящий виноградный сок; его таверна, где его можно было выпить; его саки — плоть и кровь, которые пролили его для него». ^{[ 66 ]}^: 62 Садег Хедаят — один из самых известных сторонников философии Хайяма как агностического скептицизма, и, по словам Яна Рипки (1934), он даже считал Хайяма атеистом . ^{[ 67 ]} Хедаят (1923) утверждает, что «хотя Хайям верит в трансмутацию и трансформацию человеческого тела, он не верит в отдельную душу; если нам повезет, частицы нашего тела будут использованы для изготовления кувшина с вином». ^{[ 68 ]}^: 138 Поэзия Омара Хайяма цитировалась в контексте нового атеизма , например, в «Портативном атеисте» Кристофера Хитченса . ^{[ 69 ]}^: 7

Аль-Кифти ( ок. 1172–1248 ), кажется, подтверждает этот взгляд на философию Хайяма. ^{[ 7 ]}^: 663 В своем труде «История ученых людей» он сообщает, что стихи Хайяма лишь внешне были в суфийском стиле, но были написаны с антирелигиозной направленностью. ^{[ 61 ]}^: 365 Он также упоминает, что однажды ему было предъявлено обвинение в нечестии, но он отправился в паломничество, чтобы доказать, что он благочестив. ^{[ 8 ]}^: 29 В сообщении сообщается, что по возвращении в родной город он скрывал свои самые глубокие убеждения и вел строго религиозную жизнь, посещая утром и вечером места богослужений. ^{[ 61 ]}^: 355 Хайям о Коране (цитата 84): ^{[ 70 ]}

Коран! Что ж, приходите и испытайте меня, Прекрасная старая книга в ужасной ошибке, Поверьте мне, я тоже могу цитировать Коран, Неверующий знает свой Коран лучше всех. И вы думаете, что таким, как вы, команде червячных, голодных и фанатичных, Бог открыл Тайну, а мне отказал в ней? Ну-ну, какое это имеет значение! тоже верь в это.

Не смотрите выше, там нет ответа; Не молись, ибо никто не слушает твоей молитвы; Близко так же близко к Богу, как и Далеко, И Здесь такой же обман, как и Там. ^{[ 70 ]}

Люди говорят о рае: нет другого рая, кроме здесь; Люди говорят об аде: ада нет, кроме здесь; Люди в будущей жизни говорят, и в будущих жизнях, о любовь, нет другой жизни, кроме этой. ^{[ 70 ]}

Отчет о нем, написанный в тринадцатом веке, показывает, что он «сведущ во всей мудрости греков» и имел обыкновение настаивать на необходимости изучения науки по греческим образцам. Из его прозаических произведений два, пользующиеся авторитетом, посвящены соответственно драгоценным камням и климатологии. Несомненно, поэт-астроном был неблагочестивым человеком; и его астрономия, несомненно, помогла ему стать таким. Один современник пишет: «Я не заметил, чтобы он сильно верил в астрологические предсказания; я также не видел и не слышал ни о ком из великих (ученых), которые бы верили в такую веру. Он не придерживался какой-либо религиозной секты. вера является лейтмотивом его произведений. Среди сект он повсюду видел раздоры и ненависть, в которых он не мог участвовать...». ^{[ 71 ]}^{: 263, том. 1}

Персидский писатель Садег Хедайят говорит, что Хайям «с юности до самой смерти оставался материалистом, пессимистом, агностиком. Хайям смотрел на все вопросы религии скептически», продолжает Хедайят, «и ненавидел фанатизм, ограниченность и дух месть мулл, так называемых религиозных учёных». ^{[ 72 ]}^: 13

В контексте статьи под названием « О познании принципов существования » Хайям поддерживает суфийский путь. ^{[ 8 ]}^: 8 Чиллик предполагает, что Омар Хайям мог видеть в суфизме союзника против ортодоксальной религиозности. ^{[ 73 ]}^: 75 Другие комментаторы не признают, что поэзия Хайяма имеет антирелигиозную направленность, и интерпретируют его упоминания о вине и пьянстве в традиционном метафорическом смысле, распространенном в суфизме. Французский переводчик Ж. Б. Николя считал, что постоянные призывы Хайяма пить вино не следует понимать буквально, а следует рассматривать скорее в свете суфийской мысли, где восторженное опьянение «вином» следует понимать как метафору просветленного состояния или божественного состояния. восторг от бакаа . ^{[ 74 ]} Взгляд на Омара Хайяма как на суфия защищал Бьеррегард. ^{[ 75 ]}^: 3 Идрис Шах , ^{[ 76 ]}^{: 165–166} и Дуган, который приписывает репутацию гедонизма недостаткам перевода Фицджеральда, утверждая, что поэзию Хайяма следует понимать как «глубоко эзотерическую». ^{[ 77 ]} С другой стороны, иранские эксперты, такие как Мохаммад Али Форуги и Моджтаба Минови, отвергли гипотезу о том, что Омар Хайям был суфием. ^{[ 63 ]}^: 72 Форуги заявил, что идеи Хайяма, возможно, временами совпадали с идеями суфиев, но нет никаких доказательств того, что он формально был суфием . Аминразави утверждает, что «суфийская интерпретация Хайяма возможна только путем тщательного прочтения его Рубаийята и расширения его содержания в соответствии с классической суфийской доктриной». ^{[ 8 ]}^: 128 Более того, Бойль подчеркивает, что Хайяма крайне не любил ряд знаменитых суфийских мистиков того же века. Сюда входят Шамс Тебризи (духовный наставник Руми ), ^{[ 8 ]}^: 58 Наджм ад-Дин Дайя, назвавший Омара Хайяма «несчастным философом, атеистом и материалистом», ^{[ 63 ]}^: 71 и Аттар , который считал его не коллегой-мистиком, а вольнодумным ученым, ожидающим дальнейшего наказания. ^{[ 7 ]}^{: 663–664}

Сейед Хосейн Наср утверждает, что использовать буквальную интерпретацию его стихов (многие из которых изначально имеют неопределенную подлинность) для обоснования философии Омара Хайяма «редуктивно». Вместо этого он приводит интерпретирующий перевод Хайяма « трактата Авиценны Рассуждение о Единстве» ( аль-Хутбат ат-Таухид ), где он выражает ортодоксальные взгляды на Божественное Единство . согласные с автором ^{[ 78 ]}^{: Ч. 9, 165–183} Прозаические произведения, которые, как полагают, принадлежат Хайяму, написаны в перипатетическом стиле и носят явно теистический характер, затрагивая такие темы, как существование Бога и теодицея . ^{[ 8 ]}^: 160 Как отмечает Боуэн, эти работы свидетельствуют о его увлеченности проблемами метафизики, а не тонкостями суфизма. ^{[ 63 ]}^: 71 В качестве доказательства веры Хайяма и/или соответствия исламским обычаям Аминразави упоминает, что в своих трактатах он возносит приветствия и молитвы, восхваляя Бога и Мухаммеда . В большинстве биографических отрывков он упоминается с религиозными почетными именами , такими как Имам , Покровитель веры ( Гият ад-Дин ) и Доказательство истины ( Худжат аль-Хакк ). ^{[ 8 ]} Он также отмечает, что биографы, восхваляющие его религиозность, обычно избегают упоминаний о его поэзии, а те, кто упоминает его стихи, часто не хвалят его религиозный характер. ^{[ 8 ]}^: 48 Например, отчет Аль-Байхаки, который на несколько лет предшествует другим биографическим заметкам, говорит об Омаре как об очень набожном человеке, который исповедовал ортодоксальные взгляды до своего последнего часа. ^{[ 17 ]}^: 174

На основании всех имеющихся текстовых и биографических данных вопрос остается в некоторой степени открытым. ^{[ 8 ]}^: 11 и в результате Хайям получил резко противоречивые оценки и критику. ^{[ 61 ]}^: 350

Прием

Марка Албании 1997 года под названием «850 лет со дня рождения Омара Хайяма».

Различные биографические отрывки, относящиеся к Омару Хайяму, описывают его как человека, не имеющего себе равных в научных знаниях и достижениях своего времени. ^{[ г ]} Многие называли его эпитетом Царь Мудрый ( араб . Царь Мудрых ). ^{[ необходима латинизация ]}^{[ 56 ]}^: 436^{[ 39 ]}^: 141 Шахразури (ум. 1300) высоко ценит его как математика и утверждает, что его можно рассматривать как «преемника Авиценны в различных областях философских знаний». ^{[ 61 ]}^: 352 Аль-Кифти (ум. 1248), хотя и не согласен с его взглядами, признает, что он «не имел себе равных в своих познаниях в области натуральной философии и астрономии». ^{[ 61 ]}^: 355 Несмотря на то, что ряд биографов провозглашали Хайяма поэтом, по словам Ричарда Н. Фрая , «все еще можно утверждать, что статус Хайяма как поэта первого ранга появился сравнительно поздно». ^{[ 7 ]}^: 663

Томас Хайд был первым европейцем, обратившим внимание на Хайяма и переведшим на латынь одно из его четверостиший ( Historia religis veterum Persarum eorumque magorum , 1700). ^{[ 79 ]}^: 525 Интерес Запада к Персии вырос вместе с движением ориентализма в 19 веке. Йозеф фон Хаммер-Пургшталь (1774–1856) перевел некоторые стихотворения Хайяма на немецкий язык в 1818 году, а Гора Оузли (1770–1844) на английский в 1846 году, но Хайям оставался относительно неизвестным на Западе до тех пор, пока не была опубликована книга Эдварда Фитцджеральда . Рубаи Омара Хайяма в 1859 году. Работа Фитцджеральда поначалу не имела успеха, но с 1861 года ее популяризировал Уитли Стоукс вызвали большое восхищение этой работой , и прерафаэлиты . В 1872 году Фитцджеральд напечатал третье издание, что повысило интерес к его работе в Америке. К 1880-м годам книга была чрезвычайно известна во всем англоязычном мире, вплоть до формирования многочисленных «Клубов Омара Хайяма» и «культа Рубаи конца века». ^{[ 80 ]}^: 202 Стихи Хайяма переведены на многие языки; многие из более поздних из них более буквальны, чем у Фитцджеральда. ^{[ 81 ]}

Перевод Фитцджеральда стал фактором возрождения интереса к Хайяму как поэту даже в его родном Иране. ^{[ 82 ]}^: 55–72 Садег Хедаят в своих «Песнях Хайяма» ( Taranehha-ye Khayyam , 1934) вновь представил поэтическое наследие Хайяма современному Ирану. При династии Пехлеви над его могилой был установлен новый памятник из белого мрамора по проекту архитектора Хоушанга Сейхуна . Статуя работы Абольхасана Садиги была установлена в парке Лалех в Тегеране в 1960-х годах, а бюст того же скульптора был установлен возле мавзолея Хайяма в Нишапуре. В 2009 году государство Иран подарило Отделению павильон Организации Объединенных Наций в Вене , открытый в Венском международном центре . ^{[ 83 ]} В 2016 году были открыты три статуи Хайяма: одна в Университете Оклахомы , одна в Нишапуре и одна во Флоренции, Италия. ^{[ 84 ]} Более 150 композиторов использовали Рубайят как источник вдохновения. Самым ранним таким композитором была Лиза Леманн . ^{[ 85 ]}

Фитцджеральд перевел имя Хайяма как «Изготовитель палаток», а англизированное имя «Омар Изготовитель палаток» какое-то время находило отклик в англоязычной популярной культуре. Так, Натан Хаскелл Доул опубликовал роман под названием «Омар, изготовитель палаток: роман старой Персии». в 1898 году «Омар, изготовитель палаток из Найшапура » — исторический роман Джона Смита Кларка, опубликованный в 1910 году. «Омар, изготовитель палаток» — это также название пьеса Ричарда Уолтона Талли 1914 года в восточной обстановке, адаптированная как немой фильм в 1922 году. Генерал США Омар Брэдли во время Второй мировой войны получил прозвище «Омар-палаточник». ^{[ 86 ]}^: 13

Разнообразные таланты и интеллектуальные поиски Хайяма на протяжении всей истории пленяли многих османских и турецких писателей. ^{[ 87 ]} Ученые часто рассматривали Хайяма как средство повышения своего поэтического мастерства и интеллектуальной глубины, черпая вдохновение и признание из его произведений. ^{[ 88 ]} Для многих мусульманских реформаторов стихи Хайяма стали противовесом консервативным нормам, преобладающим в исламских обществах, давая место для независимого мышления и распутного образа жизни. ^{[ 88 ]} Такие деятели, как Абдулла Джевдет , Риза Тевфик и Яхья Кемаль, использовали темы Хайяма для оправдания своих прогрессивных идеологий или прославления либеральных аспектов своей жизни, изображая его как культурный, политический и интеллектуальный образец для подражания, продемонстрировавший совместимость ислама с современными условностями. ^{[ 88 ]} Точно так же турецкие левые поэты и интеллектуалы, в том числе Назым Хикмет , Сабахаттин Эйюбоглу , А. Кадир и Гекче, использовали Хайяма для защиты своего социалистического мировоззрения, наполняя его голос гуманистическим тоном в просторечии. ^{[ 88 ]} Возрождение Хайяма в разговорном турецком языке с 1980-х годов превратило его в народного поэта, а многочисленные книги и переводы возродили его историческое значение. ^{[ 88 ]} И наоборот, такие ученые, как Даниш, Тевфик и Гёлпинарлы, выступали за критику источников и выявление подлинных катренов, чтобы распознать подлинного Хайяма среди исторических представлений о его социокультурном образе. ^{[ 88 ]}

Четверостишие «Движущий палец»

Строка английского перевода персидской поэзии Омара Хайяма на одном из факультетских корпусов Лейденского университета. — Строка английского перевода четверостишия «Двигающийся палец». Персидские рубияты Омара Хайяма на одном из корпусов факультета Лейденского университета

Четверостишие Омара Хайяма, известное как «Движущий палец», в виде его перевода английского поэта Эдварда Фицджеральда — одно из самых популярных четверостиший в англосфере . ^{[ 89 ]} Там написано:

«Двигающийся палец» пишет; и имея письмо,
Идем дальше: ни все ваше благочестие, ни ум
Заманю его обратно, чтобы отменить половину линии,
И все ваши Слезы не смывают ни слова об этом. ^{[ 90 ]}^{[ ч ]}

Название романа «Движущийся палец» , написанного Агатой Кристи и опубликованного в 1942 году, было навеяно этим четверостишием перевода «Рубайят» Омара Хайяма Эдварда Фицджеральда . ^{[ 89 ]} Мартин Лютер Кинг также цитирует это четверостишие Омара Хайяма в одной из своих речей « За пределами Вьетнама: время нарушить молчание »: ^{[ 89 ]}^{[ 91 ]}

«Мы можем отчаянно требовать, чтобы время остановило свой путь, но время непреклонно к любым просьбам и мчится вперед. На обесцвеченных костях и перемешанных остатках многочисленных цивилизаций написаны жалкие слова: «Слишком поздно». Существует невидимая книга жизни, которая верно записывает нашу бдительность или наше пренебрежение. Омар Хайям прав: «Двигающийся палец пишет, а написав движется дальше».

В одной из своих апологетических речей по поводу скандала Клинтон-Левински Билл Клинтон , 42-й президент США, также цитирует этот катрен. ^{[ 89 ]}^{[ 92 ]}

Другие отсылки к популярной культуре

В 1934 году Гарольд Лэмб опубликовал исторический роман «Омар Хайям» . Французско-ливанский писатель Амин Маалуф основал первую половину своего историко-фантастического романа «Самарканд» на жизни Хайяма и создании его «Рубайята». Скульптор Эдуардо Чильида в 1980-х годах создал четыре массивных железных изделия под названием «Меса де Омар Хайям» («Стол Омара Хайяма»). ^{[ 93 ]}^{[ 94 ]}

Омар лунный кратер Хайям В его честь в 1970 году был назван , как и малая планета 3095 Омархайям, открытая советским астрономом Людмилой Журавлевой в 1980 году. ^{[ 95 ]}

Google выпустил два дудла Google в память о нем. Первый случился в день его 964-летия 18 мая 2012 года. Второй - в свой 971-й день рождения 18 мая 2019 года. ^{[ 96 ]}

Галерея

«Рубин загорается на лозе», иллюстрация к «Рубайяту Омара Хайяма» Аделаиды Хэнском Лисон Фитцджеральда (около 1905 г.).
«У могилы Омара Хайяма» Джея Хэмбиджа (1911).
Статуя Хайяма в офисе ООН в Вене как часть Павильона персидских ученых, подаренная Ираном .
Статуя Омара Хайяма в Бухаресте
университете Памятник Омару Хайаму в Мадридском

См. также

Ножат аль-Маджалес

Известные фильмы

Известные хайямологи

Примечания

^ [oˈmæɾ xæjˈjɒːm] ; / k aɪ ˈ j ɑː m , k aɪ ˈ j æ m /
^ С ошибкой в один день, накопленной за более чем 5000 лет, он был более точным, чем григорианский календарь 1582 года, который имеет ошибку в один день каждые 3330 лет. ^{[ 8 ]}^: 200
^ Например, у Рашид-ад-Дина Хамадани , ^{[ 13 ]}^: 409 или в Мунис аль-Ахрар . ^{[ 14 ]}^: 435
^ Например, аль-Кифти , ^{[ 8 ]}^: 55 или Байхаки . ^{[ 16 ]}^: 463^{[ 17 ]}^{: 172–175, вып. 66}
^ Кац (1998), с. 270. Отрывок: В некотором смысле его трактовка была лучше, чем у Ибн аль-Хайсама, потому что он явно сформулировал новый постулат, заменяющий постулат Евклида, а не скрывающий последний в новом определении.
^ О'Коннор и Робертсон (июль 1999 г.): Однако сам Хайям, похоже, был первым, кто разработал общую теорию кубических уравнений .
^ Например, автор Фирдавс ат-Таварих , ^{[ 61 ]}^: 356 автор Тариха альфи , ^{[ 61 ]}^: 358 и аль-Исфахани . ^{[ 8 ]}^: 49
^
Это было на вывеске
Хорошая и плохая ручка постоянно изнашивается.
Он отдаст все, что ему придется заплатить в последний день
Бесполезно горевать и пытаться

Ссылки

^ Перейти обратно: ^а ^б ^с ^д Злой, Эми (28 февраля 2023 г.). «Омар Хайям: персидский поэт и астроном » энциклопедия Британская Получено 5 апреля.
^ Перейти обратно: ^а ^б ^с ^д Наср, SH ; Аминразави, М. ; при содействии г-на Джози (2008 г.). Антология философии в Персии. Том I: От Зороастра до Омара Хайяма . Лондон и Нью-Йорк: IB Tauris, совместно с Лондонским институтом исмаилитских исследований. ISBN 978-1-84511-541-8 .
^ Деххода, А.А. «Хайям» . Лухт-намах (на персидском языке). Тегеран.
^ Леви, Рубен (2011) [1951]. Персидский язык . Издания библиотеки Рутледжа: Иран, Том: XV. Лондон и Нью-Йорк: Рутледж. ISBN 978-0-203-83301-8 .
^ Перейти обратно: ^а ^б ^с О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (июль 1999 г.), «Омар Хайям» , Архив истории математики MacTutor , Университет Сент-Эндрюс
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Струйк, диджей (1958). «Омар Хайям, математик» . Учитель математики . ЛИИ (4): 280–285. JSTOR 27955652 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л Бойл, Дж. А. (2007) [1975]. « Умар Хайям: астроном, математик и поэт» . В Ричарде Н. Фрае (ред.). Кембриджская история Ирана . Том IV: От арабского вторжения до сельджуков . Нью-Йорк: Издательство Кембриджского университета. стр. 658–664. дои : 10.1017/CHOL9780521200936.023 . ISBN 978-0-521-20093-6 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д ^р ^с ^т ^в ^v ^В ^х ^и ^С ^аа ^аб ^и Аминразави, М. (2007). Вино мудрости: жизнь, поэзия и философия Омара Хайяма . Оксфорд: Один мир. ISBN 978-1-85168-355-0 .
^ Арберри, Эй Джей (2008). Аспекты исламской цивилизации: как они изображены в оригинальных текстах . Рутледж. п. 16. ISBN 978-0-415-42600-8 . Омар слагал свои стрелы остроумия и формы красоты на своем родном персидском языке, который к десятому веку оправился от ошеломляющего удара, нанесенного ему арабским языком.
^ Аль-Халили, Джим (30 сентября 2010 г.). Следопыты: золотой век арабской науки . Пингвин Великобритания. ISBN 978-0-14-196501-7 . Позже аль-Кархи (правильно: аль-Караджи ), Ибн Тахир и великий Ибн аль-Хайсам в десятом/одиннадцатом веке пошли дальше, рассматривая уравнения кубической и четвертой степени, а затем персидский математик и поэт Омар Хайям в одиннадцатом веке. век.
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Фушекур, Шарль-Анри де; Розенфельд, Борис А. (1954–2007) [2000]. «Умар Кахайям» . В ХАР Гибб ; и др. (ред.). Энциклопедия ислама . Том. X (2-е изд.). Лейден: Брилл. стр. 827б–834а. дои : 10.1163/1573-3912_islam_COM_1284 . ISBN 90-04-07026-5 .
^ Питер Эйвери и Джон Хит-Стаббс, Рубаи Омара Хайяма (Penguin Group, 1981), 14; «Эти даты, 1048–1031 годы, говорят нам, что Хайям жил, когда турецкие султаны-сельджуки расширяли и укрепляли свою власть над Персией, и когда влияние этой власти особенно ощущалось в Нишапуре, месте рождения Хайяма».
^ Браун, Э.Г. (1899). «Еще больше света на Умар-и-Хайяма» . Журнал Королевского азиатского общества Великобритании и Ирландии . XXXI (2): 409–420. дои : 10.1017/S0035869X00026538 . JSTOR 25208104 . S2CID 163490581 .
^ Росс, ЭД (1927). « Омар Хайям» . Вестник Школы востоковедения . IV (3): 433–439. дои : 10.1017/S0041977X00102897 . JSTOR 606948 . S2CID 246638673 .
^ Перейти обратно: ^а ^б ^с ^д Бойл, Дж. А. (1966). «Омар Хайям: астроном, математик и поэт» . Бюллетень библиотеки Джона Райлендса . ЛИИ (1): 30–45. дои : 10.7227/BJRL.52.1.3 .
^ Перейти обратно: ^а ^б Росс, Эд ; Гибб, ХАР (1929). «Самое раннее повествование об Умаре Хайяме» . Вестник Школы востоковедения . В (3): 467–473. дои : 10.1017/S0041977X00084615 . JSTOR 607341 . S2CID 177947195 .
^ Перейти обратно: ^а ^б ^с Мейерхоф, Макс (1948). «Татиммат Сиван аль-Хикма» Али аль-Байхаки: биографический труд об ученых исламе» . Осирис . VIII : 122–217. дои : 10.1086/368514 . JSTOR 301524 .
^ Перейти обратно: ^а ^б Сартон, Г. (1938). «Могила Омара Хайяма» . Исида . XXIX (1): 15–19. дои : 10.1086/347379 . JSTOR 225920 . S2CID 143678233 .
^ Перейти обратно: ^а ^б Эдвард Фитцджеральд, Рубаи Омара Хайяма , Ред. Кристофер Декер (Университет Вирджинии Press, 1997), xv; «Турки-сельджуки вторглись в провинцию Хорасан в 1030-х годах, и город Нишапур добровольно сдался им в 1038 году. Таким образом, Омар Хайям достиг зрелости во время первой из нескольких инопланетных династий, которые правили Ираном до двадцатого века».
^ Розенфельд, Борис А. (2016). «Умар аль-Хайям» . В Хелейн Селин (ред.). Энциклопедия истории науки, технологий и медицины в незападных культурах (3-е изд.). Дордрехт: Спрингер – Верлаг. стр. 4330б–4332а. дои : 10.1007/978-94-007-7747-7_9775 . ISBN 978-94-007-7747-7 .
^ Аминразави, М. (2010). «Рецензия: Омар Хайям: Поэт, бунтарь, астроном, Хажир Теймурян» . Иранские исследования . XLIII (4): 569–571. дои : 10.1080/00210862.2010.495592 . JSTOR 23033230 . S2CID 162241136 .
^ Перейти обратно: ^а ^б ^с Мохамед, Мохайни (2000). Великие мусульманские математики . Малайзия: Издательство Universiti Teknologi Malaysia. ISBN 983-52-0157-9 .
^ Лэмб, Эвелин (28 октября 2014 г.). «В котором Омар Хайям раздражается на Евклида» . Сеть блогов Scientific American . Проверено 10 сентября 2023 г.
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Вахабзаде, Биджан (7 мая 2014 г.). Эхсан Яршатер (ред.). «Хайям, Омар xv. Как математик» . Энциклопедия Ираника . Фонд Энциклопедии Ираника . Проверено 8 сентября 2023 г.
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж Юшкевич, Адольф П. ; Розенфельд, Борис А. (1970–1980) [1974]. «Хайями (или Хайям)». В Чарльзе Коулстоне Гиллиспи (ред.). Словарь научной биографии . Том. VII. Нью-Йорк: Сыновья Чарльза Скрибнера. стр. 323б–334а. ISBN 0-684-16962-2 .
^ Нетингтон, Аманда (2020). «Достижение философского совершенства: успешная замена Омаром Хайямом постулата параллельности Евклида» (PDF) . Люцерна: Журнал бакалавриата с отличием . XIV : 72–97. hdl : 10355/74778 .
^ Розенфельд, Борис А. (1988). История неевклидовой геометрии: эволюция понятия геометрического пространства . Исследования по истории математики и физических наук. Том. 12. Перевод Эйба Шенитцера при редакционной поддержке Харди Гранта. Нью-Йорк: Спрингер. дои : 10.1007/978-1-4419-8680-1 . ISBN 978-1-4419-8680-1 . ISSN 0172-570X .
^ Перейти обратно: ^а ^б Кац, В. (1998). История математики: Введение (2-е изд.). Аддисон-Уэсли. ISBN 0-321-01618-1 .
^ Розенфельд, Борис А.; Юшкевич, АП (1996). "Геометрия". В Рошди Рашед ; в сотрудничестве с Режисом Морелоном (ред.). Энциклопедия истории арабской науки . Том. II. Лондон и Нью-Йорк: Рутледж. стр. 115–159. ISBN 0-415-02063-8 .
^ Ролвинг, Раймонд Х.; Левин, Майта (1969). «Постулат параллельности» . Учитель математики . LXII (8): 665–669. JSTOR 27958258 .
^ Смит, Делавэр (1935). «Евклид, Омар Хайям и Саккери». сочинения Математические III (1): 5–10. OCLC 14156259 .
^ Вахабзаде, Биджан (2005). Джафар Агаяни-Чавоши (ред.). «Омар Хайям и концепция иррациональных чисел». Фарханг: Ежеквартальный журнал гуманитарных и культурных исследований. Тема номера: День памяти Хайяма (3) . XVIII (53–54): 125–134.
^ Перейти обратно: ^а ^б Купер, Глен М. (2003). «Рецензия: Омар Хайям, математик», Р. Рашид, Б. Вахабзаде . Журнал Американского восточного общества . CXXXIII (1): 248–249. дои : 10.2307/3217882 . JSTOR 3217882 .
^ Ивс, Х. (1958). «Решение кубических уравнений Омара Хайяма» . Учитель математики . ЛИ (4): 285–286. дои : 10.5951/MT.51.4.0285 . JSTOR 27955653 .
^ « Омар Аль-Хей из Хорасана, около 1079 года нашей эры, больше всего сделал для того, чтобы возвести в метод решение алгебраических уравнений посредством пересекающихся коник ». → Гильбо, Люси (1930), «История решения кубического уравнения» , Mathematics News Letter , V (4): 8–12, doi : 10.2307/3027812 , JSTOR 3027812 , S2CID 125245433
^ Нетц, Ревель (1999). «Преобразование Архимеда: случай результата, устанавливающего максимум для кубического уравнения» . Архив истории точных наук . ЛИВ (1): 1–47. дои : 10.1007/s004070050032 . JSTOR 41134072 . S2CID 121468528 .
^ Оукс, Джеффри А. (2011). «Научная редакция алгебры Хайяма» (PDF) . Сухайл: Международный журнал истории точных и естественных наук в исламской цивилизации . Х : 47–75.
^ Перейти обратно: ^а ^б ^с Кент, Дебора А .; Мураки, Дэвид Дж. (2016). «Геометрическое решение кубического куба Омара Хайяма… в котором для большего удобства учащихся вместо букв используются цветные диаграммы» . Американский математический ежемесячник . CXXIII (2): 149–160. doi : 10.4169/amer.math.monthly.123.2.149 . JSTOR 123.2.149 . S2CID 124153443 .
^ Перейти обратно: ^а ^б ^с ^д ^и Кеннеди, Эвелин (1966). « Омар Хайям» . Учитель математики . ЛИКС (3): 140–142. дои : 10.5951/MT.59.2.0140 . JSTOR 27957296 .
^ Амир-Моэз, Арканзас (1963). «Записка Омара Хайяма». Скрипта Математика . XXVI : 323–337.
^ «Обзор: Дауд Касир «Алгебра Омара Хайяма»» . Учитель математики . XXV (4): 238–241. 1932. JSTOR 27951448 .
^ Амир-Моэз, Арканзас (1962). «Решение Хайяма кубических уравнений» . Журнал «Математика» . XXXV (5): 269–271. дои : 10.2307/2688197 . JSTOR 2688197 . Эта статья содержит расширение Мохсеном Хаштруди метода Хайяма на уравнения четвертой степени.
^ Варден, Б.Л. (2013). История алгебры: от аль-Хорезми до Эмми Нётер . Нью-Йорк: Springer Science & Business Media. ISBN 978-3-642-51599-6 .
^ Ван Браммелен, Глен (2014). «Обзор исследований математических наук в средневековом исламе с 1996 по 2011 год» . У Натана Сидоли; Глен Ван Браммелен (ред.). Из Александрии через Багдад: обзоры и исследования древнегреческих и средневековых исламских математических наук в честь Дж. Л. Берггрена . Нью-Йорк: Спрингер. стр. 101–138. дои : 10.1007/978-3-642-36736-6_6 . ISBN 978-3-642-36736-6 .
^ Кнобель, Арт; Лаубенбахер, Рейнхард; Лоддер, Джерри (2007). Математические шедевры: дальнейшие хроники исследователей . Спрингер. ISBN 978-0-387-33060-0 .
^ Перейти обратно: ^а ^б ^с Уинфилд, Э.Х. (2000). Четверостишия Омара Хайяма: персидский текст с английским стиховым переводом . Нью-Йорк: Psychology Press Ltd.
^ О'Коннор, Джон Дж.; Робертсон, Э.Ф. (2006). «Мусульманское извлечение корней» . MacTutor Архив истории математики . Университет Сент-Эндрюс.
^ Кулидж, Дж. Л. (1985). «История биномиальной теоремы» . Американский математический ежемесячник . ЛВИ (3): 147–157. дои : 10.2307/2305028 . JSTOR 2305028 .
^ Николс, Сьюзен (2017). Аль-Караджи: математик и инженер десятого века . Нью-Йорк: Издательство Rosen Publishing.
^ Акрами, Муса (11 февраля 2014 г.). «Развитие иранского календаря: исторические и астрономические основы». arXiv : 1111.4926v2 [ physical.hist-ph ].
^ Абдоллахи, Молитва (15 декабря 1990 г.). Эхсан Яршатер (ред.). «Календари II. В исламский период » Энциклопедия Ираника Фонд Энциклопедии Ираника . Получено 21 ноября.
^ Фаррелл, Шарлотта (1996). «Возрождение девятого века в астрономии». Учитель физики . XXXIV (5): 268–272. Бибкод : 1996PhTea..34..268F . дои : 10.1119/1.2344432 .
^ Хейдари-Малаери, М. (21 октября 2004 г.). «Краткий обзор иранского календаря». arXiv : astro-ph/0409620v2 .
^ Салиба, Г. (2002). «Обзор: Аль-Хайам Математик Р. Рашеда; Б. Вахабзаде; Омар Хайям Математик Р. Рашеда; Б. Вахабзаде» . Иранские исследования . XXXV (1–3): 220–225. дои : 10.1017/S0021086200003686 . JSTOR 4311451 .
^ Перейти обратно: ^а ^б ^с Али Дашти (перевод LP Элвелл-Саттона), В поисках Омара Хайяма , Издания библиотеки Routledge: Иран (2012)
^ Перейти обратно: ^а ^б Росс, ЭД (1927). « Омар Хайям» . Вестник Школы востоковедения . IV (3): 433–439. дои : 10.1017/S0041977X00102897 . JSTOR 606948 . S2CID 246638673 .
^ Перейти обратно: ^а ^б ^с Блуа, Франсуа де (2004). Персидская литература - биобиблиографический обзор. Том 5: Поэзия домонгольского периода . Лондон и Нью-Йорк: Рутледж. ISBN 9780947593476 .
^ Амброуз Джордж Поттер, Библиография Рубайята Омара Хайяма (1929).
^ Мосс, Джойс (2004). Ближневосточная литература и их времена . Томсон Гейл. ISBN 9780787637316 .
^ Боскалья, Фабрицио (2015). «Пессоа, Борхес и Хайям» . Вариации Борхеса . XL (40): 41–64. JSTOR 24881234 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час Росс, ЭД (1898). «Мусаффарие: недавний вклад в изучение Омара Хайяма» . Журнал Королевского азиатского общества Великобритании и Ирландии . ХХХ (2): 349–366. дои : 10.1017/S0035869X00025235 . JSTOR 25207968 . S2CID 162611227 .
^ Аминразави, М. ; Ван Бруммелен, Г. (весна 2017 г.). «Умар Хайям» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .
^ Перейти обратно: ^а ^б ^с ^д Боуэн, JCE (1973). «Рубан Омара Хайяма: критическая оценка перевода Роберта Грейвса и Омара Али Шаха» . Иран . XI : 63–73. дои : 10.2307/4300485 . JSTOR 4300485 .
^ Дэвис, Д. (31 января 2012 г.). Эхсан Яршатер (ред.). «Фицджеральд, Эдвард» . Энциклопедия Ираника . Энциклопедия Фонда Ираника . Проверено 15 января 2017 г.
^ Фитцджеральд, Э. (2010). Рубаи Омара Хайяма (с. 12). Шампейн, Иллинойс: Проект Гутенберг
^ Шенкер, Д. (1981). «Беглая артикуляция: введение в Рубайат Омара Хайяма». Викторианская поэзия . XIX (1): 49–64.
^ «Слепая сова» Хедаята как вестерн-роман. Библиотека наследия Принстона: Майкл Бирд
^ Катузян, Х. (1991). Садек Хедаят: Жизнь и литература иранского писателя. Лондон: IB Tauris
^ Хитченс, К. (2007). Портативный атеист: необходимая литература для неверующего. Филадельфия, Пенсильвания: Да Капо.
^ Перейти обратно: ^а ^б ^с Хайям, Омар (18 мая 2017 г.). Мир в картинках. Омар Хайям. Рубаят . Издательство Эгитас. ISBN 9781773132372 .
^ Робертсон, Дж. М. (2016). Краткая история свободы: древняя и современная .
^ Хидаят, С. ; Хайям, Омар (1993). Песни Омара Хайяма . Париж: Хосе Корти. ISBN 9782714304896 .
^ Гсиллик, Б. (1960). «Настоящий Омар Хайям» . Восточный журнал Венгерской академии наук . Х (1): 59–77. JSTOR 23682646 .
^ Альбано, Джузеппе (2008). «Польза чтения «Рубайата Омара Хайяма» как пастырского» . Викторианская поэзия . XLVI (1): 55–67. дои : 10.1353/vp.0.0010 . JSTOR 40347527 . S2CID 170388817 .
^ Бьеррегард, ЦДХ (1915). Омар Хайям, Фитцджеральд, Эдвард, 1809-1883, Суфизм . Лондон: Суфийское издательское общество.
↑ Идрис Шах, Суфии , Octagon Press (1999)
^ «Каждая строка Рубаи имеет больше смысла, чем почти все, что вы можете прочитать в суфийской литературе» Абдулла Дуган Кто такой Гончар? Гностическая пресса 1991 г. ISBN 0-473-01064-X
^ Наср, С.Х. (2006). Исламская философия от ее истоков до наших дней: философия в стране пророчеств . Нью-Йорк: SUNY Press. ISBN 0-7914-6799-6 .
^ Беверидж, Х. (1905). «Омар Хайям» . Журнал Королевского азиатского общества . XXXVII (3): 521–526. дои : 10.1017/S0035869X00033530 . JSTOR 25210170 .
^ Дж. Д. Йоханнан, Персидская поэзия в Англии и Америке , 1977.
^ Сейед-Гохраб, А.А. , изд. (2012). Великий Умар Хайям: глобальное восприятие рубаята (PDF) . Лейден: Издательство Лейденского университета. ISBN 978-94-0060-079-9 .
^ Симидчиева, М. (2011). «Рубайат и агностицизм» Фитцджеральда. В книге А. Пула, К. Ван Руймбеке и У. Мартина (ред.), «Рубайат Омара Хайяма» Фитцджеральда: популярность и пренебрежение. Гимн Пресс.
^ UNIS. «Памятник будет открыт в Венском международном центре, «Павильон ученых», подаренный Ираном международным организациям в Вене» .
^ «Статуя Хайяма наконец установлена в Университете Оклахомы » Тегеран Таймс . Архивировано из оригинала 5 апреля 2016 года . Проверено 4 апреля 2016 г.
^ Мартин, Уильям Х.; Мейсон, Сандра (15 июля 2009 г.). Эхсан Яршатер (ред.). «Хайям, Омар xiii. Музыкальные произведения на основе рубаи» . Энциклопедия Ираника . Фонд Энциклопедии Ираника . Проверено 8 октября 2023 г.
^ Джеффри Д. Лавуа, Частная жизнь генерала Омара Н. Брэдли (2015)
^ Балыкчиоглу, Эфе Мурат (2024). «Четверостишия многих приемов: обзор восприятий Омара Хайяма в османских и турецких переводах» . Ирановедение : 1. doi : 10.1017/irn.2023.72 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж Балыкчиоглу, Эфе Мурат (2024). «Четверостишия многих приемов: обзор восприятий Омара Хайя в османских и турецких переводах» . Иранские исследования : 1, 22. doi : 10.1017/irn.2023.72 .
^ Перейти обратно: ^а ^б ^с ^д Сейед-Гохраб, А.А. (13 апреля 2018 г.). «Двигающийся палец: взгляд на жизнь персидского четверостишия» . Блог лейденских медиевистов . Университет Лейдена . Проверено 14 мая 2022 г.
^ Фитцджеральд, Станца LXXI, 4-е изд.
^ «17. MLK Beyond Vietnam.pdf (hawaii.edu)» (PDF) . Архивировано (PDF) из оригинала 10 октября 2022 года.
^ «Четверостишие 36» . изучая Хайям -США . 21 декабря 2006 года . Проверено 14 мая 2022 г.
^ Таблица II Омара Хайяма , получено 8 августа 2021 г.
↑ Таблица III Омара Хайяма , дата обращения 8 августа 2021 г.
^ Словарь названий малых планет . 1979. с. 255 . Проверено 8 сентября 2012 г. - через Google Книги.
^ «Как Омар Хайям изменил способ измерения времени людьми» . Независимый . 17 мая 2019 года. Архивировано из оригинала 24 мая 2022 года . Проверено 18 мая 2019 г.

Дальнейшее чтение

Бигстраатен, Йос (2008). «Омар Хайям (Влияние на литературу и общество на Западе)» . Энциклопедия Ираника . Том. 15. Фонд Энциклопедии Ираника.
Бойл, Дж. А. , изд. (1968). Кембриджская история Ирана. Том V: Салджугский и монгольский периоды . Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-06936-6 .
Рыпка, Дж. (1968). Карл Ян (ред.). История иранской литературы . Дордрехт: Д. Рейдель. ISBN 978-94-010-3481-4 .
Тернер, Ховард Р. (1997). Наука в средневековом исламе: иллюстрированное введение . Издательство Техасского университета. ISBN 0-292-78149-0 .

Внешние ссылки

Работы Омара Хайяма или о нем в Internet Archive
Работы Омара Хайяма в LibriVox (аудиокниги, являющиеся общественным достоянием)
Хашемипур, Беназ (2007). «Хайям: Гият ад-Дин Абу аль-Фатх Умар ибн Ибрагим аль-Хайами ан-Нишапури » В Томасе Хоккей; и др. (ред.). Биографическая энциклопедия астрономов Нью-Йорк: Спрингер. стр. 100-1 627–8. ISBN 978-0-387-31022-0 . ( PDF-версия .)
Умар Хайям , в Стэнфордской энциклопедии философии.
Иллюстрированный Рубайат Омара Хайяма в Интернет-архиве.

[4] [oˈmæɾ xæjˈjɒːm] ; / k aɪ ˈ j ɑː m , k aɪ ˈ j æ m /

[10] С ошибкой в один день, накопленной за более чем 5000 лет, он был более точным, чем григорианский календарь 1582 года, который имеет ошибку в один день каждые 3330 лет. ^{[ 8 ]}^: 200

[PersianName-17] Например, у Рашид-ад-Дина Хамадани , ^{[ 13 ]}^: 409 или в Мунис аль-Ахрар . ^{[ 14 ]}^: 435

[ArabicName-23] Например, аль-Кифти , ^{[ 8 ]}^: 55 или Байхаки . ^{[ 16 ]}^: 463^{[ 17 ]}^{: 172–175, вып. 66}

[Katz-1998-33] Кац (1998), с. 270. Отрывок: В некотором смысле его трактовка была лучше, чем у Ибн аль-Хайсама, потому что он явно сформулировал новый постулат, заменяющий постулат Евклида, а не скрывающий последний в новом определении.

[MacTutor-Quote-39] О'Коннор и Робертсон (июль 1999 г.): Однако сам Хайям, похоже, был первым, кто разработал общую теорию кубических уравнений .

[Biographical_extracts-85] Например, автор Фирдавс ат-Таварих , ^{[ 61 ]}^: 356 автор Тариха альфи , ^{[ 61 ]}^: 358 и аль-Исфахани . ^{[ 8 ]}^: 49

[98] 
Это было на вывеске
Хорошая и плохая ручка постоянно изнашивается.
Он отдаст все, что ему придется заплатить в последний день
Бесполезно горевать и пытаться

[Britannica-1] Перейти обратно: ^а ^б ^с ^д Злой, Эми (28 февраля 2023 г.). «Омар Хайям: персидский поэт и астроном » энциклопедия Британская Получено 5 апреля.

[NasrRazavi-2] Перейти обратно: ^а ^б ^с ^д Наср, SH ; Аминразави, М. ; при содействии г-на Джози (2008 г.). Антология философии в Персии. Том I: От Зороастра до Омара Хайяма . Лондон и Нью-Йорк: IB Tauris, совместно с Лондонским институтом исмаилитских исследований. ISBN 978-1-84511-541-8 .

[3] Деххода, А.А. «Хайям» . Лухт-намах (на персидском языке). Тегеран.

[5] Леви, Рубен (2011) [1951]. Персидский язык . Издания библиотеки Рутледжа: Иран, Том: XV. Лондон и Нью-Йорк: Рутледж. ISBN 978-0-203-83301-8 .

[mactutor-6] Перейти обратно: ^а ^б ^с О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (июль 1999 г.), «Омар Хайям» , Архив истории математики MacTutor , Университет Сент-Эндрюс

[Struik-7] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Струйк, диджей (1958). «Омар Хайям, математик» . Учитель математики . ЛИИ (4): 280–285. JSTOR 27955652 .

[The_Cambridge_History_of_Iran-8] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л Бойл, Дж. А. (2007) [1975]. « Умар Хайям: астроном, математик и поэт» . В Ричарде Н. Фрае (ред.). Кембриджская история Ирана . Том IV: От арабского вторжения до сельджуков . Нью-Йорк: Издательство Кембриджского университета. стр. 658–664. дои : 10.1017/CHOL9780521200936.023 . ISBN 978-0-521-20093-6 .

[The_Wine_of_Wisdom-9] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д ^р ^с ^т ^в ^v ^В ^х ^и ^С ^аа ^аб ^и Аминразави, М. (2007). Вино мудрости: жизнь, поэзия и философия Омара Хайяма . Оксфорд: Один мир. ISBN 978-1-85168-355-0 .

[11] Арберри, Эй Джей (2008). Аспекты исламской цивилизации: как они изображены в оригинальных текстах . Рутледж. п. 16. ISBN 978-0-415-42600-8 . Омар слагал свои стрелы остроумия и формы красоты на своем родном персидском языке, который к десятому веку оправился от ошеломляющего удара, нанесенного ему арабским языком.

[Al-Khalili-12] Аль-Халили, Джим (30 сентября 2010 г.). Следопыты: золотой век арабской науки . Пингвин Великобритания. ISBN 978-0-14-196501-7 . Позже аль-Кархи (правильно: аль-Караджи ), Ибн Тахир и великий Ибн аль-Хайсам в десятом/одиннадцатом веке пошли дальше, рассматривая уравнения кубической и четвертой степени, а затем персидский математик и поэт Омар Хайям в одиннадцатом веке. век.

[EI2-Khayyam-13] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Фушекур, Шарль-Анри де; Розенфельд, Борис А. (1954–2007) [2000]. «Умар Кахайям» . В ХАР Гибб ; и др. (ред.). Энциклопедия ислама . Том. X (2-е изд.). Лейден: Брилл. стр. 827б–834а. дои : 10.1163/1573-3912_islam_COM_1284 . ISBN 90-04-07026-5 .

[14] Питер Эйвери и Джон Хит-Стаббс, Рубаи Омара Хайяма (Penguin Group, 1981), 14; «Эти даты, 1048–1031 годы, говорят нам, что Хайям жил, когда турецкие султаны-сельджуки расширяли и укрепляли свою власть над Персией, и когда влияние этой власти особенно ощущалось в Нишапуре, месте рождения Хайяма».

[15] Браун, Э.Г. (1899). «Еще больше света на Умар-и-Хайяма» . Журнал Королевского азиатского общества Великобритании и Ирландии . XXXI (2): 409–420. дои : 10.1017/S0035869X00026538 . JSTOR 25208104 . S2CID 163490581 .

[16] Росс, ЭД (1927). « Омар Хайям» . Вестник Школы востоковедения . IV (3): 433–439. дои : 10.1017/S0041977X00102897 . JSTOR 606948 . S2CID 246638673 .

[Boyle-18] Перейти обратно: ^а ^б ^с ^д Бойл, Дж. А. (1966). «Омар Хайям: астроном, математик и поэт» . Бюллетень библиотеки Джона Райлендса . ЛИИ (1): 30–45. дои : 10.7227/BJRL.52.1.3 .

[Earliest_Account_of_Khayyam-19] Перейти обратно: ^а ^б Росс, Эд ; Гибб, ХАР (1929). «Самое раннее повествование об Умаре Хайяме» . Вестник Школы востоковедения . В (3): 467–473. дои : 10.1017/S0041977X00084615 . JSTOR 607341 . S2CID 177947195 .

[Bayhaqi-20] Перейти обратно: ^а ^б ^с Мейерхоф, Макс (1948). «Татиммат Сиван аль-Хикма» Али аль-Байхаки: биографический труд об ученых исламе» . Осирис . VIII : 122–217. дои : 10.1086/368514 . JSTOR 301524 .

[Sarton-21] Перейти обратно: ^а ^б Сартон, Г. (1938). «Могила Омара Хайяма» . Исида . XXIX (1): 15–19. дои : 10.1086/347379 . JSTOR 225920 . S2CID 143678233 .

[FitzGerald-22] Перейти обратно: ^а ^б Эдвард Фитцджеральд, Рубаи Омара Хайяма , Ред. Кристофер Декер (Университет Вирджинии Press, 1997), xv; «Турки-сельджуки вторглись в провинцию Хорасан в 1030-х годах, и город Нишапур добровольно сдался им в 1038 году. Таким образом, Омар Хайям достиг зрелости во время первой из нескольких инопланетных династий, которые правили Ираном до двадцатого века».

[Rosenfeld-24] Розенфельд, Борис А. (2016). «Умар аль-Хайям» . В Хелейн Селин (ред.). Энциклопедия истории науки, технологий и медицины в незападных культурах (3-е изд.). Дордрехт: Спрингер – Верлаг. стр. 4330б–4332а. дои : 10.1007/978-94-007-7747-7_9775 . ISBN 978-94-007-7747-7 .

[25] Аминразави, М. (2010). «Рецензия: Омар Хайям: Поэт, бунтарь, астроном, Хажир Теймурян» . Иранские исследования . XLIII (4): 569–571. дои : 10.1080/00210862.2010.495592 . JSTOR 23033230 . S2CID 162241136 .

[Great_Muslim_Mathematicians-26] Перейти обратно: ^а ^б ^с Мохамед, Мохайни (2000). Великие мусульманские математики . Малайзия: Издательство Universiti Teknologi Malaysia. ISBN 983-52-0157-9 .

[27] Лэмб, Эвелин (28 октября 2014 г.). «В котором Омар Хайям раздражается на Евклида» . Сеть блогов Scientific American . Проверено 10 сентября 2023 г.

[EIr-KhayyamMath-28] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Вахабзаде, Биджан (7 мая 2014 г.). Эхсан Яршатер (ред.). «Хайям, Омар xv. Как математик» . Энциклопедия Ираника . Фонд Энциклопедии Ираника . Проверено 8 сентября 2023 г.

[DSB-Khayyam-29] Перейти обратно: ^а ^б ^с ^д ^и ^ж Юшкевич, Адольф П. ; Розенфельд, Борис А. (1970–1980) [1974]. «Хайями (или Хайям)». В Чарльзе Коулстоне Гиллиспи (ред.). Словарь научной биографии . Том. VII. Нью-Йорк: Сыновья Чарльза Скрибнера. стр. 323б–334а. ISBN 0-684-16962-2 .

[30] Нетингтон, Аманда (2020). «Достижение философского совершенства: успешная замена Омаром Хайямом постулата параллельности Евклида» (PDF) . Люцерна: Журнал бакалавриата с отличием . XIV : 72–97. hdl : 10355/74778 .

[31] Розенфельд, Борис А. (1988). История неевклидовой геометрии: эволюция понятия геометрического пространства . Исследования по истории математики и физических наук. Том. 12. Перевод Эйба Шенитцера при редакционной поддержке Харди Гранта. Нью-Йорк: Спрингер. дои : 10.1007/978-1-4419-8680-1 . ISBN 978-1-4419-8680-1 . ISSN 0172-570X .

[Katz-1998-32] Перейти обратно: ^а ^б Кац, В. (1998). История математики: Введение (2-е изд.). Аддисон-Уэсли. ISBN 0-321-01618-1 .

[EHAS-34] Розенфельд, Борис А.; Юшкевич, АП (1996). "Геометрия". В Рошди Рашед ; в сотрудничестве с Режисом Морелоном (ред.). Энциклопедия истории арабской науки . Том. II. Лондон и Нью-Йорк: Рутледж. стр. 115–159. ISBN 0-415-02063-8 .

[35] Ролвинг, Раймонд Х.; Левин, Майта (1969). «Постулат параллельности» . Учитель математики . LXII (8): 665–669. JSTOR 27958258 .

[36] Смит, Делавэр (1935). «Евклид, Омар Хайям и Саккери». сочинения Математические III (1): 5–10. OCLC 14156259 .

[37] Вахабзаде, Биджан (2005). Джафар Агаяни-Чавоши (ред.). «Омар Хайям и концепция иррациональных чисел». Фарханг: Ежеквартальный журнал гуманитарных и культурных исследований. Тема номера: День памяти Хайяма (3) . XVIII (53–54): 125–134.

[Cooper-38] Перейти обратно: ^а ^б Купер, Глен М. (2003). «Рецензия: Омар Хайям, математик», Р. Рашид, Б. Вахабзаде . Журнал Американского восточного общества . CXXXIII (1): 248–249. дои : 10.2307/3217882 . JSTOR 3217882 .

[40] Ивс, Х. (1958). «Решение кубических уравнений Омара Хайяма» . Учитель математики . ЛИ (4): 285–286. дои : 10.5951/MT.51.4.0285 . JSTOR 27955653 .

[41] « Омар Аль-Хей из Хорасана, около 1079 года нашей эры, больше всего сделал для того, чтобы возвести в метод решение алгебраических уравнений посредством пересекающихся коник ». → Гильбо, Люси (1930), «История решения кубического уравнения» , Mathematics News Letter , V (4): 8–12, doi : 10.2307/3027812 , JSTOR 3027812 , S2CID 125245433

[42] Нетц, Ревель (1999). «Преобразование Архимеда: случай результата, устанавливающего максимум для кубического уравнения» . Архив истории точных наук . ЛИВ (1): 1–47. дои : 10.1007/s004070050032 . JSTOR 41134072 . S2CID 121468528 .

[43] Оукс, Джеффри А. (2011). «Научная редакция алгебры Хайяма» (PDF) . Сухайл: Международный журнал истории точных и естественных наук в исламской цивилизации . Х : 47–75.

[Kent&Muraki-44] Перейти обратно: ^а ^б ^с Кент, Дебора А .; Мураки, Дэвид Дж. (2016). «Геометрическое решение кубического куба Омара Хайяма… в котором для большего удобства учащихся вместо букв используются цветные диаграммы» . Американский математический ежемесячник . CXXIII (2): 149–160. doi : 10.4169/amer.math.monthly.123.2.149 . JSTOR 123.2.149 . S2CID 124153443 .

[Evelyn_Kennedy-45] Перейти обратно: ^а ^б ^с ^д ^и Кеннеди, Эвелин (1966). « Омар Хайям» . Учитель математики . ЛИКС (3): 140–142. дои : 10.5951/MT.59.2.0140 . JSTOR 27957296 .

[amirmoez-46] Амир-Моэз, Арканзас (1963). «Записка Омара Хайяма». Скрипта Математика . XXVI : 323–337.

[Kasir_review-47] «Обзор: Дауд Касир «Алгебра Омара Хайяма»» . Учитель математики . XXV (4): 238–241. 1932. JSTOR 27951448 .

[48] Амир-Моэз, Арканзас (1962). «Решение Хайяма кубических уравнений» . Журнал «Математика» . XXXV (5): 269–271. дои : 10.2307/2688197 . JSTOR 2688197 . Эта статья содержит расширение Мохсеном Хаштруди метода Хайяма на уравнения четвертой степени.

[49] Варден, Б.Л. (2013). История алгебры: от аль-Хорезми до Эмми Нётер . Нью-Йорк: Springer Science & Business Media. ISBN 978-3-642-51599-6 .

[50] Ван Браммелен, Глен (2014). «Обзор исследований математических наук в средневековом исламе с 1996 по 2011 год» . У Натана Сидоли; Глен Ван Браммелен (ред.). Из Александрии через Багдад: обзоры и исследования древнегреческих и средневековых исламских математических наук в честь Дж. Л. Берггрена . Нью-Йорк: Спрингер. стр. 101–138. дои : 10.1007/978-3-642-36736-6_6 . ISBN 978-3-642-36736-6 .

[51] Кнобель, Арт; Лаубенбахер, Рейнхард; Лоддер, Джерри (2007). Математические шедевры: дальнейшие хроники исследователей . Спрингер. ISBN 978-0-387-33060-0 .

[Whinfield-52] Перейти обратно: ^а ^б ^с Уинфилд, Э.Х. (2000). Четверостишия Омара Хайяма: персидский текст с английским стиховым переводом . Нью-Йорк: Psychology Press Ltd.

[53] О'Коннор, Джон Дж.; Робертсон, Э.Ф. (2006). «Мусульманское извлечение корней» . MacTutor Архив истории математики . Университет Сент-Эндрюс.

[54] Кулидж, Дж. Л. (1985). «История биномиальной теоремы» . Американский математический ежемесячник . ЛВИ (3): 147–157. дои : 10.2307/2305028 . JSTOR 2305028 .

[55] Николс, Сьюзен (2017). Аль-Караджи: математик и инженер десятого века . Нью-Йорк: Издательство Rosen Publishing.

[56] Акрами, Муса (11 февраля 2014 г.). «Развитие иранского календаря: исторические и астрономические основы». arXiv : 1111.4926v2 [ physical.hist-ph ].

[57] Абдоллахи, Молитва (15 декабря 1990 г.). Эхсан Яршатер (ред.). «Календари II. В исламский период » Энциклопедия Ираника Фонд Энциклопедии Ираника . Получено 21 ноября.

[58] Фаррелл, Шарлотта (1996). «Возрождение девятого века в астрономии». Учитель физики . XXXIV (5): 268–272. Бибкод : 1996PhTea..34..268F . дои : 10.1119/1.2344432 .

[59] Хейдари-Малаери, М. (21 октября 2004 г.). «Краткий обзор иранского календаря». arXiv : astro-ph/0409620v2 .

[60] Салиба, Г. (2002). «Обзор: Аль-Хайам Математик Р. Рашеда; Б. Вахабзаде; Омар Хайям Математик Р. Рашеда; Б. Вахабзаде» . Иранские исследования . XXXV (1–3): 220–225. дои : 10.1017/S0021086200003686 . JSTOR 4311451 .

[Dashti-61] Перейти обратно: ^а ^б ^с Али Дашти (перевод LP Элвелл-Саттона), В поисках Омара Хайяма , Издания библиотеки Routledge: Иран (2012)

[Ross_1927-62] Перейти обратно: ^а ^б Росс, ЭД (1927). « Омар Хайям» . Вестник Школы востоковедения . IV (3): 433–439. дои : 10.1017/S0041977X00102897 . JSTOR 606948 . S2CID 246638673 .

[Blois-63] Перейти обратно: ^а ^б ^с Блуа, Франсуа де (2004). Персидская литература - биобиблиографический обзор. Том 5: Поэзия домонгольского периода . Лондон и Нью-Йорк: Рутледж. ISBN 9780947593476 .

[64] Амброуз Джордж Поттер, Библиография Рубайята Омара Хайяма (1929).

[65] Мосс, Джойс (2004). Ближневосточная литература и их времена . Томсон Гейл. ISBN 9780787637316 .

[66] Боскалья, Фабрицио (2015). «Пессоа, Борхес и Хайям» . Вариации Борхеса . XL (40): 41–64. JSTOR 24881234 .

[E.D._Ross-67] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час Росс, ЭД (1898). «Мусаффарие: недавний вклад в изучение Омара Хайяма» . Журнал Королевского азиатского общества Великобритании и Ирландии . ХХХ (2): 349–366. дои : 10.1017/S0035869X00025235 . JSTOR 25207968 . S2CID 162611227 .

[Stanford_Encyclopedia_of_Philosophy-68] Аминразави, М. ; Ван Бруммелен, Г. (весна 2017 г.). «Умар Хайям» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .

[Bowen-69] Перейти обратно: ^а ^б ^с ^д Боуэн, JCE (1973). «Рубан Омара Хайяма: критическая оценка перевода Роберта Грейвса и Омара Али Шаха» . Иран . XI : 63–73. дои : 10.2307/4300485 . JSTOR 4300485 .

[70] Дэвис, Д. (31 января 2012 г.). Эхсан Яршатер (ред.). «Фицджеральд, Эдвард» . Энциклопедия Ираника . Энциклопедия Фонда Ираника . Проверено 15 января 2017 г.

[71] Фитцджеральд, Э. (2010). Рубаи Омара Хайяма (с. 12). Шампейн, Иллинойс: Проект Гутенберг

[72] Шенкер, Д. (1981). «Беглая артикуляция: введение в Рубайат Омара Хайяма». Викторианская поэзия . XIX (1): 49–64.

[73] «Слепая сова» Хедаята как вестерн-роман. Библиотека наследия Принстона: Майкл Бирд

[74] Катузян, Х. (1991). Садек Хедаят: Жизнь и литература иранского писателя. Лондон: IB Tauris

[75] Хитченс, К. (2007). Портативный атеист: необходимая литература для неверующего. Филадельфия, Пенсильвания: Да Капо.

[Khayyam2017-76] Перейти обратно: ^а ^б ^с Хайям, Омар (18 мая 2017 г.). Мир в картинках. Омар Хайям. Рубаят . Издательство Эгитас. ISBN 9781773132372 .

[77] Робертсон, Дж. М. (2016). Краткая история свободы: древняя и современная .

[78] Хидаят, С. ; Хайям, Омар (1993). Песни Омара Хайяма . Париж: Хосе Корти. ISBN 9782714304896 .

[Csillik-79] Гсиллик, Б. (1960). «Настоящий Омар Хайям» . Восточный журнал Венгерской академии наук . Х (1): 59–77. JSTOR 23682646 .

[80] Альбано, Джузеппе (2008). «Польза чтения «Рубайата Омара Хайяма» как пастырского» . Викторианская поэзия . XLVI (1): 55–67. дои : 10.1353/vp.0.0010 . JSTOR 40347527 . S2CID 170388817 .

[81] Бьеррегард, ЦДХ (1915). Омар Хайям, Фитцджеральд, Эдвард, 1809-1883, Суфизм . Лондон: Суфийское издательское общество.

[82] Идрис Шах, Суфии , Octagon Press (1999)

[83] «Каждая строка Рубаи имеет больше смысла, чем почти все, что вы можете прочитать в суфийской литературе» Абдулла Дуган Кто такой Гончар? Гностическая пресса 1991 г. ISBN 0-473-01064-X

[nasrkhayyamphil-84] Наср, С.Х. (2006). Исламская философия от ее истоков до наших дней: философия в стране пророчеств . Нью-Йорк: SUNY Press. ISBN 0-7914-6799-6 .

[86] Беверидж, Х. (1905). «Омар Хайям» . Журнал Королевского азиатского общества . XXXVII (3): 521–526. дои : 10.1017/S0035869X00033530 . JSTOR 25210170 .

[87] Дж. Д. Йоханнан, Персидская поэзия в Англии и Америке , 1977.

[Reception-88] Сейед-Гохраб, А.А. , изд. (2012). Великий Умар Хайям: глобальное восприятие рубаята (PDF) . Лейден: Издательство Лейденского университета. ISBN 978-94-0060-079-9 .

[Simidchieva-89] Симидчиева, М. (2011). «Рубайат и агностицизм» Фитцджеральда. В книге А. Пула, К. Ван Руймбеке и У. Мартина (ред.), «Рубайат Омара Хайяма» Фитцджеральда: популярность и пренебрежение. Гимн Пресс.

[90] UNIS. «Памятник будет открыт в Венском международном центре, «Павильон ученых», подаренный Ираном международным организациям в Вене» .

[91] «Статуя Хайяма наконец установлена в Университете Оклахомы » Тегеран Таймс . Архивировано из оригинала 5 апреля 2016 года . Проверено 4 апреля 2016 г.

[92] Мартин, Уильям Х.; Мейсон, Сандра (15 июля 2009 г.). Эхсан Яршатер (ред.). «Хайям, Омар xiii. Музыкальные произведения на основе рубаи» . Энциклопедия Ираника . Фонд Энциклопедии Ираника . Проверено 8 октября 2023 г.

[93] Джеффри Д. Лавуа, Частная жизнь генерала Омара Н. Брэдли (2015)

[Balıkçıoğlu1-94] Балыкчиоглу, Эфе Мурат (2024). «Четверостишия многих приемов: обзор восприятий Омара Хайяма в османских и турецких переводах» . Ирановедение : 1. doi : 10.1017/irn.2023.72 .

[Balıkçıoğlu1-22-95] Перейти обратно: ^а ^б ^с ^д ^и ^ж Балыкчиоглу, Эфе Мурат (2024). «Четверостишия многих приемов: обзор восприятий Омара Хайя в османских и турецких переводах» . Иранские исследования : 1, 22. doi : 10.1017/irn.2023.72 .

[Moving_Finger-96] Перейти обратно: ^а ^б ^с ^д Сейед-Гохраб, А.А. (13 апреля 2018 г.). «Двигающийся палец: взгляд на жизнь персидского четверостишия» . Блог лейденских медиевистов . Университет Лейдена . Проверено 14 мая 2022 г.

[97] Фитцджеральд, Станца LXXI, 4-е изд.

[99] «17. MLK Beyond Vietnam.pdf (hawaii.edu)» (PDF) . Архивировано (PDF) из оригинала 10 октября 2022 года.

[100] «Четверостишие 36» . изучая Хайям -США . 21 декабря 2006 года . Проверено 14 мая 2022 г.

[101] Таблица II Омара Хайяма , получено 8 августа 2021 г.

[102] Таблица III Омара Хайяма , дата обращения 8 августа 2021 г.

[103] Словарь названий малых планет . 1979. с. 255 . Проверено 8 сентября 2012 г. - через Google Книги.

[104] «Как Омар Хайям изменил способ измерения времени людьми» . Независимый . 17 мая 2019 года. Архивировано из оригинала 24 мая 2022 года . Проверено 18 мая 2019 г.

[ 1 ]

[ 2 ]

[ 3 ]

[ а ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ б ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ с ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ д ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ и ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ ж ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ 44 ]

[ 45 ]

[ 46 ]

[ 47 ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ 52 ]

[ 53 ]

[ 54 ]

[ 55 ]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

[ 68 ]

[ 69 ]

[ 70 ]

[ 71 ]

[ 72 ]

[ 73 ]

[ 74 ]

[ 75 ]

[ 76 ]

[ 77 ]

[ 78 ]

[ г ]

[ 79 ]

[ 80 ]

[ 81 ]

[ 82 ]

[ 83 ]

[ 84 ]

[ 85 ]

[ 86 ]

[ 87 ]

[ 88 ]

[ 89 ]

[ 90 ]

[ ч ]

[ 91 ]

[ 92 ]

[ 93 ]

[ 94 ]

v т и Жители Хорасана
Scientists	Abu Hatam Isfizari Abu Ma'shar al-Balkhi Abu Wafa Abu Ubayd Juzjani Abu Zayd Balkhi Alfraganus Ali Qushji Avicenna Birjandi Biruni Hasib Marwazi Ibn Hayyan Abu Ja'far al-Khazin Khazini Khojandi Khwarizmi Nasawi Nasir al-Din al-Tusi Omar Khayyam Sharaf al-Din al-Tusi Sijzi
Philosophers	Algazel Amiri Avicenna Farabi Haji Bektash Veli Nasir Khusraw Sijistani Shahrastani
Islamic scholars	Abu Dawud al-Sijistani Abu Barakat Nasafi Abu Hanifa Abu Hafs Nasafi Abu Layth Samarqandi Abu Mu'in Nasafi Abu Qasim Samarqandi Ansari Baghavi Bayhaqi Bazdawi Bukhari Dabusi Fatima Samarqandi Ghazali Ghaznawi Hakim Tirmidhi Hakim Nishapuri Ibn Hibban Ibn Mubarak Ibn Tayfour Sajawandi Juwayni Kasani Kashifi Lamishi Marghinani Maturidi Mulla al-Qari Muqatil Muslim Nasa'i Qushayri Razi Sabuni Sajawandi Sarakhsi Shaykh Tusi Taftazani Tha'labi Nishapuri Tirmidhi Zamakhshari
Poets and artists	Abu Sa'id Abu'l-Khayr Anvari Aruzi Samarqandi Asadi Tusi Attar Nishapuri Behzad Daqiqi Farrukhi Sistani Ferdowsi Jami Kashifi Nasir Khusraw Rabia Balkhi Rudaki Rumi Sanā'ī
Historians and political figures	Abu'l-Fadl Bayhaqi Abu'l-Hasan Isfarayini Abu'l-Ma'ali Nasrallah Abu Muslim Khorasani Gardizi Ali-Shir Nava'i Ata-Malik Juvayni Aufi Abu Ali Bal'ami Gawhar Shad Ibn Khordadbeh Khalid ibn Barmak Minhaj al-Siraj Juzjani Nizam al-Mulk Tahir ibn Husayn Yahya Barmaki Ahmad ibn Nizam al-Mulk Shihab al-Nasawi

Базы данных авторитетного контроля
International	FAST ISNI 2 VIAF
National	Norway Chile Spain France BnF data Germany Italy Israel Finland Belgium United States Sweden Latvia Japan Czech Republic Australia Greece Korea Croatia 2 Netherlands Poland Portugal 2 Vatican
Academics	CiNii MathSciNet Mathematics Genealogy Project zbMATH
Artists	MusicBrainz Victoria ULAN
People	Deutsche Biographie Trove
Other	RISM SNAC IdRef İslâm Ansiklopedisi Te Papa (New Zealand)