Программное обеспечение для генерации фракталов

Программное обеспечение для генерации фракталов — это любой тип графического программного обеспечения , которое генерирует изображения фракталов . Существует множество программ для генерации фракталов, как бесплатных, так и коммерческих. Доступны мобильные приложения, позволяющие играть или возиться с фракталами. Некоторые программисты создают для себя фрактальное программное обеспечение из-за новизны и из-за сложности понимания соответствующей математики. Генерация фракталов привела к некоторым очень большим проблемам для чистой математики . [1]
Программное обеспечение для генерации фракталов создает математическую красоту посредством визуализации . Современным компьютерам могут потребоваться секунды или минуты, чтобы создать одно фрактальное изображение высокого разрешения . Изображения генерируются как для симуляции (моделирования), так и для случайных фракталов для искусства . Фрактальная генерация, используемая для моделирования, является частью реализма в компьютерной графике. [2] Программное обеспечение для генерации фракталов можно использовать для имитации природных ландшафтов с помощью программ создания фрактальных ландшафтов и пейзажей . Фрактальные изображения можно использовать для внесения неравномерностей в стерильную компьютерную среду. [3]
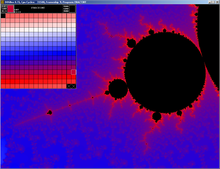
Фракталы генерируются с помощью программного обеспечения для визуализации музыки , заставок и обоев генераторов . Это программное обеспечение предоставляет пользователю более ограниченный набор настроек и функций, иногда полагаясь на ряд заранее запрограммированных переменных. Поскольку сложные изображения могут быть созданы из простых формул, фракталы часто используются на демосцене . [4] Генерация фракталов, таких как множество Мандельброта, занимает много времени и требует большого количества вычислений, поэтому ее часто используют в устройствах для сравнительного анализа . [5]
История
[ редактировать ]
Генерация фракталов путем расчета без помощи компьютера была предпринята немецким математиком Георгом Кантором в 1883 году для создания множества Кантора . [6] В последующие годы математики постулировали существование многочисленных фракталов. Некоторые из них были задуманы до того, как фракталы были названы в 1975 году, например, дерево Пифагора голландским учителем математики Альбертом Э. Босманом в 1942 году.
Разработка первого программного обеспечения для генерации фракталов началась с Бенуа Мандельбротом поиска обобщенной функции для класса фигур , известных как множества Жюлиа . В 1979 году Мандельброт обнаружил, что одно изображение сложной плоскости можно создать путем итерации . Он и программисты, работающие в IBM, создали первые элементарные фрактальные распечатки. [7] Это ознаменовало собой первый случай генерации фракталов с помощью нелинейных законов творения или «фрактала времени ускользания». [8] [9] Лорен Карпентер создала двухминутный цветной фильм под названием Vol Libre для презентации на SIGGRAPH в 1980 году. [10] В октябрьском выпуске журнала Acorn User за 1983 год был опубликован список BBC BASIC по созданию фрактальных форм Сьюзан Степни, ныне профессора компьютерных наук в Йоркском университете . [11] [12] Она продолжила это в мартовском номере журнала Acorn User за 1984 год, написав «Снежинки и другие фрактальные монстры». [13] Фракталы были визуализированы в компьютерных играх еще в 1984 году, когда была создана Rescue on Fractalus! . С начала 1980-х годов примерно до 1995 года были сформулированы сотни различных типов фракталов. [14]
Популярность создания фрактальных изображений возросла по мере того, как в 1990-е годы стали распространяться компьютеры с математическим сопроцессором или устройством с плавающей запятой в центральном процессоре. В настоящее время рендеринг изображений стандарта VGA высокого разрешения может занять много часов. [ нужна ссылка ] Алгоритмы фрактальной генерации демонстрируют исключительную распараллеливаемость . Программное обеспечение для генерации фракталов было переписано для использования многопоточной обработки . Впоследствии внедрение графических процессоров в компьютеры значительно увеличило скорость рендеринга и позволило в реальном времени изменять параметры, что ранее было невозможно из-за задержки рендеринга. [15] Генерация 3D-фракталов появилась примерно в 2009 году. Ранний список программного обеспечения для генерации фракталов был составлен для книги Джона Бриггса «Фракталы: закономерности хаоса», опубликованной в 1992 году. [16] Среди ведущих писателей в этой области — Дитмар Саупе , Хайнц-Отто Пейтген и Клиффорд А. Пиковер .
Методы
[ редактировать ]
Существует два основных метода генерации двумерных фракталов. Один из них — применить итерационный процесс к простым уравнениям с помощью порождающей рекурсии . [6] Динамические системы производят ряд значений. В фрактальном программном обеспечении значения для набора точек на комплексной плоскости рассчитываются, а затем отображаются в виде пикселей . Эта компьютерная генерация фрактальных объектов представляет собой бесконечный процесс. Теоретически изображения можно рассчитывать бесконечно, но на практике они аппроксимируются до определенного уровня детализации . [17] Мандельброт использовал квадратичные формулы, описанные французским математиком Гастоном Жюли . [14] Максимальная фрактальная размерность , которую можно получить, варьируется в зависимости от типа и иногда ограничивается в зависимости от реализованного метода. Существует множество методов окраски, которые можно применить. Одним из первых был алгоритм времени выхода. [14] Цветные полосы могут появляться на изображениях в зависимости от используемого метода окраски, а также плотности градиентного цвета.
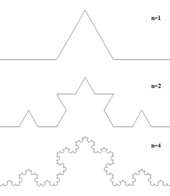
Некоторые программы генерируют геометрические самоподобные или детерминированные фракталы, такие как кривая Коха . Эти программы используют инициатор, за которым следует генератор, повторяющийся по шаблону . Эти простые фракталы возникли благодаря методу, впервые предложенному Кохом в 1904 году. [18]
Другой основной метод — это системы итерированных функций, состоящие из ряда аффинных преобразований . [19] В первом методе каждый пиксель фрактального изображения оценивается в соответствии с функцией, а затем окрашивается, прежде чем тот же процесс применяется к следующему пикселю. Первый метод представляет собой классический стохастический подход, а второй реализует линейную фрактальную модель. [3] Использование рекурсии позволило программистам создавать сложные изображения способом простым . [20]
Трехмерные фракталы генерируются различными способами, в том числе с использованием алгебры кватернионов . [21] Фракталы возникают в результате моделирования гидродинамики в виде турбулентности, когда контурная адвекция используется для изучения хаотического перемешивания . [ нужна ссылка ] Метод Буддхброта был представлен в 1993 году. Программы могут использовать фрактальные карты высот для создания ландшафта. Фракталы были созданы на компьютерах с использованием следующих методов: губка Менгера , гиперкомплексное многообразие , броуновское дерево , броуновское движение , разложение , L-системы , фракталы Ляпунова , фракталы Ньютона , стебли Пиковера и странные аттракторы .
Функции
[ редактировать ]


В пакеты программного обеспечения для генерации фракталов включено множество различных функций. Таким образом, возможно соответствующее разнообразие создаваемых изображений. Большинство из них имеют ту или иную форму выбора алгоритма , интерактивное масштабирование изображения и возможность сохранять файлы в формате JPEG , TIFF или PNG , а также возможность сохранять файлы параметров, что позволяет пользователю легко вернуться к ранее созданным изображениям для последующего использования. модификация или исследование. Формулы, параметры, переменные и алгоритмы раскраски фрактальных изображений могут обмениваться между пользователями одной и той же программы. Не существует общепринятого стандартного формата файлов фракталов .
Одной из особенностей большинства фрактальных программ времени выхода или алгебраических фракталов является настройка максимального количества итераций. Увеличение количества итераций требуется, если изображение увеличивается, чтобы мелкие детали не потерять . Ограничение максимального количества итераций важно, когда вычислительная мощность устройства низкая. Параметры окраски часто позволяют выбирать цвета в случайном порядке . Варианты плотности цвета распространены, поскольку некоторые градиенты выдают очень переменные величины, что приводит к многочисленным повторяющимся полосам или большим областям одного и того же цвета. Из-за удобной возможности добавления эффектов постобработки наложения слоев и альфа-композиции, были включены функции имеющиеся в других графических программах. Могут быть включены как 2D-, так и 3D-эффекты рендеринга, такие как эффект плазмы и освещение . Многие пакеты также позволяют пользователю вводить свою собственную формулу, чтобы обеспечить больший контроль над фракталами, а также выбирать цветопередачу, а также использовать фильтры и другие методы манипулирования изображениями. Некоторые пакеты фрактального программного обеспечения позволяют создавать фильмы из последовательности фрактальных изображений. Другие отображают время рендеринга и допускают некоторую форму цветового цикла и создания цветовой палитры инструменты .
| Внешние СМИ | |
|---|---|
| Изображения | |
| Видео | |
Стандартное графическое программное обеспечение (например, GIMP ) содержит фильтры или плагины, которые можно использовать для генерации фракталов. Blender содержит фрактальный (или случайный) модификатор. Многие автономные программы, генерирующие фракталы, можно использовать в сочетании с другими графическими программами (например, Photoshop ) для создания более сложных изображений. POV-Ray — это программа трассировки лучей, которая генерирует изображения на основе текстового описания сцены, способного генерировать фракталы. сценарии в 3ds Max и Autodesk Maya Можно использовать . Ряд веб-интерфейсов для генерации фракталов доступен бесплатно, включая Turtle Graphics Renderer. [22] Fractal Lab может генерировать как 2D, так и 3D фракталы и доступна через Интернет с помощью WebGL . [23] с открытым исходным кодом на основе Java JWildfire — это генератор фрактального пламени . [24] Mandelbrot Fractal — исследователь фракталов, написанный на JavaScript . [25] Fractal Grower — это программное обеспечение, написанное на Java для генерации фракталов замещения Линденмайера (L-систем). [26]
Программы
[ редактировать ]
Из-за эффекта бабочки генерация фракталов может оказаться сложной задачей. Небольшое изменение одной переменной может иметь непредсказуемый эффект. Некоторое программное обеспечение требует от пользователя сложного обучения , и понимание теории хаоса является преимуществом. Сюда входят характеристики фрактальной размерности , рекурсии и самоподобия, присущие всем фракталам.

Существует множество программ для генерации фракталов, как бесплатных, так и коммерческих. Известные программы генерации фракталов включают:
- Apophys - программное обеспечение IFS с открытым исходным кодом для Microsoft Windows. систем на базе
- Bryce - кроссплатформенное коммерческое программное обеспечение, частично разработанное Кеном Масгрейвом.
- Chaotica — коммерческое программное обеспечение IFS для Windows, Linux и Mac OS . Бесплатно для некоммерческого использования.
- Electric Sheep — распределенная программа-заставка с открытым исходным кодом, разработанная Скоттом Дрейвсом .
- Fractint — MS-DOS бесплатное программное обеспечение для , первоначально выпущенное в 1988 году с доступным исходным кодом , позже портированное на Linux и Windows (как WinFract).
- Fyre — это кроссплатформенный инструмент с открытым исходным кодом для создания изображений на основе гистограмм повторяющихся хаотических функций.
- Called Fractaler — фрактальный зум на базе Windows.
- Milkdrop — плагин визуализации музыки, распространяемый вместе с Winamp.
- MojoWorld Generator - несуществующий генератор ландшафтов для Windows.
- openPlaG – создает фракталы путем построения простых функций.
- Picogen — кроссплатформенный генератор ландшафта с открытым исходным кодом.
- Sterling – бесплатное программное обеспечение для Windows
- Terragen — генератор фрактальных ландшафтов , который может отображать анимацию для Windows и Mac OS X.
- Ultra Fractal — собственный генератор фракталов для Windows и Mac OS X.
- Wolfram Mathematica – может использоваться специально для создания фрактальных изображений.
- XaoS - кроссплатформенная программа фрактального масштабирования с открытым исходным кодом.
Большинство из вышеперечисленных программ создают двумерные фракталы, а некоторые создают трехмерные фрактальные объекты, такие как мандельбульбы и мандельбоксы . Mandelbulber — экспериментальная кроссплатформенная программа с открытым исходным кодом, генерирующая трехмерные фрактальные изображения. [27] Мандельбулбер является экспертом в создании 3D- анимации . [28] Mandelbulb 3D — бесплатное программное обеспечение для создания 3D-изображений со множеством эффектов, встречающихся в средах 3D-рендеринга. [29] Incendia — это 3D-фрактальная программа, использующая системы итерированных функций (IFS) для генерации фракталов. [30] Visions of Chaos, Boxplorer и Fragmentarium также отображают 3D-изображения.
Доступен GnoFract 4D с открытым исходным кодом. [31] ChaosPro — бесплатная программа для создания фракталов. [32] Fraqtive — кроссплатформенный генератор фракталов с открытым исходным кодом. [33] MandelX — бесплатная программа для рендеринга фрактальных изображений в Windows. [34] WinCIG, Chascope, Tierazon, Fractal Forge и Malsys также генерируют фрактальные изображения.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Фрейм, Майкл; Амелия Урри (2016). Фрактальные миры: выращенные, построенные и воображаемые . Издательство Йельского университета. п. 129. ИСБН 978-0300197877 . Проверено 5 мая 2017 г.
- ^ Ф. против, Хеселер против; Х.-О Пейтген; Г. Скордев (2012). «Линейные клеточные автоматы, замены, иерархические системы итерированных функций и аттракторы» . В Энкарнакао, Хосе Л.; Пейтген, Хайнц-Отто; Сакас, Георгиос; Энглерт, Габриэле (ред.). Фрактальная геометрия и компьютерная графика . Springer Science & Business Media. п. 3. ISBN 9783642956782 . Проверено 7 мая 2017 г.
- ^ Jump up to: а б Никиэль¹, Славомир С. (октябрь 1998 г.). «Настоящие цветные изображения и системы итерированных функций». Компьютеры и графика . 22 (5): 635–640. дои : 10.1016/S0097-8493(98)00072-7 .
- ^ Янус Копфштейн (14 мая 2014 г.). «Эта 4-килобайтная демо-версия сжимает вселенную фракталов до размера документа Word» . Грань . Вокс Медиа . Проверено 5 марта 2017 г.
- ^ Малышкин, Виктор (2013). Параллельные вычислительные технологии: 12-я Международная конференция PaCT 2013, Санкт-Петербург, Россия, 30 сентября-4 октября 2013 г., Тезисы докладов . Спрингер. п. 267. ИСБН 9783642399589 . Проверено 7 мая 2017 г.
- ^ Jump up to: а б Дэниел Шиффман. «Глава 8. Фракталы» . Природа кода . Проверено 22 января 2024 г.
- ^ Глейк, Джеймс (1987). Хаос: создание новой науки . Кардинал. стр. 222–223. ISBN 978-0143113454 .
- ^ Том Ван Катсем. «Сессия 5 – Фракталы времени побега» . Проверено 7 марта 2017 г.
- ^ Рёсс, Дитер (2011). Изучение и преподавание математики с использованием моделирования: плюс 2000 примеров из физики . Вальтер де Грюйтер. п. 56. ИСБН 9783110250077 . Проверено 7 мая 2017 г.
- ^ «Vol Libre: первый фрактальный компьютерный фильм» . История информации . Джереми Норман и компания . Проверено 5 марта 2017 г.
- ^ «Сьюзан Степни, профессор компьютерных наук, Йоркский университет, Великобритания» . www-users.cs.york.ac.uk . Университет Йорка . Проверено 29 декабря 2018 г.
- ^ Степни, Сьюзен (октябрь 1983 г.). «Невероятные фракталы, стр. 37, 39, 41 и 43» . www-users.cs.york.ac.uk . Пользователь Acorn . Проверено 29 декабря 2018 г.
- ^ Степни, Сьюзен (март 1984 г.). «Снежинки и другие монстры, стр. 25, 28, 29» . www-users.cs.york.ac.uk . Пользователь Acorn . Проверено 29 декабря 2018 г.
- ^ Jump up to: а б с Гарсия, Франциско; Фернандес, Анхель; Барралло, Хавьер; Мартин, Луис. «Раскраска динамических систем на комплексной плоскости». CiteSeerX 10.1.1.393.9370 .
- ^ У. Д. Мэйфилд; Джей Си Эйлан; Ти Джей Ху; М. К. Полсен; Б.М. Вятт (2016). «Генерация фрактального искусства с использованием графических процессоров». arXiv : 1611.03079 [ cs.GR ].
- ^ Бриггс, Джон (1992). Фракталы: закономерности хаоса . Саймон и Шустер. п. 182 . ISBN 978-0671742171 .
- ^ Чен, JN; Н. М. Тельманн; З.С. Цанг; Д. Тельманн (1994). Основы компьютерной графики . Всемирная научная. п. 100. ИСБН 9789814603744 . Проверено 5 мая 2017 г.
- ^ Расс, Джон К. (2013). Фрактальные поверхности . Springer Science & Business Media. п. 150. ИСБН 978-1489925787 . Проверено 5 мая 2017 г.
- ^ Чэнь, Ян Цю; Би, Гоань (май – июнь 1997 г.). «Трехмерные фракталы IFS как графическая модель реального времени». Компьютеры и графика . 21 (3): 367–370. дои : 10.1016/S0097-8493(97)00014-9 .
- ^ Пейтген, Хайнц-Отто; Питер Рихтер (1986). Красота фракталов . Спрингер-Верлаг. п. 2. ISBN 978-0883859711 . Проверено 7 мая 2017 г.
- ^ Лейс, Джос (июнь 2005 г.). «Сферические инверсные фракталы». Компьютеры и графика . 29 (3): 463–466. дои : 10.1016/j.cag.2005.03.011 .
- ^ «Средство визуализации черепаховой графики» . Проверено 2 марта 2017 г.
- ^ «Фрактальная лаборатория» . subblue.com . Проверено 5 марта 2017 г.
- ^ «Добро пожаловать на официальный сайт программного обеспечения JWildfire!» . Проверено 7 марта 2017 г.
- ^ Майк Уильямс (17 июля 2016 г.). «Фрактал Мандельброта» . PCAdvisor . IDG Великобритания . Проверено 5 марта 2017 г.
- ^ «Фрактальный производитель» . Университет Нью-Мексико . Проверено 6 марта 2017 г.
- ^ Джои Бернард (7 января 2014 г.). «Убираем фракталы со страницы» . Linux-журнал . Проверено 5 мая 2017 г.
- ^ Майк Уильямс (25 ноября 2013 г.). «Создавайте эффектные 3D-фракталы с помощью Mandelbulber» . БетаНьюс . Проверено 5 марта 2017 г.
- ^ «Программное обеспечение для фрактального рендеринга Mandelbulb 3D (MB3D)» . Сфералаб. 17 января 2014 года . Проверено 7 марта 2017 г.
- ^ «Пожары» . Рамиро Перес Клэр Нэш Проверено 7 марта 2017 г.
- ^ «Гнофракт 4D» . Архивировано из оригинала 6 марта 2020 года . Проверено 2 марта 2017 г.
- ^ «ХаосПро Релиз 4.0» . Проверено 2 марта 2017 г.
- ^ «Фрактивный» . Проверено 2 марта 2017 г.
- ^ «Бесплатное программное обеспечение от Falcosoft» . Фалькософт. 27 января 2017 года . Проверено 5 марта 2017 г.
Внешние ссылки
[ редактировать ]- Программное обеспечение для генерации фракталов в Curlie
- Введение во фракталы Пола Бурка, май 1991 г.
