Уравнение Суэйна – Луптона

В физической органической химии уравнение Суэйна-Луптона представляет собой линейное соотношение свободной энергии (LFER), которое используется при изучении механизмов реакции и при разработке количественных соотношений структура-активность для органических соединений . Оно было разработано К. Гарднером Суэйном и Элмером К. Луптоном-младшим в 1968 году как уточнение уравнения Хэммета , включающее как эффекты поля, так и резонансные эффекты.

Фон

В органической химии график Хэммета позволяет оценить влияние заместителей реакции на равновесие или скорость с помощью уравнения Хэммета ( 1 ):

$\log {\frac {K_{{\ce {X}}}}{K_{{\ce {H}}}}}=\sigma \rho$ ( 1 )

Хэммет разработал это уравнение на основе констант равновесия диссоциации бензойной кислоты и ее производных (рис. 1):

Рис. 1. Диссоциация замещенных бензойных кислот.

Хэммет определил уравнение на основе двух параметров: константы реакции (ρ) и параметра заместителя (σ). При изучении других реакций с использованием этих параметров корреляция не всегда обнаруживалась из-за специфического вывода этих параметров из равновесия диссоциации замещенных бензойных кислот и первоначального пренебрежения резонансными эффектами. Следовательно, влияние заместителей на ряд соединений необходимо изучать на основе отдельной реакции, используя уравнение Хэммета, полученное либо для полевых, либо для резонансных эффектов, но не для того и другого.

Переопределение уравнения

К. Гарднер Суэйн и Элмер К. Луптон-младший из Массачусетского технологического института переопределили параметр заместителя σ, основываясь на идее о том, что для описания эффектов любого данного фактора необходимо не более двух переменных (резонансные эффекты и эффекты поля). заместитель. Эффекты поля F включают все эффекты (индуктивные и чистое поле). обусловленные резонансом Аналогичным образом, эффекты , R , обусловлены средним значением способности отдавать электроны и способности принимать электроны. Предполагается, что эти два эффекта независимы друг от друга и поэтому могут быть записаны в виде линейной комбинации:

$\sigma \rho =fF+rR$ ( 2 )

Эти два параметра рассматриваются как независимые члены из-за предположения, сделанного Суэйном и Луптоном; заместитель удален тремя или более насыщенными центрами или если заместитель представляет собой (CH ₃ ) ₃ N ⁺ . Все остальные члены тогда пренебрежимо малы и приводят к уравнению Суэйна-Луптона ( 2 ).

Новый параметр заместителя

Параметр заместителя теперь определяется эффектами поля и резонанса F и R , которые зависят от отдельного заместителя. Константы r и f учитывают важность каждого из двух эффектов. Эти константы не зависят от заместителя, а зависят от набора параметров заместителя Гаммета (σ ^м , п ^п , п ^р+ , п ^' , и т. д.).

Чтобы найти взвешенные константы r и f для каждого набора параметров заместителей, необходимо установить тот факт, что каждый новый параметр заместителя σ _X можно записать как линейную комбинацию конкретных параметров заместителей в реакции, т.е.

$\sigma _{X}=c_{1}\sigma _{1X}+c_{2}\sigma _{2X}$ ( 3 )

где σ _1X и σ _2X — параметры конкретных заместителей (т.е. σ ⁺ , п ⁻ и т. д.), а c ₁ и c ₂ — константы, не зависящие от заместителя (зависят от условий реакции, т. е. температуры, растворителя и индивидуальной изучаемой реакции). В более общем смысле это можно выразить так:

$Z=aX+bY+i$ ( 4 )

где я - перехват, позволяющий не фиксировать начало координат в (0,0). Если бы этого не было сделано, уравнение придало бы гораздо больший вес незамещенным соединениям, которые пытаются сравнить с использованием этого уравнения. Для определения коэффициентов/констант a , b и i используется линейный анализ наименьших квадратов (Суэйн и Луптон использовали процедуру под названием DOVE: Dual Obligate Vector Evaluation). Константы сначала были основаны на трех предыдущих реакциях (σ ^м , п ^п , п ^р+ ), что приводит к большему количеству возможных ошибок, поскольку скомпилированные данные представляют собой лишь минимальную комбинацию гораздо большего пула. Видя возможную ошибку в этом ограниченном пуле, пул данных был увеличен путем первоначального назначения масштаба. Нулевая шкала используется для водорода, поскольку известно, что он не отдает и не принимает электронную плотность при присоединении к атому углерода из-за одинаковой электроотрицательности. Значение 1 было присвоено NO ₂ , поскольку предыдущие исследования показали, что эффект этого заместителя преимущественно обусловлен резонансом. Наконец, F был установлен равным R для обоих компонентов, чтобы эффекты поля можно было напрямую сравнить с резонансными эффектами. Это приводит к:

F = R = 0 для H ( Водород ).

F = R = 1 для NO ₂ ( Нитрогруппа ).

На рис. 2 показаны некоторые относительные значения F и R, полученные Суэйном и Луптоном.

Категории заместителей

Алкильные группы имеют значение F но разумные значения R. от низкого до нуля , Чаще всего это объясняется гиперконъюгацией , что означает практически полное отсутствие индуктивных эффектов, но лишь эффекты частичного резонанса.

Рис. 2а Значения F для общих заместителей.

CF ₃ имеет гораздо более высокое соотношение R / F , чем другие заместители с высокой степенью сопряжения. Это было более подробно изучено Суэйном, но все же лучше всего объясняется гиперконъюгацией фторида.

Рис. 2б Значения R для общих заместителей.

Положительно заряженные заместители (т.е. Н(СН ₃ ) ³⁺ и С(СН ₃ ) ²⁺ ) имеют большие положительные значения F из-за положительного заряда, который насыщается вблизи рассматриваемого углеродного каркаса. Отрицательно заряженные заместители (т.е. CO ²⁻ и так ³⁻ ) имеют гораздо более низкие значения F из-за их способности резонировать электронную плотность между атомами кислорода и стабилизировать ее за счет водородных связей с растворителями.

Линейные отношения свободной энергии по-прежнему полезны, несмотря на их недостатки, когда они доведены до предела. Новые методы определения параметров заместителей Суэйна-Луптона включают изучение химических сдвигов с помощью спектроскопии ядерного магнитного резонанса . Недавно, ¹⁵ Изучены химические сдвиги ЯМР N и эффекты заместителей 1,2,3,4,5,6,7,8-октагидроакридина и его производных. Значения R и F были найдены для -N(COCH ₃ ) ₂ группа, которую ранее не удалось обнаружить известными методами.

Значения f и r

Иногда полезно посмотреть на процентный резонанс (% r ), поскольку r зависит от реакции и одинаков для всех заместителей.

$\%r=100{\frac {r}{f+r}}$ ( 5 )

Можно предсказать разницу в данных, сравнивая два заместителя, используя % r :

${\frac {\rho \sigma _{{\ce {X}}}-\rho \sigma _{{\ce {H}}}}{f}}=F_{X}+{\frac {(\%r)R_{{\ce {X}}}}{100-\%r}}$ ( 6 )

если посмотреть на соотношение R и F. Наиболее доминирующий эффект очевиден , Например, было показано, что комплекс вольфрама алкилирует А и В. аллилкарбонаты Соотношение продуктов A1 и B1 можно объяснить пара-заместителем X ( рис. 3 ). Используя параметры Суэйна-Луптона (σ = 0,2 F + 0,8 R ), было обнаружено, что значение ρ -2,5 соответствует наклону.

Рис. 3а Аллиловое алкилирование карбонатов.

Рис. 3б График параметров Суэйна–Луптона.

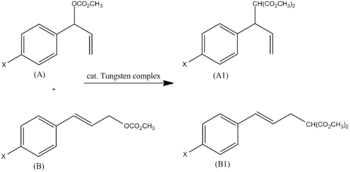
Это согласуется с предложенным механизмом (на бензильном углероде образуется положительный заряд, который стабилизируется резонансом; R доминирует в соотношении 0,8/0,2).

Недостатки

Как и любое другое установленное линейное соотношение свободной энергии , уравнение Суэйна-Луптона также не работает, когда возникают особые обстоятельства, то есть изменение скорости, определяющей шаг механизма или сольватной структуры.

См. также

• Уравнение Хэммета
• Уравнение Тафта
• Уравнение Грюнвальда–Винштейна
• Уравнение Юкавы–Цуно
• Принцип Белла – Эванса – Поланьи
• Отношения свободной энергии
• Количественная связь структура-активность