6

← 5 6 7 →
−1 0 1 2 3 4 5 6 7 8 9 → Список номеров ; Целые числа ; ← 0 10 20 30 40 50 60 70 80 90 →
Кардинал	шесть
Порядковый номер	6-е место ; (шестой)
Система счисления	шестерка
Факторизация	2 × 3
Делители	1, 2, 3, 6
Греческая цифра	Ϛ´
Римская цифра	МЫ, мы, ↅ
Греческий префикс	гекса- / гекс-
Латинский префикс	шесть- / шесть-
Двоичный	110 2
тройной	20 3
Сенарий	10 6
Восьмеричный	6 8
Двенадцатеричный	6 12
Шестнадцатеричный	6 16
Греческий	f (или F или s)
арабский , курдский , синдхи , урду	٦
персидский	۶
амхарский	፮
Бенгальский	৬
Китайская цифра	Шесть, земля
Деванагари	६
Гуджарати	૬
иврит	и
кхмерский	6
тайский	๖
телугу	౬
тамильский	௬
Сараики	٦
малаялам	൬
Армянский	З:
Вавилонская цифра	𒐚
Египетский иероглиф	𓏿
Азбука Морзе	_ ....

6 ( шесть ) — натуральное число, следующее за 5 и предшествующее 7 . Это составное число и наименьшее совершенное число. ^{[ 1 ]}

По математике

Шесть — наименьшее положительное целое число, которое не является ни квадратным , ни простым числом . Это второе наименьшее составное число после четырёх , равное сумме и произведению трёх собственных делителей ( 1 , 2 и 3 ). ^{[ 1 ]} Таким образом, шесть — единственное число, которое является одновременно суммой и произведением трёх последовательных положительных чисел. 6 — наименьшее совершенное число , то есть числа, равные их аликвотной сумме или сумме своих собственных делителей. ^{[ 1 ]}^{[ 2 ]} Это самое большое из четырех чисел Харшада (1, 2, 4 и 6), ^{[ 3 ]} где он представляет собой сумму первого простого числа и составного числа 2 и 4.

6 — проническое число и единственное полупростое число. ^{[ 4 ]} Это первое дискретное двупростое число (2 × 3) ^{[ 5 ]} что делает его первым членом дискретного бипростого семейства (2 × q ), где q — высшее простое число. Все простые числа выше 3 имеют вид 6 n ± 1 для n ≥ 1.

Как идеальное число:

6 связано с простым числом Мерсенна 3, поскольку 2 ¹(2 ² – 1) = 6 . (Следующее совершенное число — 28. )
6 — единственное четное совершенное число , не являющееся суммой последовательных нечетных кубов. ^{[ 6 ]}
6 является корнем дерева 6-аликвот и само является аликвотной суммой только одного другого числа; квадрат номер 25 .

Шесть — первое унитарное совершенное число , поскольку оно представляет собой сумму своих положительных собственных унитарных делителей , не включая само себя. Известно, что существует только пять таких чисел; шестьдесят (10 × 6) и девяносто (15 × 6) — следующие два. ^{[ 7 ]}

Это первое примитивное псевдосовершенное число . ^{[ 8 ]} и все целые числа $n$ числа, кратные 6, являются псевдосовершенными (все кратные совершенному числу псевдосовершенные); шесть также является наименьшим числом Гранвилля , или ${\mathcal {S}}$ - идеальное число. ^{[ 9 ]}

Независимо от того, что 6 является идеальным числом, линейка Голомба длиной 6 является «совершенной линейкой». ^{[ 10 ]} Шесть – соответствующее число . ^{[ 11 ]}

6 — второе первичное псевдосовершенное число , ^{[ 12 ]} и номер гармонического делителя . ^{[ 13 ]} Это также второе по важности составное число . ^{[ 14 ]} и последний, который также является первобытным .

Существует 6 неэквивалентных способов, которыми 100 можно выразить в виде суммы двух простых чисел: (3+97), (11+89), (17+83), (29+71), (41+59). и (47+53). ^{[ 15 ]}

Нет никакого простого числа $p$ такой, что мультипликативный порядок 2 по модулю $p$ равно 6, то есть $ord_{p}(2)=6$ По теореме Жигмонди , если $n$ - натуральное число, отличное от 1 или 6, то существует простое число $p$ такой, что $ord_{p}(2)=n$ . См . A112927 для получения такой информации . $p$ .

Кольцо целых шестого кругового поля $Q (ζ6),$ называемое целым числом Эйзенштейна , имеет 6 единиц: ±1, ±ω, ±ω. ², где $\omega ={\frac {1}{2}}(-1+i{\sqrt {3}})=e^{2\pi i/3}$ .

Теорема о шести экспонентах гарантирует (при правильных условиях для экспонент) трансцендентность хотя бы одной экспоненты из набора экспонент. ^{[ 16 ]}

Существует шесть основных тригонометрических функций : sin, cos , sec, csc, tan и cot. ^{[ 17 ]}

Наименьшая неабелева группа — это симметрическая группа. $\mathrm {S_{3}}$ у которого 3! = 6 элементов. ^{[ 1 ]}

Шесть – треугольное число ^{[ 18 ]} и его квадрат ( 36 ). Это первое октаэдрическое число , предшествующее 19 . ^{[ 19 ]}

Шестигранный многоугольник – это шестиугольник , ^{[ 1 ]} один из трех правильных многоугольников, способных замостить плоскость . Фигурные числа, изображающие шестиугольники (в том числе и шестиугольники), называются шестиугольными числами . Поскольку 6 является произведением степени двойки (а именно 2 ¹) не имея ничего, кроме различных простых чисел Ферма (в частности, 3), правильный шестиугольник представляет собой многоугольник, который можно построить только с помощью циркуля и линейки . Гексаграмма — это шестиконечная геометрическая фигура звезды (с символом Шлефли {6/2}, 2{3} или {{3}}).

Шесть одинаковых монет можно расположить вокруг центральной монеты того же радиуса так, чтобы каждая монета соприкасалась с центральной (и касалась обоих своих соседей без зазора), но семь расположить таким образом нельзя. Это делает число 6 ответом на двумерную задачу о числе поцелуев . ^{[ 20 ]} Самая плотная упаковка сфер на плоскости получается путем расширения этого шаблона до шестиугольной решетки , в которой каждый круг касается только шести других.

Существует только один нетривиальный магический шестиугольник : он имеет порядок 3 и состоит из девятнадцати ячеек с магической константой 38. Все строки и столбцы в магическом квадрате 6 × 6 в совокупности генерируют магическую сумму 666 ( что составляет двоякотреугольный ). С другой стороны, греко-латинских квадратов шестого порядка не существует; если $n$ - натуральное число , отличное от 2 или 6, то существует греко-латинский квадрат порядка $n$ . ^{[ 21 ]}

Куб , является одним из пяти Платоновых тел которого шесть квадратов являются гранями . Это единственный правильный многогранник, который может порождать однородные соты сам по себе , которые также являются самодвойственными . Кубооктаэдр квазиправильных , который представляет собой архимедово тело, являющееся одним из двух многогранников , имеет в качестве граней восемь треугольников и шесть квадратов. Внутри расположение его вершин можно интерпретировать как три шестиугольника, которые пересекаются, образуя экваториальную шестиугольную полугрань , посредством которой кубооктаэдр расчленяется на треугольные купола . Это тело также является единственным многогранником с радиальной равносторонней симметрией , где его ребра и длинные радиусы имеют одинаковую длину; это один из четырех многогранников с этим свойством — остальные — шестиугольник, тессеракт (как четырехмерный аналог куба) и 24-клеточный . Только шесть многоугольников являются гранями непризматических однородных многогранников , таких как Платоновы тела или Архимедовы тела: треугольник , квадрат , пятиугольник , шестиугольник, восьмиугольник и десятиугольник . Если самодвойственные изображения тетраэдра считаются отдельными, тогда всего существует шесть правильных многогранников, которые образованы тремя различными группами Вейля в третьем измерении (на основе тетраэдрической , октаэдрической и икосаэдрической симметрии).

Насколько форма объекта похожа на идеальную сферу , называется его сферичностью и рассчитывается по формуле: ^{[ 22 ]}

$\Psi ={\frac {\pi ^{\frac {1}{3}}\left(6V_{p}\right)^{\frac {2}{3}}}{A_{p}}}={\frac {A_{s}}{A_{p}}},$ где $A_{s}$ - площадь поверхности сферы, $V_{p}$ объем объекта и $A_{p}$ площадь поверхности объекта.

В четырех измерениях всего существует шесть выпуклых правильных многогранников : 5-ячеечный , 8-ячеечный , 16-ячеечный , 24-ячеечный , 120-ячеечный и 600-ячеечный .

$\mathrm {S_{6}}$ , при этом 720 = 6 ! элементы — единственная конечная симметрическая группа, имеющая внешний автоморфизм . Этот автоморфизм позволяет нам построить ряд исключительных математических объектов , таких как система Штейнера S(5,6,12) , проективная плоскость порядка 4, четырехмерная 5-ячейка и граф Хоффмана-Синглтона . Близким результатом является следующая теорема: 6 — единственное натуральное число. $n$ для чего ведется строительство $n$ изоморфные объекты на $n$ - набор $A$ , инвариантный относительно всех перестановок $A$ , но не естественно во взаимно однозначном соответствии с элементами $A$ . Это также можно выразить категорией теоретически : рассмотрим категорию , объектами которой являются $n$ наборы элементов и чьи стрелки являются биекциями между наборами. Эта категория имеет нетривиальный функтор для самой себя только для $n=6$ .

В классификации конечных простых групп двадцать из двадцати шести спорадических групп входят счастливого семейства в три семейства групп, которые делят порядок дружественного гиганта , самую большую спорадическую группу: пять первого поколения групп Матье , семь второго поколения. подфакторов решетки Лича и восемь третьего поколения подгрупп дружественного гиганта. Остальные шесть групп не делят отряд дружественных гигантов, которых ( Ly , O'N , Ru , J4 , _J1 J3 и _{париями} называют ) _{спорадических} . ^{[ 23 ]}

Перечень основных расчетов

Умножение	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	25	50	100	1000
6 × х	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120	150	300	600	6000

Разделение	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15
6 ÷ х	6	3	2	1.5	1.2	1	0. 857142	0.75	0. 6	0.6		0. 54	0.5	0. 461538	0. 428571	0.4
х ÷ 6	0.1 6	0. 3	0.5	0. 6	0.8 3	1	1.1 6	1. 3	1.5	1. 6		1.8 3	2	2.1 6	2. 3	2.5

Возведение в степень	1	2	3	4	5	6	7	8	9	10		11	12	13
6 ^х	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176		362797056	2176782336	13060694016
х ⁶	1	64	729	4096	15625	46656	117649	262144	531441	1000000		1771561	2985984	4826809

Части греческого и латинского слова

Гекса

Гекса – это классическое греческое слово «шесть». ^{[ 1 ]} Таким образом:

« Шестнадцатеричный » объединяет шестнадцатеричную и латинскую десятичную дробь для обозначения числа по основанию 16. ^{[ 24 ]}
Шестиугольник – с правильный многоугольник шестью сторонами ^{[ 25 ]}
- L'Hexagone — французское прозвище континентальной части метрополии Франции из-за ее сходства с правильным шестиугольником.
Шестигранник – это многогранник с шестью гранями, куб – частный случай. ^{[ 26 ]}
Гексаметр — поэтическая форма, состоящая из шести футов в строке.
«Шестигранная гайка» — это гайка с шестью сторонами, а болт с шестигранной головкой имеет шестигранную головку.
Приставка « гекса- » также встречается в систематических названиях многих химических соединений , таких как гексан , который имеет 6 атомов углерода ( С ₆ Н ₁₄ ).

Приставка секс-

Секс — латинская приставка, означающая «шесть». ^{[ 1 ]} Таким образом:

Сенарий — порядковое прилагательное, означающее «шестой». ^{[ 27 ]}
У людей с сексдактилией по шесть пальцев на каждой руке.
Измерительный прибор секстант получил свое название потому, что его форма составляет одну шестую часть целого круга.
Группа из шести музыкантов называется секстетом.
Шесть детей, рожденных за один раз, являются шестернями.
Сексуальные простые пары. Пары простых чисел, отличающиеся на шесть, являются сексуальными , потому что секс — это латинское слово, обозначающее шесть. ^{[ 28 ]}^{[ 29 ]}

Префикс SI для 1000 ⁶ является exa- (E), а для его взаимного отношения- (a).

Эволюция индуистско-арабской цифры

Эволюция нашей современной цифры 6 кажется довольно простой по сравнению с другими цифрами. Современное число 6 можно проследить до цифр Брахми в Индии , которые впервые известны из Указов Ашоки ок. 250 г. до н.э. ^{[ 30 ]}^{[ 31 ]}^{[ 32 ]}^{[ 33 ]} Оно было написано одним росчерком, как строчная буква «е», повернутая на 90 градусов по часовой стрелке. Постепенно верхняя часть штриха (над центральной закорючкой) стала более изогнутой, а нижняя часть штриха (ниже центральной закорючки) стала более прямой. Арабы опустили часть штриха ниже закорючки. С этого момента европейская эволюция до нашей современной цифры 6 была очень простой, если не считать заигрывания с глифом, который больше походил на заглавную букву G. ^{[ 34 ]}

На семисегментных дисплеях калькуляторов и часов цифра 6 обычно пишется шестью сегментами. В некоторых исторических моделях калькуляторов вместо цифры 6 используется всего пять сегментов, без верхней горизонтальной полосы. Этот вариант глифа не прижился; для калькуляторов, которые могут отображать результаты в шестнадцатеричном формате, цифра 6, похожая на «b», нецелесообразна.

Как и в большинстве современных шрифтов , в шрифтах с текстовыми цифрами символ цифры 6 обычно имеет восходящий элемент , как, например, в . ^{[ 35 ]}

Эта цифра напоминает перевернутую 9 . Чтобы устранить двусмысленность на объектах и документах, которые можно перевернуть, цифру 6 часто подчеркивали как в рукописном виде, так и на печатных этикетках.

В музыке

В художниках

Les Six («Шестёрка» на английском языке) — группа, состоящая из французских композиторов Жоржа Орика , Луи Дюрей , Артюра Онеггера , Дариуса Мийо , Франсиса Пуленка и Жермен Тайлефер в 1920-х годах. ^{[ 36 ]}
Группы с цифрой шесть в названии включают Six Organs of Admittance , ^{[ 37 ]} 6 O'Clock Saints, Electric Six , ^{[ 38 ]} Eve 6 , Los Xey ( sei по-баскски означает «шесть»), Out On Blue Six, Six In Six, Sixpence None the Richer , ^{[ 39 ]} Наклонная 6 , ^{[ 40 ]} Тщеславие 6, и ты меня в шесть ^{[ 41 ]}
#6 — псевдоним американского музыканта Шона Крэхана , во время выступления с группой Slipknot.

В инструментах

Стандартная гитара имеет шесть струн. ^{[ 42 ]}
Большинство деревянных духовых инструментов имеют шесть основных отверстий или клавиш (например, фагот, кларнет, свисток, саксофон); этим отверстиям или клавишам обычно не присвоены цифры или буквы в аппликатурных таблицах.

В теории музыки

В октаве шесть целых тонов. ^{[ 43 ]}
В тритоне шесть полутонов. ^{[ 44 ]}

В работе

«Шесть несущихся гусей» были подарком на шестой день популярной рождественской песни « Двенадцать дней Рождества ». ^{[ 45 ]}
Разделенная на шесть арий, Hexachordum Apollinis обычно считается одной из вершин Иоганна Пахельбеля . творчества ^{[ 46 ]}
Темой шестого альбома Dream Theater, Six Degrees of Inner Turbulence , стала цифра шесть: в альбоме шесть песен, а шестая песня — то есть полный второй диск — исследует истории шести людей, страдающих различными психическими расстройствами. болезни. ^{[ 47 ]}
Аристотель выделил шесть элементов трагедии, первый из которых — «Миф» . ^{[ 48 ]}

В религии

иудаизм

Шесть точек на Звезде Давида ^{[ 49 ]}
Шесть порядков Мишны ^{[ 50 ]}
Шесть символических блюд, помещенных на тарелку пасхального седера ^{[ 51 ]}
Богу потребовалось шесть дней, чтобы сотворить мир В ветхозаветной книге Бытия ; ^{[ 52 ]} человечество было создано на шестой день. В Божием Городе Августин Гиппопотам предположил (книга 11, глава 30), что сотворение мира Богом заняло шесть дней, потому что 6 — совершенное число . ^{[ 53 ]}
Еврейский . праздник Шавуот начинается в шестой день еврейского месяца Сиван ^{[ 54 ]}
У серафимов шесть крыльев. ^{[ 55 ]}

ислам

Есть шесть догматов веры ^{[ 56 ]}
Шесть точек на Печати Соломона
Пост в течение шести дней Шавваля вместе с месяцем Рамадан приравнивается к посту в течение всего года. ^{[ 57 ]}
Согласно Корану, небеса и земля были созданы за шесть дней : ^{[ 58 ]}

Воистину, Мы сотворили небеса, землю и всё, что между ними, за шесть дней. ¹ и Нас «даже» не коснулась усталость. ²
— Сура Каф :38

Примечание 1: Слово день не всегда используется в Коране для обозначения 24-часового периода. Согласно суре « Аль-Хадж» («Паломничество»)47, небесный День — это 1000 лет нашего времени. будет Судный день через 50 000 лет нашего времени - Сура Аль-Мааридж (Восходящая лестница):4. Следовательно, шесть Дней творения относятся к шести эонам времени, известным только Аллаху.

Примечание 2: Некоторые исламские ученые полагают, что этот стих является ответом на Исход 31:17, в котором говорится: «Господь сотворил небо и землю за шесть дней, а на седьмой день Он почил и освежился».

Другие

В индуистской теологии трасарену — это комбинация шести небесных параману ( атомов ).
В даосизме:
- Шесть линий гексаграммы
- Шесть министерств Хуан Ди ^{[ 59 ]}

В науке

Астрономия

Объект Мессье M6 магнитудой 4,5 , рассеянное скопление в созвездии Скорпиона , также известное как Скопление Бабочек. ^{[ 60 ]}
Объект Нового общего каталога . NGC 6 , спиральная галактика в созвездии Андромеды
Римская цифра VI:
- Обозначает субкарликов в схеме спектральной классификации Йеркса.
- (Обычно) обозначает шестой открытый спутник планеты или малой планеты (например, Юпитер VI ).
6 Есть

Биология

Ячейки улья шестигранные . ^{[ 61 ]}
У насекомых шесть ног (см. Шестиногие ). ^{[ 62 ]}
Шесть королевств в таксономическом ранге ниже области (биология) ; Animalia , Plantae , Fungi , Protista , Archaea / Archeabacteria и Bacteria / Eubacteria . См. Королевство (биология) . ^{[ 63 ]}
Шесть элементов, наиболее распространенных в биомолекулах, называются элементами CHNOPS; буквы обозначают химические сокращения углерода , водорода , азота , кислорода , фосфора и серы . См . ЧОН . ^{[ 64 ]}

Химия

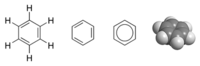
Молекула бензола имеет кольцо из шести атомов углерода. ^{[ 65 ]}
6 — атомный номер углерода. ^{[ 66 ]}
Шестикратная симметрия снежинок гексагональной возникает из-за кристаллической структуры обычного льда . ^{[ 67 ]}
Гексамер . – это олигомер, состоящий из шести субъединиц

Лекарство

) существует шесть вкусов В традиционной индийской медицине ( Аюрведе : сладкий, кислый, соленый, горький, острый и вяжущий. Эти вкусы используются, чтобы предложить диету, основанную на симптомах организма. ^{[ 68 ]}
Фаза 6 является одной из шести фаз пандемического гриппа . ^{[ 69 ]}

Физика

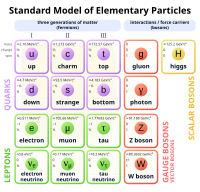
В Стандартной модели физики элементарных частиц существует шесть типов кварков и шесть типов лептонов . ^{[ 70 ]}
В статистической механике шестивершинная модель имеет шесть возможных конфигураций стрелок в каждой вершине. ^{[ 71 ]}
Цветовой круг RGB состоит из шести цветов: (первичный) красный, синий, зеленый, (вторичный) голубой, пурпурный и желтый. (См. Третичный цвет ) ^{[ 72 ]}
В трехмерном евклидовом пространстве существует шесть неизвестных опорных реакций для статически определенной структуры: по одной силе в каждом из трех измерений и по одному моменту в каждой из трех возможных ортогональных плоскостей .

В технологии

6 as a resin identification code, used in recycling.

На большинстве телефонов клавиша 6 связана с буквами M , N и O , но на BlackBerry Pearl это клавиша для J и K , а на сериях BlackBerry 8700 и Curve 8900 с полной клавиатурой это клавиша. для Ф
В « 6-метровый диапазон » любительского радио входят частоты от 50 до 54 МГц.
6 — идентификационный код смолы , используемый при переработке для идентификации полистирола. ^{[ 73 ]}

В календарях

В древнеримском Секстилис календаре был шестым месяцем. После реформы юлианской июнь стал шестым месяцем, а секстилис был переименован в август. ^{[ 74 ]}
Секстиди был шестым днем десятилетия в календаре Французской революции. ^{[ 75 ]}

Антропология

Название самой маленькой группы скаутов-детенышей и эквивалента домовых-проводников , традиционно состоящей из шести человек и возглавляемой «шестеркой».
Гроб традиционно закапывают на шесть футов под землю; таким образом, фраза «шесть футов под землей» означает, что человек (или вещь, или концепция) мертв. ^{[ 76 ]}
Говорят, что между любыми двумя людьми на Земле существует не более шести степеней разделения . ^{[ 77 ]}
В западной астрологии Дева — шестой астрологический знак Зодиака. ^{[ 78 ]}
Шесть династий являются частью китайской истории. ^{[ 79 ]}
Шесть – счастливое число в китайской культуре . ^{[ нужна ссылка ]}
« Бирмингемская шестерка» была британской судебной ошибкой и провела в тюрьме 16 лет. ^{[ 80 ]}
«Шесть» используется как неофициальный жаргонный термин для обозначения британской секретной разведывательной службы МИ-6. ^{[ 81 ]}

См. также

Ссылки

^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г Вайсштейн, Эрик В. «6» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Хиггинс, Питер (2008). История чисел: от счета к криптографии . Нью-Йорк: Коперник. п. 11 . ISBN 978-1-84800-000-1 .
^ Вайсштейн, Эрик В. «Число Харшада» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ «А002378 Слоана: числа Проника» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 30 ноября 2020 г.
^ Слоан, Нью-Джерси (ред.). «Последовательность A001358 (Полупростые (или бипростые числа): произведения двух простых чисел.)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 03 августа 2023 г.
^ Дэвид Уэллс, Словарь любопытных и интересных чисел Penguin . Лондон: Penguin Books (1987): 67.
^ Слоан, Нью-Джерси (ред.). «Последовательность A002827 (Унитарные совершенные числа)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.
^ Слоан, Нью-Джерси (ред.). «Последовательность A005835 (Псевдосовершенные (или полусовершенные) числа n: некоторое подмножество правильных делителей n в сумме дает n.)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 2 декабря 2023 г.
^ «Число Гранвиля» . OeisWiki . Интернет-энциклопедия целочисленных последовательностей. Архивировано из оригинала 29 марта 2011 года . Проверено 27 марта 2011 г.
^ Брайан Банч, Королевство бесконечных чисел . Нью-Йорк: WH Freeman & Company (2000): 72.
^ Слоан, Нью-Джерси (ред.). «Последовательность A003273 (Согласованные номера)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.
^ Слоан, Нью-Джерси (ред.). «Последовательность A054377 (Первичные псевдосовершенные числа)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 2 ноября 2018 г.
^ Слоан, Нью-Джерси (ред.). «Последовательность A001599 (Гармонические числа или числа Руды)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.
^ Вайсштейн, Эрик В. «Превосходное весьма составное число» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Слоан, Нью-Джерси (ред.). «Последовательность A065577 (количество разделов Гольдбаха 10^n)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 31 августа 2023 г.
^ Вайсштейн, Эрик В. «Теорема о шести экспонентах» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Вайсштейн, Эрик В. «Тригонометрические функции» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Вайсштейн, Эрик В. «Треугольное число» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Слоан, Нью-Джерси (ред.). «Последовательность A005900 (Октаэдрические числа)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.
^ Вайсштейн, Эрик В. «Номер поцелуев» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Вайсштейн, Эрик В. «Гипотеза Эйлера о греко-римских квадратах» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Уоделл, Хакон (1935). «Объем, форма и округлость частиц кварца» . Журнал геологии . 43 (3): 250–280. Бибкод : 1935JG.....43..250W . дои : 10.1086/624298 . JSTOR 30056250 . S2CID 129624905 .
^ Грисс-младший, Роберт Л. (1982). «Дружелюбный великан» (PDF ) изобретения Математические 69 : 91–96. Бибкод : 1982InMat..69.... 1G дои : 10.1007/BF01389186 . hdl : 2027.42/46608 . МР 0671653 . S2CID 123597150 . Збл 0498.20013 .
^ Вайсштейн, Эрик В. «Шестнадцатеричный» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Вайсштейн, Эрик В. «Шестиугольник» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Вайсштейн, Эрик В. «Шестигранник» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Вайсштейн, Эрик В. «База» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Крис К. Колдуэлл; Г. Л. Хонакер младший (2009). Prime Curios!: Словарь простых чисел . Независимая издательская платформа CreateSpace. п. 11. ISBN 978-1-4486-5170-2 .
^ Вайсштейн, Эрик В. «Сексуальные простые числа» . mathworld.wolfram.com . Проверено 3 августа 2020 г.
^ Холлингдейл, Стюарт (2014). Создатели математики . Курьерская корпорация. стр. 95–96. ISBN 978-0-486-17450-1 .
^ Издательство Britannica Educational (2009). Британский путеводитель по теориям и идеям, изменившим современный мир . Образовательное издательство Британника. п. 64. ИСБН 978-1-61530-063-1 .
^ Кац, Виктор Дж.; Паршалл, Карен Хангер (2014). Укрощение неизвестного: история алгебры от античности до начала двадцатого века . Издательство Принстонского университета. п. 105. ИСБН 978-1-4008-5052-5 .
^ Пиллис, Джон де (2002). 777 Начало математического разговора . МАА. стр. 286. ИСБН 978-0-88385-540-9 .
^ Жорж Ифра, Всеобщая история чисел: от предыстории до изобретения компьютера пер. Дэвид Беллос и др. Лондон: The Harvill Press (1998): 395, рис. 24.66.
^ Негр, Джон (1988). Компьютерная верстка . Ван Ностранд Рейнхольд. п. 59. ИСБН 978-0-442-26696-7 . небольшие зажимы, возвышающиеся над высотой колпачка (в 4 и 6)
^ Аурик, Жорж; Дьюри, Луи; Онеггер, Артур; Мийо, Дариус; Пуленк, Франсис; Тайлефер, Жермен (20 августа 2014 г.). Карамельный Му и другие великие фортепианные произведения из "Les Six": пьесы Орика, Дюри, Онеггера, Мийо, Пуленка и Тайлефера (на французском языке). Курьерская корпорация. ISBN 978-0-486-49340-4 .
^ «Шесть органов приема» . www.sixorgans.com . Проверено 3 августа 2020 г.
^ «Electric Six | Биография, альбомы, ссылки на потоки» . Вся музыка . Проверено 3 августа 2020 г.
^ «Нет шестипенсовика, богаче» . ГРЭММИ.com . 19 мая 2020 г. Проверено 4 августа 2020 г.
^ «Наклон 6 | Биография и история» . Вся музыка . Проверено 4 августа 2020 г.
^ «Ты мне в шесть лет | Биография и история» . Вся музыка . Проверено 4 августа 2020 г.
^ «Определение ГИТАРЫ» . www.merriam-webster.com . Проверено 4 августа 2020 г.
^ Д'Аманте, Эльво (1 января 1994 г.). Основы музыки: структура звука и ритмический дизайн . Пугало Пресс. п. 194. ИСБН 978-1-4616-6985-2 . Деление октавы на шесть равных частей называется полнотоновой шкалой.
^ Хорсли, Чарльз Эдвард (1876). Учебник гармонии: для школ и студентов . Сэмпсон Лоу, Марстон, Сирл и Ривингтон. п. 4. Как и тритон, он содержит шесть полутонов.
^ Триббл, Мими (2004). 300 способов сделать Рождество самым лучшим!: украшения, гимны, поделки и рецепты для всех видов рождественских традиций . Стерлинг Паблишинг Компани, Инк. 145. ИСБН 978-1-4027-1685-0 . Шесть гусей лежат
^ Стейнс, Джо (17 мая 2010 г.). Грубое руководство по классической музыке . Пингвин. п. 393. ИСБН 978-1-4053-8321-9 . ...шесть арий с вариациями, собранные под названием Hexachordum Apollinis (1699)...
^ Хегарти, Пол; Холливелл, Мартин (23 июня 2011 г.). За гранью и до: прогрессивный рок с 1960-х годов . Издательство Блумсбери США. п. 169. ИСБН 978-1-4411-1480-8 . Шесть степеней внутренней турбулентности
^ Карран, Анджела (5 октября 2015 г.). Путеводитель по философии Рутледжа по Аристотелю и поэтике . Рутледж. п. 133. ИСБН 978-1-317-67706-2 . ШЕСТЬ КАЧЕСТВЕННЫХ ЭЛЕМЕНТОВ ТРАГЕДИИ
^ Плаут, В. Гюнтер (1991). Маген Давид: как шестиконечная звезда стала эмблемой еврейского народа . Книги Бнай Брит. ISBN 978-0-910250-16-0 . Как шестиконечная звезда стала эмблемой еврейского народа
^ Лаутербах, Якоб Залель (1916). Мидраш и Мишна: исследование ранней истории Галахи . Блох. п. 9. Шесть порядков Мишны
^ Розен, Сейл; Розен, Мойше (1 мая 2006 г.). Христос на Пасхе . Издательство Муди. п. 79. ИСБН 978-1-57567-480-3 . Шесть символических продуктов
^ Репчек, Джек (15 декабря 2008 г.). Человек, который нашел время: Джеймс Хаттон и открытие древности Земли . Основные книги. ISBN 978-0-7867-4399-5 . на самом деле создание Земли заняло всего шесть дней
^ «ОТЦЫ ЦЕРКВИ: Град Божий, Книга XI (Св. Августин)» . www.newadvent.org . Проверено 4 августа 2020 г. Записано, что эти работы были завершены за шесть дней (один и тот же день повторяется шесть раз), потому что шесть — совершенное число.
^ Гроссман, Грейс Коэн; Альборн, Ричард Э.; Институт, Смитсоновский институт (1997). Иудаика в Смитсоновском институте: культурная политика как культурная модель . Издательство Смитсоновского института. п. 228. Шавуот приходится на шестой день еврейского месяца Сиван.
^ Робертсон, Уильям Арчибальд Скотт (1880). Склеп Кентерберийского собора; его архитектура, его история и его фрески . Митчелл и Хьюз. п. 91. ...но серафимы с шестью крыльями
^ Шапера, Пол М. (15 августа 2009 г.). Религиозные лидеры Ирана . The Rosen Publishing Group, Inc. с. 10. ISBN 978-1-4358-5283-9 . В исламе шесть догматов веры.
^ Алгюль, Хусейн (2005). Благословенные дни и ночи исламского года . Книги Тугры. п. 65. ИСБН 978-1-932099-93-5 . ...было благословенно поститься шесть дней в месяце Шавваль...
^ «Сура Каф-38» . Коран.com . Проверено 28 августа 2023 г.
^ Бэри, Уильям Теодор Де; ДеБэри, Уильям Т.; Чан, Винг-цит; Луфрано, Ричард; Чинг, Джулия; Джонсон, Дэвид; Лю, Гуан-Чинг; Мунгелло, Дэвид (1999). Источники китайской традиции . Издательство Колумбийского университета. ISBN 978-0-231-11270-3 . ...и были созданы Шесть Министерств...
^ Роудс, Сэмюэл Э. (1996). Небо сегодня вечером: экскурсия по звездам над Гавайями . Издательство Музея епископа. ISBN 978-0-930897-93-2 . В этой части неба видны три объекта Мессье: М6, М7 и М8.
^ Седжвик, Маркус (5 июля 2011 г.). Белая Ворона . Ревущий Брук Пресс. п. 145. ИСБН 978-1-4299-7634-3 . Ячейки сот шестигранные, поскольку шестиугольник является наиболее экономичной мозаикой.
^ Паркер, Стив (2005). Муравьиные львы, осы и другие насекомые . Замковый камень. п. 16. ISBN 978-0-7565-1250-7 . У насекомых по шесть ног...
^ Пендарвис, Мюррей П.; Кроули, Джон Л. (01 февраля 2019 г.). Изучение биологии в лаборатории: основные концепции . Издательство Мортон. п. 10. ISBN 978-1-61731-899-3 . ... в настоящее время признано как минимум шесть королевств;
^ Мадер, Сильвия С. (2004). Биология . МакГроу-Хилл. п. 20. ISBN 978-0-07-291934-9 . Аббревиатура CHNOPS помогает нам запомнить эти шесть элементов.
^ Дюфур, Фриц (19 сентября 2018 г.). Реалии реальности. Часть II: понимание того, почему современная наука развивается . Том. 1. Фриц Дюфур. п. 100. Молекула бензола состоит из шести атомов углерода в кольце. ^{[ самостоятельно опубликованный источник? ]}
^ Старр, Сеси; Эверс, Кристина (10 мая 2012 г.). Биология сегодня и завтра без физиологии . Cengage Обучение. п. 25. ISBN 978-1-133-36536-5 . Например, атомный номер углерода равен 6,
^ Уэбб, Стивен; Уэбб, профессор австралийских исследований Стивен (25 мая 2004 г.). Из этого мира: сталкивающиеся вселенные, браны, струны и другие дикие идеи современной физики . Springer Science & Business Media. п. 16. ISBN 978-0-387-02930-6 . снежинка с ее знакомой шестикратной вращательной симметрией
^ Ву, Тери Мозер; Робинсон, Мэрилу В. (3 августа 2015 г.). Фармакотерапия для медсестер продвинутой практики . Ф.А. Дэвис. п. 145. ИСБН 978-0-8036-4581-3 . Аюрведическая гербология основана на тридошической теории, согласно которой существует шесть основных вкусов.
^ Руководство по обеспечению готовности к пандемическому гриппу и реагированию на него для работников здравоохранения и работодателей здравоохранения . OSHA, Министерство труда США. 2007. с. 8. План ВОЗ описывает шесть этапов увеличения риска для общественного здравоохранения, связанного с появлением нового гриппа.
^ Сангера, Пол (8 марта 2011 г.). Квантовая физика для ученых и технологов: фундаментальные принципы и приложения для биологов, химиков, компьютерщиков и нанотехнологов . Джон Уайли и сыновья. п. 64. ИСБН 978-0-470-92269-9 . ...есть шесть типов кварков и шесть типов лептонов.
^ Джимбо, М.; Джимбо, Мичио; Мива, Тецудзи; Цучия, Акихиро (1989). Интегрируемые системы в квантовой теории поля и статистической механике . Академическая пресса. п. 588. ИСБН 978-0-12-385342-4 . Разрешенные конфигурации в шестивершинной модели и их статистические веса
^ Слоан, Робин Джеймс Стюарт (7 мая 2015 г.). Дизайн виртуальных персонажей для игр и интерактивных медиа . ЦРК Пресс. п. 34. ISBN 978-1-4665-9820-1 . размещение шести основных цветов вокруг колеса в следующем порядке: красный, желтый, зеленый, голубой, синий, пурпурный.
^ Стивенс, ES (2002). Зеленые пластмассы: введение в новую науку о биоразлагаемых пластмассах . Издательство Принстонского университета. п. 45. ИСБН 978-0-691-04967-0 .
^ Бансон, Мэтью (14 мая 2014 г.). Энциклопедия Римской империи Издательство информационной базы. п. 90. ИСБН 978-1-4381-1027-1 . Первоначально Августа также называли Секстилис, шестой месяц.
^ Николас, сэр Николас Харрис (1833). Хронология истории: содержащие таблицы, расчеты и утверждения, необходимые для установления дат исторических событий, а также государственных и частных документов от древнейшего периода до настоящего времени . Лонгхэм, Рис, Орм, Браун, Грин, Лонгман и Джон Тейлор. п. 172. СЕКСТИДИ, или «Jour de la Revolution»,
^ Раймс, Венди (01 апреля 2016 г.). «Причина, по которой мертвых хоронят на шесть футов ниже земли» . Элитные читатели . Проверено 6 августа 2020 г.
^ «Шесть градусов Пегги Бэкон» . www.aaa.si.edu . 27 июня 2012 года . Проверено 6 августа 2020 г.
^ «Дева | созвездие и астрологический знак» . Британская энциклопедия . Проверено 6 августа 2020 г.
^ Уилкинсон, Эндимион Портер; Уилкинсон, ученый и дипломат (посол ЕС в Китае 1994–2001 гг.) Эндимион (2000 г.). История Китая: Учебное пособие . Азиатский центр Гарвардского университета. п. 11. ISBN 978-0-674-00249-4 . {{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка )
^ Пирс, Гарет (12 марта 2011 г.). «Бирмингемская шестерка: извлекли ли мы уроки из нашего позорного прошлого?» . Хранитель . ISSN 0261-3077 . Проверено 6 августа 2020 г.
^ Смит, Майкл (31 октября 2011 г.). Шестая: Настоящие Джеймсы Бонды 1909-1939 годов . Издательство Bitback. ISBN 978-1-84954-264-7 .

Нечетное число 6 , Дж. А. Тодд, Матем. Учеб. Кэмб. Фил. Соц. 41 (1945) 66–68
Свойство числа шесть , Глава 6, П. Кэмерон, Дж. Х. против Линта, Проекты, графики, коды и их связи ISBN 0-521-42385-6
Уэллс, Д. Словарь любопытных и интересных чисел Penguin, Лондон: Penguin Group. (1987): 67–69

Внешние ссылки

[:0-1] Jump up to: ^а ^б ^с ^д ^и ^ж ^г Вайсштейн, Эрик В. «6» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[2] Хиггинс, Питер (2008). История чисел: от счета к криптографии . Нью-Йорк: Коперник. п. 11 . ISBN 978-1-84800-000-1 .

[3] Вайсштейн, Эрик В. «Число Харшада» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[4] «А002378 Слоана: числа Проника» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 30 ноября 2020 г.

[5] Слоан, Нью-Джерси (ред.). «Последовательность A001358 (Полупростые (или бипростые числа): произведения двух простых чисел.)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 03 августа 2023 г.

[6] Дэвид Уэллс, Словарь любопытных и интересных чисел Penguin . Лондон: Penguin Books (1987): 67.

[7] Слоан, Нью-Джерси (ред.). «Последовательность A002827 (Унитарные совершенные числа)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.

[8] Слоан, Нью-Джерси (ред.). «Последовательность A005835 (Псевдосовершенные (или полусовершенные) числа n: некоторое подмножество правильных делителей n в сумме дает n.)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 2 декабря 2023 г.

[OEIS-9] «Число Гранвиля» . OeisWiki . Интернет-энциклопедия целочисленных последовательностей. Архивировано из оригинала 29 марта 2011 года . Проверено 27 марта 2011 г.

[10] Брайан Банч, Королевство бесконечных чисел . Нью-Йорк: WH Freeman & Company (2000): 72.

[11] Слоан, Нью-Джерси (ред.). «Последовательность A003273 (Согласованные номера)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.

[12] Слоан, Нью-Джерси (ред.). «Последовательность A054377 (Первичные псевдосовершенные числа)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 2 ноября 2018 г.

[13] Слоан, Нью-Джерси (ред.). «Последовательность A001599 (Гармонические числа или числа Руды)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.

[14] Вайсштейн, Эрик В. «Превосходное весьма составное число» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[15] Слоан, Нью-Джерси (ред.). «Последовательность A065577 (количество разделов Гольдбаха 10^n)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 31 августа 2023 г.

[16] Вайсштейн, Эрик В. «Теорема о шести экспонентах» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[17] Вайсштейн, Эрик В. «Тригонометрические функции» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[18] Вайсштейн, Эрик В. «Треугольное число» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[19] Слоан, Нью-Джерси (ред.). «Последовательность A005900 (Октаэдрические числа)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 1 июня 2016 г.

[20] Вайсштейн, Эрик В. «Номер поцелуев» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[21] Вайсштейн, Эрик В. «Гипотеза Эйлера о греко-римских квадратах» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[22] Уоделл, Хакон (1935). «Объем, форма и округлость частиц кварца» . Журнал геологии . 43 (3): 250–280. Бибкод : 1935JG.....43..250W . дои : 10.1086/624298 . JSTOR 30056250 . S2CID 129624905 .

[23] Грисс-младший, Роберт Л. (1982). «Дружелюбный великан» (PDF ) изобретения Математические 69 : 91–96. Бибкод : 1982InMat..69.... 1G дои : 10.1007/BF01389186 . hdl : 2027.42/46608 . МР 0671653 . S2CID 123597150 . Збл 0498.20013 .

[24] Вайсштейн, Эрик В. «Шестнадцатеричный» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[25] Вайсштейн, Эрик В. «Шестиугольник» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[26] Вайсштейн, Эрик В. «Шестигранник» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[27] Вайсштейн, Эрик В. «База» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[28] Крис К. Колдуэлл; Г. Л. Хонакер младший (2009). Prime Curios!: Словарь простых чисел . Независимая издательская платформа CreateSpace. п. 11. ISBN 978-1-4486-5170-2 .

[29] Вайсштейн, Эрик В. «Сексуальные простые числа» . mathworld.wolfram.com . Проверено 3 августа 2020 г.

[30] Холлингдейл, Стюарт (2014). Создатели математики . Курьерская корпорация. стр. 95–96. ISBN 978-0-486-17450-1 .

[31] Издательство Britannica Educational (2009). Британский путеводитель по теориям и идеям, изменившим современный мир . Образовательное издательство Британника. п. 64. ИСБН 978-1-61530-063-1 .

[32] Кац, Виктор Дж.; Паршалл, Карен Хангер (2014). Укрощение неизвестного: история алгебры от античности до начала двадцатого века . Издательство Принстонского университета. п. 105. ИСБН 978-1-4008-5052-5 .

[33] Пиллис, Джон де (2002). 777 Начало математического разговора . МАА. стр. 286. ИСБН 978-0-88385-540-9 .

[34] Жорж Ифра, Всеобщая история чисел: от предыстории до изобретения компьютера пер. Дэвид Беллос и др. Лондон: The Harvill Press (1998): 395, рис. 24.66.

[35] Негр, Джон (1988). Компьютерная верстка . Ван Ностранд Рейнхольд. п. 59. ИСБН 978-0-442-26696-7 . небольшие зажимы, возвышающиеся над высотой колпачка (в 4 и 6)

[36] Аурик, Жорж; Дьюри, Луи; Онеггер, Артур; Мийо, Дариус; Пуленк, Франсис; Тайлефер, Жермен (20 августа 2014 г.). Карамельный Му и другие великие фортепианные произведения из "Les Six": пьесы Орика, Дюри, Онеггера, Мийо, Пуленка и Тайлефера (на французском языке). Курьерская корпорация. ISBN 978-0-486-49340-4 .

[37] «Шесть органов приема» . www.sixorgans.com . Проверено 3 августа 2020 г.

[38] «Electric Six | Биография, альбомы, ссылки на потоки» . Вся музыка . Проверено 3 августа 2020 г.

[39] «Нет шестипенсовика, богаче» . ГРЭММИ.com . 19 мая 2020 г. Проверено 4 августа 2020 г.

[40] «Наклон 6 | Биография и история» . Вся музыка . Проверено 4 августа 2020 г.

[41] «Ты мне в шесть лет | Биография и история» . Вся музыка . Проверено 4 августа 2020 г.

[42] «Определение ГИТАРЫ» . www.merriam-webster.com . Проверено 4 августа 2020 г.

[43] Д'Аманте, Эльво (1 января 1994 г.). Основы музыки: структура звука и ритмический дизайн . Пугало Пресс. п. 194. ИСБН 978-1-4616-6985-2 . Деление октавы на шесть равных частей называется полнотоновой шкалой.

[44] Хорсли, Чарльз Эдвард (1876). Учебник гармонии: для школ и студентов . Сэмпсон Лоу, Марстон, Сирл и Ривингтон. п. 4. Как и тритон, он содержит шесть полутонов.

[45] Триббл, Мими (2004). 300 способов сделать Рождество самым лучшим!: украшения, гимны, поделки и рецепты для всех видов рождественских традиций . Стерлинг Паблишинг Компани, Инк. 145. ИСБН 978-1-4027-1685-0 . Шесть гусей лежат

[46] Стейнс, Джо (17 мая 2010 г.). Грубое руководство по классической музыке . Пингвин. п. 393. ИСБН 978-1-4053-8321-9 . ...шесть арий с вариациями, собранные под названием Hexachordum Apollinis (1699)...

[47] Хегарти, Пол; Холливелл, Мартин (23 июня 2011 г.). За гранью и до: прогрессивный рок с 1960-х годов . Издательство Блумсбери США. п. 169. ИСБН 978-1-4411-1480-8 . Шесть степеней внутренней турбулентности

[48] Карран, Анджела (5 октября 2015 г.). Путеводитель по философии Рутледжа по Аристотелю и поэтике . Рутледж. п. 133. ИСБН 978-1-317-67706-2 . ШЕСТЬ КАЧЕСТВЕННЫХ ЭЛЕМЕНТОВ ТРАГЕДИИ

[49] Плаут, В. Гюнтер (1991). Маген Давид: как шестиконечная звезда стала эмблемой еврейского народа . Книги Бнай Брит. ISBN 978-0-910250-16-0 . Как шестиконечная звезда стала эмблемой еврейского народа

[50] Лаутербах, Якоб Залель (1916). Мидраш и Мишна: исследование ранней истории Галахи . Блох. п. 9. Шесть порядков Мишны

[51] Розен, Сейл; Розен, Мойше (1 мая 2006 г.). Христос на Пасхе . Издательство Муди. п. 79. ИСБН 978-1-57567-480-3 . Шесть символических продуктов

[52] Репчек, Джек (15 декабря 2008 г.). Человек, который нашел время: Джеймс Хаттон и открытие древности Земли . Основные книги. ISBN 978-0-7867-4399-5 . на самом деле создание Земли заняло всего шесть дней

[53] «ОТЦЫ ЦЕРКВИ: Град Божий, Книга XI (Св. Августин)» . www.newadvent.org . Проверено 4 августа 2020 г. Записано, что эти работы были завершены за шесть дней (один и тот же день повторяется шесть раз), потому что шесть — совершенное число.

[54] Гроссман, Грейс Коэн; Альборн, Ричард Э.; Институт, Смитсоновский институт (1997). Иудаика в Смитсоновском институте: культурная политика как культурная модель . Издательство Смитсоновского института. п. 228. Шавуот приходится на шестой день еврейского месяца Сиван.

[55] Робертсон, Уильям Арчибальд Скотт (1880). Склеп Кентерберийского собора; его архитектура, его история и его фрески . Митчелл и Хьюз. п. 91. ...но серафимы с шестью крыльями

[56] Шапера, Пол М. (15 августа 2009 г.). Религиозные лидеры Ирана . The Rosen Publishing Group, Inc. с. 10. ISBN 978-1-4358-5283-9 . В исламе шесть догматов веры.

[57] Алгюль, Хусейн (2005). Благословенные дни и ночи исламского года . Книги Тугры. п. 65. ИСБН 978-1-932099-93-5 . ...было благословенно поститься шесть дней в месяце Шавваль...

[58] «Сура Каф-38» . Коран.com . Проверено 28 августа 2023 г.

[59] Бэри, Уильям Теодор Де; ДеБэри, Уильям Т.; Чан, Винг-цит; Луфрано, Ричард; Чинг, Джулия; Джонсон, Дэвид; Лю, Гуан-Чинг; Мунгелло, Дэвид (1999). Источники китайской традиции . Издательство Колумбийского университета. ISBN 978-0-231-11270-3 . ...и были созданы Шесть Министерств...

[60] Роудс, Сэмюэл Э. (1996). Небо сегодня вечером: экскурсия по звездам над Гавайями . Издательство Музея епископа. ISBN 978-0-930897-93-2 . В этой части неба видны три объекта Мессье: М6, М7 и М8.

[61] Седжвик, Маркус (5 июля 2011 г.). Белая Ворона . Ревущий Брук Пресс. п. 145. ИСБН 978-1-4299-7634-3 . Ячейки сот шестигранные, поскольку шестиугольник является наиболее экономичной мозаикой.

[62] Паркер, Стив (2005). Муравьиные львы, осы и другие насекомые . Замковый камень. п. 16. ISBN 978-0-7565-1250-7 . У насекомых по шесть ног...

[63] Пендарвис, Мюррей П.; Кроули, Джон Л. (01 февраля 2019 г.). Изучение биологии в лаборатории: основные концепции . Издательство Мортон. п. 10. ISBN 978-1-61731-899-3 . ... в настоящее время признано как минимум шесть королевств;

[64] Мадер, Сильвия С. (2004). Биология . МакГроу-Хилл. п. 20. ISBN 978-0-07-291934-9 . Аббревиатура CHNOPS помогает нам запомнить эти шесть элементов.

[65] Дюфур, Фриц (19 сентября 2018 г.). Реалии реальности. Часть II: понимание того, почему современная наука развивается . Том. 1. Фриц Дюфур. п. 100. Молекула бензола состоит из шести атомов углерода в кольце. ^{[ самостоятельно опубликованный источник? ]}

[66] Старр, Сеси; Эверс, Кристина (10 мая 2012 г.). Биология сегодня и завтра без физиологии . Cengage Обучение. п. 25. ISBN 978-1-133-36536-5 . Например, атомный номер углерода равен 6,

[67] Уэбб, Стивен; Уэбб, профессор австралийских исследований Стивен (25 мая 2004 г.). Из этого мира: сталкивающиеся вселенные, браны, струны и другие дикие идеи современной физики . Springer Science & Business Media. п. 16. ISBN 978-0-387-02930-6 . снежинка с ее знакомой шестикратной вращательной симметрией

[68] Ву, Тери Мозер; Робинсон, Мэрилу В. (3 августа 2015 г.). Фармакотерапия для медсестер продвинутой практики . Ф.А. Дэвис. п. 145. ИСБН 978-0-8036-4581-3 . Аюрведическая гербология основана на тридошической теории, согласно которой существует шесть основных вкусов.

[69] Руководство по обеспечению готовности к пандемическому гриппу и реагированию на него для работников здравоохранения и работодателей здравоохранения . OSHA, Министерство труда США. 2007. с. 8. План ВОЗ описывает шесть этапов увеличения риска для общественного здравоохранения, связанного с появлением нового гриппа.

[70] Сангера, Пол (8 марта 2011 г.). Квантовая физика для ученых и технологов: фундаментальные принципы и приложения для биологов, химиков, компьютерщиков и нанотехнологов . Джон Уайли и сыновья. п. 64. ИСБН 978-0-470-92269-9 . ...есть шесть типов кварков и шесть типов лептонов.

[71] Джимбо, М.; Джимбо, Мичио; Мива, Тецудзи; Цучия, Акихиро (1989). Интегрируемые системы в квантовой теории поля и статистической механике . Академическая пресса. п. 588. ИСБН 978-0-12-385342-4 . Разрешенные конфигурации в шестивершинной модели и их статистические веса

[72] Слоан, Робин Джеймс Стюарт (7 мая 2015 г.). Дизайн виртуальных персонажей для игр и интерактивных медиа . ЦРК Пресс. п. 34. ISBN 978-1-4665-9820-1 . размещение шести основных цветов вокруг колеса в следующем порядке: красный, желтый, зеленый, голубой, синий, пурпурный.

[73] Стивенс, ES (2002). Зеленые пластмассы: введение в новую науку о биоразлагаемых пластмассах . Издательство Принстонского университета. п. 45. ИСБН 978-0-691-04967-0 .

[74] Бансон, Мэтью (14 мая 2014 г.). Энциклопедия Римской империи Издательство информационной базы. п. 90. ИСБН 978-1-4381-1027-1 . Первоначально Августа также называли Секстилис, шестой месяц.

[75] Николас, сэр Николас Харрис (1833). Хронология истории: содержащие таблицы, расчеты и утверждения, необходимые для установления дат исторических событий, а также государственных и частных документов от древнейшего периода до настоящего времени . Лонгхэм, Рис, Орм, Браун, Грин, Лонгман и Джон Тейлор. п. 172. СЕКСТИДИ, или «Jour de la Revolution»,

[76] Раймс, Венди (01 апреля 2016 г.). «Причина, по которой мертвых хоронят на шесть футов ниже земли» . Элитные читатели . Проверено 6 августа 2020 г.

[77] «Шесть градусов Пегги Бэкон» . www.aaa.si.edu . 27 июня 2012 года . Проверено 6 августа 2020 г.

[78] «Дева | созвездие и астрологический знак» . Британская энциклопедия . Проверено 6 августа 2020 г.

[79] Уилкинсон, Эндимион Портер; Уилкинсон, ученый и дипломат (посол ЕС в Китае 1994–2001 гг.) Эндимион (2000 г.). История Китая: Учебное пособие . Азиатский центр Гарвардского университета. п. 11. ISBN 978-0-674-00249-4 . {{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка )

[80] Пирс, Гарет (12 марта 2011 г.). «Бирмингемская шестерка: извлекли ли мы уроки из нашего позорного прошлого?» . Хранитель . ISSN 0261-3077 . Проверено 6 августа 2020 г.

[81] Смит, Майкл (31 октября 2011 г.). Шестая: Настоящие Джеймсы Бонды 1909-1939 годов . Издательство Bitback. ISBN 978-1-84954-264-7 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ 44 ]

[ 45 ]

[ 46 ]

[ 47 ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ 52 ]

[ 53 ]

[ 54 ]

[ 55 ]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

[ 68 ]

[ 69 ]

[ 70 ]

[ 71 ]

[ 72 ]

[ 73 ]

[ 74 ]

[ 75 ]

[ 76 ]

[ 77 ]

[ 78 ]

[ 79 ]

[ 80 ]

[ 81 ]