3

← 2 3 4 →
−1 0 1 2 3 4 5 6 7 8 9 → Список чисел ; Целые числа ; ← 0 10 20 30 40 50 60 70 80 90 →
Кардинал	три
Порядок	3 -й ; (третий)
Система цифр	тройной
Факторизация	основной
Основной	2 -й
Делители	1, 3
Греческое число	Γ´
Римская цифра	III, II
Греческий префикс	три-
Латинский префикс	три- / тер-
Бинарный	11 2
Тройной	10 3
Сенарь	3 6
Восьми	3 8
Двенадцатиперстная кишка	3 12
Шестнадцатеричный	3 16
Arabic, Kurdish, Persian, Sindhi, Urdu	٣
Бенгальский , ассамский	৩
китайский	Три, петь, три
Деванагагар	३
Ge'ez	፫
Греческий	C (или c)
иврит	третий
Японский	Три/См
Кхмер	3
Армянский	В
Малаялам	൩
Тамильский	௩
телугу	౩
Каннада	೩
Тайский	๓
N'ko	߃
Туберкулин	3
Грузинец	Ⴂ/ⴂ/g ( Гани )
Вавилонское число	𒐗
Мия цифры	•••
Код Морзе	... _ _

3 ( три ) - это число , цифра и цифра . Это естественное число после 2 и предшествующего 4 , и является наименьшим нечетным числом и единственным прайм, предшествующим квадратному номеру. Это имеет религиозное и культурное значение во многих обществах.

Эволюция арабской цифры

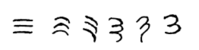
Использование трех строк для обозначения числа 3 произошло во многих системах письма, в том числе некоторые (например, римские и китайские цифры ), которые все еще используются. Это также было первоначальным представлением 3 в брахмской (индийской) численной нотации, его самые ранние формы выровнены вертикально. ^{[ 1 ]} Однако во время империи Гупта знак был изменен путем добавления кривой на каждой линии. Скрипт Нагагара повернул линии по часовой стрелке, поэтому они появились горизонтально и заканчивали каждую линию коротким нисходящим ходом справа. В курсивом сценарии три удара были в конечном итоге подключены, чтобы сформировать глиф, напоминающий ⟨3⟩ с дополнительным ходом внизу: ३ .

Индийские цифры распространились на халифат в 9 веке. Нижний ход был сброшен около 10-го века в западных частях халифата, таких как Магриб и Аль-Андалус , когда развивался отдельный вариант («западный арабский») символов цифр, включая современный западный 3. Напротив, в отличие Восточные арабы сохранили и увеличили этот ход, поворачивая цифру еще раз, чтобы дать современную («восточную») арабскую цифру « ٣ ». ^{[ 2 ]}

В большинстве современных западных шрифтов цифра 3, как и другие десятичные цифры , имеет высоту заглавной буквы и расположена на базовой линии . В шрифтах с текстовыми фигурами , с другой стороны, глиф обычно имеет высоту строчной буквы «x» и потомка : " «В некоторых французских шрифтах текста, однако, он имеет восхождение вместо потомка.

Общий графический вариант цифры трех имеет плоский верх, похожий на букву ʒ (EZH). Эта форма иногда используется для предотвращения фальсификации 3 как 8. Она обнаруживается на штрих-кодах UPC-A и на стандартных 52-картных палубах .

Математика

Согласно Пифагору и Пифагорской школе, число 3, которое они назвали триадой , является единственным числом, которое равняется сумме всех терминов под ним, и единственным числом, сумма которой с теми, которые ниже равны продукту их и себя. ^{[ 3 ]}

Правило разделимости

Естественное число делится сумма на три, если его цифр в основании 10 делится на 3. Из этого обратное любого числа, которое делится на три (или действительно, любая перестановка его цифр) также делится на три. Например, 1368 и его обратный 8631 оба делятся на три (а также 1386, 3168, 3186, 3618 и т. Д.). См. Также Правило разделимости . Это работает в основании 10 и в любой позиционной системе цифр которой , основание разделена на три листа оставшегося от одного (базы 4, 7, 10 и т. Д.).

Свойства числа

3 is the second smallest prime number and the first odd prime number. Это первое уникальное прайм , так что длины периода значение 1 из десятичного расширения его взаимного , 0,333 ..., является уникальным. 3 - двойник с 5 , и двоюродный брат с 7 с 7 , и единственное известное число $n$ так что $n$ ! - 1 и $n$ ! + 1 - главное, а также единственное первое число $p$ так что $p$ - 1 дает еще одно главное число, 2 . Треугольник сторон сделан с . трех , не предпринимающий я, Это самый маленький полигон и единственный многоугольник, который не имеет надлежащей диагонали . При быстрых оценках 3 - грубое приближение $π$ , 3.1415 ... и очень грубое приближение E , 2,71828 ...

3 является первым Mersenne Prime , а также вторым показателем Mersenne Prime и вторым двойным представителем Mersenne Prime , для 7 и 127 соответственно. 3 также является первым из пяти известных простых чисел Fermat , которые включают 5, 17 , 257 и 65537 . Это второй Фибоначчи Прайм (и второй Лукас Прайм ), вторая Софи Жермен Прайм , третье суровое число в базе 10 и второй факторный прайм , так как он равен 2! + 1.

3 is the second and only prime triangular number, and Gauss proved that every integer is the sum of at most 3 triangular numbers.

Три - единственный простой, который на один меньше, чем идеальный квадрат . Любой другой номер, который $n^{2}$ - 1 для некоторого целого числа $n$ не просто, так как это ( $n$ − 1)( $n$ + 1). Это верно и для 3 (с $n$ = 2), но в этом случае меньший фактор составляет 1. Если $n$ больше 2, оба $n$ - 1 и $n$ + 1 больше 1, поэтому их продукт не является ярким.

Связанные свойства

Трисекция угла была одной из трех известных проблем древности.

3 is the number of non-collinear points needed to determine a plane, a circle, and a parabola.

Есть только три различных панмагических квадрата 4 × 4 .

Три из пяти платонических твердых веществ имеют треугольные лица - тетраэдр , октаэдр и икосаэдр . Кроме того, у трех из пяти платонических твердых веществ есть вершины , где встречаются три лица - тетраэдр , гексаэдр ( куб ) и Додекаэдр . Кроме того, только три различных типа многоугольников составляют лица пяти платонических веществ - треугольник , квадрат и Пентагон .

В трех измерениях существует три конечных выпуклых политопных групп , кроме бесконечных семейств призмов и антипризмов : тетраэдрическая группа , октаэдрическая группа и икосаэдрическая группа . В измерениях $n$ ⩾ 5, есть только три обычных политопа: $n$ - Simplexes , $n$ - кубики и $n$ - Ортоплексы . В измерениях $n$ ⩾ 9 , единственные три равномерные семейства политопных, кроме многочисленных бесконечных профизматических семей, являются $\mathrm {A} _{n}$ простое, $\mathrm {B} _{n}$ кубический, и $\mathrm {D} _{n}$ Демигиперкубические семьи. Для паракопактных гиперболических сотовых компаний есть три группы в размерах 6 и 9 или эквивалентно ранга 7 и 10, без других форм в более высоких измерениях. Из последних трех групп самая большая и наиболее важная - это ${\bar {T}}_{9}$ , это связано с важной алгеброй Kac -Moody Lie $\mathrm {E} _{10}$ . ^{[ 4 ]}

Системы цифр

Есть некоторые доказательства того, что ранний человек, возможно, использовал системы подсчета, которые состояли из «одного, двух, трех» и после этого «многих» для описания пределов подсчета. У ранних народов было слово, чтобы описать количества одного, двух и трех, но любое количество за ее пределами было просто обозначено как «много». Скорее всего, это основано на распространенности этого явления среди людей в таких разрозненных регионах, как глубокие джунгли Amazon и Borneo, где исследователи западной цивилизации имеют исторические записи о своих первых встречах с этими коренными народами. ^{[ 5 ]}

Список основных расчетов

Умножение	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	50	100	1000	10000
3 × x	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60	63	66	69	72	75	150	300	3000	30000

Разделение	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15	16	17	18	19	20
3 ÷ x	3	1.5	1	0.75	0.6	0.5	0. 428571	0.375	0. 3	0.3		0. 27	0.25	0. 230769	0.2 142857	0.2	0.1875	0.1 7647058823529411	0.1 6	0.1 57894736842105263	0.15
x ÷ 3	0. 3	0. 6	1	1. 3	1. 6	2	2. 3	2. 6	3	3. 3		3. 6	4	4. 3	4. 6	5	5. 3	5. 6	6	6. 3	6. 6

Экспонент	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15	16	17	18	19	20
3 ^х	3	9	27	81	243	729	2187	6561	19683	59049		177147	531441	1594323	4782969	14348907	43046721	129140163	387420489	1162261467	3486784401
х ³	1	8	27	64	125	216	343	512	729	1000		1331	1728	2197	2744	3375	4096	4913	5832	6859	8000

Наука

Три - количество лития атомное .
Три - это количество измерений , которые люди могут воспринимать. Люди воспринимают вселенную иметь три пространственных измерения , но некоторые теории, такие как теория струн , предполагают больше. ^{[ 6 ]}
Три - количество элементарных поколений фермиона в соответствии со стандартной моделью физики частиц. ^{[ 7 ]}
В физике частиц каждый протон или нейтрон состоит из трех четвертей . ^{[ 8 ]}
Есть три основных цвета в аддитивных и субтрактивных моделях.
Способность человеческого глаза различать цвета основана на различной чувствительности различных клеток в сетчатке к свету разных длин волн . Люди трихроматические , сетчатка содержит три типа цветовых рецепторных клеток или конусов . ^{[ 9 ]}
В физике проблемы с тремя телами не имеют общего решения с закрытой формой , в отличие от проблем с двумя телами . ^{[ 10 ]}

Инженерный

Треугольник многоугольник , , является с тремя краями и тремя вершинами наиболее стабильной физической формой. По этой причине он широко используется в строительстве, технике и дизайне. ^{[ 11 ]}

Протологика

В европейской алхимии тремя простыми числами ( латынь : триа Прима ) были солью ( ), сера ( ) и ртуть ( 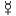). ^{[ 12 ]}^{[ 13 ]}
Три доша (слабости) и их антидоты являются основой аюрведической медицины в Индии. ^{[ 14 ]}

Псевдонаука

Три - символическое представление для MU , Августа Ле Плонгеона и Джеймса Черчворда . потерянного континента ^{[ 15 ]}

Философия

Philosophers such as Aquinas, Kant, Hegel, C. S. Peirce, and Karl Popper have made threefold divisions, or trichotomies, which have been important in their work.^{[ Цитация необходима ]}
Гегеля Диалектика = синтез создает три- из тезиса + антитеза двух. ^{[ Цитация необходима ]}
В интервью 1931 года Никола Тесла якобы сказала: «Если бы вы знали только великолепие 3, 6 и 9, то у вас будет ключ во вселенную». ^{[ Цитация необходима ]}

Религия

концепции Троицы, в тримурти и тридеви , триглав ( горит Многие том индуистские числе или религии содержат . мировые тройные божества Христианская . Троица и Богиня Викки Святая Тройная

Щит Троицы - это диаграмма христианской доктрины Троицы.

христианство

Трехедневная должность Христа - это христианская доктрина , в которой говорится, что Христос выполняет функции Пророка , священника и Царя .
Во время агонии в саду Христос три раза просил от него чашку.
Иисус поднялся из мертвых на третий день после его смерти.
Дьявол искушал Иисуса . трижды
Святой Петр Трис отрицал Иисуса , и Трис подтвердил свою веру в Иисуса .
Волшебные люди , которые были астрономами/астрологами из Персии ^{[ 16 ]} - дал Иисусу три дара. ^{[ 17 ]}^{[ 18 ]}
Есть три синоптических Евангелия и три послания Иоанна .
Павел Апостол ослепил в течение трех дней после его обращения в христианство .

Иудаизм

У Ноя было три сына: Хэм , Шем и Джафет
Три патриарха : Авраам , Исаак и Иаков
Пророк Балаам победил своего осла три раза.
Пророк Иона провел три дня и ночи в животе большой рыбы
Три подразделения письменной Торы : Тора (пять книг Моисея), Неви'им (Пророки), Кетувим (Писания) ^{[ 19 ]}
Три дивизии еврейского народа: Коэн , Левит , Исраэль
Три ежедневных молитвы : Шахахарит , Минча , Маарив
Три Шаббата блюда
Шаббат заканчивается, когда три звезды видны в ночном небе ^{[ 20 ]}
Три фестиваля паломничества : Пасха , Шавуот , Суккот
Три маца на седина пасхальном столе ^{[ 21 ]}
Три недели , период траура, соединяющего быстрые дни семнадцатого от Таммуза и Тиша Б'Ав
Три кардинальных греха, за которые еврей должен умереть, а не нарушать: идолопоклонство , убийство , сексуальная безнравственность ^{[ 22 ]}
Апшерин , первая стрижка еврейского мальчика в 3 года ^{[ 23 ]}
Бет Дин состоит из трех членов
Potential converts are traditionally turned away three times to test their sincerity^{[ 24 ]}
В еврейской мистической традиции Каббалы считается , что душа состоит из трех частей, причем наиболее высокая из которых из - нешама («дыхание»), среднее из которых - руах («ветер» или «дух») и самым низким существом («дыхание» (среднее из существования («ветер» или «дух») и самое низкое из которых - Нейфеш ( «Покой»). ^{[ 25 ]} два элемента чая («жизнь» или «животного») и йахиды («единица»). Иногда упоминаются
провинции Чаима последнему дерево относится к В

ислам

Три основных принципа традиции шиитов: Таухид (единство Бога), Набувва (концепция пророчества), Имама (концепция имама)

буддизм

Тройной Бодхи (способы понять конец рождения) являются Будху, Пасебудху и Махарахат.
Три драгоценности , три вещи, в которых укрываются буддисты.

Синто

Имперские регалии Японии меча, зеркала и драгоценного камня.

Даосизм

Три сокровища ( китайцы : 三三寶 ; пинин : санбǎо ; Уэйд-Гилс : Сан-Пао ), основные достоинства в даосизме .
Три дантиане
Три строки триграммы
Три суверена : Небеса Фу Си (Рука - Голова - 3º Глаз), Человечество Шен Нонг ( Блок 69 ), Ад Нюва (Фут - живот - Umbiculus).

индуизм

Тримюрти хранитель : Брахма Создатель, Вишну, , и Шива - эсминец.
Три гунаса ( Тригуна ), найденные в Самкхья . Школе индуистской философии ^{[ 26 ]}
The three paths to salvation in the Bhagavad Gita named Karma Yoga, Bhakti Yoga and Jnana Yoga.

Зороастризм

Три достоинства Humata , Hukhta и Huvarshta (хорошие мысли, хорошие слова и добрые дела) являются основным принципом в зороастризме .

Скандинавская мифология

Три - очень значительное число в скандинавской мифологии , а также ее способности 9 и 27.

До Рагнарёка будет три жестких зимы без промежуточного лета, Fimbulwinter .
Один пережил три трудности на мировом дереве в своем стремлении к рунам : он повесился, ранил себя копьем и страдал от голода и жажды.
Бора было три сына, Один , Вили и В. У

Другие религии

Правило Виккана трех из .
Тройная богиня : Дева, мать, Крона; Три судьбы.
Сыновья Кронуса : Зевс , Посейдон и Аид .
Славянский Бог Триглав имеет три головы.

Эзотерическая традиция

Теософское общество имеет три условия членства .
и Гурджиефа Три центра закон трех .
Liber Al Vel Legis , Центральное Писание религии Телемы , состоит из трех глав, соответствующих трем божественным рассказчикам соответственно: Nuit , Hadit и Ra-Hoor-Khuit .
Тройное величие Hermes Trismegistus является важной темой герметизма .

Как счастливчик или неудачный номер

Три ( три , формальное письмо: три , пийнин Сан , Кантонский : Саам ¹) считается хорошим числом в китайской культуре, потому что это звучит как слово «живое» ( 生 пининьин Шанг , Кантонский: Саанг ¹), появилось до 四四 четырех 四 ( 四四四四四四四四四四四四四四四四四四四四四四四四四四四 ¹), которое звучит как слово «Смерть» ( 死 Pinyin Sǐ , Кантонский: SEI ²).

Подсчет трех - это обычное дело в ситуациях, когда группа людей хочет выполнить действие в синхронности : теперь, по графу из трех, все тянут! Предполагая, что счетчик работает по однородной ставке, первые два пункта необходимы для установления скорости, а количество «трех» прогнозируется на основе времени «одного» и «двух» до него. Три, вероятно, используются вместо какого -то другого числа, потому что это требует минимального количества количества при установлении ставки.

Существует еще одно суеверие, что не повезло взять третий свет , то есть быть третьим человеком, зажигающим сигарету от того же матча или легкого. Это суеверие иногда утверждается, что возникало среди солдат в окопах Первой мировой войны, когда снайпер может увидеть первый свет, примите цель на второй и стреляйте на третьем. ^{[ Цитация необходима ]}

Фраза « Третий раз » относится к суевериям, что после двух неудач в любом усилиях третья попытка с большей вероятностью достигнет успеха. Это также иногда можно увидеть в обратном направлении, как в «Третий человеке [сделать что -то, предположительно запрещенное] поймается». ^{[ Цитация необходима ]}

Удача , особенно неудача, часто говорят, что «приходит в тройку». ^{[ 27 ]}

Смотрите также

Куб (алгебра) - (3 суперпидки )
Трижды
Третий
Триада
Трио
Правило трех
ɜ , U+025C ɜ Латинская маленькая буква перевернута, открывая E, также известная как обратный Epsilon
Список шоссе пронумеровано 3

Ссылки

^ Смит, Дэвид Юджин ; Карпински, Луи Чарльз (1911). Индуистские цифры . Бостон; Лондон: Джинн и Компания. С. 27–29, 40–41.
^ Жорж Ифра, Универсальная история чисел: от предыстории до изобретения компьютера перевод. Дэвид Беллос и соавт. Лондон: Harvill Press (1998): 393, рис. 24.63
^ Прия Хеменвэй (2005), Божественная пропорция: PHI в искусстве, природе и науке , Sterling Publishing Company Inc., с. 53–54, ISBN 1-4027-3522-7
^ Allcock, Daniel (май 2018). «Пенилопотентные пары в решетке корня E10» (PDF) . Математические разбирательства Кембриджского философского общества . 164 (3): 473–483. Bibcode : 2018mpcps.164..473a . doi : 10.1017/s0305004117000287 . S2CID 8547735 . Архивировано (PDF) из оригинала на 2022-11-03 . Получено 2022-11-03 .
«Детали предыдущего раздела были специфичными для E10, но такая же философия, вероятно, будет применить к другим симметризируемым гиперболическим корневым системам ... кажется ценным дать обзор того, как будут проходить расчеты», относительно E10 как модели Пример симметризируемости других корневых гиперболических E _N Systems.
^ Гриббин, Мэри; Гриббин, Джон Р.; Эдни, Ральф; Хэллидей, Николас (2003). Большие числа . Кембридж: Волшебник. ISBN 1840464313 .
^ Цвибах, Бартон (2009). Первый курс по теории строк (2 -е изд.). Кембридж; Нью -Йорк: издательство Кембриджского университета. ISBN 978-0-521-88032-9 .
^ Harari, H. (1977). «Три поколения кварков и лептонов» (PDF) . В Ван Гоелере, E.; Вайнштейн, Р. (ред.). Материалы XII Rencontre de Moriond . п. 170. SLAC-PUB-1974.
^ Adair, RK (1989). Великий дизайн: частицы, поля и творение . Издательство Оксфордского университета . п. 214. Bibcode : 1988gdpf.book ..... a .
^ «Стержни и конусы человеческого глаза» . Hyperphysics.phy-astr.gsu.edu . Получено 2024-06-04 .
^ Барроу-Грин, июнь (2008). «Проблема с тремя телами». В гоусерах Тимоти; Барроу-зеленый, июнь; Лидер, Имре (ред.). Принстонский компаньон по математике . ПРИЗНАЯ УНИВЕРСИТЕТА ПРИСЕТА. С. 726–728.
^ " Самый стабильный форм-треугольник ". Математика в городе . Получено 23 февраля 2015 года.
^ Эрик Джон Холмард. Алхимия. 1995. С. 153
^ Walter J. Friedlander. Золотая палочка медицины: история символа Caduceus в медицине. 1992. С.76-77
^ Крейдлер, Марк (2017-12-14). «Аюрведа: древнее суеверие, а не древняя мудрость» . Скептически скептический запросчик . Получено 2024-06-04 .
^ Церковь, Джеймс (1931). «Потерянный континент MU - символы, виньетки, таблицы и диаграммы» . Biblioteca Pleyades . Архивировано с оригинала 2015-07-18 . Получено 2016-03-15 .
^ Виндл, Брайан (2022-12-22). "Кто были волминиями?" Полем Библейский археологический отчет . Получено 2024-07-05 .
^ «Энциклопедия Британская». Лексикон всей книжной системы онлайн (на немецком языке). Doi : 10.1163/978900437862_lgbo_com_050367 .
^ «Энциклопедия Британская» . Природа . XV (378): 269–271. 25 января 1877 года. Архивировано с оригинала 24 июля 2020 года . Получено 12 июля 2019 года .
^ Маркус, раввин Йосси (2015). "Почему в иудаизме делается много вещей три раза?" Полем Спросите Моисея . Архивировано с оригинала 2 апреля 2015 года . Получено 16 марта 2015 года .
^ "Шаббат" . Иудаизм 101 . 2011. Архивировано из оригинала 29 июня 2009 года . Получено 16 марта 2015 года .
^ Китов, Элияху (2015). «Три мацца» . Chabad.org . Архивировано с оригинала 24 марта 2015 года . Получено 16 марта 2015 года .
^ Каплан, раввин Арие (28 августа 2004 г.). «Иудаизм и мученичество» . Aish.com. Архивировано с оригинала 20 марта 2015 года . Получено 16 марта 2015 года .
^ «Основы Апшерина: первая стрижка мальчика» . Chabad.org . 2015. Архивировано с оригинала 22 марта 2015 года . Получено 16 марта 2015 года .
^ "The Conversion Process" . Центр обращения в иудаизм. Архивировано из оригинала 23 февраля 2021 года . Получено 16 марта 2015 года .
^ Kaplan, Aryeh. « Душа архивировала 2015-02-24 на машине Wayback ». Айш . Из «Справочника еврейской мысли» (том 2, Maznaim Publishing . Перепечатано с разрешения.) 4 сентября 2004 г. Получено 24 февраля 2015 года.
^ Джеймс Г. Лохтефельд, Гуна, в иллюстрированной энциклопедии индуизма: Am, Vol. 1, Rosen Publishing, ISBN 978-0-8239-3179-8 , стр. 265
^ См. « Плохое архив 2009-03-02 в The Wayback Machine » в Оксфордском словаре фразы и басни , 2006, через encyclopedia.com.

Уэллс, Д. Словарь пингвинов любопытных и интересных чисел Лондон: Пингвин Группа. (1987): 46–48

Внешние ссылки

Трициклопедическая книга тройков Майкла Эка
Тройки в анатомии человека Джона А. Макналти
Грама, Джеймс. «3 везде» . Numberphile . Брэди Харан . Архивировано из оригинала 2013-05-14 . Получено 2013-04-13 .
Номер 3
Положительное целое число 3
Основные курьезы: 3

[Smith_Karpinski_1911-1] Смит, Дэвид Юджин ; Карпински, Луи Чарльз (1911). Индуистские цифры . Бостон; Лондон: Джинн и Компания. С. 27–29, 40–41.

[2] Жорж Ифра, Универсальная история чисел: от предыстории до изобретения компьютера перевод. Дэвид Беллос и соавт. Лондон: Harvill Press (1998): 393, рис. 24.63

[3] Прия Хеменвэй (2005), Божественная пропорция: PHI в искусстве, природе и науке , Sterling Publishing Company Inc., с. 53–54, ISBN 1-4027-3522-7

[4] Allcock, Daniel (май 2018). «Пенилопотентные пары в решетке корня E10» (PDF) . Математические разбирательства Кембриджского философского общества . 164 (3): 473–483. Bibcode : 2018mpcps.164..473a . doi : 10.1017/s0305004117000287 . S2CID 8547735 . Архивировано (PDF) из оригинала на 2022-11-03 . Получено 2022-11-03 .
«Детали предыдущего раздела были специфичными для E10, но такая же философия, вероятно, будет применить к другим симметризируемым гиперболическим корневым системам ... кажется ценным дать обзор того, как будут проходить расчеты», относительно E10 как модели Пример симметризируемости других корневых гиперболических E _N Systems.

[5] Гриббин, Мэри; Гриббин, Джон Р.; Эдни, Ральф; Хэллидей, Николас (2003). Большие числа . Кембридж: Волшебник. ISBN 1840464313 .

[6] Цвибах, Бартон (2009). Первый курс по теории строк (2 -е изд.). Кембридж; Нью -Йорк: издательство Кембриджского университета. ISBN 978-0-521-88032-9 .

[7] Harari, H. (1977). «Три поколения кварков и лептонов» (PDF) . В Ван Гоелере, E.; Вайнштейн, Р. (ред.). Материалы XII Rencontre de Moriond . п. 170. SLAC-PUB-1974.

[8] Adair, RK (1989). Великий дизайн: частицы, поля и творение . Издательство Оксфордского университета . п. 214. Bibcode : 1988gdpf.book ..... a .

[9] «Стержни и конусы человеческого глаза» . Hyperphysics.phy-astr.gsu.edu . Получено 2024-06-04 .

[10] Барроу-Грин, июнь (2008). «Проблема с тремя телами». В гоусерах Тимоти; Барроу-зеленый, июнь; Лидер, Имре (ред.). Принстонский компаньон по математике . ПРИЗНАЯ УНИВЕРСИТЕТА ПРИСЕТА. С. 726–728.

[11] " Самый стабильный форм-треугольник ". Математика в городе . Получено 23 февраля 2015 года.

[Eric_John_Holmyard_1990._p.153-12] Эрик Джон Холмард. Алхимия. 1995. С. 153

[13] Walter J. Friedlander. Золотая палочка медицины: история символа Caduceus в медицине. 1992. С.76-77

[14] Крейдлер, Марк (2017-12-14). «Аюрведа: древнее суеверие, а не древняя мудрость» . Скептически скептический запросчик . Получено 2024-06-04 .

[Three_is_for_the_Lost_Continent_of_Mu-15] Церковь, Джеймс (1931). «Потерянный континент MU - символы, виньетки, таблицы и диаграммы» . Biblioteca Pleyades . Архивировано с оригинала 2015-07-18 . Получено 2016-03-15 .

[16] Виндл, Брайан (2022-12-22). "Кто были волминиями?" Полем Библейский археологический отчет . Получено 2024-07-05 .

[17] «Энциклопедия Британская». Лексикон всей книжной системы онлайн (на немецком языке). Doi : 10.1163/978900437862_lgbo_com_050367 .

[18] «Энциклопедия Британская» . Природа . XV (378): 269–271. 25 января 1877 года. Архивировано с оригинала 24 июля 2020 года . Получено 12 июля 2019 года .

[why-19] Маркус, раввин Йосси (2015). "Почему в иудаизме делается много вещей три раза?" Полем Спросите Моисея . Архивировано с оригинала 2 апреля 2015 года . Получено 16 марта 2015 года .

[20] "Шаббат" . Иудаизм 101 . 2011. Архивировано из оригинала 29 июня 2009 года . Получено 16 марта 2015 года .

[21] Китов, Элияху (2015). «Три мацца» . Chabad.org . Архивировано с оригинала 24 марта 2015 года . Получено 16 марта 2015 года .

[22] Каплан, раввин Арие (28 августа 2004 г.). «Иудаизм и мученичество» . Aish.com. Архивировано с оригинала 20 марта 2015 года . Получено 16 марта 2015 года .

[23] «Основы Апшерина: первая стрижка мальчика» . Chabad.org . 2015. Архивировано с оригинала 22 марта 2015 года . Получено 16 марта 2015 года .

[24] "The Conversion Process" . Центр обращения в иудаизм. Архивировано из оригинала 23 февраля 2021 года . Получено 16 марта 2015 года .

[25] Kaplan, Aryeh. « Душа архивировала 2015-02-24 на машине Wayback ». Айш . Из «Справочника еврейской мысли» (том 2, Maznaim Publishing . Перепечатано с разрешения.) 4 сентября 2004 г. Получено 24 февраля 2015 года.

[26] Джеймс Г. Лохтефельд, Гуна, в иллюстрированной энциклопедии индуизма: Am, Vol. 1, Rosen Publishing, ISBN 978-0-8239-3179-8 , стр. 265

[27] См. « Плохое архив 2009-03-02 в The Wayback Machine » в Оксфордском словаре фразы и басни , 2006, через encyclopedia.com.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]